Еще больше физических формул и свойств — Физика — Теория, тесты, формулы и задачи
На этой странице представлен исчерпывающий список формул по физике и важнейших физических свойств для успешной подготовки к ЦТ или ЕГЭ. Список составлен в формате «вопрос-ответ» на основе многолетнего опыта, и является самым полным на этом сайте. Успешное изучение всех формул по физике и физических свойств из этого файла позволит абитуриентам, не просто очень уверенно чувствовать себя на ЦТ или ЕГЭ, но и с легкостью, чуть ли не автоматически, решить большую часть экзаменационных заданий. Знание всех этих формул позволит Вам набрать очень солидный балл на экзамене, даже если у Вас нет феноменальных способностей в физике. А если Вы хотите набрать максимальный балл на ЦТ или ЕГЭ, то выучив эти формулы, Вы с легкостью и очень быстро прорешаете основную часть теста, и у Вас останется много времени на решение самых сложных задач теста, в которых Вам, к слову, также понадобится знание этих формул.
Изучать еще больше формул по физике и физических свойств онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
educon.by
| № п/п | Наименование параметра | Формула | Обозначения |
|---|---|---|---|
| 3.1 | Закон Кулона | Q1 и Q2 ― точечные заряды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, ε ― диэлектрическая проницаемость среды, r ― расстояние между зарядами | |
| 3.2 | Емкость плоского конденсатора | ε ― диэлектрическая проницаемость среды между пластинами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, S ― площадь пластины, d ― расстояние между пластинами | |
| 3.3 | Емкость сферического конденсатора | ε ― диэлектрическая проницаемость среды между сферами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, R1 и R2 ― радиусы внутренней и внешней сфер соответственно | |
| 3.4 | Потенциал электрического поля, созданного точечным зарядом | Q ― точечный заряд, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от точечного заряда | |
| 3.5 | Потенциал электрического поля, созданного металлической сферой на расстоянии r от центра сферы: внутри сферы и на поверхности (r ≤ R) вне сферы (r > R) | q ― заряд сферы, R ― радиус сферы, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от центра сферы | |
| 3.6 | Теорема Гаусса-Остроградского | S ― площадь гауссовой поверхности, Еn ― нормальная к поверхности составляющая вектора напряженности электростатического поля, Q ― заряд, охваченный поверхностью интегрирования, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная | |
| 3.7 | Напряженность поля, создаваемого зарядом бесконечной пластины | вывод формулы | σ ― поверхностная плотность заряда, ε ― диэлектрическая проницаемость среды, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от пластины |
| 3.8 | Напряженность электрического поля, создаваемого металлической заряженной сферой: внутри сферы (r на поверхности сферы (r = R) вне сферы (r > R) | Q ― заряд сферы; ε ― диэлектрическая проницаемость среды; ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная; R ― радиус сферы; r ― расстояние от центра сферы | |
| 3.9 | Напряженность электрического поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) | вывод формулы | τ ― линейная плотность заряда; ε ― диэлектрическая проницаемость среды между пластинами, ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, r ― расстояние от оси нити |
| 3.10 | Энергия конденсатора | С ― емкость конденсатора; U ― напряжение на пластинах | |
| 3.11 | Сопротивление провода | ρ0 ― удельное сопротивление материала провода, S ― площадь сечения провода; для меди ρ0 = 0,0175∙10−6 Ом∙м; для алюминия ρ0 = 0,028∙10−6 Ом∙м; для вольфрама ρ0 = 0,055∙10−6 Ом∙м; для железа ρ0 = 0,1∙10−6 Ом∙м | |
| 3.12 | Работа, совершаемая электрическим полем при перемещении точечного заряда q из точки 1 поля в точку 2 | φ1 и φ2 ― потенциалы точек 1 и 2 соответственно | |
| 3.13 | Электрический момент диполя | ||
| 3.14 | Напряженность поля точечного диполя | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α ― угол между радиус-вектором и плечом диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная | |
| 3.15 | Напряженность поля точечного диполя в точке, лежащей на оси диполя (α = 0) | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная | |
| 3.16 | Напряженность поля точечного диполя в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины (α = π/2) | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная | |
| 3.17 | Потенциал поля точечного диполя | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α ― угол между радиус-вектором и плечом диполя; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная | |
| 3.18 | Потенциал поля точечного диполя в точке A, лежащей на оси диполя | р ― электрический момент диполя; r ― абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; ε ― диэлектрическая проницаемость; ε0 ― электрическая постоянная | |
| 3.19 | Механический момент, действующий на диполь | ― электрический момент диполя, ― напряженность однородного электрического поля, α ― угол между направлениями векторов и | |
| 3.20 | Период колебаний колебательного контура | L ― индуктивность катушки, C ― емкость конденсатора |
reshenie-zadach.com.ua
| Cвязь индукции и напряженности магнитного поля В=?0?Н Индукция магнитного поля а) бесконечно длинного проводника в) внутри бесконечно длинного соленоида на его оси. B=?0?nI Принцип суперпозиции Закон Ампера Сила взаимодействия двух параллельных проводников Сила Лоренца Магнитный момент контура с током рm=IS Механический момент, действующий на контур с током в магнитном поле M=BISsin?=Bpmsin? Магнитный поток Ф=BSּcos? Работа магнитного поля по перемещению проводника А=I?Ф Закон Фарадея ; Разность потенциалов, индуцируемая в движущемся проводнике Индуктивность контура Закон Фарадея для самоиндукции Индуктивность длинного соленоида Энергия магнитного поля: а) проводника с током
в) объемная плотность энергии магнитного поля ; | В – индукция магнитного поля Н – напряженность магнитного поля ?0 – магнитная постоянная ? – относительная магнитная проницаемость среды r – расстояние от проводника R – радиус кругового витка n – число витков на единицу длины — длина проводника sin? – sin угла между током и магнитной индукцией d – расстояние между проводниками рm – магнитный момент S – площадь, охватываемая контуром Ф – магнитный поток cos? – cos угла между нормалью к поверхности и индукцией ?i – ЭДС индукции L – индуктивность N – число витков в соленоиде S – площадь поперечного сечения соленоида — длина соленоида W – энергия магнитного поля n – число витков на единицу длины соленоида V – объем соленоида ? – объемная плотность энергии | 1Тл 1А/м 4?ּ10-7Гн/м 1м 1м 1м 1м2 1В 1Гн 1Дж 1м-1 1Дж/м3 |
nashaucheba.ru
формулы « Учи физику!
Второе уравнение Максвелла выражает закон электромагнитной индукции Фарадея: ЭДС в любом замкнутом контуре равна скорости изменения (т. е. производной по времени) магнитного потока. Но ЭДС равна касательной составляющей вектора напряженности электрического поля Е, помноженной на длину контура. Чтобы перейти к ротору, как и в первом уравнении Максвелла, достаточно разделить ЭДС на площадь контура, а последнюю устремить к нулю, т. е. взять маленький контур, охватывающий рассматриваемую точку пространства (рис. 9,в). Тогда в правой части уравнения будет уже не поток, а магнитная индукция, поскольку поток равен индукции, помноженной на площадь контура.
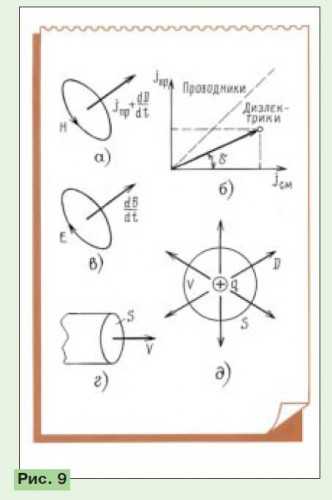
Итак, получаем: rotE=-dB/dt
Таким образом, вихревое электрическое поле порождается изменениями магнитного, что и подано на рис. 9,в и представлено только что приведенной формулой.
Третье и четвертое уравнения Максвелла имеют дело с зарядами и порождаемыми ими полями. Они основаны на теореме Гаусса, утверждающей, что поток вектора электрической индукции через любую замкнутую поверхность равен заряду внутри этой поверхности.
Подробнее…
Ещё ни кто не комментировалФормулы по физике за курс средней школы

Подробнее…
В данной шпаргалке есть все основные формулы за курс средней школы.
На рисунке показана уменьшенная копия этой шпаргалки
Подробнее…
Для многих учеников при изучении физики большой проблемой является запоминание формул. Часто спрашивают как их можно быстро запомнить.
Главный совет – это постараться понять смысл формулы. Понимать, что означает каждая буква, в чем измеряется. Помнить, что единицы измерения слева, должно совпадать с единицами измерения справа.
Подробнее…
Скачать шпаргалку с формулами по физике
Ещё ни кто не комментировалШпаргалки по физике. Приведены основные формулы по всем разделам физики.
Шпоры выполнены в виде трех колонок. Необходимо их разрезать и склеить в единую узкую ленту.
Данные шпоры будут полезны и при повторении пройденного материала и изучении формул.
Настоятельно рекомендуем пользоваться данный материал исключительно в подготовительных целях.
Не ищите дополнительных приключений на свою молодую и красивую голову.

Шпаргалки по физике
Другие задачи
Другие опыты и эксперименты
На главную
Ещё ни кто не комментировалuchifiziku.ru
