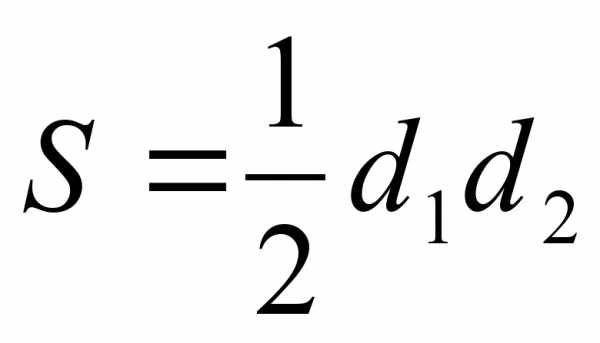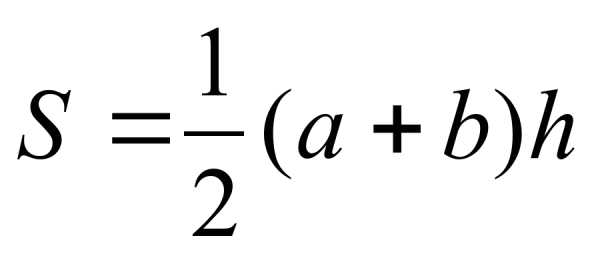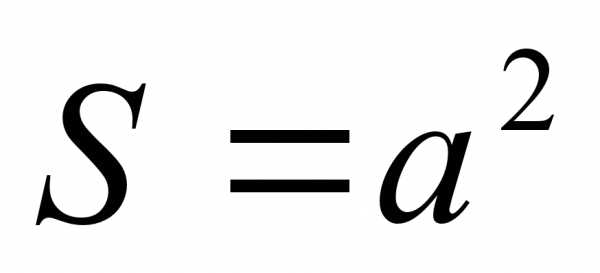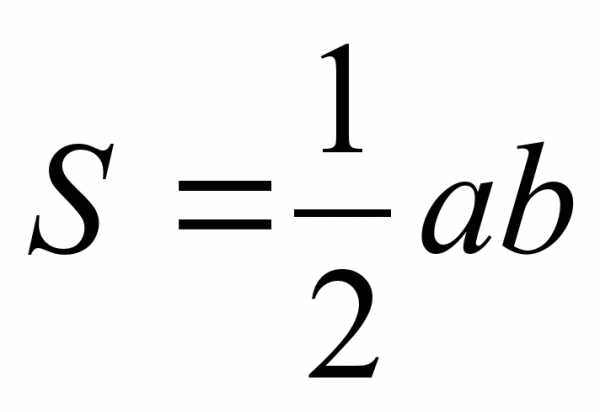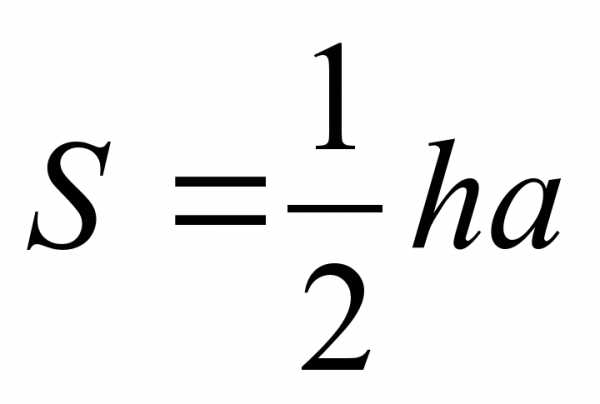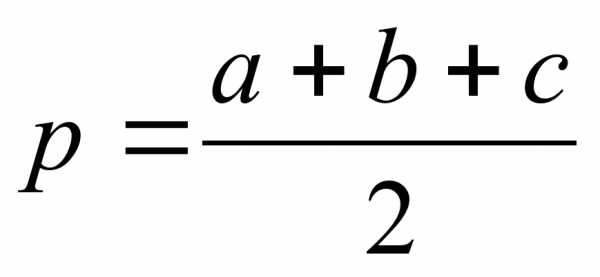11 класс подготовка к егэ математика – ЛЕГКО | Образовательный проект: ЕГЭ по математике 2015, подготовка к егэ по математике с нуля 2015 онлайн, решение задач профильного уровня, тесты математика подготовка к егэ, математика 11 класс егэ подготовка, математика подготовка к егэ решебник

Демонстрационные варианты ЕГЭ по математике (11 класс)

      Начиная с 2015 года, ЕГЭ по математике проводится в виде двух отдельных экзаменов – базового уровня и профильного уровня.

      Базовый ЕГЭ организуется для выпускников, изучающих математику для общего развития и успешной жизни в обществе, а также абитуриентов вузов, в которых не требуется высокий уровень владения математикой. Баллы, полученные на базовом ЕГЭ по математике, не переводятся в стобалльную шкалу и не дают возможности участия в конкурсе на поступление в вузы.

      Профильный ЕГЭ проводится для выпускников и абитуриентов, планирующих использовать математику и смежные дисциплины в будущей профессиональной деятельности. Результаты профильного ЕГЭ по математике переводятся в стобалльную шкалу и могут быть представлены абитуриентом на конкурс для поступления в вуз.

      Демонстрационный вариант для ЕГЭ базового уровня содержит только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы базового уровня на каждую позицию предлагается только одно задание.

      При выполнении заданий экзаменационной работы ЕГЭ по математике базового уровня разрешено использовать справочные материалы, которые выдаются учащемуся вместе с вариантом ЕГЭ.

      Демонстрационный вариант профильного экзамена ЕГЭ состоит из двух частей: часть 1 содержит задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом.

      Все демонстрационные варианты ЕГЭ по математике содержат ответы ко всем заданиям,а также критерии оценивания для заданий с развернутым ответом.

      В демонстрационных вариантах ЕГЭ по математике 2019 года как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2018 года изменений не было.

      Приведенные материалы опубликованы на официальном информационном портале Единого Государственного Экзамена.

Демонстрационные варианты ЕГЭ по математике

      Отметим, что демонстрационные варианты за 2008 — 2019 годы представлены в формате pdf, и для их просмотра необходимо, чтобы на Вашем компьютере был установлен, например, свободно распространяемый программный пакет Adobe Reader.

Изменения в демонстрационных вариантах ЕГЭ по математике

      Демонстрационные варианты ЕГЭ по математике для 11 класса за 2002-2009 годы включали в себя три раздела: А (задачи с выбором ответа из нескольких предложенных), В (задачи с кратким ответом) и С (задания, для выполнения которых требовалось привести полное решение задачи).

      В 2010 году из демонстрационного варианта ЕГЭ по математике были исключены задачи с выбором ответа, ранее составлявшие раздел А. Таким образом, демонстрационный вариант ЕГЭ стал состоять уже только из двух разделов В и С.

      Демонстрационный вариант ЕГЭ 2011 года почти полностью совпадал с демонстрационным вариантом ЕГЭ 2010 года: были изменены лишь задания C1 и C5.

      В 2014 году в демонстрационном варианте ЕГЭ по математике тематических изменений по сравнению с предыдущим годом не было: задачи В3, В9, В14, С2 и С4 были заменены на другие задачи той же тематики. Кроме того, было добавлено задание базового уровня сложности с кратким ответом, проверяющее практические навыки применения математики в повседневной жизни и изменен порядок заданий.

      В 2015 году в порядке проведения ЕГЭ по математике произошли серьезные изменения: было решено проводить два отдельных экзамена – базового уровня и профильного уровня.

    В связи с этим в 2015 году было представлено 2 демонстрационных варианта: новая модель демонстрационного варианта для ЕГЭ базового уровня и модернизированная модель демонстрационного варианта 2014 года для проведения ЕГЭ профильного уровня.

      Демонстрационный вариант для ЕГЭ базового уровня содержал только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте было представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию было предложено только одно задание.

      Демонстрационный вариант профильного экзамена 2015 года разработан на основе демонстрационного варианта ЕГЭ по математике 2014 года со следующими изменениями:

• Вариант стал состоять из двух частей (часть 1 — задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом).
• Нумерация заданий стала сквозной по всему варианту без буквенных обозначений В, С.
• Во второй части добавлено 1 задание высокого уровня сложности с развёрнутым ответом, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
• Из первой части исключено 1 задание базового уровня сложности.
• Произведены несущественные изменения формы и тематики заданий 16 и 17

      В демонстрационном варианте ЕГЭ по математике базового уровня 2016 года изменений не было .

      В демонстрационном варианте ЕГЭ по математике профильного уровня 2016 года произошли следующие изменения:

• Из первой части варианта были исключены два задания: задание практического содержания базового уровня сложности и задание по стереометрии повышенного уровня сложности.
• Максимальный первичный балл за выполнение всей работы был уменьшен с 34 до 32 баллов.

      В демонстрационных вариантах ЕГЭ по математике 2017 — 2019 годов как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2016 года изменений не было.

      На нашем сайте можно также ознакомиться с подготовленными преподавателями нашего учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Рабочая программа «Подготовка к ЕГЭ по математике» (11 класс)

РАБОЧАЯ ПРОГРАММА

Подготовка к ЕГЭ

по математике

Автор: Панфилова Надежда Ивановна

2014 г.

Пояснительная записка

Программа курса Математика «Подготовка к ЕГЭ по математике» составлена на основе федерального компонента государственного образовательного стандарта среднего (полного) общего образования, требований к уровню подготовки выпускников основной школы, примерных программ среднего (полного) общего образования по математике, контрольно-измерительных материалов для подготовки к ЕГЭ.
Программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам предметного курса.

Курс позволит школьникам систематизировать, расширить и укрепить знания, подготовиться для дальнейшего изучения тем, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере. Преподавание курса строится как повторение, предусмотренное программой основного общего образования. Повторение реализуется в виде обзора теоретических вопросов по теме и решение задач в виде тестов с выбором ответа. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих применения логической и операционной культуры, развивающих научно-теоретическое и алгоритмическое мышление учащихся.

Цели курса: обобщение и систематизация, расширение и углубление знаний по изучаемым темам; приобретение практических навыков выполнения заданий, повышение математической подготовки школьников.

Задачи курса:

• вооружить учащихся системой знаний по решению уравнений;

• сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

• подготовить учащихся к итоговой аттестации;

• формировать навыки самостоятельной работы;

• формировать навыки работы со справочной литературой;

• формировать умения и навыки исследовательской деятельности;

• способствовать развитию алгоритмического мышления учащихся.

Программа курса предполагает знакомство с теорией и практикой рассматриваемых вопросов и рассчитана на 34 часа занятий — 1 час в неделю.

Содержание курса состоит из шести разделов.

В процессе изучения данного курса предполагается использование различных методов активизации познавательной деятельности школьников. А также различных форм организации их самостоятельной работы.

Ожидаемые результаты:

— овладение математическими знаниями и умениями, необходимыми для итоговой аттестации, продолжения образования и освоения избранной специальности на современном уровне;

— развитие логического мышления, алгоритмической культуры математического мышления и интуиции, необходимых для продолжения образования ;

— формирование навыков самообразования, критического мышления, самоорганизации и самоконтроля, умения находить, формулировать и решать проблемы.

Учебно — тематическое планирование

№ п/п

Название раздела

Количество часов

1

Алгебра

5

2

Уравнения и неравенства

4

3

Функции

5

4

Начала математического анализа

4

5

Геометрия

6

6

Элементы комбинаторики, статистики и теории вероятностей

3

7

Решение тренировочных экзаменационных работ в формате ЕГЭ

7

Итого

34

Содержание разделов:

1. Алгебра

Целые числа. Дроби, проценты, рациональные числа. Свойства степени с действительным показателем. Корень степени n > 1 и его свойства.

Синус, косинус, тангенс, котангенс произвольного угла. Основные тригонометрические тождества. Формулы тригонометрии.

Логарифм числа и его свойства. Десятичный и натуральный логарифмы, число е.

Преобразование выражений, включающих арифметические операции. Преобразования выражений, включающих операцию возведения в степень. Преобразования выражений, включающих корни натуральной степени. Преобразования тригонометрических выражений. Преобразование выражений, включающих операцию логарифмирования. Модуль (абсолютная величина) числа.

2. Уравнения и неравенства.

Квадратные уравнения. Рациональные уравнения. Иррациональные уравнения. Тригонометрические уравнения. Показательные уравнения. Логарифмические уравнения. Равносильность уравнений, систем уравнений. Простейшие системы уравнений с двумя неизвестными. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных.

Квадратные неравенства. Рациональные неравенства. Показательные неравенства. Логарифмические неравенства. Системы линейных неравенств. Системы неравенств с одной переменной. Равносильность неравенств, систем неравенств Использование свойств и графиков функций при решении неравенств. Метод интервалов. Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем.

3. Функции.

Функция, область определения функции. Множество значений функции. График функции. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. График обратной функции. Свойства функции. Функции, их свойства и графики: линейная, квадратичная, степенная, тригонометрические, показательная, логарифмическая.

4. Начала математического анализа.

Понятие о производной функции, ее геометрический и физический смысл. Уравнение касательной к графику функции. Производные основных элементарных функций, вторая производная и ее физический смысл. Применение производной к исследованию функций и решения прикладных задач. Первообразные элементарных функций. Примеры применения интеграла в физике и геометрии.

5. Геометрия.

Расположение прямых на плоскости. Расположение прямых и плоскостей в пространстве. Свойства геометрических фигур (аксиомы, определения, теоремы). Формулы для вычисления геометрических величин. Решение планиметрических и стереометрических задач. Понятие вектора на плоскости и в пространстве. Координаты вектора.

6. Элементы комбинаторики, статистики и теории вероятностей.

Поочередный и одновременный выбор. Формулы сочетаний и перестановок. Бином Ньютона. Табличное и графическое представление данных. Числовые характеристики рядов данных. Вероятности событий. Примеры использования вероятностей и статистики при решении прикладных задач.

В результате изучения курса учащиеся должны знать / уметь:

-проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

— моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи;

— решать рациональные, иррациональные, тригонометрические, показательные и логарифмические уравнения, неравенства, системы уравнений и неравенств;

— решать задачи с параметрами и модулями;

— решать практические задачи, связанные с нахождением геометрических, алгебраических величин, применяя изученные математические формулы, уравнения и неравенства;

— решать прикладные задачи с применением производных и интегралов;

— проводить доказательные рассуждения при решении задач, оценивать логическую правильность полученных результатов;

— пользоваться справочной литературой и таблицами.

Календарно — тематический план

Дата

№ урока

Тема

1

АЛГЕБРА

Числа, корни и степени.

2

Основы тригонометрии.

3

Логарифмы.

4

Преобразование выражений.

5

Преобразование выражений.

6

УРАВНЕНИЯ И НЕРАВЕНСТВА

Уравнения.

7

Уравнения.

8

Неравенства.

9

Неравенства.

10

ФУНКЦИИ

Определение и график функции.

11

Элементарное исследование функций.

12

Основные элементарные функции.

13

Основные элементарные функции.

14

Основные элементарные функции.

15

НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

Производная.

16

Исследование функций.

17

Исследование функций.

18

Первообразная и интеграл.

19

ГЕОМЕТРИЯ

Планиметрия.

20

Прямые и плоскости в пространстве.

21

Многогранники.

22

Тела и поверхности вращения.

23

Измерение геометрических величин.

24

Координаты и векторы.

25

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

Элементы комбинаторики.

26

Элементы статистики.

27

Элементы теории вероятностей.

28

Решение типовых экзаменационных работ.

29

Решение типовых экзаменационных работ.

30

Решение типовых экзаменационных работ.

31

Тренировочная экзаменационная работа.

32

Тренировочная экзаменационная работа.

33-34

Повторение.

Перечень учебно — методического обеспечении

1. 1. Алгебра и начала математического анализа: Учеб. Для 10, 11 кл. общеобразоват. учреждений: базовый и профильный уровни / Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин – М.: Просвещение, 2011.

2. ЕГЭ-2014 Математика самое полное издание типовых вариантов заданий.

3. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. Автор Ершова А.П., Голобородько В.В. –М.: Илекса, 2007.

4. А.С. Атанасян, В.Ф. Бутузов и др. Учебник. Геометрия 10 – 11.- М.: Просвещение, 2009.

5. Н.А.Ким. Математика. Технология подготовки учащихся к ЕГЭ 10-11классы . Волгоград Изд. Учитель, 2010год.

Список литературы:

1. Под ред. А.Л. Семенов, И.В. Ященко. Типовые варианты заданий ЕГЭ 2014, АСТ Астрель, Москва, 2013.

2. Л.Д. Лаппо, М.А. Попов. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ. Изд. «Экзамен» Москва, 2013.

3. И.В. Ященко, С.А. Шестаков, П.И. Захаров. Математика ЕГЭ. Тематическая рабочая тетрадь. Изд. МЦНМО «Экзамен», Москва, 2012.

4. Под ред. А.Л. Семенов, И.В. Ященко. Математика ЕГЭ. Типовые тестовые задания. Изд. «Экзамен» Москва, 2010.

5. Белошистая А.В. Математика: Тематическое планирование уроков подготовки к экзамену-М: Издательство «Экзамен» 2007

6. Мирошин В.В. Алгебра и начала анализа. 11 класс. 180 диагностических вариантов-М: Национальное образование, 2012г.

Перечень сайтов

1.http://www.prosv.ru – сайт издательства ,,Просвещение,, /рубрика,,Математика,,/

2.http://www.drofa.ru-сайт издательства ,,Дрофа,, /рубрика,,Математика,,/

3.http://www.legion.ru-сайт издательства ,,Легион,,

4.http://www. fipi. ru-портал информационной поддержки мониторинга качества образования здесь содержится Федеральный банк тестовых заданий.

5.http://zadachi.mccme.ru-Задачи по геометрии :информационно-поисковая система.

6.http://www.intelekt centre.ru-Сайт издательства ,, Интеллект центр,,

Где можно найти учебно-тренировочные материалы, банк тренировочных заданий с ответами , методические рекомендации и образцы решений.

7.http://www.edu.ru-Центральный образовательный портал, содержит нормативные документы Министерства, стандарты и информацию о проведении эксперимента.

infourok.ru

задачники для 10-11 класса — Колпаков Александр Николаевич

Предлагаю свой каталог учебной литературы: краткие описания пособий для 10-11 классов, ориентированных на подготовку к ЕГЭ по математике. Вместе с рекомендованными книжками от ФИПИ здесь представлены несколько классических сборников, не связанных напрямую с форматом Единого Государственного Экзамена. Несмотря на несоответствие его стандартам, они имеют достаточно высокий КПД на развитие ученика. Как мне кажется, при фундаментальной подготовке к ЕГЭ именно репетитор по математике мог бы дать ребенку хорошую практику в решении разнообразных задач. Для этой цели, на мой взгляд, луше всего использовать серьезные сборники конкурсных заданий прошлых лет со вступительных экзаменов и олимпиад в различные ВУЗы. Их эффективность проверена годами. При таком направлении занятий репетитор по математике выиграет больше, чем при натаскивании ученика на решения однотипных номеров из ЕГЭ ориентированных пособий. Особенно если подготовка к ЕГЭ начинается задолго его проведения. Стандарты могут в любой момент измениться и только тот абитуриент, который был натренирован репетитором на решение широкого спектра математических задач сможет не растеряться на реальном ЕГЭ.

Лучшие учебники активно используется в работе. Их здесь большинство. Остальные занимают место на полке только потому, что имеют отношение к любимой математике и их жалко выбрасывать. Вы сами поймете о каких книжках я говорю.

В.М. Говоров. Математика. Сборник задач для поступающих в ВУЗы Замечательная книжка, из которой я регулярно беру классические задания на уравнения и неравенства по всем разделам школьного курса. Репетитор по математике оценит очень хорошую организацию пособия. Представлен и отсортирован широкий круг конкурсных и базовых номеров, имеются все ответы и решения особенно трудных заданий. Ошибок и опечаток не замечено. Номера расположены примерно по возрастанию их уровня сложности (как и должно быть). Книга толстая и тяжелая, так что если репетитор математики положит ее в сумку, то возможно для кругих учебников в ней уже места не хватит. Незначительным недостаткам я бы отнес слабую базу заданий на вычисление логарифмов (их очень мало) и лишнюю (в свете подготовки к ЕГЭ) главу по комбинаторике и математическому анализу.
Оценка репетитора: 9 баллов из 10

И. Шарыгин. Математика для поступающих в ВУЗы. Еще один хороший и крепкий задачник по математике. Главным достоинством книжки является наличие в ней очень толковых комментариев по поиску решений трудных уравнений, неравенств, др. номеров. Описывается стратегия размышлений над задачей. Одновременно с этим разбираются хитрых и нестандартные приемы и алгоритмы. Уровень в среднем несколько выше чем у Говорова и поэтому я бы рекомендовал данный сборник не только для подготовки к ЕГЭ, но и для полноценной подготовки в МГУ. Сборник ориентирован только на школу. Элементы высшей математики в ней не представлены. Репетитор оценит качество и разнообразие номеров. Имеются ответы и указания к ним. Кое что решено полнотстью. К недостаткам можно отнести не очень разнообразную базу функциональных заданий: на касательную, на экстремумы.
Оценка репетитора: 9 баллов из 10

Закрытый сегмент ЕГЭ. 3000 задач части «B» с ответами. Официальный МИОО сборник, являющийся печатной версией их официального сайта с он-лайн решением задач части «B». Это его база. Главным недостатком этого пособия является наличие в нем огромного количества опечаток и неверных ответов. Надеюсь, что со временем все они исправятся и мы получим очень хороший путеводителей по ЕГЭ номерам. Что мне еще не понравилось? Слишком много одинаковых номеров, в потоке которых можно запутаться. Если репетитор по математике не выбирает задания заранее (не выписывает номера в рабочий листочек), то для поиска чего-нибудь новенького приходится просматривать по нескольку страниц. Это не удобно. Достоинством книжки является 100% соответствие реальным ЕГЭ прошлых лет. Никакого отклонения в сторону. Для репетитора по математике, преследующего с учеником прагматичные цели при подготовке к ЕГЭ — данная книжка является настоящим кладом. Чего-либо большего от нее ждать не приходится.
Оценка репетитора: 7 баллов из 10.

А.С. Бортаковский. Экзаменационные задачи и варианты по математике. Базовый задачник для подготовки к экзамену в МАИ выпущенный для подготовительных курсов в указанный ВУЗ. В нем собраны задачи, которые в разное время встречались на реальных экзаменах и представляющих дидактический интерес для преподавателей и учеников. Репетитор по математике найдет в книге широкий набор конкурсных задач: уравнения, неравенства, планиметрия, стереометрия, функции, текстовые задачи д. р. Рядом с каждым номером указан ответ и поэтому не нужно тратить время на его поиск конце книги. Имеется очень толково изложенная теоретическая часть с формулами и теоремами, а также база реальных экзаменационных вариантов МАИ. К недостаткам я бы отнес недостаточную плавность при переходе от простых заданий к сложным. Легких тригонометрических и логарифмических уравнений школьного уровня в задачнике почти нет. Объяснение этому простое: они редко включались в МАИ варианты.
Оценка репетитора: 9 баллов из 10.

И.В. Ященко. Подготовка к ЕГЭ по математике.
Одна из первых книжек выпущенных еще в 2010 году для подготовки к ЕГЭ в новой форме. Самое ценное в ней — описание стандартов будущего экзамена (в 2010 году он впервые проводился в новой форме) и отдельные тренировочные номера. Однако само качество пособия в плане точности и объема дидактики оставляет желать лучшего. Такое впечатление, что подготовительные номера были придуманы за полчаса до сдачи брошюры в печать 🙂 Репетитору по математике будут крайне сложно провести по ней полноценную подготовку к ЕГЭ. Задач и вариантов очень мало. Я взял из нее несколько номеров «С5» и «С6» и отложил в сторону.
Оценка репетитора: 4 балла из 10.

Постепенно перечень пособий будет дополняться новыми описаниями и комментариями. Жаль только что свободного времени у меня не так много. Если вас привлекло то или иное печатное издание — Вы можете прислать свою рецензию на него. Я опубликую ее от Вашего имени.

О новых пособиях. Опытные репетиторы по математике со стажем от 10 лет, как правило, весьма неохотно перестраивают свою систему работы с выпускниками под новые формы проведения экзамена в виде ЕГЭ. Поэтому все равно задачи для «С» части предпочитают брать из старых сборников. Предлагаются уравнения и неравенства? Старо как мир. Показательный пример: в пробники ЕГЭ прошлого года попало несколько диофантовых уравнений (в номера «C6») из старых номеров журнала «Квант». В далекие 90-е оды, когда я сам учился на математика в МПГУ и ходил на спецкурс «решение уравнений в целых числах» я решал у доски (как сейчас помню) уравнение методом спуска. Именно его пришлось показывать ученику Денису при подготовке к ЕГЭ в этом году.

Варинтов ЕГЭ наклепали уже столько, что в пору открывать для них музей, однако просматриваешь задания и замечаешь: этот номер один в один с древнего варианта вступительного экзамена в РЭА им.Плеханова, этот МГУ повторяет, здесь Финансовая Академия след оставила и т.д. Поэтому для работы в «С» части репетитору по математике совсем необязательно закупать пачками эти новые брошюры. Большинство из них не имеют проработанной дидактики, содержат немало опечаток и повторений. Я предпочитаю серьезные Говорова, Крамера, Шарыгина, Бортаковского, отчасти Сканави и очень люблю методичку Плехановской Академии. Поэтому не удивляйтесь, если на занятих для фундаментальной подготовки к ЕГЭ мы сначала проработаем ЕГЭ материал по этим учебникам. Тогда варианты ЕГЭ покажутся Вам легкой прогулкой по конкурсной математике.

Для задач с параметрами я однозначно останавливаю свою выбор на специализированных книжках. В скором времени я сделаю для них отдельную страницу.

Колпаков А.Н. Репетитор математики, Москва.

ankolpakov.ru

Урок математики в 11 классе «Повторение. Подготовка к ЕГЭ»

Урок математики в 11 классе.

Тема: «Повторение. Подготовка к ЕГЭ».

Цель урока:

1. Повторение материала, подготовка учащихся к экзаменам.

2. развитие логического мышления, навыков самостоятельной и групповой деятельности.

3. Воспитание коллективизма.

План урока:

1. Оргмомент.

2. Устная работа. Задания типа В2

3. Повторение темы « Площади». Составление кластера.

4. Повторение темы «Логарифмы», использование ЭОРов.

5. Подведение итогов урока

(Тип урока:  урок повторения и закрепления пройденного материала.

Методы обучения: словесный,  наглядный, практический (частично-поисковый,  метод самостоятельной работы).

Средства обучения:  наглядный материал  (карточки, плакаты, учебное пособие «Банк открытых заданий ЕГЭ»).

Формы работы:  групповая, индивидуальная.

Триединая цель урока:

Задачи урока:

• Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»

• Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда

• Научить учащихся находить главное

• Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства      товарищества, культуры общения, чувства ответственности. )

Ход урока.

1. Оргмомент.

1. Устные упражнения: Разрешите открыть урок с высказывания Декарта: «Я мыслю, следовательно, существую». Сейчас вам дается возможность проявить свою мысль при выполнении ряда заданий для подготовки к ЕГЭ.

ЕГЭ это вершина ,к которой мы медленно поднимаемся, переходя из класса в класс, изучая одну тему за другой. Задания ЕГЭ это ступени, по которым легче покорить эту вершину. Сегодня на уроке мы преодолеем вместе с вами некоторые из этих ступеней.

Итак , первая ступенька на которую мы с вами сегодня поднимемся -задания В2. Их можно решить устно. Мы сейчас рассмотрим несколько разных заданий этого типа.

Задание B2

На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.

Определите по графику, сколько дней из данного периода осадков выпало между 2 и 8 мм.

Ответ: 3

Задание B2

На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.

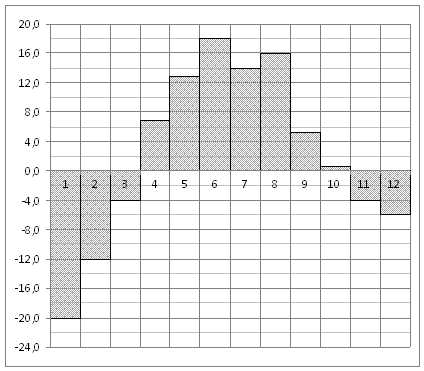
Ответ: 38

Задание B2

Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее  ° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы.

Ответ: 7

Задание B2

На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.

Ответ: 10

Задание B2

На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 19 декабря.

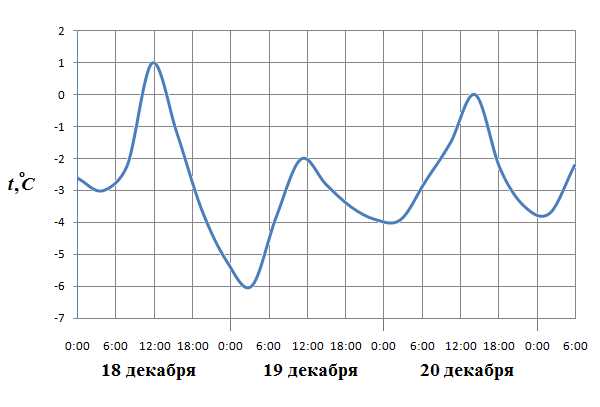
Ответ: 4

Задание B2 (18881)

(показов: 1885, ответов: 1026)

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа выпало наибольшее количество осадков.

Ответ: 15

Задание B2

На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года.

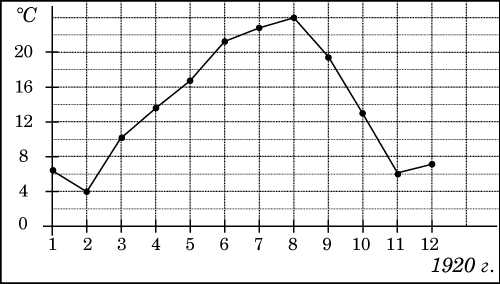
Ответ: 6

Задание B2

На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1988 году.

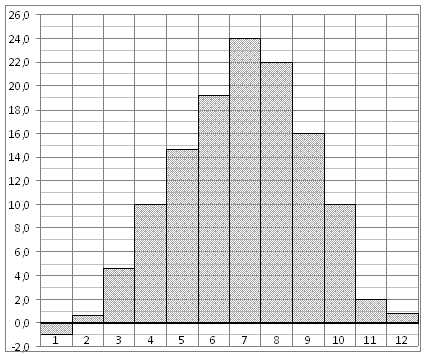
Ответ: 24

Задание B2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

Ответ: 3

1. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Формулы для кластера

(ромб) (трапеция) (параллелепипед) S = ha S= аbsinγ S= (d1×d2×sinγ) 2 (прямоугольник) S = a*b (квадрат) (прямоугольный треугольник) (треугольник) Формула Геррона S= 1/2ab sinγ S=1/2 r×P S= abc 4R (круг) (круговой сектор) S=πR²α 360 (правильные многоугольники) n=3, S=a²√3 4 n =4, S=a² n=6, S=3√3a² 2

(пирамида) (правильная пирамида) Sбок=1/2Pоснd (апофему) (усеченная пирамида) Sбок=1/2(P1 +P2)d (апофему) (куб) S = 6a² (прямоугольный параллелепипед) S = 2(ab+bc+ac) (цилиндра) S бок= 2πRh Sпол=2πR(R + h) (призма)S= Sбок + 2Sосн (прямой призмы) Sбок= Ph (конус) Sбок=πrl Sпол=πr(l + r) (усеченный конус) Sбок=π (r + r1) l (сфера)

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.
После небольшого обсуждения в парах, ответы вслух. Обсуждение.
Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

• Площадь какой фигуры находили?

• Какую формулу применяли?

• Можно ли решить данную задачу другим способом?

Предлагаемые задачи для устной работы:

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура.  Найдите его площадь.

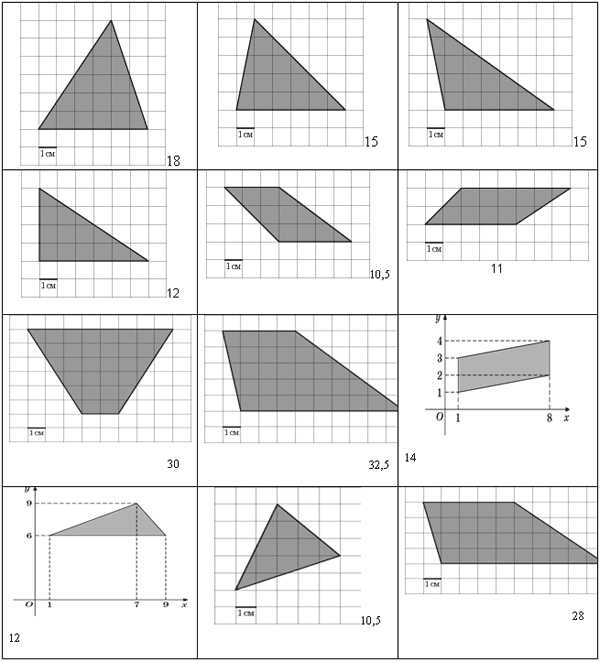
1. Теперь давайте перейдем к заданиям типа В5, В7. Логарифмы. Перед вами лежат формулы, выражающие свойства логарифмов. При работе можете ими пользоваться.

ЭОРы: а) работа вместе с учителем

Б) самостоятельная работа ученика.

Одновременно класс работает с ним, корректирует знания.

1. Откройте «Репетитор по математике. Варианты ЕГЭ, 2012 год». Выполняете каждый свой вариант. Начинаем выполнять тест. Результаты тестирования отправьте на печать.

2. Подведение итогов урока

3. 1. Домашнее задание.

4. – Задачи из банка открытых задач ЕГЭ: №5061, 5067,5201, 21337.
   – Оформить кластер, ответить на вопросы, отмеченные в кластере

5. 2. Выставление оценок

6. 3. Рефлексия

7. – Что дает нам прием «Кластер»?
   – Имеет ли практическое значение данная тема?
   – Понравился ли вам урок?

9. Сегодня мы проводим урок – отчет самостоятельного решения

задачи. Вы решали одну задачу разными способами. Мы ждем от вас красивого решения, а добиться этого можно лишь в результате кропотливой работы над задачей.

Красивое решение приходит тогда, когда придумано несколько вариантов решения задачи. Метода, который гарантировал бы решение любой задачи – нет. Но все же существуют весьма общие приемы, которые при умелом применении заметно облегчают решение многих трудных задач. Разработка этих приемов называется — эвристика. Слово происходит от знаменитого «Эврика».

«Эврика» — нашел! – воскликнул, согласно легенде, древнегреческий ученый Архимед, выскочив из ванны, он понял как решить, возникшую перед ним задачу.

Стихотворение (читает ученица)

Преданье старинное знает весь свет,

Как, нежась горячею ванной,

Открыл свой великий закон Архимед,

Связав его с выходкой странной.

Сияющий выскочил вон Архимед,

Из ванны горячей, где мылся,

И прямо из бани, как был, неодет,

Куда-то бежать он пустился.

Картина, достойная кисти богов,

По улице, солнцем согретой,

Пунктир оставляя из мокрых следов,

Бежит Архимед неодетый.

Толпа сиракузцев несется во след,

В восторге от бешеной гонки,

И громко ликует, когда Архимед,

Выкрикнул «Эврика» звонко.

«Нашел!» Он нашел тот желанный ответ,

Который искал так упорно.

«Нашел!» В упоенье кричал Архимед,

«Нашел!» — повторяли задорно.

Подобно Архимеду, вы искали решение задачи, каждая группа предлагает свой способ. Когда вы получили задание сделать проект решения задачи, то вы думали, что это невозможно, но сейчас посмотрим, что из этого получилось

1. Заключение.

Сейчас, прослушав несколько способов решения одной задачи, мы повторили несколько тем. Вы должны выбрать тот способ решения, который вам больше понравился, и если на экзамене вам встретилась задача, которую не можете решить, то вспомните, что можно попытаться решить другим способом.

В этом году вы выпускаетесь из школы и вас ждут большие жизненные испытания. Так вы должны знать, что безвыходных ситуаций не бывает.

В любой ситуации можно найти решение.

Закончим наш урок словами Эйнштейна: «Каждый важный успех приносит новые вопросы».

kopilkaurokov.ru

Математика для 11 класса • Светоч

Что утомительно? Праздность”. Фалес

Математика 11 класс (подготовка к ЕГЭ)

По окончании 11-го класса всем школьникам предстоит сдать обязательный единый государственный экзамен (ЕГЭ) по математике, включающий в себя задания из всего школьного курса математики, включая планиметрию и стереометрию.

Предлагаемый курс математики образовательного Центра «Светоч» для учащихся 11-го класса направлен в первую очередь на успешную подготовку учащихся к сдаче ЕГЭ. Программа курса построена таким образом, чтобы максимально эффективно распределять учебное время между изучением нового материала, повторением и закреплением ранее пройденного материала, решением типовых задач и типовых контрольно-экзаменационных вариантов ЕГЭ.

Программа предлагаемого курса полностью соотносится со школьной программой по математике. Учащиеся узнают о характерных сложностях, специфике, организационных особенностях предстоящего экзамена. В течение курса учащиеся несколько раз напишут тестовый экзамен.

Таким образом, по окончании нашего курса вы будете готовы к ЕГЭ на 100%.

1-2 Четверть

Содержание курса

Алгебра

1. Функции. Первообразная.
2. Интегрирование. Неопределенный и определенный интеграл.
3. Формула Ньютона-Лейбница. Площадь.

Геометрия

1. Стереометрия.
2. Тела вращения.
3. Объем и площадь поверхности.

По завершении курса вы будете:

• уверенно проводить полный анализ функций;
• интегрировать функции;
• решать задачи на определенный интеграл;
• находить объем и площадь поверхности тел;
• уверенно решать типовые задачи и примеры, предлагаемые на ЕГЭ.

3-4 Четверть

Содержание курса

Алгебра и геометрия

1. Повторение и систематизация изученного теоретического материала.
2. Решение типовых задач и примеров.
3. Решение задач повышенной сложности.
4. Решение типового варианта ЕГЭ.

По завершении курса вы:

• повторите и систематизируете весь необходимый теоретический материал;
• в полной мере отработаете навык решения типовых задач ЕГЭ;
• отработаете навык быстрого и правильного решения задач в условиях реального экзамена;
• будете уверенно решать задачи по планиметрии и стереометрии;
• знать специфику и формат предстоящего экзамена;
• научитесь решать задачи повышенной сложности;
• будете готовы к ЕГЭ 2010 по математике на 100%.

www.svetoch-msk.ru

ЕГЭ по математике, подготовка к ЕГЭ по математике 11 класс

Числа, корни и степени
1.1 Целые числа
1.2 Степень с натуральным показателем
1.3 Дроби, проценты, рациональные числа
1.4 Степень с рациональным показателем
1.5 Корень степени n>1 и его свойства
1.6 Степень с рациональным показателем и его свойства
1.7 Свойства степени с действительным показателем

Решение заданий 1, 2, 3, 9, 11, 19

Основы тригонометрии
1.8 Синус, косинус, тангенс, котангенс произвольного числа
1.9 Радианная мера угла
1.10 Синус, косинус, тангенс и котангенс числа
1.11 Основные тригонометрические тождества
1.12 Формулы приведения
1.13 Синус, косинус, тангенс суммы и разности 2-х углов
1.14 Синус и косинус двойного угла

Решение заданий 6, 9, 13

Логарифмы
1.15 Логарифм числа
1.16 Логарифмы произведения, частного, степени
1.17 Десятичный и натуральный логарифм числа

Решение заданий 5, 9, 15

Преобразование выражений
1.18 Преобразование выражений , содержащих арифметические операции, включающих операцию возведения в степень
корня натуральной степени
1.19 Преобразование тригонометрических выражений, включающих операцию логарифмирования
1.20 Модуль числа

Решение заданий 5, 10, 13, 17, 19

Уравнения
2.1 Квадратные уравнения
2.2 Рациональные уравнения
2.3 Иррациональные уравнения
2.4 Тригонометрические уравнения
2.5 Показательные уравнения
2.6 Логарифмические уравнения
2.7 Равносильность уравнений, системы уравнения
2.8 Простейшие системы уравнений с двумя переменными
2.9 Основные приемы – подстановки, сложения, введения новой переменной
2.10 Использование свойств и графиков функций при решении уравнений
2.11 Изображение на координатной плоскости множества решений уравнений
2.12 Применение математических методов для решения содержательных задач из различных областей науки и
практики

Решение заданий 12, 20

Неравенства
2.13 Квадратные неравенства
2.14 Рациональные неравенства
2.15 Показательные неравенства
2.16 Логарифмические неравенства
2.17 Системы линейных неравенств
2.18 Системы неравенств с одной переменной
2.19 Равносильность неравенств систем неравенств
2.20 Использование свойств и графиков функций при решении неравенств
2.21 Метод интервалов
2.22 Изображение на координатной плоскости множества решений неравенств и их систем

Решение заданий 15, 17

Определения и графики функций
3.1 Функция, область определения функции
3.2 Множество значений функции
3.3 График функции. Примеры функций в реальных процессах
3.4 Обратная функция. График обратной функции
3.5 Преобразование графиков, параллельный перенос, симметрия относительно осей координат

Элементарные последования функций
3.6 Монотонность функции. Промежутки возрастания и убывания функций
3.7 Четность и нечетность функции
3.8 Периодичность
3.9 Ограниченность
3.10 Точки экстремума
3.11 Наибольшее и наименьшее значение функции

Основные элементарные функции
3.12 Линейная функция и ее графики
3.13 Обратно -пропорциональная функция и ее график
3.14 Квадратичная функция и ее график
3.15 Степенная функция с натуральным показателем и ее график
3.16 Тригонометрические функции и их графики
3.17 Показательная функция и ее график
3.18 Логарифмическая функция и ее график

Производная
4.1 Понятие о производной, геометрический смысл производной
4.2 Физический смысл производной, нахождения скорости
4.3 Уравнение касательной к графику функции
4.4 Производная суммы, произведения, частного
4.5 Производные основных элементарных функций
4.6 Вторая производная и ее физический смысл

Исследование функций
4.7 Применение производной к исследованию функции
4.8 Примеры использования производной при решении практических задач

Первообразная и интеграл
4.9 Первообразные элементарных функций
4.10 Примеры применения интеграла в физике и технике

Решение заданий 17, 12

Планиметрия
5.1 Треугольники
5.2 Параллелограммы, прямоугольник, ромб, квадрат
5.3 Трапеция
5.4 Окружность и круг
5.5 Окружность вписанная в треугольник и окружность описанная около треугольника
5.6 Многоугольник. Сумма углов выпуклого многоугольника
5.7 Правильные многоугольники. Вписанные и описанные окружности правильных многоугольников

Решение заданий 3, 6

Прямые и плоскости в пространстве
5.8 Пересекающиеся параллельные и скрещивающие прямые. Перпендикулярность прямых
5.9 Параллельность прямой и плоскости
5.10 Параллельность плоскости, признаки и свойства
5.11 Перпендикулярность прямой и плоскости, признаки и свойства
5.12 Перпендикулярность плоскостей . Признаки и свойства
5.13 Параллельное проектирование. Изображение пространственных фигур на плоскости

Решение заданий 8,14

Многогранники
5.14 Призма. Ее основания, боковые ребра, высота, боковая поверхность. Прямая и правильная призма
5.15 Параллелепипед, куб, симметрия
5.16 Пирамида
5.17 Сечения куба, призмы, пирамиды
5.18 Представление о правильных многогранниках

Решение заданий 3,6,8, 14 баз(6,8)

Многогранники
5.19 Цилиндр, основание, высота, боковая поверхность, образующая
5.20 Конус и его элементы
5.21 Шар и сфера. Их сечения

Решение заданий 8, 14

Измерение геометрической величины
5.22 Величина угла, градусная мера, соответствие между величиной угла и длиной окружности
5.23 Угол между прямыми в пространстве; между прямой и плоскостью ; между плоскостями
5.24 Длина ломаной, окружности. P многоугольника
5.25 Расстояние от точки до прямой, до плоскости, расстояние между параллельными прямыми, скрещивающимися прямыми и между параллельными плоскостями
5.26 Площадь треугольника, параллелограмма, трапеции, круга, сектора
5.27 Площадь поверхности конуса, цилиндра и сферы

Решение заданий 3, 6, 8

Координаты и векторы
5.28 Координаты на прямой, декартовы координаты на плоскости и пространстве
5.29 Формула расстояния между двумя точками. Уравнение сферы
5.30 Вектор. Модуль вектора. Сложение векторов. Умножение вектора на число
5.31 Коллинеарные векторы. Разложение по 2-м неколлинеарным векторам
5.32 Коллинеарные векторы. Разложение по 3-м неколлинеарным векторам
5.33 Координаты вектора. Скалярное произведение векторов. Угол между векторными.

Решение заданий 3

6.1 Элементы комбинаторики
6.2 Поочередный и одновременный выбор
6.3 Формула числа сочетаний, размещения и перестановок . Бином Ньютона
6.4 Элементы статистики
6.5 Табличное и графическое представление данных, числовые характеристики рядов
6.6 Элементы теории вероятностей
6.7 Вероятности событий
6.8 Примеры использования теорий вероятностей и статистики при решении задач.

Решение заданий 4,10 (баз), 11

ariadna-ege.ru

Практикум по подготовке к егэ по математике 11класс

Муниципальное общеобразовательное учреждение
« Беловская средняя общеобразовательная школа»

Практикум по подготовке к ЕГЭ

по МАТЕМАТИКЕ

11класс

Тема: Повторение логарифмов по заданиям первой части ЕГЭ.

Тип урока: закрепления изученного материала.

Форма обучения : практическое занятие.

Учитель математики: Бартенева О.Н.

Тема: Повторение логарифмов по заданиям первой части ЕГЭ.

ЦЕЛЬ: ( урок подготовки к ЕГЭ)

1. Обобщение изученного материала по теме, формирование умений применять логарифмическую функцию к решению заданий ЕГЭ.

2.Практическое применение усвоенных теоретических знаний.
Задачи:

Образовательные:

Сформировать у учащихся умение выполнять преобразования выражений, содержащих логарифмы;

Отрабатывать навыки преобразования выражений, содержащих логарифмы в режиме централизованного тестирования.

Развивающие:

Развивать и совершенствовать умения применять накопленные знания в измененной ситуации, делать выводы и обобщения.

Воспитательные:

Воспитывать настойчивость в достижении поставленной цели.

Оборудование: мультимедийная установка, презентация, тесты по вариантам на каждого ученика.

Ход урока:

1. 
   Организационный этап.
   

Задача: подготовить учащихся к работе на занятии, определить тему урока.

Деятельность учителя: раздать карточки, определить границы и объём работы на уроке.
Устная работа: (карточка дана каждому ученику)

Вычислите логарифмы. Зачеркните в таблице ответы буквы, им соответствующие. Оставшиеся буквы позволят вам прочитать название темы.

= = =

3	21	2	13	9	1	7
К	Л	Ю	О	Г	Н	А
17	32	-2	11	5	15	4
Р	И	Е	Ф	В	М	Ы

И так тема урока: логарифмы.
2.Проверка, теоретических, ранее усвоенных знаний.
Задача: проверить ранее усвоенные теоретические знания учащихся.

Деятельность учителя: Вспомните определение логарифма, основное логарифмическое тождество, свойства логарифма, формулу перехода к одному основанию.
Определение логарифма: пусть ао и а1; Логарифм положительного числа b по основанию a (обозначается ) – это показатель степени, в которую надо возвести a, чтобы получить b. Иными словами

= х = b.
Например:

=3, т.к. 2³ = 8;

=2, т.к. 7² = 49;

= -1, т.к. 5-¹ = ;

= , т.к. =

log₃ 81 = 4 , т. к.  3⁴  = 81;

log_1/3 27 = – 3 , т. к.   = 3³ = 27;

Логарифм с основанием 10 называется десятичным и обозначается . Например, ,

.

Логарифм с основанием е называется натуральным и обозначается.

Обратите внимание: логарифм определён только для положительных чисел. Причина в том, что показательная функция может принимать лишь положительные значения.

Например: число не существует; В какую бы степень мы не возводили 2, мы никогда не получим -4.

Не забывайте также про ограничения на основание 0или а .

Вышеприведенное определение логарифма можно записать в виде тождества: .

Основные свойства логарифмов:

Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы.

1. log_b b = 1, так как  b ¹ = b.
2. log_b 1 = 0, так как  b ⁰ = 1.

3. Логарифм произведения равен сумме логарифмов:

log_c (ab) = log_c a + log_c b.
4. Логарифм частного равен разности логарифмов:

log_c (a:b) = log_c a – log_c b.

5. Логарифм степени равен произведению показателя степени на логарифм её основания:  log_c (b ^k ) = k · log_c b , говорят вынесем степень за знак логарифма.

6. Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак логарифма: =

7. Два последних свойства можно объединить в одно:

, если m =n мы получаем формулу

. Например:

8.  Формула перехода (т.e. перехода от одного основания логарифма к другому основанию):

, в частности , если с = b, то и тогда

.

3.Воспроизведение изученного материала и его применение в стандартных условиях.

Задача: рассмотреть типичные задания В 7 открытого банка заданий по подготовке к ЕГЭ.(по карточкам)

Деятельность учителя: Раздать всем учащимся карточки с заданиями В7 из банка ЕГЭ.

Деятельность учащихся: Решить пять заданий на свойства логарифма, ответы проверить через мультимедийник.
Предполагаемые результаты: Учащиеся должны справиться с заданиями.

Задачи В 7: приведём несколько примеров из банка заданий ЕГЭ

(карточка)

1)

(применим формулу суммы логарифма)

2) ² = (²)² = (² = (2*2)² = 16

(применим формулы степени логарифма)

3)( )² = 3² = 9

( применим основное логарифмическое тождество)

4) = = -1

(применим формулу перехода к новому основанию)

5) = = = 9² = 81

( применим формулу разности логарифма)

4. Перенос приобретенных теоретических знаний и их первичное применение в новых условиях.

Задача: проверить умения и навыки учащихся самостоятельно выполнять преобразования выражений, содержащих логарифмы в режиме централизованного тестирования с кратким ответом (в виде целого числа или числа, записанного в виде десятичной дроби).

Деятельность учителя: Раздать учащимся тестовые задания. Работа по вариантам.

Тестовые задания

Найти значение выражения:

5. Подведение итогов.

Деятельность учителя: показать ответы учащимся, ответить на вопросы учащихся.
Деятельность учащихся: проверяют, задают вопросы, выполняют работу над ошибками.
Предполагаемые результаты: усвоение темы.

6. Постановка домашнего задания:

Задания с ЕГЭ 2010г. (пробный) В7:

Найдите значение выражения:

=

2) =

3) =

4)

5) =
Самоанализ урока.

по алгебре в 11 классе по теме : «повторение»
ЦЕЛЬ: ( урок подготовки к ЕГЭ)

1. Обобщение изученного материала по теме, формирование умений применять логарифмическую функцию к решению заданий ЕГЭ.

2.Практическое применение усвоенных теоретических знаний.
Задачи:

Образовательные:

Сформировать у учащихся умение выполнять преобразования выражений, содержащих логарифмы;

Отрабатывать навыки преобразования выражений, содержащих логарифмы в режиме централизованного тестирования.

Развивающие:

Развивать и совершенствовать умения применять накопленные знания в измененной ситуации, делать выводы и обобщения.

Воспитательные:

Воспитывать настойчивость в достижении поставленной цели.

Оборудование: мультимедийная установка, презентация, тесты по вариантам на каждого ученика.

Урок – практикум по теме : логарифмы опирается на предыдущий материал: определение логарифма, свойства логарифма, формулы перехода к одному основанию, основные логарифмические тождества область определения логарифмической функции. Структура урока обобщения и систематизации знаний имеет вид: мотивация – анализ содержания учебного материала – выделение главного – обобщение и систематизация знаний – самоконтроль – контроль – коррекция. Согласно данной структуры определены следующие этапы урока:

1. 
   Организационный момент.
   
2. 
   Проверка теоретических знаний.
   
3. 
   Воспроизведение изученного материала и его применение в стандартных условиях.
   
4. 
   Перенос приобретённых теоретических знаний и их первичное применение в новых условиях. Тесты.
   
5. 
   Подведение итогов.
   
6. 
   Задание на дом.
   

Все этапы выполнены. На каждом этапе стремилась построить работу таким образом, чтобы каждый ученик чувствовал себя полноценным участником образовательного процесса. Деятельность учащихся была направлена на решение поставленных задач и развитие самого себя. Свою задачу видела в том, чтобы вовлечь каждого в работу, создать условия для сомореализации и уверенности в себе. На протяжении всего урока использовала индивидуальные, групповые, коллективные формы работы, что способствовало активизации познавательной деятельности. На данном уроке учитывались требования программы и стандарта, а также реализовывалась одна из задач школы: включение каждого школьника в работу на учебных занятиях в качестве активного участника образовательного процесса . Для более успешного повторения материала практический метод обучения, который способствует более качественной подготовке к итоговой аттестации, причём учащиеся имели возможность решить несколько заданий из банка ЕГЭ. На данном уроке были представлены: мультимедийная презентация, карточки, тесты, материал для домашней работы. Считаю, что практикум для старшей школы является основным при подготовке к ЕГЭ. При подведении итога урока учащиеся имели возможность высказать свою точку зрения об уроке, внести предложения, пожелания. Каждый для себя сделал вывод: чтобы успешно сдать ЕГЭ, необходимо заниматься в системе, что очень важно для дальнейшей деятельности учащихся. Урок детям понравился, а это самое главное в нашей работе.

..

.

5-bal.ru