Вращательное движение определение – Дать определение вращательного движения и всех величин, характеризующих данное движение?

Дать определение вращательного движения и всех величин, характеризующих данное движение?

Кафедра Физики и математики, информационных технологий

 

 

Отчет

по лабораторной работе № 1.4

 

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ

 

 

Выполнила ст. группы СБ-13-15

Новак Элина Францевна

 

Проверил:

ст. преподаватель Соболева В.В.

 

 

 

Лабораторная работа №1.4.

 

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ

 

Цель работы:

1. Изучить характеристики и основной закон динамики вращательного движения твёрдого тела.

2. Определить момент инерции крестообразного маятника (маятник Обербека).

3. Оценить момент тормозящей силы, действующий на тело в процессе вращения.

4. Определить момент инерции тела с учетом момента тормозящей силы.

5. Произвести расчет моментов, пользуясь энергетическими соотношениями.

 

Приборы и принадлежности:

1. Модульный учебный комплекс МУК-М1;

2. Блок секундомер электронный СЭ1;

3. Блок механический БМ1.

 

 

Ответы на контрольные вопросы:

Дать определение вращательного движения и всех величин, характеризующих данное движение?

 

Вращательное движение — это движение тела, при котором точки описывают окружности, размещенные в параллельных плоскостях, причем центры всех окружностей располагаются на одной прямой, которая обычно определяется как ось вращения.

Вращательное движение представляет траекторию в виде кривой линии, а скорость в каждой точке кривой линии направлена по касательной.

Кинематика вращательного движения характеризуется:

угловой скоростью и обозначается
угловым ускорением и обозначается

Угловая скорость — это скорость вращательного движения, которая определяется отношением угла поворота радиуса, соединяющего движущееся тело с центром окружности, к времени, за которое был совершен поворот и записывается формулой: , где — угол поворота радиуса, t — время поворота.

Единицу измерения угла поворота принято считать радианом, но не запрещается выражать его и в градусах. Размерность радиана:

Угловая скорость является векторной величиной, где его угловой вектор скорости направлен в том же направлении, что и поступательное движение правого винта (правило буравчика), где происходит движение по окружности.

Если вращательное движение совпадает с вращением рукоятки буравчика, то поступательное движение буравчика будет указывать на направление угловой скорости и углового ускорения, т.к. они сонаправлены.
Физический смысл угловой скорости при вращательном движении: угловая скорость будет равна углу поворота радиуса за единицу времени.

В Международной системе единиц угловая скорость имеет размерность — рад/с (радиан в секунду).
Связь между угловой и линейной скоростями: так как линейная скорость выражается следующей формулой , а во вращательном движении траектория определена формулой

Скорость во вращательном движении можно также выразить числом оборотов в единицу времени. Через число оборотов легко выразить угловую скорость, которая будет определяться формулой:

Число оборотов есть частота обращения, а величина обратная частоте есть период обращения и определяется формулой: .

Рассмотрим ускорение во вращательном движении: центро-стремительное ускорение и угловое ускорение.
Центростремительное ускорение — это такое ускорение, которое образуется при движении тела по окружности и направлено к центру по радиусу окружности. Центростремительное ускорение равно отношению квадрата скорости к радиусу окружности и записывается формулой:

Также центростремительное ускорение выражается в виде про- изведения линейной и угловой скоростей и записывается формулой:

Угловое ускорение — это ускорение, которое определяется отношением изменения угловой скорости ко времени, за которое произошло изменение этой скорости и записывается в виде формулы: , где — изменение угловой скорости, t — время, за которое произошло изменение угловой скорости.

Физический смысл углового ускорения: при вращательном движении угловое ускорение будет определяться как изменение угловой скорости за единицу времени.

Единицей углового ускорения в международной системе единиц является рад/с (радиан на секунду).
С изменением угловой скорости происходит изменение частоты вращения. Частота вращения характеризуется отношением числа оборотов ко времени и записывается в виде формулы:

Средняя частота вращения определяется соотношением:

являются соответственно начальной и конечной частотой.

Угловое ускорение имеет взаимосвязь с углом поворота. Эта связь определяется следующей формулой:

 

megaobuchalka.ru

Вращательное движение и угловая скорость твердого тела :: SYL.ru

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

φ = φ(t).

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с².

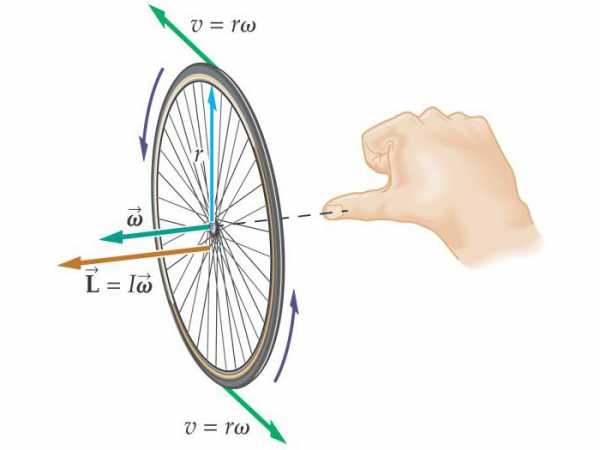
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt²/2.

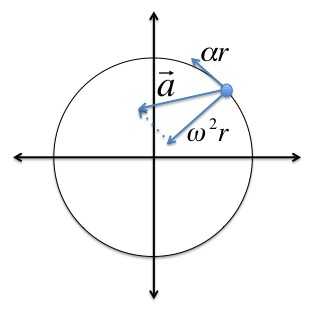
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц= v²/R = (ωR)²/R = ω²R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t= ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R²mβ, β= M/mR² = M/I, где I = mR² — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10⁴ об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Решение

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω₀— εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с²).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt²/2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10⁴ (об.).

Ответ: угловое ускорение равно 4,36 рад/с²; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10⁴ об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Решение

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR² = F/mR.

Найдем время, за которое диск остановится: t = ω₀/ε, где ω₀ — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

www.syl.ru

Лабораторная работа № 11

1. Дайте определение основных кинематических величин, характеризующих вращательное движение твёрдого тела.

Углова́я ско́рость— векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе)rот оси вращения можно считать так:v = rω.Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

Ине́рция(от лат.inertia—бездеятельность, косность) — явление сохранения скорости тела в случае, если внешние воздействия на него отсутствуют или взаимно скомпенсированы.

Существование явления инерции в классической механике постулируется Первым законом Нью́тона, который также называется Зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:

«Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.»

Современная формулировка закона:

«Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.»

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными. Проявлением неинерциальности в них является возникновение фиктивных сил, называемых «силами инерции».

2. Связь линейных и угловых параметров вращательного движения.

Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скоростиопределяется скоростью вращения телаи расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток временитело повернулось на угол(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный

Линейная скорость точки по определению.

(2.6)

Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:

подставляя значение скорости из (2.6), находим:

(2.7)

Тангенциальное ускорение

Воспользовавшись тем же отношением (2.6) получаем

(2.8)

Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.

studfiles.net

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА

План

1. Абсолютное твёрдое тело. Вращательное движение. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями вращающегося твёрдого тела.

2. Момент инерции тела. Кинетическая энергия вращающегося твёрдого тела.

3. Вычисление моментов инерции. Теорема Штейнера. Свободные оси.

4. Момент силы. Момент импульса.

5. Уравнение моментов. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.

6. Гироскопы. Гироскопический эффект.

 

1. Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками тела остаётся неизменным.

Всякое движение твёрдого тела можно разложить на два основных вида движения – поступательное и вращательное.

Вращательнымназывается такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Введём понятие угловой скорости и углового ускорения. Пусть твёрдое тело вращается вокруг неподвижной в данной системе отсчёта оси и за время совершает бесконечно малый поворот (рис. 3.1).

Соответствующий угол поворота будем характеризовать вектором , модуль которого равен углу поворота, а направление совпадает с осью , причём так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора .

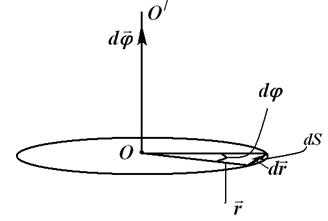
Рис. 3.1

Из рис. 3.1 следует, что . Вектор как бесконечно малую величину можно считать по модулю равным соответствующей дуге окружности , его направление соответствует правилу правого винта по отношению к векторам и

Разделим обе части на :

. (*)

Производная угла поворота по времени называется угловой скоростью.

Вектор совпадает по направлению с вектором . Изменение вектора со временем характеризуют вектором углового ускорения:

Из выражения * получаем связь линейной и угловой скоростей:

(**)

То есть скорость любой точки А твёрдого тела, вращающегося вокруг неподвижной оси с угловой скоростью , равна векторному произведению на радиус-вектор точки А относительно произвольной точки на оси вращения.

Если выбрать в качестве точки отсчёта для радиус-вектора центр окружности вращения (точка О), при неизменном радиусе окружности выражение (**) можно записать в скалярном виде:

Продифференцируем это выражение по времени: , отсюда получаем связь тангенциального и углового ускорений:

Нормальное ускорение можно представить как

Модуль полного ускорения:

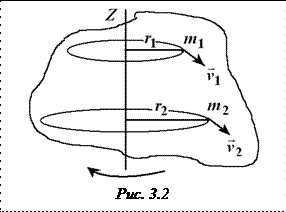2. Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки ( ). Обозначим массу i-го элемента , а скорость этого элемента .

Кинетическая энергия этого элемента

.

Просуммировав кинетическую энергию всех элементов, получим кинетическую энергию вращательного движения тела:

.

Линейная скорость связана с угловой скоростью вращения тела ( постоянна для всех точек тела).

.

Определение. Моментом инерции материальной точки относительно оси z называется произведение массы этой точки на квадрат её расстояния от оси вращения:

Определение. Моментом инерции твёрдого тела относительно некоторой оси z называется сумма моментов инерций материальных точекотносительно данной оси.

В соответствии с этими определениями:

(Сравните с выражением для кинетической энергии поступательного движения , очевидно соответствие ).

Физический смысл момента инерции. Момент инерции во вращательном движении играет такую же роль, как масса при поступательном движении, характеризует меру инертности тела при вращательном движении. Чем больше момент инерции тела, тем труднее при прочих равных условиях привести его во вращательное движение. Момент инерции определяется не только массой, но и тем, как эта масса распределена относительно оси вращения.

Соотношение является приближённым, причём тем более точным, чем меньше элементарные массы . Задача нахождения моментов инерции сводится к интегрированию.

(Интегрирование ведётся по всей массе тела ).

 

3. Вычисление моментов инерции. 1. Кольцо (полый цилиндр) (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии от центра.

Относительно оси, проходящей через центр кольца:

,

.

2. Однородный диск (сплошной цилиндр)

Дано: радиус диска, масса диска.

Найти: момент инерции диска относительно оси, проходящей через центр диска.

Разобьём диск (рис. 3.4) на кольца с радиусом , толщиной . По определению момента инерции . Пусть поверхностная плотность диска , тогда масса кольца , где площадь кольца, . Интегрируя по радиусу, находим момент инерции диска:

= ,

3. Тонкий однородный стержень

Дано: масса стержня, длина стержня.

Найти: (момент инерции относительно оси ОО, проходящей через конец стержня перпендикулярно ему) (рис. 3.5).

 

 

Рис. 3.5

 

Ввиду одномерного характера задачи выражение можно заменить на , где , тогда .

Теорема Штейнера (без вывода)

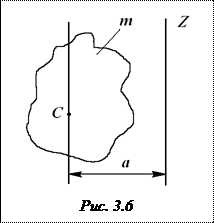Постановка задачи. Известен момент инерции произвольного тела массой относительно оси, проходящей через его центр тяжести (рис. 3.6). Требуется найти, каков момент инерции относительно какой-либо оси , параллельной первой и находящейся на расстоянии от неё.

Теорема. Момент инерции тела относительно произвольной оси z равен сумме момента инерции относительно оси, проходящей через центр масс тела С и параллельной данной, и произведения массы тела на квадрат расстояния между осями a:

.

Пример применения теоремы Штейнера.

Требуется найти момент инерции тонкого однородного стержня массой и длиной относительно перпендикулярной к нему оси , проходящей через центр стержня (рис. 3.7).

Рис. 3.7

Решение:

Воспользуемся полученным ранее выражением для момента инерции стержня относительно оси, проходящей через его конец:

. Используя теорему Штейнера, получаем:

отсюда .

Свободные оси

Определение. Ось вращения тела, положение которой в пространстве остаётся неизменным без действия на неё внешних сил, называется свободной.

Можно доказать, что в любом теле существует три взаимно перпендикулярных оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела. Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Вращение вокруг главных осей с наибольшим и наименьшим (экстремальными) моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом – неустойчивым. Этот факт является достаточно важным при проектировании конструкций с вращающимися частями.

4. Момент силы. Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы. Обозначим радиус-вектор, проведённый из этой точки к точке приложения силы (Рис. 3.8).

Рис. 3.8

Определение. Моментом силы относительно точки О называется векторное произведение радиуса-вектора на силу :

Раскрывая векторное произведение, получим где плечо силы (длина перпендикуляра, опущенного из точки О на линию действия силы).

В соответствии с определением векторного произведения вектор направлен перпендикулярно плоскости, в которой лежат векторы и в соответствии с правилом правого винта (буравчика).

Определение. Момент силы относительно оси , проходящей через точку О, есть проекция на эту ось вектора момента силы относительно точки, лежащей на этой же оси.

как проекция на ось является скалярной величиной.

 

Момент импульса

Пусть материальная точка массой движется со скоростью относительно точки О, а радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).

Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора на вектор импульса :

Направление перпендикулярно плоскости, в которой лежат векторы и , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.

Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор некоторой частицы массой лежит в плоскости рис. 3.10, скорость перпендикулярна ей («от нас»), частица движется по окружности радиусом .

Модуль момента импульса . Линейную скорость можно связать с угловой относительно оси как , тогда . Проекция вектора на ось вращения равна

. Как видно из рис. 3.10, , т.е.

Для системы материальных точек (твёрдого тела) выражение связи , и формально такое, как и для материальной точки:

Но под здесь подразумевается сумма моментов инерции материальных точек системы:

Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела . Он направлен вдоль оси вращения в ту же сторону, что и , т.е.

(Для несимметричного тела в общем случае не совпадает по направлению с вектором ).

 

5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у , и других величин не писать, но подразумевать, что он есть.

Продифференцируем выражение для момента импульса материальной точки: . .

Учтём, что , а .

Рассмотрим первое слагаемое (см. в лекции № 1 «Векторное произведение»).

= (так как угол между и равен нулю).

Второе слагаемое в выражении для

(по определению момента силы).

В результате получаем:

Уравнение моментов (оно связывает момент импульса с моментом силы).

Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.

Похожие статьи:

poznayka.org

Вращательное движение — Физическая энциклопедия

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ твёрдого тела — 1) В. д. вокруг неподвижной оси — движение твёрдого тела, при к-ром все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной

неподвижной прямой, наз. осью вращения. Тело, совершающее В. д., имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения (рис. 1). В. д. задаётся ур-нием , где t — время. Осн. кинематич. характеристики В.д. тела: его угловая скорость и угловое ускорение . Для любой точки тела, находящейся на расстоянии h от оси вращения, линейная скорость , касат. ускорение , нормальное ускорение , полное ускорение . Т.о., скорости и ускорения всех точек тела пропорциональны их расстояниям от оси вращения.

Осн. динамич. характеристиками В. д. тела являются его гл. моменты кол-в движения относительно связанных с телом осей х, у, z (z — ось вращения), равные:

и кинетич. энергий

где I_x — осевой, а 1_хz, I_yz — центробежные моменты инерции.

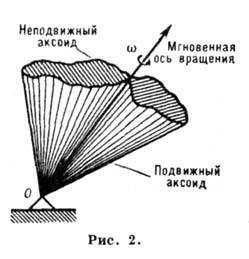
2) В. д. вокруг точки (или сферич. движение) — движение твёрдого тела, имеющего одну неподвижную точку 0 (напр., движение гироскопа ,закреплённого в кардановом подвесе). Каждая из точек тела при этом В. д. перемещается по поверхности сферы с центром в точке 0. В. д. тела вокруг точки слагается из серии элементарных или мгновенных В. д. вокруг мгновенных осей вращения, проходящих через эту точку. Мгновенная ось вращения непрерывно изменяет своё положение как по отношению к системе отсчета, в к-рой рассматривается движение тела, так и в самом теле, образуя при этом 2 конич. поверхности, наз. соответственно неподвижным и подвижным аксоидами. Качением подвижного аксоида по неподвижному можно осуществить геом. картину движения тела в этом случае (рис. 2).

Тело с неподвижной точкой имеет 3 степени свободы, и его положение по отношению к данной системе отсчёта определяется тремя параметрами, напр. Эйлера углами . Закон движения тела задаётся в этом случае ур-ниями

Кинематич. характеристиками движения являются вектор угл. скорости , направленный в каждый момент времени вдоль мгновенной оси вращения, и вектор угл. ускорения , направленный параллельно касательной к годографу вектора. Если движение задано ур-ниями (*), то проекции вектора на прямоугольные оси Oxyz, жёстко связанные с движущимся телом, определяются кинематич. ур-ниями Эйлера

I

где — производные от углов Эйлера по времени t. Векторы линейной скорости и ускорения любой точки тела равны

где — радиус-вектор, проведённый в данную точку тела из неподвижной точки 0. Проекции вектора v на оси Oxyz определяются ф-лами Эйлера

Осн. динамич. характеристиками тела с неподвижной точкой 0 являются моменты количеств движения относительно гл. осей инерции х, у, z, проведённых в точке 0:

и кинетич. энергия

где I_x, I_y, I_z — моменты инерции тела относительно упомянутых гл. осей; — проекции на эти оси. Кол-во движения тела при любом виде движения равно , где т — масса тела, — скорость центра масс.

Теория В. д. имеет важные приложения в небесной механике, внеш. баллистике, теории гироскопа, кинематике и динамике механизмов и машин и при решении др. техн. задач.

Лит.: см. при ст. Кинематика и Динамика. С. M. Тарг.

      Предметный указатель      >>   

www.femto.com.ua

Вращательное движение — «Энциклопедия»

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ твёрдого тела,

1) вращательное  движение вокруг неподвижной оси — движение тела, при котором какие-либо две его точки остаются неподвижными во всё время движения. Прямая, соединяющая эти две точки (и также остающаяся неподвижной), называется осью вращения. При таком движении все точки тела, не лежащие на оси, описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения, с центрами, находящимися на этой оси. Положение тела в пространстве определяется величиной угла поворота φ — двугранного угла, образованного неподвижной полуплоскостью, проходящей через ось вращения, и полуплоскостью, неизменно связанной с вращающимся телом и также проходящей через ось вращения (рис.).

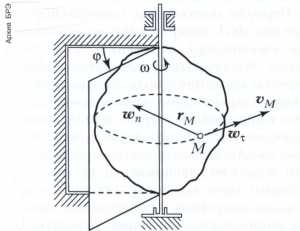Зависимость угла φ от времени φ = φ(t) выражает закон вращательного движения твёрдого тела. Производная dφ/dt = ω(t) называется угловой скоростью вращения тела, а производная da/dt = ε(t) угловым ускорением. Угловую скорость тела можно изобразить в виде вектора ω = ωk, где k — единичный вектор оси вращения. Тогда вектор скорости v_M произвольной точки М тела можно представить в виде векторного произведения:

Реклама

v_M = ω x r_M,

где  r_M — радиус-вектор точки М в неподвижной системе координат.

Величина скорости ν_Μ = ωr, где r — радиус окружности, по которой движется точка М. Вектор ускорения ν_Μ точки М вращающегося тела представляется в виде суммы w^τ_M и нормального wⁿ_M ускорений: w_M = w^τ_Μ + + wⁿ_M. Величины этих ускорений соответственно равны w^τ_M = er, wⁿ_M = ω²r.

2) вращательное движение вокруг неподвижной точки — движение тела, при котором одна из его точек остаётся неподвижной, а все другие точки тела могут двигаться лишь по сферам с общим центром в неподвижной точке. При таком вращательном движении тела в каждый момент времени скорости его точек оказываются такими, как если бы тело совершало вращательное движение вокруг некоторой оси. Это означает, что существуют такие точки тела, скорости которых в данный момент времени равны нулю. Эти точки образуют мгновенную ось вращения тела, вдоль которой направлен вектор угловой скорости ω. С течением времени эта ось непрерывно изменяет своё положение. При этом скорость любой точки М тела определяется по формуле (1).

В. М. Морозов.

knowledge.su

Вращательное движение

Вращательное движение является периодическим движением.

Период обозначается буквой T.

Чтобы найти период обращения, надо время вращения разделить на число оборотов:

Физическая величина, равная отношению числа полных оборотов тела ко времени, в течение которого эти обороты совершены, называется частотой вращения.

Частота вращения обозначается буквой n.

Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:

Частота вращения и период обращения связаны друг с другом как взаимообратные величины: Период измеряется в секундах: [T] = 1 с.

Единица частоты – секунда в минус первой степени: [n] = 1 с^–1.

Эта единица имеет собственное название – 1 герц (1 Гц).

Проведем аналогию между вращательным и поступательным движениями.

Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.

Тела, совершающие вращательное движение поворачиваются на некоторый угол.

Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.

Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:

Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.

Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.

Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1

Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.

Характеристикой равнопеременного поступательного движения является ускорение:

Соответственно, для вращательного движения можно ввести величину, определяемую отношением изменения угловой скорости ко времени, в течение которого это изменение происходит – угловое ускорение: Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени. Чтобы получить единицу углового ускорения, нужно в его определяющую формулу подставить единицы угловой скорости 1 рад/с и времени – 1 с. Получаем:

Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении

Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:

Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:

Метод, который использовался в данном случае, называется методом аналогий.

Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути. Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.

Линейная скорость точки направлена по касательной к окружности, по которой она движется.

Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.

Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.

За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости

Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:

При равномерном вращении скорость меняется по направлению, но не изменяется по величине.

Поскольку всякое изменение скорости характеризуется понятием ускорения, то для равномерного вращения следует ввести еще одно ускорение, изменяющееся не по величине, а по направлению. Это ускорение называют центростремительным.

Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.

Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости к направлению на центр вращения.

При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.

Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).

Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.

Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и

Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:

Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим

Разделив правую и левую части последнего уравнения на t, получим:

Отсюда Таким образом,

Полученная формула является формулой для расчета центростремительного ускорения.

Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:

files.school-collection.edu.ru