Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами
Курс математики в выпускном классе посвящен изучению степеней и корней, знакомству с показательной и логарифмической функцией, интегралами и элементами математической статистикой. Отдельное внимание в 11 классе посвящено повторению изученного за весь курс математики и подготовке к грядущему экзамену.
В связи с этим, для учеников 11 класса особенно важно участие в олимпиадах по математике и дополнительные занятия, посвященные решению заданий различной сложности.
На этой странице собраны задания для подготовки к олимпиаде по математике для 11 класса. Представлены уравнения, задачи и математические загадки с ответами и решениями. Этот материал может быть использован учителями или репетиторами для повышения уровня знания учеников.
Уравнения
1. Решите уравнение: = 3
2. Решите уравнение: ( − 8)² = ( + 9)²
3. Решите уравнение: log2 (5 + ) = log2 (1 − ) + 1
4. Решите уравнение: log5 ( + ) = log5 ( + 9)
5. Решите уравнение: log2 (4 − ) = 7
6. Решите уравнение: − + 72 = 0
7. Решите уравнение: ( + 7)² = ( − 1)²
8. Решите уравнение: ( − 8)² = ( − 2)²
9. Решите уравнение: ( − 6)² = −
10. Решите уравнение: + 9 = ( + 9)²
Задачи
Задача №1
Докажите, что уравнение xy = 2006 (x + y) имеет решения в целых числах.
Задача №2
Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.
Задача №3
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.
Задача №4
Докажите неравенство −< 1/6 на луче [1/4; + ∞).
Задача №5
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.
Математические загадки
Загадка №1
Сколько лет человеку, если в 2012 году его возраст оказался равным сумме цифр года его рождения.
Загадка №2
Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. Каждый участник решил не более шести задач. Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими. Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.
Загадка №3
Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?
Загадка №4
В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.
Загадка №5
Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800.
Чему равна сумма цифр числа 3n?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | 6 | 8,5 ∈ [8;9) | − 0,25 | 1,8 | -124 |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | 9; 8 | -1,5 | 1 | -6 | -4 |
Ответы к задачам
Задача 1
Преобразуем уравнение к следующему виду: (x – 2006)(y − 2006) = 20062. Уравнение имеет решения, например, x = y = 4012.
Задача 2
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos² x = (1 + cos 2x)/2, cos x = − cos (π − x), cos x + cos y = (2cos((x + y)/2)) cos((x − y)/2), получим справедливое тождество.
Задача 3
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 . Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О.
Высота «горки» из четырех шаров равна сумме OD + 2R = 2R + 1
Задача 4
Пусть = −. Тогда = − и с помощью метода интервалов получаем, что < 0 при всех >2/9. Но 1/4>2/9, следовательно, функция убывает на луче [1/4; +∞]. Это значит, что − < 1/16 − 3/64 = 1/64 < 1/64.
Задача 5
Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4. Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
Ответ: 175 центов
Ответы на загадки
Загадка 1
1 вар. Человек родился в 19mn году, тогда
2012 − 19mn= 1 + 9 + m + n
2012 − 1900 − m − n = 10 + m + n
102 = 11m + 2n
m = 8, n = 7, значит 1987 год, ему 25 лет.
2 вар. Человек родился в 200n году, тогда
2012 − 200n = 2 + n
2012 − 2000 − n = 2 + n
12 − 2 = 2n
n = 5, значит 2005 год, ему 7 лет.
Загадка 2
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.
Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).
Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.
Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.
По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 × 10 + 21 × 10 < 21²).
Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.
Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.
Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.
Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.
Загадка 3
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует
Загадка 4
Найдем произведение всех 25 чисел, записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек. Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1. А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50). Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число. А это значит, что сумма 50 написанных произведений не может равняться нулю.
Загадка 5
Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n.
Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда.
Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Олимпиадные задания по математике 10-11 класс
Просмотр содержимого документа
«10 и 11 классы »
Просмотр содержимого документа
«10 класс решение»
10 класс
Решения
Решение.
, т.к. первое слагаемое – это произведение трех последовательных натуральных чисел, т.е. оно кратно 3, а второе слагаемое содержит множитель 3, значит и вся сумма кратна 3.
Решение.
Проведем BK параллельно CD. Заметим KD || BC, KB || DC, следовательно, KBCD параллелограмм и KD = BC =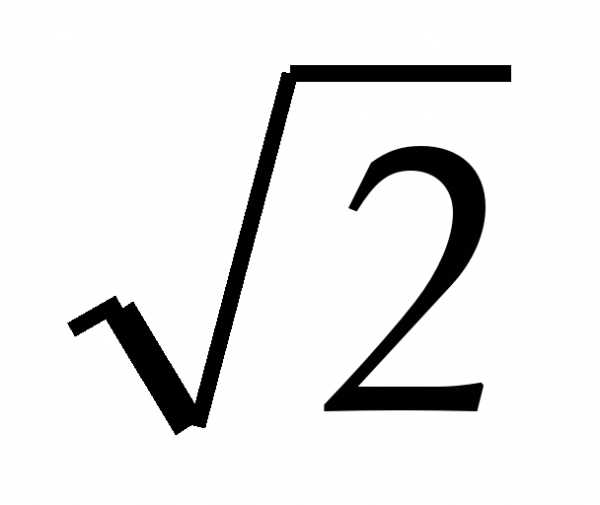 . AD – секущая параллельных прямых BK и CD, следовательно AKB =ADC = 30°.
. AD – секущая параллельных прямых BK и CD, следовательно AKB =ADC = 30°.
Далее найдем длину отрезка AK = AD – KD = . Боковую сторону AB теперь можно найти по теореме синусов для треугольника ABK: . При этом ABK = 180° – AKB – BKA = 180° – 30°– 15° = 135°.
И sin 135° =  . Теперь можно найти AB, она получается равной 1.
. Теперь можно найти AB, она получается равной 1.
Ответ: 1.
Ответ: на семь слагаемых.
Решение. Приведём пример разбиения числа 96 на семь слагаемых:
9 6 = 2 + 5 + 7 + 11 + 13 + 17 + 41.
Если слагаемых больше, то среди них не менее восьми нечётных (если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны. Но сумма восьми наименьших нечётных простых чисел равна 98.
Решение.
| Имя | Белое платье | Красное платье | Голубое платье | Туфли |
| Тамара | — | + | — | Красные |
| Лида | + | — | Голубые | |
| Валя | + | Белые |
Ответ: у Тамары были красные туфли и платье, у Вали – белые туфли и голубое платье, у Лиды – белое платье и голубые туфли.
Ответ: х = 95, у = 0, z = 94 или х = 31, у = 2, z = 32.
Решение. Вычтя из второго уравнения первое, получим (х — z)(1 — у) = 1.
По условию, х, у, z целые, тогда возможны два случая:
1) х– z = 1, 1 – у = 1, т. е. у = 0. Подставив значение у в систему, получим: z =94, x=95.
2) х –z = -1, 1 – у = — 1, т. е. z = х +1, у = 2. Подставим найденные значения у и z в первое уравнение, получим 2х + х +1 = 94, х = 31. Отсюда z = 32 .
Просмотр содержимого документа
«11 класс решение»
11 класс
Решение
Ответ. в 17.00.
Решение. Расстояние между Мишей и Колей и их скорости не меняются, а скорости Васи и Пети равны. Вася встретил Колю через 2 часа после Миши, значит, Петя встретят Колю тоже через 2 часа после Миши, т. е. в 17.00.
Ответ. 17.
Решение. Так как из 18 шаров найдется хотя бы один синий, то красных не более 17, а из любых 10 шаров найдется хотя бы один красный, то есть синих не более 9. Так как всех шаров 26, то синих – 9, а красных – 17.
Ответ. 70 кг
Решение. 5 процентов от 30 кг —  = 1,5 кг соли в 30кг морской воды,
= 1,5 кг соли в 30кг морской воды,
Х л добавили, стало (х+30)л. Х+30-100 процентов, 1,5 -1,5 процентов, тогда х=70
Ответ:
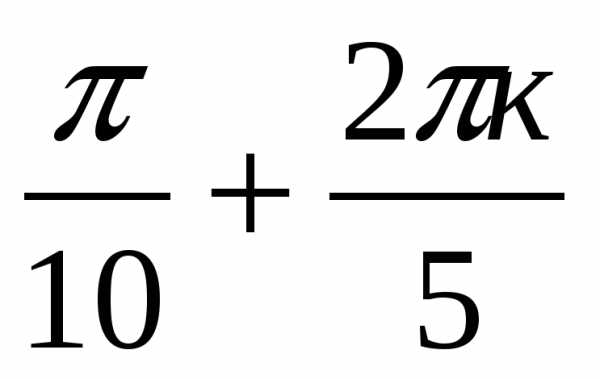 , k꞊1+5t, t
, k꞊1+5t, t
 .
.
Решение. tgx ctgx ꞊ sin5x
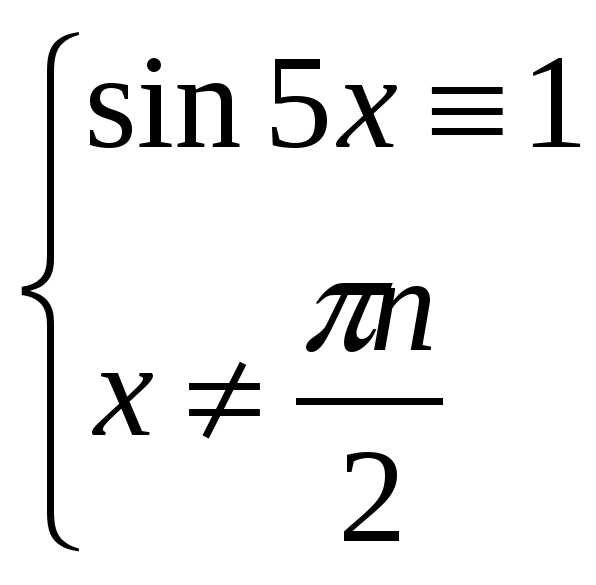 ,
, 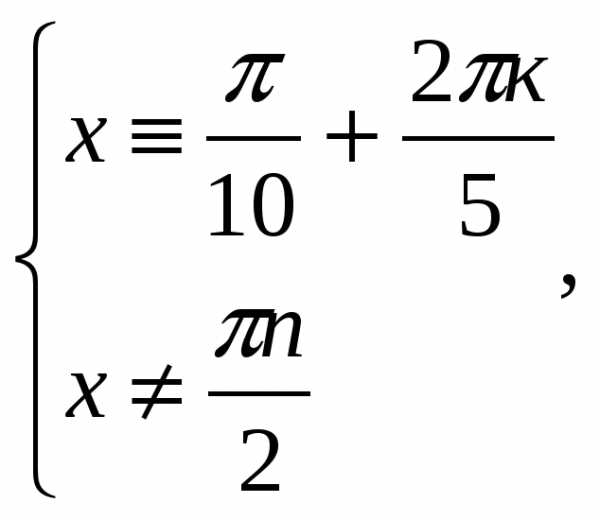 k
k
 , n
, n

Найдем теперь такие k, при которых 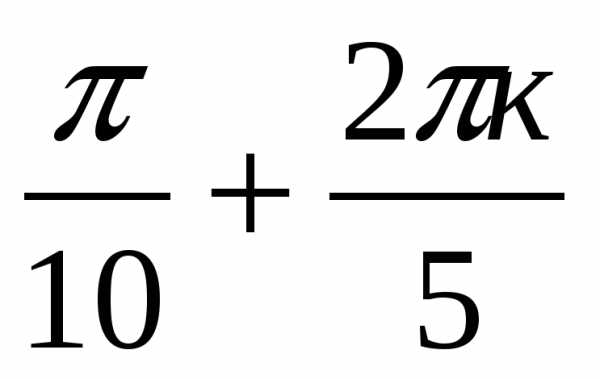 ꞊
꞊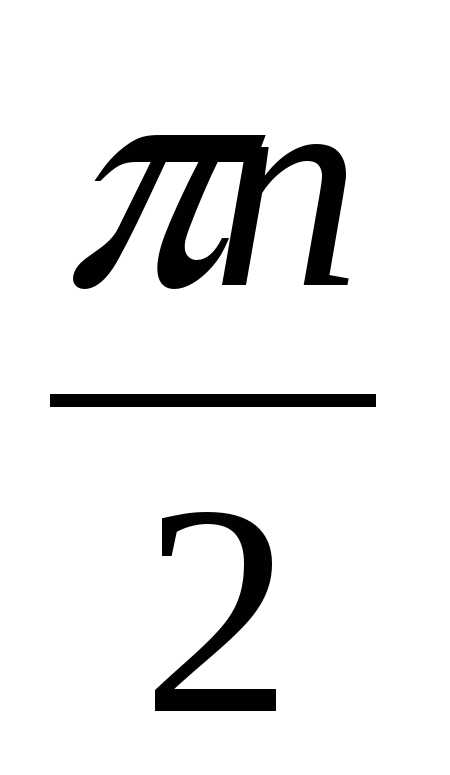 . Это уравнение перепишем в виде 5n-4k꞊1.Частное решение последнего уравнения
. Это уравнение перепишем в виде 5n-4k꞊1.Частное решение последнего уравнения
n0꞊1, k0꞊1,тогда k꞊1+5t, t
 . Итак,
. Итак, 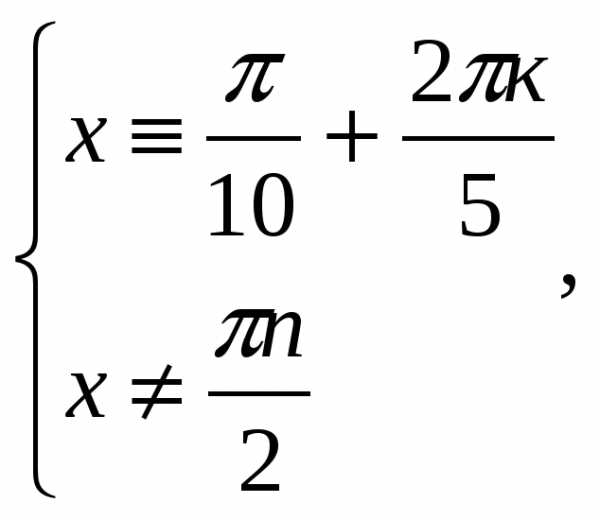
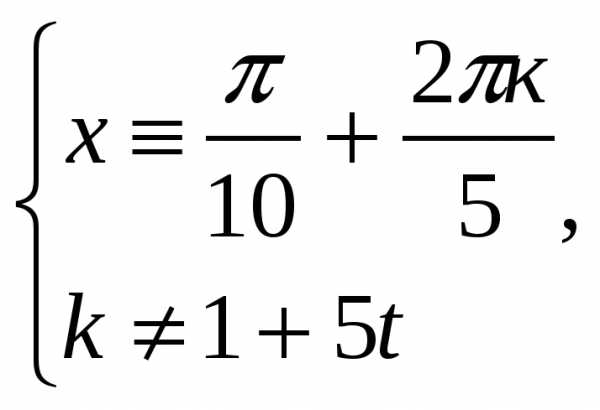 k
k
 , t
, t

Ответ:

Решение. Обозначим длину отрезка AB за 1, тогда SA=2. Найдём прежде всего длины отрезков BD и SD. Пусть BD=x. Тогда, применяя теорему Пифагора к треугольникам ABD и ASD, получаем AD²=1–x² = 4 – (2–x)², BD=x=1/2. Далее в треугольнике BMD BM꞊ и, для того чтобы воспользоваться теоремой косинусов, достаточно найти косинус угла MBD. Но из прямоугольного треугольника SBM получаем: cos SBM ꞊
и, для того чтобы воспользоваться теоремой косинусов, достаточно найти косинус угла MBD. Но из прямоугольного треугольника SBM получаем: cos SBM ꞊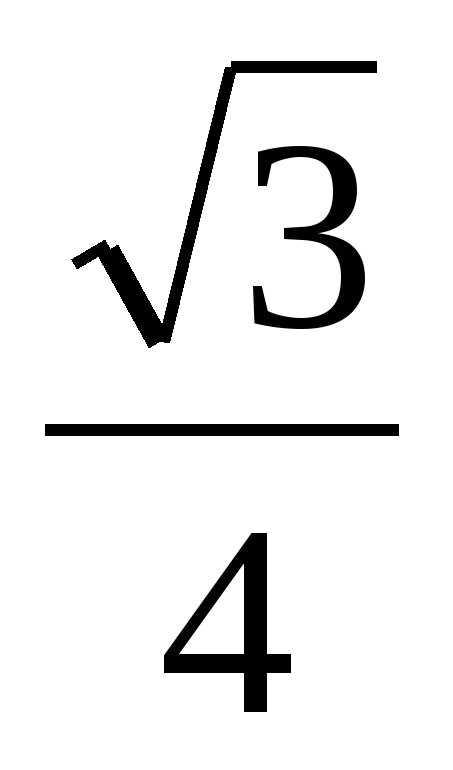
DM ² ꞊꞊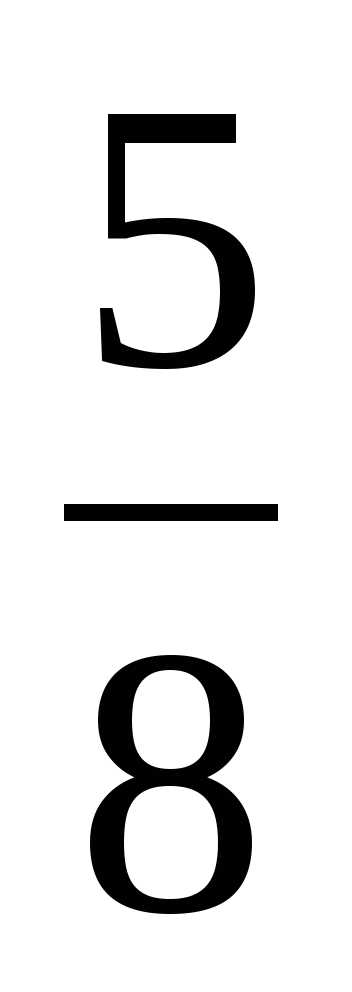 , DM ꞊
, DM ꞊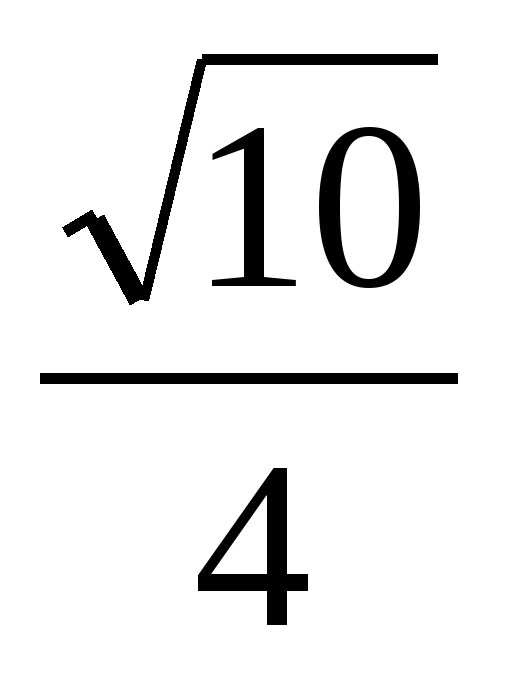
multiurok.ru
Своя игра по математике 10–11-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (12,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Оформление зала:
“Математика принадлежит к числу тех наук, которые ясны сами по себе”. (Якоби К.)
“Высшее значение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает”. (Винер Н.)
“Жизнь украшается двумя вещами: занятием математикой и её преподаванием”. (Пуассон С.Д.)
Цели:
- формирование и развитие познавательной активности школьников;
- совершенствование знаний, умений и навыков по математике;
- развитие внимания, памяти, абстрактного мышления;
- воспитание интереса к математике через нестандартные и занимательные задания.
Оборудование: мультимедийный проектор, экран, компьютерное оснащение, доска для отражения набранной суммы баллов для каждой команды
Сценарий проведения аналогичен телевизионной игре с одноименным названием. Викторина, проводится для учащихся 10 — 11 классов во время проведения декадника по математике и информатике. В игре принимают участие 3 команды (от каждого класса по 4 -5 участников). Каждая команда выбирает себе название.
Вместо денег учащиеся зарабатывают баллы, учет которых ведёт счётная комиссия. Команда набравшая наибольшее количество баллов, становится победителем игры.
Правила игры
Задача каждой команды набрать как можно большее количество баллов. Для этого необходимо правильно ответить на вопросы 2-х отборочных туров и в финальной игре не только правильно ответить, но и сделать большую ставку на свой ответ.
В отборочных турах каждый вопрос имеет свою стоимость, на обдумывание дается одна минута, отвечает та команда, которая быстрее поднимет руку. Если команда ответила правильно, то она выбирает следующий вопрос. На вопрос-аукцион право ответа имеет та команда, которая назначит большую сумму, если на счету игроков сумма, меньшая чем стоимость вопроса, то они могут предложить только номинал (стоимость вопроса). На вопрос кот в мешке отвечает та команда, которой отдает это право команда, выбравшая вопрос.
Подсчёт ведёт счетная комиссия из числа преподавателей школы и приглашенных они ведут подсчет баллов, если команда отвечает правильно – баллы прибавляются, если неправильно – вычитаются.
Ход игры
Здравствуйте, дорогие ребята и взрослые! Сегодня мы проводим викторину “Своя игра!”. Цель игры – популяризация знаний по предмету Математика. Наша цель узнать, кто из вас имеет больше всего знаний по этому предмету. Мы проверим ваши знания по математике. Победители будут награждены дипломами и призами. Внимание! Объявляю участников игры! (Представление команд – название команды и выбор капитана команды).
Счетная комиссия, которая будет считать баллы – (назвать).
Итак, игроки готовы. Зрителей прошу не выкрикивать, не подсказывать, так как в этом случае ответ засчитан не будет, и баллы будут сняты.
I тур
Темы I тура: математические формулы, толкование математических терминов, единицы измерения, крылатые фразы.
| Темы | Стоимость вопроса | ||||
| Математические формулы | 100 | 200 | 300 | 400 | 500 |
| Толкование математических терминов | 100 | 200 | 300 | 400 | 500 |
| Единицы измерения | 100 | 200 | 300 | 400 | 500 |
| Крылатые фразы | 100 | 200 | 300 | 400 | 500 |
1. Математические формулы
1. Запишите формулу корней квадратного уравнения. Ответ: х1,2 = .
2. запишите формулы суммы и разности кубов двух чисел.
Ответ: a3 — b3 = ( a — b)( a2 + ab + b2)
3. Запишите формула Герона для вычисления площади треугольника.
Ответ: S =, где р — полупериметр
4. Запишите основное тригонометрическое тождество. Ответ: sin2+ cos2= 1
5. Кот в мешке. Запишите формулу куба суммы двух чисел.
Ответ: (a + b)3 = a3 + 3a2b + 3ab2 + b3.
2. Толкование математических терминов
1. Трапеция происходит от латинского слова “трапезиум” — столик.
От этого же слова происходит наше слово “ трапеза”, означающее стол.
2. Конус – это латинская форма греческого слова “конос”, что означает сосновую шишку.
3. Аксиома. В современном понимании аксиома — высказывание некоторой теории, принимаемое при построении этой теории без доказательства, т.е. принимаемое как исходное, отправное для доказательств других положений этой теории (теорем). Аксиомы называют также постулатами.
4. Гипотенуза. Гипотенуза — от греческого слова «гипотенуза», что означает «тянущаяся под чем-либо». Название происходит, очевидно, от способа построения прямоугольных египетских треугольников с помощью натягивания веревки. Евклид вместо термина «гипотенуза» так и писал: «сторона, которая стягивает прямой угол»).
5. Радикал – знак математического действия извлечения корня, также результат такого действия
3. Единицы измерения
1. Какую часть составляет 1 ар от гектара? Ответ: .
2. Что такое баррель? Чему он равен?
Ответ: Известно, что баррель единица измерения объёма нефти. Нефтяной баррель равен 158,988 куб. дм.
3. Вопрос аукцион. Назовите любые три старинные русские единицы измерения длины.
Ответ: аршин — старинная русская мера длины, равная, в современном исчислении 0,7112 м.
Сажень — одна из наиболее распространенных на Руси мер длины.
Малая пядь — расстояние между концами расставленных большого и указательного (или среднего) пальцев = 17,78 cm
Большая пядь — расстояние между концами большого пальца и мизинца (22-23 см.).
Верста — старорусская путевая мера верста равнялась 500 саженей, в современном исчислении - 213,36 x 500 = 1066,8 м.
Локоть равнялся длине руки от пальцев до локтя.
Вершок равнялся 1/16 аршина, 1/4 четверти. В современном исчислении — 4,44 см.
Меры длины (употреблявшиеся в России после «Указа» 1835 г. и до введения метрической системы):
1 верста = 500 саженей = 50 шестов = 10 цепей = 1,0668 километра
1 сажень = 3 аршина = 7 фут = 48 вершков = 2,1336 метра
Косая сажень = 2,48 м.
Маховая сажень = 1,76 м.
1 аршин = 4 четверти (пяди) = 16 вершков = 28 дюймов = 71,12 см
(На аршин обычно наносили деления в вершках)
1 локоть = 44 см (по разным источникам от 38 до 47 cm)
1 фут = 1/7 сажени = 12 дюймов = 30,479 см
4. В некоторых зарубежных магазинах говорят: » Отпустите, пожалуйста,
тридцать декаграммов сыра». Сколько это граммов?
Ответ: 300 грамм. (Декаграмм — 10 граммов.)
5. Сколько литров воды в 1 куб. дециметре? Ответ: 1 литр.
4. Крылатые фразы
Назовите автора этих строк?
1. Математика – царица наук, арифметика – царица математики. Ответ: (К.Ф. Гаусс)
2. Математику уже затем учить надо, что она ум в порядок приводит.
Ответ: (М.В. Ломоносов)
3. Вдохновение нужно в геометрии не меньше, чем в поэзии. Ответ: (А.С. Пушкин)
4. Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств. Ответ: (Л. Эйлер)
5. Кот в мешке. Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. Ответ: (Б. Паскаль)
II тур
| Темы | Стоимость вопроса | ||||
| Вычислительная техника | 100 | 200 | 300 | 400 | 500 |
| Великие математики | 100 | 200 | 300 | 400 | 500 |
| Математические развлечения | 100 | 200 | 300 | 400 | 500 |
| Задачи в стихах | 100 | 200 | 300 | 400 | 500 |
1. Вычислительная техника
1. Как называлась счётная доска у древних греков.
Ответ: Абамк (греч. , abakion, лат. abacus — доска) — счётная доска, применявшаяся для арифметических вычислений приблизительно с IV века до н. э. в Древней Греции, Древнем.
2. В 1662 году немецкий математик Г.Лейбниц разработал счетную машину, выполняющую все четыре арифметические действия и использующую двоичную систему счисления. Это счетное устройство использовали до середины 20 века.
Как назывался прибор, выполнявший все четыре действия, который был прототипом прибора созданного в 1673 году немецким физиком и математиком Готфридом Вильгельмом Лейбницем?
Ответ: Арифмометр (от греч. — “число”, “счёт” и греч. — “мера”, “измеритель”) — настольная (или портативная) механическая вычислительная машина, предназначенная для точного умножения и деления, а также для сложения и вычитания. Арифмометры, начиная с 1820, производились серийно и ими пользовались до 1960-х годов.
3. Как называется прибор, который использовали школьники для упрощения вычислений до изобретения микрокалькулятора?
Ответ: Логарифмимческая линейка — аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб) и вычисление квадратных и кубических корней, вычисление логарифмов, тригонометрических функций и другие операции.
4. Назовите автора первой вычислительной машины, работавшей на двоичной логике и применявшее арифметику с плавающей запятой
Ответ: Изобретатель компьютера. Таким титулом награждён немецкий инженер Конрад Цузе его вычислительная машина Z1, стала первым вычислительным устройством, работавшим на двоичной логике и применявшее арифметику с плавающей запятой.
5. Кот в мешке. Назовите родоначальника науки кибернетика
Ответ: Норберт Виннер. Норберт Винер (англ. Norbert Wiener; 26 ноября 1894, Колумбия, штат Миссури, США — 18 марта 1964, Стокгольм, Швеция) — американский учёный, выдающийся математик и философ, основоположник кибернетики и теории искусственного интеллекта.
Поскольку родоначальником кибернетики в современном понимании этого слова является Норберт Винер, обратимся сначала к его собственному определению, которое он дал в своей знаменитой книге “Кибернетика, или управление и связь в животном и машине”.
Кибернетика — это новая область науки, изучающая процессы управления и связи, протекающие при любых обстоятельствах в различных системах. Основополагающим для кибернетики явилось открытие единства законов управления, действующих в различных системах - живых и неживых, физических и биологических, социальных и экономических.
2. Великие математики
1. Попробуй и отгадай.
Разгадал загадку круга,
Метод площадей нам дал,
Знаем мы, как в Сиракузах
Родину он защищал.
Свой народ спасал от бед,
Его имя …..
Ответ: (Архимед).
2. На острове Самос
Философ сей родился.
И во главу угла
Поставлены им числа.
И, говорят, за теорему
Принес богам быка он в жертву.
Был чемпионом Олимпиады,
Имел своих учеников.
Надеюсь, догадался каждый,
Что его имя ….. Ответ: (Пифагор)
3. Все, что раньше люди знали,
Он собрал в своих “Началах”.
Было их 13 книг,
Написал их все …. Ответ: (Евклид)
4. Очень слабым он родился,
Но науке все ж сгодился.
Открыл не кто иной,
А он притяжения закон.
Интеграл дал миру он,
Физик ….. Ответ: (Ньютон)
5. Вопрос аукцион.
Математики начала
По обоям изучала
И влюбилась в ту науку.
Только вот какая штука.
Ведь в России в это время
Не пускали в вузы женщин.
Чтоб в математике достичь вершин,
Пришлось уехать девушке в Берлин,
И стать для этого фальшивою невестою,
Такой мы знаем …….
Ответ: Софью Ковалевскую
3. Математические развлечения
1. В эту игру умеют играть все. Это одна из древнейших игр. Для того, чтобы играть в нее, достаточно иметь лист бумаги и ручку. Наверное поэтому в нее играют на уроках тайком от учителя. Ответ: крестики, нолики
2. Древняя игра, берущая начало в Индии и имеющая многовековую историю; сочетает в себе элементы науки, искусства и спорта. Способствует развитию фантазии и концентрации внимания, воспитанию характера и воли, приучает логически мыслить.
Что это за игра?
Существует древняя легенда, которая приписывает создание шахмат некоему брамину. За свое изобретение он попросил у раджи (тот был в восторге от новой игры) незначительную, на первый взгляд, награду: столько пшеничных зерен, сколько покажет шахматная доска, если на первую клетку положить одно зерно, а потом количество зерен удваивать. Оказалось зерен потребуется 18446744073709551615 (18 квинтильонов 446 квадрильонов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615). Этого количества не могло быть на всей планете. Ответ: Шахматы
3. Жил – был игрок, он был далек от всякой науки
Любой урок ему не впрок, ему б монетку в руки
Что в жертву рок его обрек не мог он знать заранее
Один бросок, другой бросок – и выигрыш в кармане!
Приходит срок и наутек пускается удача…
Один бросок, другой бросок – и выигрыша нету!”
Какова вероятность выигрыша при игре “Орлянка» ?
Ответ: 0,5 Орлянка — старинная азартная игра, распространённая во многих странах.
Смысл игры заключается в следующем: бросают монету любого номинала и тот, кто угадает, какой стороной она упадёт, выигрывает её.
Так как вероятность выпадения одного из двух вариантов одинакова, похожим способом иногда пользуются, когда нужно принять решение. Например, перед началом футбольного матча судья подкидывает монетку и таким образом определяется, на какой половине поля начнёт игру та или иная команда.
4. Кот в мешке. В эту игру играли еще египетские фараоны, правда, она несколько отличалась от современной. Затем игра проникла в Грецию и в Древний Рим. Предметы этой игры были найдены в гробнице Тутанхамона. Появление этой игры на Руси связано с именем Владимира Мономаха.
Ответ: Шашки — одна из самых древних игр. Известно, что ими увлекались еще египетские фараоны.
5. В 2004 году исполнилось 30 лет с тех пор, как весь мир развлекается этой игрой головоломкой. Конечно, пик популярности ее прошел, но если предмет этой игры попадет в руки думающего человека, он не откажется привести его в порядок. Назовите профессию и родину изобретателя этой игры.
Ответ: Эрно Рубик (Эрнё Рубик; венг. Rubik Erno, род. 13 июля 1944, Будапешт, Венгрия) — венгерский изобретатель, скульптор и профессор архитектуры. Всемирно известен благодаря своим объемным головоломкам и игрушкам, к числу которых принадлежит Кубик Рубика (1974). Кубик Рубика
Но рекорды популярности из всех головоломок побил «Кубик Рубика», изобретенный в 1974 году венгром Эрне Рубиком. Пластмассовый куб из 26 малых кубиков, вращающихся вокруг невидимых осей, нужно было привести в состояние, когда каждая грань состоит из одноцветных квадратов. Число состояний куба равнялось 43 252 003 274 489 856 000, при этом игрушку можно было собрать всего за 29 ходов. Внутри кубика поместили цилиндрический механизм, скрепляющий кубики, но позволяющий им вращаться. Побочным эффектом компромисса между плотностью скрепления и свободной кручения стал характерный хруст. «Кубик Рубика» стал лидером по количеству продаж. По всему миру было продано 300 млн. штук. Популярность «кубик Рубика» была так велика, что в 1982 году в Будапеште прошло первое мировое первенство по сборке, а в Кноксвилле кубику даже соорудили памятник.
4. Шарады, мегаграммы
1. Вначале — двойка.
Далее — мужчина,
Высокого он титула и чина.
А слово целиком — обозначенье,
Дробящее на дозы обученье.
Ответ: параграф
2. Читаем мы направо смело —
Геометрическое тело.
Прочтём же справа мы налево —
Увидим разновидность древа.
Ответ: куб — бук
3. Предлог стоит в моём начале,
В конце же — загородный дом.
А целое мы все решали
И у доски, и за столом
Ответ: задача
4. Счастливой цифру ту считают,
При счете её применяют.
А “М” вот на “Т” поменяли —
И рыбы немало поймали.
Ответ: Семь — сеть
5. Я – цифра меньше 10,
Меня тебе легко найти.
Но если букве “Я”
Прикажешь рядом встать:
Я – все: отец, и ты, и дедушка, и мать!
Ответ: (Семь – семья).
Финал
Каждая команда устанавливает свою цену (цена не может быть больше количества баллов набранных командой) за ответ на вопрос финального тура, записывает её на листках и передают счётной комиссии.
«Задача о гусях»
Гуси с юга к нам летели
На зеленом лугу сели.
Их увидел Елисей:
— Добрый день вам, сто гусей.
— Нас не сто, — сказал вожак,
Уважаемый гусак.
— Сколько ж вас, — он вопрошает.
— Кто сметливый, — отгадает.
Если к нам добавить столько ж
И полстолько с четверть столько
Да гуся, что сел на стог,
То нас будет ровно сто.
Вот скажите-ка, друзья,
Какова гусей семья?
Ответ: 36 гусей.
Подведение итогов игры.
Награждение победителей.
xn--i1abbnckbmcl9fb.xn--p1ai
Тест по математике с ответами (11 класс)
1.Умножьте 16*16,после чего из полученного выведите квадратный корень. Из результата вычтите 156.
А)10(верный)
Б)156
В)308
2.Чему равно число Pi(5 знаков после запятой)
А)4.15163
Б)3.14159(верный)
В)1.19514
3.Котангенс это отношение…
А)sin/tan
Б)cos/sin(верный)
В)tan/cos
4.Простое число делится на…
А)Себя и единицу(верный)
Б)Себя и 5
В)себя и 2
5.Лента Мёбиуса…
А)Имеет начало, но не имеет конца
Б)Не имеет ни начала, ни конца(верный)
В)Не имеет начала, но имеет конец
6.Прямой угол в угловых минутах равен…
А)324000
Б)90
В)5400(верный)
7.Минимальное кол-во прямых углов в прямоугольной трапеции
А)1(верный)
Б)2
В)3
8.Кронциркуль используется для измерения…
А)Это то же, что и обычный циркуль
Б)Больших расстояний
В)Малых расстояний(верный)
9.Вычлените из 25 квадратный корень, после чего умножьте результат на 500 и разделите на 200
А)2.5(верный)
Б)25
В)1.5
10.Обьём-это…
А)х2
Б)х3(верный)
В)х4
11.Какое из этих чисел не является простым?
А)3
Б)11
В)18(верный)
12.Парабола-это кривая…
А)Второго порядка(верный)
Б)Третьего порядка
В)Четвёртого порядка
13.tan555=?
А)0.26795(верный)
Б)1.42815
В)0.08749
14.Двоичная система исчисления использует цифры…
А)0 и 2
Б)0 и 1(верный)
В)0 и 5
15.1% от 1225=?
А)12255
Б)1.225
В)12.25(верный)
16.Минута обозначается как…
А)'(верный)
Б)»
В)’»
17.Минута это…
А)1/10 градуса
Б)1/60 градуса(верный)
В)1/3600 градуса
18.2 в 5 степени=?
А)10
Б)32(верный)
В)128
19.Число 19 является…
А)Простым числом(верный)
Б)Сложным числом
В)Архисложным числом
20.Полный угол=?
А)Pi rad
Б)1/2 Pi rad
В)2Pi rad(верный)
21.Как расшифровыется СГС?
А)Сантиметр-Грамм-Секунда(верный)
Б)Стандарт Геометрической Синусоидности
В)Сумма-График-Синус
22.Какой из этих законов гласит:»От перемены места слагаемых сумма не меняется»?
ПРИМЕЧАНИЯ:Pi(число Пи),Rad(Радиан),sin(Синус),cos(косинус),tan(тангенс)
А)Дистрибутивный закон
Б)Ассоциативный закон
В)Коммутативный закон(верный)
23.Абелева группа это…
А)Коммутативная группа(верный)
Б)Группа простых чисел
В)Соединение нескольких групп в одну
24.Определение константы
А)Переменная
Б)Постоянное число, не изменяющееся в рамках математического процесса(верный)
В)Второе название синусоида
25.Иррациональное число…
А)Является вещественным и может быть представлено как дробь
Б)Рациональная дробь, где первое число целое, а второе натуральное
В)Нерациональное число, которое не может быть представлено как дробь(верный)
likedoc.ru
Викторина по математике 11 класс с ответами — 22 Ноября 2014
Знаете ли вы, что такие, на первый взгляд, скучные и трудно запоминающиеся математические термины очень часто используются в повседневной жизни людьми, далекими от математической науки?Веселая «математическая» викторина докажет это!
Вопросы:
1. Что является «нулем» на карте железных дорог России? (Москва: по железным дорогам России все расстояния считаются от Москвы, кроме Октябрьской железной дороги, где отсчет идет от Санкт-Петербурга.)
2. Где находится «нуль» в вашем городе? (В Воронеже это главный почтамт: от него считаются все расстояния на автодорогах.)
3. В каком европейском городе находится памятник нулю? (В центре Будапешта, столицы Венгрии. Это точка, от которой отсчитываются расстояния в Венгрии.)
4. Названия многих русских городов произошли от числительных: Семипалатинск, Семилуки, Пятигорск. А какой город был назван в честь наибольшего числа? (Тюмень, от тюркского слова «тумен» – 10 000.)
5. Какой город России назван «в честь» знака математической операции? (Минусинск, Красноярский край.)
6. Назовите «математические» растения. (Тысячелистник, столетник, золототысячник.)
7. В какие «цифры» люди одеваются? (В костюм-двойку и в костюм-тройку.)
8. Какие цифры «пишут» летчики в небе? (Восьмерки.)
9. Назовите «математические» упражнения «школы» фигурного катания. (Круг, тройка, двукратная тройка, скобка, восьмерка.)
10. Какая цифра широко известна в мировой политике – да еще с эпитетом «большая»? («Большая восьмерка» – неформальный клуб президентов восьми государств: США, Великобритании, Франции, Германии, Италии, Японии, Канады, России.)
11. Цифра в классном журнале – это… (отметка).
12. Какое число можно найти в каждом автомобильном бензобаке? (Октановое число.)
13. Над каким предприятием можно увидеть вывеску с надписью «СТО»? (Над станцией технического обслуживания.)
14. Без чего не могут обойтись охотники, барабанщики и математики? (Без дроби.)
15. Что отличает один поезд от другого с точки зрения математика? (Номер.)
16. Какой математический знак напоминает движение губ верблюда, когда он жует жвачку? (Знак бесконечности. Чтобы в этом убедиться, сходите в зоопарк.)
17. Как называется математическое выражение типа А:А в спортивных играх? (Ничья.)
18. Что есть у каждого слова, растения и уравнения? (Корень.)
19. Чему равна колесная формула армейского восьмиколесного грузовика КамАЗ–6350? (8×8 – все восемь колес являются ведущими.)
20. Название какого государства скрывается в математическом выражении А3? (Куб А – Куба.)
21. С какой формулой нас познакомил Марк Захаров и Отар Мгалоблишвили? («Формула любви» – название кинофильма.)
22. Какой математический закон, известный всем с младших классов, стал популярной пословицей? (От перемены мест слагаемых сумма не изменяется.)
23. Какую формулу прославили Фанхио, Лауда, Сенна, Прост, Шумахер? (Автогонки «Формула–1».)
24. Какие мужские имена имеют «математическое» происхождение? (Константин, от латинского слова «constant» – стойкий, постоянный. Максим, от латинского слова «maximus» – самый большой, величайший.)
25. Какая школьная принадлежность сможет отвезти вас куда угодно? (Транспортир, ведь в нем спрятан транспорт.)
26. В каком слове можно найти целый метр букв О? (В слове «метрО».)
27. Какая цифра всегда катается в электричке? (Цифра три – элекТРИчка.)
28. Какая цифра красуется в центре каждой витрины? (Три – виТРИна.)
29. Что общего у числа и слова? (Слог СЛО – чиСЛО, СЛОво.)
30. Локоть человека является старинной мерой длины, а какая часть человека служит единицей времени? (Век – челоВЕК.)
31. Какую математическую фигуру украшают брильянтами? (Кольцо.)
32. Какой геометрической фигурой названа любовь в одной очень известной песне? (Кольцом. «Любовь – кольцо, а у кольца начала нет и нет конца».)
33. Эмблемой какого автомобиля являются четыре кольца? («Ауди».)
34. Какие геометрические фигуры дружат с солнцем? (Лучи.)
35. Какая геометрическая фигура нужна для наказания детей? (Угол.)
36. Какие геометрические фигуры есть у нас во рту? (Углы, угол рта.)
37. На какой угол поворачивается солдат по команде «кругом»? (На 180°.)
38. Какую форму имеет президентский кабинет в Белом доме США? (Овальный кабинет.)
39. Какие «математические» созвездия вы знаете? (Треугольник, Южный треугольник, Циркуль.)
40. Какую геометрическую фигуру прикрепляют к лацканам костюмов выпускников вузов? (Ромб. Значок в виде ромба.)
41. Как называется географическое кольцо? (Атолл – коралловое сооружение, имеющее форму сплошного или разорванного кольца, окружающего мелководную лагуну.)
42. А как называют военно-историческое кольцо? (Блокада.)
43. Какая дуга вошла в историю 20 века? (Курская дуга.)
44. Какой многоугольник является высоким военным начальством? (Пятиугольник, по-гречески – «pentagonon». Пентагон – здание военного министерства США близ Вашингтона в форме пятиугольника, в переносном смысле – военное ведомство США.)
45. На какой фигуре основана форма любой снежинки? (При всем разнообразии узоров, форма у всех снежинок одна и та же: любая снежинка – это шестиугольник, или гексагон.)
46. Какую форму имеют соты пчел и ос, ячейки глаз насекомых? (Форму правильного шестиугольника.)
47. Какую страну Европы ее жители называют «наш шестиугольник»? (Францию.)
48. Составление карты какой страны получило название «Великое тригонометрическое исследование»? (Индии, она на карте имеет форму треугольника.)
49. Какая объемная геометрическая фигура очень больно кусается, иногда со смертельным исходом? (Конус – хищный морской моллюск с конической яркой раковиной, имеющий ядовитую железу.)
50. Географический конус – это… (вулкан).
51. Вечнозеленый конус – это… (кипарис).
52. Какую математическую фигуру носят на голове мужчины? (Цилиндр.)
53. Многогранник из Египта – это… (пирамида).
54. Обманный финансовый многогранник – это… (пирамида).
55. Назовите «геометрический» вид тополя. (Пирамидальный тополь.)
56. Какую форму имеют бульонные кубики? (Форму параллелепипеда, а вовсе не куба.)
57. Какую форму имеет спасательный круг? (Приблизительно форму тора. Тор – геометрическое тело, образованное вращением круга вокруг не пересекающей его и лежащей в одной с ним плоскости прямой.)
58. Назовите музыкальную меру длины. (Ми-ля – миля.)
59. Имя какой сказочной героини произошло от названия единицы измерения длины? (Дюймовочка, от единицы измерения дюйм, который равен 2,54 см.)
60. Какая домашняя птица хорошо знает и очень часто называет единицу измерения земельной площади, равную 10 000 м2? («Га-га-га» – так гогочет гусь.)
61. Назовите меру для лиха и изюма. (Фунт. Выражения: «фунт лиха» и «фунт изюма».)
62. Как называется перпендикуляр к рельсам? (Шпала.)
63. Какие животные имеют ось симметрии? (ОСЬминог, лОСЬ.)
64. Какие две буквы каждое ребро геометрического тела сделают драгоценным? (Буквы С и Е: ребро – СЕребро.)
65. Как нужно уважительно обращаться к учителю на уроке геометрии? (Ваше ПреПОДОБИЕ!)
doshvozrast.ucoz.ru
|
РАЗРАБОТКИ |
11 классВ категории разработок: 136 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Диагностическая контрольная работа состоит из двух частей, включающих в себя 12 заданий. Часть 1 содержит 8 заданий базового уровня с кратким ответом. Часть 2 содержит 3 задания повышенного уровня сложности с кратким ответом и 1 задание с развёрнутым ответом. На выполнение работы отводится 90 минут.
Целевая аудитория: для 11 класса Данный тест можно предлагать учащимся в конце изучения темы. Уровень заданий средний. Тест содержит 11 заданий. Тест так же можно использовать для определении уровня изучения темы в индивидуальном порядке. Тест включает основные понятия, которые изучают по теме «Логарифмическая функция» Целевая аудитория: для 11 класса 2 варианта по 10 заданий. Есть критерии оценки работ и правильные ответы.
Источник: 4ege.ru Целевая аудитория: для 11 класса Подготовку к ЕГЭ по математике необходимо начинать заранее и заниматься постоянно. Эта дисциплина не терпит суеты и неточности. Важно четко понимать, что нужно знать на экзамене, и как решать задачи. Контрольно-измерительные материалы — 2018 содержат 20 заданий. Экзаменационная работа включает в себя один уровень, определяющий:
Целевая аудитория: для 11 класса 21 вариант! Секрет успешной подготовки к ЕГЭ по математике — это продуманная и системная работа. Важнейшим элементом подготовки является правильный подбор заданий. В подготовку должны быть включены все типы заданий, которые могут встретиться на экзамене. Все задания взяты из Официального Банка заданий ФИПИ, Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.
Целевая аудитория: для 11 класса На выполнение диагностической работы по математике даётся 45 минут. Работа состоит из двух частей, включающих в себя 8 заданий. Часть 1 содержит 7 заданий базового уровня сложности, проверяющих наличие практических математических навыков, знаний и умений. Ответом к каждому из заданий 1 — 7 является целое число или конечная десятичная дробь. Часть 2 содержит одно задание №8 — повышенного уровня сложности. При его выполнении надо записать полное решение и записать ответ.
Целевая аудитория: для 11 класса Экзаменационная работа включает в себя 20 заданий. На выполнение работы отводится 3 часа (180 минут). Содержание работы соответствует демоверсии ЕГЭ-2017 по математике (базовый уровень).
Целевая аудитория: для 11 класса Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развернутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Целевая аудитория: для 11 класса На выполнение диагностической работы по математике даётся 45 минут. Работа состоит из двух частей, включающих в себя 8 заданий. Часть 1 содержит 7 заданий базового уровня сложности, проверяющих наличие практических математических навыков, знаний и умений. Ответом к каждому из заданий 1 — 7 является целое число или конечная десятичная дробь. Часть 2 содержит одно задание №8 — повышенного уровня сложности. При его выполнении надо записать полное решение и записать ответ.
Целевая аудитория: для 11 класса На выполнение диагностической работы по математике дается 45 минут. Работа состоит из двух частей, включающих в себя 8 заданий. Часть 1 содержит 7 заданий (задания 1–7) базового уровня сложности, проверяющих наличие практических математических знаний и умений. Ответом к каждому из заданий 1–7 является целое число или конечная десятичная дробь. Часть 2 содержит одно задание №8 – повышенного уровня сложности. При его выполнении надо записать полное решение и записать ответ.
Целевая аудитория: для 11 класса |
Конкурсы Диплом и благодарность каждому участнику! |
www.uchportal.ru
