В чем измеряется сила индукционного тока – Физика 10-11 класс. Самоиндукция. Индуктивность. Энергия магнитного поля тока :: Класс!ная физика

Эдс индукции

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

— магнитный поток, — ток в контуре, — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током^[4]:

.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри

[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10⁹см)^[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz)^{[источник не указан 1017 дней]}. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)^[8]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года^{[источник не указан 1017 дней]}.

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре:  (1)  где коэффициент пропорциональности L называется

индуктивностью контура.  При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией.  Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

·c/А . 

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ₀μ(N²I/l)S . Подставив в (1), найдем  (2)  т. е. индуктивность соленоида зависит от длины

l солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида.  Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.  Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна  Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3)  где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем.  Если ток со временем увеличивается, то (dI/dt<0) и ξ _s>0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξ_s<0 т. е. индукционный ток имеет такое же направление, как и уменьшающийся ток в контуре, и замедляет его уменьшение. Значит, контур, обладая определенной индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока уменьшается тем сильнее, чем больше индуктивность контура.

 

42. Ток при размыкании и замыкании цепи.

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. , резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток

(внутренним сопротивлением источника тока пренебрегаем).

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент време­ни ток в цепи определяется законом Ома I=_s/R, или

(127.1)

Разделив в выражении (127.1) переменные, получим Интегрируя это уравнение по I (от I₀ до I) и 

t (от 0 до t), находим ln (I /I₀) = –Rt/L, или

(127.2)

где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что  есть время, в течение которого сила тока уменьшается в е раз.

Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше  и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э. д. с.  возникает э. д. с. самоиндукции препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома, или

Введя новую переменную преобразуем это уравнение к виду

где  — время релаксации.

В момент замыкания (t=0) сила тока 

I = 0 и u = –. Следовательно, интегрируя по и (от – до IR–) и t (от 0 до t), находим ln[(IR–)]/–= —t/, или

(127.3)

где — установившийся ток (при t).

Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению . Скорость нарастания тока определяется тем же временем релаксации =L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индук­тивность цепи и больше ее сопротивление.

Оценим значение э.д.с. самоиндукции , возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R₀ до R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток . При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение для

I₀ и , получим

Э.д.с. самоиндукции

т. е. при значительном увеличении сопротивления цепи (R/R₀>>1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I

1, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда   (1)  где L₂₁ — коэффициент пропорциональности. 

Рис.1

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй:    Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то    Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1

 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый:    Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е.   (2)  Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн).  Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ₀(N₁I₁/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф₂ = BS = μμ₀(N₁I₁/l)S 

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков,    Поток Ψ создается током I₁, поэтому, используя (1), найдем   (3)  Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,   

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

studfiles.net

Электромагнитная индукция

01. Электромагнитная индукция – это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Фарадеем в 1831 г.

Для демонстрации этого явления возьмем неподвижный магнит и проволочную катушка, концы которой соединим с гальванометром. Если катушку приблизить к одному из полюсов магнита, то во время движения стрелка гальванометра отклоняется – в катушке возбуждается электрический ток. При движении катушки в обратном направлении направление тока меняется на противоположное. То же самое происходит, если повернуть магнит на 180 градусов, не меняя направления движения катушки.

Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающий при движении проводника.

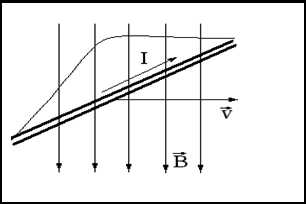
Рассмотрим случай, когда два параллельных провода АВ и CD замкнуты, справа – разомкнуты. Вдоль проводов может свободно скользить проводящий мостик BC. Когда мостик движется вправо со скоростью v, вместе с ним движутся электроны и положительные ионы. На каждый движущий заряд в магнитном поле действует сила Лоренца . На положительные ион она действует вниз, на отрицательные вверх. В результате электроны начнут перемещаться по мостику вверх, т.е. по нему потечет электрический ток, направленный вниз. Перераспределившись заряды создадут электрическое поле, которое возбудит токи и в остальных участках контураABCD.

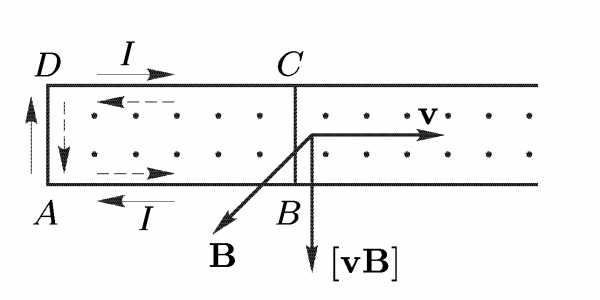
Сила Лоренца F в опыте играет роль сторонней силы, возбуждающей электрический ток.

02. Электродвижущая сила индукции (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока.

Знак минус поставлен потому, что стороннее поле направлено против положительного обхода контура.

Величина lv есть приращение площади контура ABCD в единицу времени, или скорость приращении этой площади. Поэтому равна

Основной закон электромагнитной индукции.(Дифференциальная форма закона электромагнитной индукции)

При движении замкнутого провода в магнитном поле в нем возбуждается электродвижущая сила, пропорциональная скорости приращения магнитного потока, пронизывающего контур провода.

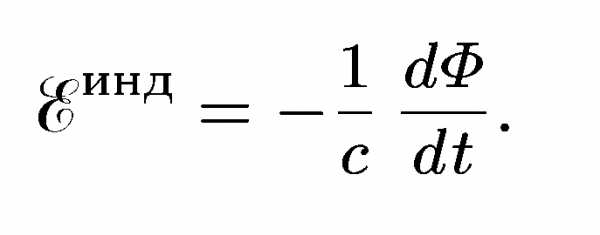
03. Правило Ленца (принцип Ле Шателье)

Индукционный ток всегда имеет такой направление, что он ослабляет действие причины, возбуждающий этот ток.

Возьмем в магнитном поле замкнутый проволочный виток, положительное направление обхода которого составляет с направлением поля правовинтовую систему. Допустим, что магнитный поток Ф возрастает. Тогда, согласно формуле 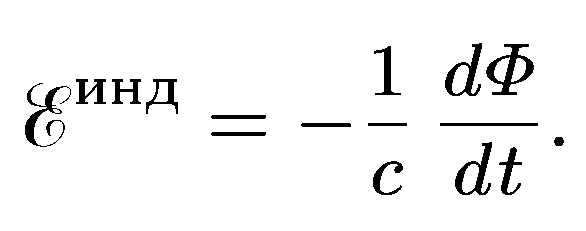, величинабудет отрицательна, а индукционный ток в витке потечет в отрицательном направлении. Такой ток, ослабляя внешнее магнитное поле, будет препятствовать возрастанию магнитного потока.

Пусть теперь магнитный поток Ф убывает. Тогда величина станет положительной, а индукционный ток в витке потечет в положительном направлении и будет препятствовать убыванию магнитного поля и магнитного потока.

04. Индуктивность проводов.

Рассмотрим тонкий замкнутый провод, по которому течет постоянный ток I. Внутри провода параллельно его оси проведем произвольный замкнутый математический контур s и установим на нем положительное направление. Если в пространстве нет ферримагнитных тел, то величина B(магнитное поле тока) и Ф(магнитный поток) будут пропорционально току.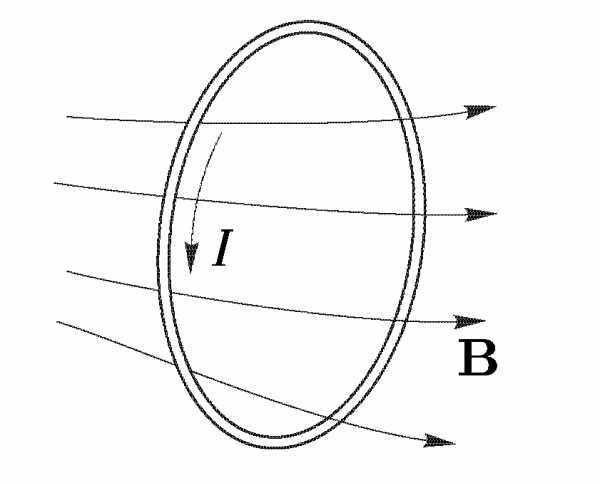

здесь — сила тока в гауссовской системе единиц, а- сила тока в системе СГСМ.

• — самоиндукция, или коэффициент самоиндукции провода. Он не зависит от силы тока, определяется только размерами и конфигурацией самого провода.

Пример: Вычислим индуктивность соленоида. Пусть — длина соленоида,- общее число витков,- площадь одного витка.

Индукция магнитного поля внутри соленоида

Магнитный поток через один виток равен , я черезвитков -т.е.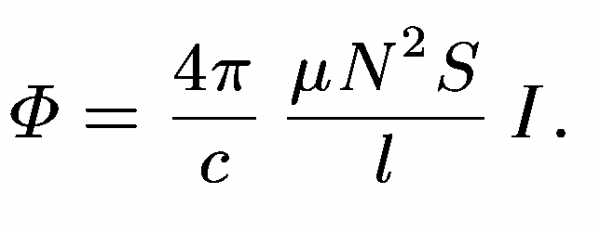

Получим индуктивность ( в сантиметрах)

Магнитный поток — это поток Ф вектора магнитной индукции B через конечную поверхность S. За единицу магнитного потока принимают максвелл.

Максвелл есть магнитный поток, создаваемый магнитным полем в один гаусс через перпендикулярную к нему площадь в один квадратный сантиметр.

05. Явления при замыкании тока

Процесс замыкания

Пусть цепь состоит из источника постоянного ЭДС, катушки самоиндукции и омического сопротивления. Полную индуктивность цепи обозначим через , а полное сопротивление– через . При замыкании ключа К ток не сразу достигает предельного значения, определяемого законом Ома, а нарастает постепенно. При этом возрастает также магнитный поток, пронизывающий контур цепи. Возникает электродвижущая сила индукции и соответствующий ей индукционный ток. Этот ток называют экстратоком замыкания. Согласно правилу Ленца направление экстратока замыкания противоположно направлению основного тока.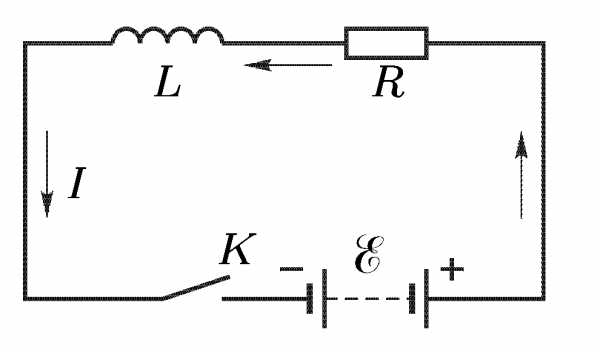

Сила переменного тока не обязательно должна быть одной и той же на всех участках провода, так как в отдельных местах возможно накопление зарядов. Однако мы рассмотрим здесь только такие переменные токи, которые меняются во времени сравнительно медленно. Тогда мгновенные значения токов во всех участках неразветвленной цепи с высокой степенью точности одинаковы, а магнитный поля внутри проводов могут вычисляться по закону Био и Савара, как если бы токи были постоянными. Такие токи называются квазистационарными.

Сила тока определяется выражением

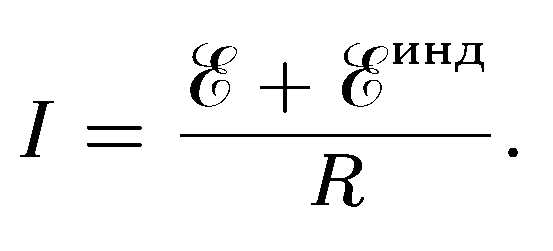
В практических единицах

Дифференциальное уравнение для квазистационарных токов

Если за время изменения тока провода не деформируются, то индуктивность , постоянна и может быть вынесена из-под знака производной

При постоянном значении общее решение этого уравнения имеет вид

Постоянная интегрирования C должна определяться из начального условия: в момент замыкания, т.е. при , то ток равен нулю. Используя это условие, находим. Эта формула применима в любой системе единиц.

Где — постоянная, имеющая размерность времени:

В гауссовской системе единиц:

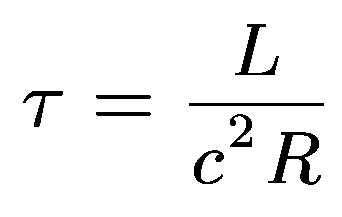
Полный ток I состоит из двух слагаемых, из которых второе, т.е. , определяет силу экстратока замыкания. Приэкстра ток стремится к нулю, а полный токI – к своему предельному значению . Таким образом, окончательное значение тока устанавливается постепенно. Быстроту установления определяется временем: по истечении временисила экстратока убывает враз.

06. Явления при размыкании тока

Ключ К сначала замкнут. Направление токов показаны сплошными стрелками. Общий ток распределяется между параллельно включенными самоиндукцией и омическим сопротивлением. Если внутреннее сопротивление батареи пренебрежимо мало, то ток в катушке самоиндукции будет равен. После размыкания ключа К замкнутым останется только контур ABCD. Первоначальный ток, существовавший в катушке самоиндукции, обладал определенным запасом магнитной энергии, которая исчезает не сразу. Магнитное поле начнет убывать. Это возбудит электродвижущую силу и индукционный ток в контуре ABCD. Такой ток называется экстратоком размыкания. Экстраток показан пунктирными стрелками. В катушке самоиндукции экстраток течет в том же направлении , что и первоначальный ток, в остальных участках контура ABCD— в противоположном направлении. Если — общее сопротивление контура ABCD, то сила тока определится из дифференциального уравнения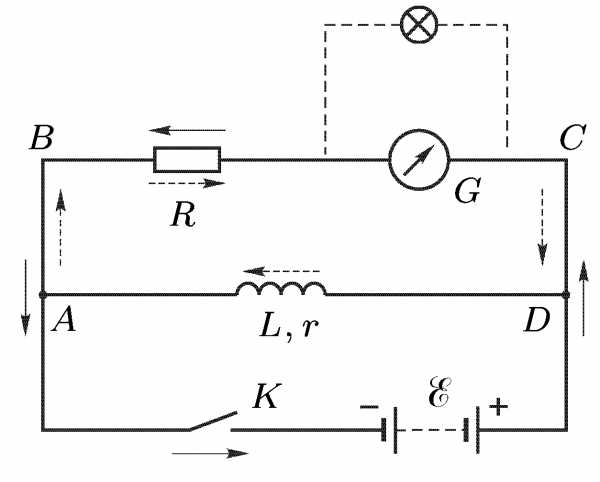

и начального условия: . Это дает, гдеопределяется прежним выражением. Электродвижущая сила индукции равна

Если , то эта величина может значительно превзойти ЭДС батареи. В этом причина электрического пробоя, наблюдающегося иногда при выключении тока в цепях, содержащих большие индуктивности.

Для демонстрации явления можно взять катушку длиной 50-60 см и диаметром 8-10 см сердечником из железных прутьев и обмоткой из нескольких слоев проволоки диаметром около 1 мм. Параллельно катушке присоединена лампочка. Лампочка рассчитана на напряжение, несколько превышающее ЭДС батареи. При замкнутой цепи лампочка горит тускло. При размыкании ключа К она ярко вспыхивает и даже может перегореть, так как ЭДС индукции превосходит в несколько раз ЭДС батареи.

Рассмотрим теперь два витка (или две катушки), по которым текут постоянные токи и. Установим произвольно на этих витках положительные направления обхода. Если в окружающем пространстве нет ферромагнетиков, то магнитные потоки через виткиипропорциональны токам и могут быть представлены в виде

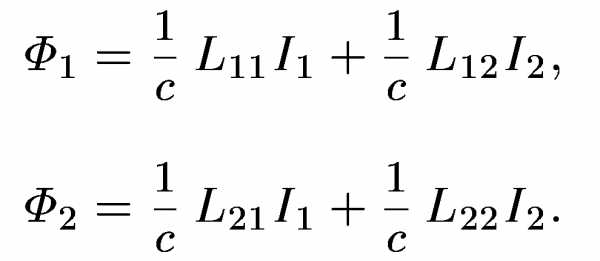
Коэффициенты не зависят от токов, а определяются лишь формой, размерами и взаимным расположением витков. Они называются коэффициентами индуктивности. Если. Поэтомуесть индуктивность первого, а- второго витка. Оставшиеся два коэффициентаиназываются взаимными индуктивностями или коэффициентами взаимной индукции.

07. Энергия магнитного поля.

Электрический ток обладает запасом энергии, называемой магнитной.

Магнитная энергия может зависеть только от величины и распределения токов, а таксисе от магнитных свойств среды, заполняющей пространство.

Рассмотрим сначала одиночный неподвижный замкнутый виток проволоки. Пусть в начальный момент сила тока в нем равна нулю. Будем каким-либо способом создавать и наращивать ток в витке . Тогда будет нарастать и магнитный поток через виток Ф. Возникнет электродвижущая сила индукции. Элементарная работа, которую должен совершить внешний источник против электродвижущей силы индукции, будет

Полученное соотношение носит общий характер. Оно справедливо и для ферромагнитных материалов, так как при его выводе относительно магнитных свойств среды не вводилось никаких предположений. Однако если среда не обладает гистерезисом, в частности является пара- или диамагнитной, то работа пойдет только на увеличение магнитной энергии, так что

Предположим, что ферромагнетики отсутствуют. Тогда причем для неподвижного провода самоиндукция L остается постоянной. Используя это и интегрируя, получим

Для справедливости формулы несущественно, что во время нарастания тока виток оставался неподвижным, так как энергия зависит от состояния системы, но не от способа, каким было достигнуто это состояние

Формула для произвольного числа витков. Предположим, что все витки неподвижны, будем увеличивать токи в них. Тогда для элементарной работы против электродвижущей силы индукции будет:

Магнитная энергия в конечном состоянии представится интегралом:

, где текущее значения соответствующих величин

Для упрощения расчета будем наращивать все токи одновременно и притом так, чтобы они оставались пропорциональными друг другу. Таким образом, в любой момент будет соблюдаться соотношение — переменная величина, не зависящая отi. В начальном состоянии , в конечном. Так как при отсутствии ферромагнитных материалов магнитные потоки связаны с токами линейно, то для них справедливы такие же соотношения, т. е.. Таким образом

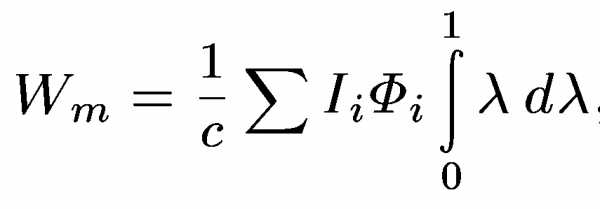или после интегрирования

08. Локализация магнитной энергии в пространстве.

Выражение для магнитной энергии можно преобразовать в другую форму, которая соответствует иному представлению о месте нахождения энергии. Покажем это на примере длинного соленоида, по поверхности которого циркулирует ток с линейной плотностью . Пренебрегая краевыми эффектами, можно написать для поля Н внутри соленоида. ПустьS – площадь поперечного сечения соленоида. Тогда , получим

Если — магнитная энергия, приходящаяся на единицу объема соленоида, то для ее дифференциала можно написать

В случае пара- и диамагнитных сред и выражение можно проинтегрировать

В общем случае постоянных электрических токов выражение для магнитной энергии можно преобразовать. Считая ток неподвижным и полагая в формуле , получим

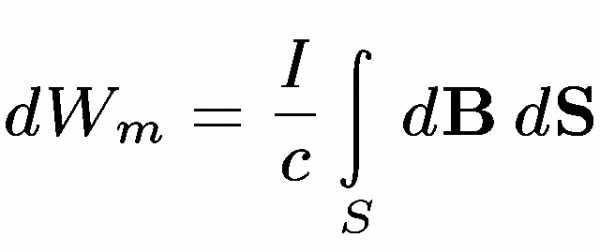
Вектор А и называется векторным потенциалом магнитного поля. Используя это соотношение и применяя теорему Стокса, находим

Вместо линейного введем объемный элемент тока и воспользуемся теоремой о циркуляции

09. Основы теории Максвелла. Ток смещения.

Основные уравнения электромагнитного поля в неподвижных средах, применимые не только к постоянным, но и к переменным электромагнитным полям, были установлены Максвеллом. К уравнениям Максвелла можно прийти путем последовательного обобщения опытных фактов.К основным уравнениям электродинамики присоединим закон сохранения электрического заряда. В дифференциальной форме он имеет вид

Если электромагнитное поле стационарно, то уравнение переходит

Теорема о циркуляции

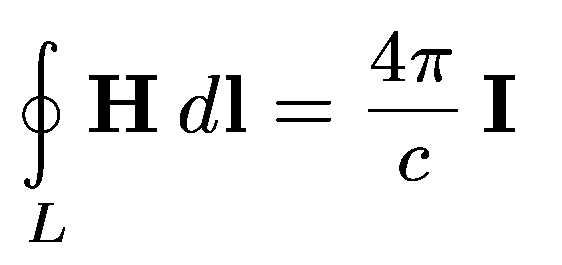также может быть преобразована в дифференциальную форму

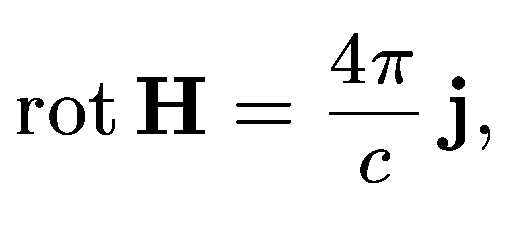
Эти соотношения верны только для стационарных токов.

Чтобы прийти к обобщенным уравнениям, воспользуемся следующим наводящим рассуждением. Поскольку дивергенция левой части уравнения тождественно равна нулю, в правой части этого уравнения должен стоять вектор, дивергенция которого также всегда равна нулю. В случае стационарных электромагнитных полей этот вектор должен переходить в j. Легко указать вектор, удовлетворяющий этим условиям. Дифференцируя по времени соотношениеполучаем

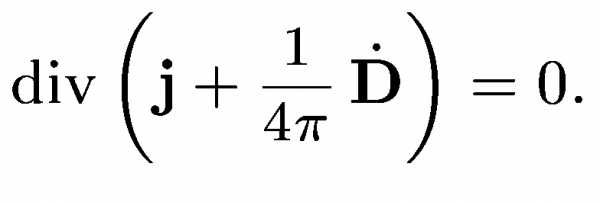
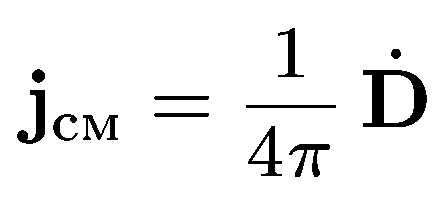— ток смещения

Таким образом , т.е полный ток всегда соленоидален.

Если в уравнении 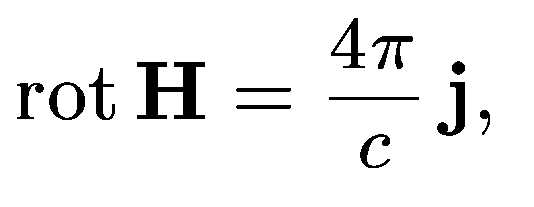ток проводимостиj заменить полным током

Для обобщения уравнени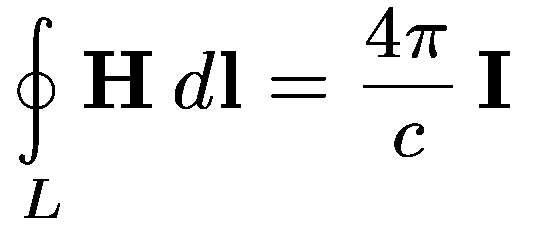й и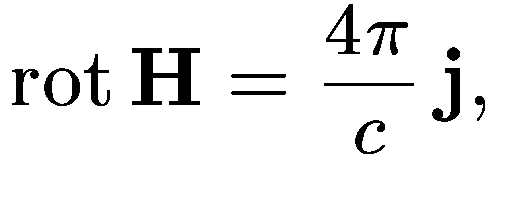

В вакууме всякое изменение электрического поля во времени возбуждает в окружающем пространстве магнитное поле.

10. Система уравнений Максвелла.

Система фундаментальных уравнений электродинамики

В дифференциальной форме:

теорема о циркуляции + ток смещения

закон электромагнитной индукции

теорема Гаусса в веществе

теорема Гаусса для магнитного поля

В Интегральной форме:

Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами {электрическими токами), либо переменными электрическими полями.

11. Граничные условия.

Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Можно, однако, достигнуть полной математической эквивалентности обеих форм уравнений Максвелла. Для этого надо дифференциальные уравнения дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия содержатся в интегральной форме уравнений Максвелла. Они были выведены в соответствующих местах курса и имеют вид

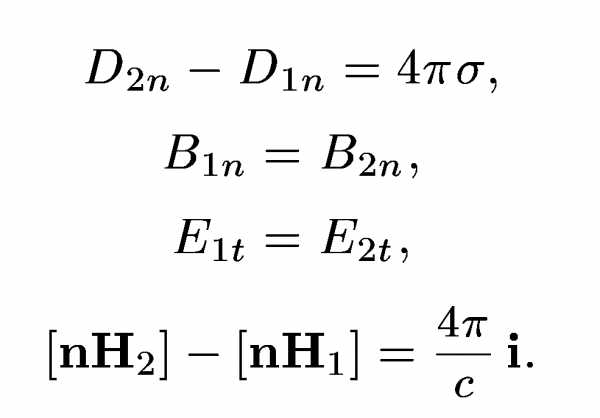
Здесь — поверхностная плотность тока проводимости на рассматриваемой границе раздела, а i — поверхностная плотность тока проводимости на рассматриваемой границе раздела. В частном случае, когда поверхностных токов нет, последнее условие переходит в.

12. Материальные уравнения.

Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе таких теорий лежат какие-то идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами Р, I, j, с одной стороны, и векторами Е и В — с другой. Таким путем, в зависимости от характера среды и электромагнитного поля, получаются более или менее сложные соотношения, которые и дополняют фундаментальные уравнения Максвелла до полной системы уравнений электродинамики. Наиболее просты материальные уравнения в случае слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных неферромагнитных и несегнетоэлектрических сред материальные уравнения могут быть записаны в виде

, где — постоянные, характеризующие электромагнитные свойства среды. Они называются диэлектрической и магнитной проницаемостью и электрической проводимостью среды.

Когда поля стационарны , уравнения Максвелла распадаются на две группы независимых уравнений. Первую группу составляют уравнения электростатики

вторую — уравнения магнитостатики

В этом случае электрическое и магнитное поля независимы друг от друга. Источниками электрического поля будут только электрические заряды, источниками магнитного поля — только токи проводимости.

13. Электромагнитные волны.

электромагнитные волны, или возмущения, распространяющиеся в пространстве с определенной скоростью.

Рассмотрим бесконечно протяженную однородную диэлектрическую среду с диэлектрической и магнитной проницаемостями и. Поместим в нее бесконечную равномерно заряженную плоскость, которую примем за координатную плоскость XY

studfiles.net

Репетитор-онлайн — подготовка к ЦТ

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10⁻¹⁰ Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм². Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение. Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф₁ = B ₁S cos α,

где B ₁ — первоначальное значение модуля индукции магнитного поля, B ₁ = 250 мТл; S — площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф₂ = B ₂S cos α = 0,

где B ₂ — значение модуля индукции после выключения магнитного поля, B ₂ = 0.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = Ф₂ − Ф₁ = −Ф₁,

или, с учетом явного вида Ф₁,

∆Ф = −B ₁S cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

|ℰi|=|ΔФΔt|=|−B1ScosαΔt|=B1S|cosα|Δt,

где ∆t — интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

Ii=|ℰi|R=B1S|cosα|RΔt,

где R — сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

qi=IiΔt=B1S|cosα|R.

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

qimax=IiΔt=B1SR.

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца — площадь круга радиусом r, периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr,

где l — длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r=l2π,

а его площадь —

S=πr2=πl24π2=l24π.

Сопротивление кольца задается формулой

R=ρlS0,

где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10⁻¹⁰ Ом ⋅ м; S ₀ — площадь поперечного сечения проволоки, S ₀ = = 0,100 мм².

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

qimax=B1l2S04πρl=B1lS04πρ.

Вычислим:

qimax=250⋅10−3⋅1,57⋅0,100⋅10−64⋅3,14⋅50,0⋅10−10=0,625 Кл=625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

vedy.by

что это такое, основные формулы, в чем измеряется, от чего зависит.

В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.

Магнитный поток

Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.

При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.

ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Законы Фарадея и Ленца

Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.

Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.

Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.

Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:

Е = — dФ/dt.

Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.

Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.

Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.

Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.

Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.

Движение провода в магнитном поле

Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.

Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.

Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.

Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.

Вращающаяся катушка

Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).

Согласно формуле, на Ф воздействуют изменения в ситуациях:

• при изменении магнитного потока меняется вектор направления;
• изменяется площадь, заключенная в контур;
• меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.

На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.

ЭДС самоиндукции

При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.

В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:

Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.

Взаимоиндукция

При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.

Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.

Значение взаимоиндуктивности второй катушки в отношении первой:

М21 = (N2 x F21)/I1.

Значение магнитного потока:

Ф21 = (М21/N2) x I1.

Индуцированная ЭДС вычисляется по формуле:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt.

В первой катушке значение индуцируемой ЭДС:

Е1 = — M12 x dI2/dt.

Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.

Тогда взаимоиндуктивность считается равной:

М12 = М21 = М.

Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.

Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.

Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.

Похожие статьи

odinelectric.ru

формула. Измерение индуктивности. Индуктивность контура

Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.

Электрическая цепь и индуктивность

Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Как найти индуктивность

Формула, которая является простейшей для нахождения величины, следующая:

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN²R² : 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N²R² :^{2Π(6R + 9l + 10w).}

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от «витков в квадрате».
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:

Xc = 1 : W х C.

Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

Работа конденсатора

Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.

Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:

1. Конденсаторы с газообразным диэлектриком.
2. Вакуумные.
3. С жидким диэлектриком.
4. С твердым неорганическим диэлектриком.
5. С твердым органическим диэлектриком.
6. Твердотельные.
7. Электролитические.

Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:

1. Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
2. Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
3. Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

fb.ru

Электромагнитная индукция. Самоиндукция — Мегаобучалка

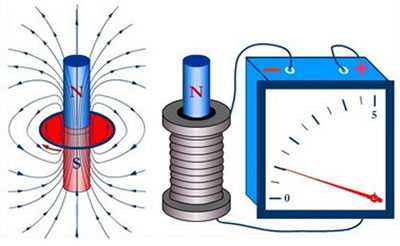
Как мы уже выяснили, электрический ток способен порождать магнитные поля. Возникает вопрос: может ли магнитное поле вызывать появление электрического тока? Эта задача была решена английским физиком Майклом Фарадеем, открывшим явление электромагнитной индукции в 1831 г.^Свитый в катушку проводник замыкается на гальванометре (рис. 3.19). Если вдвигать в катушку постоянный магнит, то гальванометр покажет наличие тока в течение всего промежутка времени, пока магнит перемещается относительно катушки. При выдергивании магнита из катушки гальванометр показывает наличие тока противоположного направления. Изменения направления тока происходит при изменении вдвигаемого или выдвигаемого полюса магнита.

Аналогичные результаты наблюдались при замене постоянного магнита электромагнитом (катушкой с током). Если обе катушки закрепить неподвижно, но в одной из них менять значение тока, то в этот момент в другой катушке наблюдается индукционный ток.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ состоит в возникновении электродвижущей силы (э.д.с.) индукции в проводящем контуре, через который меняется поток вектора магнитной индукции. Если контур является замкнутым, то в нем возникает индукционный ток.

Открытие явления электромагнитной индукции:

1) показало взаимосвязь между электрическим и магнитным полем;

2) предложило способ получения электрического тока с помощью магнитного поля.

Основные свойства индукционного тока:

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

 

Опытами Фарадея было установлено, что величина электродвижущей силы индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника (закон электромагнитной индукции Фарадея)

, или , (3.46)

где (dF) – изменение потока в течении времени (dt).МАГНИТНЫМ ПОТОКОМ или ПОТОКОМ МАГНИТНОЙ ИНДУКЦИИназывается величина, которая определяется на основе следующего соотношения: (магнитный поток через поверхность площадью S): Ф=ВScosα, (3.45), угол a – угол между нормалью к рассматриваемой поверхности и направлением вектора индукции магнитного поля

единица магнитного потока в системе СИ носит название вебер – [Вб=Тл×м²].

Знак «–» в формуле означает, что э.д.с. индукции вызывает индукционный ток, магнитное поле которого противодействует всякому изменению магнитного потока, т.е. при >0 э.д.с. индукции e_И<0 и наоборот.

э.д.с. индукции измеряется в вольтах

 

Для нахождения направления индукционного тока существует правило Ленца (правило установлено в 1833 г.): индукционный ток имеет такое направление, что создаваемое им магнитное поле стремится компенсировать изменение магнитного потока, вызвавшее этот индукционный ток.

Например, если вдвигать северный полюс магнита в катушку, т. е. увеличивать магнитный поток через его витки, в катушке возникает индукционный ток такого направления, что на ближайшем к магниту конце катушки возникает северный полюс (рис.3.20). Итак, магнитное поле индукционного тока стремится нейтрализовать вызвавшее его изменение магнитного потока.

Не только переменное магнитное поле порождает индукционный ток в замкнутом проводнике, но и при движении замкнутого проводника длиной l в постоянном магнитном поле (В) со скоростью v в проводнике возникает эдс:

a (B Ùv) (3.47)

Как вы уже знаете, электродвижущая силав цепи– это результат действия сторонних сил. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца (которая действует со стороны магнитного поля на движущийся электрический заряд). Под действием этой силы происходит разделение зарядов и на концах проводника возникает разность потенциалов. Э.д.с. индукции в проводнике является работой по перемещению единичных зарядов вдоль проводника.

Направление индукционного токаможно определитьпо правилу правой руки:Вектор В входит в ладонь, отведенный большой палец совпадает с направлением скорости проводника, а 4 пальца укажут направление индукционного тока.

Таким образом переменное магнитное поле вызывает появление индуцированного электрического поля. Оно не потенциально( в отличие от электростатического), т.к. работапо перемещению единичного положительного заряда равна э.д.с. индукции, а не нулю.

Такие поля называются вихревыми. Силовые линии вихревогоэлектрического поля – замкнуты сами на себя,в отличие от линий напряженности электростатического поля.

 

Э.д.с. индукции возникает не только в соседних проводниках, но и в самом проводнике при изменении магнитного поля тока, идущего по проводнику. Возникновение э.д.с. в каком-либо проводнике при изменении в нем самом силы тока (следовательно, магнитного потока в проводнике) называется самоиндукцией, а ток, индуцируемый в этом проводнике, – током самоиндукции.

Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, напряженность которого пропорциональна силе тока I. Поэтому магнитный поток Ф, пронизывающий контур, пропорционален силе тока в контуре

Ф=L×I, (3.48).

 

L – коэффициент пропорциональности, который носит название коэффициента самоиндукции, или, просто, индуктивности. Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости среды, окружающей контур.

В этом смысле индуктивность контура — аналогэлектрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.

Единица индуктивности — генри (Гн): 1Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1А равен 1Вб (1Гн=1Вб/А=1В·с/А).

Если L=const, то э.д.с. самоиндукции можно представить в следующем виде:

, или , (3.49)

где DI (dI) – изменение тока в цепи, содержащей катушку индуктивности (или контур) L, за время Dt (dt). Знак «–» в этом выражении означает, что э.д.с. самоиндукции препятствует изменению тока (т. е. если ток в замкнутом контуре уменьшается, то э.д.с. самоиндукции приводит к возникновению тока того же направления и наоборот).

 

Одним из проявлений электромагнитной индукции является возникновение замкнутых индукционных токов в сплошных проводящих средах: металлических телах, растворах электролитов, биологических органах и т.д. Такие токи носят название вихревых токов или токов Фуко. Эти токи возникают при перемещении проводящего тела в магнитном поле и/или при изменении со временем индукции поля, в которое помещены тела. Сила токов Фуко зависит от электрического сопротивления тел, а также от скорости изменения магнитного поля.

Токи Фуко также подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему вихревые токи.

Поэтому массивные проводники тормозятся в магнитном поле. В электрических машинах, для того чтобы минимизировать влияние токов Фуко, сердечники трансформаторов и магнитные цепи электрических машин собирают из тонких пластин, изолированных друг от друга специальным лаком или окалиной.

Вихревые токи вызывают сильное нагревание проводников. Джоулево тепло, выделяемое токами Фуко, используется в индукционных металлургических печах для плавки металлов, согласно закону Джоуля-Ленца:

 

megaobuchalka.ru

От чего зависит индукционный ток?

Поиск Лекций

---

Введение

 

Се­го­дняш­ний урок будет по­свя­щен яв­ле­нию элек­тро­маг­нит­ной ин­дук­ции. Яв­ле­ни­ем элек­тро­маг­нит­ной ин­дук­ции на­зы­ва­ет­ся яв­ле­ние воз­ник­но­ве­ния элек­три­че­ско­го тока в про­вод­ни­ке под дей­стви­ем пе­ре­мен­но­го маг­нит­но­го поля.

Важно, что в дан­ном слу­чае про­вод­ник дол­жен быть за­мкнут. В на­ча­ле XIX в. после опы­тов дат­ско­го уче­но­го Эр­сте­да стало ясно, что элек­три­че­ский ток со­зда­ет во­круг себя маг­нит­ное поле. После встал во­прос о том, нель­зя ли по­лу­чить элек­три­че­ский ток за счет маг­нит­но­го поля, т.е. про­из­ве­сти об­рат­ные дей­ствия. Если элек­три­че­ский ток со­зда­ет маг­нит­ное поле, то, на­вер­ное, и маг­нит­ное поле долж­но со­зда­вать элек­три­че­ский ток. В пер­вой по­ло­вине XIX века уче­ные об­ра­ти­лись имен­но к таким опы­там: стали ис­кать воз­мож­ность со­зда­ния элек­три­че­ско­го тока за счет маг­нит­но­го поля.

Опыты Фарадея

Впер­вые уда­лось до­стичь успех в этом (т.е. по­лу­чить элек­три­че­ский ток за счет маг­нит­но­го поля) ан­глий­ско­му фи­зи­ку Май­к­лу Фа­ра­дею. Итак, об­ра­тим­ся к опы­там Фа­ра­дея.

Рис. 1. Опыт, ана­ло­гич­ный опыту Фа­ра­дея. При дви­же­нии маг­ни­та в ка­туш­ке, в ее цепи ре­ги­стри­ру­ет­ся элек­три­че­ский ток

 

 

Пер­вая схема была до­воль­но про­стой. Во-пер­вых, М. Фа­ра­дей ис­поль­зо­вал в своих опы­тах ка­туш­ку с боль­шим чис­лом вит­ков. Ка­туш­ка на­ко­рот­ко была при­со­еди­не­на к из­ме­ри­тель­но­му при­бо­ру, мил­ли­ам­пер­мет­ру (мА). Нужно ска­зать, что в те вре­ме­на не было до­ста­точ­но хо­ро­ших ин­стру­мен­тов для из­ме­ре­ния элек­три­че­ско­го тока, по­это­му поль­зо­ва­лись необыч­ным тех­ни­че­ским ре­ше­ни­ем: брали маг­нит­ную стрел­ку, рас­по­ла­га­ли рядом с ней про­вод­ник, по ко­то­ро­му про­те­кал ток, и по от­кло­не­нию маг­нит­ной стрел­ки су­ди­ли о про­те­ка­ю­щем токе. Так вот в дан­ном слу­чае токи могли быть очень неве­ли­ки, по­это­му ис­поль­зо­вал­ся при­бор мА, т.е. тот, ко­то­рый из­ме­ря­ет ма­лень­кие токи.

Вдоль ка­туш­ки М. Фа­ра­дей пе­ре­ме­щал по­сто­ян­ный маг­нит – от­но­си­тель­но ка­туш­ки маг­нит дви­гал­ся вверх и вниз.

Об­ра­ща­ем ваше вни­ма­ние на то, что в этом экс­пе­ри­мен­те впер­вые было за­фик­си­ро­ва­но на­ли­чие элек­три­че­ско­го тока в цепи в ре­зуль­та­те из­ме­не­ния маг­нит­но­го по­то­ка, ко­то­рый про­хо­дит сквозь ка­туш­ку.

Фа­ра­дей об­ра­тил вни­ма­ние и на тот факт, что стрел­ка мА от­кло­ня­ет­ся от сво­е­го ну­ле­во­го зна­че­ния, т.е. по­ка­зы­ва­ет, что в цепи су­ще­ству­ет элек­три­че­ский ток толь­ко тогда, когда маг­нит дви­жет­ся. Стоит толь­ко маг­ни­ту оста­но­вить­ся, стрел­ка воз­вра­ща­ет­ся в пер­во­на­чаль­ное по­ло­же­ние, в ну­ле­вое по­ло­же­ние, т.е. ни­ка­ко­го элек­три­че­ско­го тока в цепи в этом слу­чае нет.

Вто­рая за­слу­га Фа­ра­дея – уста­нов­ле­ние за­ви­си­мо­сти на­прав­ле­ния ин­дук­ци­он­но­го элек­три­че­ско­го тока от по­ляр­но­сти маг­ни­та и на­прав­ле­ния его дви­же­ния. Сто­и­ло Фа­ра­дею из­ме­нить по­ляр­ность маг­ни­тов и про­пус­кать маг­нит через ка­туш­ку с боль­шим чис­лом вит­ков, как тут же ме­ня­лось на­прав­ле­ние ин­дук­ци­он­но­го тока, того, ко­то­рый воз­ни­ка­ет в за­мкну­той элек­три­че­ской цепи.

Т.о. мы при­шли к тому, с чего на­чи­на­ли урок: под­твер­ди­лась ги­по­те­за, что элек­три­че­ский ток воз­ни­ка­ет, когда из­ме­ня­ет­ся маг­нит­ное поле.

Итак, неко­то­рое за­клю­че­ние. Из­ме­ня­ю­ще­е­ся маг­нит­ное поле со­зда­ет элек­три­че­ский ток. На­прав­ле­ние элек­три­че­ско­го тока за­ви­сит от того, какой полюс маг­ни­та про­хо­дит в дан­ный мо­мент через ка­туш­ку, в каком на­прав­ле­нии дви­жет­ся маг­нит.

И еще: ока­зы­ва­ет­ся, на зна­че­ние элек­три­че­ско­го тока вли­я­ет ко­ли­че­ство вит­ков в ка­туш­ке. Чем боль­ше вит­ков, тем и зна­че­ние тока будет боль­ше.

Об­ра­тим­ся те­перь ко вто­ро­му экс­пе­ри­мен­ту Фа­ра­дея. В чем он за­клю­чал­ся?

Рис. 2. Вто­рой экс­пе­ри­мент по ис­сле­до­ва­нию яв­ле­ния элек­тро­маг­нит­ной ин­дук­ции

 

 

Две ка­туш­ки раз­ме­ща­лись близ­ко друг с дру­гом. Одна ка­туш­ка с боль­шим чис­лом вит­ков под­клю­ча­лась к ис­точ­ни­ку тока, в этой цепи был ключ, ко­то­рый за­мы­кал и раз­мы­кал цепь. Вто­рая ка­туш­ка, тоже с боль­шим чис­лом вит­ков, под­клю­чен­ная к мил­ли­ам­пер­мет­ру на­пря­мую, ни­ка­ких ис­точ­ни­ков тока нет. Как толь­ко цепь за­мы­ка­лась, мил­ли­ам­пер­метр по­ка­зы­вал на­ли­чие элек­три­че­ско­го тока в цепи. Как толь­ко цепь раз­мы­ка­лась, мил­ли­ам­пер­метр вновь ре­ги­стри­ро­вал на­ли­чие элек­три­че­ско­го тока, но на­прав­ле­ние элек­три­че­ско­го тока из­ме­ня­лось на про­ти­во­по­лож­ное. Пока цепь была за­мкну­та, т.е. пока в цепи про­те­кал элек­три­че­ский ток, мил­ли­ам­пер­метр ни­ка­ко­го тока в элек­три­че­ской цепи не ре­ги­стри­ро­вал.

Выводы из экспериментов

Какие вы­во­ды были сде­ла­ны М.Фа­ра­де­ем в ре­зуль­та­те этих экс­пе­ри­мен­тов? Ин­дук­ци­он­ный элек­три­че­ский ток по­яв­ля­ет­ся в за­мкну­той цепи толь­ко тогда, когда су­ще­ству­ет пе­ре­мен­ное маг­нит­ное поле. При­чем это маг­нит­ное поле долж­но из­ме­нять­ся.

От чего зависит индукционный ток?

Если из­ме­не­ния маг­нит­но­го поля не про­ис­хо­дит, то не будет ни­ка­ко­го элек­три­че­ско­го тока. Даже если маг­нит­ное поле су­ще­ству­ет. Мы можем ска­зать, что ин­дук­ци­он­ный элек­три­че­ский ток прямо про­пор­ци­о­на­лен, во-пер­вых, числу вит­ков, во-вто­рых, ско­ро­сти маг­нит­но­го поля, с ко­то­рой из­ме­ня­ет­ся это маг­нит­ное поле от­но­си­тель­но вит­ков ка­туш­ки.

Рис. 3. От чего за­ви­сит ве­ли­чи­на ин­дук­ци­он­но­го тока?

 

Для ха­рак­те­ри­сти­ки маг­нит­но­го поля ис­поль­зу­ет­ся ве­ли­чи­на, ко­то­рая на­зы­ва­ет­ся маг­нит­ный поток. Она ха­рак­те­ри­зу­ет маг­нит­ное поле в целом, мы об этом будем го­во­рить на сле­ду­ю­щем уроке. Сей­час от­ме­тим лишь, что имен­но из­ме­не­ние маг­нит­но­го по­то­ка, т.е. числа линий маг­нит­но­го поля, про­ни­зы­ва­ю­щих кон­тур с током (ка­туш­ку, на­при­мер), при­во­дит к воз­ник­но­ве­нию в этом кон­ту­ре ин­дук­ци­он­но­го тока.

 

poisk-ru.ru