Posted in Советы по обучению

Умножение восьмеричная система счисления – СЛОЖЕНИЕ ДЕЛЕНИЕ УМНОЖЕНИЕ ЧИСЕЛ В ЛЮБОЙ СИСТЕМЕ СЧИСЛЕНИЯ ОНЛАЙН

§12. Арифметические операции в позиционных системах счисления

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Арифметические операции в позиционных системах счисления





12.3. Умножение чисел в системе счисления с основанием q
12.1. — 12.2. Сложение и вычитание чисел в системе счисления с основанием q12.4. Деление чисел в системе счисления с основанием q

12.3. Умножение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц умножения в троичной (табл. 3.5), восьмеричной (табл. 3.6) и шестнадцатеричной (табл. 3.7) системах счисления.

Таблица 3.5

Умножение в троичной системе счисления

Таблица 3.6

Умножение в восьмеричной системе счисления

Таблица 3.7

Умножение в шестнадцатеричной системе счисления

Рассмотрим алгоритм умножения многозначного числа на однозначное.

Чтобы в системе счисления с основанием q получить произведение М многозначного числа А и однозначного числа b, надо вычислить произведения b и цифр, образующих число А по разрядам i справа налево:

• если ai • b < q, то mi = ai • b, старший (i + 1)-й разряд не изменяется;
• если аi • b ≥ q, то mi = аi • b mod q, старший (i + 1)-й разряд увеличивается на ai • b div q (где div — операция целочисленного деления).

Примеры:

Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы в одном столбце оказались их самые младшие разряды с цифрами, отличными от нуля. Нули переносятся в итоговое произведение, а в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат.

Примеры:


Cкачать материалы урока


xn—-7sbbfb7a7aej.xn--p1ai

Восьмеричная система счисления

В восьмеричной системе счисления используется восемь цифр: 0,1,2 … 7, а основание записывается как 10(8) (810=1·81+0·80). Рассмотрим примеры выполнения операций в восьмеричной системе счисления. При их выполнении используются правила представленные в таблицах сложения и умножения восьмеричных цифр.

Сложение

Умножение

1

2

3

4

5

6

7

1

2

3

4

5

6

7

1

2

3

4

5

6

7

10

1

1

2

3

4

5

6

7

2

3

4

5

6

7

10

11

2

2

4

6

10

12

14

16

3

4

5

6

7

10

11

12

3

3

6

11

14

17

22

25

4

5

6

7

10

11

12

13

4

4

10

14

20

24

30

34

5

6

7

10

11

12

13

14

5

5

12

17

24

31

36

43

6

7

10

11

12

13

14

15

6

6

14

22

30

36

44

52

7

10

11

12

13

14

15

16

7

7

16

25

34

43

52

61

Шестнадцатеричная система счисления

В шестнадцатеричной системе счисления используются шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,B,C,D,E,F. Основание записывается как 10(16)(1610=1*161+0*160).

Сложение

Умножения

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

1

2

3

4

5

6

7

8

9

а

b

c

d

e

f

10

1

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

2

3

4

5

6

7

8

9

a

b

c

d

e

f

10

11

2

2

4

6

8

a

c

e

10

12

14

16

18

1a

1c

1e

3

4

5

6

7

8

9

a

b

c

d

e

f

10

11

12

3

3

6

9

c

f

12

15

18

1b

1e

21

24

27

2a

2d

4

5

6

7

8

9

A

b

c

d

e

f

10

11

12

13

4

4

8

c

10

14

18

1c

20

24

28

2c

30

34

38

3c

5

6

7

8

9

a

B

c

d

e

f

10

11

12

13

14

5

5

a

f

14

19

1e

23

28

2d

32

37

3c

41

46

4b

6

7

8

9

a

b

C

d

e

f

10

11

12

13

14

15

6

6

c

12

18

1e

24

2a

30

36

3c

42

48

4e

54

5a

7

8

9

a

b

c

D

e

f

10

11

12

13

14

15

16

7

7

e

15

1c

23

2a

31

38

3f

46

4d

54

5b

62

69

8

9

a

b

c

d

E

f

10

11

12

13

14

15

16

17

8

8

10

18

20

28

30

38

40

48

50

50

60

68

70

78

9

a

b

c

d

e

F

10

11

12

13

14

15

16

17

18

9

9

12

1b

24

2d

36

3f

48

51

5a

63

6c

75

7e

87

a

b

c

d

e

f

10

11

12

13

14

15

16

17

18

19

a

a

14

1e

28

32

3c

46

50

5a

64

6e

78

82

8c

96

b

c

d

e

f

10

11

12

13

14

15

16

17

18

19

20

b

b

16

21

2c

37

42

4d

58

63

6e

79

84

8f

9a

a5

c

d

e

f

10

11

12

13

14

15

16

17

18

19

20

21

c

c

18

24

30

3c

48

54

60

6c

78

84

90

9c

a8

84

d

e

f

10

11

12

13

14

15

16

17

18

19

20

21

22

d

d

1a

27

34

41

4e

5b

68

75

82

8f

9c

a9

b6

c3

e

f

10

11

12

13

14

15

16

17

18

19

20

21

22

23

e

e

1c

2a

38

46

54

62

70

7e

8c

9a

a8

b6

c4

d2

f

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

f

f

1e

2d

3c

4b

5a

69

78

87

96

a5

b4

c3

d2

e1

studfiles.net

Восьмеричная система счисления — Программирование на C, C# и Java

Оглавление:
Перевод из десятичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в десятичную
Перевод из двоичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в двоичную
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
Применение восьмеричной системы счисления

Восьмеричная система – одна из основных систем счислений наряду с двоичной, десятичной и шестнадцатеричной, применяемая в информационных технологиях.

Как мы знаем, компьютеры «воспринимают» лишь двоичную систему счисления, состоящую только из нулей и единиц. Однако человеку довольно непривычно и неудобно работать с такими числами. Например, привычное нам десятичное число 2 143 в двоичной системе будет выглядеть как 100001011111.  Переводить числа из двоичной системы в десятеричную также не очень удобно и бывает довольно муторно.

В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и наоборот гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.

Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе. Так, например, в восьмеричной системе то же число 2 143 будет записываться как 4137.

В восьмеричной системе счисления, как уже можно было догадаться, основанием является цифра 8 и, соответственно, она вмещает в себя только восемь цифр: от 0 до 7. Поэтому числа в восьмеричной системе счисления очень похожи на десятичные, в отличие от шестнадцатеричных, где присутствуют буквы латинского алфавита или двоичных, состоящих только из двух цифр. Отличают эти две системы тем, что в восьмеричной отсутствуют цифры 8 и 9, а также, очевидно, нижними индексами: у числа в десятичной системе прибавляют нижний индекс с цифрой 10, а к числам в восьмеричной системе приписывают цифру 8, например:

 Теперь давайте научимся переводу чисел в восьмеричную систему счисления и наоборот.

Перевод из десятичной системы счисления в восьмеричную

Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.

Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.

Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.

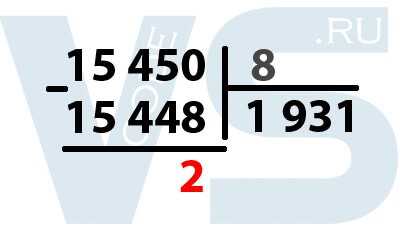
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.
Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:

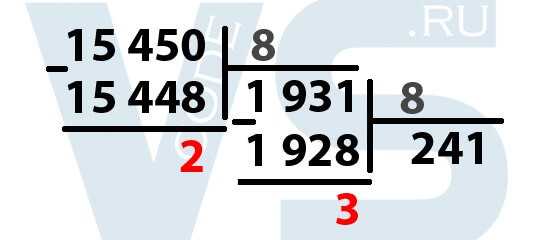
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241. При умножении 241 на 8 получается число 1 928. Ищем разность между 1 931 и 1928 – получается 3. Выделяем её. Далее делим 241 на 8.

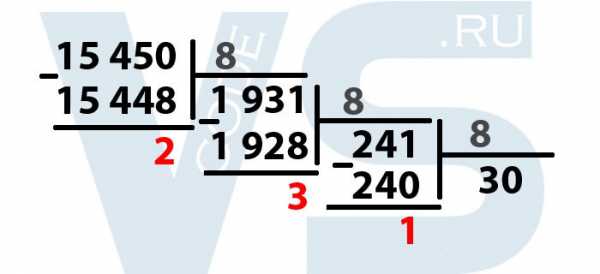
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.
Продолжаем деление до тех пор, пока частное не станет меньше 8!

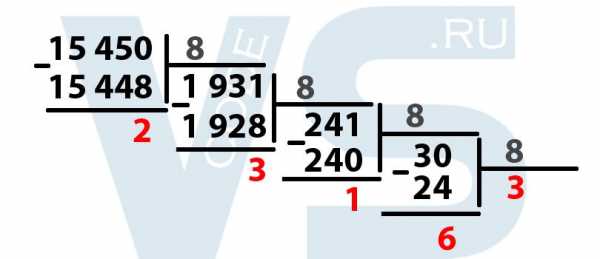Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 – 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).

Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.

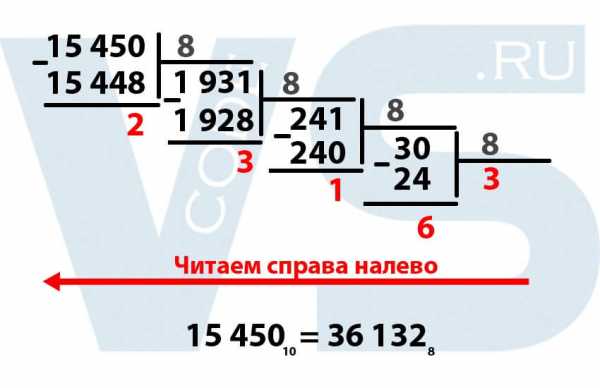
Таким образом, десятичное число 15 45010 в восьмеричной системе будет выглядеть как 36 1328.

Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:

  1. Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.
  2. Умножить полученное частное на 8. Записать его под исходным числом.
  3. Найти остаток между этими числами и выделить его – это кусочек переведённого в восьмеричную систему числа.
  4. Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
  5. Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
  6. Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.

Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.

Перевод из восьмеричной системы счисления в десятичную

Перевести восьмеричное число в десятичное даже проще, чем наоборот. Давайте рассмотрим пример: переведём восьмеричное число 36078 в десятичное.

Для начала мы делаем такую запись: с конца берём каждую цифру нашего исходного числа, каждое из них умножаем на 8, и все в целом складываем. Должно получиться примерно так:

Однако, это ещё не всё! После того, как мы сделали подобную запись, ко всем числам 8, на которые умножаются цифры исходного числа, необходимо добавить степени в порядке возрастания: 0, 1, 2 и т.д. Обязательно необходимо начинать с нулевой степени!

Всё, что остаётся после этого – просто посчитать. В итоге у нас получилось число 1927 в десятичной системе.

Перевод из двоичной системы счисления в восьмеричную

Перевод чисел из двоичной системы счисления в восьмеричную – довольно необычное дело для тех, кто никогда с этим не сталкивался. Однако на деле всё не так пугающе, как может показаться с первого раза.

Давайте попробуем. Допустим, у нас есть двоичное число 1010010001011101100.

Для начала нам необходимо разбить это число на триады – группы из трёх цифр. Почему именно три цифры? Как мы знаем, у систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8. Математически это можно записать так:

Найти i, пожалуй, не составит труда: i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или, говоря иначе – 3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо с младшего бита. Бит – это одна цифра в двоичном числе. Чем дальше бит от начала числа, тем он младше. Самый младший бит – это последняя цифра двоичного числа. Иными словами, мы разбиваем число на триады, начиная с конца.

Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.

Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:

Для этого в каждой отдельной триаде (начиная с первой) нужно каждую цифру (начиная с последней) умножить на 2, возведённую в степени от 0 до 2, и сложить полученные три числа.

Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.

Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:

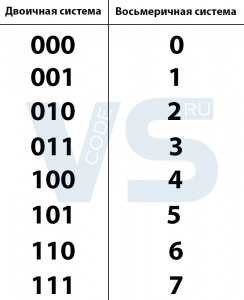
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.

Перевод из восьмеричной системы счисления в двоичную

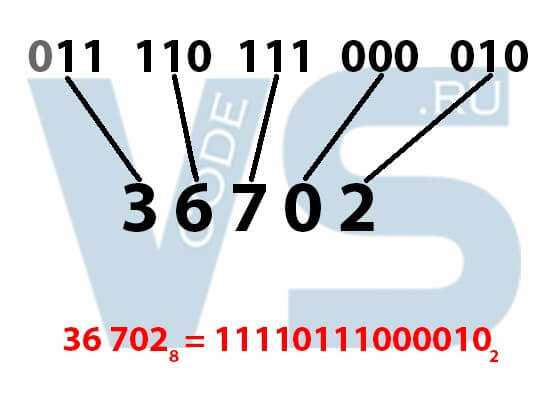
Самым удобным способом перевода из восьмеричной системы счисления в двоичную является использование таблицы соответствий. Итак, допустим, мы хотим перевести восьмеричное число 36702 в двоичную систему. Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.

Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы. Например, как на изображении ниже. В старшем бите у нас получился ноль при переводе восьмеричной тройки, и мы убрали его. Это делается для удобства, потому что зачем хранить и писать незначащие цифры.

Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную

К сожалению, несмотря на то, что эти системы счисления близки друг к другу, напрямую перевести друг в друга нельзя. Легче всего при переводе этих двух систем друг в друга воспользоваться посредничеством двоичной системы. То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.

Применение восьмеричной системы счисления

В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году – это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.

Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.

 

Восьмеричная система счисления

5 (100%) 11 votes


Поделиться в соц. сетях:

vscode.ru

Восьмеричная система счисления

В восьмеричной системе счисления используется восемь цифр: 0,1,2 … 7, а основание записывается как 10(8) (810=1·81+0·80). Рассмотрим примеры выполнения операций в восьмеричной системе счисления. При их выполнении используются правила представленные в таблицах сложения и умножения восьмеричных цифр.

Сложение

Умножение

1

2

3

4

5

6

7

1

2

3

4

5

6

7

1

2

3

4

5

6

7

10

1

1

2

3

4

5

6

7

2

3

4

5

6

7

10

11

2

2

4

6

10

12

14

16

3

4

5

6

7

10

11

12

3

3

6

11

14

17

22

25

4

5

6

7

10

11

12

13

4

4

10

14

20

24

30

34

5

6

7

10

11

12

13

14

5

5

12

17

24

31

36

43

6

7

10

11

12

13

14

15

6

6

14

22

30

36

44

52

7

10

11

12

13

14

15

16

7

7

16

25

34

43

52

61

Шестнадцатеричная система счисления

В шестнадцатеричной системе счисления используются шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,B,C,D,E,F. Основание записывается как 10(16)(1610=1*161+0*160).

Сложение

Умножения

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

1

2

3

4

5

6

7

8

9

а

b

c

d

e

f

10

1

1

2

3

4

5

6

7

8

9

a

b

c

d

e

f

2

3

4

5

6

7

8

9

a

b

c

d

e

f

10

11

2

2

4

6

8

a

c

e

10

12

14

16

18

1a

1c

1e

3

4

5

6

7

8

9

a

b

c

d

e

f

10

11

12

3

3

6

9

c

f

12

15

18

1b

1e

21

24

27

2a

2d

4

5

6

7

8

9

A

b

c

d

e

f

10

11

12

13

4

4

8

c

10

14

18

1c

20

24

28

2c

30

34

38

3c

5

6

7

8

9

a

B

c

d

e

f

10

11

12

13

14

5

5

a

f

14

19

1e

23

28

2d

32

37

3c

41

46

4b

6

7

8

9

a

b

C

d

e

f

10

11

12

13

14

15

6

6

c

12

18

1e

24

2a

30

36

3c

42

48

4e

54

5a

7

8

9

a

b

c

D

e

f

10

11

12

13

14

15

16

7

7

e

15

1c

23

2a

31

38

3f

46

4d

54

5b

62

69

8

9

a

b

c

d

E

f

10

11

12

13

14

15

16

17

8

8

10

18

20

28

30

38

40

48

50

50

60

68

70

78

9

a

b

c

d

e

F

10

11

12

13

14

15

16

17

18

9

9

12

1b

24

2d

36

3f

48

51

5a

63

6c

75

7e

87

a

b

c

d

e

f

10

11

12

13

14

15

16

17

18

19

a

a

14

1e

28

32

3c

46

50

5a

64

6e

78

82

8c

96

b

c

d

e

f

10

11

12

13

14

15

16

17

18

19

20

b

b

16

21

2c

37

42

4d

58

63

6e

79

84

8f

9a

a5

c

d

e

f

10

11

12

13

14

15

16

17

18

19

20

21

c

c

18

24

30

3c

48

54

60

6c

78

84

90

9c

a8

84

d

e

f

10

11

12

13

14

15

16

17

18

19

20

21

22

d

d

1a

27

34

41

4e

5b

68

75

82

8f

9c

a9

b6

c3

e

f

10

11

12

13

14

15

16

17

18

19

20

21

22

23

e

e

1c

2a

38

46

54

62

70

7e

8c

9a

a8

b6

c4

d2

f

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

f

f

1e

2d

3c

4b

5a

69

78

87

96

a5

b4

c3

d2

e1

studfiles.net

Author: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *