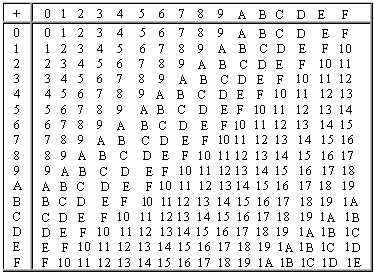
Таблица чисел в системах счисления

Таблица умножения чисел в шестнадцатеричной системе счисления
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F | |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 | 5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
2 |
0 |
2 |
4 |
6 |
8 |
A |
C |
E |
10 |
12 |
14 |
16 |
18 |
1A |
1C |
|
|
3 |
0 |
3 |
6 |
9 |
C |
F |
12 |
15 |
18 |
1B |
1E |
21 |
24 |
27 |
2A |
2D |
|
4 |
0 |
4 |
8 |
C |
10 |
14 |
18 | 1C |
20 |
24 |
28 |
2C |
30 |
34 |
38 |
3C |
|
5 |
0 |
5 |
A |
F |
14 |
19 |
1E |
23 |
28 |
2D |
32 |
37 |
3C |
41 |
46 |
4B |
|
|
0 |
6 |
C |
12 |
18 |
1E |
24 |
2A |
30 |
36 |
3C |
42 |
48 |
4E |
54 |
5A |
|
7 |
0 |
7 |
E |
15 |
1C |
23 |
2A |
31 |
38 | 3F |
46 |
4D |
54 |
5B |
62 |
69 |
|
8 |
0 |
8 |
10 |
18 |
20 |
28 |
30 |
38 |
40 |
48 |
50 |
58 |
60 |
68 |
70 |
78 |
|
9 |
0 |
|
12 |
1B |
24 |
2D |
36 |
3F |
48 |
51 |
5A |
63 |
6C |
75 |
7E |
87 |
|
A |
0 |
A |
14 |
1E |
28 |
32 |
3C |
46 |
50 |
5A |
64 |
6E |
78 |
82 |
8C |
96 |
|
B |
0 |
B |
16 |
21 |
2C |
37 |
42 |
4D |
58 |
63 |
6E |
79 |
84 |
8F |
9A |
A5 |
|
C |
0 |
C |
18 |
24 |
30 |
3C |
48 |
54 |
60 |
6C |
78 |
84 |
90 |
9C |
A8 |
B4 |
|
D |
0 |
D |
1A |
27 |
34 |
41 |
4E |
5B |
68 |
75 |
82 |
8F | 9C |
A9 |
B6 |
C3 |
|
E |
0 |
E |
1C |
2A |
38 |
46 |
54 |
62 |
70 |
7E |
8C |
9A |
A8 |
B6 |
C4 |
D2 |
|
F |
0 |
F |
1E |
2D |
|
4B |
5A |
69 |
78 |
87 |
96 |
A5 |
B4 |
C3 |
D2 |
E1 |
Таблица сложения чисел в шестнадцатеричной системе счисления
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F | |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
|
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
|
4 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
|
5 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
|
6 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
8 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
9 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
A |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
B |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
|
C |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
|
D |
D |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
|
E |
E |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
1D |
|
F |
F |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
1A |
1B |
1C |
1D |
1E |
Таблица сложения чисел в восьмеричной системе счисления
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
|
3 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
|
4 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
|
5 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
|
6 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Таблица умножения чисел в восьмеричной системе счисления
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
0 |
2 |
4 |
6 |
10 |
12 |
14 |
16 |
|
3 |
0 |
3 |
6 |
11 |
14 |
17 |
22 |
25 |
|
4 |
0 |
4 |
10 |
14 |
20 |
24 |
30 |
34 |
|
5 |
0 |
5 |
12 |
17 |
24 |
31 |
36 |
43 |
|
6 |
0 |
6 |
14 |
22 |
30 |
36 |
44 |
52 |
|
7 |
0 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |
studfiles.net
Арифметические операции с числами в позиционных системах счисления
17
Практическое занятие № 2
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только надо пользоваться особыми таблицами сложения и умножения для каждой системы.
1. Сложение
Таблицы сложения легко составить, используя правила счета.
|
Сложение в двоичной системе |
Сложение в восьмеричной системе
|
|
Сложение в шестнадцатиричной системе
| |
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
|
Шестнадцатеричная:F16+616 |
Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2.81 + 5.80 = 16 + 5 = 21, 1516 = 1.161 + 5.160 = 16+5 = 21. |
Пример 2. Сложим числа 15, 7 и 3.
-
Шестнадцатеричная: F16+716+316
Ответ:
15+7+3 = 2510 = 110012 = 318 = 1916.
Проверка:
110012 = 24 + 23 + 20 = 16+8+1=25,
318 = 3.81 + 1.80 = 24 + 1 = 25,
1916 = 1.161 + 9.160 = 16+9 = 25.
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25
311,28 = 3.82 + 1.81 + 1.80 + 2.8-1 = 201,25
C9,416 = 12.161 + 9.160 + 4.16-1 = 201,25
2. Вычитание
|
Вычитание в двоичной системе счисления
заем |
Вычитание в шестнадцатеричной системе счисления
Заем единицы из старшего разряда | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычитание в восьмеричной системе счисления
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заем единицы из старшего разряда
Пример 4. Вычтем единицу из чисел 102, 108 и 1016
Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016.
Пример 6. Вычтем число 59,75 из числа 201,25.
Ответ: 201,2510 — 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2.82 + 1.81 + 5.80 + 4.8-1 = 141,5;
8D,816 = 8.161 + D.160 + 8.16-1 = 141,5.
studfiles.net
Разработайте таблицы сложения и умножения для восьмеричной системы счисления. + 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 * 0 1
+ 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7 10
2 2 3 4 5 6 7 10 11
3 3 4 5 6 7 10 11 12
4 4 5 6 7 10 11 12 13
5 5 6 7 10 11 12 13 14
6 6 7 10 11 12 13 14 15
7 7 10 11 12 13 14 15 16
* 0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7
2 0 1 4 6 10 12 14 16
3 0 2 6 11 14 17 22 25
4 0 3 10 14 20 24 30 34
5 0 4 12 17 24 31 36 43
6 0 5 14 22 30 36 44 52
7 0 6 16 25 34 43 52 61
Место для вычислений:
8(10)=10(8)
9(10)=11(8)
10(10)=12(8)
ll(10)=13(8)
12(10)=14(8)
13(10)=15(8)
vashurok.ru
Таблицы сложения и умножения
Таблицы сложения и умноженияТаблицы сложения и умножения в различных системах счисления
Двоичная система счисления
Троичная система счисления
| Таблица сложения | Таблица умножения | ||
| 1+1=2 | 1*1=1 | ||
| 1+2=10 | 2+2=11 | 1*2=2 | 2*2=11 |
Восьмеричная система счисления
| Таблица сложения | ||||||
| 1+1=2 | ||||||
| 1+2=3 | 2+2=4 | |||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=10 | |||
| 1+5=6 | 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | ||
| 1+6=7 | 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | |
| 1+7=10 | 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
| Таблица умножения | ||||||
| 1*1=2 | ||||||
| 1*2=2 | 2*2=4 | |||||
| 1*3=3 | 2*3=6 | 3*3=11 | ||||
| 1*4=4 | 2*4=10 | 3*4=14 | 4*4=20 | |||
| 1*5=5 | 2*5=12 | 3*5=17 | 4*5=24 | 5*5=31 | ||
| 1*6=6 | 2*6=14 | 3*6=22 | 4*6=30 | 5*6=36 | 6*6=44 | |
| 1*7=7 | 2*7=16 | 3*7=25 | 4*7=34 | 5*7=43 | 6*7=52 | 7*7=61 |
Шестнадцатеричная система счисления
| Таблица сложения | ||||||||||||||
| 1+1=2 | ||||||||||||||
| 1+2=3 | 2+2=4 | |||||||||||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||||||||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 | |||||||||||
| 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | 5+5=A | ||||||||||
| 1+6=7 | 2+6=8 | 3+6=9 | 4+6=A | 5+6=B | 6+6=C | |||||||||
| 1+7=8 | 2+7=9 | 3+7=A | 4+7=B | 5+7=C | 6+7=D | 7+7=E | ||||||||
| 1+8=9 | 2+8=A | 3+8=B | 4+8=C | 5+8=D | 6+8=E | 7+8=F | 8+8=10 | |||||||
| 1+9=A | 2+9=B | 3+9=C | 4+9=D | 5+9=E | 6+9=F | 7+9=10 | 8+9=11 | 9+9=12 | ||||||
| 1+A=B | 2+A=C | 3+A=D | 4+A=E | 5+A=F | 6+A=10 | 7+A=11 | 8+A=12 | 9+A=13 | A+A=14 | |||||
| 1+B=C | 2+B=D | 3+B=E | 4+B=F | 5+B=10 | 6+B=11 | 7+B=12 | 8+B=13 | 9+B=14 | A+B=15 | B+B=16 | ||||
| 1+C=D | 2+C=E | 3+C=F | 4+C=10 | 5+C=11 | 6+C=12 | 7+C=13 | 8+C=14 | 9+C=15 | A+C=16 | B+C=17 | C+C=18 | |||
| 1+D=E | 2+D=F | 3+D=10 | 4+D=11 | 5+D=12 | 6+D=13 | 7+D=14 | 8+D=15 | 9+D=16 | A+D=17 | B+D=18 | C+D=19 | D+D=1A | ||
| 1+E=F | 2+E=10 | 3+E=11 | 4+E=12 | 5+E=13 | 6+E=14 | 7+E=15 | 8+E=16 | 9+E=17 | A+E=18 | B+E=19 | C+E=1A | D+E=1B | E+E=1C | |
| 1+F=10 | 2+F=11 | 3+F=12 | 4+F=13 | 5+F=14 | 6+F=15 | 7+F=16 | 8+F=17 | 9+F=18 | A+F=19 | B+F=1A | C+F=1B | D+F=1C | E+F=1D | F+F=1E |
| Таблица умножения | ||||||||||||||
| 1*1=1 | ||||||||||||||
| 1*2=2 | 2*2=4 | |||||||||||||
| 1*3=3 | 2*3=6 | 3*3=9 | ||||||||||||
| 1*4=4 | 2*4=8 | 3*4=C | 4*4=10 | |||||||||||
| 1*5=5 | 2*5=A | 3*5=F | 4*5=14 | 5*5=19 | ||||||||||
| 1*6=6 | 2*6=C | 3*6=12 | 4*6=18 | 5*6=1E | 6*6=24 | |||||||||
| 1*7=7 | 2*7=E | 3*7=15 | 4*7=1C | 5*7=23 | 6*7=2A | 7*7=31 | ||||||||
| 1*8=8 | 2*8=10 | 3*8=18 | 4*8=20 | 5*8=28 | 6*8=30 | 7*8=38 | 8*8=40 | |||||||
| 1*9=9 | 2*9=12 | 3*9=1B | 4*9=24 | 5*9=2D | 6*9=36 | 7*9=3F | 8*9=48 | 9*9=51 | ||||||
| 1*A=A | 2*A=14 | 3*A=1E | 4*A=28 | 5*A=32 | 6*A=3C | 7*A=46 | 8*A=50 | 9*A=5A | A*A=64 | |||||
| 1*B=B | 2*B=16 | 3*B=21 | 4*B=2C | 5*B=37 | 6*B=42 | 7*B=4D | 8*B=58 | 9*B=63 | A*B=6E | B*B=79 | ||||
| 1*C=C | 2*C=18 | 3*C=24 | 4*C=30 | 5*C=3C | 6*C=48 | 7*C=54 | 8*C=60 | 9*C=6C | A*C=78 | B*C=84 | C*C=90 | |||
| 1*D=D | 2*D=1A | 3*D=27 | 4*D=34 | 5*D=41 | 6*D=4E | 7*D=5B | 8*D=68 | 9*D=75 | A*D=82 | B*D=8F | C*D=9C | D*D=A9 | ||
| 1*E=E | 2*E=1C | 3*E=2A | 4*E=38 | 5*E=46 | 6*E=54 | 7*E=62 | 8*E=70 | 9*E=7E | A*E=8C | B*E=9A | C*E=A8 | D*E=B6 | E*E=C4 | |
| 1*F=F | 2*F=1E | 3*F=2D | 4*F=3C | 5*F=4B | 6*F=5A | 7*F=69 | 8*F=78 | 9*F=87 | A*F=96 | B*F=A5 | C*F=B4 | D*F=C3 | E*F=D2 | F*F=E1 |
Задачи
Контрольная работа
К оглавлению
slbazhenova.narod.ru
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических операций (сложение, вычитание, умножение и деление) в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Таблицы сложения и умножения составляются по правилу счета и для разных систем счисления сведены в табл. 3.
Таблица 3. Таблицы сложения и умножения в разных системах счисления
|
Сложение и умножение в двоичной системе |
Сложение и умножение в восьмеричной системе |
|
Сложение в шестнадцатеричной системе
| |
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
2. Единицы измерения информации
Информатика неразрывно связана с машинной обработкой, хранением и передачей информации. Но, для того, чтобы ЭВМ могла каким-то образом обрабатывать, хранить и передавать информацию, необходимо, чтобы, информация была представлена в понятном для нее виде.
Известны различные формы представления информации. Однако, ЭВМ — это техническое устройство, основанное на работе электронных компонентов, а значит, обладающее определенными физическими характеристиками. Поэтому, информация, предназначенная для ЭВМ, должна иметь физическое представление, причем это представление должно быть наиболее простым.
Этим требованиям отвечает, так называемое, битовое представление информации, основанное на двоичной системе счисления, при котором каждая запоминаемая частица может принимать только два значения — либо 0, либо 1. В технических устройствах двоичная система счисления используется для обозначения систем с двумя возможными состояниями: 1 — включено 0 — выключено; 1 — есть напряжение 0 — нет напряжения.
Причем каждая двоичная цифра содержит один битинформации.
В информатике битом(binary digit— двоичная единица) называется количество информации, заключающееся в определении одного из двух возможных состояний.
Если объединить два бита в одно целое, то в таком объеме можно хранить уже больше состояний: 00, 01, 10, 11. Если объединить три, то появляется возможность для хранения еще большей информации: 000, 001, 010, 011, 100, 101, 110, 111 и т.д.
Чтобы было нагляднее, изобразим это в таблице:
|
Количество битов |
Возможные комбинации |
Количество комбинаций |
|
1 |
0,1 |
21 |
|
2 |
00, 01, 10, 11 |
22 |
|
3 |
000, 001, 010, 011, 100, 101, 110, 111 |
23 |
|
… |
… | |
|
n |
00…0, 00…1, … , 11…1 |
2n |
Объединение, состоящее из восьми битов, называется байтом(1 байт = 8 бит)
Бит — это наименьшая единица информации. Но ЭВМ довольно редко работают с конкретными битами. Как правило, они оперируют байтом, воспринимая его как единое целое. Поэтому в информатике и ее приложениях принято считать, что байттакже является единицей измерения информации.
Современные электронно-вычислительные машины обрабатывают, хранят, передают очень большие объемы информации. Если попробовать выразить подобный объем в байтовом виде, то получится громоздкое, неудобное для восприятия число. Поэтому, для обозначения больших объемов информации существуют более крупные единицы измерения:
1 Кбайт = 1024 байт = 210 байт = 1024 байт = 8192 бит;
1 Мбайт = 1024 Кбайт = 220 байт = 1048576 байт = 8388608 бит;
1 Гбайт = 1024 Мбайт = 230 байт = 1073741824 байт = 8589934592 бит;
1 Тбайт = 1024 Гбайт = 240 байт = 1099511627776 байт = 8796093022208 бит;
1 Пбайт = 1024 Тбайт = 250 байт = 1125899906842620 байт = 9007199254740990 бит
studfiles.net
iMath Wiki — Арифметические операции в традиционных системах счисления. Правила преобразования чисел между системами счисления.
Из доказанной в предыдущей лекции теоремы существуют несколько интересных следствий. В частности, о правилах арифметических операций в P-ичных системах счисления, и о преобразовании чисел между системами счисления.
Рассмотрим два числа, \[ X_1 = \sum_{i=0}^n a_i P^i, \] \[ X_2 = \sum_{i=0}^m b_i P^i \]
Правила сложения
Правила сложения выводятся очевидным образом:
\[ Y = X_1 + X_2, \] \[ Y = \sum_{i=0}^{\mathrm{max}(m,n)} (a_i+b_i) P^i = \sum_{i=0}^{p} c_i P^i \]
Теперь, по условиям теоремы, \(0\leq c_i < P\). Поскольку так же \(0\leq a_i < P\), \(0\leq b_i < P\), то \(0\leq a_i+b_i \leq P+P-2\). Таким образом, имеем два варианта для каждого разряда:
- \(a_i + b_i < P\). Тогда \(c_i = a_i + b_i\) удовлетворяет условиям теоремы.
- \(P\leq a_i+b_i < 2P-1\). Тогда \[ Y = \ldots + (a_{i+1} + b_{i+1}) P^{i+1} + (a_i+b_i) P^i + \ldots,\] \[ Y = \ldots + (a_{i+1} + b_{i+1}) P^{i+1} + (a_i+b_i-P+P) P^i + \ldots,\] \[ Y = \ldots + (a_{i+1} + b_{i+1}) P^{i+1} + P^{i+1}+ (a_i+b_i-P) P^i + \ldots,\] \[ Y = \ldots + (a_{i+1} + b_{i+1}+1) P^{i+1} + (a_i+b_i-P) P^i + \ldots,\] и тогда \(c_i = a_i+b_i-P < P-1\) удовлетворяет условиям теоремы, а \(a_{i+1}+b_{i+1} +1 < 2P\) может быть рассмотрено аналогично.
Получаем правила сложения: числа складываются поразрядно, начиная с младшего. Если в результате сложения получается число меньшее основания системы счисления, переходим к следующему разряду. Иначе, из результата вычитается основание системы счисления \(P\) и “переносится” как 1 в следующий разряд.
Для облегчения задачи сложения, можно использовать так называемые таблицы сложения. Таблицы сложения составляются достаточно легко для любой P-ичной системы счисления. Рассмотрим несколько примеров.
| 0 | 0 | 1 |
| 1 | 1 | 10 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
| C | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B |
| D | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
| E | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D |
| F | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E |
Пример:
\(\begin{matrix} & A & 4 & D & {}_{16} \\ + & & 8 & C & {}_{16} \\ \hline &&&&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & A & 4 & D & {}_{16} \\ + & & 8 & C & {}_{16} \\ \hline &&\overset{1}{}&9&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & A & 4 & D & {}_{16} \\ + & & 8 & C & {}_{16} \\ \hline &&\overset{1}{C}&9&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & A & 4 & D & {}_{16} \\ + & & 8 & C & {}_{16} \\ \hline &A&\overset{1}{C}&9&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & A & 4 & D & {}_{16} \\ + & & 8 & C & {}_{16} \\ \hline &A&\overset{1}{C}&9&{}_{16} \\ \hline &A&D&9&{}_{16} \end{matrix}\qquad\)
Правила умножения
\[ Y = X_1 \cdot X_2, \] \[ Y = \left(\sum_{i=0}^n a_i P^i\right) \cdot \left(\sum_{i=0}^m b_i P^i\right) \]
Раскрывая вторые скобки, получаем:
\[ Y = \sum_{i=0}^m b_i P^i \left(\sum_{j=0}^n a_j P^j\right) \]
Внося \(P^i\) в скобку,
\[ Y = \sum_{i=0}^m b_i \left(\sum_{j=0}^n a_j P^{j+i}\right) \]
Обозначим \[ Y_i = b_i \cdot \sum_{j=0}^n a_j P^j \]
Тогда \[ Y = \sum_{i=0}^m Y_i P^i \]
Таким образом, каждый разряд \(b_i\) умножается на число \(X_1\), результат смещается на \(i\) разрядов влево (умножается на \(P^i\)), затем все промежуточные результаты складываются (правила сложения нам уже известны).
Рассмотрим теперь умножение на один разряд:
\[ Y_i = b_i \cdot \sum_{j=0}^n a_j P^j = \sum_{j=0}^n a_j b_i P^j = \sum_{j=0}^n c_j P^j .\]
По условиям теоремы, \(0\le c_j < P\). В то же время, \(0 \le a_j b_j \le (P-1)^2\). \((P-1)^2 = P^2 — 2P + 1 < P^2\).
Тогда, имеем два варианта:
- \(a_j b_i<P\). Тогда \(c_j = a_j b_i\) удовлетворяет условиям теоремы.
- \(P \le a_j b_i \le (P-1)^2\). Тогда можем разложить \(a_j b_i = p_j P + c_j\). В разложении не может быть больше двух членов, поскольку \(a_j b_i < P^2\). \(c_j\) очевидно удовлетворяет условиям теоремы, а следующий разряд получает “перенос” \(p_j\): \(a_j b_i + p_j \le P^2 — 2P + 1 + P-1 = P^2-P < P^2\) и может быть рассмотрен аналогично.
Получаем правила умножения: Каждый разряд второго операнда умножается на первый операнд, причем результат смещается на положение этого разряда. Первый операнд умножается на разряд второго поразрядно, начиная с младшего, причем, если результат больше основания системы счисления P, то, записанный в P-ичной системе счисления результат будет иметь два разряда, младший из которых определит текущий разряд промежуточного результата \(Y_i\), а старший будет аддитивно перенесен в следующий.
Для облегчения умножения, существуют таблицы умножения. Их составление немного сложнее, чем таблиц сложения, однако при наличии таблиц сложения оказывается тоже достаточно простым.
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 2 | 0 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E |
| 3 | 0 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D |
| 4 | 0 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C |
| 5 | 0 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B |
| 6 | 0 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A |
| 7 | 0 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 |
| 8 | 0 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 |
| 9 | 0 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 |
| A | 0 | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 |
| B | 0 | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 |
| C | 0 | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 |
| D | 0 | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 |
| E | 0 | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 |
| F | 0 | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 |
Пример:
\(\begin{matrix} & & A & E & {}_{16} \\ \times & & 3 & E & {}_{16} \\ \hline \end{matrix}\qquad\) \(\begin{matrix} & & A & \underline E & {}_{16} \\ \times & & 3 & \underline E & {}_{16} \\ \hline & & C & 4 & {}_{16} \end{matrix}\qquad\) \(\begin{matrix} & & \underline A & E & {}_{16} \\ \times & & 3 & \underline E & {}_{16} \\ \hline & & C & 4 & {}_{16} \\ + & 8 & C & & {}_{16} \end{matrix}\qquad\) \(\begin{matrix} & & A & \underline E & {}_{16} \\ \times & & \underline 3 & E & {}_{16} \\ \hline & & C & 4 & {}_{16} \\ + & 8 & C & & {}_{16} \\ + & 2 & A & & {}_{16} \\ \end{matrix}\qquad\) \(\begin{matrix} & & \underline A & E & {}_{16} \\ \times & & \underline 3 & E & {}_{16} \\ \hline & & & C & 4 & {}_{16} \\ + & & 8 & C & & {}_{16} \\ + & & 2 & A & & {}_{16} \\ + & 1 & E & & & {}_{16} \\ \end{matrix}\qquad\) \(\begin{matrix} & & A & E & {}_{16} \\ \times & & 3 & E & {}_{16} \\ \hline & & & C & 4 & {}_{16} \\ + & & 8 & C & & {}_{16} \\ + & & 2 & A & & {}_{16} \\ + & 1 & E & & & {}_{16} \\ \hline & \overset{1}{1} & \overset{2}{8} & 2 & 4 & {}_{16} \\ \hline & 2 & A & 2 & 4 & {}_{16} \end{matrix}\qquad\)
Правила вычитания и деления
Правила вычитания и деления, как можно понять, абсолютно аналогичны правилам вычитания и деления в столбик в десятичной системе счисления, с той поправкой, что максимальная цифра ограничивается основанием системы счисления \(P\).
Для вычитания можно использовать таблицы сложения, а для деления – таблицы умножения и сложения.
Пример вычитания:
\(\begin{matrix} & A & 4 & D & {}_{16} \\ — & & 8 & C & {}_{16} \\ \hline &&&&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & A & 4 & D & {}_{16} \\ — & & 8 & C & {}_{16} \\ \hline &&&1&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & \dot A & 4 & D & {}_{16} \\ — & & 8 & C & {}_{16} \\ \hline &&C&1&{}_{16} \end{matrix}\qquad\) \(\begin{matrix} & \dot A & 4 & D & {}_{16} \\ — & & 8 & C & {}_{16} \\ \hline &9&C&1&{}_{16} \end{matrix}\qquad\)
Пример деления:
\(\begin{matrix} 8 & D & 6 & {}_{16} \\ & & & \end{matrix}\begin{array}{|llll} D_{16} & \\ \hline & \\ \end{array}\)
\(\begin{matrix} & 8 & D & 6 & {}_{16} \\ — & 8 & 2 & & \\ \hline & & B & 6 \end{matrix} \begin{matrix} \begin{array}{|llll} D & {}_{16} & \\ \hline A \end{array} \\ & \end{matrix}\)
\(\begin{matrix} & 8 & D & 6 & {}_{16} \\ — & 8 & 2 & & \\ \hline & & B & 6 \\ & — & B & 6 \\ \hline &&& 0 \end{matrix} \begin{matrix} \begin{array}{|llll} D & {}_{16} & \\ \hline A & E & {}_{16} \end{array} \\ & \\ & \\ & \end{matrix}\)
Другим интересным следствием теоремы о единственности представления чисел является преобразование чисел между системами счисления.
Если дано число \(X\) в P-ичной системе счисления, то для его перевода в десятичную, достаточно записать представление в виде числового ряда в десятичной системе и вычислить получившееся выражение. Другими словами, каждую цифру перевести в десятичную систему, домножить на ее “вес” (в десятичной системе) и сложить полученные числа.
Например:
\[ ACE_{16} = 10 \cdot 16^2 + 12 \cdot 16 + 14 = 2560 + 192 + 14 = 2766 \]
\[ 10100101110110_2 = 2 + 4 + 16 + 32 + 64 + 256 + 2048 + 8192 = 10614 \]
Рассмотрим разложение числа \(X\) в P-ичной системе счисления:
\[ X = a_n P^n + \ldots + a_1 P^1 + a_0 \]
Если разделить \(X\) на \(P\) с остатком, то получим
\[ \frac{X}{P} = \frac{a_n P^n + \ldots + a_1 P^1 + a_0}{P} \] \[ \frac{X}{P} =a_n P^{n-1} + \ldots + a_1 + \frac{a_0}{P}, \]
то есть \(a_0\) – остаток, а \((a_n P^{n-1} + \ldots + a_1)\) – частное. Если теперь разделить частное на \(P\), получим:
\[\frac{a_n P^{n-1} + \ldots + a_1}{P}= a_n P^{n-2} + \ldots + a_2 + \frac{a_1}{P}.\]
Ясно, что мы можем повторить эту процедуру \(n\) раз, и в результате получим \(0\) в частном и \(a_n\) в остатке.
Таким образом, мы можем получить значения всех разрядов в P-ичном числе, пользуясь его десятичным представлением.
Пример:
\[ 9283_{10} = {?}_2 \] \[ 9283/2 = 4641\;(1)\] \[ 4641/2 = 2320\;(1)\] \[ 2320/2 = 1160\;(0)\] \[ 1160/2 = 580\;(0)\] \[ 580/2 = 290\;(0)\] \[ 290/2 = 145\;(0)\] \[ 145/2 = 72\;(1)\] \[ 72/2 = 36\;(0)\] \[ 36/2 = 18\;(0)\] \[ 18/2 = 9\;(0)\] \[ 9/2 = 4\;(1)\] \[ 4/2 = 2\;(0)\] \[ 2/2 = 1\;(0)\] \[ 1/2 = 0\;(1)\]
Получаем, \[ 9283_{10} = 10010001000011_2 \]
Аналогично, \[ 9283_{10} = {?}_{16} \] \[ 9283/16 = 580\;(3)\] \[ 580/16 = 36\;(4)\] \[ 36/16 = 2\;(4)\] \[ 2/16 = 0\;(2)\] \[ 9283_{16} = 2443_{16}\]
- Смешанная система счисления
- это система счисления с основанием \(Q\), в которой для записи цифр используются числа в системе счисления с основанием \(P\).
Пример смешанного двоично-шестнадцатиричного числа: \[ {[1011_2][1110_2][1110_2][1111_2]}_{16} \]
Пример смешанного десятично-шестнадцатиричного числа:
\[ {[11][14][14][15]}_{16} \]
Интересная особенность проявляется в PQ-ичных системах счисления, в которых основание Q – это степень основания P.
Рассмотрим две системы счисления с основаниями \(P\) и \(Q\), причем \(Q = P^k\), где \(m\in\mathbb{N}\). Тогда число \(X\) можно разложить как \[ X = \sum_{i=0}^n a_i P^i, \] \[ X = \sum_{j=0}^{m} b_j Q^j.\]
Приравняв оба представления и подставив \(Q = P^k\),
\[ \sum_{i=0}^n a_i P^i = \sum_{j=0}^{m} b_j P^{kj}\] \[ a_n P^n + \ldots + a_{2k-1} P^{2k-1} + \ldots + a_{k} P^{k} + a_{k-1} P^{k-1} + \ldots + a_0 = b_m P^{km} + \ldots + b_1 P^k + b_0\] \[ a_n P^n + \ldots + \left( a_{2k-1} P^{k-1} + \ldots + a_{k}\right) P^{k} + a_{k-1} P^{k-1} + \ldots + a_0 = b_m P^{km} + \ldots + b_1 P^k + b_0.\]
Пользуясь методом неопределенных коэффициентов, можем сказать, что
\[b_0 = a_{k-1} P^{k-1} + \ldots + a_0,\] \[b_1 = a_{2k-1} P^{k-1} + \ldots + a_k,\] \[\ldots\]
Получаем, что каждая Q-ичная цифра соответствует P-ичному числу из \(k\) цифр, и наоборот.
Эта связь позволяет легко переводить числа между системами счисления с основаниями \(P\) и \(Q\), если \(Q = P^k\).
Для перевода из P-ичной в Q-ичную, число разбивается на группы по \(k\) P-ичных цифр, и каждая из групп переводится в Q-ичную систему счисления.
Для перевода из Q-ичной в P-ичную, каждая Q-ичная цифра переводится в P-ичную систему счисления, и при необходимости дополняется слева нулями до \(k\) цифр.
Пример:
\[ BEEF_{16} = {?}_{2} \] \[ B_{16} = 1011_{2} \] \[ E_{16} = 1110_{2} \] \[ F_{16} = 1111_{2} \] \[ BEEF_{16} = {[1011_2][1110_2][1110_2][1111_2]}_{16} = {1011\,1110\,1110\,1111}_{2} \]
Несложно оказывается написать программу, которая автоматически строит таблицы сложения и умножения.
Некоторые примеры:
wiki.livid.pp.ru
|
Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
Пример 2. Сложим числа 15, 7 и 3.
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416 Проверка. Преобразуем полученные суммы к десятичному виду: 311,28 = 3*82 + 1•81 + 1*80 + 2*8-1 = 201,25 C9,416 = 12*161 + 9*160 + 4*16-1 = 201,25
Вычитание Пример 4. Вычтем единицу из чисел 102, 108 и 1016 Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016. Пример 6.Вычтем число 59,75 из числа 201,25. Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816. Проверка. Преобразуем полученные разности к десятичному виду: 215,48 = 2*82 + 1*81 + 5*80 + 4*8–1 = 141,5; 8D,816 = 8*161 + D*160 + 8*16–1 = 141,5.
Умножение Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям. Пример 7. Перемножим числа 5 и 6. Ответ: 5*6 = 3010 = 111102 = 368. Проверка. Преобразуем полученные произведения к десятичному виду: 368 = 3•81 + 6•80 = 30. Пример 8. Перемножим числа 115 и 51. Ответ: 115*51 = 586510 = 10110111010012 = 133518. Проверка. Преобразуем полученные произведения к десятичному виду: 133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865. Деление Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей. Пример 9. Разделим число 30 на число 6. Ответ: 30 : 6 = 510 = 1012 = 58. Пример 10. Разделим число 5865 на число 115. Восьмеричная: 133518 :1638 Ответ: 5865 : 115 = 5110 = 1100112 = 638. Проверка. Преобразуем полученные частные к десятичному виду: Пример 11. Разделим число 35 на число 14. Восьмеричная: 438 : 168 Ответ: 35 : 14 = 2,510 = 10,12 = 2,48. Проверка. Преобразуем полученные частные к десятичному виду:
Упражнения 2.1. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: (№ варианта соответствует № рабочего места)
2.2. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: (№ варианта соответствует № рабочего места)
2.3. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: (№ варианта соответствует № рабочего места)
2.4. Выпишите целые числа: а) от 1011012 до 1100002 в двоичной системе; б) от 2023 до 10003 в троичной системе; в) от 148 до 208 в восьмеричной системе; г) от 2816 до 3016 в шестнадцатеричной системе.
2.5. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
2.6. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
2.7. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: (№ варианта соответствует № рабочего места)
2.8. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:
2.9. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
2.10. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
|
megapredmet.ru