1.18
1.18. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ХАРАКТЕРИСТИКИ
Определение гармонических колебаний. Характеристики гармонических колебаний: смещение от положения равновесия, амплитуда колебаний, фаза колебания, частота и период колебаний. Скорость и ускорение колеблющейся точки. Энергия гармонического осциллятора. Примеры гармонических осцилляторов: математический, пружинный, крутильный и физический маятники.
Акустика, радиотехника, оптика и другие разделы науки и техники базируются на учении о колебаниях и волнах. Большую роль играет теория колебаний в механике, в особенности в расчетах на прочность летательных аппаратов, мостов, отдельных видов машин и узлов.
Колебания являются процессами, повторяющимися через одинаковые промежутки времени (при этом далеко не все повторяющиеся процессы являются колебаниями!). В зависимости от физической природы повторяющегося процесса различают колебания механические, электромагнитные, электромеханические и т.п. При механических колебаниях периодически изменяются положения и координаты тел.
Возвращающая сила — сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.
В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.
В зависимости от характера воздействия на колеблющуюся систему различают свободные колебания, вынужденные, автоколебания и параметрические колебания.
Свободными (собственными) колебаниями называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она была выведена из положения равновесия, т.е. когда на колеблющееся тело действует только возвращающая сила.. Примером могут служить колебания шарика, подвешенного на нити. Для того, чтобы вызвать колебания, надо либо толкнуть шарик, либо, отведя в сторону, отпустить его. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).
· Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы (например, колебания моста, возникающие при прохождении по нему людей, шагающих в ногу). Во многих случаях системы совершают колебания, которые можно считать гармоническими.
· Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако, моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой. То есть система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.
· Параметрические колебания осуществляются при периодическом изменении параметров колеблющейся системы (качающийся на качелях человек периодически поднимает и опускает свой центр тяжести, тем самым меняя параметры системы). При определенных условиях система становится неустойчивой — случайно возникшее отклонение из положения равновесия приводит к возникновению и нарастанию колебаний. Это явление называется параметрическим возбуждением колебаний (т.е. колебания возбуждаются за счет изменения параметров системы), а сами колебания – параметрическими.
Несмотря на разную физическую природу, для колебаний характерны одни и те же закономерности, которые исследуются общими методами. Важной кинематической характеристикой является форма колебаний. Она определяется видом той функции времени, которая описывает изменение той или иной физической величины при колебаниях. Наиболее важными являются такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Они называются гармоническими.
Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).
Этот вид колебаний особенно важен по следующим причинам. Во-первых, колебания в природе и в технике часто имеют характер очень близких к гармоническим. Во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение, или суперпозиция,
Уравнение гармонического осциллятора
Гармоническое колебание описывается периодическим законом:
. (18.1)
Рис. 18.1. Гармоническое колебание
З
десь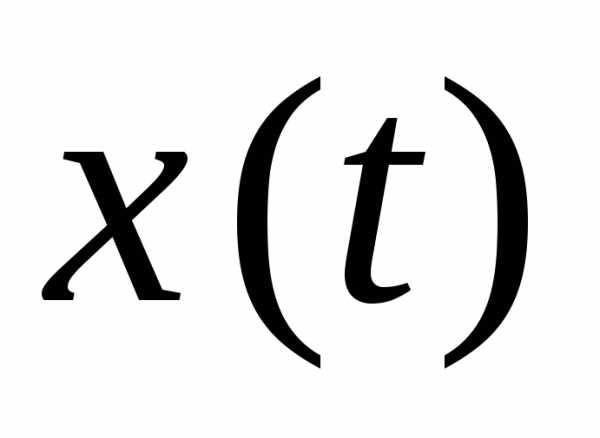 —
характеризует изменение
какой-либо физической величины при
колебаниях (смещение положения маятника
из положения равновесия; напряжение на
конденсаторе в колебательном контуре
и т.д.), A
— амплитуда
колебаний,
—
характеризует изменение
какой-либо физической величины при
колебаниях (смещение положения маятника
из положения равновесия; напряжение на
конденсаторе в колебательном контуре
и т.д.), A
— амплитуда
колебаний,
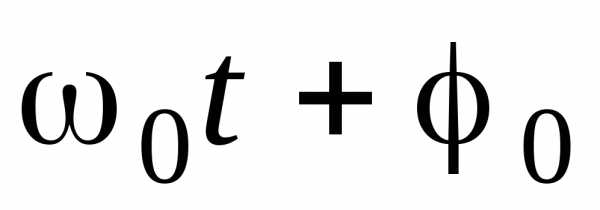 —
фаза
колебаний,
—
фаза
колебаний,
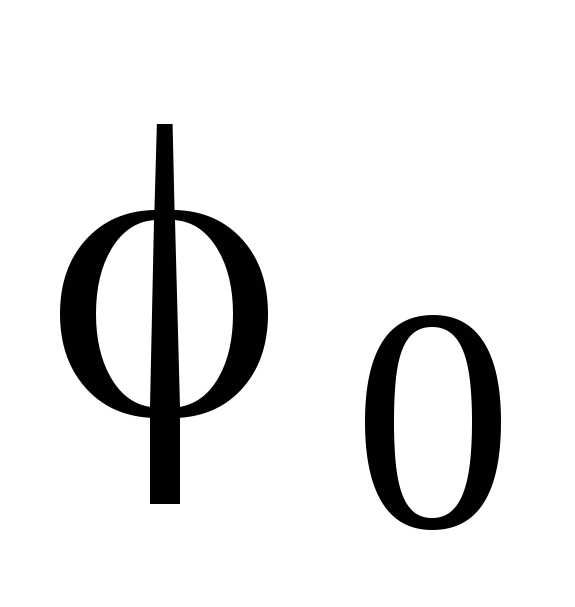 —
начальная
фаза,
—
начальная
фаза,
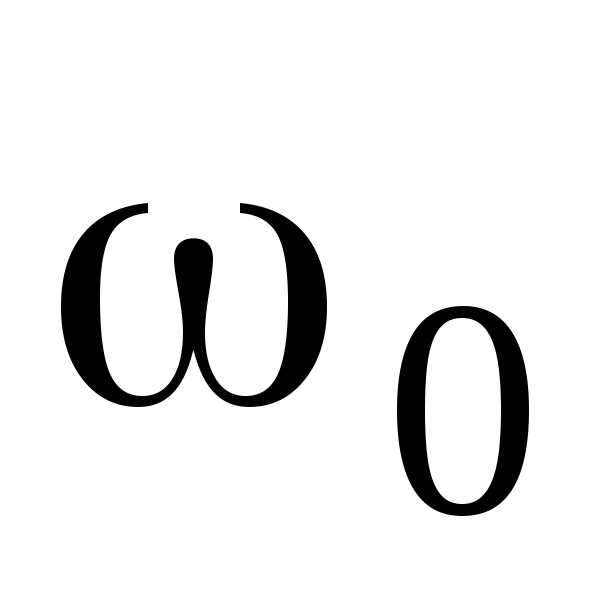 —
циклическая
частота;
величину
—
циклическая
частота;
величину 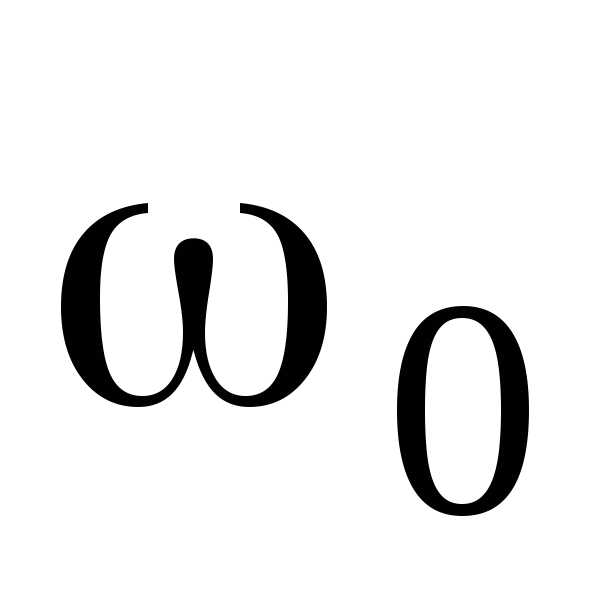 называют
также
собственной
частотой
колебаний. Такое название подчеркивает,
что эта частота определяется параметрами
колебательной системы. Система, закон
движения которой имеет вид (18.1), называется
одномерным
гармоническим осциллятором.
Помимо перечисленных величин для
характеристики колебаний вводят понятия
периода,
т.е. времени одного колебания.
называют
также
собственной
частотой
колебаний. Такое название подчеркивает,
что эта частота определяется параметрами
колебательной системы. Система, закон
движения которой имеет вид (18.1), называется
одномерным
гармоническим осциллятором.
Помимо перечисленных величин для
характеристики колебаний вводят понятия
периода,
т.е. времени одного колебания.
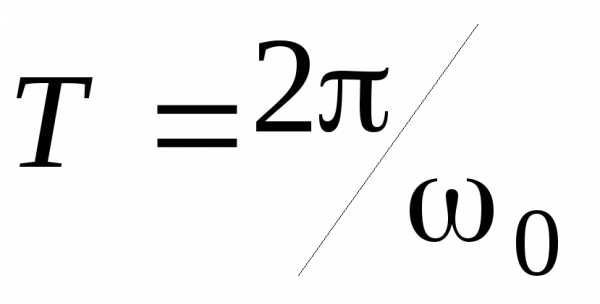
(Периодом колебаний
и частоты , определяющей число колебаний в единицу времени. За единицу частоты принимается частота такого колебания, период которого равен 1 с. Эту единицу называют герцем (Гц).
Частотой колебаний n называется величина обратная периоду колебаний — число полных колебаний, совершаемых в единицу времени.
Амплитуда — максимальное значение смещения или изменения переменной величины при колебательном или волновом движении.
Фаза колебаний — аргумент периодической функции или описывающей гармонический колебательный процесс (ω— угловая частота, t— время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0).
Первая и вторая производные по времени от гармонически колеблющейся величины также совершают гармонические колебания той же частоты:
,
. (18.2)
В данном случае за основу взято уравнение гармонических колебаний, записанное по закону косинуса. При этом первое из уравнений (18.2) описывает закон, по которому изменяется скорость колеблющейся материальной точки (тела), второе уравнение описывает закон, по которому изменяется ускорение колеблющейся точки (тела).
Амплитуды
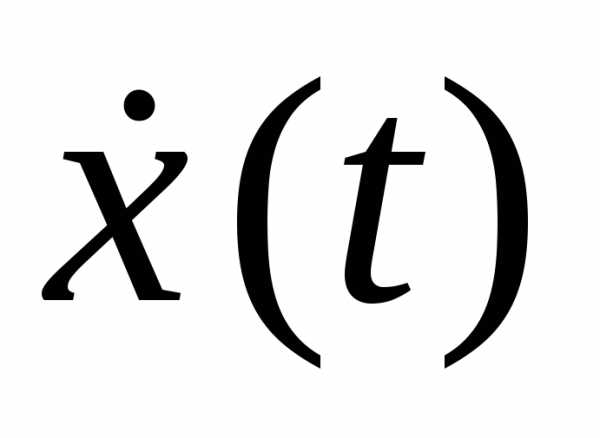 и
и
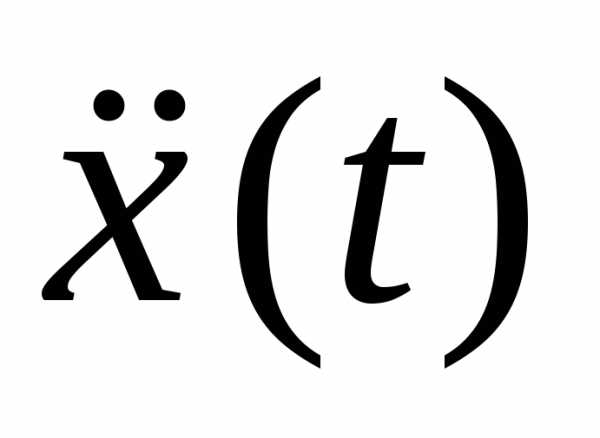 равны
соответственно
равны
соответственно 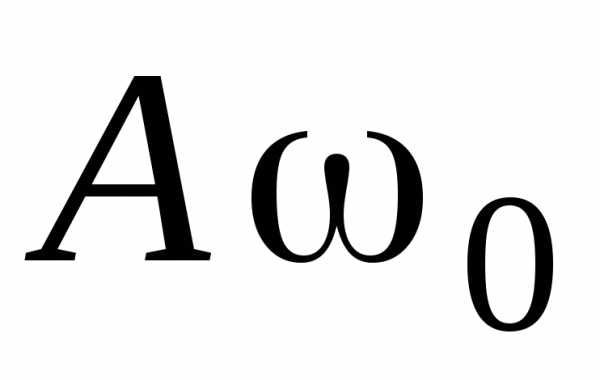
 .
Колебание
.
Колебание 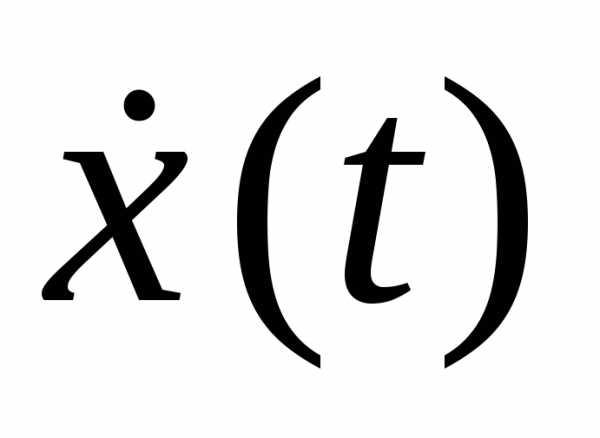 опережает
опережает
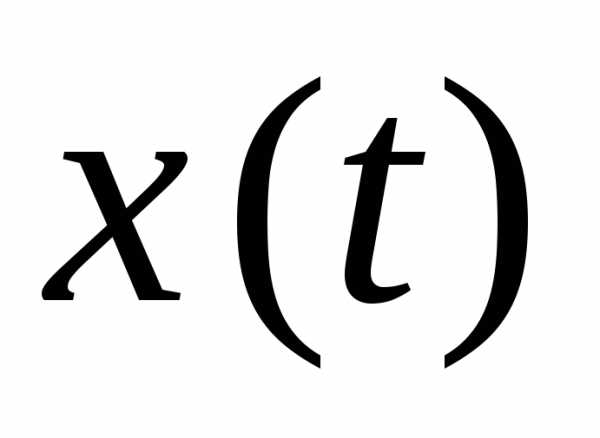 по
фазе на
по
фазе на  ;
а колебание
;
а колебание 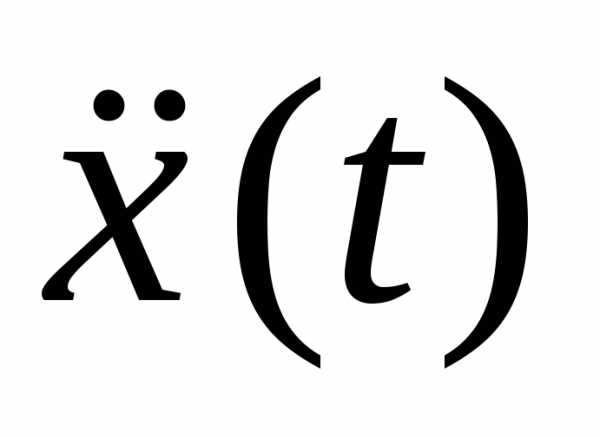 опережает
опережает
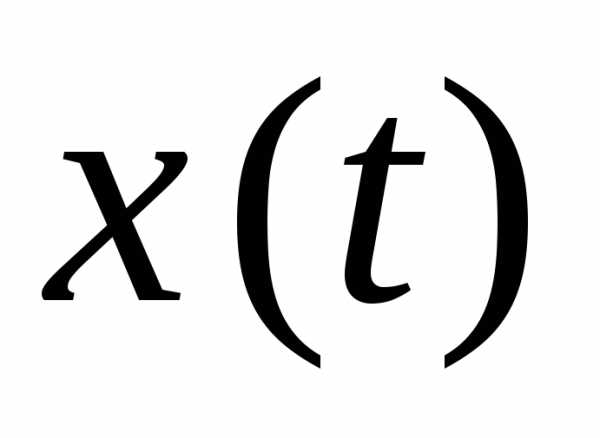 на
на
 .
Значения A
и
.
Значения A
и 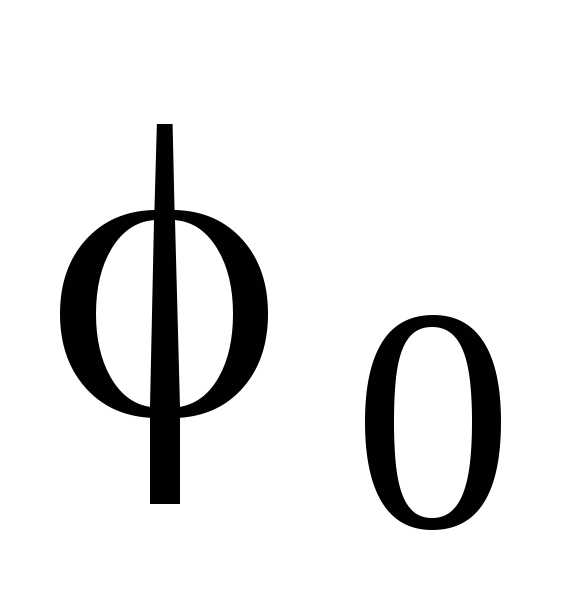 могут
быть определены из заданных начальных
условий
могут
быть определены из заданных начальных
условий 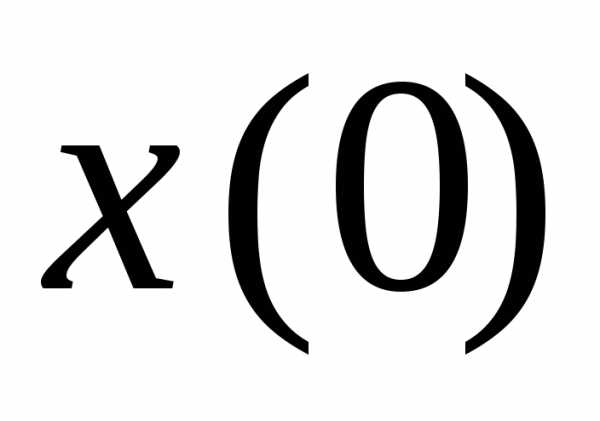 и
и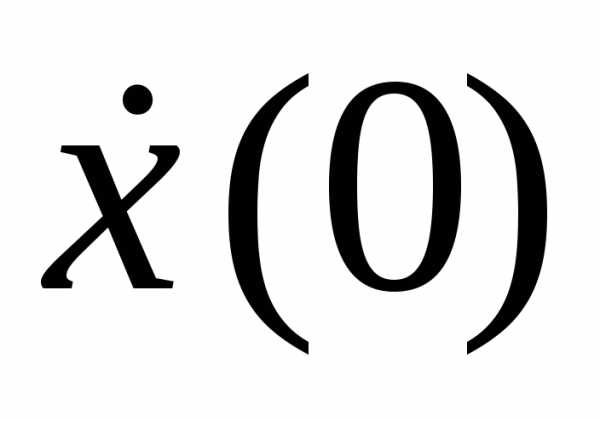 :
:
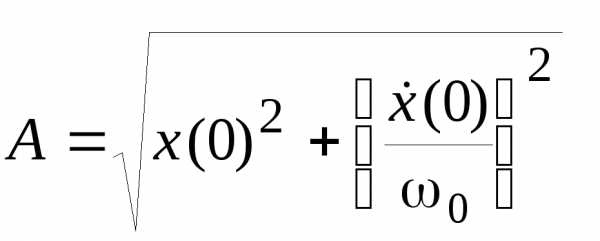 ,
,
 . (18.3)
. (18.3)
Энергия колебаний осциллятора
П
|
Рис. 18.2. Пружинный маятник |
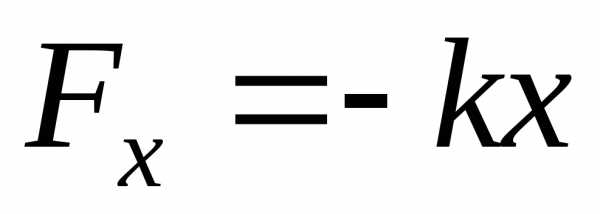 (к
примеру, пружинный маятник, см. рис.
18.2). Силы иной природы, чем упругие, но
в которых выполняется условие F
= -kx,
называются
(к
примеру, пружинный маятник, см. рис.
18.2). Силы иной природы, чем упругие, но
в которых выполняется условие F
= -kx,
называются |
смещение: | |
|
скорость: | |
|
ускорение: |
Т.е.
уравнение таких колебаний имеет вид
(18.1) с собственной частотой 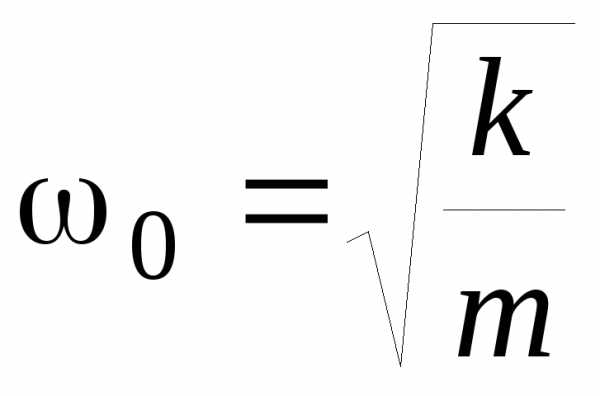 .
Квазиупругая сила является консервативной.
Поэтому полная энергия таких гармонических
колебаний должна оставаться постоянной.
В процессе колебаний происходит
превращение кинетической энергии Eк
в потенциальную Eп
и обратно, причем в моменты наибольшего
отклонения от положения равновесия
полная энергия равна максимальному
значению потенциальной энергии, а при
прохождении системы через положение
равновесия полная энергия равна
максимальному значению кинетической
энергии. Выясним, как изменяется со
временем кинетическая и потенциальная
энергия:
.
Квазиупругая сила является консервативной.
Поэтому полная энергия таких гармонических
колебаний должна оставаться постоянной.
В процессе колебаний происходит
превращение кинетической энергии Eк
в потенциальную Eп
и обратно, причем в моменты наибольшего
отклонения от положения равновесия
полная энергия равна максимальному
значению потенциальной энергии, а при
прохождении системы через положение
равновесия полная энергия равна
максимальному значению кинетической
энергии. Выясним, как изменяется со
временем кинетическая и потенциальная
энергия:
Кинетическая энергия:
|
(18.4) |
Потенциальная энергия:
(18.5)
Учитывая то, что т.е. , последнее выражение можно записать в виде:
|
(18.6) |
Полная энергия колеблющегося тела равна сумме кинетической и потенциальной энергий
|
(18.7) |
Таким
образом, полная энергия гармонического
колебания оказывается постоянной. Из
соотношений (18.4) и (18.5) также следует,
что средние значения кинетической и
потенциальной энергии равны друг другу
и половине полной энергии, поскольку
средние значения и
за
период равны 0,5. Используя тригонометрические
формулы, можно получить, что кинетическая
и потенциальная энергия изменяются с
частотой 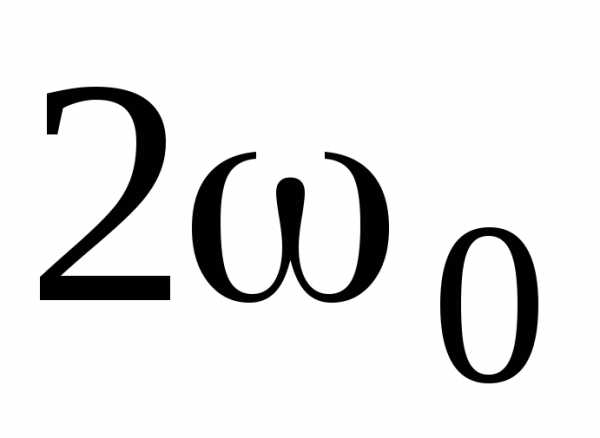 ,
т.е. с частотой в два раза превышающей
частоту гармонического колебания.
,
т.е. с частотой в два раза превышающей
частоту гармонического колебания.
В качестве примеров гармонического осциллятора могут быть пружинный, физический, математический маятники и крутильный маятники.
1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или (18.8) Из формулы (18.8) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
(18.9) и периодом
(18.10) Формула (18.10) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (18.9) и формулу потенциальной энергии предыдущего раздела, равна (см.18.5)
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).
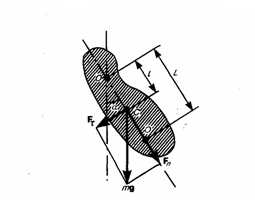
Рис.18.3 Физический маятник
Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы (18.11) где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (18.11) запишем как
или Принимая (18.12) получим уравнение
идентичное с (18.8), решение которого найдем и запишем как:
(18.13) Из формулы (18.13) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
(18.14) где введена величина L=J/(ml) — приведенная длина физического маятника. Точка О’ на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 18.3). Применяя теорему Штейнера для момента инерции оси, найдем
т. е. ОО’ всегда больше ОС. Точка подвеса О маятника и центр качаний О’ имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника
(8) где l — длина маятника.
Поскольку
математический маятник есть частный
случай физического маятника, если
предположить, что вся его масса
сосредоточена в одной точке — центре
масс, то, подставив (8) в (7), найдем выражение
для периода малых колебаний математического
маятника
(18.15)
Сопоставляя формулы (18.13) и (18.15),
видим, что если приведенная длина L
физического маятника равна длине l
математического маятника, то периоды
колебаний этих маятников одинаковы.
Значит, приведенная
длина физического маятника
— это длина такого математического
маятника, у которого период колебаний
совпадает с периодом колебаний данного
физического маятника. Для математического
маятника (материальной точки массой m,
подвешенной на невесомой нерастяжимой
нити длиной l
в поле силы тяжести с ускорением
свободного падения равным g)
при малых углах отклонения (не превышающих
5-10 угловых градусов) от положения
равновесия собственная частота колебаний:
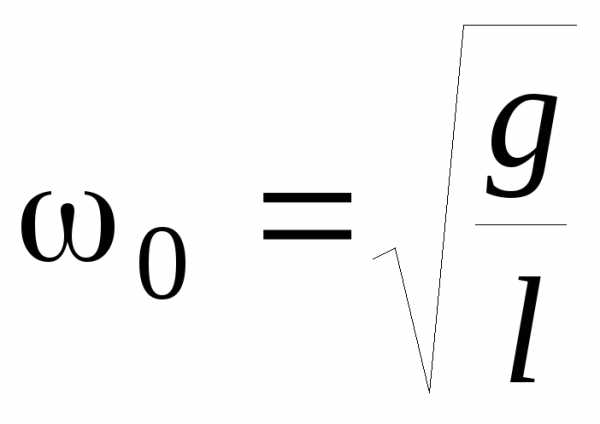 .
.
4. Тело, подвешенное на упругой нити или другом упругом элементе, совершающее колебания в горизонтальной плоскости, представляет собой крутильный маятник.
Эта механическая колебательная система, которая использует силы упругих деформаций. На рис. 18.4 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол θ возникает момент сил Mупр упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина χ аналогична жесткости пружины k. Второй закон Ньютона для вращательного движения диска записывается в виде
где I = IC – момент инерции диска относительно оси, проходящий через центр масс, ε – угловое ускорение.
По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.
|
Рисунок 18.4. Крутильный маятник |
10
studfiles.net
Свободные гармонические колебания
Колебания, которые совершает система около положения равновесия после того, как она была выведена из состояния равновесия, носят название собственных или свободных колебаний. Свободные колебания возникают в результате достаточно быстрого изменения действующей на тело силы, т.е. воздействия, имеющего характер толчка.
Рассмотрим
цилиндрическую пружины, один конец
которой закреплён, а к другому подвешено
тело (например, металлический шарик)
массой m.
Будем считать, что на тело действуют
сила тяжести
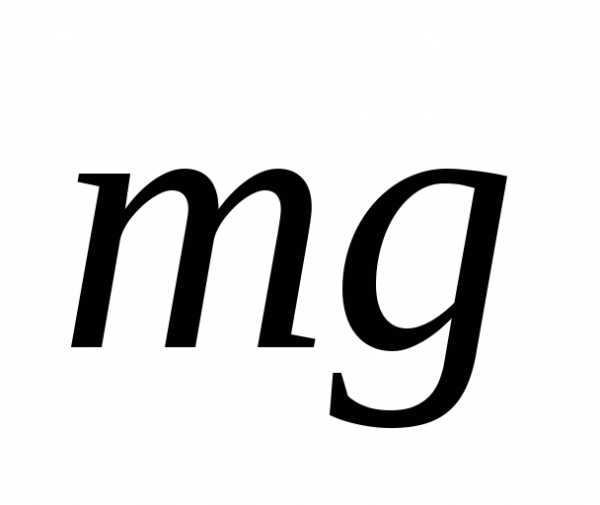 и сила упругости
и сила упругости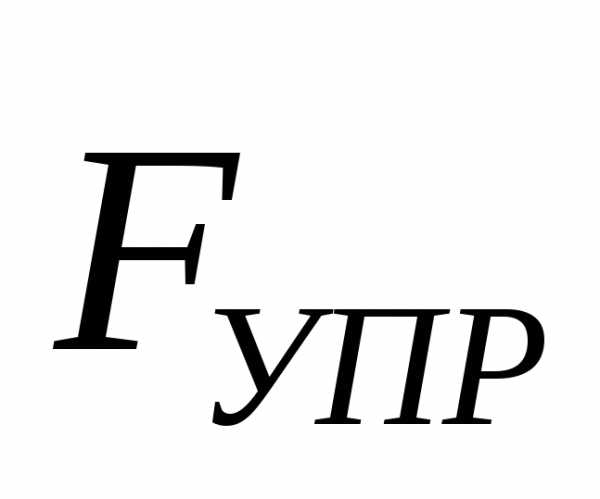 (силу сопротивления, действующую на
тело при движении в реальной среде,
считаем пренебрежимо малой величиной).
Запишем теорему о движении центра масс
тела в случае простой упругой деформации
пружины – продольного растяжения
(сжатия):
(силу сопротивления, действующую на
тело при движении в реальной среде,
считаем пренебрежимо малой величиной).
Запишем теорему о движении центра масс
тела в случае простой упругой деформации
пружины – продольного растяжения
(сжатия):
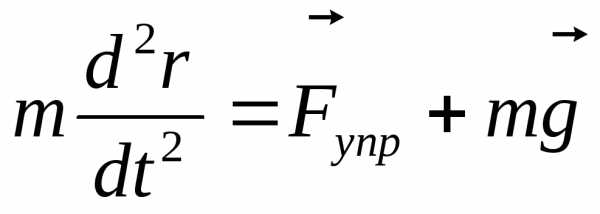 .
.
Рассмотрим
задачу, в которой сила тяжести
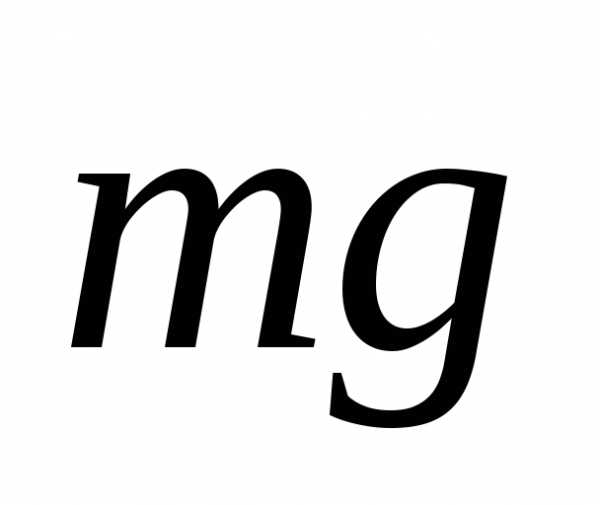 и сила упругости
и сила упругости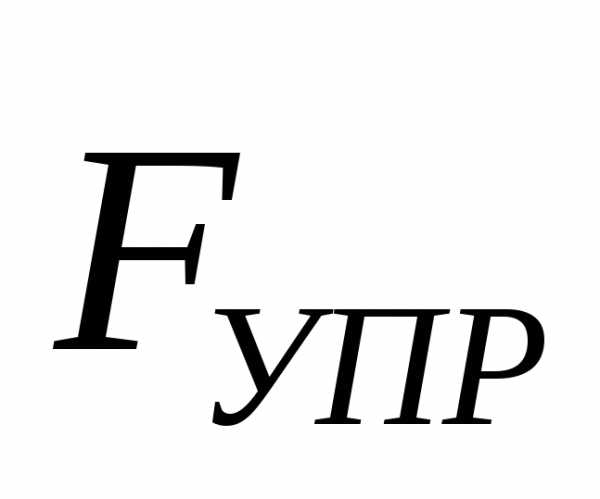 направлены
вдоль одной прямой, совпадающей с осью
пружины. Направив ось0Х
вдоль оси пружины, получаем одномерную
задачу. Теорема о движении центра масс,
записанная в проекции на ось 0Х,
имеет вид:
направлены
вдоль одной прямой, совпадающей с осью
пружины. Направив ось0Х
вдоль оси пружины, получаем одномерную
задачу. Теорема о движении центра масс,
записанная в проекции на ось 0Х,
имеет вид:
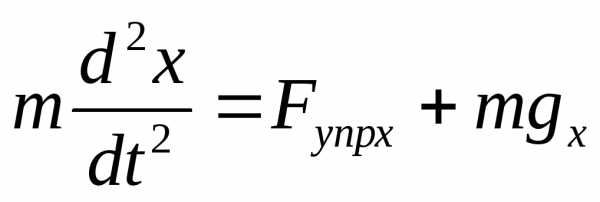 . (1)
. (1)
В
положении равновесия
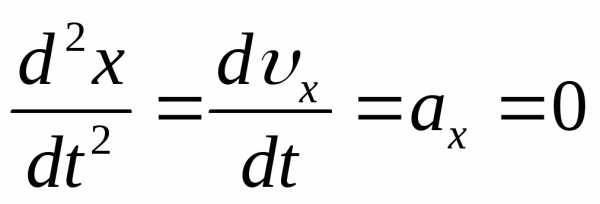 и
сумма сил, действующих на шарик равна
нулю. Отсюда, обозначив координату
центра масс груза в положении равновесия
и
сумма сил, действующих на шарик равна
нулю. Отсюда, обозначив координату
центра масс груза в положении равновесия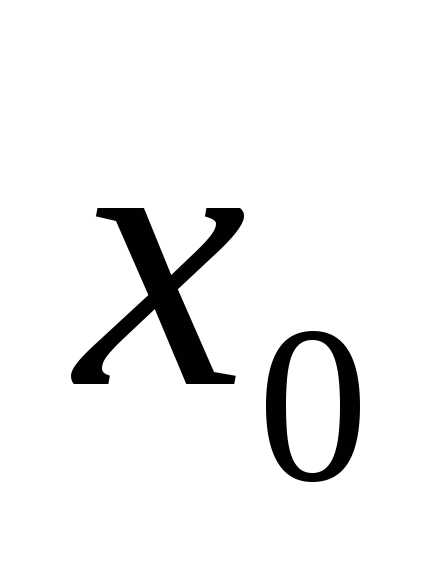 ,
имеем:
,
имеем:
;
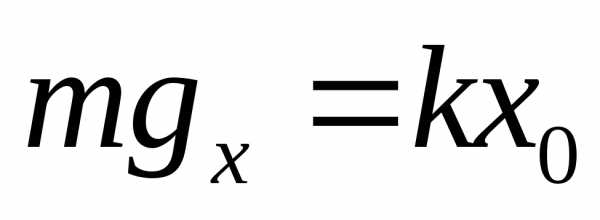 . (2)
. (2)
Подставляя (2) в (1):
 ,
но
,
но
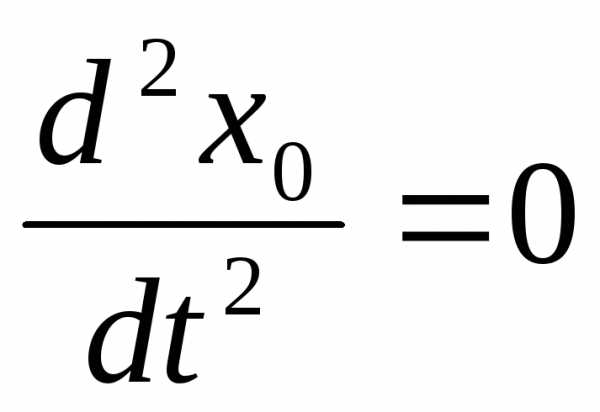 .
.
Следовательно:
 ,
где
или
,
где
или
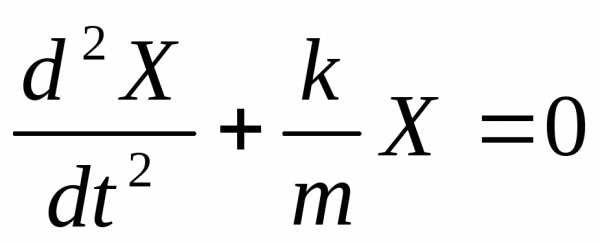 (3)
(3)
Величина Х определяет смещение груза из положения равновесия. Само положение равновесия смещается под действием силы тяжести, но это не затрагивает математическую сторону колебательного процесса.
 ,
где
,
где
 ,
,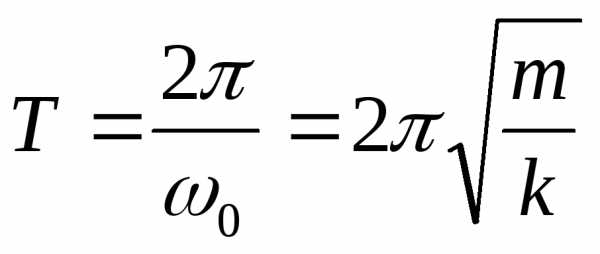 – циклическая частота и период колебаний.
Период колебаний не зависит от амплитудыА
(это свойство называется изохронностью
колебаний).
– циклическая частота и период колебаний.
Период колебаний не зависит от амплитудыА
(это свойство называется изохронностью
колебаний).
Затухающие колебания материальной точки
Ранее мы рассматривали случаи колебаний, при которых на движущееся тело не действуют силы сопротивления. Во всякой реальной колебательной системе силы сопротивления имеются. На преодоление сопротивления затрачивается энергия колебательного движения и, в конечном счёте, колебания затухают.
Рассмотрим один из наиболее часто встречающихся на практике случаев, когда сила сопротивления пропорциональна скорости материальной точки:
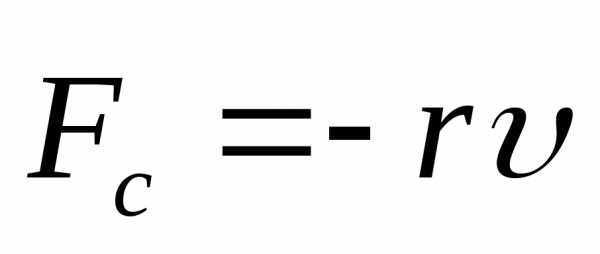 .
.
В одномерном случае
, (4)
где r – коэффициент сопротивления. Тогда уравнение, описывающее затухающие колебания при наличии действующих на материальную точку силы упругости и силы сопротивления, будет иметь вид:
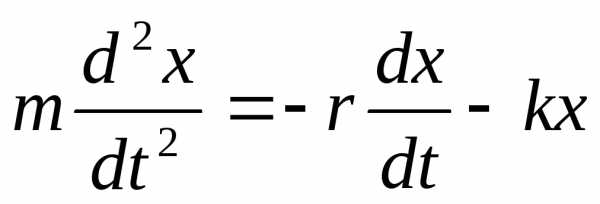 .
.
Введя
обозначения
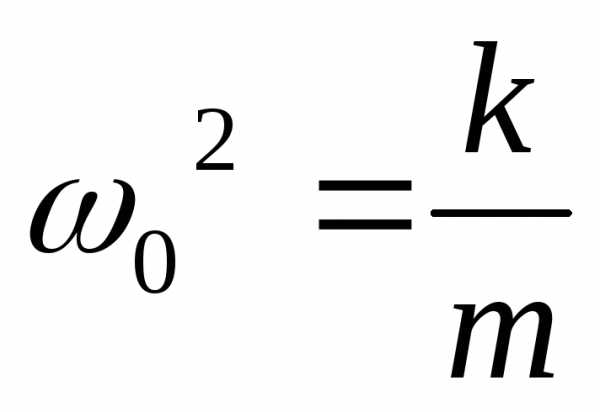 ,
,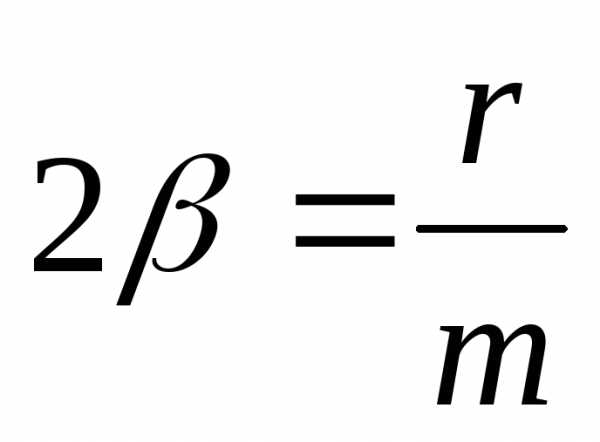 ,
получаем следующее уравнение:
,
получаем следующее уравнение:
. (5)
В случае гармонического осциллятора размах колебаний, определяемый амплитудой А, остаётся постоянным. Наличие сопротивления среды приводит к тому, что размах колебаний уменьшается. Поэтому будем искать решение уравнения (5) в виде:
, (6)
где А(t) – некоторая функция времени. Продифференцировав (6) по времени, находим:
.
После подстановки этих выражений в (5) получаем:
.
Отсюда:
 ;
;
(7)
;
;
(7)
Запишем первое уравнение в виде:
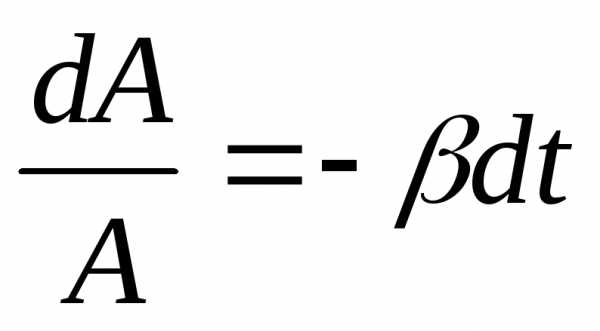 .
.
Проинтегрировав полученное уравнение, получим: . В результате потенцирования имеем:. Легко видеть, что:
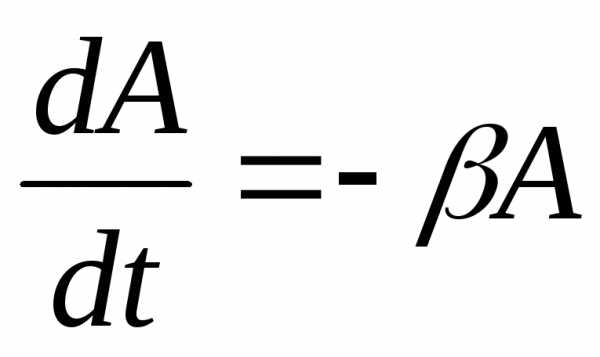 ;
;
 .
.
Подставим данные соотношения в (7):
.
Величина
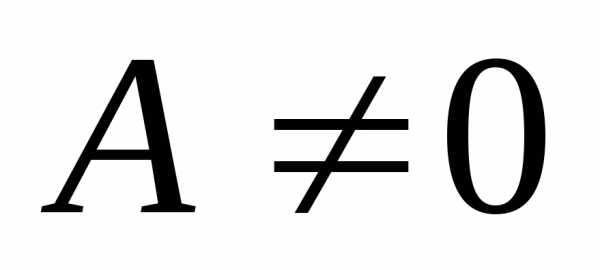 .
Отсюда:
.
Отсюда:
.
При
условии, что
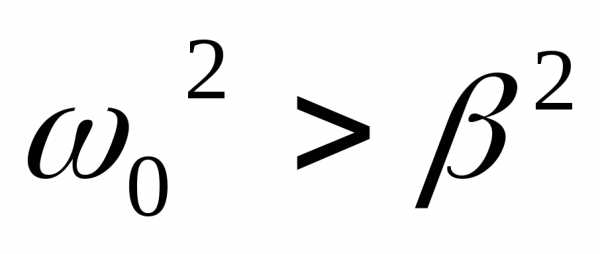 ,
величина
,
величина
 будет
вещественной, и решение уравнения (5)
может быть представлено в виде:
будет
вещественной, и решение уравнения (5)
может быть представлено в виде:
З десь
десь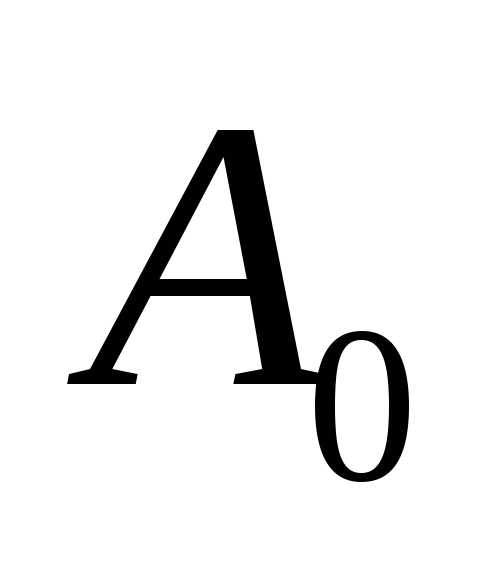 – начальная амплитуда,
– начальная амплитуда,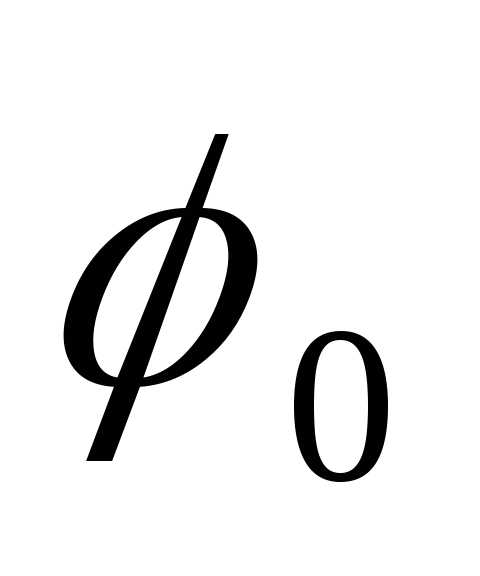 – начальная фаза колебаний.
– начальная фаза колебаний.
Период колебаний:
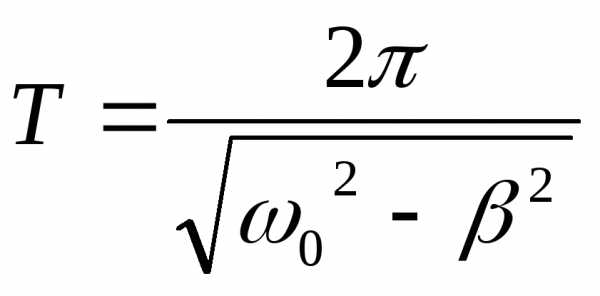 . (8)
. (8)
Амплитуда
колебаний уменьшается по закону:
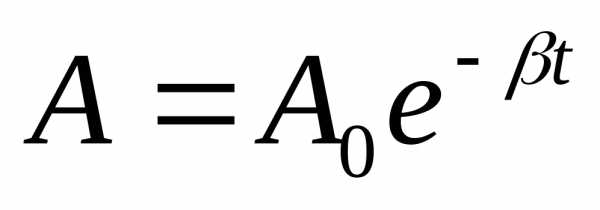 (
(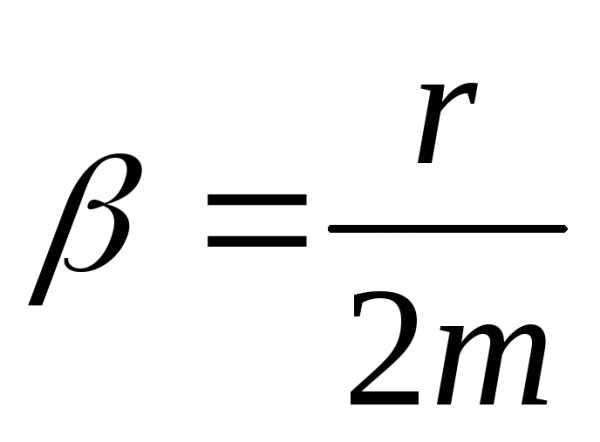 – коэффициент затухания).
– коэффициент затухания).
При процесс перестаёт быть периодическим.
В
результате затухания колебаний состояние
системы (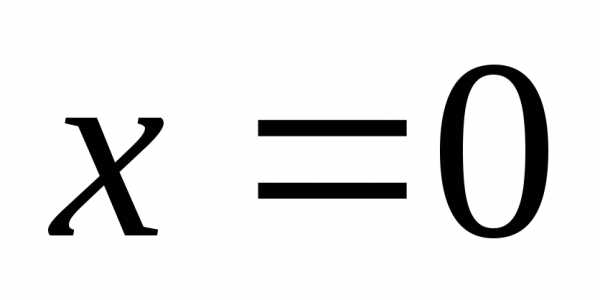
 )
переходит в равновесие. Процесс, в
результате которого параметры,
характеризующие физическую систему,
переходят к своим равновесным значениям,
называютпроцессом
релаксации.
Время, в течение которого отклонения
системы от равновесия уменьшается в е
раз, называют временем релаксации.
Найдём время релаксации
)
переходит в равновесие. Процесс, в
результате которого параметры,
характеризующие физическую систему,
переходят к своим равновесным значениям,
называютпроцессом
релаксации.
Время, в течение которого отклонения
системы от равновесия уменьшается в е
раз, называют временем релаксации.
Найдём время релаксации
 :
:
 или
,
или
,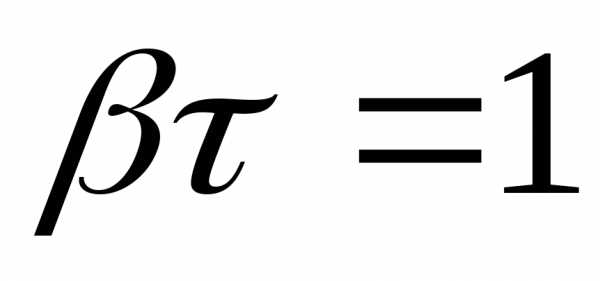 и
и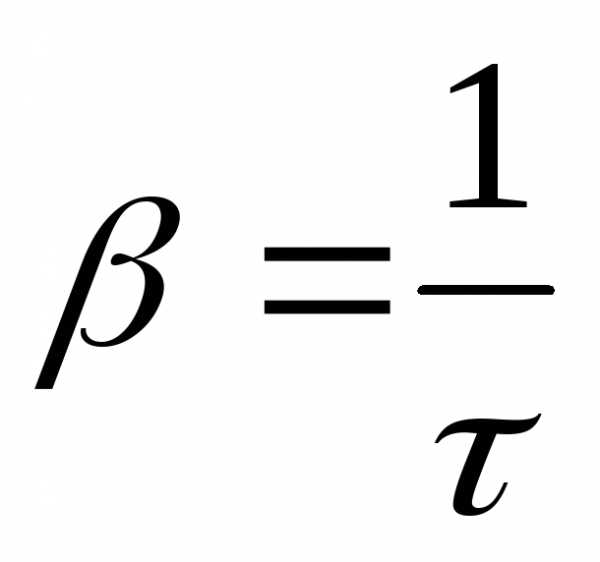 .
.
Таким образом, коэффициент затухания есть величина обратная промежутку времени, за который амплитуда колебаний уменьшается в е раз.
Отношение двух произвольных последовательных амплитуд при затухающих колебаниях есть величина постоянная:
.
Это отношение называют декрементом затухания, а логарифм этого отношения – логарифмическим декрементом затухания:
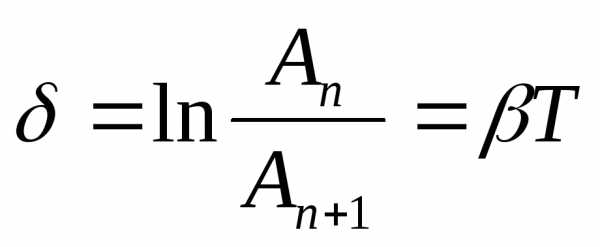 . (9)
. (9)
Логарифмический
декремент затухания является естественной
характеристикой затухания, которая
показывает, как амплитуда колебаний
изменяется за один период. Тогда как
коэффициент затухания
 определяет время, в течение которого
амплитуда уменьшается ве
раз.
определяет время, в течение которого
амплитуда уменьшается ве
раз.
Часто
колебательные системы характеризуют
также добротностью. Добротностью
называют отношение энергии в системе
в данный момент времени и убыли энергии
за период, умноженный на
 .
.
. (10)
Поскольку энергия E(t) пропорциональна квадрату амплитуды колебаний:
.
Учитывая (9):
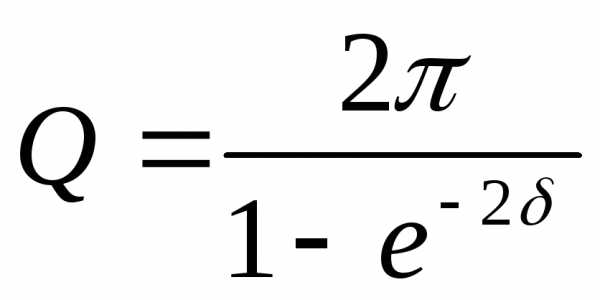 .
.
Разлагая в ряд и ограничиваясь первыми двумя членами разложения, получим:
 .
.
Добротность системы обратно пропорциональна логарифмическому декременту затухания.
studfiles.net
Свободные гармонические колебания
Гармонические колебания — периодический процесс, в котором рассматриваемый параметр изменяется по гармоническому закону. Если на колебательную систему не действуют внешние переменные силы, то такие колебания называются свободными. Рассмотрим массу, которая колеблется на пружине как показано на рисунке. Если амплитуда колебаний мала, то координата x массы по вертикальной оси изменяется по гармоническому закону:
x = Asin(wt + j)
где A — амплитуда колебаний, t — время, j — фаза колебаний, w — угловая частота колебаний, w = 2pn = 2p /T, n — частота колебаний, T — период колебаний.
Далее мы найдём период колебаний T пружинного маятника, состоящего из грузика массой m и пружины жёсткостью k. Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояние x, то на грузик со стороны пружины будет действовать сила -kx. Помимо этого на грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a — ускорение. Таким образом, мы можем записать дифференциальное уравнение для пружинного маятника:
md2x/dt2 = -kx + mg
где g — ускорение свободного падения в гравитационном поле,d2x/dt2 — вторая производная координаты x по времени t. Это уравнение имеет следующее решение:
x = Asin[(k/m)1/2t + j] + mg/k
Мы можем видеть из этой формулы, что период колебаний равен
T = 2p(m/k)1/2
и, соответственно, угловая частота w равна
w = (k/m)1/2
Амплитуда колебаний A и фаза колебаний j зависят от начальных условий (в момент времени t=0): начального смещение грузика x0 и начальной скорости v0. В состоянии равновесия пружина растянута на величину mg/k.
Предположим, что колеблющийся грузик связан с пером, который рисует линию на бумажной ленте. Если лента движется равномерно в горизонтальном направлении, то перо будет рисовать на ней синусоиду. Зная скорость движения ленты и период синусоиды, мы можем вычислить период колебаний грузика на пружине.
В общем случае на осциллятор действует сила трения, пропорциональная скорости движения грузика: F=av. В случае пружинного маятника эта сила возникает из-за сопротивления воздуха и неупругих свойств самого материала, из которых изготовлена пружина. В результате, амплитуда колебаний будет со временем уменьшаться. Уравнение свободного гармонического осциллятора с затуханием может быть записано следующим образом:
m(d2x/dt2) + a (dx/dt) + kx = mg
где a — коэффициент трения. Это уравнение может быть переписано в виде
d2x/dt2+ 2g(dx/dt) + W2x = g
где 2g = a / m; W2=k /m
В случае, когда W2 > g2 уравнение колебаний свободного гармонического осциллятора с затуханием имеет следующее решение:
x = Ae-gtcos(wt + j )
При этом период колебаний зависит от коэффициента затухания g :
T = 2p/w = 2p/(W2 -g2)1/2
www.examen.ru
09_гармонические колебания
Федун В.И. Конспект лекций по физике Механические колебания и волны
Колебания и упругие волны.
Лекция 9.
8. Гармонические колебания и их основные характеристики.
8. 1. Свободные колебания и их основные характеристтики. Представления гармонических колебаний.
Колебательным движением называется движение, обладающее той или иной степенью повторяемости во времени. Движение называется периодическим, если значения величин, изменяющихся в процессе движения. Повторяются через равные промежутки времени.
Систему, совершающую колебания, независимо от ее природы называют осциллятором.
Свободные
колебания. Для
тела (точки), совершающей колебания,
существует положение устойчивого
равновесия. Вывести тело из этого
состояния можно, приложив внешнюю силу.
Тело, выведенное из состояния равновесия
и представленное самому себе, совершает
колебания около положения равновесия.
Такие
колебания называются собственными
или
свободными.
Частота
 ,
с которой система совершает такие
колебания, называетсясобственной.
,
с которой система совершает такие
колебания, называетсясобственной.
|
Простейшим типом колебаний являются гармонические, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Гармоническое колебание может быть представлено в трех видах: графическом, аналитическом и векторным. Графическое представление колебаний изображено на рис. 8.1. | |
|
Рисунок 8.1. |
Аналитическое представление гармонических колебаний не менее известно:
|
(8.1) |
где
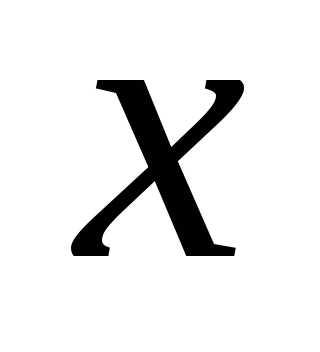 —
колеблющаяся величина (смещение,
скорость, ускорение, сила и т.п.),
—
колеблющаяся величина (смещение,
скорость, ускорение, сила и т.п.),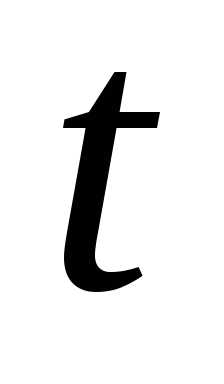 —
время,
—
время, —
амплитуда колебания (амплитуда равна
максимальному абсолютному значению
отклонения колеблющейся величины от
положения равновесия),
—
амплитуда колебания (амплитуда равна
максимальному абсолютному значению
отклонения колеблющейся величины от
положения равновесия), — циклическая или круговая частота.
— циклическая или круговая частота.
Физический смысл
циклической частоты состоит в том, что
она численно равна числу колебаний,
совершаемых за
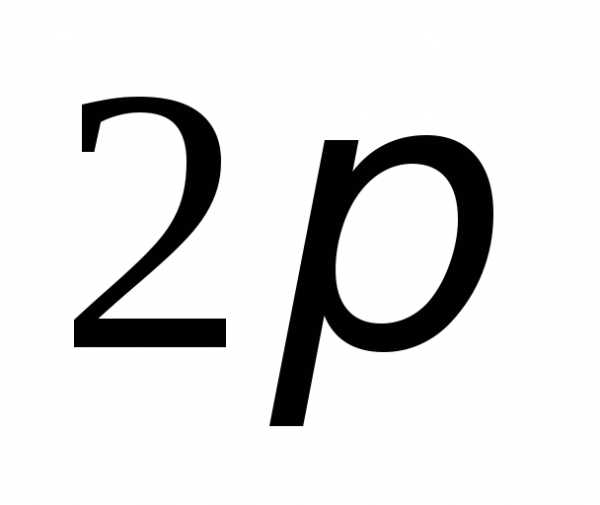 секунд, т.е.
секунд, т.е.
|
(8.2) |
где
 —
частота колебаний, т.е. число колебаний,
совершаемых за единицу времени,
—
частота колебаний, т.е. число колебаний,
совершаемых за единицу времени,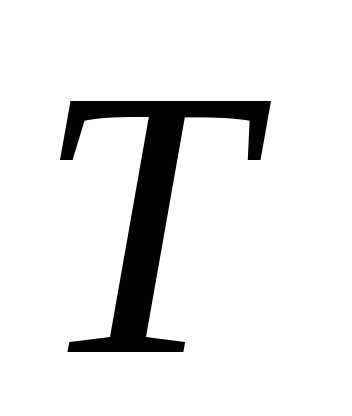 —
период колебаний – время, за которое
совершается одно полное колебание.
—
период колебаний – время, за которое
совершается одно полное колебание.
Величина
называется фазой колебания. Фаза
колебания – функция времени, которая
определяет значение колеблющейся
величины в данный момент времени
в данный момент времени .
Она показывает, какую часть от амплитуды
.
Она показывает, какую часть от амплитуды составляет смещение в данный момент
времени:.
Величина
составляет смещение в данный момент
времени:.
Величина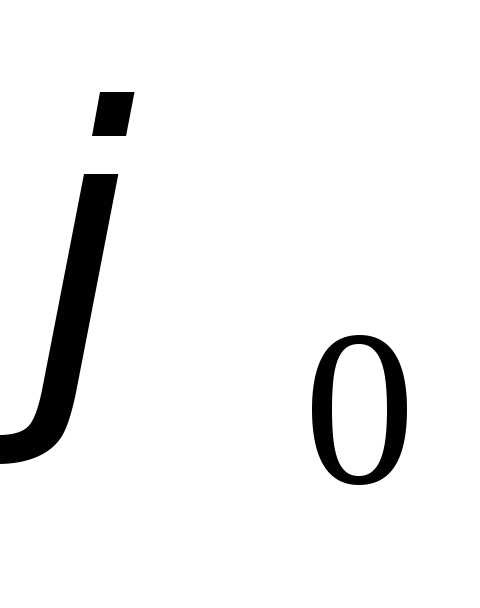 называется начальной фазой колебания.
Она определяет значение величины
называется начальной фазой колебания.
Она определяет значение величины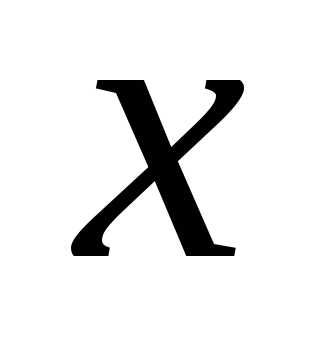 в начальный момент времени
в начальный момент времени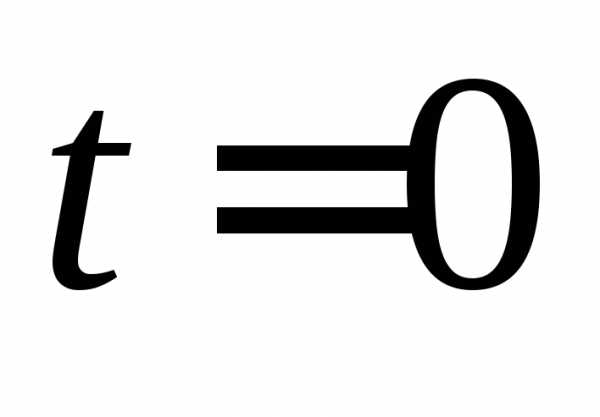 .
.
Наконец, в векторном представлении колебание представляется в виде вектора, длина которого пропорциональна амплитуде колебаний (см. рис.8.2). Сам вектор вращается в плоскости чертежа с угловой скоростью вокруг оси, перпендикулярной этой плоскости и проходящей через начало вектора
|
колебания. Первоначальное отклонение вектора от горизонтали изображает начальную фазу колебания. Этот вид представления колебаний особенно удобен для сложения колебаний, когда результирующее колебание находится как векторная сумма всех слагаемых, и будет использоваться во всем курсе. | |
|
Рисунок 8.2. |
8. 2. Пружинный маятник. Дифференциальное уравнение свободных колебаний.
Пружинный маятник.
Примером гармонического осциллятора
является пружинный маятник. Пружинный
маятник
– это груз
массой т,
закрепленный на абсолютно упругой
пружине (см. рис. 8.3) и совершающий
гармонические колебания под действием
упругой или квазиупругой силы
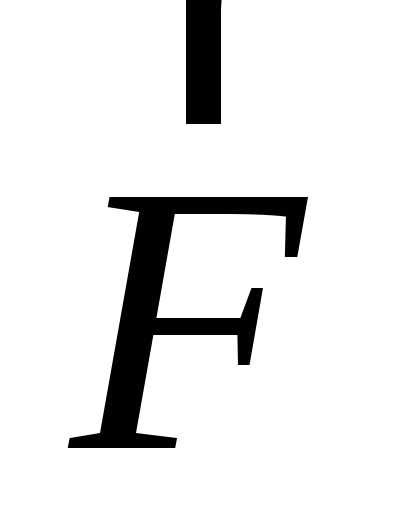 (силы, имеющие иную природу, чем упругие
силы, но также
(силы, имеющие иную природу, чем упругие
силы, но также
|
удовлетворяющие
уравнению
| |
|
Рисунок 8.3. |
Такая сила называется возвращающей силой. По второму закону Ньютона для возвращающей силы имеем
|
|
(8.3) |
где
 —
масса груза,
—
масса груза,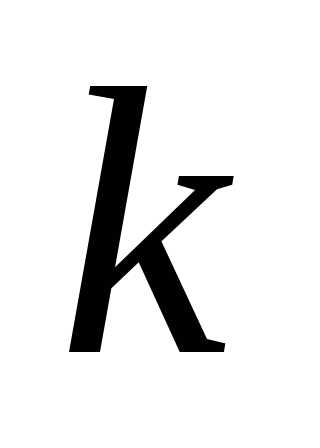 —
коэффициент упругости пружины.
—
коэффициент упругости пружины.
Отсюда введя величину
|
|
(8.4) |
получаем дифференциальное уравнение собственных колебаний
|
. |
(8.5) |
В математике такое уравнение относят к классу дифференциальных уравнений с постоянными коэффициентами, которое имеет решение
|
. |
(8.6) |
или после перехода от комплексной формы к тригонометрической
|
. |
(8.7) |
Таким образом,
выражения (1) и (7) совпадают. Следовательно,
величина
есть циклическая частота, а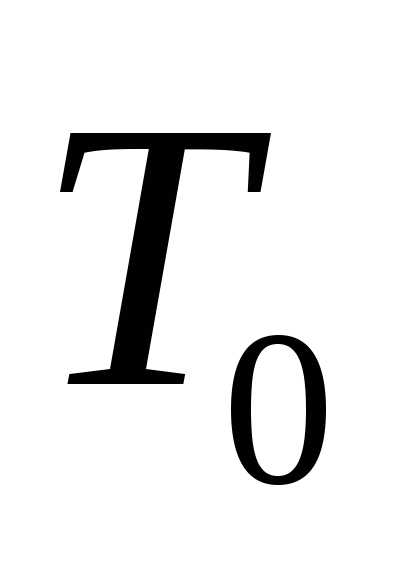 —
период собственных колебаний можно
определить по формуле:
—
период собственных колебаний можно
определить по формуле:
|
|
(8.8) |
8. 3. 1. Физический маятник.
Рассмотрим вращение массивного тела (см. рис.8.4) вокруг неподвижной оси при малых отклонениях этого тела от положения равновесия. В этом случае такое тело называют физическим маятником. Уравнением движение этого тела является основное уравнение динамики вращательного движения
|
|
(8.9) |
где
 — момент инерции тела, вычисленный
относительно оси вращения,
— момент инерции тела, вычисленный
относительно оси вращения,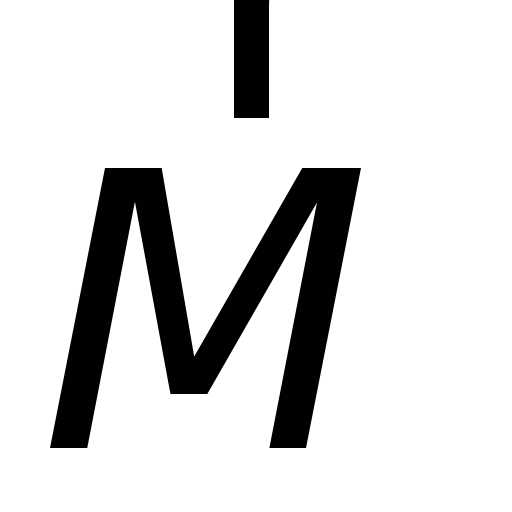 — главный вектор моментов сил,
— главный вектор моментов сил, — угол поворота тела,
— угол поворота тела,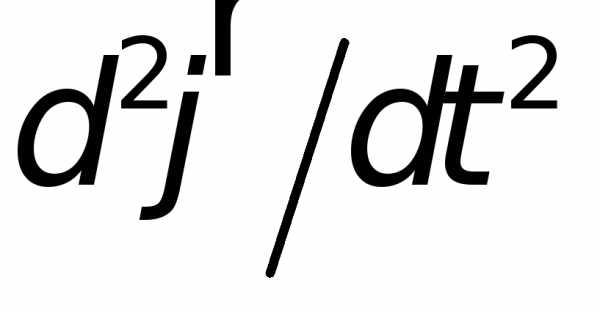 — угловое ускорение тела.
— угловое ускорение тела.
Напомним, что
 является псевдовектором, который
направлен вдоль оси вращения и подчиняется
правилу правого винта. Поэтому на рис.
8.4 вектор
является псевдовектором, который
направлен вдоль оси вращения и подчиняется
правилу правого винта. Поэтому на рис.
8.4 вектор направлен за плоскость рисунка.
направлен за плоскость рисунка.
К вращению тело
приводит только момент силы тяжести
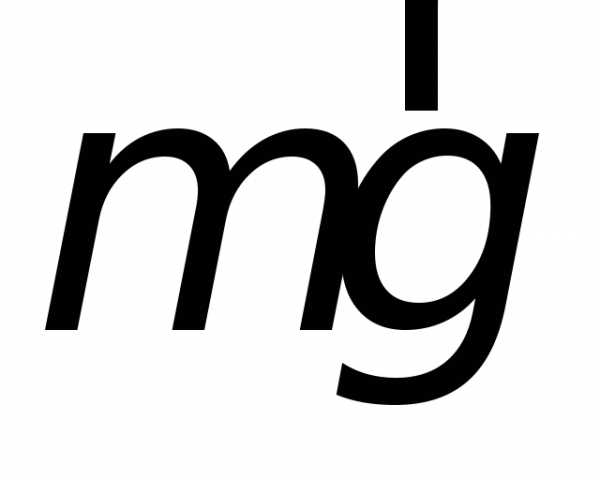 ,
точка приложения которой совпадает с
центром инерции тела. Поэтому главный
вектор моментов сил
,
точка приложения которой совпадает с
центром инерции тела. Поэтому главный
вектор моментов сил
|
(8.10) |
где
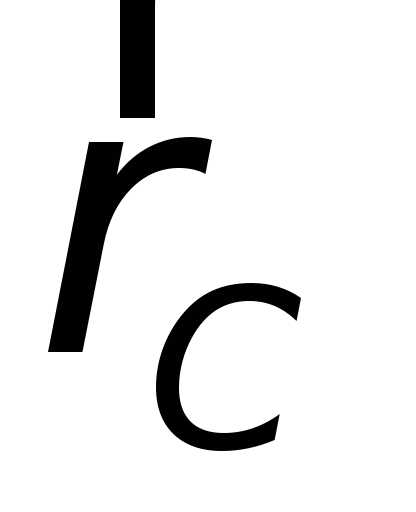 — радиус-вектор центра инерции, берущий
начало на оси вращения. Проектируя
вектор
— радиус-вектор центра инерции, берущий
начало на оси вращения. Проектируя
вектор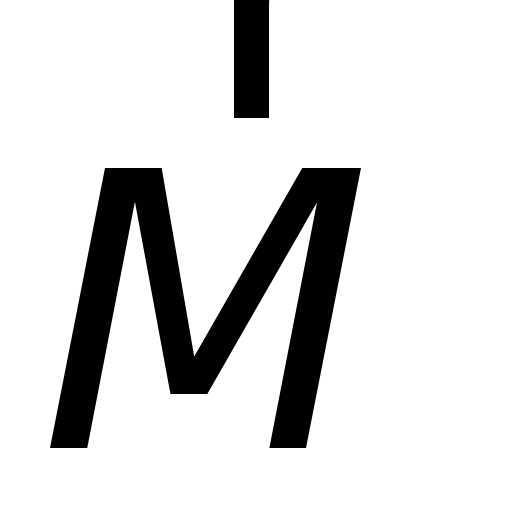 на ось вращения получаем
на ось вращения получаем
|
(8.11) |
где
 — расстояние от оси вращения до центра
инерции,
— расстояние от оси вращения до центра
инерции,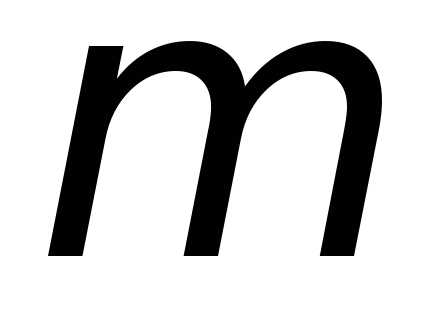 -масса тела
-масса тела
|
Знак «минус» в
(11) означает, что векторы
При малых отклонениях физического маятника от положения равновесия можно считать, что
Такое
приближение дает расхождение между
углом (измеряемом в радианах) и его
синусом при
| |
|
Рисунок 8. |
Проектируя (9) на ось вращения получаем дифференциальное уравнение колебаний физического маятника
|
(8.12) |
где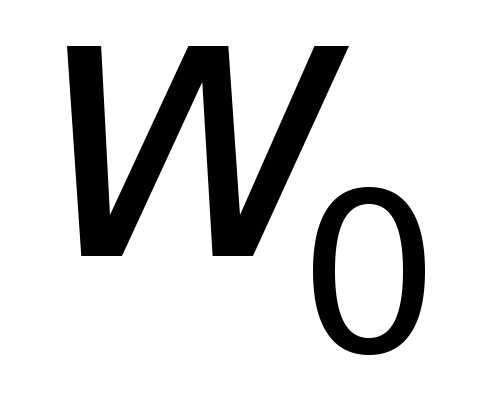 — собственная частота колебаний
физического маятника:
— собственная частота колебаний
физического маятника:
|
|
(8.13) |
8. 3. 2. Математический маятник.
Если размеры тела много меньше расстояния от оси вращения до центра инерции, то физический маятник можно считать математическим. Здесь проверим справедливость этого утверждения сделав предельный переход для частоты колебаний, определяемой по (8.13).
По теореме Штейнера
момент инерции
,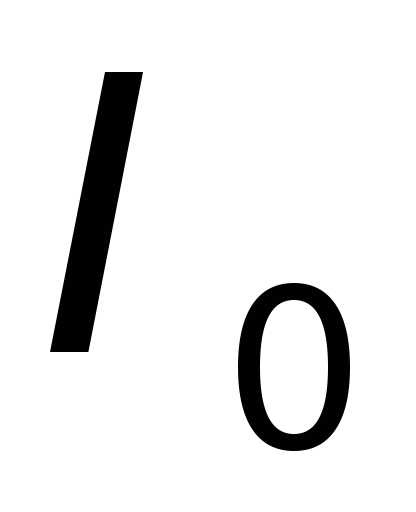 — момент инерции относительно оси,
проходящей через центр инерции. Если
— момент инерции относительно оси,
проходящей через центр инерции. Если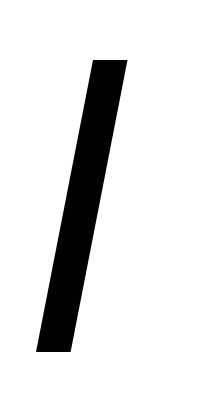 достаточно велико, то
достаточно велико, то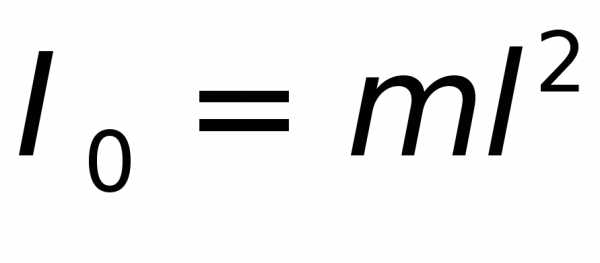 .
Следовательно,
.
Следовательно,
|
. |
Таким образом, получено известное из школьного курса выражение для круговой частоты собственных колебаний математического маятника
|
|
(8.14) |
8. 4. Скорость и ускорение тела, участвующего в гармонических колебаниях. Кинетическая, потенциальная и полная механическая энергия осциллятора.
На примере пружинного
маятника найдем скорость и ускорение
тела, совершающего колебательное
движение. По определению скорость тела
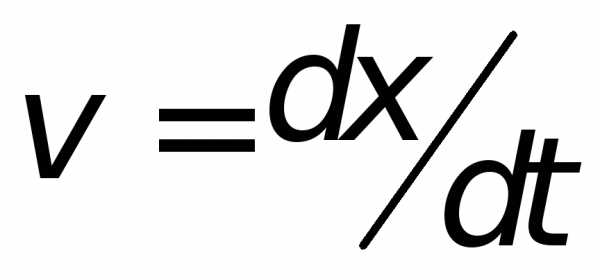 .
Следовательно, при гармонических
колебаниях согласно (8.1)
.
Следовательно, при гармонических
колебаниях согласно (8.1)
|
, |
(8.15) |
а ускорение тела
|
. |
(8.16) |
Тогда по основному закону динамики возвращающая сила
|
. |
(8.17) |
Кинетическая энергия осциллятора по определению
|
. |
(8.18) |
Потенциальная энергия деформированной пружины
|
. |
(8.19) |
Следовательно, полная механическая энергия гармонического осциллятора
|
. |
(8.20) |
113
studfiles.net
физика лекцыи_1 / Часть 2 / 1.18
1.18. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ХАРАКТЕРИСТИКИ
Определение гармонических колебаний. Характеристики гармонических колебаний: смещение от положения равновесия, амплитуда колебаний, фаза колебания, частота и период колебаний. Скорость и ускорение колеблющейся точки. Энергия гармонического осциллятора. Примеры гармонических осцилляторов: математический, пружинный, крутильный и физический маятники.
Акустика, радиотехника, оптика и другие разделы науки и техники базируются на учении о колебаниях и волнах. Большую роль играет теория колебаний в механике, в особенности в расчетах на прочность летательных аппаратов, мостов, отдельных видов машин и узлов.
Колебания являются процессами, повторяющимися через одинаковые промежутки времени (при этом далеко не все повторяющиеся процессы являются колебаниями!). В зависимости от физической природы повторяющегося процесса различают колебания механические, электромагнитные, электромеханические и т.п. При механических колебаниях периодически изменяются положения и координаты тел.
Возвращающая сила — сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.
В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.
В зависимости от характера воздействия на колеблющуюся систему различают свободные колебания, вынужденные, автоколебания и параметрические колебания.
Свободными (собственными) колебаниями называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она была выведена из положения равновесия, т.е. когда на колеблющееся тело действует только возвращающая сила.. Примером могут служить колебания шарика, подвешенного на нити. Для того, чтобы вызвать колебания, надо либо толкнуть шарик, либо, отведя в сторону, отпустить его. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).
· Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы (например, колебания моста, возникающие при прохождении по нему людей, шагающих в ногу). Во многих случаях системы совершают колебания, которые можно считать гармоническими.
· Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако, моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой. То есть система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.
· Параметрические колебания осуществляются при периодическом изменении параметров колеблющейся системы (качающийся на качелях человек периодически поднимает и опускает свой центр тяжести, тем самым меняя параметры системы). При определенных условиях система становится неустойчивой — случайно возникшее отклонение из положения равновесия приводит к возникновению и нарастанию колебаний. Это явление называется параметрическим возбуждением колебаний (т.е. колебания возбуждаются за счет изменения параметров системы), а сами колебания – параметрическими.
Несмотря на разную физическую природу, для колебаний характерны одни и те же закономерности, которые исследуются общими методами. Важной кинематической характеристикой является форма колебаний. Она определяется видом той функции времени, которая описывает изменение той или иной физической величины при колебаниях. Наиболее важными являются такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Они называются гармоническими.
Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).
Этот вид колебаний особенно важен по следующим причинам. Во-первых, колебания в природе и в технике часто имеют характер очень близких к гармоническим. Во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение, или суперпозиция, гармонических колебаний.
Уравнение гармонического осциллятора
Гармоническое колебание описывается периодическим законом:
. (18.1)
Рис. 18.1. Гармоническое колебание
З
десь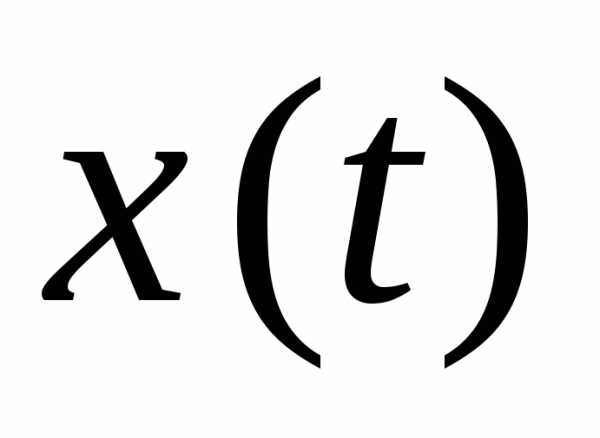 —
характеризует изменение
какой-либо физической величины при
колебаниях (смещение положения маятника
из положения равновесия; напряжение на
конденсаторе в колебательном контуре
и т.д.), A
— амплитуда
колебаний,
—
характеризует изменение
какой-либо физической величины при
колебаниях (смещение положения маятника
из положения равновесия; напряжение на
конденсаторе в колебательном контуре
и т.д.), A
— амплитуда
колебаний,
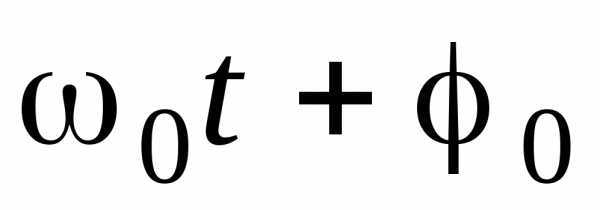 —
фаза
колебаний,
—
фаза
колебаний,
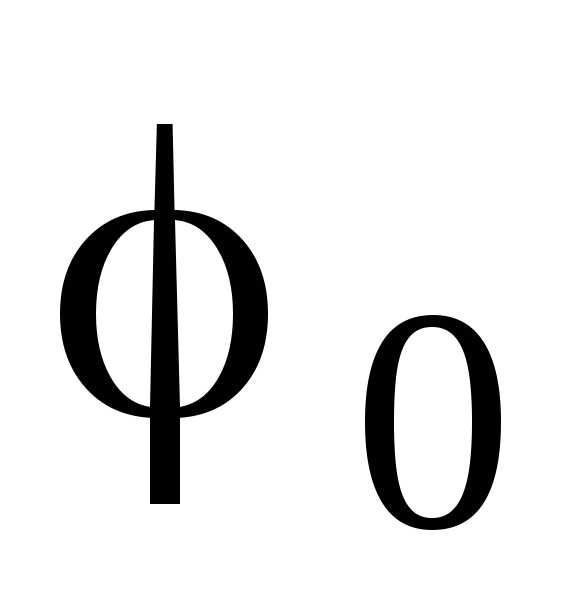 —
начальная
фаза,
—
начальная
фаза,
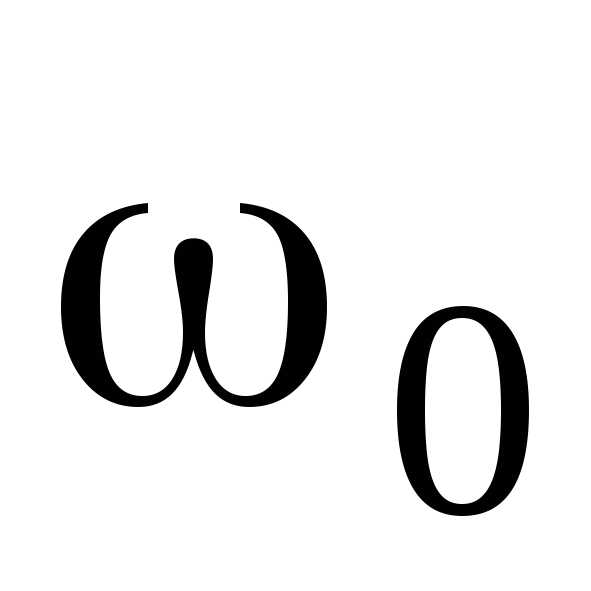 —
циклическая
частота;
величину
—
циклическая
частота;
величину  называют
также
собственной
частотой
колебаний. Такое название подчеркивает,
что эта частота определяется параметрами
колебательной системы. Система, закон
движения которой имеет вид (18.1), называется
одномерным
гармоническим осциллятором.
Помимо перечисленных величин для
характеристики колебаний вводят понятия
периода,
т.е. времени одного колебания.
называют
также
собственной
частотой
колебаний. Такое название подчеркивает,
что эта частота определяется параметрами
колебательной системы. Система, закон
движения которой имеет вид (18.1), называется
одномерным
гармоническим осциллятором.
Помимо перечисленных величин для
характеристики колебаний вводят понятия
периода,
т.е. времени одного колебания.
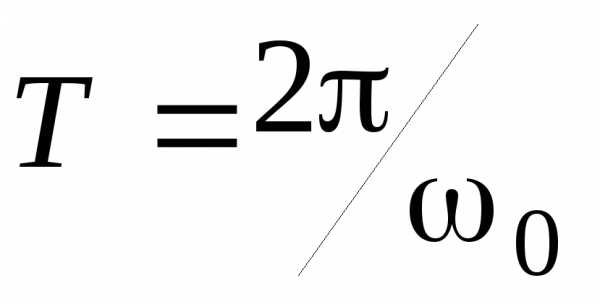
(Периодом колебаний T называется наименьший промежуток времени, по истечении которого повторяются состояния колеблющейся системы (совершается одно полное колебание) и фаза колебания получает приращение 2p).
и частоты , определяющей число колебаний в единицу времени. За единицу частоты принимается частота такого колебания, период которого равен 1 с. Эту единицу называют герцем (Гц).
Частотой колебаний n называется величина обратная периоду колебаний — число полных колебаний, совершаемых в единицу времени.
Амплитуда — максимальное значение смещения или изменения переменной величины при колебательном или волновом движении.
Фаза колебаний — аргумент периодической функции или описывающей гармонический колебательный процесс (ω— угловая частота, t— время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0).
Первая и вторая производные по времени от гармонически колеблющейся величины также совершают гармонические колебания той же частоты:
,
. (18.2)
В данном случае за основу взято уравнение гармонических колебаний, записанное по закону косинуса. При этом первое из уравнений (18.2) описывает закон, по которому изменяется скорость колеблющейся материальной точки (тела), второе уравнение описывает закон, по которому изменяется ускорение колеблющейся точки (тела).
Амплитуды
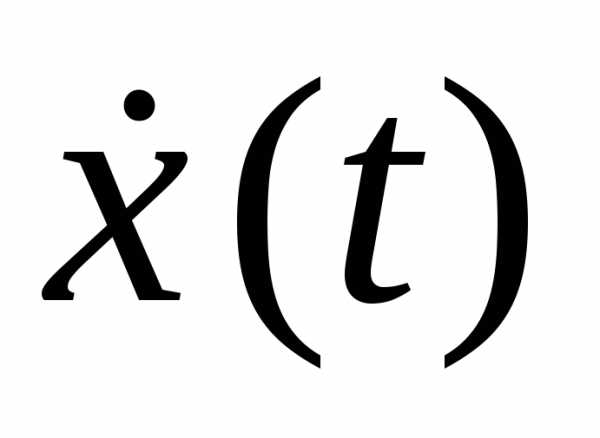 и
и
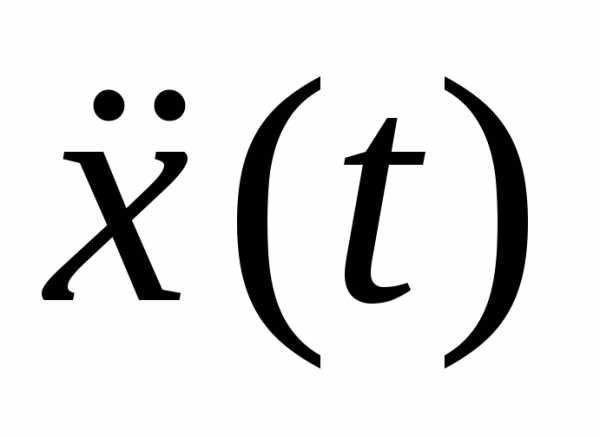 равны
соответственно
равны
соответственно 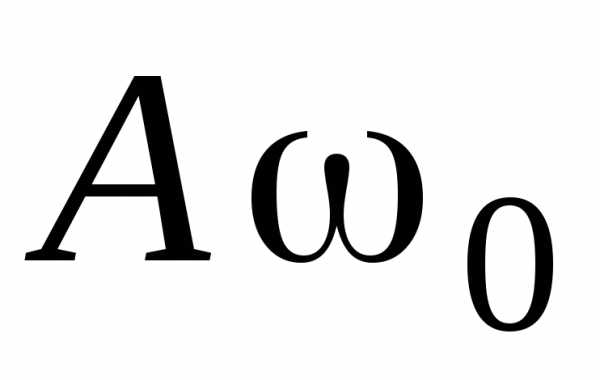 и
и
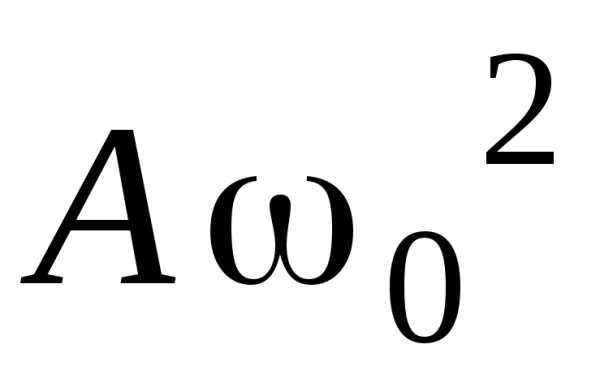 .
Колебание
.
Колебание 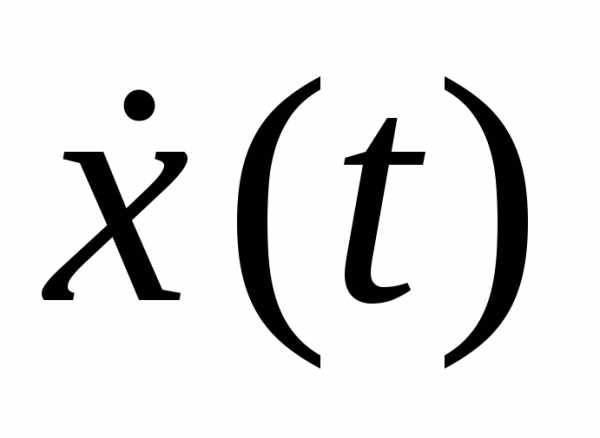 опережает
опережает
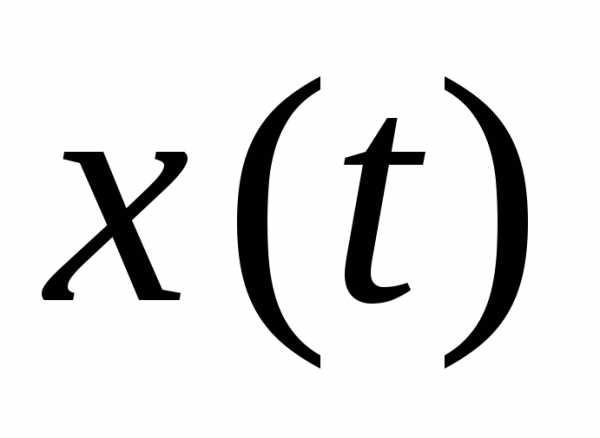 по
фазе на
по
фазе на  ;
а колебание
;
а колебание 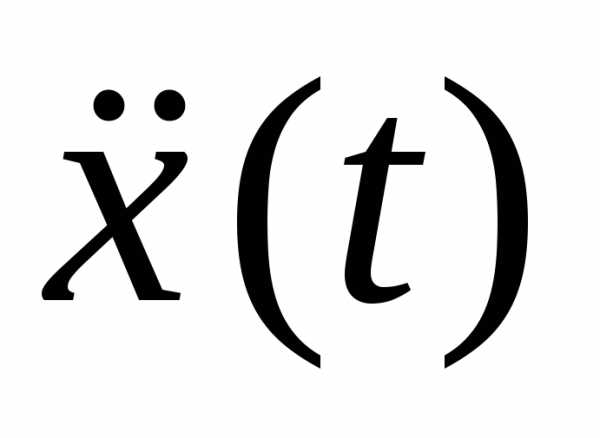 опережает
опережает
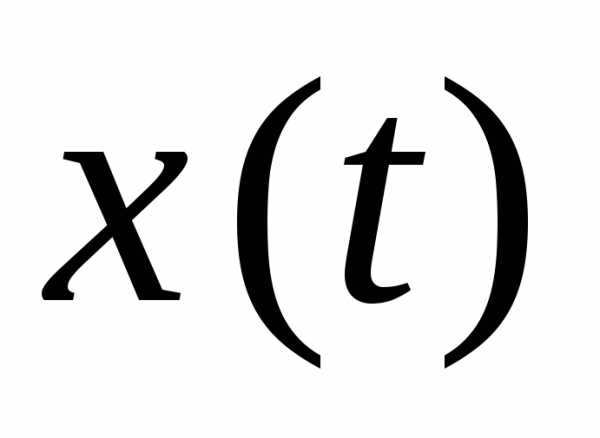 на
на
 .
Значения A
и
.
Значения A
и 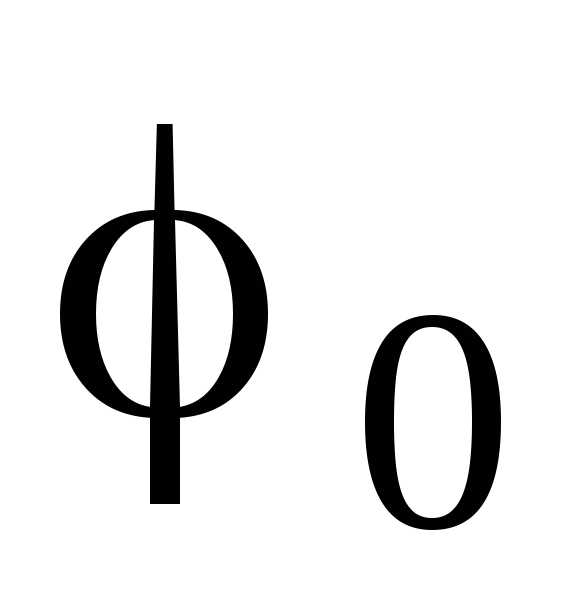 могут
быть определены из заданных начальных
условий
могут
быть определены из заданных начальных
условий 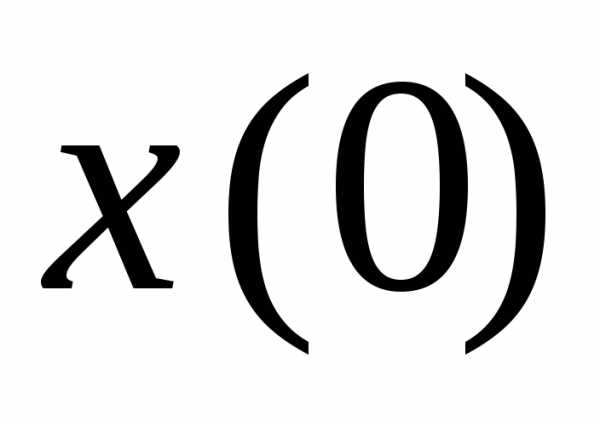 и
и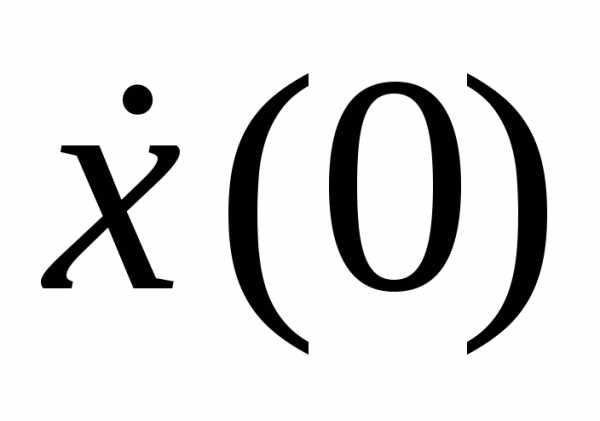 :
:
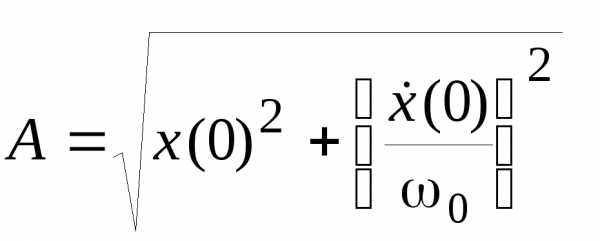 ,
,
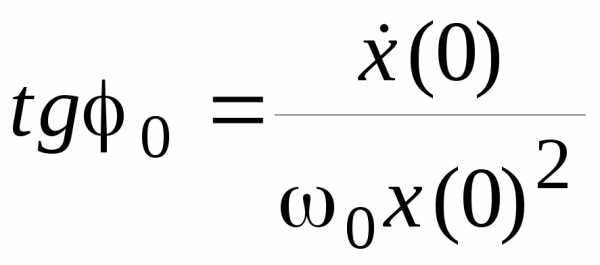 . (18.3)
. (18.3)
Энергия колебаний осциллятора
П
|
Рис. 18.2. Пружинный маятник |
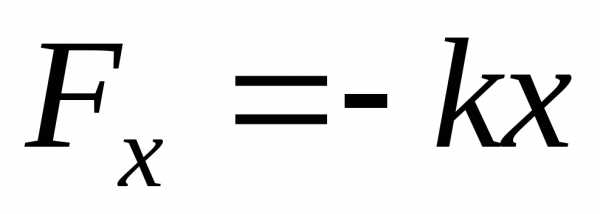 (к
примеру, пружинный маятник, см. рис.
18.2). Силы иной природы, чем упругие, но
в которых выполняется условие F
= -kx,
называются квазиупругими.
Под действием этих сил тела тоже совершают
гармонические колебания. Пусть:
(к
примеру, пружинный маятник, см. рис.
18.2). Силы иной природы, чем упругие, но
в которых выполняется условие F
= -kx,
называются квазиупругими.
Под действием этих сил тела тоже совершают
гармонические колебания. Пусть:
|
смещение: | |
|
скорость: | |
|
ускорение: |
Т.е.
уравнение таких колебаний имеет вид
(18.1) с собственной частотой  .
Квазиупругая сила является консервативной.
Поэтому полная энергия таких гармонических
колебаний должна оставаться постоянной.
В процессе колебаний происходит
превращение кинетической энергии Eк
в потенциальную Eп
и обратно, причем в моменты наибольшего
отклонения от положения равновесия
полная энергия равна максимальному
значению потенциальной энергии, а при
прохождении системы через положение
равновесия полная энергия равна
максимальному значению кинетической
энергии. Выясним, как изменяется со
временем кинетическая и потенциальная
энергия:
.
Квазиупругая сила является консервативной.
Поэтому полная энергия таких гармонических
колебаний должна оставаться постоянной.
В процессе колебаний происходит
превращение кинетической энергии Eк
в потенциальную Eп
и обратно, причем в моменты наибольшего
отклонения от положения равновесия
полная энергия равна максимальному
значению потенциальной энергии, а при
прохождении системы через положение
равновесия полная энергия равна
максимальному значению кинетической
энергии. Выясним, как изменяется со
временем кинетическая и потенциальная
энергия:
Кинетическая энергия:
|
(18.4) |
Потенциальная энергия:
(18.5)
Учитывая то, что т.е. , последнее выражение можно записать в виде:
|
(18.6) |
Полная энергия колеблющегося тела равна сумме кинетической и потенциальной энергий
|
(18.7) |
Таким
образом, полная энергия гармонического
колебания оказывается постоянной. Из
соотношений (18.4) и (18.5) также следует,
что средние значения кинетической и
потенциальной энергии равны друг другу
и половине полной энергии, поскольку
средние значения и
за
период равны 0,5. Используя тригонометрические
формулы, можно получить, что кинетическая
и потенциальная энергия изменяются с
частотой 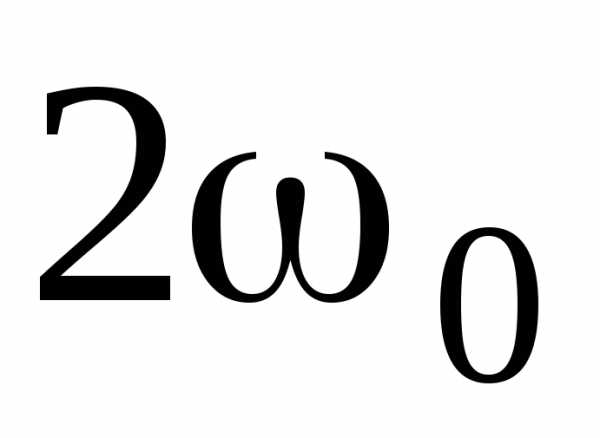 ,
т.е. с частотой в два раза превышающей
частоту гармонического колебания.
,
т.е. с частотой в два раза превышающей
частоту гармонического колебания.
В качестве примеров гармонического осциллятора могут быть пружинный, физический, математический маятники и крутильный маятники.
1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или (18.8) Из формулы (18.8) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
(18.9) и периодом
(18.10) Формула (18.10) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (18.9) и формулу потенциальной энергии предыдущего раздела, равна (см.18.5)
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).
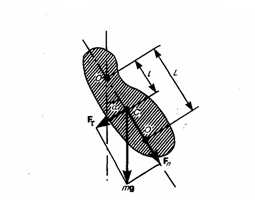
Рис.18.3 Физический маятник
Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы (18.11) где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (18.11) запишем как
или Принимая (18.12) получим уравнение
идентичное с (18.8), решение которого найдем и запишем как:
(18.13) Из формулы (18.13) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
(18.14) где введена величина L=J/(ml) — приведенная длина физического маятника. Точка О’ на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 18.3). Применяя теорему Штейнера для момента инерции оси, найдем
т. е. ОО’ всегда больше ОС. Точка подвеса О маятника и центр качаний О’ имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника
(8) где l — длина маятника.
Поскольку
математический маятник есть частный
случай физического маятника, если
предположить, что вся его масса
сосредоточена в одной точке — центре
масс, то, подставив (8) в (7), найдем выражение
для периода малых колебаний математического
маятника
(18.15)
Сопоставляя формулы (18.13) и (18.15),
видим, что если приведенная длина L
физического маятника равна длине l
математического маятника, то периоды
колебаний этих маятников одинаковы.
Значит, приведенная
длина физического маятника
— это длина такого математического
маятника, у которого период колебаний
совпадает с периодом колебаний данного
физического маятника. Для математического
маятника (материальной точки массой m,
подвешенной на невесомой нерастяжимой
нити длиной l
в поле силы тяжести с ускорением
свободного падения равным g)
при малых углах отклонения (не превышающих
5-10 угловых градусов) от положения
равновесия собственная частота колебаний:
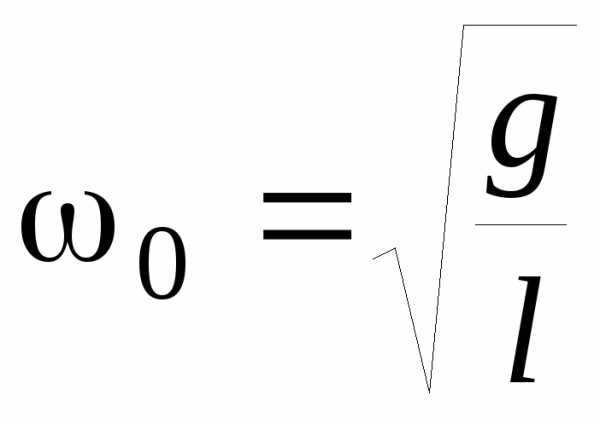 .
.
4. Тело, подвешенное на упругой нити или другом упругом элементе, совершающее колебания в горизонтальной плоскости, представляет собой крутильный маятник.
Эта механическая колебательная система, которая использует силы упругих деформаций. На рис. 18.4 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол θ возникает момент сил Mупр упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина χ аналогична жесткости пружины k. Второй закон Ньютона для вращательного движения диска записывается в виде
где I = IC – момент инерции диска относительно оси, проходящий через центр масс, ε – угловое ускорение.
По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.
|
Рисунок 18.4. Крутильный маятник |
10
studfiles.net
Физика
1.Определение колебательного движения
Колебательное движение — это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Учение о колебательном движении в физике выделяют особо. Это обусловлено общностью закономерностей колебательного движения различной природы и методов его исследования. Механические, акустические, электромагнитные колебания и волны рассматриваются с единой точки зрения. Колебательное движение свойственно всем явлениям природы. Внутри любого живого организма непрерывно происходят ритмично повторяющиеся процессы, например биение сердца.
Механические колебания Колебания — это любой физический процесс, характеризующийся повторяемостью во времени.
Волнение моря, качание маятника часов, вибрации корпуса корабля, биение человеческого сердца, звук, радиоволны, свет, переменные токи — все это колебания.
В процессе колебаний значения физических величин, определяющих состояние системы, через равные или неравные промежутки времени повторяются. Колебания называются периодическими, если значения изменяющихся физических величин повторяются через равные промежутки времени.
Наименьший промежуток времени Т, черезкоторый значение изменяющейся физической величины повторяется (по величине и направлению, если эта величина векторная, по величине и знаку, если она скалярная), называетсяпериодом колебаний.
Число полных колебаний n , совершаемых за единицу времени, называется частотой колебаний этой величины и обозначается через ν . Период и частота колебаний связаны соотношением :
Любое колебание обусловлено тем или иным воздействием на колеблющуюся систему. В зависимости от характера воздействия, вызывающего колебания, различают следующие виды периодических колебаний: свободные, вынужденные, автоколебания, параметрические.
Свободные колебания — это колебания, происходящие в системе, предоставленной самой себе, после выведения ее из состояния устойчивого равновесия (например, колебания груза на пружине).
Вынужденные колебания — это колебания, обусловленные внешним периодическим воздействием (например, электромагнитные колебания в антенне телевизора).
Механические колебания
Автоколебания — свободные колебания, поддерживаемые внешним источником энергии, включение которого в нужные моменты времени осуществляет сама колеблющаяся система (например, колебания маятника часов).
Параметрические колебания — это колебания, в процессе которых происходит периодическое изменение какого-либо параметра системы (например, раскачивание качелей: приседая в крайних положениях и выпрямляясь в среднем положении, человек, находящийся на качелях, изменяет момент инерции качелей).
Различные по своей природе колебания обнаруживают много общего: они подчиняются одним и тем же закономерностям, описываются одними и теми же уравнениями, исследуются одними и теми же методами. Это дает возможность создать единую теорию колебаний.
Простейшими из периодических колебаний
являются гармонические колебания.
Гармонические колебания- это колебания, в процессе совершения которых значения физических величин изменяются с течением времени по закону синуса или косинуса. Большинство колебательных процессов описываются этим законом или может быть приставлено в виде суммы гармонических колебаний.
Возможно и другое «динамическое» определение гармонических колебании как процесса, совершаемого под действием упругой или «квазиупругой»
силы.
2. Периодическими называются колебания, при которых происходит точное повторение процесса через равные промежутки времени.
Периодом периодических колебаний называется минимальное время, через которое система возвращается в первоначальное
х — колеблющаяся величина (например, сила тока в цепи, состояние и начинается повторение процесса. Процесс, происходящий за один период колебаний, называется «одно полное колебание».
периодических колебаний называется число полных колебаний за единицу времени (1 секунду) — это может быть не целое число.
Т — период колебаний Период — время одного полного колебания.
Чтобы вычислить частоту v, надо разделить 1 секунду на время Т одного колебания (в секундах) и получится число колебаний за 1 секунду или координата точки) t — время
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
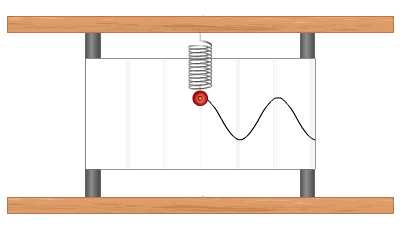
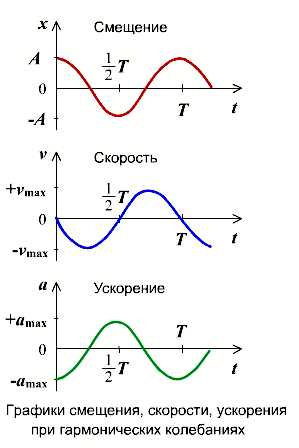
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

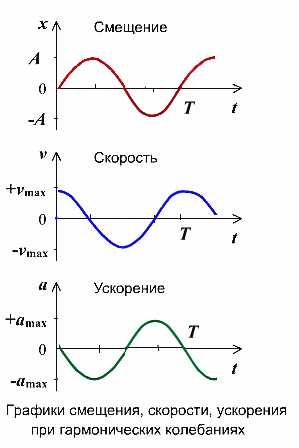
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, каксила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
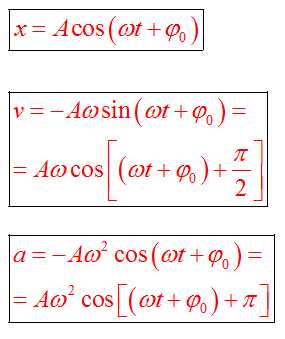
Если колебание описывать по закону синуса
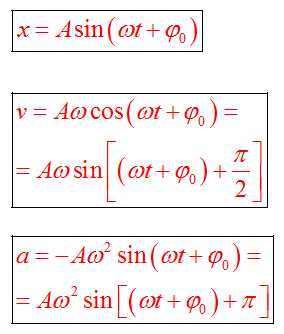
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
studfiles.net
Колебания. Характеристики гармонических колебаний — Мегаобучалка
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
План
1. Колебания. Характеристики гармонических колебаний.
2. Свободные (собственные) колебания. Дифференциальное уравнение гармонических колебаний и его решение. Гармонический осциллятор.
3. Энергия гармонических колебаний.
4. Сложение одинаково направленных гармонических колебаний. Биение. Метод векторной диаграммы.
5. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
6. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Частота затухающих колебаний. Изохронность колебаний. Коэффициент, декремент, логарифмический декремент затухания. Добротность колебательной системы.
7. Вынужденные механические колебания. Амплитуда и фаза вынужденных механических колебаний.
8. Механический резонанс. Соотношение между фазами вынуждающей силы и скорости при механическом резонансе.
9. понятие об автоколебаниях.
Колебания. Характеристики гармонических колебаний.
Колебания – движение или процессы, обладающие той или иной степенью повторности во времени.
Гармонические (или синусоидальные) колебания – разновидность периодических колебаний, которые могут быть заменены в виде
(1)
где a – амплитуда, — фаза, — начальная фаза, — циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).
Амплитуда (а) – наибольшее отклонение от среднего значения величины, совершающей колебания.
Фаза колебаний ( ) – изменяющийся аргумент функции, описывающей колебательный процесс (величина t+ , стоящая под знаком синуса в выражении (1) ).
Фаза характеризует значение изменяющейся величины в данный момент времени. Значение в момент времени t=0 называется начальной фазой ( ).
В качестве примера на рисунке 27.1 представлены математические маятники в крайних положениях с разностью фаз колебаний =0 (27.1.а) и = (27.1б)
Разность фаз колебаний маятников проявляется отличием в положении колеблющихся маятников.
Циклической или круговой частотой называется количество колебаний, совершаемое за 2 секунд.
Частотой колебаний (или линейной частотой) называется число колебаний в единицу времени. За единицу частоты принимается частота таких колебаний, период которых равен 1с. Эту единицу называют Герц (Гц).
Промежуток времени, за который совершается одно полное колебание, а фаза колебания получает приращение, равное 2 , называется периодом колебания (рис. 27.2).
Частота связана с пе-
риодом Т соотношении-
ем
| |
| |
рис. 27.2
2. Свободные колебания. Свободными или собственными называются такие колебания, которые происходят в системе, выведенной из положения равновесия и предоставленной самой себе.
Рассмотрим колебания груза на пружине, совершаемые на гладкой горизонтальной поверхности (рис. 27.3). Если растянуть пружину на некоторое расстояние х, и затем отпустить, то на груз будет действовать упругая
 |
.
Поделив обе части уравнений на m
и перенеся в левую часть
.
Обозначив , получим линейное дифференциальное однородное уравнение второго порядка
| |
(линейное – т.е. и сама величина х, и ее производная в первой степени; однородное – т.к. нет свободного члена, не содержащего х ; второго порядка – т.к. вторая производная х).
Уравнение (2) решается (*) подстановкой х = . Подставляя в (2) и проводя дифференцирование
.
Получаем характеристическое уравнение
.
Это уравнение имеет мнимые корни: ( -мнимая единица).
Общее решение имеет вид
где и — комплексные постоянные.
Подставляя корни, получим
(3)
(Замечание: комплексным числом z называется число вида z = x + iy, где x,y – вещественные числа, i – мнимая единица ( = -1). Число х называется вещественной частью комплексного числа z.. Число у называется мнимой частью z).
(*) В сокращенном варианте решение можно опустить
Выражение вида можно представить в виде комплексного числа с помощью формулы Эйлера
аналогично
(т.к. .
Положим и в виде комплексных постоянных = А , а = А , где А и произвольные постоянные. Из (3) получим
Обозначив получим
Используя формулу Эйлера
| |
(4)
где — собственная круговая частота колебаний, А – амплитуда.
Смещение х применяется со временем по закону косинуса, т.е. движение системы под действием упругой силы f = -кх представляет собой гармоническое колебание.
Если величины, описывающие колебания некоторой системы периодически изменяются со временем, то для такой системы пользуются термином «осциллятор».
Линейным гармоническим осциллятором называется такой, движение которого описывается линейным уравнением .
3. Энергия гармонических колебаний. Полная механическая энергия системы, изображенной на рис. 27.2 равна сумме механической и потенциальной энергий.
Продифференцируем по времени выражение ( , получим
= = -a sin( t + ).
Кинетическая энергия груза (массой пружины пренебрегаем) равна
E = .
Потенциальная энергия выражается известной формулой подставляя х из (4), получим
т.к. .
Полная энергия
величина постоянная. В процессе колебаний потенциальная энергия переходит в кинетическую и наоборот, но каждая энергия остается неизменной.
4. Сложение одинаково направленных колебаний.. Обычно одно и то же тело участвует в нескольких колебаниях. Так, например, звуковые колебания, воспринимаемые нами при слушании оркестра представляют собой сумму колебаний воздуха, вызываемых каждым из музыкальных инструментов в отдельности.
Рассмотрим сложение двух гармонических колебаний одинакового направления. Смещение х колеблющегося тела будет суммой смещений и . Положим равными, для простоты, амплитуды и начальные фазы Тогда
.
Воспользовавшись формулой суммы косинусов, получим
| |
(5)
Биения. Пусть два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Обозначим частоту одного из колебаний , частоту второго . При этом Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Начальные фазы для упрощения задачи положим равными нулю. Тогда
Сложим эти колебания, воспользовавшись формулой (5), получим
| |
(6)
Во втором сомножителе (6) пренебрегли по сравнению с . Множитель меняется гораздо медленнее, чем (т.к. ). Результирующее колебание х можно рассматривать как гармоническое с частотой , амплитуда которого меняется по закону от -2а до +2а (амплитуда – величина положительная). Такие колебания называются биениями. Они представлены на рис.27.4.
 |
Частота пульсаций амплитуды называется частотой биений.Промежуток времени между соседними моментами времени, когда амплитуда максимальна, называется периодом биений Тб. За это время разность фаз изменяется на , т.е.
Таким образом период биений
| |
megaobuchalka.ru

 ,
называютсяквазиупругими).
Эта сила всегда направлена к положению
равновесия, а смещение
,
называютсяквазиупругими).
Эта сила всегда направлена к положению
равновесия, а смещение
 —
в противоположную сторону, поэтому
значения силы и смещения имеют
противоположные знаки.
—
в противоположную сторону, поэтому
значения силы и смещения имеют
противоположные знаки.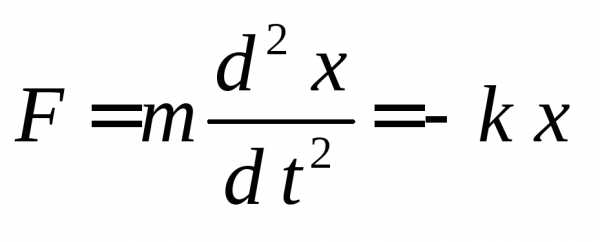
 .
.
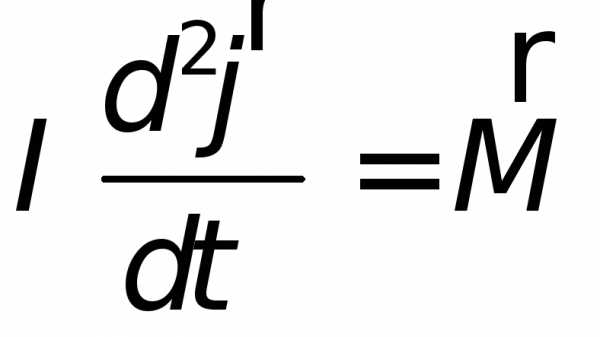
 и
и имеют противоположные направления.
имеют противоположные направления. .
. менее чем три процента.
менее чем три процента.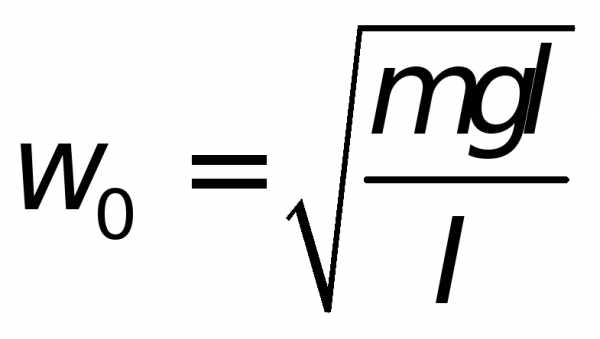 .
. .
.