две задачи с применением теоремы Менелая.
Обе задачи очень интересные. Взяты из пособия В.В. Мирошина “ЕГЭ 2018. Тренировочные задания” – первая из варианта 4, вторая – из 27.
Задача 1. Основанием пирамиды является параллелограмм . Точки , и расположены на ребрах соответственно, и при этом
А) Докажите, что прямые и пересекаются.
Б) Найдите отношение объема пирамиды к объему пирамиды .
Рисунок 1
Проведем высоту пирамиды. Основание высоты пирамиды – точка пересечения диагоналей параллелограмма . Проведем прямую и рассмотрим треугольник .
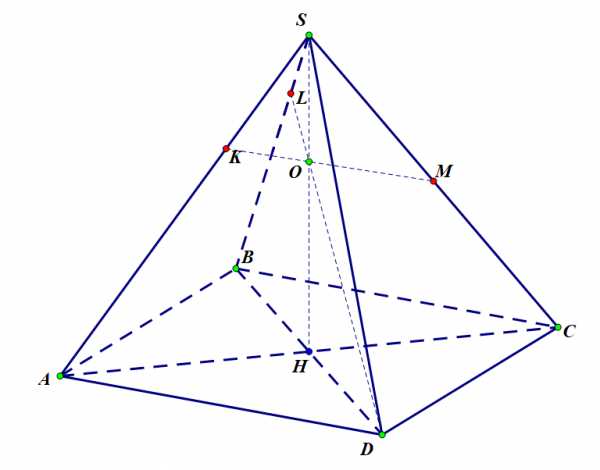
Рисунок 2
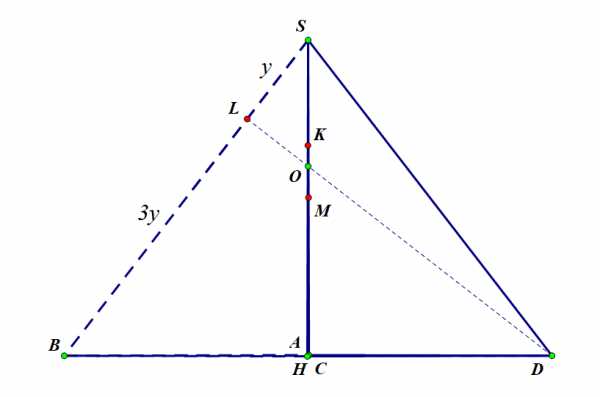
Рисунок 3
Пусть прямая пересекает высоту в точке . Определим, в каком отношении точка делит высоту . По теореме Менелая для треугольника
– диагональ параллелограмма, точка пересечения диагоналей в параллелограмме делит каждую из них пополам, поэтому . Ребро по условию разделили на 4 части, отрезок – одна из них, поэтому , . Тогда . Следовательно,
И тогда
Теперь рассмотрим плоскость и треугольник . Пусть прямая пересекает высоту в точке . Тогда, если точка делит высоту в таком же отношении, как и точка , то это одна и та же точка, и тогда именно в ней и пересекаются прямые и .
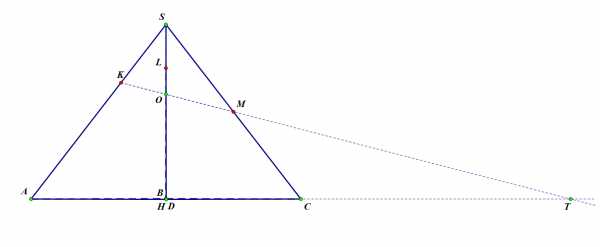
Рисунок 4
Продлим прямые и до пересечения. Точку пересечения обозначим . Запишем теорему Менелая для треугольника :
Отношение по условию (ребро разделили на три части, одна из них – отрезок , две – отрезок ).
Далее необходимо определить длины отрезков и . Для этого рассмотрим подобные треугольники и . Запишем отношения для его сходственных сторон:
Или
Так как , то из подобных треугольников и . Из этих же треугольников , следовательно, .
Так как , то из подобных треугольников и . Из этих же треугольников , следовательно, .
Тогда
Или
Или , то есть .
Тогда . Возвращаемся к нашей теореме Менелая:
Или
Перепишем:
Мы получили то же отношение, следовательно, точки и совпадают и прямые и в точке пересекаются.
Теперь определим объем пирамиды .
Объем пирамиды можно представить как сумму объемов пирамид и , у которых объемы равны:
Объем пирамиды можно представить как сумму объемов пирамид и :
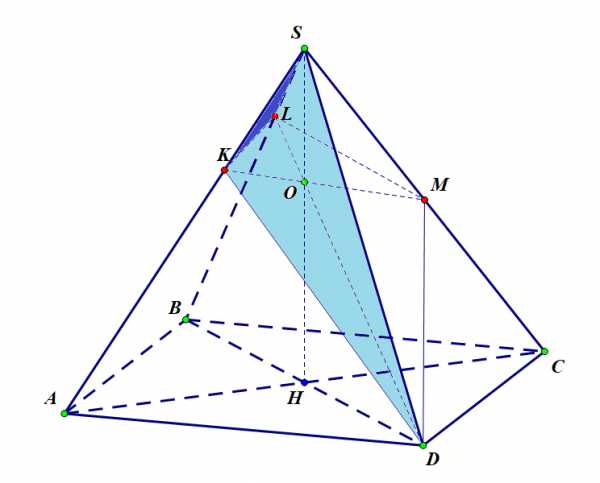
Рисунок 5
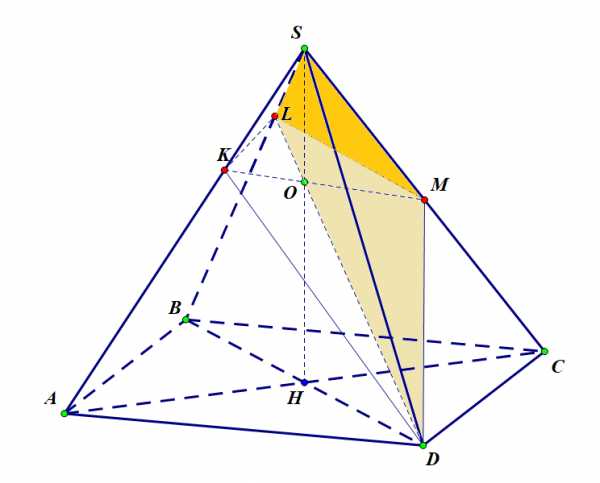
Рисунок 6
Причем у пирамид и одна и та же высота, а также у пирамид и также одна и та же высота. Поэтому
И
Определим отношения площадей:
Поэтому
Ответ: Б) .
Задача 2. Точки , и расположены на ребрах правильной четырехугольной пирамиды соответственно, и при этом
А) Докажите, что плоскость проходит через вершину пирамиды .
Б) Найдите угол между плоскостью и плоскостью основания пирамиды , если , .
Рисунок 7
Если внимательно посмотреть на данные отношения, то можно заметить, что , то есть точки и расположены на одной высоте. Проведем прямую до пересечения с прямой , а прямую – до пересечения с прямой . Обозначим точки этих пересечений соответственно и . Тогда прямая – линия пересечения плоскостей и .
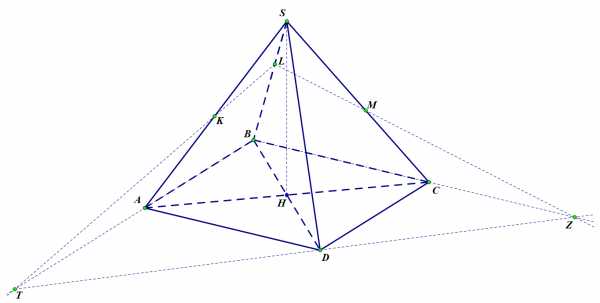
Рисунок 8
Рассмотрим треугольник и пересекающую его прямую . Запишем теорему Менелая:
Отношение , тогда
Откуда
В силу того, что , при записи теоремы Менелая для треугольника и пересекающей его прямой можно найти, что
Это означает, что треугольник – равнобедренный прямоугольный, и прямая обязательно пройдет через точку – это можно установить через площадь, например, или определив длину гипотенузы .
Таким образом, – высота треугольника , а по теореме о трех перпендикулярах наклонная . Следовательно, угол – искомый угол между плоскостями. Определим тангенс этого угла.
Найдем длины этих отрезков.
Высота пирамиды равна
Рассмотрим подобные треугольники и , где – основание перпендикуляра, опущенного из точки к плоскости основания.
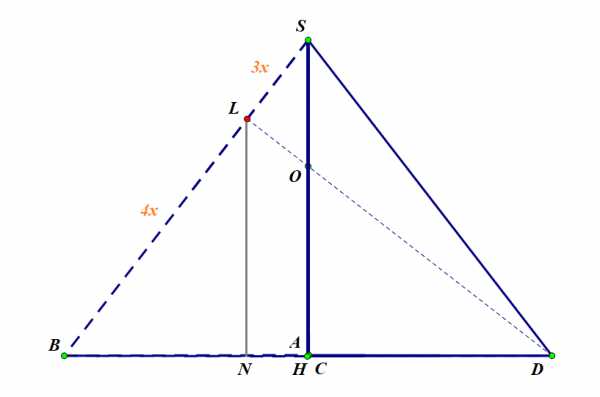
Рисунок 9
Запишем отношения сходственных сторон:
Тогда , а
Тогда
Угол будет равен
Ответ: .
easy-physic.ru
| Задания реальных ЕГЭ прошлых лет Skip Navigation Links.
|
egeprof.ru
Решение задач на применение аксиом и их следствий (разные задачи)
Тема: Аксиомы стереометрии и их следствия
Урок: Решение задач на применение аксиом и их следствий (разные задачи)
Аксиомы стереометрии и следствия из них устанавливают взаимоотношения между основными фигурами стереометрии: точкой, прямой и плоскостью.
Точка может лежать на прямой, может не лежать на прямой.
Прямая может принадлежать плоскости, может не принадлежать плоскости.
Плоскость может проходить через прямую, не проходить через нее, содержать точку, не содержать точку.
Подобные задачи мы решали для пирамиды и для параллелепипеда. Теперь мы будем решать задачи в общем виде.
Вспомним для этого сначала аксиомы и теоремы-следствия.
Аксиома 1 (А1)
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Иллюстрация аксиомы А1.
Рис. 1.
Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость , и притом только одна. Плоскость можно также обозначить через три точки АВС.
Аксиома 2 (А2)
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Иллюстрация аксиомы А2. (Рис. 2.)
Рис. 2.
Аксиома 3 (А3).
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).
Иллюстрация аксиомы А3. (Рис. 3.)
Рис. 3.
Повторение теорем, которые следуют из аксиом стереометрии.
Теорема 1
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Иллюстрация теоремы 1. (Рис. 4.)
Рис. 4.
единственная
Теорема 2
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Иллюстрация теоремы 2. (Рис. 5.)
Рис. 5.
Задача 1.
Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).
Рис. 6.
Решение:
Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.
Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее .
Две разные точки А и В прямой с принадлежат плоскости . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.
Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости.
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
Решение:
Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).
Рис. 7.
Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость
Прямая АВ целиком лежит в плоскости , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости .
Аналогично и с другими отрезками. Прямая ВС лежит в плоскости , потому что две ее точки В и С лежат в плоскости, значит, и отрезок ВС лежит в плоскости .
И аналогично, отрезок АС лежит в плоскости . Что и требовалось доказать.
Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли 2 другие вершины параллелограмма в плоскости ?
Решение:
Рис. 8.
Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.
Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка С, точка прямой АО, лежит в плоскости .
Аналогично, прямая ВО целиком лежит в плоскости , значит, точка D этой прямой тоже лежит в плоскости .
Ответ: Да, вершины С и D лежат в плоскости .
Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Рис. 9.
Решение:
Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.
Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через . Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости , в силу 2 аксиомы.
Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости . Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости , что и требовалось доказать.
Верно ли утверждение:
а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;
б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
Рис. 10.
Решение:
а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно.
Ответ: нет.
б) Даны три точки окружности А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость .
Теперь докажем, что любая точка М окружности лежит в плоскости . Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости , потому что две ее точки А и D лежат в плоскости . Значит, и точка М окружности лежит в плоскости . Значит, данное утверждение верно.
Ответ: да.
Точки А, В, С и D не лежат в одной плоскости (Рис. 11.).
а) Могут ли какие-то три из них лежать на одной прямой?
б) Могут ли прямые АВ и СD пересекаться?
interneturok.ru
Сборник задач по стереометрии
Пирамида.
1. В правильной четырехугольной пирамиде высота составляет с боковой гранью угол, равный 37º. Найдите угол между апофемами противоположных боковых граней. (37º).
2. Боковое ребро правильной пирамиды вдвое больше её высоты. Определите угол наклона бокового ребра к плоскости основания. (30º).
3. Периметр основания пирамиды равен 20 см, а площадь её основания 16 см². Найдите периметр и площадь сечения пирамиды, проведенного параллельно основанию через середину бокового ребра. (10 см, 4 см²).
4. Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника, лежащего в основании, и равны 12 см. Вычислите высоту пирамиды. (6√3см).
5. В правильной четырехугольной пирамиде боковое ребро равно 20 см, оно составляет с основанием угол 45º. Определите расстояние от центра основания до бокового ребра.
Решение: Искомое расстояние d равно длине высоты, опущенной из вершины равнобедренного прямоугольного треугольника на гипотенузу, которой является боковое ребро, d=10 см.
6. Используя рис.1, на котором изображена правильная треугольная пирамида, заполните пустые ячейки в табл.1 и табл.2.
Таблица 1.
№ п/п
a
b
h
k
β
1
6
4
2
12
45º
3
4
60º
4
4
2√7
Таблица 2.
№ п/п
a
k
h
b
α
1
2√3
√3
2
1
45º
3
4
2
4
4√3
60º
Ответы
К табл. 1:
1)h=2, k=√7, β=30º;
2)b=4√6, h=4√3, k=2√15;
3)a=2√3, h=2√3, k=√13;
4)a=12, b=8, β=30º.
К табл. 2:
1) k=2, b=√7, α=60º;
2) a=2√3, k=√2, b=√3;
3) a=12, b=2√13, a=30º;
4) k=4, h=2√3, b=2√7.
Указание: Перед решением задачи следует повторить и затем записать на доске формулы
NC=a√3/2, ON=a√3/6, OC=a√3/3.
7. Используя рис. 2, на котором изображена правильная четырехугольная пирамида, заполните пустые ячейки в табл. 3 и табл.4.
Таблица 3.
№ п/п
a
k
h
b
α
1
2
√3
2
2√2
45º
3
6
3
4
4
30º
Таблица 4.
№ п/п
a
b
h
k
β
1
4
60º
2
2
45º
3
8
4
4
4√2
8
Табл. 3 (1- 2, √5, 60º;
2- 2, √2, √6;
3- 6√3, 3√5, 30º;
4- 4√3, 2, 2√5).
Табл. 4 (1- 2√2, 2√3, √14;
2- 2√2, 2√2, √6;
3- 4√6, 2√10, 30º;
4- 4√3, 2√14, 60º).
Указание: Перед решением этой задачи следует повторить и затем записать на доске формулы
AC=a√2, AO=a√2/2, ON=a/2.
8. Площадь боковой поверхности пирамиды, в основании которой лежит трапеция, равна 2Q. Боковые грани пирамиды составляют с плоскостью основания равные углы. Найдите сумму площадей боковых граней, проходящих через непараллельные стороны трапеции. (Q)
9. В основании пирамиды лежит ромб. Боковые грани пирамиды образуют с основанием равные углы. Площадь одной из боковых граней равна Q. Найдите площадь боковой поверхности пирамиды. (4Q)
10. Вычислите площадь боковой поверхности правильной пятиугольной пирамиды, если известно, что ее боковое ребро, равное a, со стороной основания составляет угол 60º. (5a²√3/4)
11. Дана правильная треугольная пирамида, у которой а- сторона основания, k- апофема, P- периметр основания, S1- площадь боковой поверхности, S- площадь пирамиды. Заполните табл. 5.
Таблица 5.
№ п/п
a
k
P
S1
S
1
5
75
2
24
24
3
18
297
4
45
315
5
198√3
202√3
(1-10, 15, 75+25√3/4;
2- 8, 288, 288+16√3;
3- 11, 33, 297+121√3/4;
4- 15, 14, 315+225√3/4;
5- 4, 12, 33√3).
Указание: Задачу следует решать по заранее заготовленному чертежу. Перед решением необходимо повторить и записать на доске формулы:
S=Pk/2, P=3a, S=S1+S2, S2=a²√3/4.
(S2- площадь основания пирамиды).
12. Дана правильная четырехугольная пирамида, у которой a- сторона основания, k- апофема, P- периметр основания, S1- площадь боковой поверхности, S- площадь пирамиды.
Таблица 6.
№ п/п
a
k
P
S1
S
1
6
12
2
13
689
3
16
288
4
44
396
5
352
416
(1- 24, 144, 180;
2- 52, 520, 20;
3-36, 9, 369;
4- 11,18, 517;
5- 8, 32, 22).
Указание: Задачу следует решать по заранее заготовленному чертежу.
S= Pk/2, P=4a, S=S1+S2, S2=a².
(S2- площадь основания пирамиды).
Усеченная пирамида.
1. Два односторонних плоских угла при ребре боковой грани усеченной пирамиды. Найдите эти углы.
2. Высота усеченной пирамиды равна 2h. Сходственные стороны ее основания относятся как 1:3. Вычислить высоту полной пирамиды. (3h)
3. Основание усеченной пирамиды — прямоугольник со сторонами 27 см и 15 см. Найти стороны верхнего основания, если его периметр равен 56 см.
Решение: У усеченной пирамиды основания являются подобными многоугольниками, т.е. отношение сторон верхнего и нижнего оснований пропорционально. Полупериметр верхнего основания равен 28 см, а остальные стороны равны x см и 28-x см. Тогда
27/15 = 28-x/x
и стороны верхнего основания равны 10 см и 18 см.
4. Стороны оснований правильной четырехугольной усеченной пирамиды равны 4 см и 2 см, высота пирамиды – 3 см. Вычислите площади диагональных сечений данной усеченной пирамиды.
Решение: Диагональными сечениями данной правильной усеченной пирамиды являются равнобедренные трапеции, стороны оснований которых равны 4√2 см и 2√2, а площадь равна:
S=(4√2+2√2)/2*3=9√2 (см²).
5. Дана правильная треугольная усеченная пирамида (рис. 3), у которой a- сторона нижнего основания; a1 – сторона верхнего основания, b — боковое ребро, h — высота, k — апофема, α — угол между боковой гранью и основанием, β — угол между боковым ребром и основанием. Заполнить табл.7 и табл.8.
Таблица 7.
№ п/п
a
a1
b
h
k
β
1
9√2
3√2
4√3
2
12
3
30º
3
3
8
4
4
6
2√3
60º
(1 – 2√6, √30, 45º; 2 – 6, 3, √91/2;
3 – 15, 2√7, 30º; 4 – 9, 3, √39/2).
Таблица 8.
№ п/п
a
a1
b
h
k
α
1
6
2√3
60º
2
9
3
2
3
12
6
45º
4
3
6
60º
12, √21, 3;
√13, 1, 30º;
√15, √3, √6;
15, 2√21, 4√3).
Указание: Перед решением задачи следует повторить и затем записать на доске формулы
CO = a/√3 , C1O1 = a1/√3, ON = a/2√3, O1N1 = a1/2√3.
6. Заполните табл. 9, если a и b – стороны оснований пирамиды, h – высота, k – апофема, S1 – площадь боковой поверхности, S – площадь поверхности пирамиды.
Таблица 9.
№
Вид усеченной правильной пирамиды
a
b
h
k
S1
S
1
3-угольная
12
6
1
2
4-угольная
8
2
4
3
6-угольная
4
2
1
(1 — 2 , 54, 54+45√3;
2- 5, 100, 168;
3 – 2, 36 , 36+30 √3).
Указание: Задачу следует решать по заранее заготовленному чертежу. Перед решением повторить и записать на доске необходимые формулы.
Цилиндр.
1. Радиус основания цилиндра равен 2 см, высота – 3 см. Найдите диагональ осевого сечения.
(5 см).
2. Осевое сечение цилиндра – квадрат, площадь которого равна 4 см². Найдите площадь основания.
(π см²).
3. Чему равна высота цилиндра, радиус основания которого равен 1 м, а площадь осевого сечения равновелика основанию.
(π/2 м).
4. Диаметр основания цилиндра равен его высоте. Найдите отношение площади осевого сечения S к площади его основания.
(Sосн/S=π/4).
5. Дан прямой круговой цилиндр, у которого буквой c обозначена длина окружности основания, d – диаметр основания, H – высота цилиндра, d1 – диагональ осевого сечения, B0 – площадь основания, Q – площадь осевого сечения. Используя известные формулы, заполните пустые ячейки в табл.1.
Указание: Перед решением задачи следует выполнить рисунок на доске, повторить и затем записать на доске формулы
с = πd, d²1 = d²+H²; B0 = πd²/4; Q = dH.
Таблица 1.
№
с
d
H
d1
B0
Q
1
c
H
2
d
d1
3
H
B0
4
d1
Q
5
B0
Q
6. Квадрат, площадь которого равна Q, свернули так, что получилась боковая поверхность цилиндра. Найдите площадь основания этого цилиндра.
(Qπ/4)
7. Пусть S – площадь боковой поверхности цилиндра, d – диаметр основания, H – высота цилиндра. Заполните пустые ячейки в табл. 2.
Таблица 2.
№
S (см²)
d (см)
H (см)
1
12
5
2
100π
25
3
225π
15
(1 — 60π; 2 – 4; 3 – 15).
8. Радиус основания цилиндра равен 2 см, а диагональ осевого сечения – 5см. Найдите: a) высоту цилиндра; б) площадь осевого сечения цилиндра; в) площадь боковой поверхности; г) площадь поверхности цилиндра.
(а) – 3 см; б) – 12 см²; в) – 12π см²; г) – 20π см²)
9. Найдите площадь боковой поверхности цилиндра, если а) диаметр основания цилиндра равен 1, а высота равна длине окружности основания; б) осевое сечение цилиндра – квадрат с высотой h; в) площадь осевого сечения равна Q. (а) — π²; б) -πh²; в)- πQ).
Конус.
1. Найдите площадь осевого сечения конуса, если образующая равна l, а угол при вершине осевого сечения составляет: а) 30º; б) 45º; в) 90º.
(а) — l²/4; б) — √2 l²/4; в) — l²/2).
2. Осевое сечение конуса – равносторонний треугольник со стороной 1. Определите радиус и высоту конуса.
(R=1/2; H=1√3/2).
3. Высота конуса равна радиусу основания R. Найдите площадь осевого сечения, если R=3 см.
(9 см²)
4. Через середину высоты конуса проведена плоскость параллельно основанию. Найдите площадь сечения, если радиус основания конуса равен 2 см.
(π см²)
5. На каком расстоянии от вершины конуса надо провести плоскость параллельно основанию, чтобы площадь сечения была равна половине площади основания?
(H√2/2, где H- высота конуса).
6. Дан конус, осевое сечение которого- равносторонний треугольник. Через две образующие , составляющие между собой угол 30º, проведена плоскость. Найдите площадь сечения, если радиус основания равен r.
(r²)
7. Полукруг радиуса R свернут в конус. Найдите: а) радиус основания конуса; б) угол α при вершине осевого сечения.
(R/2; 60º)
8. Дан прямой круговой конус, у которого буквой обозначена длина окружности основания, d-диаметр основания, H-высота конуса, l-образующая конуса, α- угол наклона образующей к основанию, B-площадь основания, Q- площадь осевого сечения. Используя известные формулы, заполните пустые ячейки в табл.3.
Указание: Перед решением задачи сделайте на доске рисунок, повторите и запишите на доске формулы
c=πd, l²=H²+d²/2, B=πd²/4, Q=dH/2. Таблица 3.
№
с
d
H
l
α
B
Q
1
c
H
2
c
L
3
d
α
4
l
α
B
5
α
Q
9. Образующая конуса удалена от центра его основания на расстояние l см и наклонена к плоскости основания под углом 30º. Вычислите площадь основания конуса. (4π см²)
10. Боковая поверхность конуса равна 132π см², образующая – 11 см. Найдите площадь основания. (144π см²)
11. Какое минимальное количество картона необходимо для изготовления модели конуса, высота которого 12 см, а диаметр – 10 см? (90π см²)
12. Осевое сечение конуса – прямоугольный треугольник с гипотенузой, равной 2√2 см. Найдите площадь боковой поверхности конуса. (2 π√2 см²)
13. Разверткой боковой поверхности конуса является сектор, дуга которого равна 60º, а хорда – b. Найдите боковую поверхность конуса. (π/6 b²)
Усеченный конус.
1. Высота H усеченного конуса равна разности радиусов оснований. Найдите площадь осевого сечения, если радиусы оснований равны R и r.
((R²-r²)/2)
2. Чему равна площадь сечения, проведенного через середину высоты усеченного конуса параллельно основаниям, если радиусы оснований усеченного конуса равны 4 см и 2 см? (9 π см²)
3. Дан усеченный конус, у которого буквами с1 и с2 обозначены длины окружностей соответственно нижнего и верхнего оснований, d1 и d2- диаметры соответственно нижнего и верхнего оснований, H – высота, l – образующая усеченного конуса, α – угол наклона образующей к плоскости нижнего основания, Q – площадь диагонального сечения. Используя известные формулы, заполните пустые ячейки в табл.4.
Указание: Перед решением задачи сделайте на доске чертеж, повторите и затем запишите формулы
c1= πd1, c2= πd2, l²=H²+(R-r)², Q=((R+r)/2)*H.
Таблица 4.
№
с1
с2
d1
d2
H
l
α
Q
1
с1
H
α
2
d2
H
l
3
d1
l
Q
4
с2
d1
α
5
с1
H
Q
4. Площадь боковой поверхности усеченного конуса равна 132π дм², образующая – 11 дм. Найдите радиусы оснований, если известно, что их отношение равно 2. (8 дм и 4 дм)
5. Радиусы оснований усеченного конуса равны 3 дм и 6 дм, образующая – 5 дм. Найдите: а) высоту усеченного конуса; б) площадь осевого сечения; в) угол наклона образующей к плоскости основания; г) площадь боковой поверхности усеченного конуса; д) площадь поверхности усеченного конуса.
(а) 4 дм; б) 18 дм²; и) arcsin 0,8; г) 45π дм²; 90π дм²)
6. Дан усеченный конус, у которого R, r – радиусы нижнего и верхнего оснований, H, l – высота и образующая усеченного конуса, α – угол наклона образующей к плоскости нижнего основания, Sбок – боковая поверхность, S – поверхность усеченного конуса. Заполните пустые ячейки в табл. 5.
Указание: Перед решением сделать на доске чертеж, повторить и затем на доске записать формулы
S=π(R+r)l, S=Sбок+πR²+πr².
Таблица 5.
№
R
r
H
l
α
Sбок
S
1
16
10
8
2
6
3
5
3
7
6
45º
4
6
3
45π
5
3√3
8
30º
( 1) – 10 ; arcsin 0,8; 260π; 616 π;
2) – 4; arcsin 0,8; 45π, 90π;
3) – 1; 6√2; 48 π√2; 50 π+48 π√2;
4) – 5; 4; arcsin 0,8; 90π;
5) – 4; 7√3; 80π√3; 80π√3+174π)
Шар и сфера.
1. В шаре проведены два параллельных сечения на расстоянии 1 см и 2 см от центра. Найдите расстояние между сечениями. (3 см и 1 см)
2. Найдите расстояние от центра до плоскости, если расстояние от центра этого шара до плоскости равно d, а радиус шара – R. ( 0 или d-R)
3. Две сферы, радиусы которых равны R1 и R2, имеют единственную общую точку. Найдите расстояние между их центрами. (R1+R2, |R1-R2|)
4. Площадь поверхности полушара на Q площади его основания. Найдите площадь основания. (Q)
5. Шар радиуса 5 см пересечен плоскостью, отстоящей от центра на 3 см. Найдите площадь круга, полученного в сечении. (16π см²)
www.metod-kopilka.ru
стереометрия 10 -11 класс. Решения задач для подготовки к ЕГЭ — Колпаков Александр Николаевич
Эта страница создана для учащихся 10 — 11 классов и абитуриентов, кого интересует качественная подготовка к ЕГЭ по математике в виртуальном он-лайн режиме. Многие школьники испытывают серьезные проблемы с решением задач по стереометрии (в новой спецификации ЕГЭ 2012 года это номера 9, B11 и С2) и почти всегда нуждаются в квалифицированной помощи профессионального преподавателя. Для многих из них фраза репетитор по математике ассоциируется с реальными занятиями, однако не все могут позволить себе нанять хорошего репетитора. Для этой категории учащихся сайт предоставляет возможность получить отдельные он-лайн консультации по вопросам решения различных задач (как с ЕГЭ, так и с традиционных контрольных работ).
Регулярно просматривайте опубликованные учебные материалы, изучайте решения задач, вникайте в доказательства, и задавайте репетитору по математике любые вопросы по стереометрии через специальную приведенную ниже форму. Их спектр не ограничивается только одними задачами подготовки к ЕГЭ по математике и распространяется на любые темы по стереометрии 10 — 11 класс: призмы, пирамиды, тела вращения, объемы, площади поверхностей, доказательства теорем, правила для нахождения углов между стереометрическими объектами, растояний, вектора, элементы аналитической геометрии и многое другое. Кроме меня оформлением решений занимаются мои коллеги — репетиторы по математике и физике, которых я лично знаю и держу их анкеты в базе репетиторов сайта. Если вы сами репетитор по математике и хотите принять участие в он-лайн решениях — укажите при регистрации те страницы, которые вы хотели бы курировать.
Задача для репетитора по математике от Катерины.
Имеется правильная усеченная четырехугольная пирамида. Ее стороны оснований равны 4 , а боковое ребро с большим основанием образует угол в 45 град. Найдите площадь диагонального сечения пирамиды.
Решение репетитора (Колпаков А.Н.)
Напомню, что пирамиду называют правильной, когда в основании у нее лежит правильный многоугольник (в нашем случае — квадрат), а основание O высоты является его центром (точкой пересечения диагоналей). Если усеченная пирамида получена из правильной, то она тоже называется правильной. Идеально, если на рисунке репетитор по математике изображает усеченную пирамиду вместе с обычной.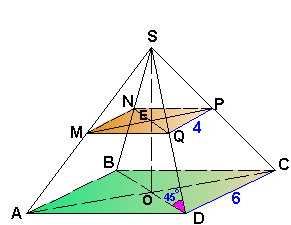 
В этом случае ее удобнее строить и легче проводить обоснования используемых свойств. Эти обоснования опустим, считая их известными, а именно: 1) диагональное сечение BNQD — равнобедренная трапеция, 2) угол между боковым ребром QD и основанием ABCD — это угол данной трапеции, то есть . Поэтому согласно условию. Основания трапеции — диагонали квадратов ABCD и MNPQ. Применим свойство о том, что диагональ квадрата в раз больше его стороны и получим, что , (аналогичные результаты можно получить при помощи теоремы Пифагора). Осталось вычислить площадь трапеции (диагональное сечение BNQD): ее удобнее вынести из стереометрического рисунка и изобразить в «полный рост»:
Для нахождения площади необходимо выяснить длину отрезка QK (высота трапеции). Проведем вторую высоту NH. Получим . Так как — прямоугольный с углом , то и второй его угол — равнобедренный . Тогда
Вопрос репетитору по математике от Татьяны.
Здравствуйте. Как можно решать такую задачу? В правильной треугольной пирамиде SABC M-середина ребра BC, S-вершина. Известно, что SM=7, а площадь боковой поверхности равна 63. Найти длину AB.
Решение репетитора (Колпаков А.Н.) Применим формулу, вычисляющую площадь боковой поверхности правильной пирамиды (она верна для любых пирамид с равными апофемами): , где p — полупериметр основания пирамиды, а h-ее апофема. Поскольку наша пирамида является правильной и стороны ее основания равны, то . Подставляя в указанную формулу значение площади, равное 63 и указанное выражение для полупериметра основания, получим:
или
, откуда находим
Ответ: AB=6.
Задача Алены.
Через сторону AD ромба проведена плоскость альфа, удалённая от BC на расстоянии 3 корня из 3 (см). Сторона ромба — 12 см, угол BCD равен 30 град. Найдите угол между плоскостью ромба и плоскостью альфа.
Решение и рисунок репетитора по математике для Алены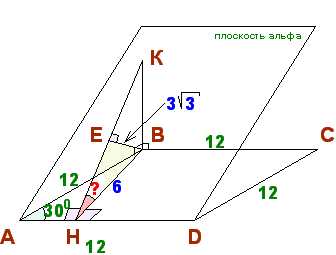
Восстановим из точки B перпендикуляр к альфа и пусть К — его точку пересечения с альфа (см.рисунок). В плоскости ромба проведем высоту BH и соединим ее точку H с точкой K. Тогда по теореме о 3-х перпендикулярах KH перепндикулярна AD. Плоскость BHK будет перпендикулярна линии пересечения интересующих нас плоскостей, а также самим плоскостям (по признакам перпендикулярности прямой и плоскости, двух плоскостей). Поэтому — линейный угол двугранного угла между ромбом и альфа. Расстояние от B до альфа — есть перпендикуляр BE, лежащей в плоскости BKH (доказательство этого факта я пропускаю). Остается найти в треугольнике BHK. Для этого через треугольник ABH найдем . В итоге
Вопрос репетитору по математике от Светланы
Как построить сечение параллелепипеда плоскостью, проходящей через три точки, лежащих на взаимно скрещивающихся ребрах? Спасибо.
Решение: Рассмотрим параллелепипед ABCDMNKP и точки H,E и F, принадлежащие скрещивающимся ребрам. Для построения таких сечений (плоскостью HEF) необходимо построить вспомогательную плоскость AHEQ, в которой В этой плоскости проводим HE до пересечения с продолжением AQ в точке S. Соединяем S и F, пересекая AD в точке T. Полученная точка T лежит с F в одной грани основания. Далее действуем стандартно (репетитор по математике предполагает, что дальнейшее построение сечения — дело техники и не вызовет особых проблем). Достаточно пересечь FT с продолжением BC и замкнуть таким образом контур сечения. Вы можете кликнуть на фотографию для ее увеличения.
ankolpakov.ru
расстояние от точки до плоскости и другие задачи
В этой статье будем определять различные расстояния: от точки до плоскости, между прямыми, и даже будем определять кратчайшее расстояние от точки до точки по поверхности куба.
Задача 1. В основании прямой треугольной призмы с боковым ребром лежит прямоугольный треугольник с катетами и . Точка -середина ребра , а точка делит ребро в отношении 1 : 2 , считая от вершины . Плоскость пересекает ребро в точке .
a) Докажите, что точка -середина ребра ;
б) Найдите расстояние от точки до плоскости .
Рисунок 1 к задаче 1
Строим плоскость . Найдем точку пересечения прямых и – точку . Эта точка принадлежит плоскости грани , поэтому можно провести прямую . Прямая пересечет ребро в точке .
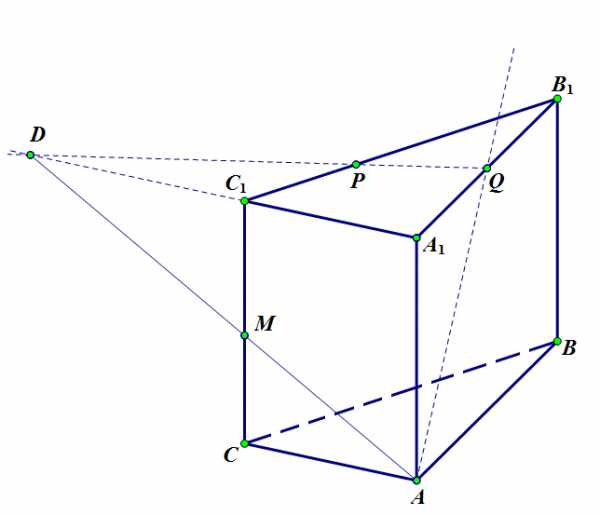
Рисунок 2 к задаче 1
Соединяем точки и штрихуем сечение.
Рисунок 3 к задаче 1
Решим эту задачу координатно-векторным способом. Введем систему координат так, что ее начало совпадет с вершиной прямого угла треугольника, лежащего в основании призмы. Направим ось вдоль ребра , ось – вдоль ребра , а ось – вверх. Определим координаты точек, принадлежащих плоскости сечения.
Рисунок 4 к задаче 1
Длина отрезка , поэтому . Поскольку точка – середина отрезка , то ее координаты . Координаты точки .
Определим уравнение плоскости. Коэффициент , так как плоскость не проходит через начало координат.
Вычтем из первого второе уравнение:
Тогда из первого уравнения:
Уравнение плоскости:
Точка принадлежит плоскости, поэтому ее координаты должны удовлетворять полученному уравнению. Координаты этой точки по двум осям известны, так как она принадлежит ребру :
Тогда при подстановке в уравнение плоскости получим:
Таким образом, доказано, что точка – середина ребра .
Теперь определим расстояние от точки до плоскости. Координаты точки : . Расстояние определим по формуле
Ответ: .
Задача 2. В правильной треугольной призме сторона основания равна 6, а боковое ребро равно 3. На ребре отмечена точка так, что . Точки и -середины ребер и соответственно. Плоскость параллельна прямой и содержит точки и .
а) Докажите, что прямая ВМ перпендикулярна плоскоcти .
б) Найдите расстояние от точки до плоскости .
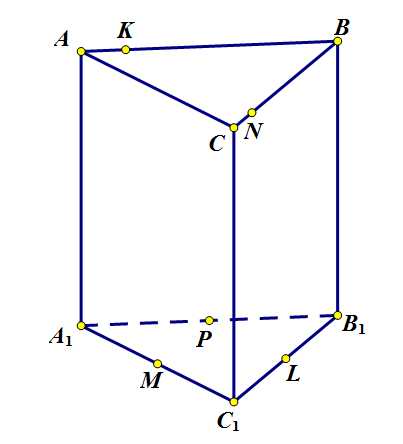
Рисунок 1 к задаче 2
Построим плоскость . Так как она параллельна , то и прямые этой плоскости параллельны , поэтому, зная точки, принадлежащие плоскости, построим прямые, проходящие через эти точки и одновременно параллельные – и .
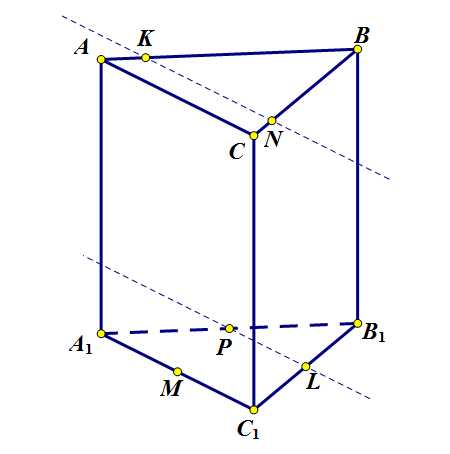
Рисунок 2 к задаче 2
Теперь соединяем точки сечения отрезками и штрихуем его:
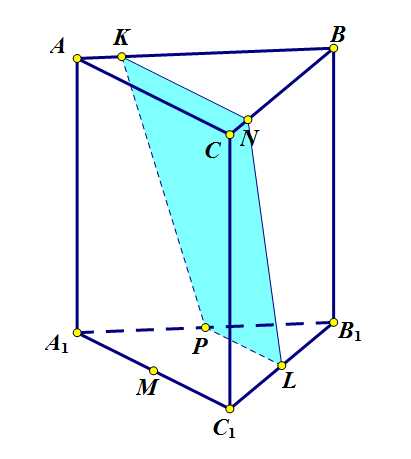
Рисунок 3 к задаче 2
Решим эту задачу координатно-векторным способом. Введем систему координат так, что ее начало совпадет с точкой . Направим ось вдоль ребра , ось – вдоль высоты основания , а ось – вверх. Определим координаты точек, принадлежащих плоскости сечения.
Для этого понадобится знание высот ы основания – длины отрезка :
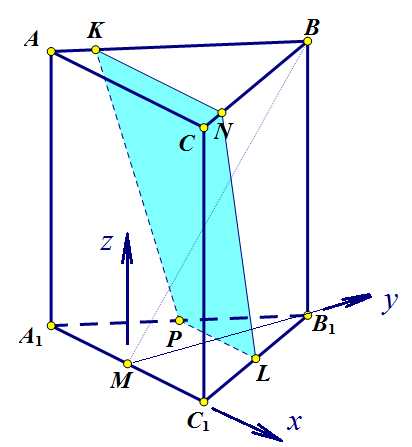
Рисунок 4 к задаче 2
Тогда
Определяем коэффициенты уравнения плоскости:
Вычитание третьего уравнения из первого дает , следовательно, , .
Уравнение плоскости
Координаты нормали
Найдем координаты направляющего вектора прямой . Координаты точки – они и будут координатами направляющего вектора прямой.
Так как соответствующие координаты вектора нормали и координаты вектора относятся друг к другу с постоянным коэффициентом:
То указанные вектора коллинеарны, а следовательно, вектор перпендикулярен плоскости.
Определим расстояние от точки до плоскости.
Координаты точки : .
Ответ: .
Задача 3. В правильной четырехугольной пирамиде боковое ребро равно , а высота пирамиды равна . Точки и – середины ребер и соответственно, -высота пирамиды с вершиной и основанием .
a) докажите, что точка Т -середина отрезка ;
б) Найдите расстояние между прямыми и .
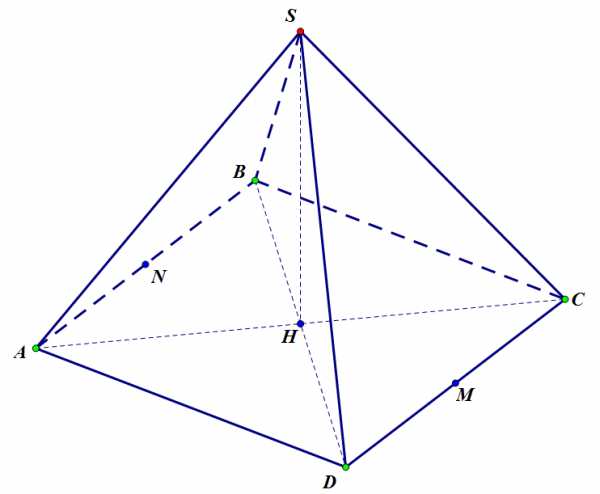
Рисунок 1 к задаче 3
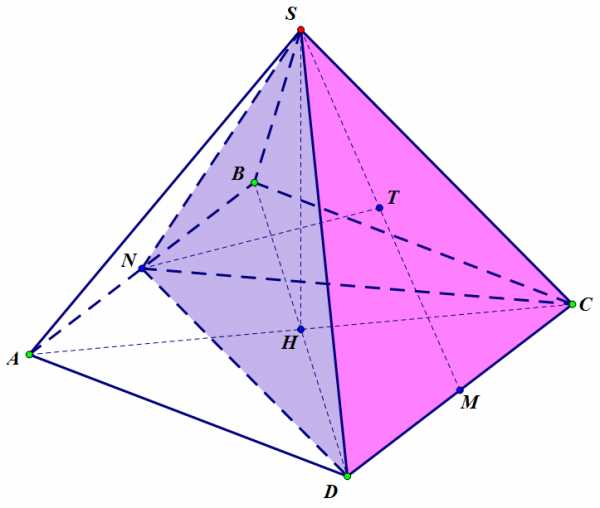
Рисунок 2 к задаче 3
Определим апофему пирамиды.
Тогда треугольник – равносторонний со стороной, равной 2. Следовательно, высота пирамиды с вершиной и основанием – отрезок – его высота, медиана и биссектриса. Пункт а) доказан.
Рисунок 3 к задаче 3
Рассмотрим треугольник . Длина отрезка – искомое расстояние.
Для подобных треугольников и запишем отношение сходственных сторон:
Ответ: .
Задача 4. На ребре куба взята середина , а на ребре – такая точка ‚ что . Найдите длину кратчайшего пути из точки в точку по поверхности куба.
Чтобы найти кратчайший путь из пункта А в пункт В – нужно срезать. То есть в идеале – пройти по гипотенузе. Нарисовать кратчайший путь нам мешает ребро куба – сгиб. Так давайте разогнем – развернем поверхность куба!
Рисунок 1 к задаче 4
В треугольнике катеты , а , поэтому искомое расстояние :
Ответ: .
easy-physic.ru
