Очень сложные задачи : Физика
Здравствуйте. Помогите пожалуйста решить несколько задач. Их всего 5 и они сложные. Хотя бы идейку подкиньте пожалуйста…
1. Полусферический тонкостенный «колокол» с небольшим отверстием в верхней части плотно (без зазора) лежит на горизонтальном столе. Через отверстие в колокол медленно наливают воду. Когда вода доходит до отверстия, она приподнимает колокол и начинает вытекать из под него снизу. Найдите массу колокола m, если его радиус R=10 см. Плотность воды ρ=10^3 кг/м3.2. Маленькая шайба находится на горизонтальной поверхности стола, состоящей из двух панелей: гладкой и шероховатой. Коэффициент трения между шайбой и шероховатой панелью возрастает по мере удаления от стыка панелей по линейному закону μ(x)=αx, где α=const, а координатная ось Ox направлена перпендикулярно стыку панелей. Шайба скользит по гладкой панели параллельно оси Ox и в некоторый момент времени попадает на шероховатую панель. Какое расстояние x0 пройдет по шероховатой панели шайба до полной остановки, если
ее скорость на гладкой панели равна v0? Ускорение свободного падения g.
3. Катер приближается к пристани со скоростью v=72 км/ч. Стоит безветренная погода. На пристани играет оркестр. На сколько полутонов п должны изменить свое исполнение музыканты оркестра для того, чтобы пассажиры катера слышали мелодию в неискаженной тональности? Скорость звука в воздухе примите равной c=340 м/с.
Указание. Один полутон соответствует изменению частоты звучания в Корень двенадцатой степени из 2 раза.
4. Дождевая капля радиусом R падает с высоты h. При падении капля пролетает через заряженное облако и приобретает потенциал φ0. Под действием сил кулоновского отталкивания капля разделяется на две одинаковые части, относительные скорости которых направлены горизонтально. Какую максимальную скорость может приобрести каждая из капелек в момент достижения поверхности Земли? Сопротивлением воздуха и электростатическим взаимодействием капелек с поверхностью Земли и с заряженным облаком, а также поверхностным натяжением воды можно пренебречь. Плотность воды ρ. Электрическая постоянная ε0, ускорение свободного падения g.
5. Водитель видит приближающийся сзади автомобиль в панорамное (выпуклое)
зеркало заднего вида. Во сколько раз m отличается угловой размер изображения
автомобиля от углового размера самого автомобиля, если фокусное расстояние зеркала f=1 м, а расстояние от глаз водителя до зеркала s=0,5 м? Считайте, что это расстояние значительно меньше расстояния l от зеркала до приближающегося сзади автомобиля.
dxdy.ru
Колебания: интересные задачи
Сложные и средней сложности задачи предлагаю вам в этой статье. Они взяты из задачника Г.А. Никуловой и А.Н. Москалева. После решения этих задач вы будете более уверенно чувствовать себя на ЕГЭ по физике.
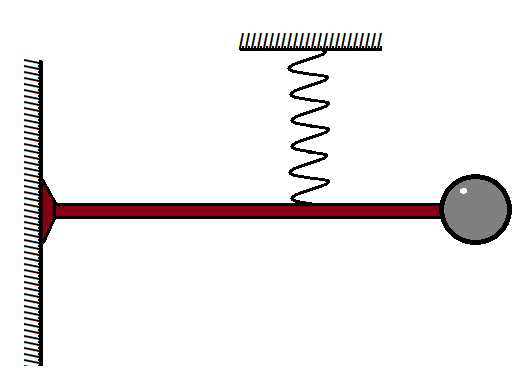
Задача 1. Найдите период колебаний бруска массой кг в системе, изображенной на рисунке. Жесткость пружин Н/м, Н/м. Трением пренебречь.

К задаче 1
На брусок будут действовать две силы упругости: от первой и второй пружин. Причем если одна пружина растянута, то другая сжата, следовательно, обе силы всегда направлены в одну сторону, так как одна пружина стремится сжаться, а другая, наоборот, растянуться. Таким образом, равнодействующая будет суммой обеих сил:
Тогда общий коэффициент жесткости
Следовательно, период равен
Ответ: с.
Задача 2. Определите среднюю скорость при колебаниях пружинного маятника с амплитудой см и периодом колебаний с за время движения маятника а) от положения равновесия до отклонения в 0,5 см; б) от максимального отклонения до отклонения 0,5 см.
Средняя скорость – это весь пройденный телом путь, деленный на все время. Определим и то, и другое. Общая форма записи координаты при колебательном движении
Где – начальная фаза. Предположим, она равна нулю – для нашей задачи это совершенно неважно. Тогда, если тело прошло пол-амплитуды, то
Отсюда следует, что
А . Это составляет двенадцатую часть периода:

К задаче 2
Теперь можно определять среднюю скорость: разделим путь на время.
Теперь второй случай. Теперь грузик перемещается от точки с максимальной амплитудой до отклонения 0,5 см. Но если положение равновесия он проходит с максимальной скоростью, и на последующие за положением равновесия 0,5 см у него уходит одно время, то на путь из точки с максимальной амплитудой до 0,5 см у него уйдет больше времени: ведь в точке с максимальной амплитудой он неподвижен. Определим, сколько понадобится на тот же путь времени в этот раз. Движение из точки в точку занимает , а движение из точки в точку – время , уже определенное нами ранее. Тогда
Тогда средняя скорость равна
Ответ: 0,06 и 0,03 м/с.
Задача 3. Груз массой колеблется на пружине жесткостью с амплитудой . Найдите в точке с координатой : а) кинетическую энергию; б) скорость прохождения грузом этой точки.
Общая форма записи координаты при колебательном движении
Где – начальная фаза. Предположим, она равна нулю. Тогда
Максимальная потенциальная энергия пружины равна
Потенциальная энергия пружины в точке
Тогда кинетическая энергия груза будет равна разности этих потенциальных энергий:
Так как
То скорость в этой точке
Ответ: , .
Задача 4. Какова частота собственных колебаний соснового бруска массой кг и площадью поперечного сечения см, плавающего в вертикальном положении в озере? Плотность древесины кг/м.
Брусок плавает в озере, сила Архимеда уравновешивает силу тяжести.
Если мы чуть надавим и погрузим брусок чуть больше, то возникнет добавка к уже ранее погруженной части, дополнительный погруженный объем, и «излишек» силы Архимеда, который и станет возвращающей силой и вызовет колебания бруска, когда мы его отпустим.
Этот «излишек» Архимедовой силы равен
Где – дополнительная глубина, на которую мы погрузили брусок.
Эту силу можно считать «силой упругости воды», и записать так:
Тогда «коэффициент упругости воды» будет равен
Частота колебаний определяется формулой
Ответ: 1,76 Гц.
Задача 5. Найдите период колебаний математического маятника длиной см, подвешенного в вагоне, движущемся горизонтально с ускорением м/с.
На маятник будет воздействовать ускорение, являющееся суммой и :
Период колебаний такого маятника равен
Линия отвеса тоже поменяет положение, отклонившись от вертикали на угол:
Ответ: с, .
Задача 6. С каким ускорением и в каком направлении должна двигаться кабина лифта, чтобы находящийся в ней секундный маятник за время мин с совершил колебаний?
Период колебаний математического маятника определяется формулой:
Период был равен 1 с, а потом под действием ускорения изменился, и стал равен
Так как длина нити не менялась, а период вырос в полтора раза, следовательно, изменилось ускорение: ускорение свободного падения уменьшилось на величину ускорения лифта. Из этого делаем вывод, что лифт идет вниз.
Длину нити найдем из условия, что истинный период маятника – секунда:
И подставим:
Ответ: 5,6 м/с.
Задача 7. Определите период колебаний маятника. Масса груза 400 г, жесткость пружины Н/м. Массой стержня пренебречь. Точка прикрепления пружины к стержню делит ее длину в отношении , считая от шарика. В положении равновесия стержень горизонтален, а ось пружины вертикальна.
К задаче 7
По правилу моментов запишем
Где – сила, растягивающая пружину.
Тогда растяжение пружины
Если таково растяжение пружины, то «ход» груза на конце стержня будет в 1,5 раза больше – из подобия треугольников. Тогда
То есть эквивалентная масса груза ()
Следовательно, период колебаний
Ответ: 1,88 с
easy-physic.ru
Задания по физике 11 класс
Задача 1. На полу лежит доска массы m. Как должен двигаться на доске человек массы М, чтобы она начала скользить по полу? Коэффициент трения между доской и полом равен k.
Ответ: На доску, по которой идет человек, действуют сила , сила реакции пола , сила трения и сила давления , производимого человеком. На человека действуют сила тяжести и сила реакции доски , причем .
Если человек движется по доске равномерно и прямолинейно, то силы и уравновешивают друг друга и, следовательно, сила будет направлена вертикально вниз. В этом случае , и доска останется в покое.
Если человек движется по доске прямолинейно с ускорением относительно пола, то силы и имеют горизонтальные составляющие (см.рис.). Из уравнения движения человека следует, что величина каждой из этих составляющих равна Ма. Вертикальные составляющие и будут иметь величину Mg. В этом случае
где — ускорение доски относительно пола. Вводя систему координат так, как показано на рисунке, и записывая последнее уравнение в проекциях на оси ОХ и ОУ, получим
(здесь учтено, что (при ≠ 0) и горизонтальная составляющая силы направлены по оси ОХ, а сила — противоположно оси ОХ). Наибольшая величина силы покоя, совпадающая с величиной силы трения скольжения, в данном случае равна . Если , то сила уравновешивает горизонтальную составляющую силы , и доска останется в покое (=0). Если же , то сила имеет наибольшую величину, но не уравновешивает горизонтальную составляющую силы . В этом случае доска скользит по полу с ускорением, имеющим величину .
Итак, для того, чтобы доска пришла в движение, человек должен двигаться по ней с ускорением, удовлетворяющим условие
Задача 2. Определите частоту колебаний пружинного маятника, который образован грузом массой m, связанным с бортами тележки одинаковыми пружинами жесткости k. В состоянии покоя пружины не деформированы. Тележка имеет массу М, может двигаться без трения в горизонтальной плоскости. Тележка симметрична так, что её центр масс и центр масс груза в состоянии покоя находятся на одной вертикали.
Ответ: Центр масс системы неподвижен, либо движется с постоянной скоростью относительно Земли. Пусть центр масс неподвижен относительно Земли. Выберем систему координат так, что её начало совпадает с центром масс системы, а ось Х параллельна Земле и направлена вдоль тележки и пружин.
В начальный момент времени выведем груз из состояния равновесия, х = 0, так что его координата определяется значением х, при этом тележка сдвинется относительно Земли на величину х0, так как центр масс должен оставаться в точке х = 0. Значение х0 найдем из определения центра масс и условия, что он находится в точке х = 0
Из модели следует, что модуль изменения длины каждой пружины по сравнению с её длиной в нормальном состоянии определяется выражением
Уравнение Ньютона для груза, совершающего колебательные движения, имеет вид
где а — ускорение груза. Из уравнения следует, что циклическая частота колебаний определяется выражением
Задача 3. Найти отношение работ расширения газа в процессах 1 – 2, 3 – 4. Массы газов одинаковы. Газ по своим свойствам близок к идеальному.
Ответ: Точки 1, 3 лежат на одной изохоре. То же самое можно сказать про точки 2 и 4. Следовательно, изменение объема ΔV в обоих процессах одинаково. Работа в процессе 3 – 4 (а оба процесса изобарические) в раза больше, так как
Задача 4. Катушка с намотанной на неё проволокой вращается вокруг своей оси. Концы проволоки с помощью скользящих контактов соединены с гальванометром. Какой заряд ΔQ пройдет через гальванометр при резкой остановке катушки? Радиус катушки r, угловая скорость её вращения ω, площадь поперечного сечения проволоки S, удельное сопротивление металла проволоки ρ.
Ответ: При остановке катушки свободные электроны в металле будут двигаться по инерции до тех пор, пока их кинетическая энергия, обусловленная вращением катушки, не превратиться в тепло
где m – масса электрона, — линейная скорость движения проволоки, n – концентрация электронов, L – длина проволоки, — её сопротивление, — средний ток в проводнике за все время торможения.
Ток в начале торможения где е – заряд электрона. Следовательно, заряд
Задача 5. Электрическая печь присоединена к сети напряжением U = 220 В. Расстояние от ввода до места, где установлена печь l = 7,5 м. Сечение провода S = 1,5 мм2, его удельное сопротивление ρ = 10-7Ом. Определите сопротивление печи, если её мощность Р = 2,1 кВт.
Ответ: Сопротивление проводов, соединяющих печь и источник тока после вычислений R = 1 Ом. Ток, протекающий в цепи где r – сопротивление печи. Мощность печи Р представляется выражением Уравнение удобно представить в виде Подставляя численные значения известных величин, получаем Откуда находим два возможных значения r. r1 = 1/21 Ом, r2 = 21 Ом. Если взять в качестве решения r1, то ток, протекающий в проводе J1 = 210 А. Такой ток недопустим. Если взять r2 = 21 Ом, то J2 = 10 А, что допустимо. Значит r = 21 Ом.
Вконтакте
Google+
Одноклассники
olimpotvet.ru
| № п/п | Название темы | Кол-во часов |
| 1 | ФИЗИЧЕСКАЯ ЗАДАЧА. | 2 |
| 1.1 | Что такое физическая задача. Состав физической задачи. Физическая теория и решение задач. Значение задач в обучении и жизни. | 1 |
| 1.2 | Классификация физических задач по требованию, содержанию, способу задания, способу решения. Примеры задач всех видов. | 1 |
| 2 | ПРАВИЛА И ПРИЕМЫ | 5 |
| 2.1 | Общие требования при решении физических задач. Этапы решения физической задачи. Работа с текстом задачи | 1 |
| 2.2 | Анализ физического явления; формулировка идеи решения (план решения). Выполнение плана решения задачи. Числовой расчет. | 1 |
| 2.3 | Использование вычислительной техники для расчетов. Анализ решения и его значение. Оформление решения задачи. | 1 |
| 2.4 | Типичные недостатки при решении и оформлении решения физических задач. | 1 |
| 2.5 | Различные приемы и способы физических задач: алгоритмы, аналогии, геометрические приемы, метод размерностей, графические решения и т.д. | 1 |
| 3 | МЕХАНИКА | 11 |
| 3.1 | Координатный метод решения задач по механике. | 1 |
| 3.2 | Решение задач на основные законы динамики: законы Ньютона. | 2 |
| 3.3 | Решение задач на законы для сил тяготения, упругости. | 2 |
| 3.4 | Решение задач на трение, сопротивление движения. | 2 |
| 3.5 | Решение задач на движение материальной точки, системы точек, твердого тела под действием нескольких сил. | 2 |
| 3.6 | Задачи на определение характеристик равновесия физических систем. | 1 |
| 3.7 | Задачи на принцип относительности: кинематические и динамические характеристики движения тела в разных инерциальных системах отсчета. | 1 |
| 4 | ЗАКОНЫ СОХРАНЕНИЯ | 8 |
| 4.1 | Решение задач средствами кинематики, динамики, с помощью законов сохранения. | 2 |
| 4.2 | Решение задач на закон сохранения импульса и реактивное движение | 2 |
| 4.3 | Решение задач на определение работы и мощности, на закон сохранения и превращения механической энергии. | 2 |
| 4.4 | Решение задач несколькими способами. Взаимопроверка решаемых задач. | 2 |
| 5 | МОЛЕКУЛЯРНАЯ ФИЗИКА. СТРОЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ. | 5 |
| 5.1 | Решение качественных задач на основные положения и основное уравнение МКТ. Решение задач на описание поведения идеального газа. | 2 |
| 5.2 | Решение задач на свойства паров: использование уравнения Менделеева-Клапейрона, характеристика критического состояния. | 1 |
| 5.3 | Решение задач на определение характеристик влажности воздуха. | 1 |
| 5.4 | Решение задач на определение характеристик твердого тела: абсолютное и относительное удлинение, тепловое расширение, запас прочности, сила упругости. | 1 |
| 6 | ОСНОВЫ ТЕРМОДИНАМИКИ | 4 |
| 6.1 | Решение комбинированных задач на 1-й закон термодинамики. | 2 |
| 6.2 | Решение задач на тепловые двигатели. | 2 |
| 7 | ЭЛЕКТРИЧЕСКОЕ И МАГНИТНОЕ ПОЛЯ | 5 |
| 7.1 | Характеристика решения задач данного раздела. | 1 |
| 7.2 | Решение задач на закон сохранения заряда и закон Кулона. | 2 |
| 7.3 | Задачи разных видов на описание магнитного поля тока и его действия: магнитная индукция, магнитный поток. | 1 |
| 7.4 | Решение задач по теме: «Сила Ампера» и «Сила Лоренца» | 1 |
| 8 | ЗАКОНЫ ПОСТОЯННОГО ЭЛЕКТРИЧЕСКОГО ТОКА. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ. | 12 |
| 8.1 | Решение задач на различные приемы расчета сопротивления сложных электрических цепей. | 2 |
| 8.2 | Решение задач разных видов на описание электрических цепей постоянного электрического тока с помощью закона Ома для замкнутой цепи. | 1 |
| 8.3 | Решение задач на закон Джоуля-Ленца. | 1 |
| 8.4 | Решение задач на последовательное и параллельное соединения проводников. | 2 |
| 8.5 | Ознакомление с правилами Кирхгофа при решении задач. | 1 |
| 8.6 | Решение задач на расчет участка цепи, имеющего ЭДС | 1 |
| 8.7 | Решение задач на описание постоянного электрического тока в электролитах, вакууме, газах, проводниках: характеристика носителей, | 1 |
| 8.8 | Решение качественных задач. | 2 |
| 8.9 | Решение комбинированных задач. | 1 |
| 9 | ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ | 15 |
| 9.1 | Решение задач разных видов на описание явления | 1 |
| 9.2 | Решение задач на закон электромагнитной индукции. | 2 |
| 9.3 | Решение задач на правило Ленца, индуктивность. | 2 |
| 9.4 | Решение задач на переменный электрический ток | 1 |
| 9.5 | Решение задач на характеристики переменного | 2 |
| 9.6 | Решение задач по теме «Трансформатор», | 1 |
| 9.7 | Решение задач на описание различных свойств электромагнитных волн: скорость, отражение, преломление, интерференция, дифракция, поляризация. | 2 |
| 9.8 | Решение задач по геометрической оптике. | 3 |
| 9.9 | Классификация задач по СТО и знакомство | 1 |
| 10 | ОБОБЩАЮЩЕЕ ЗАНЯТИЕ ПО МЕТОДАМ И ПРИЕМАМ РЕШЕНИЯ ФИЗИЧЕСКИХ ЗАДАЧ | 5 |
refdb.ru
Учитель физики сдает ЕГЭ | Мел
Физика традиционно считается одним из наиболее сложных предметов для сдачи ЕГЭ. Синусы, косинусы, векторы и хороший счет, годы не на подготовку к экзамену, а на систематическое изучение науки — почему это главные условия для получения высокого балла? Сегодня сдает ЕГЭ по физике и отвечает на вопросы учитель Григорий Лапшин.
Специальная рассылка
Для тех, кому до школы остался год. Как подготовить ребёнка и себя к походу в первый класс
Для успешной сдачи ЕГЭ нужно владеть всем школьным курсом физики, который изучается на протяжении пяти лет (с 7 по 11 классы). Сюда входят следующие разделы: механика, молекулярная физика и термодинамика, электричество и магнетизм, оптика, квантовая и ядерная физика, начало теории относительности. На все вопросы дается чуть меньше четырех часов. Попытаемся проанализировать, в чем сложность этого экзамена и что необходимо для его успешной сдачи.
Итак, экзамен состоит из трех частей: всего 36 заданий, подавляющее большинство из которых — задачи. На весь экзамен лишь два или три задания на теорию. Надо в первую очередь уметь решать задачи по физике — именно это главное и основное условие успешной сдачи ЕГЭ. Проблема состоит в том, что решать задачи в старшей школе почти не учат. Исключения составляют лишь специализированные школы с углубленным изучение физики и математики, а также профильные классы в обычных школах. Да и то при условии, что учитель с должным вниманием отнесется к этому вопросу.
Физика вызывает трудности у подавляющего большинства школьников, включая тех, для кого это профилирующий предмет при поступлении в вуз
Дело в том, что изучение физики — это не зазубривание правил, формул и алгоритмов, а усвоение идей. Достаточно большого количества непростых идей. Их суть при поверхностном подходе понять сложно. В процессе учебы надо постепенно осознавать физические идеи, каждая из которых дает ключ к решению очередного пласта физических задач. Физику нужно понимать, потому что без этого нельзя научиться решать задачи.
Одного усвоения идей недостаточно — нужно уверенно владеть математическим аппаратом. Сложить векторы, выразить нужную величину из формулы, не путаться в синусах-косинусах и так далее. Отсутствие математических знаний и навыков закрывает путь к решению задач по физике.
При этом школьные курсы физики и математики выстроены таким образом, что, начиная с 7 класса, математика не успевает за физикой
Неудивительно, что многие разделы по физике оказываются как бы недопонятыми с точки зрения математики. Усвоить физические идеи, ясно понять законы физики и научиться решать задачи можно только под руководством квалифицированного преподавателя. Пособия для подготовки к ЕГЭ составлены по материалам прошлых лет и дают лишь ограниченное представление о физике. Следующий экзамен будет содержать уже совершенно иные задачи. Физика как раз и отличается тем, что по каждой теме можно составить огромное количество задач, и они никогда не повторяются.
Задания первой части в основной своей массе весьма просты, однако сыграть в «угадайку» тут не получится по ряду причин. Во-первых, это все-таки задачи, которые требуют именно решения, и выбрать правильный ответ по наитию или руководствуясь только теорией — не наш вариант. Во-вторых, варианты ответов подобраны таким образом, что нас опять отправляют к решению задачи или к анализу графика. В первом блоке собран весь школьный курс физики.
Встречаются весьма интересные и познавательные задачи, требующие умения связывать и преобразовывать размерности физических величин. В школе к этому вопросу учителя относятся зачастую недостаточно серьезно. Уровень сложности этих задач соответствует известному школьному задачнику Рымкевича. Он содержит много простых задач, на которых хорошо набивать руку.
Первая часть
Задания первой части группируются следующим образом (в том варианте, что был у меня):
с 1 по 7 — задачи из основных разделов школьного курса физики (механическое движение, законы Ньютона, закон всемирного тяготения, закон сохранения импульса, механические колебания). Это простые задания и проблем, как правило, не вызывают.
с 8 по 12 — термодинамика. Сам раздел всегда воспринимается школьниками с некоторым трудом, однако и тут особенных подводных камней нет.
с 13 по 24 — задачи на электродинамику, элементы квантовой физики, три задачи на ядерную физику. Они редко бывают сложными, у школьников с ними проблем нет.
Показательна задача № 18 на умение работать с физическими величинами, которая может вызвать трудности. Тут нужно хорошо представлять, что такое 1H и 1Тл, и уметь их выразить через другие единицы. Если с 1H все понятно — это кг м∕с2, — то представить 1Тл через другие единицы без дополнительных знаний не получится. В итоге 1Тл — это кг∕А · с2, а А·с — это не что иное как Кл, в итоге получается кг∕Кл·с.
Вторая часть
Задания второй части с 25 по 27, как вы уже догадались, представляют собой задачи. Как правило, они из механики, термодинамики, электростатики или электродинамики. В моем варианте попались:
№ 25 на применение силы Архимеда
№ 26 термодинамика
№ 27 электродинамика
Уровень сложности этих задач уже повыше. Для их решения необходимо правильно построить рисунок, указать направления действия сил и так далее. При этом последние две могут вызвать трудности, а вот задача № 25 будет по плечу даже восьмикласснику.
Третья часть
Задания третьей части — это задачи повышенной сложности. Такие задачи в школьных учебниках и задачниках не встречаются и требуют особой подготовки. Необходимо уметь думать и иметь большой опыт в решении задач, видеть задачу не узконаправленно, а всеобъемлюще.
Ученика нужно научить пытаться решить задачу различными способами, искать оптимальные пути, а не отступать через две минуты, если что-то не получается. В третьей части нет задач, которые решаются за несколько минут, тут необходимо думать и рассуждать. Очень кстати придется опыт и навык решения олимпиадных заданий, которые предполагают наличие нестандартного мышления.
Итак, передо мной пять задач по следующим темам: механические колебания, работа энергии, термодинамика, электродинамика, квантовая физика.
Задача № 29
Два шарика, массы которых m = 0,1 кг и М = 0,2 кг, висят, соприкасаясь, на вертикальных нитях одинаковой длины L. Левый шарик отклоняют на угол 90° и отпускают с начальной скоростью, равной нулю. В результате абсолютно не упругого удара шариков выделяется количество теплоты Q=1 Дж. Определите длину нитей L.
Решение довольно простое:
Закон сохранения энергии: mgL=mv12/2 где v1 — скорость шара с массой m в момент удара.
Закон сохранения импульса: mv=(m+M)v2 где v2 — скорость шаров после неупругого удара.
Разность кинетических энергий до удара и после удара равна количеству теплоты, которое выделилось. Q= mv12/2-(m+M)v22/2
Решая совместно эти три уравнения, получаем L.
L=Q(m+M)/mMg. Численный ответ будет L=1,5 м.
Кстати, эта задача (или подобная) встречалась в ОГЭ по физике в 9 классе. Так что она вполне по силам 11 классу.
Задачи № 30 и 31 заставят школьников поломать голову, особенно первая. А вот следующая задача хоть и выглядит на первый взгляд серьезно — трудностей не представляет.
Задача № 32
Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода) сосуда, из которого откачан воздух. Электрон разгоняется однородным электрическим полем напряженностью Е = 5·104 В/м. До какой скорости электрон разгонится в этом поле, пролетев путь S = 5·10—4 м? Релятивистские эффекты не учитывать.
Решение:
Вспоминаем уравнение Эйнштейна для фотоэффекта: в соответствии с ним начальная скорость электрона равна 0.
Работа силы электрического поля идет на увеличение кинетической энергии A=mv2/2, где m- масса нашего электрона.
Работа силы связана с напряженностью электрического поля и пройденным расстоянием. A=FS=eES, где e — это заряд электрона, который нам дан в таблице.
Получаем следующее уравнение: mv2/2= eES, откуда выражаем v2=2eES/m, извлекаем квадратный корень, подставляем числа и получаем v≈3·106 м/с.
Школьный ЕГЭ по физике — достаточно серьезное испытание, к которому надо готовиться заранее и систематически. Нельзя вдруг решить за несколько месяцев до экзамена, что нужна именно физика. Тогда полноценно подготовиться при помощи репетиторов и тем более самостоятельно уже не получится.
Подготовку к экзамену надо начинать заранее и лучше всего потратить на это два года
Если хотите как следует подготовиться к ЕГЭ по физике — забудьте о ЕГЭ. Не существует каких-то особенных вопросов и задач, характерных для экзамена. Физика — это наука. Необходимо вникать в суть физических законов и понимать смысл формул. Научиться решать разнообразные примеры не из пособий для подготовки к ЕГЭ, а из задачников, ценность и качество которых проверена временем.
mel.fm
Задачи №32 ЕГЭ по физике (ядерная физика)-1
Рассмотрим последнюю задачу ЕГЭ. Чаще всего под этим номером попадаются задачи на ядерную физику. Некоторые из них совсем простые, другие – наоборот, сложные. Впрочем, судить вам.
Задача 1. Электроны, вылетевшие в положительном направлении оси под действием света с катода фотоэлемента, попадают в электрическое и магнитное поля. Какой должна быть частота падающего света , чтобы в момент попадания самых быстрых электронов в область полей действующая на них сила была направлена против оси ? Работа выхода для вещества катода эВ, напряженность электрического поля В/м, индукция магнитного поля Тл.
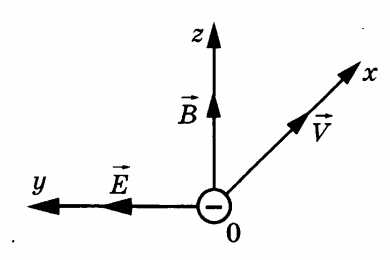
К задаче 1
Согласно рисунку, кулонова сила направлена вправо, то есть по оси в отрицательном направлении. По правилу левой руки определяем, что сила Лоренца направлена по оси в положительном направлении. Тогда для выполнения условия задачи сила Лоренца должна быть меньше кулоновой:
Распишем обе силы:
То есть
Теперь запишем уравнение Энштейна для фотоэффекта:
Подставим скорость:
Считаем:
Ответ: .
Задача 2. В открытый контейнер поместили 1,5 г изотопа полония-210 . Затем контейнер герметично закрыли. Изотоп полония радиоактивен и претерпевает альфа-распад с периодом полураспада примерно 140 дней, превращаясь в стабильный изотоп свинца. Через пять недель давление внутри контейнера составило Па. Определите объем контейнера. Температура внутри контейнера поддерживается постоянной и равна . Атмосферное давление равно Па.
Давление в контейнере будут создавать как воздух, так и образовывающийся гелий:
Давление воздуха – это атмосферное давление. Определим давление гелия из уравнения Менделеева-Клапейрона:
Количество молей гелия равно количеству молей полония (который распался):
Изначально было, предположим, атомов полония. Потом их количество уменьшалось согласно закону радиационного распада:
Где – количество оставшихся нераспавшимися атомов.
Тогда распалось число атомов, равное:
Количество молей образовавшегося гелия тогда равно
Отношение .
Теперь «вытащим» из уравнения Менделеева-Клапейрона объем и подставим все найденные величины:
Считаем:
Ответ: см.
Задача 3. Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 массой 1,4 кг, если ее мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
КПД электростанции можно посчитать как отношение энергии, вырабатываемой ею, к выделившейся в результате распада ядер энергии:
Здесь , .
Определим, сколько ядер урана в таком количестве:
Тогда КПД:
Ответ: 20%.
Задача 4. Свободный пион ( -мезон) с энергией покоя 135 МэВ движется со скоростью , которая значительно меньше скорости света. В результате его распада образовались два гамма-кванта, причем один из них распространяется в направлении движения пиона, а второй – в противоположном направлении. Энергия первого гамма-кванта на 10% больше, чем второго. Чему равна скорость пиона до распада?
По закону сохранения импульса
Импульс пиона равен , энергия равна
По условию , поэтому можно упростить последнее выражение:
Снова упрощаем с условием :
Энергия пиона поделится между квантами:
То есть
Пришло время закона сохранения импульса:
Приравняем обе энергии:
Сокращаем:
Ответ: м/c.
easy-physic.ru
