Олимпиадные задания по математике 8
Ответы и решения олимпиадных задач по математике
8 – 9 класс
8 класс
1. В классе 37 учеников. Докажите, что среди них найдутся 4 ученика, отмечающих день рождения в один месяц.
Ответ: Если в каждый месяц родилось не более 3 учеников, то всего учеников будет не больше 36. А по условию их 37, значит, такого быть не может. Поэтому найдется 4 ученика, отмечающих день рождения в один месяц.
2. Длины сторон треугольника равны 6,82 м и 0,31 м, а длина третьей стороны выражена целым числом метров. Найти длину третьей стороны.
Решение: a, b, c – стороны треугольника: a = 6,82; b = 0,31; известно, что
a – b c a + b, то есть 6,51 c так как c €
3. Разложите на множители: 4(а2 + b2) + 21b2 – 20ab – 36.
Ответ: (2a – 5b – 6)( 2a – 5b + 6).
4. Четырех кошек взвесили попарно во всех возможных комбинациях. Получились массы 7 кг, 8 кг, 9 кг, 10 кг, 11 кг, 12 кг. Какова общая масса всех кошек?
Решение:

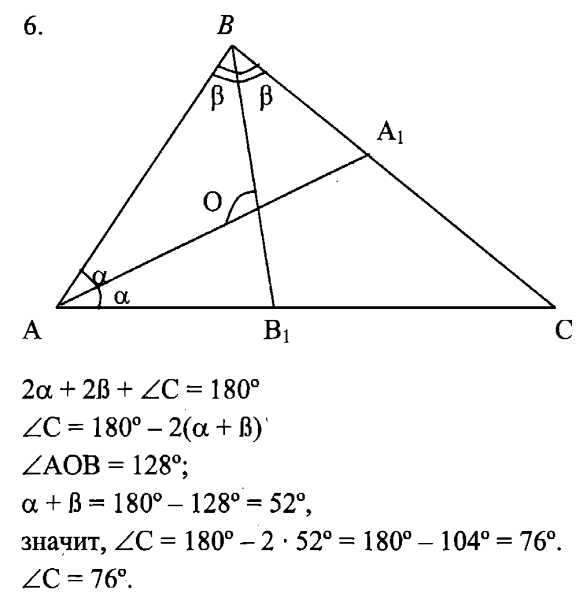
5. В ∆АВС биссектриссы углов А и В пересекаются под углом 1280. Найдите угол С.
Решение:
9 класс
1. Решить уравнение: x2 + xy + y2 – 2x + 2y + 4 = 0
Решение: Умножим на 2 обе части уравнения и сгруппируем. В итоге получим: (x 2 + 2xy + y2) + (x2 – 4x + 4) + (y2 + 4y + 4) = 0,
(x + y)2 + (x – 2)2 + (y + 2)2 = 0, x = 2; y = -2.
2. Автомобиль проехал 600 км. Первую половину пути он двигался со скоростью 100 км/ч, а вторую – 60 км/ч. Найдите среднюю скорость движения автомобиля.
Решение:
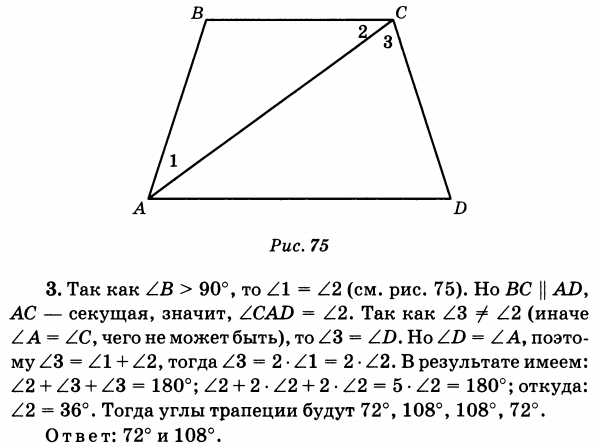
3. Равнобокая трапеция АВСD разбивается диагональю АС на 2 равнобедренных треугольника. Определите углы трапеции.
Решение:
4. Решите систему уравнений:
(3x + y)2 + 2(x – y)2 = 96,
3x + y = 2(x – y).
Решение:
5. Четверо ребят – Алексей, Борис, Владимир и Григорий участвовали в лыжных гонках. На следующий день, на вопрос кто какое место занял, они ответили так:
Алексей: Я не был ни первым и ни последним;
Борис: Я не был последним;
Владимир: Я был первым;
Григорий: Я был последним.
Известно, что три из этих ответов были правдивыми, а один – ложью. Кто сказал правду? Кто был первым?
Решение:
6. Найдите четыре последовательных натуральных числа, произведение которых равно 1680.
Решение:

multiurok.ru
Задания для проведения школьного этапа Всероссийской олимпиады школьников по математике в 5 – 11 классах
Муниципальное бютжетное общеобразовательное учреждение
«Полевской лицей»
Курского района Курской области
Задания для проведения школьного этапа Всероссийской олимпиады школьников по математике в 5 – 11 классах
Подготовила
учитель математики
Праведникова Галина Викторовна
д. Полевая
2014
Школьный этап Всероссийской олимпиады школьников
по математике
5 класс
Задания.
На прямой линии посажено 10 кустов так, что расстояние между любыми соседними кустами одно и то же. Найдите это расстояние , если расстояние между крайними кустами 90 дм.
В записи 1 ☼ 2 ☼ 3 ☼ 4 ☼ 5 = 100 замените «☼» знаками действия и расставьте скобки так, чтобы получилось верное равенство.
Мальчик по чётным числам всегда говорит правду, а по нечётным всегда врёт. Как-то его три октябрьских дня подряд спрашивали: «Как тебя зовут?». На первый день он ответил: «Андрей», на второй: «Борис», на третий: «Виктор». Как зовут мальчика? Объясните, как вы рассуждали.
В 9.00 Юра вышел из дома и пошёл по прямой дороге со скоростью
6 км/ч. Через некоторое время он развернулся и с той же скоростью пошёл домой. В 12.00 Юре оставалось до дома два километра. На каком расстоянии от дома он развернулся? Объясните, как был найден ответ.
Кот Матроскин прикинул, что он может выложить пол квадратной комнаты квадратной плиткой, и ему не понадобится ни одну из них разрезать. Сначала он положил плитки по краям комнаты, и на это у него ушло 84 плитки. Сколько всего ему надо иметь плиток, чтобы покрыть весь пол?
Ответы , указания, решения.
(может быть предложено другое решение)
Ответ.10 дм.
Решение.Так как посажено 10 кустов, то промежутков между ними будет 9. Поэтому расстояние между соседними кустами будет 90 : 9 = 10дм.
Ответ.1 · ( 2 + 3 ) · 4 · 5 = 100.
Ответ.Борис.
Решение. Так как мальчик дал три разных ответа, то он два раза соврал. Поэтому два дня из трёх, когда мальчику задавали вопросы, пришлись на нечётные числа. Поскольку чётные и нечётные числа месяца чередуются, это должны были быть первый и третий дни. Стало быть, второй день пришёлся на чётное число. В этот день мальчик и назвал своё настоящее имя.
Ответ.На расстоянии 10 км.
Решение. За 3 часа, с 9.00 до 12.00, Юра прошёл 18 км. Если он пройдет еще два километра, то он попадет домой. То есть 18 + 2 = 20 км. – это путь до места разворота и обратно. Значит, он развернулся на расстоянии
20:2 = 10 км от дома.
Ответ.484.
Решение. На каёмке, не считая угловых, лежит 84 – 4 = 80 плиток. Значит, на каждой стороне лежит 20 плиток, не считая угловых, а вместе с угловыми – 22 плитки. Поэтому общее число плиток равно 22 · 22 = 484.
www.prodlenka.org
Школьный этап всероссийской олимпиады школьников по математике год. Решения.
Требования. Введение
Требования к организации и проведению школьного этапа всероссийской олимпиады школьников по общеобразовательным предметам в 2016-2017 учебном году Введение Требования к организации и проведению школьного
ПодробнееМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
СОГЛАСОВАНО: Проректор ГУДПО ДРИДПО В.Г. Зарицкая МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ по проведению муниципального этапа Республиканской ученической олимпиады и І этапа Республиканской олимпиады школьников для обучающихся
ПодробнееРешения заданий День 2
III Кавказская математическая олимпиада Решения заданий День 2 Д. К. Мамий П. А. Кожевников В. А. Брагин Д. А. Белов А. В. Антропов Л. А. Емельянов А. А. Полянский М. Сагафиян С. И. Токарев 15 20 марта
ПодробнееОММО решения для жюри общие критерии
ОММО 01.0.015 решения для жюри общие критерии Общие критерии оценивания По результатам проверки каждого задания выставляется одна из следующих оценок (перечислены в порядке убывания): «+» задача решена
ПодробнееРешение задач 3 тура 2010/2011 года. (3 балла)
Приносим свои извинения за то, что в решении последней задачи предыдущего тура была допущена ошибка, решение исправлено, баллы полученные участниками подкорректированы. В соответствующих файлах были внесены
ПодробнееЗАДАНИЯ ДЛЯ 7 КЛАССА
ЗАДАНИЯ ДЛЯ 7 КЛАССА Задание 1 (Задача предложена А.В. Ястребовым). Сформулируйте математическое утверждение, которое ставит под сомнение представленные на рисунке 1 результаты эксперимента. Нужно ли считать
ПодробнееОтветы и решения. 7 класс
Задания для муниципального тура Всероссийской олимпиады школьников по математике в 06/07 учебном году Ответы и решения 7 класс. Ответ. Можно. Решение. Первым взвешиванием можно получить 3 кг песка, если
ПодробнееТРЕНИРОВОЧНЫЙ КИМ 02102
ТРЕНИРОВОЧНЫЙ КИМ 0202 ОГЭ-9, 206 г. Математика, 9 класс Тренировочный вариант 2 от 05.09.205 / 8 Основной государственный экзамен по МАТЕМАТИКЕ Инструкция по выполнению работы Общее время экзамена 25
Подробнееa = p 1p 2, b = p 1p 3
9.1. Известно, что ни одно из чисел a, b, c не является целым. Может ли случиться так, что каждое из чисел ab, bc, ca, abc целое? Ответ. Может. Решение. Например, выберем три различных простых числа p
Подробнееtg MN M 1 = MM 1. M 1 N = 6 5
Математика. класс. Вариант (без логарифмов) Критерии оценивания заданий с развёрнутым ответом C Решите систему уравнений y + sinx =, (4 sinx )(y + ) =. y = Из второго уравнения получаем, или sinx =. 6
ПодробнееЭкзаменационная работа
Экзаменационная работа для проведения государственной (итоговой) аттестации выпускников IX классов общеобразовательных учреждений 008 года (в новой форме) по ГЕОМЕТРИИ Демонстрационный вариант 008 года
ПодробнееРешения заданий варианта ЕГЭ 2007 года. Часть 1
Решения заданий варианта ЕГЭ 007 года Часть Сайт элементарной математики Дмитрия Гущина wwwmathnetspbru A Упростите выражение b b, 0,,6 b 0,, b, b 0,,6 b, 0,, 0,, Решение: b b = b + = b Правильный ответ:
ПодробнееОтветы к заданиям части 1. задания Ответ В В2 12 В3 12 В4 820 В5 3 В6 140 В7 2 В8-0,25 В9 64 В10 0,5 В11 0,3 В12 27,5 В13 10 В14 7
МАТЕМАТИКА, класс.. (0-3 — / 8) Ответы к заданиям части задания Ответ В 9000 В В3 В4 80 В5 3 В6 40 В7 В8-0,5 В9 64 В0 0,5 В 0,3 В 7,5 В3 0 В4 7 Ответы к заданиям части задания Ответ С а) x = πk, k ; б)
ПодробнееРайонная олимпиада по математике г. Хабаровск, 1997 год 9 КЛАСС. n 3. 3x x (3x 2 + 1) + 3x , + 1, b = a = 3x 2 1
Районная олимпиада по математике г. Хабаровск, 997 год 9 КЛАСС Задача. При каких целых n дробь 5n n целое число? Решение. Заметим, что 5n n = 5 + n. Поэтому это число целое только в случаях n =, 6, 4,,,,,,,
ПодробнееТРЕНИРОВОЧНЫЙ КИМ 02101
ОГЭ-9, 2016 г. Математика, 9 класс Тренировочный вариант 1 от 30.08.2015 1 / 9 Основной государственный экзамен по МАТЕМАТИКЕ Инструкция по выполнению работы Общее время экзамена 235 минут. Характеристика
docplayer.ru
