Самостоятельная работа производная суммы и разности – План-конспект занятия по алгебре (11 класс) на тему: ПЛАН – КОНСПЕКТ УЧЕБНОГО ЗАНЯТИЯ по учебной дисциплине ОУД(п).10 Математика: алгебра и начала математического анализа; геометрия Тема урока: Производные суммы, разности, произведения, частного | скачать бесплатно

Самостоятельная работа по теме «Производная»

1 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

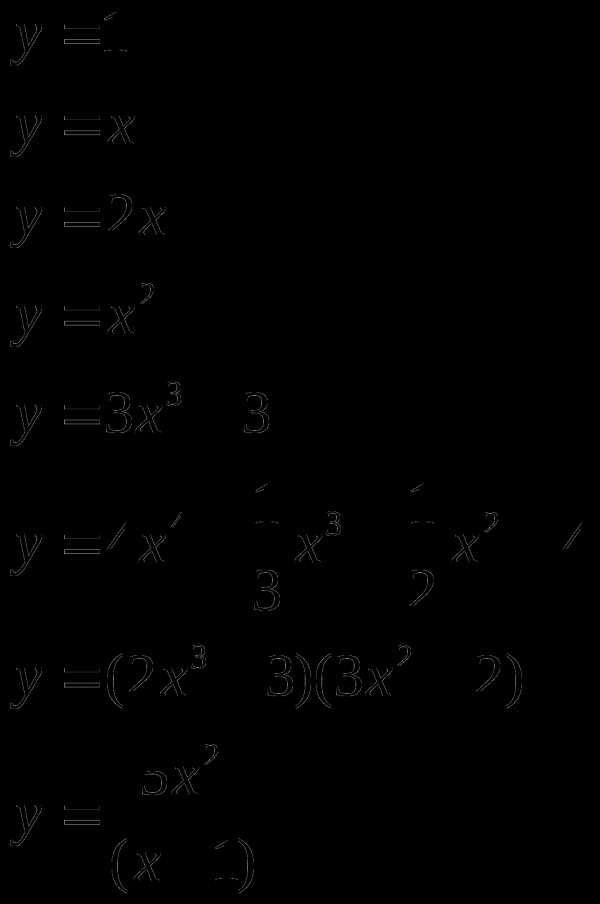
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по закону  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 9 с.

2. вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

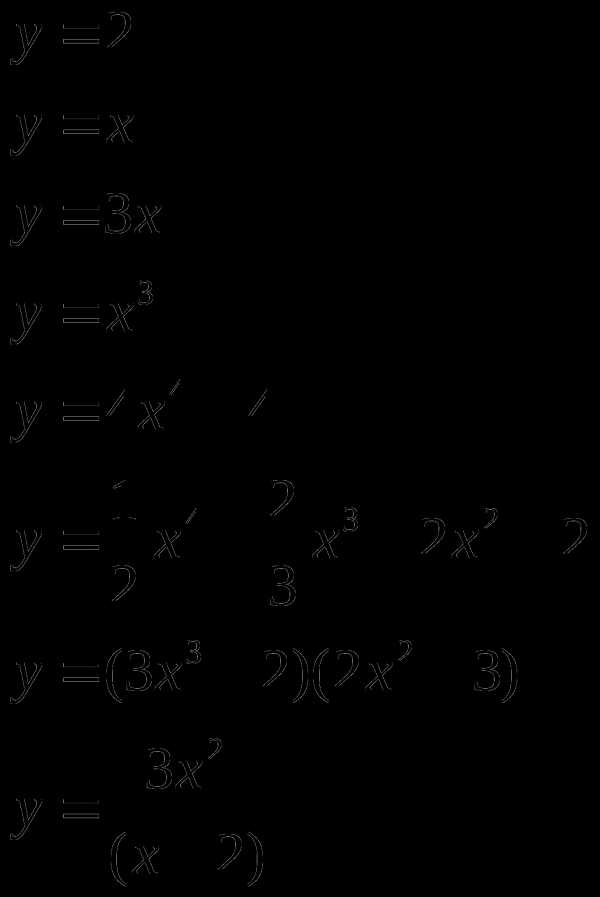
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по закону

  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни 

t = 6 с.

3 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

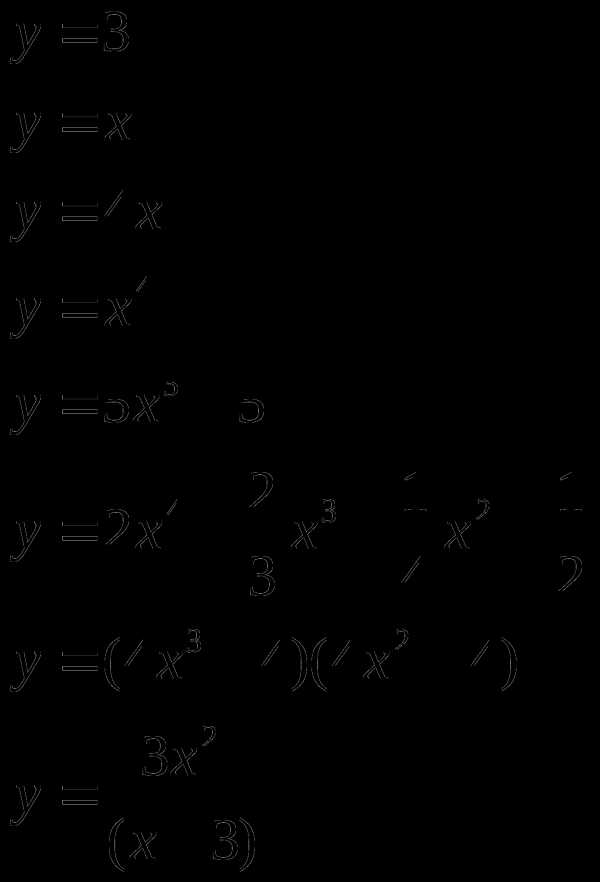
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по

закону (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни  с.

4 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

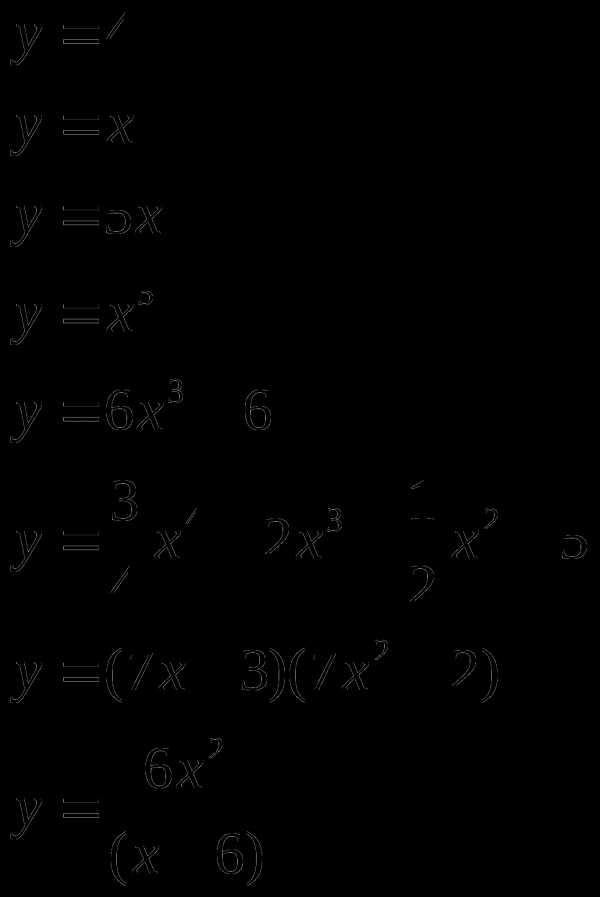
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, 

   t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 3 м/с?

 

5 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

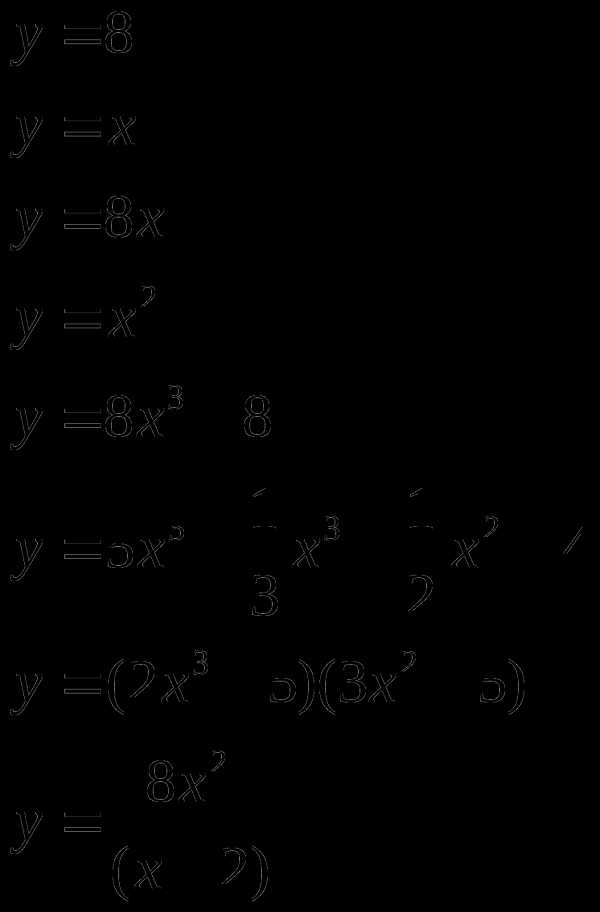
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  

(где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 2 м/с?

6 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

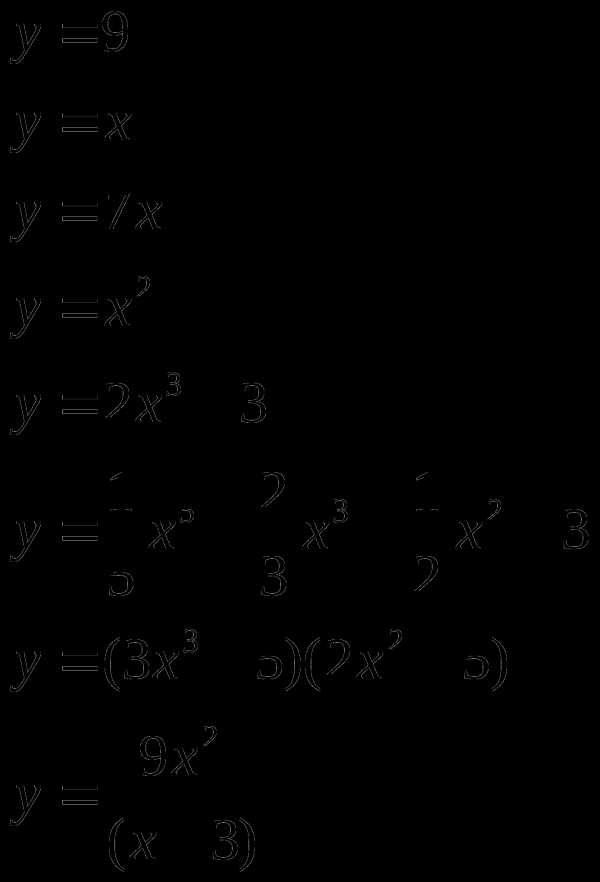
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни  с.

7 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

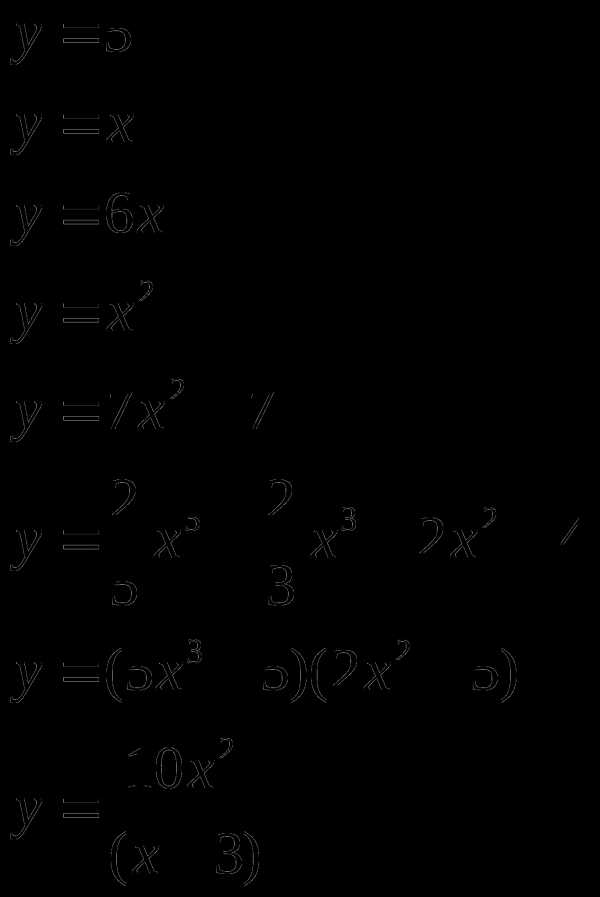
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни  с.

8 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

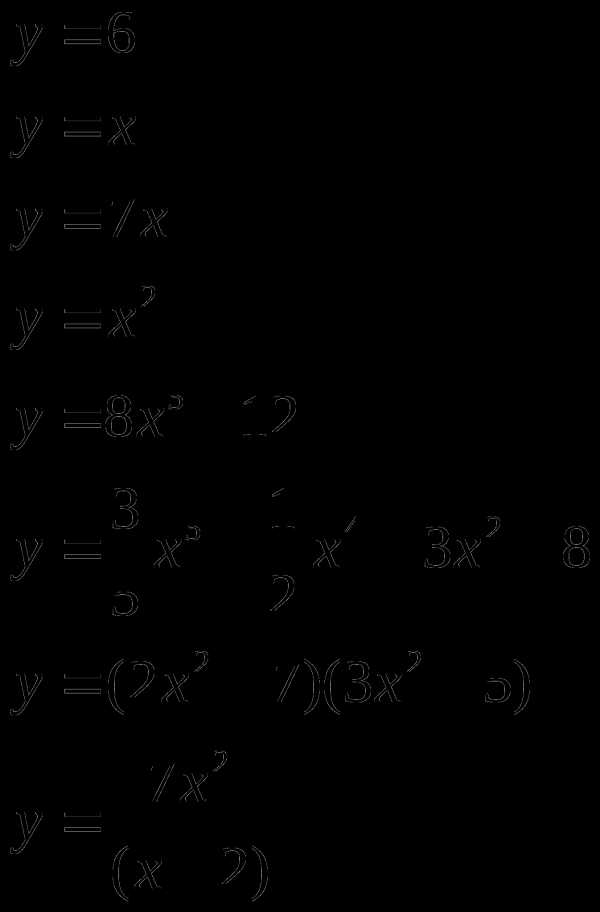
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни  с.

9 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

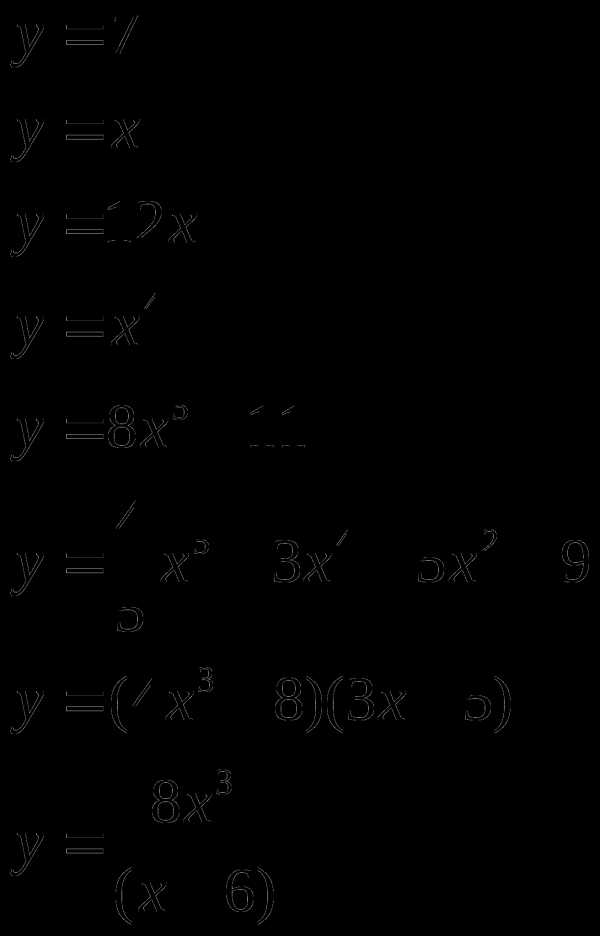
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни  с.

10 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

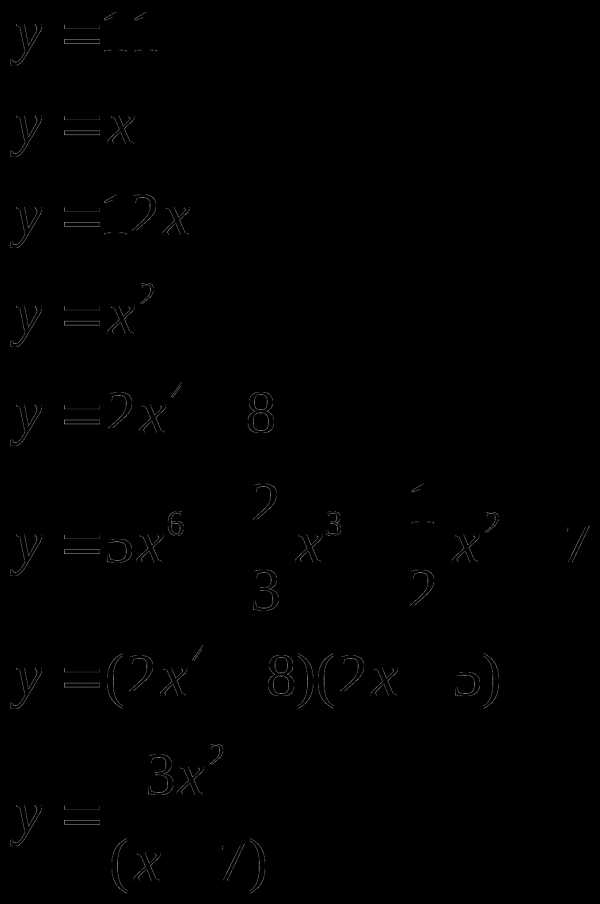
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где  — рас­сто­я­ние от точки от­сче­та в мет­рах,  — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни 

11 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

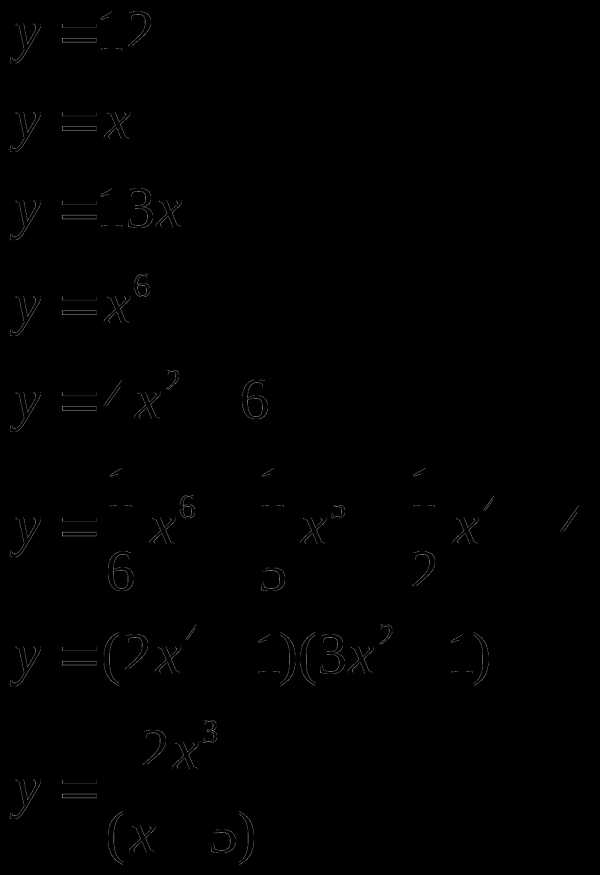
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни  с.

12 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

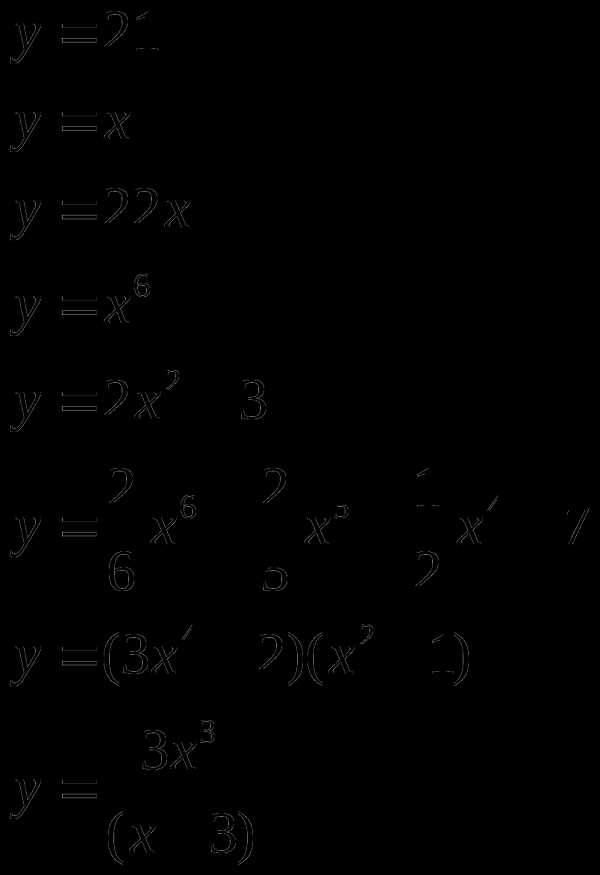
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну где 

   х — рас­сто­я­ние от точки отсчёта (в мет­рах), t — время дви­же­ния (в се­кун­дах). Най­ди­те её ско­рость (в мет­рах в се­кун­ду) в мо­мент вре­ме­ни t = 2 с.

13 вариант

1. Найти производную (с помощью формул и правил сложения, умножения, частного)

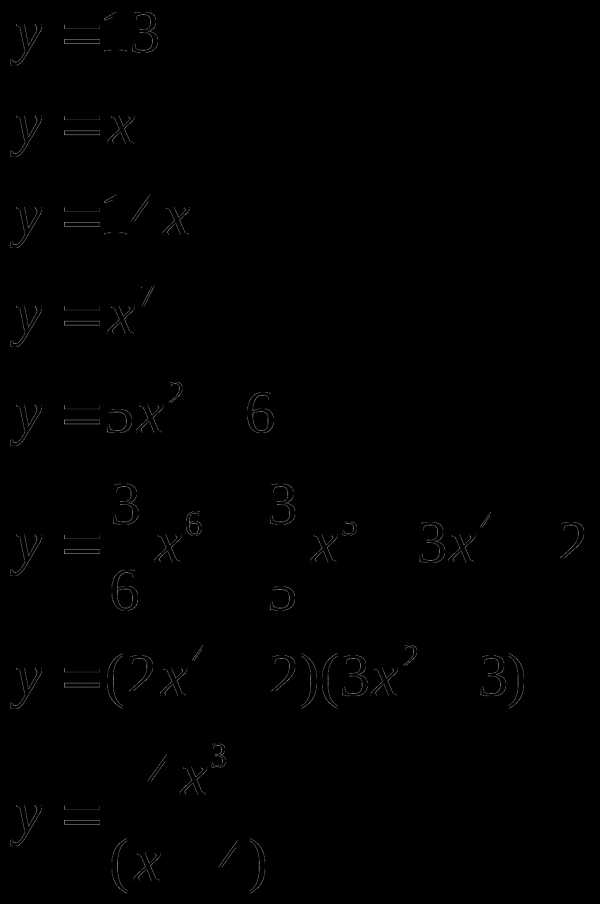
2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 96 м/с?

infourok.ru

Самостоятельная работа «Нахождение производных функций»

Инфоурок › Математика › Другие методич. материалы › Самостоятельная работа «Нахождение производных функций»

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-125098

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

infourok.ru

Самостоятельные работы по алгебре на тему «Производная функции»(10 класс)

Самостоятельная работа №1

«Производная функции. Правила дифференцирования.»

Цели: 1)закрепить правила нахождения производных в ходе решения упражнений; тренировать навык устного счета;

2) развивать мыслительную деятельность обучающихся;

3) воспитывать аккуратность при оформлении записей.

Найти производную функции:

1.

2.

y=cosx-2cosx

4.

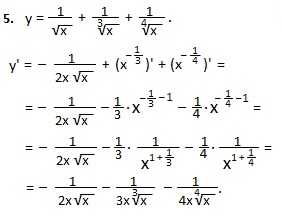
6.

7.

8.

9.

10.

Самостоятельная работа №2

«Производная сложной и обратной функции»

Цель: 1) Научить учащихся применять знания, полученные в основной школе в нестандартных условиях, углубить знания по теме.

2) Развивать гибкость мышления, логическое мышление, воображение, математическую речь. Повысить качество успеваемости.

Найти производную сложной и обратной функции:

1.

2.

3.

4.

5.

6.

y = arсctg x.

7.

y = arcos x

8.

Обратной функцией будет функция

9.

10. Пользуясь правилом дифференцирования обратной функции, найти производную у’х для функции

Решение: обратная функция х=у³+1 имеет производную х’_у =3у².

Следовательно,

Самостоятельная работа №3

«Производная высших порядков»

Цели : 1) ввести понятие производной высших порядков;

2)рассмотреть задачи по данной теме;

3) развить логическое мышление и интерес к теме.

1 Найти производную второго порядка функции

2

3

4

5 Вычислить третью производную функции

6

7

8 Найти производную 13-го порядка функции у=sinx.

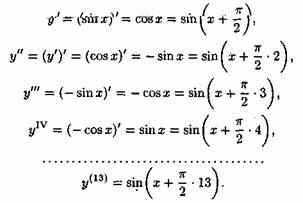
9 Найти производную n-го порядка

10 Найти все производные функции n-го порядка

………………………………………………………

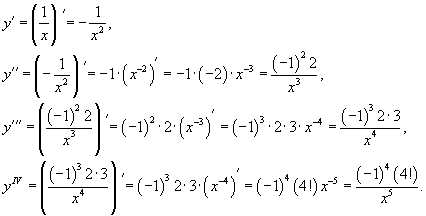
www.metod-kopilka.ru

«Вычисление производных, суммы, разности, произведения, частного»

Методическая разработка урока математики по теме: «Вычисление производных, суммы, разности, произведения, частного»

Пояснительная записка

В настоящее время актуален вопрос о целях образования и их практическом применении, выраженной в мотивации учебной деятельности обучающихся. Очень трудно бывает объяснить студенту, для чего ему нужна математика, если он собирается быть электриком или автомехаником. Поэтому главной своей задачей считаю, необходимость формирования у обучающихся умений самопознания, самосозидания и самореализации. В этом мне помогают элементы новых педагогических технологий, которые я включаю в каждый из своих уроков.

Урок закрепления и систематизации знаний по теме «Вычисление производных суммы, разности, произведения, частного» разработан для студентов СПО, 1 курса (на базе 9 классов) по специальности «Техническая эксплуатация и обслуживание электротехнического и электромеханического оборудования (по отраслям)», квалификация «техник». Изучающих программу общеобразовательного цикла, по учебникам А.Н. Колмогоров «Алгебра и начала математического анализа 10-11 класс».

Готовясь к проведению урока, преподаватель дает творческое задание, для исследовательской работы студентам по теме. Тема исследовательской работы на уроке освещается лишь тезисным выступлением авторов в защиту своей работы. Данный прием относится к инновационной технологии проектного обучения.

В данной разработке представлены задания для проверки теоретического материала, путем закрепления решения практических и тестовых заданий. Использование разноуровневых заданий для самостоятельной работы позволяет проверить знания и умения сформированных навыков у каждого студента индивидуально. Данный прием относится к инновационной технологии уровневой дифференциации.

Особое значение урока заключается в использовании информационно-коммуникационных технологий. Презентация к уроку включает задания для устного счета и закрепления, способствует решению задач по реализации объема учебного материала, где прослеживается межпредметная связь.

Работа с интерактивной доской позволяет сделать урок более насыщенным.

Данная разработка урока направленна на формирование профессиональных компетенций.

Тема: Вычисление производных суммы, разности, произведения, частного.

Цели урока:

• Создать условия для углубления и обобщения знаний студентов по нахождению производной суммы, произведения, частного и производной степенной функции.

• Активизировать умения по нахождению производной функций, используя правила дифференцирования, умения применять их на практике.

• Содействовать воспитанию у студентов самостоятельности, самопознания, самосозидания и самореализации.

Средства обучения: Презентация, приложение для интерактивной доски, учебник, разноуровневые карточки, интерактивная доска, жетоны, координатная прямая (для рефлексии), наклеивающиеся точки (на каждого ученика)

Тип урока: урок систематизации и обобщения знаний

Форма урока: эвристическая и практическая работа с элементами исследования.

Ход урока:

I. Организационный момент

а) Скажи мне, и я забуду.

Покажи мне, и я запомню.

Вовлеки меня, и я научусь. ( Китайская мудрость.)

Моя цель на этом уроке – обобщить и закрепить полученные знания при изучении темы, а ваша задача созвучна китайской мудрости.

б) Постановка целей и задач урока

в) Активность каждого на уроке будет оцениваться жетонами, в конце урока все жетоны суммируются и выставляется оценка, число жетонов соответствуют оценке.

II. Актуализация учебного материала

1. На прошлых уроках мы познакомились с понятием производная и с основными правилами вычисления производных, давайте вспомним: (Презентация)

а) Что такое производная? (ответ, слайд 3)

б) Как она обозначается (штрих)

в) Какие смыслы производной существуют? (физический, геометрический)

г) Что значит продифференцировать?(Найти производную функции)

д) Какая функция называется дифференцируемой в точке х_о?

(Функцию, имеющую производную в точке х_о)

2. Соотнесите формулы и прочитайте их (приложение 1)

III. Устный счет.

Применение теоретического материала к решению задач. Найдите производную функции (Вопросы высвечиваются на интерактивной доске, студенты отвечают по «цепочке») (слайд, 4)

IV. Закрепление

1. «Найдите ошибку» № 209 (б), № 210 (а), № 215 а,в (приложение 2 )

Студенты выходят по 1 человеку к интерактивной доске, читают решение примера и исправляют ошибки

№ 209 (г)

Решение

№ 210 (а)

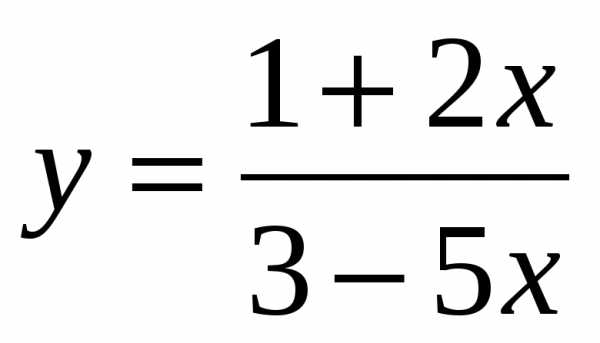
Решение

№ 215 а

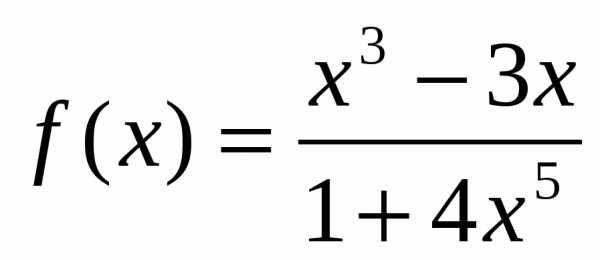
2. Тест с использованием интерактивной доски.

В тесте зашифрована фамилия ученого-математика. Основное понятие дифференциального исчисления — понятие производной, возникло в 17веке в связи с необходимостью решать задачи по физике, математике. Кто явился создателем дифференциального исчисления? Фамилия одного из первых кто ввел понятие производной, вы сможете узнать, решив задания теста. Ответ (Лейбниц ) (слайд 5-19)

3. Сообщение студента

Кравченко Иван готовил сообщение «История появления производных», краткое содержание Иван изложит. (Приложение 3)

V. Повторение. Решение задач с профессиональной направленностью

(Слайд 20-21)

1. Посмотрите на эти предметы, это все нас окружает в жизни. Найдите среди предметов среднее число потребляемой энергии каждого, и ответе на вопрос: «Какой предмет потребляет большего всего энергии?». Подойдите к доске и выберите ответ.

2. Мощность некоторых предметов обозначено звездочкой, что означает:

* — Данное электрооборудование имеет пусковые токи.
** — Данное электрооборудование имеет большие пусковые токи.
Расшифруйте пожалуйста, что означает пусковые токи?

VI. Разноуровневая самостоятельная работа

Ребята! У вас у каждого на столе лежат красная карточка, это оценка «5», желтая – оценка «4», зеленая – оценка «3». Выберите для себя одну карточку, рассчитав свои силы, все задания выбранной карточки должны быть решены верно, для получения соответствующей оценки.

Оценка «5»

Вычислите производные функций:

1.

2.

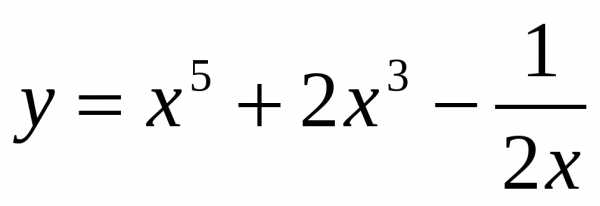
3.

4.

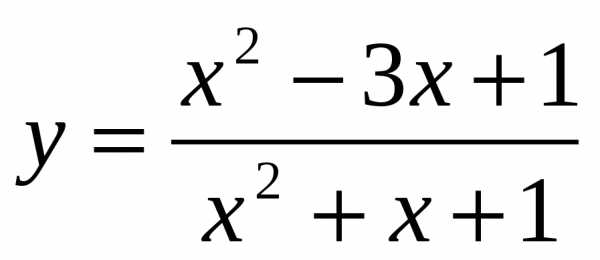
5.

Оценка «4»

Вычислите производные функций:

1.

2.

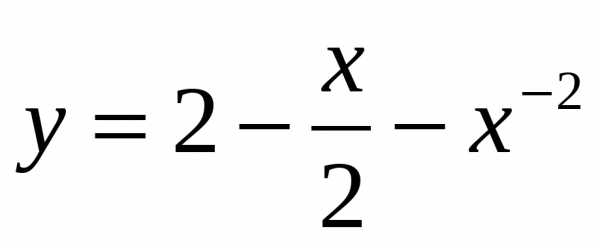
3.

4.

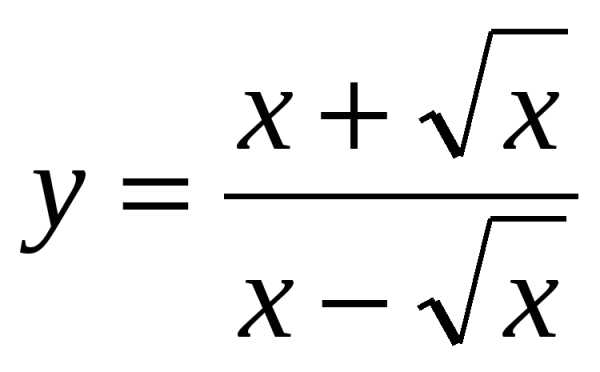
5.

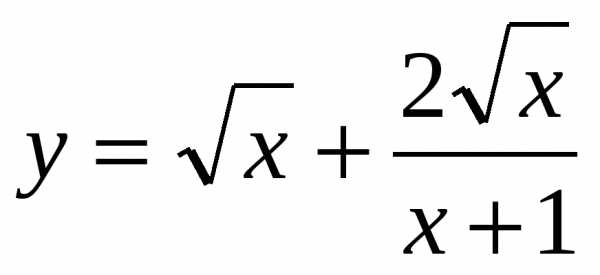
Оценка «3»

Вычислите производные функций:

1.

2.

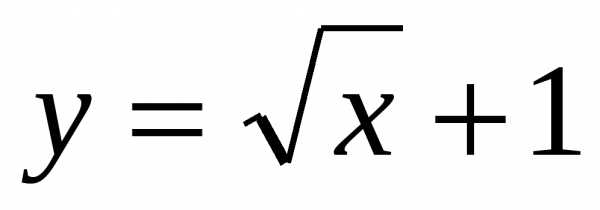
3.

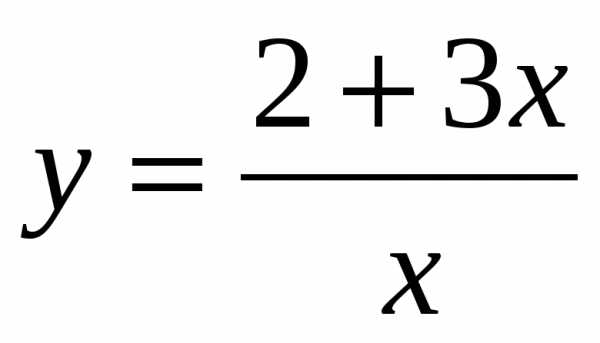
4.

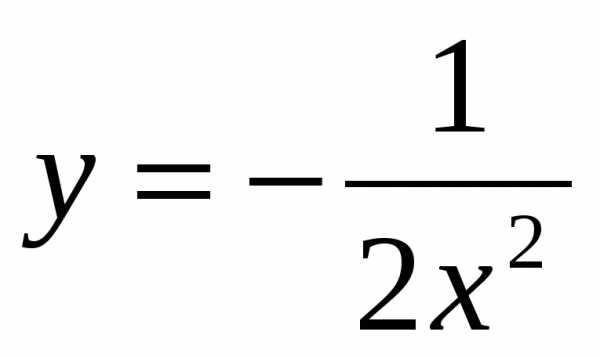
5.

VII. Итог занятия.

1. Чем мы занимались сегодня на уроке?

2. Что понравилось, какие виды деятельности?

3. Анализ работы студентов, выставление оценок

VIII. Рефлексия

Ребята! У выхода висит координатная прямая, наклейте точки соответствующие вашему эмоциональному состоянию на уроке.

Точка: (-1) «Мне было скучно, не интересно, урок не понравился»

Точка: (0) «Мне безразлично»

Точка (1) «Мне было интересно, урок понравился»

IX. Домашнее задание

Задания на дом выдается аналогичное тем, что мы сегодня выполняли.

П. 15 прочитать

№ 214, 216 решить

multiurok.ru

Открый урок по математике на тему «Производная суммы, разности, произведения и частного функций»

Областное государственное автономное

профессиональное образовательное учреждение

«Шебекинский агротехнический ремесленный техникум»

ОТКРЫТЫЙ УРОК

тема: «Производная суммы, разности,
произведения и частного функций»

Разработал: Черникова Елена Сергеевна,

преподаватель математики

Шебекино,

2017 год

Группа: 2 С1 (мастер сухого строительства).

Дисциплина: Математика: алгебра и начала математического анализа, геометрия.

Тема занятия: «Производная суммы, разности, произведения и частного функций».

Вид занятия (тип урока): комбинированный (фронтальный опрос, индивидуальная работа, лекция с элементами объяснения, практическая работа).

Задачи урока:

Образовательная: продолжить формирование знаний по теме «Производная», изучить основные правила дифференцирования; отработать навыки нахождения производных суммы, разности, произведения и частного функций.

Развивающая: развивать общие компетенции и универсальные учебные действия; умение применять основные формулы и правила дифференцирования при решении; развитие математического мышления; совершенствование навыков.

Воспитательная: формировать коммуникативную компетентность, вовлечь в активную деятельность; формировать умения, осуществлять самоконтроль в процессе самостоятельной работы обучающихся; продолжить воспитание усердия и упорства, желания добиваться поставленной цели.

Цели занятия:

Учебные:

• • закрепить знания по теме «Производная»,

  • рассмотреть и изучить основные правила дифференцирования;

  • отработать навыки нахождения производных суммы, разности, произведения и частного функций

Воспитательные: 

• • воспитывать познавательный интерес к предмету;

  • способствовать формированию ответственного отношения к учебному труду.

Развивающие:

• • развивать память и логическое мышление;

  • развивать речевую активность путем обогащения математической терминологии;

  • развивать коммуникативные навыки и навыки самоконтроля.

Основные методы обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, информационно-коммуникационная технология.

Ожидаемый результат: освоение общих компетенций посредством демонстрации знаний и умений.

Оборудование: компьютер, проектор, презентация к уроку, раздаточный материал.

Ход урока

Скажи мне, и я забуду.

Покажи мне, и я запомню.

Вовлеки меня, и я научусь.

Китайская мудрость

1. Организационный момент

1. Взаимное приветствие;

2. Проверка внешнего вида и состояния рабочих мест,

3. Проверка отсутствующих.

2. Постановка целей и задач урока

1. Повторение предыдущего материала;

2. Изучение основных правил дифференцирования в нахождении производной суммы, разности, произведения и частного функций;

3. Упражнения для закрепления пройденной темы.

3. Основная часть.

Преподаватель: Здравствуйте! Садитесь. Мы очень рады видеть на нашем уроке гостей. Сегодня мы продолжаем работу по теме «Производная». Цель нашего урока — еще раз повторить необходимый материал для успешного нахождения производных функций и дать возможность каждому из вас самому оценить степень усвоения материала по изученной теме.

Эпиграфом к нашему уроку послужит китайская мудрость: Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеки меня, и я научусь.

Проверка домашнего задания

3 обучающихся получают задание на карточках:

Карточка №1. Найти производную функции в точке х₀

Карточка №2. Найти производную функции в точке х₀

Карточка №3. Найти производную функции в точке х₀

Пока 3 учащихся выполняют задания по карточкам, остальные отвечают на вопросы.

1. Что называется приращением аргумента.

2. Что называется приращением функции.

3. В чем состоит геометрический смысл производной функции.

4. В чем состоит механический смысл производной функции.

5. Дайте определение производной функции f(x) в точке х₀.

4. Подготовка обучающихся к активному и сознательному усвоению нового материала

Преподаватель. Повторили как находятся производные элементарных функций. Как решить задачи с более сложной функцией?

Найдите производную следующих функций:

(Ответят, скорее всего, неправильно, потому что не знают правил дифференцирования.)

– Сегодня изучим эти правила.

5. Объяснение новой темы

– Запишите новую тему «Производная суммы(разности), произведения и частного функций». (Слайд 1)

Рассмотрим основные правила дифференцирования без доказательств.

Обозначим для краткости функции

Правило 1. Если функции U и V дифференцируемы в т. x, то их сумма (разность) дифференцируема в этой точке  (Слайд 2)

Пример:

Правило 2.  Если функции U и V дифференцируемы в т. x, то их произведение дифференцируемо в этой точке (Слайд 3)

Пример:

Следствие. Если функция дифференцируема в т. Х, а С –постоянная, то функция СU дифференцируема в этой точке и

(CU)’=CU‘. (Слайд 4).

Пример:

Правило 3. Если функции U и V дифференцируемы в т.х и функция V не равна 0 в этой точке, то частное  дифференцируемо в х и  (Слайд 5)

Пример:

6. Закрепление материала

Вернемся к тем примерам которые рассматривали ранее. Теперь зная правила дифференцирования, как бы вы их решили? (Слайд 6)

7. Самостоятельная работа (дифференцированная) (карточки).

Вариант 1 – на «3»

Вариант 2 – на «4»

Вариант 3 – на «5»

Вариант 1

1)

2)

3)

4)

Вариант 2

1)

2)

3)

4)

Вариант 3

1)

2)

3)

4)

(№4 — при наличии времени)

Самостоятельно в тетрадях выполняем упражнения

Упражнение № 208(а, б), 209(а, б), 210(а, б).

Домашнее задание

1) Повторить основные правила дифференцирования.

2) Выучить 3 правила дифференцирования.

3) Выполнить упражнения №208(в, г), 209(в, г), 210(в, г) [2].

8. Подведение итогов

Преподаватель подводит итоги работы обучающихся, дает качественную оценку работы группы, отдельных обучающихся.

— Как Вы считаете, достигнута ли цель сегодняшнего урока?

Сообщение оценок. Анализ деятельности обучающихся на занятии.

ЛИСТ ОТВЕТОВ

Ф.И.______________________________________________

Самостоятельная работа (дифференцированная)

Вариант 1 – на «3» Вариант 2 – на «4» Вариант 3 – на «5»

Вариант 1 Вариант 2 Вариант 3

1) 1) 1)

2) 2) 2)

3) 3) 3)

4) 4) 4) решение_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ОТВЕТЫ:

1 вариант

1)

2)

3)

4)

2 вариант

1)

2)

3)

4)

3 вариант

1)

2)

3)

4)

Карточка №1.

Найти производную функции в точке х₀

Карточка №2.

Найти производную функции в точке х₀

Карточка №3.

Найти производную функции в точке х₀

infourok.ru

Самостоятельная работа по теме «Производная функции»

Просмотр содержимого документа
«Самостоятельная работа по теме «Производная функции»»

Самостоятельная работа

по теме «Производная»

Вариант № 1

1) Вычислить производную функции:

a)

б)

в)

г)

д)

2) Найти (1), если:

Самостоятельная работа

по теме «Производная»

Вариант № 2

1) Вычислить производную функции:

a)

б) 12

в)

г)

д)

2) Найти (1), если:

Самостоятельная работа

по теме «Производная»

Вариант № 1

1) Вычислить производную функции:

a)

б)

в)

г)

д)

2) Найти (1), если:

Самостоятельная работа

по теме «Производная»

Вариант № 2

1) Вычислить производную функции:

a)

б) 12

в)

г)

д)

2) Найти (1), если:

Самостоятельная работа

по теме «Производная»

Вариант № 1

1) Вычислить производную функции:

a)

б)

в)

г)

д)

2) Найти (1), если:

Самостоятельная работа

по теме «Производная»

Вариант № 2

1) Вычислить производную функции:

a)

б) 12

в)

г)

д)

2) Найти (1), если:

multiurok.ru

Самостоятельная работа по теме «Производная функции».

Самостоятельная работа

Тема: «Производная»

Вариант 1

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 2

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 3

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 4

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 5

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 6

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 7

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

Самостоятельная работа

Тема: «Производная»

Вариант 8

1. Найдите производную функции

2. Найдите значение производной функции в точке

3. Решите уравнение , если

4. Найдите производные функций:

a) в)

б) г)

infourok.ru