Самостоятельная работа производная 11 класс – Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) на тему: Самостоятельные работы по теме «Производная» | скачать бесплатно

Самостоятельная работа по алгебре. Тема «Геометрический смысл производной». 11 класс.

Самостоятельная работа по алгебре. Тема «Геометрический смысл производной». 11 класс.

Вариант 1

1. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(х) в точке .

а) б)

2. Найдите угловой коэффициент касательной к графику функции у = в точке с абсциссой

3. Написать уравнение касательной к графику функции у = f(х) в точке .

у = 2 ,

 4. Прямая  является касательной к графику функции . Найдите абсциссу точки касания.

Вариант 2

1. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(х) в точке .

a) б)

2. Найдите угловой коэффициент касательной к графику функции у = в точке с абсциссой

3. Написать уравнение касательной к графику функции у = f(х) в точке .

у = ,

4. Прямая  является касательной к графику функции . Найдите абсциссу точки касания.

Вариант 3

1. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(х) в точке .

a) б)

2. Найдите угловой коэффициент касательной к графику функции у = в точке с абсциссой

3. Написать уравнение касательной к графику функции у = f(х) в точке .

У =

4. Прямая  является касательной к графику функции . Найдите абсциссу точки касания.

Вариант 4

1. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(х) в точке .

a) б)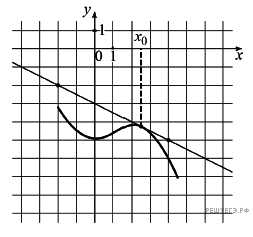

2. Найдите угловой коэффициент касательной к графику функции у = в точке с абсциссой

3. Написать уравнение касательной к графику функции у = f(х) в точке .

у =

4. Прямая  является касательной к графику функции . Найдите абсциссу точки касаний.

infourok.ru

Самостоятельная работа по алгебре 11 кл «Правила дифференцирования» 12 вариантов

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 1 А 11

1. Найдите производную функции

а) y = 3x² – 7x³ б) y = x³(x² – 5)

в) г) y = (3x² — 1)³

2. Запишите формулой функцию f (g(x)), если

y = g(x) = sin x

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 2 А 11

1. Найдите производную функции

а) y = 2x³ – 5x² б) y = (x³ – 2) x²

в) г) y = (2x³ — 3)²

2. Запишите формулой функцию f (g(x)), если

F(y) = cos y

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 3 А 11

1. Найдите производную функции

а) y = -4x³ +5x² б) y = x²(x³ +2)

в) г) y = (2x³ +3)²

2. Запишите формулой функцию f (g(x)), если

y = g(x) = cos x

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 4 А 11

1. Найдите производную функции

а) y = 5x² – 3x³ б) y = (– 2 + x²) x³

в) г) y = (-3x² +1)³

2. Запишите формулой функцию f (g(x)), если

F(y) = sin y

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 5 А 11

1. Найдите производную функции

а) y = 5x³ – 2x² б)

y = x²(4 – x²)

в) г) y = (2x³ — 3)²

2. Запишите формулой функцию f (g(x)), если

y = g(x) = tg x

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 6 А 11

1. Найдите производную функции

а) y = 5x² + 3x³ б) y = (2x² – 3) x³

в) г) y = (4x

² – 8)²

2. Запишите формулой функцию f (g(x)), если

F(y) = ctg y

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 7 А 11

1. Найдите производную функции

а) y = 3x² – 7x³ б) y = (x³ – 2) x²

в) г) y = (-3x² +1)³

2. Запишите формулой функцию f (g(x)), если

3. y = g(x) = sin x

__________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 8 А 11

1. Найдите производную функции

а) y = 2x³ – 5x² б) y = x³(x² – 5)

в) г) y = (2x³ — 3)²

2. Запишите формулой функцию f (g(x)), если

F(y) = cos y

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 9 А 11

1. Найдите производную функции

а) y = -4x³ +5x² б) y = (– 2 + x²) x³

в) г) y = (4x² – 8)²

2. Запишите формулой функцию f (g(x)), если

F(y) = sin y

____________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 10 А 11

1. Найдите производную функции

а) y = 5x² + 3x³ б) y = x²(

x³ +2)

в) г) y = (2x³ — 3)²

2. Запишите формулой функцию f (g(x)), если

y = g(x) = tg x

___________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 11 А 11

1. Найдите производную функции

а) y = 5x² – 3x³ б) y = x²(4 – x²)

в) г) y = (3x² — 1)³

2. Запишите формулой функцию f (g(x)), если

F(y) = ctg y

___________________________________________________

Самостоятельная работа «Правила дифференцирования»

ВАРИАНТ 12 А 11

1. Найдите производную функции

а) y = 5x³ – 2x² б) y = (2x² – 3) x³

в) г) y = (2x³ +3)²

2. Запишите формулой функцию f (g(x)), если

y = g(x) = cos x

__________________________________________

infourok.ru

«Физический смысл производной» (11 класс)

Физический смысл производной

Вариант №1

1.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=t⁴+1/3t³-t²+8. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?

2.Материальная точка движется по закону х(t)= 1/3t³-t²+9t+11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с² ?

3. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=5t² — 3t+6. Через сколько секунд после начала движения произойдет остановка?

4. Материальная точка движется по закону х(t)= t³-4t²+3t — 17 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 10 м/с² ?

5. Материальная точка движется по закону х(t)= t³-5t²+6t +7 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 8 м/с² ?

6. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=1/4t⁴+t³-1/2t²+12. Чему будет равна мгновенная скорость (м/с) через 4 с после начала движения?

_____________________________________________________________________________________

Физический смысл производной

Вариант №2

1. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t² — 24t-13. Через сколько секунд после начала движения произойдет остановка?

2. Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=3t³-4t+5 м. Определите скорость движения тела через 2 с после начала движения.

3.Материальная точка движется по закону х(t)=2 t³-3t² -14t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с² ?

4. Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=3/4t⁴-2/3t³+3t²-21. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?

5.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=3/4t⁴-2/3t³+3t²-21. Чему будет равна мгновенная скорость (м/с) через 3 с после начала движения?

6.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=2t⁴-1/3t³+5t²-4. Чему будет равна мгновенная скорость (м/с) через 2 с после начала движения?

Физический смысл производной

Вариант №3

1. Материальная точка движется по закону х(t)=1/4 t³-3t²+21t — 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с² ?

2.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t² — 18t+19. Через сколько секунд после начала движения произойдет остановка?

3. Материальная точка движется по закону х(t)=1/6 t³-4t²+35t — 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с² ?

4.Материальная точка движется по закону х(t)=1/3 t³-6t²+35t +61 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с² ?

5.Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=2t²+4 -9 м. Определите скорость движения тела через 4 с после начала движения.

6.Материальная точка движется по закону х(t)=1/2 t³-7t²+16t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 4 м/с² ?

_____________________________________________________________________________________

Физический смысл производной

Вариант №3

1. Материальная точка движется по закону х(t)=1/4 t³-3t²+21t — 18 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 3 м/с² ?

2.Тело движется по прямой так, что расстояние S (в м) от него до точки М этой прямой изменяется по закону S(t)=6t² — 18t+19. Через сколько секунд после начала движения произойдет остановка?

3. Материальная точка движется по закону х(t)=1/6 t³-4t²+35t — 11 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 2 м/с² ?

4.Материальная точка движется по закону х(t)=1/3 t³-6t²+35t +61 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 6 м/с² ?

5.Тело движется прямолинейно, его расстояние S (в м) от начала отсчета изменяется по закону S(t)=2t²+4 -9 м. Определите скорость движения тела через 4 с после начала движения.

6.Материальная точка движется по закону х(t)=1/2 t³-7t²+16t -27 (х –перемещение в м, t – время в с). Через сколько секунд после начала движения ускорение точки будет равно 4 м/с² ?

infourok.ru

Самостоятельная работа на тему: «Производная»

Самостоятельная работа по теме: «Производная»

11 класс

Вариант 1

1. Найдите производную функции:

а) б) ; в) ;

г) ; д) ; e) .

2. Найти значение производной функции в точках 1 и 5, если

3. При каких значениях значение производной равно нулю, положительно, отрицательно: а) ; б) .

__________________________________________________________________________

Вариант 2

1. Найдите производную функции:

а) б) ; в) ;

г) ; д) ; e) .

2. Найти значение производной функции в точках 2 и 4, если

3. При каких значениях значение производной равно нулю, положительно, отрицательно: а) ; б) .

Вариант 3

1. Найдите производную функции:

а) б) ; в) ;

г) ; д) ; e) .

2. Найти значение производной функции в точках 1 и -2, если

3. При каких значениях значение производной равно нулю, положительно, отрицательно: а) ; б) .

infourok.ru

Самостоятельная работа по теме: «Геометрический смысл производной» (11 класс)

Геометрический смысл производной№1

1.Определите абсциссу точки, в которой касательная к графику функции у=4х²-8х+4 параллельна оси абсцисс.(1)

2.На кривой у= х²-х+1 найдите точку, в которой касательная параллельна прямой у=3х-1. В ответе укажите абсциссу этой точки.(2)

3.К графику функции f(х)=3х²-8х+15 проведена касательная параллельно прямой у=4х-3. Найдите абсциссу точки касания.(2)

4.Определите абсциссу точки, в которой касательная к графику функции у=4х²-8х+4 параллельна прямой у=8х-4(2)

5. На кривой у=х²-х+1 найдите точку, в которой касательная параллельна прямой у=9х-1. Укажите абсциссу этой точки.(5)

6.Касательная к графику функции у=lnх+х параллельна прямой у=2х-3. Определите абсциссу точки касания.(1)

7.Касательная к графику функции у=1/х² параллельна прямой у=-2х+4. Определите абсциссу точки касания.(1)

8.Касательная к графику функции у=3х²-5х параллельна прямой у=7х-2. Найдите абсциссу точки касания.(2)

9. В какой точке касательная к графику функции у=х² -5х параллельна прямой у=-х?(2;-6)

10. Дана функция у=1/3х³ -4х+2. Найдите координаты точек, в которых касательная к графику функции параллельна оси абсцисс.(2; -10/3) ; (-2; 22/3)

Геометрический смысл производной№2

1.Определите угол в градусах, который образует касательная, проведенная к графику функции у=х²-5х+7 в точке с абсциссой х₀=2, с положительным направлением оси Ох. (135)

2.Через точку графика функции f(х)=-1/2х²+4х+7 с абсциссой х₀=2 проведена касательная. Найдите тангенс угла наклона касательной к положительному направлению оси абсцисс.(2)

3.Определите угол, который образует касательная, проведенная к графику функции у=4/х в точке с абсциссой х₀=-2, с положительным направлением оси абсцисс.(135)

4.Укажите градусную меру угла, образованного положительным направлением оси абсцисс и касательной к графику функции у=х+sin3х в точке х₀= π/2.(45)

5. Найдите угол (в градусах), образованный с положительным направлением оси Ох и касательной к графику функции у=2е^х -3х в точке х₀ =0.(135)

6.Найдите тангенс угла наклона касательной к графику функции у=х(х-2) в точке с абсциссой х₀ =4.(6)

7.Найдите тангенс угла наклона касательной к графику функции у=2х⁴ +5х² -3 в точке с абсциссой х₀ =-1.(-18)

8. Известно, что производная функции в точке х₀ равна -1. Тогда касательная к графику функции у=f(х) в точке х₀ образует с положительным направлением оси Ох угол …..? (135)

9.Под каким углом к оси Ох наклонена касательная, проведенная к кривой у=х³ –х² -7х+6 в точке М₀ (2;4)? (45)

10. К графику функции у=3х² +5х-15 в точке с абсциссой х₀=1/6 проведена касательная. Найдите тангенс угла наклона касательной к оси Ох. (6)

Геометрический смысл производной№3

1.Найдите абсц
иссу точки графика функции f(х)= π (4х²+3), в которой угловой коэффициент касательной равен π/4.(1/32)

2.Найдите абсциссу точки графика функции f(х)=14х²-27х+15, в которой касательная наклонена под углом 45⁰ к оси абсцисс.(1)

3.Найдите произведение абсцисс точек, принадлежащих графику функции (х)=х³ /3-4х ² +5х+7, в которых касательная наклонена под углом 135⁰ к оси абсцисс.(6)

4.На графике функции f(х)=х²+х-5 взята точка А. Касательная к графику, проведенная через точку А, наклонена к положительному направлению оси Ох под углом, тангенс которого равен 5. Найдите абсциссу точки А.(2)

5.К графику функции f(х)= х²+3х+2 проведена касательная. Найдите абсциссу точки касания, если касательная образует угол 45⁰ с положительным направлением оси абсцисс.(-1)

6. Прямая у=1-2х является касательной к графику функции у=-х². Укажите абсциссу точки касания.(1)

7. Прямая у=-6х-10 является касательной к графику функции у=х³+4х²-6х-10. Найдите абсциссу точки касания.(0)

8. Найдите абсциссу точки, в которой касательная к графику функции у=х² /8+2 наклонена к оси Ох под углом, тангенс которого равен ½.(2)

9. Прямая у=-5х+14 является касательной к графику функции у=х³+3х²-2х+15. Найдите абсциссу точки касания.(-1)

10. Прямая у=3х+9 является касательной к графику функции у=х³+х²+2х+8. Найдите абсциссу точки касания.(-1)

Геометрический смысл производной№4

1.Найдите угловой коэффициент касательной, проведенной к графику функции у=3х³-2х²+5 в его точке с абсциссой

х₀=-3.(93)

2.Найдите угловой коэффициент касательной, проведенной к графику функции у=3х³-2х²+5 в его точке с абсциссой х₀=3.

(69)

3. Найдите угловой коэффициент касательной, проведенной к графику функции f(х)=sinх-cosх в точке с абсциссой х₀= π/4.

().

4. Найдите угловой коэффициент касательной к графику функции f(х)=4х²-4х+1 в точке пересечения графика с осью ординат.(-4)

5. К графику функции f(х)=х²+3х+2 в точке с абсциссой х₀ =1 проведена касательная. Найдите ординату точки графика касательной, абсцисса которой равна 11.(56)

6. К графику функции f(х)=х²+х+1 в точке с абсциссой х₀=1 проведена касательная. Найдите абсциссу точки пересечения касательной с осью Ох.(0)

7.Найдите угловой коэффициент касательной к графику функции у=2х³-х в точке х₀=-2.(-23)

8.Найдите угловой коэффициент касательной к графику функции у=хlnх в точке х₀=е.(2)

9.Найдите угловой коэффициент касательной к графику функции у=х⁴-2х³+3х-13 в точке х₀=-1.(-7)

10. Найдите угловой коэффициент касательной к графику функции у=х⁶-2х⁵+3х4 +х²+4х+5 в точке х₀=-1.(-26)

11. Найдите угловой коэффициент касательной к графику функции у=х⁵+2х⁴ +х³+12 в точке х₀=1.(16)

12. Дана функция f(х)=х²-4х+1. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.(3;-2)

13. Угловой коэффициент касательной, проведенной к графику функции у=4х³ -7х² +2х-1 в точке с положительной абсциссой х_0, равен 2. Найдите х₀.(7/6)

referat-4all.ru

Самостоятельная работа по теме «Нахождение производных элементарных функций. Правила дифференцирования. » (11 класс)

Алгебра-11

Самостоятельная работа по теме

«Нахождение производной элементарных функций. Правила дифференцирования»

Вариант 1

Вариант 2

I.Продолжить формулу

1) (x^p)=…

2) (a^x)’ =…

3) ()’ =…

4) (cos x)’ =…

5) ()’ =…

6) =…

I.Продолжить формулу

1) (e^x)=…

2) ()’ =…

3) ()’ =…

4) ()’ =…

5) (e^kx)’ =…

6) =…

II.Дополнить формулу (u=f(x), v=g(x))

1. (uv)’ = u’ …+ v’ …

2. (…)’ = k ‘

II.Дополнить формулу (u=f(x), v=g(x))

1. (…)’ = u’ + v’

2. =

III.Установить соответствие между левыми и правыми частями формул

III.Установить соответствие между левыми и правыми частями формул

1)(e^x)’

2)(x^p)

3)()’

4)(sin x)’

А)cos x

Б)p x^p—1

В)e^x

Г)e^kx

Д) kcos kx

1)( cos x)’

2)(a ^x)

3)()’

4)

А)

Б)-sin x

В)a ^x

Г)

Д)

IV.Найти ошибку, записать верное решение.

(e^3x )’ = (e^3x)’ – e ^3x = e^3x — e^3x = e^3x

IV.Найти ошибку, записать верное решение.

()’=

infourok.ru

Самостоятельная работа 11класс Производная (1)

Вариант 1
1. Найдите производную функции
а)у = 3х2- 12х.
б) у = 13х2- 2
2. Найдите значение производной функции
а) y=(x2 — 6)(5×2 +1 2) в точке х0 = 1.
б)y=х-6х в точке х0 = 2.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 2)(x2 + 2).
4. Найти все значения x, при которых f/(х) > 0 если f (х) = (х + 3)(х + 14). Вариант 2
1.Найдите производную функции
а) у = 4х2- 16х.
б) y=32х2+ 16.
2. Найдите значение производной функции
а) y=(x2 — 2)(x2 + 12x) в точке х0 = 1
б) y= х-18х в точке х0 = 3.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 3)(x2 + 3).
4. Найти все значения x, при которых
f/(х) > 0 если f (х) = (12-3x)(х + 4).
Вариант 1
1. Найдите производную функции
а)у = 3х2- 12х.
б) у = 13х2- 2
2. Найдите значение производной функции
а) y=(x2 — 6)(5×2 +1 2) в точке х0 = 1.
б)y=х-6х в точке х0 = 2.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 2)(x2 + 2).
4. Найти все значения x, при которых f/(х) > 0 если f (х) = (х + 3)(х + 14). Вариант 2
1.Найдите производную функции
а) у = 4х2- 16х.
б) y=32х2+ 16.
2. Найдите значение производной функции
а) y=(x2 — 2)(x2 + 12x) в точке х0 = 1
б) y= х-18х в точке х0 = 3.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 3)(x2 + 3).
4. Найти все значения x, при которых
f/(х) > 0 если f (х) = (12-3x)(х + 4).
Вариант 1
1. Найдите производную функции
а)у = 3х2- 12х.
б) у = 13х2- 2
2. Найдите значение производной функции
а) y=(x2 — 6)(5×2 +1 2) в точке х0 = 1.
б)y=х-6х в точке х0 = 2.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 2)(x2 + 2).
4. Найти все значения x, при которых f/(х) > 0 если f (х) = (х + 3)(х + 14). Вариант 2
1.Найдите производную функции
а) у = 4х2- 16х.
б) y=32х2+ 16.
2. Найдите значение производной функции
а) y=(x2 — 2)(x2 + 12x) в точке х0 = 1
б) y= х-18х в точке х0 = 3.
3. Решите уравнение f/(x) = 0 , если
f (x) = (x2 — 3)(x2 + 3).
4. Найти все значения x, при которых
f/(х) > 0 если f (х) = (12-3x)(х + 4).

Приложенные файлы

profhelp.net