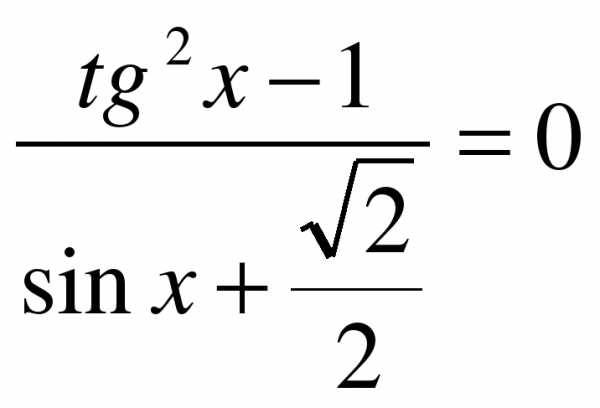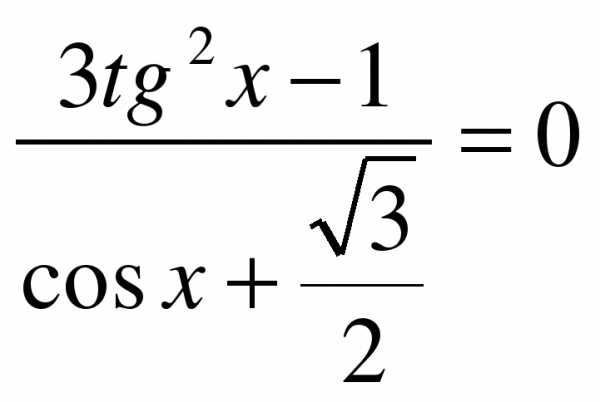Самостоятельная работа по алгебре в 11 классе по теме: «Тригонометрия»
Самостоятельная работа по алгебре в 11 классе по теме: «Тригонометрия»
Вариант 1
Часть А
1. Найдите множество значений функции у = 3 – 2sinx
[ 1; 5]; 2) [ — 1; 1]; 3) [ 3; 5 ]; 4) [ 1; 3]
2. Вычислите значение sin2x, если cosx = и
– ; 2) ; 3) ; 4) – .
3. Найдите сумму всех целых чисел, которые входят в область значений функции у = 4cos2x – 7
– 25; 2) 25; 3) – 22; 4) 0.
4. Упростите выражение 5sin2x – 4 + 5cos2x
1; 2) 9; 3) – 9; 4) – 4.
5. Решите уравнение cosx – = 0
2) 3) 4)
Часть
6. Найдите значение выражения при
7. Упростите выражение
Часть С
8. Определите, сколько корней уравнения 2сos2x + 7cosx – 4 = 0, принадлежит отрезку [ — 2
Самостоятельная работа по алгебре в 11 классе по теме: «Тригонометрия»
Вариант 2.
Часть
1. Найдите множество значений функции у = 3cosx – 2
[ – 5; 1]; 2) [ – 1; 1]; 3) [ – 5; –2]; 4) [ 1; 3].
2. Вычислите значение cos2 , если sin = – и
– ; 2) ; 3) – 0,5 ; 4) 0,5.
3. Найдите произведение всех целых чисел, которые входят в область значений функции у = 5 – 3sin2x
120; 2) 14; 3) – 15; 4) 0.
4. Упростите выражение – 4sin2x + 5 – 4cos2x
1; 2) 9; 3) 5; 4) 4.
5. Решите уравнение sinx – = 0
1) 2) 3) 4)
Часть В
6. Найдите значение выражения при cos =
7. Упростите выражение
Часть С
8. Определите, сколько корней уравнения 2sin2x + 5sinx – 3 = 0, принадлежит отрезку [ — 2
Самостоятельная работа по алгебре в 11 классе по теме: «Тригонометрия»
Работа состоит из 8 заданий. К каждому заданию А1 – А5 приведены 4 варианта ответа, из которых только один верный . При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ. К заданию С1 — записать решение.
Система оценивания работы.
За каждое верно решенное задание части А обучающийся получает 1 балл, части В – 2 балла, части С – 3 балла. Таким образом, максимальное число баллов, которое можно получить за верное решение всех заданий, равно 12. Оценка «3» ставится, если ученик набрал от 4 до 7 баллов; оценка «4», если ученик набрал от 8 до 9 баллов; оценка «5», если ученик набрал от 10 до 12 баллов.
gigabaza.ru
Урок алгебры 11 класс , контрольная работа по теме»Тригонометрические функции»
Контрольная работа № 1
Тригонометрические функции
Вариант 1
А1. Найдите область определения функции  .
.
А2. Найдите множество значений функции .
А3. Выяснить, является ли данная функция четной или нечетной:
А4. Докажите, что функция является периодической с периодом Т = p.
А5. Сравните числа:  .
.
A6. Найдите значение функции .
В1. Сравните числа: 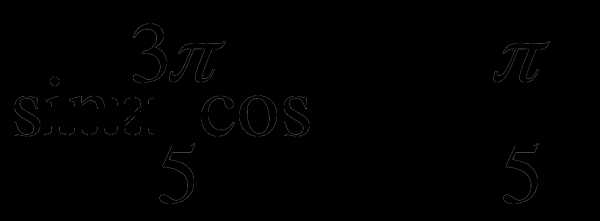 .
.
В2. Найдите все корни уравнения , принадлежащие промежутку [0;2p].
С1. Найдите наибольшее и наименьшее значение функции на отрезке 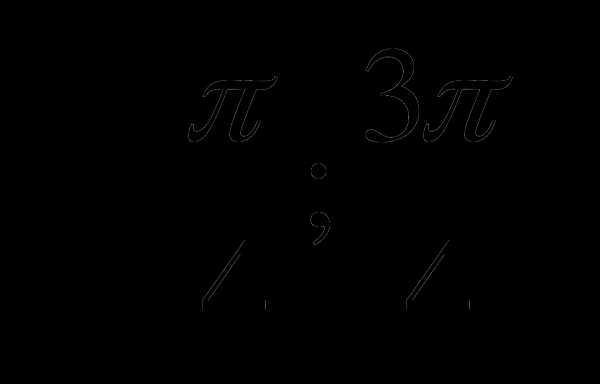 .
.
С2. Постройте график функции .
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
_________________________________________________________________
Контрольная работа № 1.
Тригонометрические функции
Вариант 2
А1. Найдите область определения функции .
А2. Найдите множество значений функции .
А3. Выясните, является ли данная функция четной или нечетной: .
А4. Докажите, что функция у = tg 3x является периодической с периодом Т =  .
.
А5. Сравните числа: sin  и sin
и sin  .
.
A6. Найдите значение функции .
В1. Сравните числа: 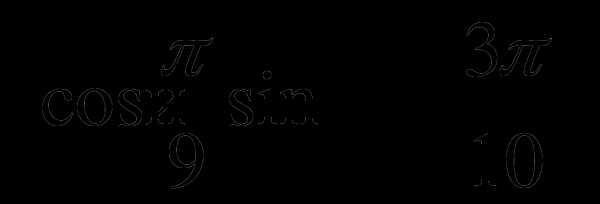
В2.Найти все корни уравнения , принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции на отрезке 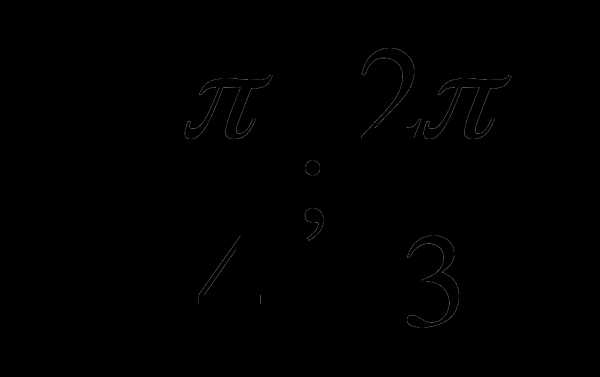 .
.
С2. Построить график функции 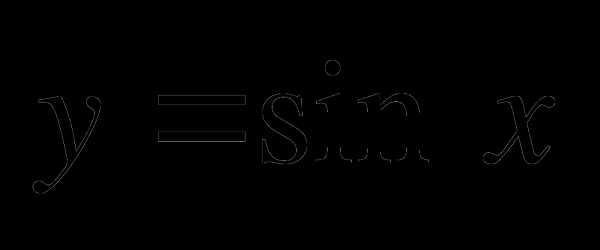 .
.
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 3
А1. Найдите область определения функции у = sin  .
.
А2. Найдите множество значений функции у = 1 –2sin x.
А3. Выяснить, является ли данная функция четной или нечетной:
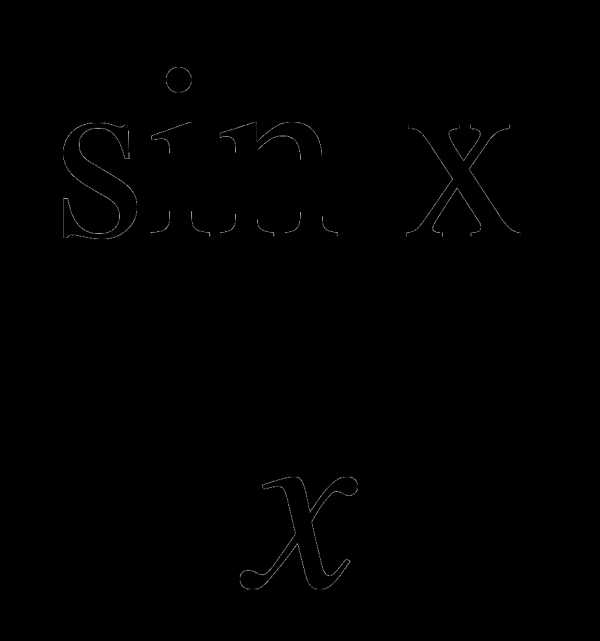 .
. А4. Докажите, что функция у = cos  является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Сравните числа: tg  и tg
и tg  .
.
A6. Найдите значение функции у=3cos при х =
при х =  .
.
В1. Сравните числа: sin  и cos
и cos  .
.
В2. Найдите все корни уравнения 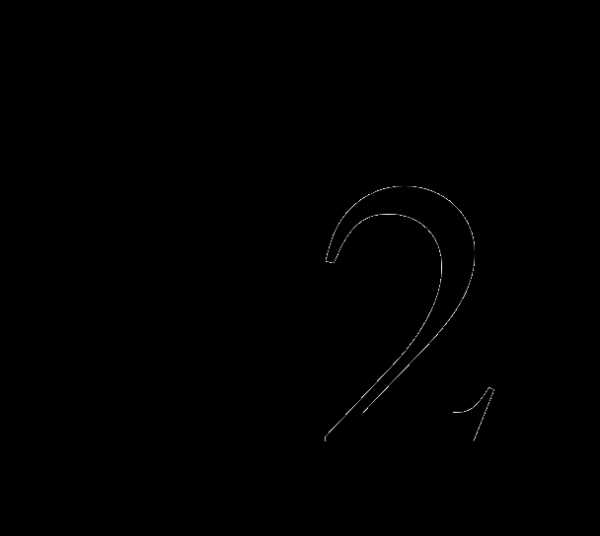 sin x = 1, принадлежащие промежутку [-p;p].
sin x = 1, принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции у=4tgx на отрезке 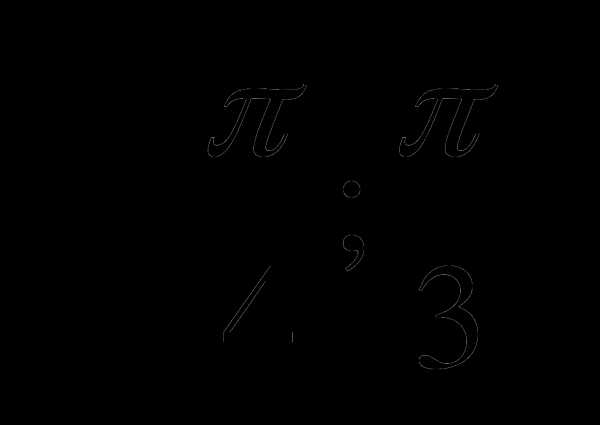 .
.
С2. Построить график функции 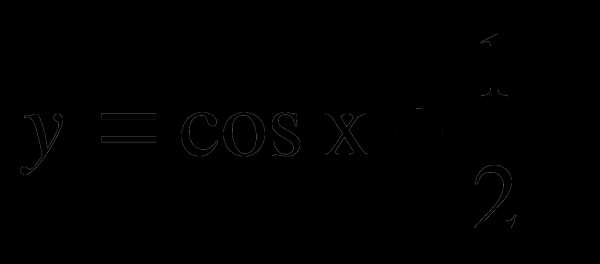 .
.
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 4
А1. Найти область определения функции у = cos  .
.
А2. Найти множество значений функции у = 3sin x.
А3. Выяснить, является ли данная функция четной или нечетной: у = tg x – x3.
А4. Доказать, что функция у = cos  является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Возрастает или убывает функция у = sin x на отрезке 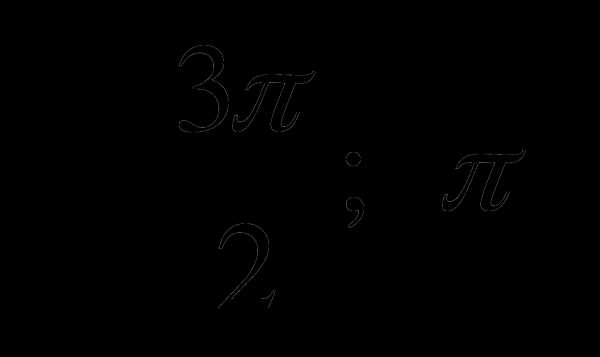
A6. Найдите значение функции у=4sin при х =
при х =  .
.
В1. Сравните числа: cos  и sin
и sin  .
.
В2. Найдите все корни уравнения 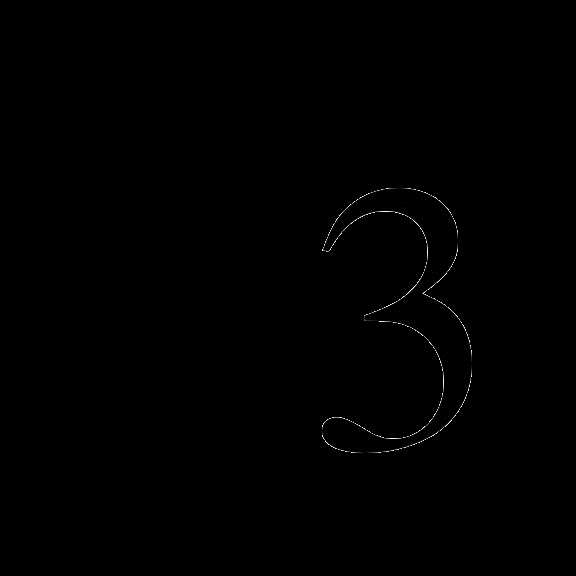 + 2cos x = 0, принадлежащие промежутку
+ 2cos x = 0, принадлежащие промежутку
[0; 2p].
С1. Найдите наибольшее и наименьшее значение функции у=4cosx на отрезке 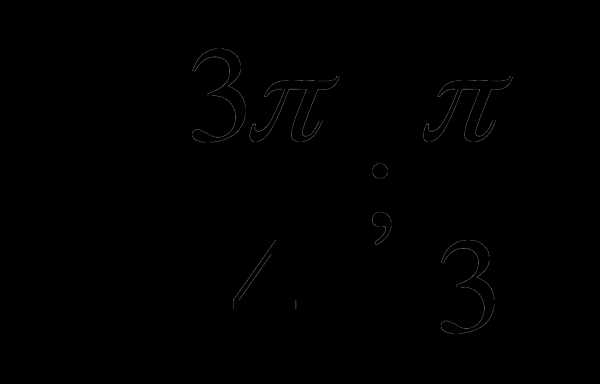
С2. Построить график функции у = |sin x| +1
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
infourok.ru
а y = sin3x; б у = соs; в
скачать 11А Самостоятельная работа по теме «Тригонометрические функции» В- 1-
Найдите область определения функции: а) y = sin3x; б) у = соs; в) .
-
Найдите множество значений функции: а) у = 5+sinx; б) у = -3cos 5x- 2; в) .
|
3. На каком рисунке изображено решение неравенства |
|
|
11А Самостоятельная работа по теме «Тригонометрические функции» В- 2
-
Найдите область определения функции: а) y = cos3x; б) у =sin; в) . -
Найдите множество значений функции: а) у = 1 + sinx; б) у = 2 — 4cos x; в) .
|
3. На каком рисунке изображено решение неравенства cosx > |
|
|
11А Самостоятельная работа по теме «Тригонометрические функции» В- 3
-
Найдите область определения функции: а) y =tg 3x; б) у =cos; в) . -
Найдите множество значений функции: а) у = 1 -3sinx; б) у = 2cos4 x+ 2; в)
|
3. На каком рисунке изображено решение уравнения cosx = 0 |
|
|
11А Самостоятельная работа по теме «Тригонометрические функции» В- 4
-
Найдите область определения функции: а) y = sin2 x б) у =ctg2x в) -
Найдите множество значений функции: а) у = 1 + 2sinx; б) у = 3cos x-1; в)
|
3. На каком рисунке изображено решение неравенства |
|
|
11А Самостоятельная работа по теме «Тригонометрические функции» В- 5
-
Найдите область определения функции: а) y = cos2 x; б) у =tg2x в) . -
Найдите множество значений функции: а) у = sin2x; б) у = 2cos x + 1; в) y = 1 + 2sinx∙cosx
|
3. На каком рисунке изображено решение уравнения sinx = 0 |
|
|
11 A Самостоятельная работа по теме «Тригонометрические функции» В- 6
-
Найдите область определения функции: а) y = cos2x; б) у =sin; в) -
Найдите множество значений функции: а) у = 1 + 4sinx; б) у = 2cos4 x — 1; в)
|
3. На каком рисунке изображено решение неравенства sinx > |
|
|
скачать
nenuda.ru
Самостоятельные работы по алгебре для 11 класса
ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ 10 — 11 КЛАССА ПО АЛГЕБРЕ
ДЛЯ ПОДГОТОВКИ К ЕГЭ
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Пределы)
Вычислить пределы:
1) 5)
2) 6)
3) 7)
4) 8)
9) Найти сумму геометрической прогрессии 32, 16, 8, 4, 2, …
10) Найти первый член геометрической прогрессии (), если S = 10, q = 0,1.
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Производные)
За правильное выполнение 20 заданий оценка «5»;
За правильное выполнение 18 — 19 заданий оценка «4»;
За правильное выполнение 11 — 17 заданий оценка «3»;
Найти производные следующих функций:
1). 8). 14).
2). 9). 15).
3).
4). 10). 16).
5). 11). 17).
6). 12). 18).
7). 13). 19).
20).
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Производная)
Найти производную функции:
1). 7). 13). 19).
2). 8). 14). 20).
3). 9). 15). 21).
4). 10). 16). 22).
5). 11). 17). 23).
6). 12). 18). 24).
26).
Вычислить тангенс угла между касательной к графику функции в точке с абсциссой :
26). ; =
27). ; = 0
Вычислить угловой коэффициент касательной к графику функции в точке с абсциссой :
28). ; =
29). ; =
30). Вычислить скорость изменения функции в точке с абсциссой = 0.
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Производная)
1). Материальная точка движется прямолинейно по закону , где
Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 9 сек.
2). Материальная точка движется прямолинейно, её скорость выражается формулой
V=2+5t. Найти закон движения, если известно, что в момент времени t = 2 координата точки равнялась числу 20.
3). Материальная точка движется прямолинейно по закону , где
Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 9 сек.
4). Скорость прямолинейного движения материальной точки задаётся формулой
. Найти закон движения ,если S(0) = 9.
5). Материальная точка движется прямолинейно по закону , где
Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 6 сек.
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Интеграл. Площадь фигуры)
1). Вычислить определённый интеграл: а) ; б) ; в) ;
г) ;
2). Вычислить площадь фигуры, ограниченной прямыми
3). Вычислить площадь фигуры, ограниченной графиками функций
и
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Преобразования алгебраических выражений и дробей)
1. Найдите значение выражения .
2. Найдите значение выражения при .
3. Найдите , если .
4. Найдите значение выражения , если .
5. Найдите значение выражения , если , а .
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Преобразование числовых и буквенных иррациональных выражений)
1). Найдите значение выражения при .
2). Найдите значение выражения при .
3). Найдите значение выражения при .
4). Найдите , если при .
5). Найдите значение выражения .
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Преобразование буквенных показательных выражений)
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Найдите значение выражения при .
4. Найдите значение выражения при .
5. Найдите значение выражения при .
6. Найдите значение выражения при .
7. Найдите значение выражения при .
8. Найдите значение выражения при .
9. Найдите значение выражения , если .
10. Найдите значение выражения при .
11. Найдите значение выражения при .
12. Найдите значение выражения при .
13. Найдите значение выражения
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Преобразование числовых и буквенных логарифмических выражений)
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения .
7. Найдите значение выражения .
8. Найдите значение выражения .
9. Найдите значение выражения .
10. Найдите значение выражения .
11. Найдите значение выражения .
12. Найдите значение выражения .
13. Найдите значение выражения .
14. Найдите значение выражения .
15. Найдите значение выражения .
16. Найдите значение выражения .
17. Найдите значение выражения .
18. Вычислите значение выражения: .
19. Найдите значение выражения
20. Найдите значение выражения
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Преобразование числовых и буквенных тригонометрических выражений)
1. Найдите , если и
2. Найдите , если и .
3. Найдите , если и .
4. Найдите , если .
5. Найдите , если и .
6. Найдите , если .
7. Найдите , если .
8. Найдите , если .
9. Найдите значение выражения , если .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
Найдите значение выражения .
14. Найдите значение выражения .
15. Найдите значение выражения .
16. Найдите значение выражения .
17. Найдите значение выражения .
18. Найдите значение выражения .
19. Найдите значение выражения .
20. Найдите значение выражения .
21. Найдите значение выражения .
22. Найдите значение выражения: .
23. Найдите значение выражения .
24. Найдите значение выражения
25. Найдите значение выражения
САМОСТОЯТЕЛЬНАЯ РАБОТА
(Тема: Линейные, квадратные, кубические, рациональные уравнения)
1. Найдите корень уравнения
2. Решите уравнение .
3. Решите уравнение .
4. Решите уравнение .
5. Найдите корень уравнения .
6. Найдите корень уравнения .
7. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
8. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
9. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
10. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.
11. Найдите корень уравнения .
12. Найдите корень уравнения .
13. Решите уравнение .
14. Решите уравнение .
infourok.ru
| СР 1 | Тригонометрия повторение к ЕГЭ Вариант 1 | СР1 | Тригонометрия повторение к ЕГЭ Вариант 2 |
| 1 | Найти значение выражения | 1 | Найти значение выражения |
| а | а | ||
| б | ,если | б | ,если |
| в | в | ||
| г | , если . | г | ,, если |
| д |
| д | |
| 2 | 2 | ||
| 3 | Решите уравнение cos3x =1 Укажите наибольшее отрицательное решение | 3 | Решите уравнение Укажите наименьшее положительное решение |
| 4 | Решите уравнение | Решите уравнение | |
| СР1 | Тригонометрия повторение к ЕГЭ Вариант 3 | СР1 | Тригонометрия повторение к ЕГЭ Вариант 4 |
| 1 | Найти значение выражения | 1 | Найти значение выражения |
| а | а | ||
| б | б | ||
| в | , если. | в | Найдите значение выражения |
| г | г | ||
| д | д | ||
| 2 | Найдите значение | 2 | Найдите , если и . |
| 3 | Решите уравнение Укажите наибольшее отрицательное решение | 3 | Решите уравнение = Укажите наименьшее положительное решение |
| Решите уравнение | Решите уравнение |
multiurok.ru
Подготовка к контрольной работе «Тригонометрические функции» конспект урока с презентацией и карточками для проведения контрольной работы в 11 классе по алгебре и началам анализа – УчМет
Автор Турукина Е.В.
Муниципальное бюджетное общеобразовательное учреждение
МБОУ Еткульская СОШ с.Еткуль Еткульского района Челябинской области
Класс 11
Тема Подготовка к контрольной работе по теме «Тригонометрические функции»
Цели:
1.Повторить определение четной (нечетной) функции, свойства и построение графиков тригонометрических функций
2.Воспитание мотивов учения
3.Развитие умения применять теорию на практике
План урока
-
Устная работа (слайд 3)
Функция у=f(x), для которой область определения симметрична относительно начала координат и выполняется равенство f(-x)=f(x)
Функция у= f(x), для которой область определения симметрична относительно относительно начала координат и выполняется равенство f(-x)=-f(x)
2.Проверить функцию на четность (слайд 4)
а) у= Sin x+ Cos x (ни четная ни нечетная)
б) у= х2 + Сos x (четная)
в) y= Sin x +2tg x (нечетная)
г) y = Cos2x –Sin2x (четная)
3.Найти область определения и область значений функции (слайд 5)
а) у= Сos 2x
б) y=2sin 0,5 x
в) y= -0,5 Cos2x
г) y=0,4Sinx +2
д) y= -0,07Cos x
е) y=5tg x +1
Ответы: а) Д(у)=R, Е(у)=[-1;1]
б) Д(у)=R, Е(у)=[-2;2]
в) Д(у)=R, Е(у)=[-0,5;0,5]
г) Д(у)=R, Е(у)=[1,6;2,4]
д) Д(у)=R,Е(у)=[-0,07;0,07]
е) Е(у)=R Д(у) : все х≠π/2 +πn, где n€Z
4.Найти наибольшее и наименьшее значение функции (слайд 6)
Ответ : у наибольшее =5, у наименьшее=1
Ответ : у наибольшее =9, у наименьшее=1
5.Повторим построение графиков тригонометрических функций(слайд 8-11)
6.Запишем домашнее задание: готовиться к контрольной работе, выполнить №717(а), 767,(766, 719)
7. При наличии времени можно предложить учащимся построить графики функций
1. у= 2Sin x -1
2. y= -0,5Cos x+2
3. y=2Sin0,5x
4. y= Cos2x+3
5. y= 3Sin2x-0,5
6. y= Cos(x — π/3 )
7. y= Sin (x+ π/4 )
Следующий урок контрольная работа
Используемая литература
1. Учебник Алгебра и начала анализа для 10-11 класса
Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, Н.Е.Федорова, М.И. Шабунин
Москва, Просвещение , 2010 год
2. Готовимся к Единому Государственному Экзамену Математика
Л.О. Денищева, Е.М.Бойченко, Ю.А.Глазков и др.
Москва, Дрофа, 2009
3. Учебно-тренировочные материалы для подготовки учащихся
ЕГЭ Математика 2009 ,Интеллект –центр
4. Дидактические материалы по алгебре и началам анализа 11 класс
М.И. Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г. Газарян
Москва, Просвещение, 2008 год
5. А.П.Ершова, В.В.Голобородько Алгебра и начала анализа 10-11 классы. Математика. Самостоятельные и контрольные работы. Разноуровневые дидактические материалы. Москва, «Илекса» 2008
www.uchmet.ru
Тема: «Тригонометрические функции». 11 класс
Контрольная работа по алгебре № 1.
Тема: «Тригонометрические функции».11 класс
Вариант 1 Вариант 2
|
1.(1б) Найти область определения и множество значений функции y=2cos(-x)+6. 2. (1б) Построить график функции y= 0,5cosx-2. При каких значениях х функция возрастает ? 3.(1б) Выяснить, является ли функция y = 3sinx — 2cosx четной или нечетной. 4.(1б) С помощью графика функции выяснить, сколько корней имеет уравнение . ___________________________ 5. (2б) Доказать, что функция периодическая с наименьшим положительным периодом и найдите ее область определения. 6. (3б) Найти наибольшее и наименьшее значения функции: у=3sinx ∙cosx+1. 7* Построить график функции . |
1.(1б)Найти область определения и множество значений функции y=0,5sinx-5. 2. (1б) Построить график функции y=2sinx+1. При каких значениях х функция убывает ? 3.(1б) Выяснить, является ли функция y = 3sin2 x – cos2x четной или нечетной. 4.(1б) С помощью графика функции выяснить, сколько корней имеет уравнение . ___________________________ 5.(2б) Доказать, что функция периодическая с наименьшим положительным периодом и найдите ее область определения. 6. (3б) Найти наибольшее и наименьшее значения функции:
7* Построить график функции . |
Контрольная работа по алгебре № 1.
Тема: «Тригонометрические функции».11 класс
Время выполнения – 45 минут (2мин – организационный момент, 43 мин – решение и оформление работы).
Данная контрольная работа содержит 7 заданий различной степени сложности:
4 задания – 57%-уровень обязательной подготовки (УОП)
2 задания – 29%-уровень возможностей (УВ)
1 задание – *14%- для одаренных детей.
Система оценивания:
-за каждое верно выполненные задания 1-4 ученик получает 1 балл;
— за верно выполненное задание 5 ученик получает 2 балла;
— за верно выполненное задание 6 ─ 3 балла.
Система выставления отметок представлена в таблице 1.
|
Отметка |
«3» |
«4» |
«5» |
|
Количество баллов |
4 балла |
6 баллов |
9 баллов |
|
За задание 7* выставляется отдельная отметка |
|||
Таблица1
gigabaza.ru

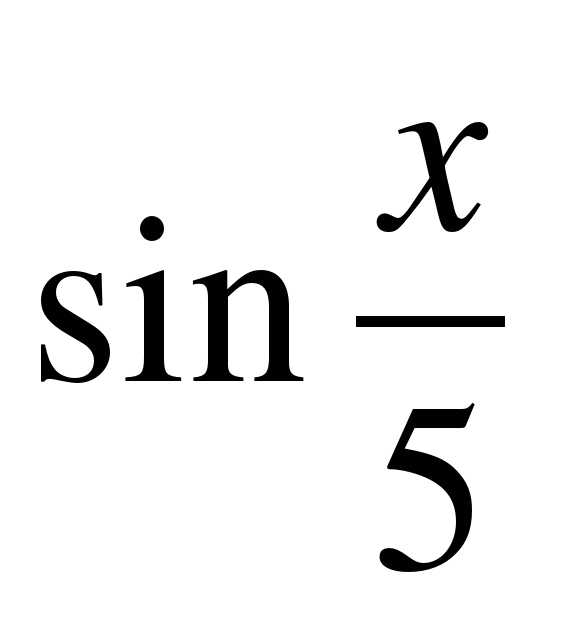 = — 1
= — 1