С решением система счисления – Система счисления троичная — таблица. Как перевести в троичную систему счисления

Онлайн калькулятор систем счисления с решением онлайн

Переведем целую часть 12 числа 12.3₁₀ в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

12	:	2	=	6	остаток: 0
6	:	2	=	3	остаток: 0
3	:	2	=	1	остаток: 1
1	:	2	=	0	остаток: 1

12₁₀ = 1100₂

Переведем дробную часть 0.3 числа 12.3₁₀ в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

0.3	·	2	=	0.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2

0.3₁₀ = 0.010011001100110011001100110011₂
12.3₁₀ = 1100.010011001100110011001100110011₂

matematika-club.ru

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:

0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 10³ + 4 * 10² + 7 * 10¹ + 6 * 10⁰

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 137₁₀

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹

 + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

inf1.info

основание, примеры и перевод в другие системы счисления

С того момента, как человек впервые осознал себя автономным объектом в мире, огляделся вокруг, прервав замкнутый круг бездумного выживания, он начал изучать. Смотрел, сравнивал, считал, делал выводы. Именно на этих, казалось бы, элементарных действиях, которые сейчас под силу и ребенку, начали основываться современные науки.

С чем работать будем?

Для начала необходимо определиться с тем, что вообще представляет собой система счисления. Это условный принцип записи чисел, их наглядное представление, которое упрощает процесс познания. Сами по себе числа не существуют (да простит нас Пифагор, который считал число основой мироздания). Это просто абстрактный объект, что имеет физическое обоснование лишь при вычислениях, своеобразное мерило. Цифры — объекты, из которых число составляется.

Начало

Первый осознанный счет носил самый примитивный характер. Теперь его принято называть непозиционной системой счисления. На практике она представляет собой число, в которых позиция составляющих его элементов неважна. Взять, к примеру, обыкновенные черточки, каждая из которых соответствует определенному объекту: три человека эквивалентны |||. Как ни крути, три черточки — это все те же три черточки. Если брать более близкие примеры, то древние новгородцы пользовались при счете славянским алфавитом. При необходимости выделения именно числа над буквой просто проставляли знак ~. Также буквенная система счисления была в почете у древних римлян, где числа – это опять же буквы, но принадлежащие уже латинскому алфавиту.

В силу обособленности древних держав, каждая из них развивала науку самостоятельно, кто во что горазд. Примечателен тот факт, что альтернативная десятичная система счисления была выведена еще египтянами. Однако «родственницей» привычного нам понятия считать ее нельзя, так как принцип счета отличался: жители Египта использовали число десять как основание, оперируя степенями.

С развитием и усложнением процесса познания мира появилась потребность выделения разрядов. Представим, что нужно как-то зафиксировать численность армии государства, которая измеряется тысячами (в лучшем случае). Что ж теперь, бесконечно выписывать палочки? Из-за этого шумерские ученые тех лет выделили систему счисления, в которой месторасположение символа было обусловлено его разрядом. Опять же, пример: числа 789 и 987 имеют один и тот же «состав», но, в силу смены расположения цифр, второе существенно больше.

Что это такое — десятичная система счисления? Обоснование

Конечно, позиционность и закономерность были не едиными для всех методов подсчета. Например, в Вавилоне базой выступало число 60, в Греции — алфавитная система (число составляли буквы). Примечательно то, что метод подсчета жителей Вавилона жив и по сей день — он нашел свое место в астрономии.

Однако прижилась и распространилась та, у которой основание системы счисления — десятка, так как прослеживается откровенная параллель с пальцами человеческих рук. Посудите сами — поочередно сгибая пальцы, можно досчитаться чуть ли не до бесконечного множества.

Начало этой системе было положено в Индии, причем она появилась сразу на базе «10». Формирование названий чисел было двояким – например, 18 можно было прописать словом и как «восемнадцать», и как «без двух двадцать». Также именно индийские ученые вывели такое понятие, как «ноль», официально его появление зафиксировано в IX веке. Именно этот шаг стал основополагающим в формировании классических позиционных систем счисления, потому что ноль, несмотря на то, что символизирует пустоту, ничто, способен поддержать разрядность числа, дабы оно не потеряло свой смысл. Например: 100000 и 1. Первое число включает в себя 6 цифр, первая из которых – единица, а пять последних обозначают пустоту, отсутствие, а второе число – просто единица. По логике, они должны быть равны, но на практике это далеко не так. Нули в 100000 обозначают присутствие тех разрядов, которых во втором числе нет. Вот вам и «ничто».

Современность

Десятичная система счисления состоит из цифр от нуля до девяти. Числа, составленные в её рамках, строятся по следующему принципу:

крайняя справа цифра обозначает единицы, сместитесь на один шаг влево – получите десятки, еще шаг влево – сотни и так далее. Сложно? Ничего подобного! На самом деле, десятичная система примеры может предоставить весьма наглядные, взять хотя бы число 666. Состоит из трех цифр 6, каждая из которых обозначает свой разряд. Причем эта форма записи является свернутой. Если вы хотите подчеркнуть, о каком именно числе идет речь, то его можно развернуть, придав письменную форму тому, что «проговаривает» ваш внутренний голос каждый раз, когда вы видите число – «шестьсот шестьдесят шесть». Само написание включает в себя все те же единицы, десятки и сотни, то есть каждая цифра позиции умножается на определенную степень числа 10. Развернутая форма представляет собой следующее выражение:

666₁₀ = 6х10² + 6*10¹ + 6*10⁰ = 600 + 60 + 6.

Актуальные альтернативы

Второй по популярности после десятичной системы счисления является достаточно молодая разновидность — двоичная (бинарная). Появилась она благодаря вездесущему Лейбницу, который считал, что в особо сложных случаях в исследовании теории чисел бинарность будет удобнее, нежели десятизначность. Свое повсеместное распространение она получила с развитием цифровых технологий, так как имеет в основании число 2, и элементы в ней составляются из цифр 1 и 2. Кодирование информации происходит в данной системе, так как 1 — наличие сигнала, 0 — его отсутствие. На основании этого принципа можно показать несколько наглядных примеров, демонстрирующих перевод в десятичную систему счисления.

С течением времени процессы, связанные с программированием, усложнялись, поэтому ввели способы записи чисел, у которых в основании лежат 8 и 16. Почему именно они? Во-первых, количество знаков больше, а значит, само число будет короче, во-вторых — в их основе лежит степень двойки. Восьмеричная система состоит из цифр 0-7, а шестнадцатеричная — из тех же цифр, что и десятичная, плюс буквы от A до F.

Принципы и методы перевода числа

Перевести в десятичную систему счисления просто, достаточно придерживаться следующего принципа: исходное число записывается как многочлен, который состоит из сумм произведений каждого числа на основу «2», возведенную в соответствующую разрядности степень.

Основная формула для вычисления:

_x2 = y_k2^k-1 + y_k-12^k-2 + y_k-22^k-3 + …+ y₂2¹ + y₁2⁰.

Примеры перевода

Для закрепления рассмотрим несколько выражений:

101111₂ = (1×2⁵) + (0x2⁴) + (1×2³) + (1×2²) + (1×2¹) + (1×2⁰) = 32 + 8 + 4 + 2 + 1 = 47₁₀.

Усложним задачу, ибо система включает в себя перевод и дробных чисел, для этого рассмотрим отдельно целую и отдельно дробную часть — 111110,11_2. Итак:

111110,11₂ = (1×2⁵) + (1×2⁴) + (1×2³) + (1×2²) + (1×2¹) + (0x2⁰) = 32 + 16 + 8 + 4 + 2 = 62₁₀;

11₂ = 2^-1x1 + 2^-2x1 = 1/2 + 1/4 = 0,75_10.

В итоге получаем, что 111110,11₂ = 62,75₁₀.

Вывод

Несмотря на всю «древность», десятичная система счисления, примеры которой мы рассмотрели выше, все еще «на коне», и списывать ее со счетов не стоит. Именно она становится математической основой в школе, на ее примере познаются законы математической логики, выводится умение строить выверенные взаимосвязи. Да что уж там — практически весь мир пользуется именно этой системой, не смущаясь ее неактуальностью. Причина для этого одна: она удобная. В принципе, вывести основу счета можно любую, ею при необходимости станет даже яблоко, но зачем усложнять? Идеально выверенное количество цифр при необходимости и по пальцам пересчитать можно.

fb.ru

Решение задач по теме «Системы счисления » с ответами

Задачи по теме «Системы счисления»

Примеры решения

Задание №1. 
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 3? 
Решение: 
Переведём число 35710 в троичную систему счисления: 
 
Итак, 35710 = 1110203. Число 1110203 содержит 6 значащих цифр. 
Ответ: 6.  

Задание №2. 
Дано А=A715, B=2518. Какое из чисел C, записанных в двоичной системе, отвечает условию A
1) 101011002 
2) 101010102 
3) 101010112 
4) 101010002 
Решение: 
Переведём числа А=A715 и B=2518 в двоичную систему счисления, заменив каждую цифру первого числа соответствующей тетрадой, а каждую цифру второго числа – соответствующей триадой: A715= 1010 01112; 2518 = 010 101 0012. 

Условию a

Задание №3. 
На какую цифру оканчивается запись десятичного числа 123 в системе счисления с основанием 6? 
Решение: 
Переведём число 12310 в систему счисления с основанием 6: 
 
12310 = 3236. 
Ответ: Запись числа 12310 в системе счисления с основанием 6 оканчивается на цифру 3. 
Задания на выполнение арифметических действий над числами, представленными в разных системах счисления 

Задание №4. 
Вычислите сумму чисел X и Y, если X=1101112, Y=1358. Результат представьте в двоичном виде. 
1) 100100112 2) 100101002 3) 110101002 4) 101001002 
Решение: 
Переведём число Y=1358 в двоичную систему счисления, заменив каждую его цифру соответствующей триадой: 001 011 1012. Выполним сложение: 
 
Ответ: 100101002 (вариант 2). 

Задание №5. 
Найдите среднее арифметическое чисел 2368, 6С16 и 1110102. Ответ представьте в десятичной системе счисления. 
Решение: 
Переведём числа 2368, 6С16 и 1110102 в десятичную систему счисления: 

 
Вычислим среднее арифметическое чисел: (158+108+58)/3 = 10810. 
Ответ: среднее арифметическое чисел 2368, 6С16 и 1110102 равно 10810. 

Задание №6. 
Вычислите значение выражения 2068 + AF16 ? 110010102. Вычисления производите в восьмеричной системе счисления. Переведите ответ в десятичную систему. 
Решение: 
Переведём все числа в восьмеричную систему счисления: 
2068 = 2068; AF16 = 2578; 110010102 = 3128 
Сложим числа: 
 
Переведём ответ в десятичную систему: 
 
Ответ:51110. 

Задания на нахождение основания системы счисления 

Задание №7. 
В саду 100q фруктовых деревьев: из них 33q яблони, 22q груши, 16q слив и 17q вишен. Найдите основание системы счисления, в которой посчитаны деревья. 
Решение: 
Всего в саду 100q деревьев: 100q = 33q+22q+16q+17q. 
Пронумеруем разряды и представим данные числа в развёрнутой форме: 

 
Ответ: Деревья посчитаны в системе счисления с основанием 9. 

Задание №8. 
Найдите основание x системы счисления, если известно, что 2002x = 13010. 
Решение: 
Пронумеруем разряды и запишем данные числа в развёрнутой форме: 
 
Ответ:4.

Задание №9. 
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание. 
Решение: 
Примем за х основание неизвестной системы счисления и составим следующее равенство: 
1810 = 30x; 
Пронумеруем разряды и запишем данные числа в развёрнутой форме: 
 
Ответ: десятичное число 18 записывается в виде 30 в системе счисления с основанием 6. 

infourok.ru

Перевод целых чисел из одной системы счисления в другую онлайн

См. также: перевод дробных чисел.

Число — это понятие в математике, испульзующееся для счёта предметов (объектов) и их количественного описания.

Цифры — это знаки, используемые для записи чисел.

Система счисления — способ записи чисел с помощью знаков (цифр). Нижний индекс у числа показывает, в какой системе счисления оно записано. Например, 765₈ — число записано в восьмеричной системе счисления.

Как перевести целое число из одной системы счисления в другую?

Сначала представляем число в десятичной системе счисления:

   

где — наше число в десятичной системе счисления, — основание исходной системы счисления, а — цифры числа в десятичной системе счисления, — первая цифра числа, а — последняя.

Далее, чтобы перевести число в некоторую систему счисления с основанием (цифры числа лежит в диапазоне ), иначе говоря, в -ичную систему счисления, следует представить его в виде:

   

где — цифры записи числа в системе счисления с основанием , причём — первая цифра числа, а — последняя.

Чтобы получить такое представление, будем делать так:

Находим остаток от деления числа на . Этот остаток равен последней цифре числа — . Затем находим целую часть от деления на . Пусть она равна . Находим остаток от деления на — это будет предпоследняя цифра числа . И так далее.

Рассмотрим алгортим перевода числа на примере.

Пример. Перевести число 111₁₀ в двоичную систему счисления.

Решение. Находим остаток от деления 111 на 2. 111 = 55 · 2 + 1 — остаток равен 1, следовательно, 1 — последняя цифра числа 111₁₀ в двоичном представлении.

Теперь рассматриваем число 55 — это целая часть от деления 111 на 2. 55 = 27 · 2 + 1, остаток равен 1, поэтому 1 — предпоследняя цифра. 111 = 27 · 2² + 1 · 2 + 1.

27 = 13 · 2 + 1, следующая цифра — 1.

13 = 6 · 2 + 1, следующая цифра — 1.

6 = 3 · 2 + 0, следующая цифра — 0.

3 = 1 · 2 + 1, следующая цифра — 1.

1 = 0 · 2 + 1, следующая цифра — 1. Окончательный результат —

Перевод чисел между системами счисления онлайн

Программа быстро переведёт число из одной системы счисления в другую онлайн. Она работает с числами до 20000000000000₁₆, записанными в системе счисления с основанием от 2 до 36. Основания систем счисления нужно записывать в десятичном представлении.

umath.ru

Система счисления троичная — таблица. Как перевести в троичную систему счисления

В информатике, кроме привычной нам десятичной системы счисления, существуют различные варианты целочисленных позиционных систем. Одной из таких является троичная.

Какие бывают системы счисления

В обычной жизни людьми применяется десятичная система счисления, включающая цифры от 0 до 9. В информатике принято использовать двоичную систему, включающую только 0 и 1. Однако это не мешает существовать и другим системам, вроде троичной, которая состоит из цифр 0,1 и 2. Она менее популярна, чем названные выше, однако понимание того, как переводить в троичную систему счисления, будет полезно изучающим информатику. В статье приведены простые примеры перевода.

Как переводить в троичную систему счисления из десятичной

Данный способ перевода весьма прост и схож с переводом в двоичную систему. Необходимо взять десятичное число, и поделить на основание системы (в троичной — число 3), пока в остатке не останется число меньше трёх. Затем все остатки записываются в обратном порядке.

Этот же способ подходит для большинства систем счисления. Сложности могут возникнуть с шестнадцатеричной системой, в которой числа от 10 до 15 обозначаются первыми буквами английского алфавита. Для простоты вычислений можно делить в столбик число. Это удобнее, чем запись в строчку, поскольку не даст запутаться и упустить значения.

Пример перевода

В качестве примера того, как переводить в троичную систему счисления, можно использовать число 100. Для начала запишите число и делите его на 3. Получается: 100/3=33(остаток 1)/3=11(остаток 0)/3=3(остаток 2)/3=1(остаток 0). Затем следует выписать все цифры:10201. Напишите число наоборот (от последней цифре к первой). В данном примере получится тоже самое число, однако может быть иное число, вроде 22102, которое запишется как 20122.

Перевод из троичной системы в десятичную

Как перевести троичную систему счисления в десятичную? Требуется владеть базовыми навыками сложения, умножения и возведения в степень числа. Для начала следует записать переводимое троичное число и над каждой цифрой написать сверху порядковый номер (начиная с последней, которая имеет цифру 0, до первой, в порядке возрастания на единицу).

Затем необходимо каждое число умножить на основание численной системы ( в данном случае — тройку), при этом цифра 3 будет возводиться в степень, равную порядковому номеру той цифры, на которую умножается. Все нули можно опустить (такое умножение не имеет смысла в данном случае), при этом над ними тоже следует записывать номер, чтобы не допустить путаницы. Затем все полученные значения складываются, и итоговое число будет ответом.

Пример перевода

Для примера того, как счисление чисел в троичной системе можно вернуть к десятичной, используем ранее названное число 20122. Для начала над каждой цифрой укажите её порядковый номер 2⁴ 0³ 1² 2¹ 2⁰. Затем каждое число следует умножить на основание троичной системы, которое возводится в степень по номеру числа: 2*3⁴+1*3²+2*3¹+2*3⁰. Полученные результаты суммируются (162+9+6+2). В результате будет число 179. При этом можно заметить, что цифра 0 была не записана. При желании её тоже можно учитывать, однако она даст лишь нулевой результат.

Как просто переводить числа из разных систем

Если такой способ подсчёта кажется слишком долгим, то всегда можно воспользоваться онлайн-калькуляторами. Большое число современных сервисов работает с троичной системой и многими другими. Вместе с этим можно посмотреть, как выполнялся перевод в троичную систему счисления и вспомнить, как правильно считать или проверить на ошибки.

При этом не следует забывать про учебные пособия. Необходимость перевода в разные системы счисления зачастую возникает у школьников и студентов, которые изучают информатику. Большая часть учебников имеет в своём содержании раздел со значениями перевода. Также для учащихся вузов существует множество справочников с огромным объемом данных, в том числе троичной системой счисления, правилами перевода и основными целыми значениями.

Что делать с дробными выражениями

Работать с подобными числами тоже возможно. Способ перевода схож с описанным ранее, однако необходимо учитывать отдельные детали. В процессе перевода дробное число также делится на 3, однако если полученный результат не целый, к примеру 1,236. В таком случае записывается лишь число перед запятой (даже 0 учитывается). Затем полученные числа записываются уже после запятой в новой системе счисления, к примеру 0,21022 в троичной системе.

Если само выражение имеет как целую, так и дробную часть, то стоит выполнять раздельные перевод. Для начала возьмите целую часть, и поделитесь её описанным способом, затем рассчитайте дробную часть, и напишите её после запятой.

Перевод отрицательных чисел

В случае с троичной системой счисления работать с отрицательными числами просто. При переводе отрицательного десятичного числа в троичное, знаки сохраняются.

Однако это правильно не действует на двоичную систему, где процедура будет более трудоёмкой. В связи с этим нельзя так просто перевести десятичное отрицательное число в двоичное, как в случае с троичной системой счисления.

Варианты троичной системы счисления

В отличие от прочих систем, троичная может быть несимметричной и симметричной. Во всех предыдущих вариантах была описана именно первая, несимметричная система. Отличия сильно заметны. В симметричной системе используются знаки (-;0+), (-1;0+1). Возможен вариант с верхним или нижним подчеркиванием ненулевого числа, для обозначения минуса. Этот вариант не так часто встречается в школьной программе, однако необходимо учитывать и его, ведь достаточно легко спутать с двоичной системой. Однако последняя не имеет знаков перед числом.

Также заслуживает внимание обозначение троичной системы буквами. Обычно это A,B,C, при этом указывается, какое число больше и меньше (A>B>C).

Таблица

Не лишним будет упомянуть основные значения перевода из десятичной системы в троичную. Хотя это достаточно просто, но на начальных этапах вычисления стоит проверять полученный результат, прежде чем браться за более серьезные расчеты. Троичная система счисления и таблица помогут понять, на чем основывается перевод разных систем.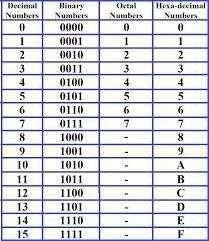

Из данной таблицы становится понятна логика, по которой формируются числа. Также её достаточно просто запомнить.

Существует несколько различных систем счислений. В повседневной жизни человеку приходится сталкиваться разве что с десятичной, однако стоит знать, что существует система счисления троичная. Она отличается от остальных наличием трех цифр и двумя вариантами записи (симметричный и несимметричный). Вместе с этим, в ней достаточно просто работать с отрицательными числами и дробными. Благодаря этому, данная система весьма проста в понимании. Симметричный вариант может напоминать двоичную систему, однако между ними имеется существенная разница. Она заключается в наличии знаков, по которым отличают положительное число от отрицательного. В двоичной системе их нет.

fb.ru