Решение логарифмических неравенств с подробным решением – 11 класс. Алгебра. Показательная и логарифмическая функции. Логарифмические уравнения и неравенства. — Решение логарифмических неравенств.

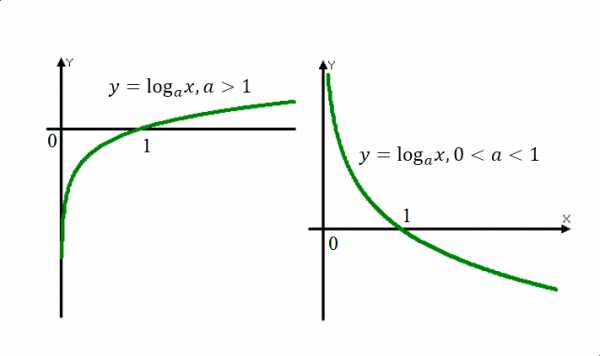
Логарифмические неравенства, примеры решений

Теория по логарифмическим неравенствам

Решение логарифмических неравенств основывается на свойстве монотонности логарифмической функции: функция монотонно возрастает, если , и монотонно убывает, если . При этом учитывается, что подлогарифмическое выражение может принимать только положительные значения. Таким образом, для неравенства вида

   

при потенцировании, для значений знак неравенства сохраняется; а для значений , меняется на противоположный.

В случае если переменная содержится и в основании, и в подлогарифмическом выражении, например , решение разбивается два случая, когда и, когда , то есть

   

Так же некоторые логарифмические неравенства можно решить методом замены переменной.

Примеры

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Логарифмические неравенства. Как решать логарифмические неравенства?

Если проще: это неравенства, в которых неизвестные (иксы) или выражения с ними находятся внутри логарифмов.

Примеры:

\(\log_3⁡x≥\log_3⁡9\)
\(\log_3⁡ {(x^2-3)}< \log_3⁡{(2x)}\)
\(\log_{x+1}⁡{(x^2+3x-7)}>2\)
\(\lg^2⁡{(x+1)}+10≤11 \lg⁡{(x+1)}\)

Как решать логарифмические неравенства:

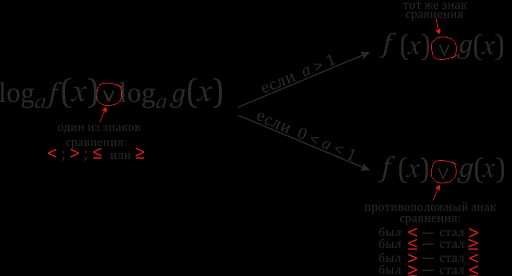
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a⁡{f(x)} ˅ \log_a{⁡g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).

Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.

Примеры:

\(\log_2⁡{(8-x)}<1\) ОДЗ: \(8-x>0\) \(-x>-8\) \(x<8\) Решение: \(\log\)\(_2\)\((8-x)<\log\)\(_2\)\({2}\) \(8-x\)\(<\)\(2\) \(8-2<x\) \(x>6\) Ответ: \((6;8)\)

\(\log\)\(_{0,5⁡}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)⁡\({(x+1)}\) ОДЗ: \(\begin{cases}2x-4>0\\x+1 > 0\end{cases}\) \(\begin{cases}2x>4\\x > -1\end{cases}\)   \(\Leftrightarrow\)   \(\begin{cases}x>2\\x > -1\end{cases}\)  \(\Leftrightarrow\)   \(x\in(2;\infty)\) Решение: \(2x-4\)\(≤\)\(x+1\) \(2x-x≤4+1\) \(x≤5\) Ответ: \((2;5]\)

Очень важно! В любом неравенстве переход от вида \(\log_a{⁡f(x)} ˅ \log_a⁡{g(x)}\) к сравнению выражений под логарифмами можно делать только если:

\(-\) вы написали ОДЗ для исходного неравенства. Напоминаю ОДЗ для логарифма \(\log_a⁡b\):

\(b>0\), \(a>0\), \(a≠1\).

\(-\) число в основании логарифмов слева и справа одинаково;

\(-\) логарифмы слева и справа — «чистые», то есть нет никаких коэффициентов, умножений, делений и т.д. – только одинокие логарифмы и слева, и справа;

Кстати, в конце (после решения) не забудьте пересечь решения неравенства с ОДЗ.

Например:

1) \(\log_3⁡{(x^2-3)}>\log_3⁡{(2x)}\) \(x^2-3>2x\) \(x^2-2x-3>0\) \(x∈(-∞;-1)∪(3;+∞)\)	Не написали ОДЗ и не пересекли с ним решение. Неравенство решено неверно.
2) \(\log_5⁡{(x-7)}≤\log_3{⁡4} \)	Основания логарифмов разные, переход к \(x-7≤4\) невозможен.
3) \(\log_6⁡{(x-2)}-\log_6⁡{x}<\log_6⁡{(2x)}\)	Логарифмы не «чистые», так как слева есть разность логарифмов. Переход к \((x-2)-x<2x\) невозможен.
4) \(\log_2⁡{(x^2-24)}≥-\log_2⁡x\)	Логарифмы не «чистые» т.к. справа есть минус перед логарифмом. Переход к \(x^2-24≥-x\) невозможен.

Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.

Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}⁡{\frac{3x-2}{2x-3}}\)\(≤-1\)

Решение:

\(\log\)\(_{\frac{1}{3}}⁡{\frac{3x-2}{2x-3}}\)\(≤-1\)		Выпишем ОДЗ.
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\)		ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами.
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\)		Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) Построим числовую ось и отметим на ней эти точки.
		Запишем ОДЗ в виде интервалов.
\(x∈(-∞;\)\(\frac{2}{3}\)\()∪(\)\(\frac{3}{2}\)\(;∞)\)		С ОДЗ закончили, переходим к решению.
Решение:  \(\log\)\(_{\frac{1}{3}}⁡{\frac{3x-2}{2x-3}}\)\(≤-1\)		Воспользовавшись свойствами логарифмов и свойствами степени, преобразуем правую часть: \(-1=-1 \cdot 1=-1 \cdot \log\) \(_\frac{1}{3} \frac{⁡1}{3}\)\(=\log\)\(_\frac{1}{3}⁡ {\frac{1}{3}}^{-1}\) \(=\log\) \(_\frac{1}{3}\) \(⁡3\).
\(\log\)\(_{\frac{1}{3}}⁡{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\)		Мы привели неравенство к виду \(\log_a⁡{f(x)} ˅ \log_a⁡{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем.
\(⁡\frac{3x-2}{2x-3}\)\(≥\) \(3\)		Переносим \(3\) и приводим к общему знаменателю, пользуясь свойствами дробей.
\(⁡\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\)		Раскрываем скобки, приводим подобные слагаемые.
\(⁡\frac{-3x+7}{2x-3}\)\(≥\) \(0\)		Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения.
\(⁡\frac{3x-7}{2x-3}\)\(≤\) \(0\)		Далее выносим \(3\) из числителя и \(2\) из знаменателя.
\(⁡\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\)		Построим числовую ось и отметим на ней точки \(\frac{7}{3}\) и \(\frac{3}{2}\). Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль.
\(x∈(\)\( \frac{3}{2}\)\(;\)\(\frac{7}{3}]\)		Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ.
		Записываем окончательный ответ.

Ответ:   \(x∈(\)\( \frac{3}{2}\)\(;\)\(\frac{7}{3}]\)

Пример. Решить неравенство: \(\log^2_3⁡x-\log_3⁡x-2>0\)

Решение:

\(\log^2_3⁡x-\log_3⁡x-2>0\)		Выпишем ОДЗ.
ОДЗ: \(x>0\)		Приступим к решению.
Решение: \(\log^2_3⁡x-\log_3⁡x-2>0\)		Перед нами типичное квадратно-логарифмическое неравенство. Делаем замену.
\(t=\log_3⁡x\) \(t^2-t-2>0\)		Раскладываем левую часть неравенства на множители.
\(D=1+8=9\) \(t_1= \frac{1+3}{2}=2\) \(t_2=\frac{1-3}{2}=-1\) \((t+1)(t-2)>0\)		Решаем неравенство методом интервалов.
		Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену.
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3⁡x>2 \\ \log_3⁡x<-1 \end{gathered} \right.\)		Преобразовываем \(2=\log_3⁡9\),    \(-1=\log_3⁡\frac{1}{3}\).
\(\left[ \begin{gathered} \log_3⁡x>\log_39 \\ \log_3⁡x<\log_3\frac{1}{3} \end{gathered} \right.\)		Делаем переход  к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется.
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\)		Соединим решение неравенства и ОДЗ на одном рисунке.
		Запишем ответ.

Ответ: \((0; \frac{1}{3})∪(9;∞)\)

Смотрите также:
Показательные неравенства

Скачать статью

cos-cos.ru

11 класс. Алгебра. Показательная и логарифмическая функции. Логарифмические уравнения и неравенства. — Решение логарифмических неравенств.

Комментарии преподавателя

Ре­ше­ние ло­га­риф­ми­че­ских нера­венств

Клю­чом к ре­ше­нию ло­га­риф­ми­че­ских нера­венств яв­ля­ют­ся свой­ства ло­га­риф­ми­че­ской функ­ции, т.е. функ­ции вида  (). Здесь t – неза­ви­си­мая пе­ре­мен­ная, а= кон­крет­ное число, у – за­ви­си­мая пе­ре­мен­ная, функ­ция.

Вспом­ним ос­нов­ные свой­ства ло­га­риф­ми­че­ской функ­ции.

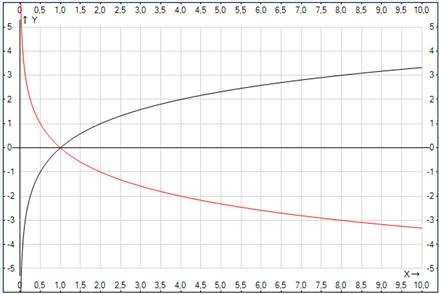
Рис. 1. Гра­фик ло­га­риф­ми­че­ской функ­ции при раз­лич­ных ос­но­ва­ни­ях

Функ­ция мо­но­тон­на на всей своей об­ла­сти опре­де­ле­ния. При  мо­но­тон­но воз­рас­та­ет, т.е. боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет боль­шее зна­че­ние функ­ции, . При  мо­но­тон­но убы­ва­ет, т.е. боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет мень­шее зна­че­ние функ­ции,, .

Имен­но мо­но­тон­ность ло­га­риф­ми­че­ской функ­ции поз­во­ля­ет ре­шать про­стей­шие ло­га­риф­ми­че­ские нера­вен­ства.

Рас­смот­рим ре­ше­ние ло­га­риф­ми­че­ско­го нера­вен­ства, когда ос­но­ва­ние ло­га­риф­ма .

То есть знак нера­вен­ства со­хра­ня­ет­ся.

При этом необ­хо­ди­мо не за­быть про ОДЗ, т.к. под ло­га­риф­мом могут сто­ять стро­го по­ло­жи­тель­ные вы­ра­же­ния. ОДЗ пред­став­ле­но си­сте­мой:

Ре­ше­ни­ем ис­ход­но­го нера­вен­ства яв­ля­ет­ся эк­ви­ва­лент­ное нера­вен­ство , по­это­му для со­блю­де­ния ОДЗ до­ста­точ­но за­щи­тить мень­шее из чисел по­лу­ча­ем си­сте­му нера­венств, ко­то­рая со­от­вет­ству­ет ис­ход­но­му нера­вен­ству:

 

При­мер 1 – ре­шить нера­вен­ство:

Со­глас­но ме­то­ди­ке ре­ше­ния про­стей­ших ло­га­риф­ми­че­ких нера­венств, пер­вым дей­стви­ем необ­хо­ди­мо урав­нять ос­но­ва­ния ло­га­риф­мов, в дан­ном слу­чае пред­ста­вить пра­вую часть в виде ло­га­риф­ма с тре­бу­е­мым ос­но­ва­ни­ем:

По­лу­ча­ем нера­вен­ство:

По­сколь­ку ос­но­ва­ние ло­га­риф­ма боль­ше еди­ни­цы, в эк­ви­ва­лент­ной си­сте­ме знак нера­вен­ства со­хра­нит­ся:

Пре­об­ра­зу­ем:

Ответ: 

При­мер 2 – ре­шить нера­вен­ство:

Учтем ОДЗ:

ОДЗ: 

Со­глас­но свой­ству ло­га­риф­ма пре­об­ра­зу­ем в левой части сумму ло­га­риф­мов с оди­на­ко­вым ос­но­ва­ни­ем в ло­га­рифм про­из­ве­де­ния:

Нам из­вест­но, что число Пи боль­ше еди­ни­цы (). По­это­му в эк­ви­ва­лент­ном нера­вен­стве знак ис­ход­но­го нера­вен­ства со­хра­ня­ет­ся:

Пре­об­ра­зу­ем по­лу­чен­ное нера­вен­ство:

Корни квад­рат­но­го урав­не­ния, сто­я­ще­го в левой части, со­глас­но тео­ре­ме Виета . Имеем па­ра­бо­лу, ветви ко­то­рой на­прав­ле­ны вверх. Ин­те­ре­су­ю­щие нас зна­че­ния на­хо­дят­ся между кор­ней урав­не­ния:

Ответ с уче­том ОДЗ:  

Све­де­ние к про­стей­ше­му ло­га­риф­ми­че­ско­му нера­вен­ству часто осу­ществ­ля­ет­ся с по­мо­щью за­ме­ны пе­ре­мен­ных.

 

При­мер 3 – ре­шить нера­вен­ство:

При­ве­дем вто­рой член к ос­но­ва­нию 5:

По­лу­чи­ли нера­вен­ство:

Оче­вид­на за­ме­на: 

Имеем:

Со­глас­но тео­ре­ме Виета корни квад­рат­но­го урав­не­ния, сто­я­ще­го в левой части: . Имеем па­ра­бо­лу, ветви ко­то­рой на­прав­ле­ны вверх. Ин­те­ре­су­ю­щие нас ре­ше­ния на­хо­дят­ся в ин­тер­ва­ле между кор­ня­ми.

Вер­нем­ся к ис­ход­ным пе­ре­мен­ным:

Пре­об­ра­зу­ем со­глас­но опре­де­ле­нию ло­га­риф­ма:

Ответ: 

 

При­мер 4 – ре­шить нера­вен­ство:

Учтем ОДЗ:

ОДЗ: 

Со­глас­но свой­ству ло­га­риф­ма пре­об­ра­зу­ем в левой части сумму ло­га­риф­мов с оди­на­ко­вым ос­но­ва­ни­ем в ло­га­рифм про­из­ве­де­ния:

Пре­об­ра­зу­ем пра­вую часть в ло­га­рифм с тре­бу­е­мым ос­но­ва­ни­ем:

Имеем нера­вен­ство:

Ос­но­ва­ние ло­га­риф­ма боль­ше еди­ни­цы, по­лу­ча­ем эк­ви­ва­лент­ное нера­вен­ство с тем же зна­ком:

Пре­об­ра­зу­ем:

www.kursoteka.ru

Логарифмические уравнения и неравенства

Автор Сергей

Суббота, Февраль 18, 2012

Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.

Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.

Логарифмическая функция

Определение

Функцию вида

   

называют логарифмической функцией.

Основные свойства

Основные свойства логарифмической функции y = log_a x:

	a > 1	0 < a < 1
Область определения	D(f) = (0; +∞)	D(f) = (0; +∞)
Область значений	E(f) = (-∞; +∞)	E(f) = (-∞; +∞)
Монотонность	Возрастает на (0; +∞)	Убывает на (0; +∞)
Непрерывность	Непрерывная	Непрерывная
Выпуклость	Выпукла вверх	Выпукла вниз

График логарифмической функции

Графиком логарифмической функции является логарифмическая кривая:

Свойства логарифмов

• Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

   

• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:

   

• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:

   

•  Равенство log 

a t = log _a s, где a > 0, a ≠ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):

   

yourtutor.info

Решение простейших логарифмических неравенств – Сайт Александра Бабаева

Теория.

Для начала рекомендуется ознакомится со статьёй “Логарифм и его свойства“, описывающей теорию про логарифмы, и статьёй “Решение простейших логарифмических уравнений“, описывающей методы решения логарифмических уравнений.

Неравенство называется логарифмическим, если в нём содержится логарифмическая функция.

Методы решения логарифмических неравенств не отличаются от методов решений логарифмических уравнений, за исключением двух вещей.

Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства. Он подчиняется следующему правилу.

Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству подлогарифмических функций знак неравенства сохраняется, а если же меньше $1$, то меняется на противоположный.

Во-вторых, решение любого неравенства – промежуток, а, значит, в конце решения неравенства подлогарифмических функций необходимо составить систему из двух неравенств: первым неравенством этой системы будет неравенство подлогарифмических функций, а вторым – промежуток области определения логарифмических функций, входящих в логарифмическое неравенство.

Практика.

Решим неравенства:

1. $\log_{2}{(x+3)} \geq 3.$

Для начала найдём область определения:

$D(y): \ x+3>0.$

$\ x>-3$

$x \in (-3;+\infty)$

Основание логарифма равно $2>1$, поэтому знак не меняется. Пользуясь определением логарифма, получим:

$x+3 \geq 2^{3},$

$x+3 \geq 8,$

$x \geq 5,$

$x \in [5; + \infty).$

Соединяя полученное решение с областью определения, получим:Ответ: $x \in [5; +\infty)$.

2.  $\log_{\frac{1}{3}}{(x-2)} > -2.$

Для начала найдём область определения:

$D(y): \ x-2>0.$

$\ x>2$

$x \in (2;+\infty)$

Основание равно $\frac{1}{3}<1$, а, значит, знак неравенства меняется на противоположный. Получаем:

$x-2<\left(\frac{1}{3}\right)^{-2},$

$x-2<9,$

$x<11,$

$x \in (- \infty; 11).$

Соединяя полученное решение с областью определения, получим:

Ответ: $x \in (2; 11).$

Разберём теперь более сложный пример из задания C1 экзамена.

3. $\log_{3}{(2x+1)} \geq \log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}$.

Для начала найдём область определения:

$D(y): \ 2x+1>0, \ \frac{1}{7-x}>0, \ 7-x \neq 0,$

$2x+1>0, \ 7-x>0, \ 7-x \neq 0,$

таким образом, третье неравенство излишне (второе уже не допускает равенства!) , получим:

$x>-0,5, \ x<7,$

$x \in (-0,5;7).$

Преобразуем логарифм, стоящий в правой части, используя пятое и шестое свойство из статьи “Логарифм и его свойства“.

$\log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}=\frac{1}{-1}\log_{3}{\left(\frac{1}{7-x}\right)}=-\log_{3}{\left(\frac{1}{7-x}\right)}=\log_{3}{\left(\frac{1}{7-x}\right)^{-1}}=$

$=\log_{3}{(7-x)}.$

Таким образом, получено следующее неравенство:

$\log_{3}{(2x+1)} \geq \log_{3}{(7-x)}$.

Основание равно $3>1$, а, значит, знак неравенства не меняется. Получаем:

$2x+1 \geq 7-x,$

$3x \geq 6,$

$x \geq 2,$

$x \in [2; +\infty).$

Соединяя полученное решение с областью определения, получаем ответ.

Ответ: $x \in [2; 7).$

babaev-an.ru

Логарифмические неравенства

\(\blacktriangleright\) На ОДЗ верны следующие формулы:

\[\large{\begin{array}{|lcl|} \hline \log_a1=0& \qquad & \log_aa=1\\ &&\\ \log_{a^n}{b^m}=\frac mn\log_{|a|}{|b|}&& a^{\log_bc}=c^{\log_ba}\\ &&\\ \log_a{bc}=\log_a{|b|}+\log_a{|c|}&& \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\\ &&\\ \log_ab\cdot \log_bc=\log_ac & \Longleftrightarrow & \log_bc=\dfrac{\log_ac}{\log_ab}\\ &&\\ \log_ab\cdot \log_ba=1 & \Longleftrightarrow & \log_ab=\dfrac1{\log_ba}\\ &&\\ \hline \end{array}}\]

\(\blacktriangleright\) Стандартное логарифмическое неравенство \[{\Large{\log_a{h(x)}\geqslant \log_a{g(x)} \quad (*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\ >,\ <\))

 

Логарифмическая функция \(f(x)=\log_ax\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех положительных \(x\) (то есть ее область определения \(x\in (0;+\infty)\)).

 

На графике приведен пример возрастающей логарифмической функции \(f_1(x)=\log_2x\) и убывающей логарифмической функции \(f_2(x)=\log_{\,0,5}x\).

 

Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).

 

Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).

 

Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:

 

если \({\large{a>1}}\), то данное неравенство равносильно системе (не забываем про ОДЗ!) \[{\Large{\begin{cases} h(x)\geqslant g(x)\\ g(x)>0 \end{cases}}}\] Заметим, что условие \(h(x)>0\) учитывается автоматически в такой системе, т.к. если \(h\geqslant g\), а \(g>0\), то и \(h>0\).

 

если \({\large{0<a<1}}\), то данное неравенство равносильно системе \[{\Large{\begin{cases} h(x)\leqslant g(x)\\ h(x)>0 \end{cases}}}\]
Заметим, что условие \(g(x)>0\) учитывается автоматически в такой системе.

 

\(\blacktriangleright\) Напомним, что область значений логарифмической функции — все числа, т.е. \(\log_ax\in \mathbb{R}\) при всех возможных \(a\) и \(x\).

 

\(\blacktriangleright\) С помощью формулы \({\Large {b=\log_a{a^b}}}\) можно любое число \(b\) представить в виде логарифма по необходимому основанию \(a>0,\ a\ne 1\).

 

Пример 1. Решить неравенство \(\log_2 {(x^2+7)}>4\)

 

Представим по формуле \(4=\log_2{2^4}=\log_2{16}\), тогда неравенство примет вид \[\log_2{(x^2+7)}>\log_2 {16} \Leftrightarrow \begin{cases} x^2+7>16\\ x^2+7>0 \end{cases}\] (знак неравенства не сменится, т.к. основание логарифмов \(2>1\)).

Второе неравенство \(x^2+7>0\) (это и есть ОДЗ) выполнено при всех \(x\).
Первое неравенство системы равносильно \(x^2-9>0 \Leftrightarrow (x-3)(x+3)>0 \Rightarrow x\in (-\infty;-3)\cup(3;+\infty)\).

 

Таким образом, после пересечения решений обоих неравенств системы решением исходного неравенства будут \(x\in (-\infty;-3)\cup(3;+\infty)\).

 

\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{\log_{h(x)}{f(x)}\geqslant \log_{h(x)}{g(x)}}}\] (на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\ >,\ <\))
То есть когда в основании логарифма находится не конкретное число, а функция, зависящая от \(x\).

 

Данное неравенство равносильно совокупности: \[{\Large{\left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x)\\ g(x)>0 \end{cases}\\[4pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x)\\ f(x)>0 \end{cases} \end{aligned} \end{gathered} \right.}}\]

Иногда удобно выписать ОДЗ отдельно. Тогда неравенство будет равносильно системе: \[{\Large{\begin{cases} f(x)>0 \quad (\textbf{ОДЗ})\\ g(x)>0 \quad (\textbf{ОДЗ})\\[3pt] \left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x) \end{cases}\\[3pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x) \end{cases} \end{aligned} \end{gathered} \right. \end{cases}}}\]

Пример 2. Решить неравенство \(\log_x{(3x-1)}>1\)

 

Данное неравенство равносильно:

\(\log_x{(3x-1)}>\log_xx \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &\begin{cases} x>1\\ 3x-1> x\\ x>0 \end{cases}\\ &\begin{cases} 0<x<1\\ 3x-1< x\\ 3x-1>0 \end{cases} \end{aligned} \end{gathered} \right. \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &x>1\\ &\dfrac13<x<\dfrac12 \end{aligned} \end{gathered} \right. \ \Leftrightarrow \quad x\in \left(\dfrac13;\dfrac12\right)\cup\Big(1;+\infty\Big)\)

 

Пример 3. Решить неравенство \(\log_{x^2}{(x+1)^2}\leq 1\)

 

Выпишем ОДЗ для аргумента логарифма: \((x+1)^2>0 \Rightarrow x\ne -1\).
Для основания логарифма ОДЗ отдельно выписывать не имеет смысла, т.к. мы будем учитывать его в самом решении: рассматривать случаи, когда основание больше \(1\) и когда оно находится между \(0\) и \(1\).

 

Таким образом, на ОДЗ неравенство равносильно совокупности (учитывая, что \(1=\log_{x^2}{x^2}\)) \[\left[ \begin{gathered} \begin{aligned} &\begin{cases} x^2>1\\ (x+1)^2\leqslant x^2 \end{cases}\\[2pt] &\begin{cases} 0<x^2<1\\ (x+1)^2\geqslant x^2 \end{cases} \end{aligned} \end{gathered} \right. \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} x^2-1>0\\ (x+1)^2-x^2\leqslant 0 \end{cases}\\[2pt] &\begin{cases} x^2<1\\ x^2>0\\ (x+1)^2- x^2\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right.\quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} (x-1)(x+1)>0\\ (x+1-x)(x+1+x)\leqslant 0 \end{cases}\\[2pt] &\begin{cases} (x-1)(x+1)<0\\ x\ne 0\\ (x+1-x)(x+1+x)\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right.\quad \Leftrightarrow \quad\]
\[\quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} x\in (-\infty;-1)\cup(1;+\infty)\\ x\in (-\infty;-\dfrac12\big] \end{cases}\\[2pt] &\begin{cases} x\in (-1;1)\\ x\ne 0\\ x\in\big[-\dfrac12;+\infty) \end{cases} \end{aligned} \end{gathered} \right. \quad \Leftrightarrow \quad x\in \Big(-\infty;-1\Big)\cup\Big[-\dfrac12;0\Big)\cup\Big(0;1\Big)\]

Пересекая данный ответ с ОДЗ (\(x\ne -1\)), получим тот же ответ.

 

\(\blacktriangleright\) Таким образом, как правило, для того, чтобы система (совокупность) не выглядела слишком огромной, удобно записывать ОДЗ неравенства отдельно, а затем просто пересекать решение системы (совокупности) с этим ОДЗ. Что мы и сделали в примере \(3\).

shkolkovo.net

Решение логарифмических неравенств. Поурочные планы

Дополнительные сочинения

В данном уроке мы рассмотрим решение более сложных логарифмических неравенств, покажем, каким образом оно сводится к решению простейших логарифмических неравенств.

Тема: Показательная и логарифмическая функция

Урок: Решение логарифмических неравенств

1. Введение

Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т. е. функции вида (). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.

2. Основные опорные факты

Вспомним основные свойства логарифмической функции.

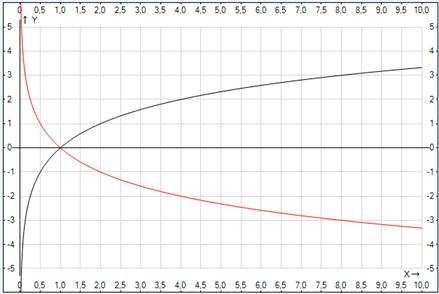
Рис. 1. График логарифмической функции при различных основаниях

Функция монотонна на всей своей области определения. При монотонно возрастает, т. е. большему значению аргумента соответствует большее значение функции, . При монотонно убывает, т. е. большему значению аргумента соответствует меньшее значение функции,, .

Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.

3. Решение простейшего логарифмического неравенства

Рассмотрим решение логарифмического неравенства, когда основание логарифма .

То есть знак неравенства сохраняется.

При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:

Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел получаем систему неравенств, которая соответствует исходному неравенству:

4. Решение более сложных логарифмических неравенств

Пример 1 – решить неравенство:

Согласно методике решения простейших логарифмичеких неравенств, первым действием необходимо уравнять основания логарифмов, в данном случае представить правую часть в виде логарифма с требуемым основанием:

Получаем неравенство:

Поскольку основание логарифма больше единицы, в эквивалентной системе знак неравенства сохранится:

Преобразуем:

Ответ:

Пример 2 – решить неравенство:

Учтем ОДЗ:

ОДЗ:

Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:

Нам известно, что число Пи больше единицы (). Поэтому в эквивалентном неравенстве знак исходного неравенства сохраняется:

Преобразуем полученное неравенство:

Корни квадратного уравнения, стоящего в левой части, согласно теореме Виета . Имеем параболу, ветви которой направлены вверх. Интересующие нас значения находятся между корней уравнения:

Ответ с учетом ОДЗ:

Сведение к простейшему логарифмическому неравенству часто осуществляется с помощью замены переменных.

Пример 3 – решить неравенство:

Приведем второй член к основанию 5:

Получили неравенство:

Очевидна замена:

       

Имеем:

Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: . Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями.

Вернемся к исходным переменным:

Преобразуем согласно определению логарифма:

Ответ:

Пример 4 – решить неравенство:

Учтем ОДЗ:

ОДЗ:

Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:

Преобразуем правую часть в логарифм с требуемым основанием:

Имеем неравенство:

Основание логарифма больше единицы, получаем эквивалентное неравенство с тем же знаком:

Преобразуем:

Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: . Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями:

Ответ с учетом ОДЗ:

Итак, мы рассмотрели решение различных типовых логарифмических неравенств. Далее мы перейдем к решению более сложных логарифмических неравенств.

Список рекомендованной литературы.

1. Мордкович А. Г. Алгебра и начала математического анализа. М.: Мнемозина

2. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. М.: Дрофа.

3. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. М.: Просвещение.

Рекомендованные ссылки на ресурсы Интернет

1. Webmath. ru .

2. Математика .

3. Tutoronline .

Рекомендованное домашнее задание

1. Алгебра и начала анализа, 10—11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, №526-528;

2. Решить неравенство:

а) ;

б) ;

в) ;

г) ;

3. Решить неравенство:

а) ;

б) ;

в) ;

г) ;

dp-adilet.kz