Разница сочетания и размещения – Чем отличается сочетание от размещения

Чем отличается сочетание от размещения

Б. Паскаль  и  Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.

Определение

Сочетания — соединения, каждое из которых составлено из  k1 элементов, выбранных из n1 различных элементов, состав которых  отличается  хотя бы на один элемент.

Размещения — cоединения, каждое из которых составлено из  k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.

к содержанию ↑

Сравнение

Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов.  Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.

Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.

Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами  1, 4 и 6. Это и есть сочетание.

Размещениями называют соединения, каждое из которых содержит k1  элементов, взятых из n1    различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.

Размещения отличают друг от друга состав элементов или их порядок.  Из n1 элементов по к1 (к1 < n1). По-другому, из n1 элементов выбирают к1 элементов и размещают их на А позиций. Число размещений из n1 элементов по к1 обозначают символом Ак1n1 (читается: А из n1 по к1).

При этом две расстановки будут считаться разными, если у них есть отличие друг от друга хотя бы на один элемент. Или они состоят из одних и тех же предметов, но они расположены в разном порядке. Например, есть три элемента, размещаем их в определенном порядке: 15, 11, 12 или 11, 12, 15 или 12, 15,11. Это и есть размещение — различные комбинации с одними и теми же элементами. Число размещений больше числа сочетаний.

к содержанию ↑

Выводы TheDifference.ru

1. Сочетания отличаются от размещений только тем, что они не зависят от порядка следования элементов.

thedifference.ru

Перестановки, сочетания, размещения Основные определения и обозначения

Различные упорядоченные множества, которые отличаются лишь порядком элементов (т.е. могут быть получены из того же самого множества), называются перестановками этого множества. Число различных перестановок 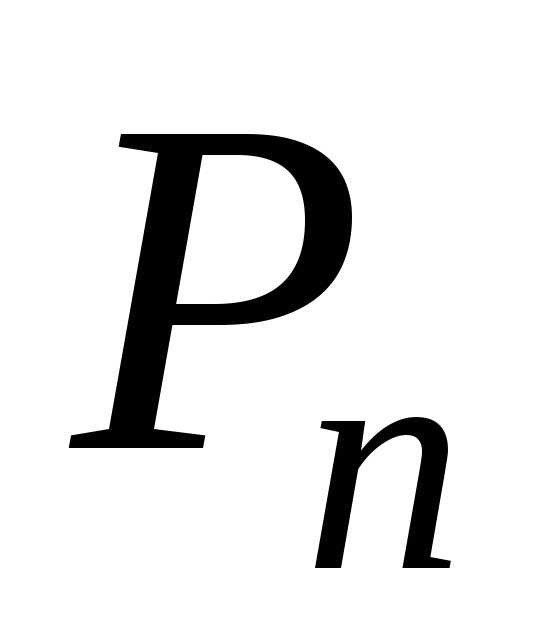изn элементов равно

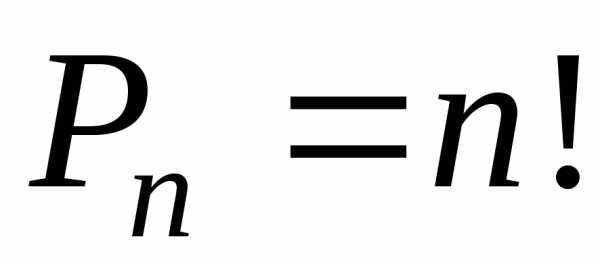
Произвольное k – элементное подмножество n – элементного множества называется сочетанием из n элементов по k.

Число сочетаний 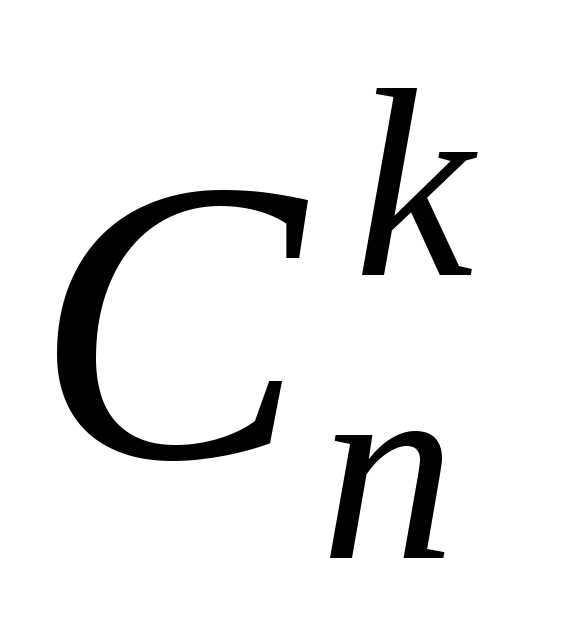изn элементов по k равно

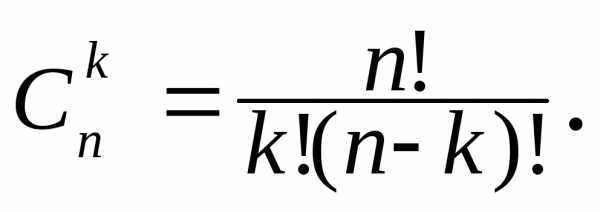
Упорядоченные k – элементные подмножества из n элементов называются размещением из n элементов по k.

Число размещений 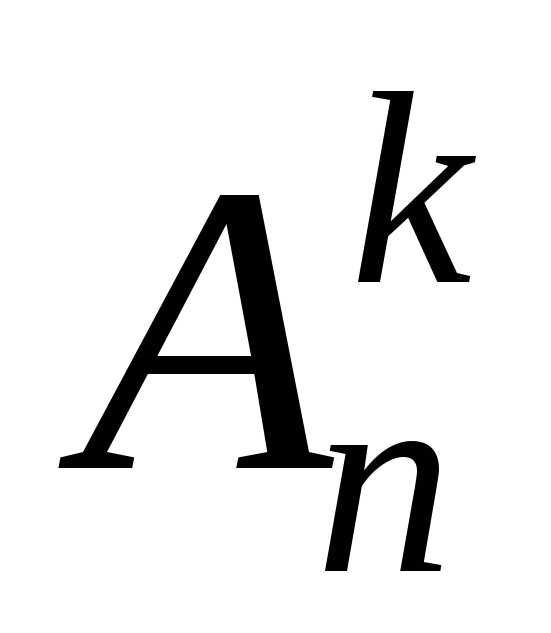изn элементов по k равно

Методические указания к решению задач

Применяя формулы числа перестановок, сочетаний и размещений, следует исходить из определений этих понятий.

Пример 7. Задано множество .

1. Составить всевозможные перестановки этого множества.

2. Всевозможные сочетания по два элемента.

3. Всевозможные размещения по два элемента.

Решение:

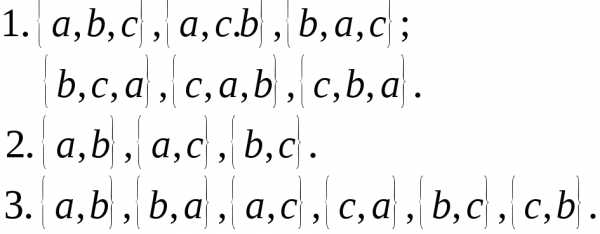
Пример 8. Сколько существует способов выбора из 7 человек комиссии, состоящей из 3 человек?

Решение. Число возможных составов комиссии равно числу всевозможных трехэлементных подмножеств множества, состоящего из 7 человек, т.е.

Пример 9. Сколькими способами можно разместить на полке 4 книги?

Решение. Искомое число способов равно числу способов упорядочения множества, состоящего из 4 элементов, т.е.

Пример 10. В студенческой группе 25 человек. Надо выбрать старосту группы, академорга и профорга. Сколькими способами может быть сделан выбор, если каждый член группы может занимать только один пост?

Решение. В данном примере из множества в 25 элементов нужно выбрать 3 элемента, но среди выбранных 3 элементов имеет значение порядок, так как здесь играет роль то, кто какой пост займет.

Например, выбор:

староста – Иванова, академорг – Алексеева, профорг – Петров отличается от выбора:

староста – Алексеева, академорг – Иванова, профорг – Петров.

Следовательно, число различных способов выбора равно числу размещений из 25 элементов по 3,

Пример 11. На профсоюзном собрании присутствует 50 человек. Необходимо выбрать делегацию из 5 человек на профсоюзную конференцию. Сколькими способами это можно сделать?

Решение. В данном примере из множества в 50 элементов нужно выбрать подмножество из 5, порядок которых не играет роли. Поэтому число способов выбора делегации равно

Пример 12. Сколькими способами можно упорядочить множество так, чтобы каждое четное число имело четный номер?

Решение. Здесь можно рассматривать 2 объекта: четные и нечетные числа.

Мест с четными номерами n. Таким образом, четные числа можно расставить n! способами. Общее число искомых перестановок по правилу умножения равно

3. Перестановки и сочетания с повторениями Основные определения и обозначения

До сих пор мы рассматривали предметы, которые были попарно различны. А теперь рассмотрим совокупности, в которых имеются одинаковые предметы.

Пусть имеются предметы k различных типов, число предметов первого типа равно 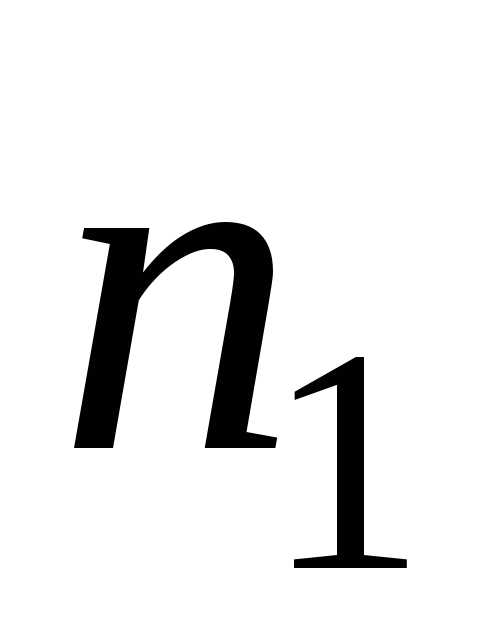, второго типа —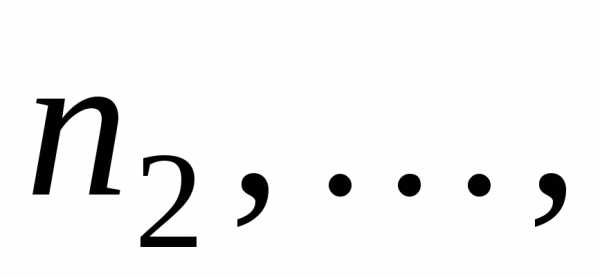k—го типа —

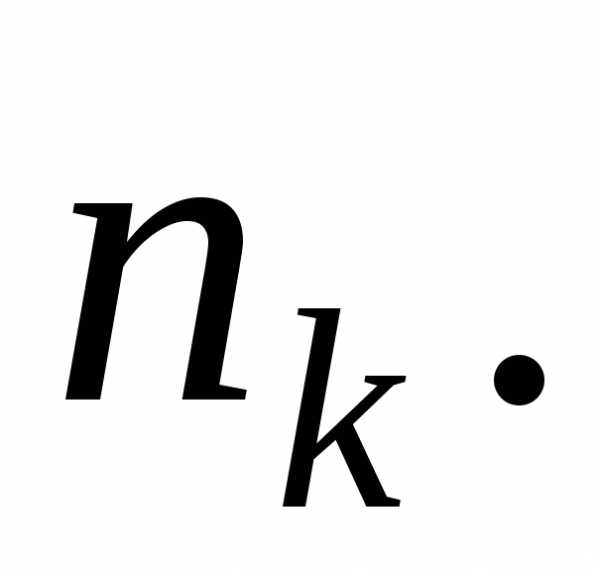
Число различных перестановок, которые можно сделать из даных элементов, равно

Число m – элементарных подмножеств, порядок в которых не принимается во внимание, равно

studfiles.net

Чем отличается сочетание от размещения |

Б. Паскаль и Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.

Сочетания — соединения, каждое из которых составлено из k1 элементов, выбранных из n1 различных элементов, состав которых отличается хотя бы на один элемент.

Размещения — cоединения, каждое из которых составлено из k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.

Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов. Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.

Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.

Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами 1, 4 и 6. Это и есть сочетание.

Размещениями называют соединения, каждое из которых содержит k1 элементов, взятых из n1 различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.

Размещения отличают друг от друга состав элементов или их порядок. Из n1 элементов по к1 (к1

При этом две расстановки будут считаться разными, если у них есть отличие друг от друга хотя бы на один элемент. Или они состоят из одних и тех же предметов, но они расположены в разном порядке. Например, есть три элемента, размещаем их в определенном порядке: 15, 11, 12 или 11, 12, 15 или 12, 15,11. Это и есть размещение — различные комбинации с одними и теми же элементами. Число размещений больше числа сочетаний.

1. Сочетания отличаются от размещений только тем, что они не зависят от порядка следования элементов.

charmsoflife.ru

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра

     При решении задач по комбинаторике используют следующие важные понятия

Размещения

      Рассмотрим следующую задачу.

      Задача.   9   карточек пронумерованы числами   1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .   Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

      Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

      На первое место можно положить одну из   9   карточек. Для этого есть   9   способов. В каждом из этих   9   способов на второе место можно положить одну из оставшихся   8   карточек. Таким образом, существует

способа, чтобы положить карточки на первое и второе места. В каждом из этих   72   способов на третье место можно положить одну из оставшихся   7   карточек. Следовательно, существует

способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих   504   способов на четвертое место можно положить одну из оставшихся   6   карточек. Отсюда вытекает, что существует

различных способа, чтобы выложить в ряд   4   карточки из набора, состоящего из   9   пронумерованных карточек. Таким образом, при выкладывании карточек можно получить   3024   различных четырехзначных числа.

      Ответ:   3024.

      При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

      Определение 1. Рассмотрим множество, содержащее   n   элементов, и все его упорядоченные подмножества, содержащие   k   элементов. Каждое из этих подмножеств называют размещением из   n   элементов по   k   элементов.

      Если обозначить символом  число размещений из   n   элементов по   k   элементов, то будет справедлива формула:

(1)

      В соответствии с определением факториала, формулу (1) можно также записать в виде:

      В задаче множеством из   n   элементов является исходный набор из   9   пронумерованных карточек, а упорядоченным подмножеством из   k   элементов –   4   карточки, выложенные в ряд.

      Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из   9   элементов по   4   элемента, т.е. число

      В соответствии с формулой (1),

что и было получено в задаче.

      Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

      Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

смысл которой заключается в следующем.

      Утверждение. Размещение из   n   элементов по   n   элементов является перестановкой из   n   элементов.

Сочетания

      Определение 2. Рассмотрим множество, состоящее из   n   элементов. Каждое его подмножество, содержащее   k   элементов, называют сочетанием из   n   элементов по   k   элементов.

      Число сочетаний из   n   элементов по   k   элементов обозначается символом

      Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие   k   элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем   k   элементов (из определения 2), совершить всевозможные перестановки, количество которых равно   k ! ,   то мы получим все размещения.

      Таким образом, справедлива формула:

      Следовательно,

откуда вытекает формула

(2)

      Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

      В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):

      Замечание 4. С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.

   С понятиями факториала числа   n   и перестановок из   n   элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.

 

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

перестановки, сочетания, размещения, правило умножения и сложения — Мегаобучалка

Классификация событий. Классическое определение вероятности.

Опытом или испытанием назыв. всякое осуществление опр. комплекса условий или действий при которых происходит соотв. явление. возможный результат опыта называется событием (А, В, С). Событие называется достоверным в данном опыте, если оно обязательно произойдет в этом опыте (Е). Событие называется невозможным в данном опыте, если оно не может произойти в этом опыте (О). Событие называется случайным в данном опыте если оно может произойти или не произойти в данном опыте. Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого в этом опыте. Два события называются несовместными если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными если они попарно несовместны. Множество событий А1, А2, …, Аn называются полной группой событий, если они попарно несовместны, появление одного и только одного из них является достоверным событием. Два события называются противоположными, если появление одного из них равносильно не появлению другого ( ).События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие. Каждое событие, которое может наступить в результате опыта называется элементарным исходом (элементарным событием). Элементарные исходы, при которых данное событие наступает называется благоприятствующим этому событию.

2. Вероятностью события А называется отношение числа элементарных исходов благоприятствующих данному событию к числу всех равновозможных образующих полную группу элементарных исходов опыта, в котором может появиться это событие. Обозначается как Р( А).

, где m – число элементарных исходов благоприятствующих событию А; n – число всех равновозможных элементарных исходов опыта, в котором может появиться событие А. Св-ва вероятности события: 1. вероятность достоверного события равна 1, т.е. Р (Е) = 1; 2. вероятность невозможного события равна 0, т.е. Р (Е) = 0; вероятность любого события удовл-ет неравенству 0 ≤ Р

Элементы комбинаторики: перестановки, сочетания, размещения, правило умножения и сложения.

Комбинаторикой называется раздел математики, изучающий вопрос о том сколько комбинаций определенного типа можно составить из данных предметов (элементов). Множество элементов, состоящее из одних и тех же различных элементов и отличающиеся друг от друга только их порядком называется перестановками этих элементов.

Число возможных перестановок из n-элементов вычисляется по ф-ле: Рn = n!, где n !- произведение первых натуральных чисел, n! = 1*2*3*…*n. По определению 0!=1.

Размещениями называются множества, составленные из n различных элементов по m-элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений:

Сочетаниями из n-различных элементов по m-элементов называются мн-ва, содержащие m-элементов из числа n-заданных и которые отличаются хотя бы одним элементом.

Число сочетаний из n-элементов по m: . Разница между сочетаниями и размещениями: в сочетании не учитывается порядок элементов. Замечание: выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляются по другим формулам. При решении задач комбинаторики используют следующие правила: правила суммы; если некоторый объект А может быть выбран из мн-ва объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами; правило произведения: если объект А можно выбрать из мн-ва объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов АВ в указанном порядке может быть выбрана m*n способами.

 

 

megaobuchalka.ru

Перестановки, размещения, сочетания

Характерная примета в задачах из области комбинаторики – вопрос в них обычно можно сформулировать так, чтобы он начинался со слов: «Сколькими способами…».

Первые задачи такого типа встречались уже, например, в древней и средневековой Индии.

«О друг, назови число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов» (Махавира, IX в.). Условие этой задачи, возможно, не очень понятно; судя по решению, здесь речь идет об ожерельях, которые бы отличались не по количеству или расположению камней одного и того же типа, а по наличию тех или иных камней – например, ожерелье из бриллиантов, из бриллиантов и кораллов, из бриллиантов, изумрудов и жемчугов и т. д.

Решение

Конечно, эту задачу можно решить простым перебором вариантов, но можно кое-что заметить. В разных ожерельях камни каждого конкретного вида могут наличествовать либо отсутствовать. Например, бриллианты могут быть, а могут не быть – две возможности. Как при наличии бриллиантов, так и при их отсутствии сапфиры могут быть, а могут или не быть – итого четыре возможности. И при наличии, и при отсутствии бриллиантов и сапфиров изумруды могут быть, а могут не быть, – итого восемь возможностей. И т. д. Следовательно, всего вариантов 25 = 32, правда, нужно еще вычесть один вариант отсутствия всех пяти камней (такое ожерелье, с точки зрения здравого смысла, ожерельем не является). Итак, ответ в задаче – 31 возможное ожерелье. БСИКЖ БСИК БСИЖ БСИ БСКЖ БСК БСЖ БС БИКЖ БИК БИЖ БИ БКЖ БК БЖ Б СИКЖ СИК СИЖ СИ СКЖ СК СЖ С ИКЖ ИК ИЖ И КЖ К Ж –

«Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи, каково число всех разновидностей» (Шридхара, IX–X вв.).

Решение

Аналогично решению предыдущей задачи получаем 26 – 1 = 64 – 1 = 63.

Классическими понятиями комбинаторики являются перестановки, размещения и сочетания.

Перестановкой называется какой-либо способ упорядочения данного множества. Чтобы найти число всех перестановок множества из n предметов (это число обозначается P_n, от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом. Первым можно поставить любой из n предметов, вторым – любой из (n – 1) оставшихся предметов, третьим любой из (n – 2) оставшихся предметов и т. д. В результате число перестановок будет равно произведению n множителей n (n – 1) (n – 2) … ∙ 3 ∙ 2 ∙ 1.

Рис. 1. Перестановки (варианты размещения четырех предметов по четырем ячейкам)

Упорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется размещением из n по m. С помощью рассуждений, аналогичных предыдущим, нетрудно найти, что число размещений из n по m (оно обозначается , от французского arrangement – размещение) равно произведению m множителей

n (n – 1) (n – 2) … (n – m + 2) (n – m + 1).

 

Рис. 2. Размещения (варианты размещения четырех предметов по трем ячейкам)

Наконец, неупорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется сочетанием из n по m. Число сочетаний обозначается , от французского combinaison – сочетание. Поскольку одному и тому же сочетанию соответствует P_m размещений (получаемых с помощью различных перестановок одного и того же набора m элементов), число сочетаний из n по m меньше числа размещений из n по m в P_m раз:

 

Рис. 3. Сочетания (неупорядоченные размещения)

Впервые понятия перестановки, размещения и сочетания в их взаимосвязи появились в написанной на древенееврейском языке арифметике (1321 г.) жившего в Провансе (Юго-Восточная Франция) Льва Герсонида, или Леви бен Гершона, однако его труд не был известен большинству последующих европейских математиков. В основном элементы комбинаторики были открыты и упорядочены математиками XVII и начала XVIII вв.

Например, термин permutation – перестановка – появился в учебнике «Теория и практика арифметика» (1656 г.) у работавшего в Лувене и Антверпене (ныне Бельгия) преподавателя математики Андре Таке, учебники которого получили большое распространение в XVII–XVIII вв. Понятие размещений и равенство вновь появились только у Я. Бернулли, давшего наиболее полное изложение комбинаторики во второй части «Искусства предположений», изданного в 1713 г. спустя четыре года после смерти автора и ставшего фундаментальной работой по теории вероятностей.

А вот история сочетаний, как мы сейчас убедимся, более давняя: а именно, числа сочетаний – оказывается, ни что иное, как давно знакомые нам биномиальные коэффициенты, которые мы (вслед за Эйлером) обозначали

Дело тут вот в чем: число – это коэффициент при a^n – mb^m в разложении выражения (a + b)ⁿ. Когда бином (a + b) возводится в n-ую степень, т. е. перемножаются n выражений (a + b), множитель b^m получается из m выражений (a + b), а a^n – m – из оставшихся (n – m) таких же выражений. Коэффициент равен числу, указывающему, сколько раз произведение a^n – mb^m появляется в этом разложении, т. е. сколько раз можно выбрать m из n множителей. Слово combinaison – сочетание – употреблял уже Б. Паскаль, который, как уже было указано, уделил большое внимание свойствам биномиальных сочетаний, образующих треугольник Паскаля.

Соответственно, на числа сочетаний переносятся все уже известные свойства биномиальных коэффициентов, в частности, свойство

Это свойство можно доказать новым способом, исходя из комбинаторного смысла чисел . Сумма – это совокупное число, которым можно выбрать последовательно из n имеющихся элементов: ноль элементов (это можно сделать только одним способом), один элемент (это, разумеется, можно сделать n способами), два элемента и т. д., наконец, n элементов (снова одним способом). Каково же это суммарное число? Обратимся к способу решения вышеприведенной задачи об ожерельях! В данном сочетании первый элемент либо присутствует, либо нет – две возможности. Независимо от первого, второй либо присутствует, либо нет – значит, для присутствия или отсутствия первого и второго четыре возможности. Независимо от первого и второго, третий может присутствовать, может не присутствовать – итого 8 возможностей и т. д. Всего получается 2ⁿ всевозможных сочетаний, где каждый элемент может присутствовать, а может и отсутствовать, вплоть до одновременного отсутствия всех n элементов (единственный возможный вариант сочетания из n по 0): правда, индийская задача как раз этот – единственный – случай и исключала: ожерелье вовсе без камней – вообще не ожерелье.

Также по-новому, исходя из комбинаторного определения сочетаний, можно доказать и свойство , гарантирующее, вместе с очевидными равенствами , что числа сочетаний можно найти с помощью треугольника Паскаля. Попробуйте!

Доказательство

Рис. 4. Треугольник Паскаля По определению, число сочетаний из n по m – это число способов, которыми можно из n предметов выбрать m, порядок которых неважен. Как-либо выделим (n – 1) предмет из данных n. Тогда составить неупорядоченную совокупность m предметов из n данных можно, либо выбрав все m лишь из выделенных (n – 1), либо взять один невыделенный предмет, а оставшиеся (m – 1) выбрать из выделенных (n – 1) предмета. Получается, что общее число способов, которым можно создать неупорядоченную совокупность m предметов из n данных, равно числу способов, которым можно из (n – 1) предметов выбрать m, плюс число способов, которым из (n – 1) предметов можно выбрать (m – 1). Таким образом, Рис. 5.

Т. н. мультипликативное представление биномиальных коэффициентов

= (n (n – 1) (n – 2) … (n – m + 2) (n – m + 1)) / (m (m – 1) (m – 2) … ∙ 3 ∙ 2 ∙ 1)

впервые (после Леви бен Гершона) установил парижский преподаватель математики П. Эригон (1634 г.), но широкую известность оно получило благодаря работе Паскаля «Трактат об арифметическом треугольнике», опубликованной в 1665 г. после смерти автора. Пожалуй, проще всего этот результат доказывается с помощью равенства . Впрочем, мы сейчас обычно записываем «мультипликативное представление» несколько иначе, с помощью знака факториала. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Факториалом 0 считается 1. Термин «факториал» впервые предложил французский математик Л. Ф. А. Арбогаст (1800 г.). Факториал числа n обозначается n! Это обозначение ввел в 1808 г. немецкий математик К. Крамп. Итак, n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n, 0! = 1. В этих обозначениях

P_n = n!,

Что касается самого слова «комбинаторика», то оно восходит к «Рассуждению о комбинаторном искусстве» двадцатилетнего Лейбница (1666 г.), которое положило начало этому разделу математики как самостоятельной науке. «Рассуждение» Лейбница содержало ряд теорем о сочетаниях и перестановках, но, кроме того, автор провозглашал весьма широкую применимость новой науки к таким разнообразным предметам, как замки, органы, силлогизмы, смешение цветов, стихосложение, логика, геометрия, военное искусство, грамматика, юриспруденция, медицина и богословие. В дальнейшем Лейбниц продолжил вынашивать грандиозный замысел комбинаторики, полагая, что, как обычная математика занимается большим и малым, единым и многим, целым и частью, так комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным местоположением. Лейбниц предвидел приложения комбинаторики к кодированию и декодированию, к играм, статистике, теории наблюдений. Следует отметить, что, хотя ныне мы понимаем комбинаторику более узко, тем не менее, предвидения Лейбница относительно развития математических теорий, относящихся к указанным предметам, ныне вовсе не выглядят такими беспочвенными, какими казались в его время.

files.school-collection.edu.ru

Перестановки сочетания и размещения (с и без повторений) — Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

Пример 1:  — это 4-элементное размещение из 6-элементного множества .

Пример 2: некоторые размещения элементов множества  по 2:     …    … …

В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы  и  являются различными, хотя состоят из одних и тех же элементов  (то есть совпадают как сочетания).

 

Содержание

• 1 Количество размещений
• 2 Размещение с повторениями
  • 2.1 Количество размещений с повторениями
• 3 См. также
• 4 Ссылки

 

Количество размещений[править ]

Количество размещений из n по k, обозначаемое , равно убывающему факториалу:

Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из nпо k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту , в то время как перестановок наk элементах ровно k! штук.

При k=n количество размещений равно количеству перестановок порядка n:^[1][2][3]

Размещение с повторениями[править ]

Размещение с повторениями или выборка с возвращением^[4] — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.

Количество размещений с повторениями[править ]

По правилу умножения количество размещений с повторениями из n по k, обозначаемое , равно:^[5][1][4]

Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

Ещё один пример: размещений с повторениями из 4 элементов a, b, c, d по 2 равно  эти размещения следующие:

В комбинаторике сочетанием из  по  называется набор  элементов, выбранных из данного множества, содержащего  различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} () являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать  элементов из множества, содержащего  различных элементов, стоит на пересечении -й диагонали и -й строки треугольника Паскаля.^[1]

 

Содержание

• 1 Число сочетаний
• 2 Сочетания с повторениями
• 3 См. также
• 4 Примечания
• 5 Ссылки

 

Число сочетаний[править ]

Основная статья: Биномиальный коэффициент

Число сочетаний из  по  равно биномиальному коэффициенту

При фиксированном  производящей функцией последовательности чисел сочетаний , , , … является:

Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями[править ]

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из  по  равно биномиальному коэффициенту

Доказательство  

При фиксированном  производящей функцией чисел сочетаний с повторениями из  по  является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

intellect.ml