Проекция скорости тела при равномерном прямолинейном движении вдоль оси x – Элементы векторной алгебры. Равномерное прямолинейное движение. Относительность механического движения. — Объяснение нового материала.

Лекции физика

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ — vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s₁ / t₁ = tg α

где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α₁ > tg α₂

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α₃ = v₃ < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х₀

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Связь угловых и линейных величин

Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скоростиопределяется скоростью вращения телаи расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток временитело повернулось на угол(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный

Линейная скорость точки по определению.

(2.6)

Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:

подставляя значение скорости из (2.6), находим:

(2.7)

Тангенциальное ускорение

Воспользовавшись тем же отношением (2.6) получаем

(2.8)

Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.

Основные понятия.

Периодическим колебанием называется процесс, при котором система (например, механическая) возвращается в одно и то же состояние через определенный промежуток времени. Этот промежуток времени называется периодом колебаний.

Возвращающая сила — сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.

В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.

Свободные колебания имеют место тогда, когда на колеблющееся тело действует только возвращающая сила. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).

Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которую называют вынуждающей. Во многих случаях системы совершают колебания, которые можно считать гармоническими.

Гармоническими колебаниями называют такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса:

(7.1)

Для иллюстрации физического смысла рассмотрим окружность, и будем вращать радиус ОК с угловой скоростью ω против часовой (7.1) стрелки. Если в начальный момент времени ОК лежал в горизонтальной плоскости, то через время t он сместится на угол. Если начальный угол отличен от нуля и равенφ₀, тогда угол поворота будет равен Проекцияна ось ХО₁ равна . По мере вращения радиуса ОК изменяется величина проекции, и точкабудет совершать колебания относительно точки- вверх, вниз и т.д. При этом максимальное значение х равно А и называется амплитудой колебаний; ω — круговая или циклическая частота;- фаза колебаний;– начальная фаза. За один оборот точки К по окружности ее проекция совершит одно полное колебание и вернется в исходную точку.

Периодом Т называется время одного полного колебания. По истечению времени Т повторяются значения всех физических величин, характеризующих колебания. За один период колеблющаяся точка проходит путь, численно равный четырем амплитудам.

Угловая скорость определяется из условия, что за период Т радиус ОК сделает один оборот, т.е. повернется на угол 2π радиан:

или

Частота колебаний — число колебаний точки в одну секунду, т.е. частота колебаний определяется как величина, обратная периоду колебаний:

Пружынный маятник упругие силы.

Пружинный маятник состоит из пружины и массивного шара, насаженного на горизонтальный стержень, вдоль которого он может скользить. Пусть на пружине укреплен шарик с отверстием, который скользит вдоль направляющей оси (стержня). На рис. 7.2,а показано положение шара в состоянии покоя; на рис. 7.2,б — максимальное сжатие и на рис. 7.2,в -произвольное положение шарика.

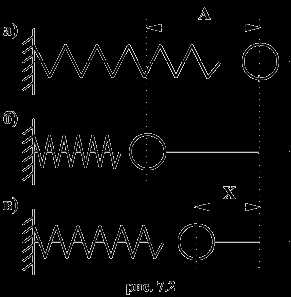
Под действием возвращающей силы, равной силе сжатия, шарик будет совершать колебания. Сила сжатия F = -kx , где k — коэффициент жесткости пружины. Знак минус показывает, что направление силы F и смещение х противоположны. Потенциальная энергия сжатой пружины

кинетическая .

Для вывода уравнения движения шарика необходимо связать х и t. Вывод основывается на законе сохранения энергии. Полная механическая энергия равна сумме кинетической и потенциальной энергии системы. В данном случае :

. В положении б) :.

Так как в рассматриваемом движении выполняется закон сохранения механической энергии, можно записать:

. Определим отсюда скорость:

Но в свою очередь и, следовательно,. Разделим переменные. Интегрируя это выражение, получим:,

где — постоянная интегрирования. Из последнего следует, что

(7.2)

Сравнивая (7.1) с (7.2), получаем

(7.3)

Таким образом, под действием упругой силы тело совершает гармонические колебания. Силы иной природы, чем упругие, но в которых выполняется условие F = -kx, называются квазиупругими. Под действием этих сил тела тоже совершают гармонические колебания. При этом:

смещение:
скорость:
ускорение:

Математический маятник.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещенияи, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: , и момент инерции:M = FL . Момент инерции J в данном случае Угловое ускорение:

С учетом этих величин имеем:

или

(7.8)

Его решение ,

где и

(7.9)

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Затухающие колебания.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают — их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r — коэффициент сопротивления, v — скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ

или

(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β — коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде где U — некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение тогда С вещественным ω решением этого уравнения, как мы знаем, является функция

Таким образом, в случае малого сопротивления среды , решением уравнения (7.19) будет функция

(7.20)

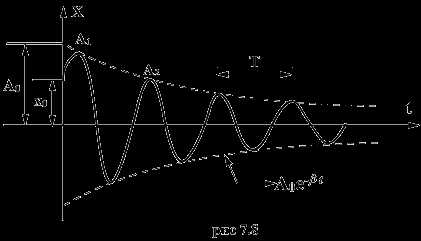
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величинуобычно называют периодом затухающих колебаний, правильнее — условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N — число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Вынужденные колебания.

В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы периодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы .

Пусть эта сила изменяется со временем по закону , гдеамплитуда вынуждающей силы. Возвращающая силаи сила сопротивленияТогда второй закон Ньютона можно записать в следующем виде:

или

(7.21)

Предположим, что возникающее под действием силы установившиеся вынужденные колебания системы также являются гармоническими: (7.22) причем их циклическая частота равна циклической частоте ω вынуждающей силы.

Дифференцируя два раза (7.22) и подставляя в (7.21), получим

Обозначим:

Тогда последнее равенство можно записать в следующем виде:

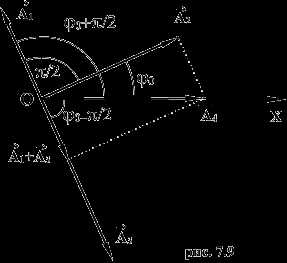
Правую часть этого выражения можно рассматривать как уравнение некоторого гармонического колебания, получившегося при сложении трех гармонических колебаний, определяемых слагаемыми левой части этого равенства. Для сложения этих колебаний воспользуемся методом векторных диаграмм. Проведем опорную линию ОХ (рис. 1.9) и отложим под углами, соответствующими начальным фазам всех четырех колебаний векторы ,,,их амплитуды таким образом, чтобы

Из рис. 7.9 видно, что Подставляя в последнее значения соответствующих амплитуд (1.22), получим:

отсюда

(7.23)

Амплитуда установившихся вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F₀, обратно пропорциональна массе m системы и уменьшается с увеличением коэффициента затухания β. При постоянных F₀, m и β амплитуда зависит только от соотношения циклических частот вынуждающей силы β и свободных незатухающих колебаний системы . При циклической частоте вынуждающей силы ω=0 амплитуда колебаний. В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F₀:

Поэтому отклонение A₀ иногда называют статической амплитудой.

Если нет диссипации т.е β=0, то амплитуда колебаний

растет с увеличением циклической частоты ω вынуждающей силы F_вн и при становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем

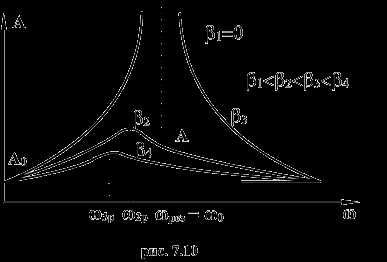
Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы называется резонансом.

Если затухание существует то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого, где- называют резонансной частотой.обозначает то значение циклической частоты ω вынуждающей силы, при котором.

Из последней формулы следует, что для консервативной системы , а для диссипативной системынесколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец приисчезает совсем.

Явление резонанса используется для усиления колебаний, например, электромагнитных. Однако при конструировании различных машин и сооружений необходимо учитывать даже самую небольшую периодическую силу с тем, чтобы предотвратить нежелательные последствия резонанса.

studfiles.net

3. Равномерное прямолинейное движение.

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

V(вектор) = s(вектор) / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

s(вектор) = V(вектор)  • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ — vt

4. Равнопеременное движение.

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

v_cp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

V=lim(^t-0) ^s/^t

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

V(вектор) = s’(вектор)

Проекция вектора скорости на ось ОХ:

v_x = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

а(вектор) = lim (t-0) ^v(вектор)/^t

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

a(вектор) = v(вектор)’ = s(вектор)»

Учитывая, что ₀ – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости,формула ускорения будет следующей:

a(вектор) = v(вектор)-v0(вектор)/t

Отсюда формула скорости равнопеременного движения в любой момент времени:

v(вектор) = v₀(вектор) + a(вектор)t

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

v_x = v_0x ± a_xt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

  Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

  Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v₀

bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

  Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

  Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

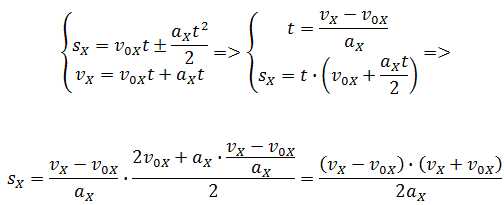
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

studfiles.net

Равномерное прямолинейное движение – FIZI4KA

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ​\( t \)​ тело совершило перемещение ​\( \vec{s} \)​, то скорость его движения ​\( \vec{v} \)​ равна ​\( \vec{v}=\frac{\vec{s}}{t} \)​.

Единица скорости: \( [\,v\,]=\frac{[\,s\,]}{[\,t\,]} \); \( [\,v\,]=\frac{1\,м}{1\,с}=1\frac{м}{с} \). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec{s}=\vec{v}t \). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть \( \vec{s} \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ​\( x_0 \)​ — координата начальной точки перемещения, ​\( x \)​ — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ​\( \vec{s}_x=x-x_0 \)​. С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec{s}_x=\vec{v}_xt \). Откуда ​\( x-x_0=\vec{v}_xt \)​ или \( x=x_0+\vec{v}_xt \). Если начальная координата ​\( x_0 \)​ = 0, то ​\( x=\vec{v}_xt \)​.

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ​\( x>x_0 \)​. Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x<x_0 \).

4. Зависимость координаты от времени можно представить графически.

Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ​\( x \)​ = 4 м/с · ​\( t \)​. Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них ​\( t \)​ = 0 и ​\( x \)​ = 0, а другая ​\( t \)​ = 1 с, ​\( x \)​ = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

Если в начальный момент времени координата тела ​\( x_0 \)​ = 2 м, а проекция его скорости ​\( v_x \)​ = 4 м/с, то уравнение движения имеет вид: ​\( x \)​ = 2 м + 4 м/с · ​\( t \)​. Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ​\( t \)​ = 0, ​\( x \)​ = 2 м (рис. 14).

В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \)​ = 2 м – 4 м/с · ​\( t \)​. График зависимости координаты такого движения от времени представлен на рисунке 15.

Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

1. Кратко записать условие задачи.
2. Проанализировать ситуацию, описанную в условии задачи:
   — выяснить, можно ли принять движущиеся тела за материальные точки;
   — сделать рисунок, изобразив на нём векторы скорости;
   — выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
3. Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
4. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
5. Решить задачу в общем виде.
6. Подставить в формулу значения величин и выполнить вычисления.
7. Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: ​\( v_1 \)​ = 15 м/с  ​\( v_2 \) ​= 12 м/с  ​\( l \) ​= 270 м. Найти: ​\( t \)​ – ?   \( x\)​ – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

Система отсчёта связана с Землёй, ось ​\( Ox \)​ направлена в сторону движения первого тела, начало отсчёта координаты — т. ​\( O \)​ — положение первого тела в начальный момент времени.

Начальные условия: ​\( t \)​ = 0; ​\( x_{01} \)​ = 0; \( x_{02} \) = 270.

Уравнение в общем виде: ​\( \vec{s}=\vec{v}t \)​; ​\( x=x_0+v_xt \).

Уравнения для каждого тела с учётом начальных условий: ​\( x_1=v_1t \)​; ​\( x_2=l-v_2t \)​. В месте встречи тел ​\( x_1=x_2 \); следовательно: ​\( v_1t=l-v_2t \)​. Откуда ​\( t=\frac{l}{v_1+v_2}\cdot t \)​. Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ​\( x \)​ = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​\( v_1 \)​ и скорости «Пежо» — \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​\( v_1 \)​ и \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​\( v_1 \)​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​\( v_1=v_2=v_3 \)​
2) \( v_1>v_2>v_3 \)​
3) \( v_1<v_2<v_3 \)​
4) ​\( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​\( x=1t \)​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

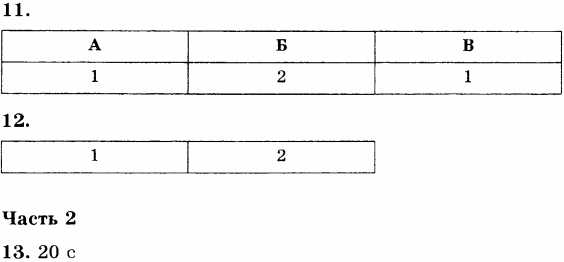
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Ответы

Равномерное прямолинейное движение

5 (100%) 2 votes

fizi4ka.ru

Прямолинейное равномерное движение | Физика для всех

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

vcp = v

 

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

vx = v,	то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x0

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x0 - vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s1 / t1 = tg α

где α – угол наклона графика к оси времени.Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α1 > tg α2

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α3 = v3 < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х0

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

av-mag.ru

Прямолинейное равномерное движение | Все формулы

Прямолинейное равномерное движение — это такое движение, при котором за одинаковые промежутки времени, тело проходит одинаковое расстояние.

Равномерное движение — это такое движение тела, при котором его скорость остается постоянной (),то есть все время движется с одной скоростью, а ускорение или замедление не происходит ().

Прямолинейное движение — это движение тела по прямой линии, то есть траектория у нас получается — прямая.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор скорости совпадает с вектором перемещения. При всем этом средняя скорость в любой промежуток времени равна начальной и мгновенной скорости:

Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела за любой промежуток времен к значению этого промежутка t:

Из данной формулы. мы легко можем выразить перемещение тела при равномерном движении:

Рассмотрим зависимость скорости и перемещения от времени

Так как тело у нас движется прямолинейно и равноускоренно (), то график с зависимостью скорости от времени будет выгладить, как параллельная прямая оси времени.

В зависимости проекции скорости тела от времени ничего сложного нет. Проекция перемещения тела численно равна площади прямоугольника АОВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

На графике мы видим зависимость перемещения от времени.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу. мы можем сказать, чем больше угол, тем быстрей движется наше тело и оно проходит больший путь за меньшее время

В Формуле мы использовали :

-Средняя скорость равномерного прямолинейного движения

— Скорость равномерного прямолинейного движения

— Перемещение тела (расстояние, на которое передвинулось тело)

— Промежуток времени перемещения (время)

— Угол наклона графика к оси времени

xn--b1agsdjmeuf9e.xn--p1ai

Равномерное прямолинейное движение

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

vcp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

vx = v,	то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x0

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

х = x0 - vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s1 / t1 = tg α

где α – угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α1 > tg α2

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α3 = v3 < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х0

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

av-physics.narod.ru

Равномерное прямолинейное движение

Равномерное прямолинейное движение — это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$

Проекция перемещения на ось ОХ равна: $s = v_t = x — x0$

где $x_0$ — начальная координата тела, $х$ — конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $

Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:

\[v=\frac{S_1}{t_1}=tg\alpha \]

Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что

tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).

tg $\alpha $3 = v3 $

Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0

Задача 2

Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения — за 6 часов.

Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с

Найти: $v_p$ — ?; $v_k$ — ?

Решение:

Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:

\[L=v_1t_1=\left(v_k+v_p\right)t_1; L=v_2t_2=\left(v_k-v_p\right)t_2\]

Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.

Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$

Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$

Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.

spravochnick.ru