Пример 1.1
Определим, какое количество информации можно получить после реализации одного из шести событий. Вероятность первого события составляет 0,15; второго – 0,25; третьего – 0,2; четвертого – 0,12; пятого – 0,12; шестого – 0,1, т. е. Р1 =0,15; Р2 =0,25; Р3 = 0,2; Р4 =0,18; Р5 =0,12; Р6 =0,1.
Решение.
Для определения количества информации применим формулу (1.1)
Для вычисления этого выражения, содержащего логарифмы, воспользуемся сначала компьютерным калькулятором, а затем табличным процессором Microsoft (MS) Excel, входящим в интегрированный пакет программ MS Office ХР.
Для вычисления с помощью компьютерного калькулятора выполним следующие действия. С помощью команды: [Кнопка Пуск– Программы – Стандартные – Калькулятор] запустим программу Калькулятор. После запуска программы выполним команду: [Вид – Инженерный] (рис. 1.3).

Рис. 1.3. Инженерный калькулятор
Кнопка log калькулятора производит вычисление десятичного (по основанию 10) логарифма отображаемого числа. Поскольку в нашем случае необходимо производить вычисления логарифмов по основанию 2, а данный калькулятор не позволяет этого делать, то необходимо воспользоваться известной формулой:
logbN =М · logaN,
где
В нашем случае соотношение примет вид: log2N = Mlog10N,
где
т. е log2N = 3,322 · log10N, и выражение для вычисления количества информации примет вид:
При вычислении на калькуляторе используем кнопки: +/‑ (изменение знака отображаемого числа), ()(открывающие и закрывающие скобки), log (логарифм числа по основанию 10) и т. д. Результат вычисления показан на рис. 1.3. Таким образом, количество информации I = 2,52 бит.
Воспользуемся теперь табличным процессором MS Excel. Для запуска программы Excel выполним команду: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel].В ячейки А1, В1, С1, D1, E1, F1 открывшегося окна Excel запишем буквенные обозначения вероятностей Р1, Р2, P3, Р4, P5, P6 а в ячейку G1 – количество информации I, которое необходимо определить. Для написания нижних индексов у вероятностей Р1 ÷ P6 в ячейках А1, В1, С1, D1, E1, F1 выполним следующую команду: [Формат – Ячейки – Шрифт – Видоизменение (поставим флажок напротив нижнего индекса)]. В ячейки А2, В2, С2, D2, Е2, F2 запишем соответствующие значения вероятностей.
После записи значений в ячейки необходимо установить в них формат числа. Для этого необходимо выполнить следующую команду: [Формат – Ячейки – Число – Числовой (устанавливаем число десятичных знаков, равное двум)]. Устанавливаем в ячейке G2 тот же числовой формат. В ячейку G2 записываем выражение = – (A2*LOG(A2;2) + B2*LOG(B2;2) + C2*LOG(C2;2) + D2*LOG(D2;2) + E2*LOG(E2;2) + F2*LOG(F2;2) ). После нажатия на клавиатуре компьютера клавиши <Enter>,в ячейке G2 получим искомый результат – I =2,52 бит (рис. 1.4).
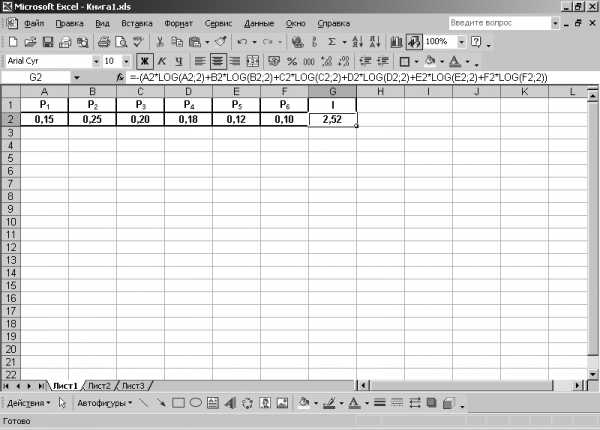
Рис. 1.4. Результат вычисления количества информации
Пример 1.2
Определим, какое количество байт и бит информации содержится в сообщении, если его объем составляет 0,25 Кбайта.
Решение.
С помощью калькулятора определим количество байт и бит информации, которое содержится в данном сообщении:
I =0,25 Кбайт · 1024 байт/1 Кбайт = 256 байт;
I =256 байт · 8 бит/1 байт = 2048 бит.
На семантическом уровне информация рассматривается по ее содержанию, отражающему состояние отдельного объекта или системы в целом. При этом не учитывается ее полезность для получателя информации.
Данный подход предполагает, что для понимания (осмысливания) и использования полученной информации приемник (получатель) должен обладать априорной информацией (тезаурусом), т. е. определенным запасом знаков, наполненных смыслом, слов, понятий, названий явлений и объектов, между которыми установлены связи на смысловом уровне. Таким образом, если принять знания о данном объекте или явлении за тезаурус, то количество информации, содержащееся в новом сообщении о данном предмете, можно оценить по изменению индивидуального тезауруса под воздействием данного сообщения. В зависимости от соотношений между смысловым содержанием сообщения и тезаурусом пользователя изменяется количество семантической информации, при этом характер такой зависимости не поддается строгому математическому описанию и сводится к рассмотрению трех основных условий, при которых тезаурус пользователя:
• стремится к нулю, т. е. пользователь не воспринимает поступившее сообщение;
• стремится к бесконечности, т. е. пользователь досконально знает все об объекте или явлении и поступившее сообщение его не интересует;
• согласован со смысловым содержанием сообщения, т. е. поступившее сообщение понятно пользователю и несет новые сведения.
Два первых предельных случая соответствуют состоянию, при котором количество семантической информации, получаемое пользователем, минимально. Третий случай связан с получением максимального количества семантической информации. Таким образом, количество семантической информации, получаемой пользователем, является величиной относительной, поскольку одно и то же сообщение может иметь смысловое содержание для компетентного и быть бессмысленным для некомпетентного пользователя.
На прагматическом уровнеинформация рассматривается с точки зрения ее полезности (ценности) для достижения потребителем информации (человеком) поставленной практической цели. Данный подход при определении полезности информации основан на расчете приращения вероятности достижения цели до и после получения информации.
Количество информации, определяющее ее ценность (полезность), находится по формуле:
где Р0, P1 –вероятность достижения цели соответственно до и после получения информации.
В качестве единицы измерения (меры) количества информации, определяющей ее ценность, может быть принят 1 бит (при основании логарифма, равном 2), т. е. это такое количество полученной информации, при котором отношение вероятностей достижения цели равно 2.
Рассмотрим три случая, когда количество информации, определяющее ее ценность, равно нулю и когда она принимает положительное и отрицательное значение.
Количество информации равно нулю при Р0=Р1, т.е. полученная информация не увеличивает и не уменьшает вероятность достижения цели.
Значение информации является положительной величиной при P1 > P0
Значение информации является отрицательной величиной при P1 < P0, т. е. полученная информация увеличивает исходную неопределенность и уменьшает вероятность достижения цели. Такую информацию называют дезинформацией.
studfiles.net
6/2(1+2) | Блог инженера
Вот сижу что-то ночью опять… Решил написать своё мнение о популярном сейчас вопросе: один или девять?
Я думаю, по изображению сверху стало уже понятно, о чём идёт речь. Знак умножения – он опущен перед скобками, и… как считать?
Посмотрим с двух позиций.
1) Знак умножения просто опущен. Тогда изначальная запись выражения выглядит так: .
Шесть делим на два, умножаем на сумму единицы и двойки и (всё просто супер, детка) получаем девять. Ответ – 9. Вроде всё красиво, но…
2) Знак умножения не просто опущен. Как так – не просто? А просто так и нельзя опустить. Итак, вот есть инфа, которую, похоже, взяли из учебника за седьмой класс (изначальный источник не найден, но нагуглил в методичке какого-то математического лицея):
Случаи возможного пропуска знака умножения: 1) между буквенными множителями; 2) между числовым и буквенным множителем; 3) между множителем и скобкой; 4) между выражениями в скобках.
Что это для нас значит? А то, что если знак умножения опустили так, как описано в предыдущем пункте, то поступили неправильно, потому что двойка в примере – не множитель перед скобкой, а просто один из трёх множителей (если рассматривать деление как частный случай умножения). Поэтому, если он опущен правильно, то имеем.
И это в том случае, если правило выше абсолютно точное. Но без конкретного источника (утверждается, что это школьный учебник) можно не рассчитывать на то, что оно точное. В школьной математике много требований, которыми даже в разделах вышки порой пренебрегают.
Это правило, к тому же, может оказаться неполным: вдруг нельзя опускать знак между скобкой и множителем в такой ситуации? Составлял бы я правила, я бы так и поступил. Спорная ситуация? Ставь ещё одну пару скобок! Будет вполне однозначно и всем понятно.
От себя скажу, что я часть после деления воспринимаю как нечто целое, т.е. скобку с множителем, мне это кажется вполне естественным. Почему же возникает спор? Многие запоминают, что «всегда можно опустить знак умножения». Но это не так. 2 умножить на 3 не есть 23, а произведение переменных c, o и s не всегда будет правильно понято.
На первый взгляд становится понятно, что человек, сказавший, что ответ – 1, просто забыл о порядке действий, его смутило отсутствие знака умножения. Здесь это чем-то напоминает мне загадку о ножках в комнате (где вопрос о том, сколько ног у животных в комнате. Вскользь упоминается, что ещё стоит и кровать. Если человек забыл про ножки кровати, он лох, если посчитал их, то тоже лох, ибо это не ноги, а ножки. Если посчитал ноги животных, то тоже лох, ибо у них лапы. Короче, вне зависимости от ответа человек – лох и ставит жирафа на аватар). А так как его действия (которые сначала нам показались такими) неправильные, то наше образование – говно и всё такое. Но если копнуть глубже, то действительно встаёт вопрос – а сколько? Если в реальной жизни в важном месте встретить такое, то, независимо от правильного ответа, нужно серьёзно поговорить с человеком, который написал это выражение и не уточнил, что он имел в виду.
Да, помню в какой-то методичке по экономике (у нас слабо вёлся этот предмет, и методички слабые были) была буквенная формула с такой же проблемой. Знак деления, справа большое достаточно выражение. Я тогда засомневался, в итоге нашёл правильную формулу. Да, там после деления всё должно было быть знаменателем. Но там это было однозначно неверно. Люди, пишите не правильно, а понятно 🙂
engineerblog.ru
1.2. Пример выполнения лабораторной работы
3) по способу границ.
Сравните полученные результаты между собой, прокомментируйте
различие методов вычислений и смысл полученных числовых значений.
1.2.2.Решение типового примера
1.Число X = 7,3344, все цифры которого верны в строгом смысле,
округлите до трех значащих цифр. Для полученного числа X1»X найдите предельную абсолютную и предельную относительную погрешности. В
записи числа X1 укажите количество верных цифр(в узком и широком смысле).
Пусть X = 7,3344.
Округлим данное число до трех значащих цифр, получим число:
X1 = 7,33.
Вычислим абсолютную погрешность:
∆X1 = |X –X1| = |7,3344 – 7,33| = 0,0044.
Определим границы абсолютной погрешности(предельную
погрешность), округляя с избытком до одной значащей цифры:
DX1 = 0,005.
Предельная относительная погрешность составляет:
d X1 = | DX1 |
|
| = | 0,005 | = 0,0007= 0,07%. |
|
| |
| X 1 |
|
| 7,33 |
|
| |||
|
|
|
| ||||||
Укажем количество верных цифр в узком и широком смысле в записи | |||||||||
числа X1 = 7,33. |
|
|
|
| |||||
Так |
| как DX1 = 0,005 £ 0,005, следовательно, | в узком | смысле | |||||
верными являются все цифры числа X1 7, 3, 3. |
|
| |||||||
Так |
| как DX1 = 0,005 £ 0,01, следовательно, в | широком | смысле | |||||
верными являются также все цифры числа X1 7, 3, 3.
2. Вычислите с помощью микрокалькулятора значение величины
Z= ab — 4c при заданных значениях параметров a = 12,762, b = 0,4534 lna + b
studfiles.net
Пример 2.1
Количество просмотров публикации Пример 2.1 — 28
На однопредметной прерывно-поточной (прямоточной) линии (ОППЛ) обрабатывается кронштейн. Технологический процесс состоит их 4х операций: токарной, сверлильной, фрезерной и шлифовальной. Длительность операций соответственно составляет, мин: t1 = 1.9, t2 = 1.1, t3 = 2.1 t4 = 1.3. Месячная программа 12600 шт. В месяце 21 рабочий день. Режим работы линии двухсменный. Продолжительность рабочей смены 8 часов. Период оборота линии 0.5 смены.
Читайте также
По дороге движутся два грузовых автомобиля, один порожний, другой с грузом на платформе. Требуется определить, какие максимальные скорости движения на поворотах с радиусом R= 50 м могут быть допущены для обоих автомобилей, не вызывая их бокового опрокидывания. Исходные… [читать подробнее].
Двигатели последовательного возбуждения являются саморегулирующимися, так как при увеличении нагрузки уменьшаются обороты и увеличивается момент и наоборот. Эти двигатели наиболее подходят к условиям тяги поездов и поэтому получили широкое… [читать подробнее].
Нисходящее и восходящее проектирование. Если решение задач высоких иерархических уровней предшествует решению задач более низких иерархических уровней, то проектирование называют нисходящим. Если раньше выполняются этапы, связанные с низшими иерархическими уровнями,… [читать подробнее].
Наиболее простыми и широко используемыми контактными устройствами центральной части, предназначенными для логической обработки информации, являются электромагнитные реле.Подробная классификация, принципы действия, конструкции, основные характеристики и параметры… [читать подробнее].
В машиностроении базовые элементы представлены деталями. Примерами деталей являются винт, шпонка, маслоотражатель, вал, зубчатое колесо. Детали рассматриваются как элементы, фигурирующие в описаниях низшего иерархического уровня, на котором системами являются… [читать подробнее].
В качестве датчика управляемой величины используется поплавок 1; в качестве задающего устройства – фиксатор поплавка 2. Поплавок с помощью рычага 3 перемещает контактный ползунок потенциометрического датчика 4. Датчик управляет исполнительным устройством – реверсивным… [читать подробнее].
Рис 1.1. Объект управления Заданный алгоритм обычно предусматривает поддержание рабочего параметра постоянным во времени или же изменение во времени по известному или неизвестному закону. Задача управления, по существу, заключается в формировании такого закона… [читать подробнее].
Примеры трансформационных упражнений Примеры подстановочных упражнений 1. Составьте предложения из заданных слов. 2. Составьте предложения по образцу. 3. Прослушайте диалог, воспроизведите его и составьте диалог по аналогии. 4. Расскажите о себе или друге,… [читать подробнее].
Тренировка грамматического материала Примеры упражнений на первичное закрепление материала. 1. Сравните употребление … в следующих ситуациях и скажите, по какому признаку они противопоставлены. 2. Сравните ситуации, найдите общее и отличительное в… [читать подробнее].
Пример 8. Свободно опертая по контуру плита перекрытия крупнопанельного здания (рис. 53). Исходные данные. Размеры плиты в плане — 3580 ´ 6580 мм. Толщина 120 мм. Размеры опорных площадок: вдоль короткого пролета — 50мм; вдоль длинного пролета — 70 мм. Расчетные пролеты плиты: l1 =… [читать подробнее].
referatwork.ru
1.2 Пример расчета
Определение конечной осадки ленточного фундамента мелкого заложения методом послойного суммирования
Ширина подошвы ленточного фундамента b= 2,4 м, грунтовые условия см. рисунок 1.2. Среднее давление под подошвой фундамента
РII = 293 кПа.
Удобна такая последовательность расчета:
Вычерчиваем в масштабе геологический разрез строительной площадки. На этот разрез наносим контуры фундамента, строго выдерживая глубину заложения. Разбиваем толщу грунта ниже подошвы фундамента на элементарные слои высотой hi= 0,4 b.
м.
Для вертикали , проходящей через середину подошвы фундамента, находим напряжения от собственного веса грунта σzqi и дополнительные давления σzpi:
В уровне подошвы фундамента (точка 0): кПа; в точке I: σzq1 = 43,4 + 19,7 . 0,96 = 62,3 кПа.
Ниже УПВ в песках учитываем взвешивающее действие воды:
kH/м3,
в точке I: σzq3 = 62.3+9.55 . 1.24 = 74.2 кПа.
Глинистые грунты с JL < 0,5 считаются водоупорами. Суглинок бурый имеет JL = 0,4. Следовательно, на кровле суглинка эпюра σzq имеет скачок:
кПа.
11
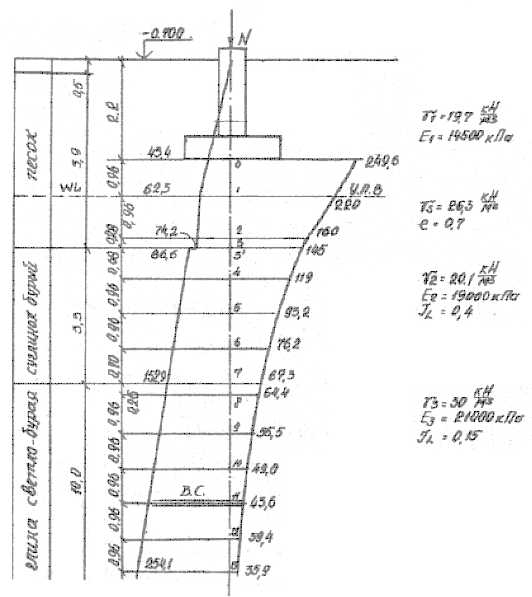
Рисунок 1.2 – Схема к расчету осадок ленточного фундамента
12
Для остальных точек значения σzqприведены в таблице 1.3.
Вычисляем дополнительные (уплотняющие) давления :
В точке 0, т.е. на отметке – 2,9 м:
РII = 293 кПа, σzq,o= 43,4 КПа.
кПа.
В точке I
Z = 0.96 м
кПа
В точке 2
Z = 1.92
кПа.
Для остальных точек величины σzpприведены в таблице 1. 3.
Таблица 1.3 – Результаты расчета
|
Грунт |
Номер точек |
Z, м |
|
,кПа |
,кПа |
E ,кПа | |
|
Песок пылеватый |
0 |
0 |
0 |
1,0 |
249,6 |
43,4 | |
|
I |
0,96 |
0,8 |
0,881 |
220 |
62,3 |
14500 | |
|
2 |
1,92 |
1.6 |
0.642 |
160 | |||
|
3 |
2,20 |
1,83 |
0,582 |
145 |
74,2 | ||
|
3 |
2,20 |
86,6 | |||||
|
Суглинок бурый |
4 |
2,88 |
2,4 |
0,477 |
119 | ||
|
5 |
3,84 |
3,2 |
0,374 |
93,2 |
19000 | ||
|
6 |
4,80 |
4,0 |
0,306 |
76,2 |
13
Продолжение таблицы 1.3
|
Грунт |
Номер точек |
Z, м |
|
|
|
E, кПа | |
|
Песок пылеватый |
8 |
5,76 |
4,8 |
0,258 |
64,4 | ||
|
9 |
6,72 |
5,6 |
0,223 |
55,5 |
21000 | ||
|
10 |
7,68 |
6,4 |
0,196 |
49 | |||
|
11 |
8,64 |
7,2 |
0,176 |
43,6 | |||
|
12 |
9,6 |
8,0 |
0,158 |
39,4 | |||
|
13 |
10,56 |
8,8 |
0,144 |
35,9 |
254,1 |
Осадка фундамента
0,6
= 4,46 см. .
.
Сравним полученную конечную осадку основания S = 0,045 м с предельно допустимой (1, приложение 4):
S = 0,045 м < Su = 0,1 м.
Следовательно, ожидаемая осадка основания фундамента находится в пределах допустимой.
studfiles.net
Пример 2.1
Количество просмотров публикации Пример 2.1 — 11
Переставить первый и последний элемент массива x[] местами. Количество элементов массива n.
Решение
В С нумерация элементов массива начинается с нуля, в связи с этим номер последнего элемента массива (n–1) .
1 способ: tmp=x[0]; x[0]=x[n-1]; x[n-1]=tmp;
2 способ: x[0]=x[0]+x[n-1]; x[n-1]=x[0]-x[n-1]; x[0]=x[0]-x[n-1];
Пример 2.2
Поменять местами заданный элемент массива x[k] с последующим.
Читайте также
По дороге движутся два грузовых автомобиля, один порожний, другой с грузом на платформе. Требуется определить, какие максимальные скорости движения на поворотах с радиусом R= 50 м могут быть допущены для обоих автомобилей, не вызывая их бокового опрокидывания. Исходные… [читать подробнее].
Двигатели последовательного возбуждения являются саморегулирующимися, так как при увеличении нагрузки уменьшаются обороты и увеличивается момент и наоборот. Эти двигатели наиболее подходят к условиям тяги поездов и поэтому получили широкое… [читать подробнее].
Нисходящее и восходящее проектирование. Если решение задач высоких иерархических уровней предшествует решению задач более низких иерархических уровней, то проектирование называют нисходящим. Если раньше выполняются этапы, связанные с низшими иерархическими уровнями,… [читать подробнее].
Наиболее простыми и широко используемыми контактными устройствами центральной части, предназначенными для логической обработки информации, являются электромагнитные реле.Подробная классификация, принципы действия, конструкции, основные характеристики и параметры… [читать подробнее].
В машиностроении базовые элементы представлены деталями. Примерами деталей являются винт, шпонка, маслоотражатель, вал, зубчатое колесо. Детали рассматриваются как элементы, фигурирующие в описаниях низшего иерархического уровня, на котором системами являются… [читать подробнее].
В качестве датчика управляемой величины используется поплавок 1; в качестве задающего устройства – фиксатор поплавка 2. Поплавок с помощью рычага 3 перемещает контактный ползунок потенциометрического датчика 4. Датчик управляет исполнительным устройством – реверсивным… [читать подробнее].
Рис 1.1. Объект управления Заданный алгоритм обычно предусматривает поддержание рабочего параметра постоянным во времени или же изменение во времени по известному или неизвестному закону. Задача управления, по существу, заключается в формировании такого закона… [читать подробнее].
Примеры трансформационных упражнений Примеры подстановочных упражнений 1. Составьте предложения из заданных слов. 2. Составьте предложения по образцу. 3. Прослушайте диалог, воспроизведите его и составьте диалог по аналогии. 4. Расскажите о себе или друге,… [читать подробнее].
Тренировка грамматического материала Примеры упражнений на первичное закрепление материала. 1. Сравните употребление … в следующих ситуациях и скажите, по какому признаку они противопоставлены. 2. Сравните ситуации, найдите общее и отличительное в… [читать подробнее].
Пример 8. Свободно опертая по контуру плита перекрытия крупнопанельного здания (рис. 53). Исходные данные. Размеры плиты в плане — 3580 ´ 6580 мм. Толщина 120 мм. Размеры опорных площадок: вдоль короткого пролета — 50мм; вдоль длинного пролета — 70 мм. Расчетные пролеты плиты: l1 =… [читать подробнее].
referatwork.ru
Пример 2.1.
Производство Пример 2.1.
Количество просмотров публикации Пример 2.1. — 34
| Наименование параметра | Значение |
| Тема статьи: | Пример 2.1. |
| Рубрика (тематическая категория) | Производство |
Имеются первичные данные о количестве работников определенного возраста.
| Возраст, лет | ||||||||||||||
| Число сотрудников |
Произведем группировку работников предприятия по возрасту. Для этого по формуле (2.1) рассчитаем число групп
m = 1+3,322·lg 39 = 6,28 ≈ 6.
Определим интервал группировки по формуле (2.2)
.
Округлим величину интервала до ближайшего целого h = 7.
Тогда группировка будет следующей:
| Возраст, лет | ||||||||||||||
| Число сотрудников | ||||||||||||||
| Границы интервалов | 20 – 27 | 27 – 33 | 33–40 | 40–47 | 47 – 54 | 54 – 60 | ||||||||
| Число сотрудников в интервале |
Граничное значение входит в тот интервал, где оно является верхней границей.
Произведем вторичную группировку с укрупнением интервалов (h = 10):
| Возраст, лет | ||||||||||||||
| Число сотрудников | ||||||||||||||
| Границы интервалов | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | ||||||||||
| Число сотрудников в интервале |
Пример 2.1. — понятие и виды. Классификация и особенности категории «Пример 2.1.» 2014, 2015.
Читайте также
По дороге движутся два грузовых автомобиля, один порожний, другой с грузом на платформе. Требуется определить, какие максимальные скорости движения на поворотах с радиусом R= 50 м могут быть допущены для обоих автомобилей, не вызывая их бокового опрокидывания. Исходные… [читать подробнее].
Двигатели последовательного возбуждения являются саморегулирующимися, так как при увеличении нагрузки уменьшаются обороты и увеличивается момент и наоборот. Эти двигатели наиболее подходят к условиям тяги поездов и поэтому получили широкое… [читать подробнее].
Нисходящее и восходящее проектирование. Если решение задач высоких иерархических уровней предшествует решению задач более низких иерархических уровней, то проектирование называют нисходящим. Если раньше выполняются этапы, связанные с низшими иерархическими уровнями,… [читать подробнее].
Наиболее простыми и широко используемыми контактными устройствами центральной части, предназначенными для логической обработки информации, являются электромагнитные реле.Подробная классификация, принципы действия, конструкции, основные характеристики и параметры… [читать подробнее].
В машиностроении базовые элементы представлены деталями. Примерами деталей являются винт, шпонка, маслоотражатель, вал, зубчатое колесо. Детали рассматриваются как элементы, фигурирующие в описаниях низшего иерархического уровня, на котором системами являются… [читать подробнее].
В качестве датчика управляемой величины используется поплавок 1; в качестве задающего устройства – фиксатор поплавка 2. Поплавок с помощью рычага 3 перемещает контактный ползунок потенциометрического датчика 4. Датчик управляет исполнительным устройством – реверсивным… [читать подробнее].
Рис 1.1. Объект управления Заданный алгоритм обычно предусматривает поддержание рабочего параметра постоянным во времени или же изменение во времени по известному или неизвестному закону. Задача управления, по существу, заключается в формировании такого закона… [читать подробнее].
Примеры трансформационных упражнений Примеры подстановочных упражнений 1. Составьте предложения из заданных слов. 2. Составьте предложения по образцу. 3. Прослушайте диалог, воспроизведите его и составьте диалог по аналогии. 4. Расскажите о себе или друге,… [читать подробнее].
Тренировка грамматического материала Примеры упражнений на первичное закрепление материала. 1. Сравните употребление … в следующих ситуациях и скажите, по какому признаку они противопоставлены. 2. Сравните ситуации, найдите общее и отличительное в… [читать подробнее].
Пример 8. Свободно опертая по контуру плита перекрытия крупнопанельного здания (рис. 53). Исходные данные. Размеры плиты в плане — 3580 ´ 6580 мм. Толщина 120 мм. Размеры опорных площадок: вдоль короткого пролета — 50мм; вдоль длинного пролета — 70 мм. Расчетные пролеты плиты: l1 =… [читать подробнее].
referatwork.ru

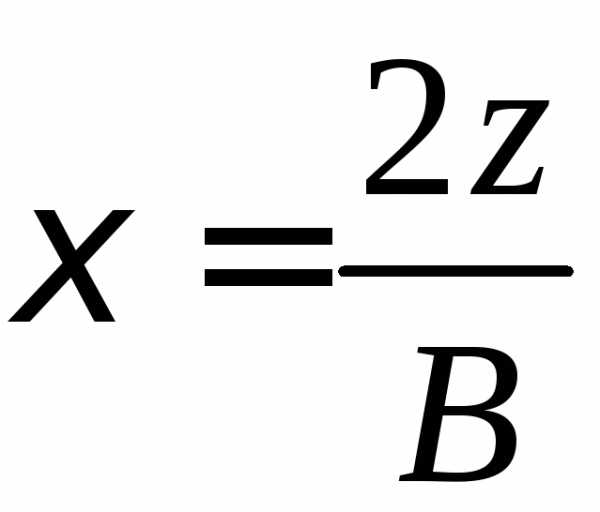
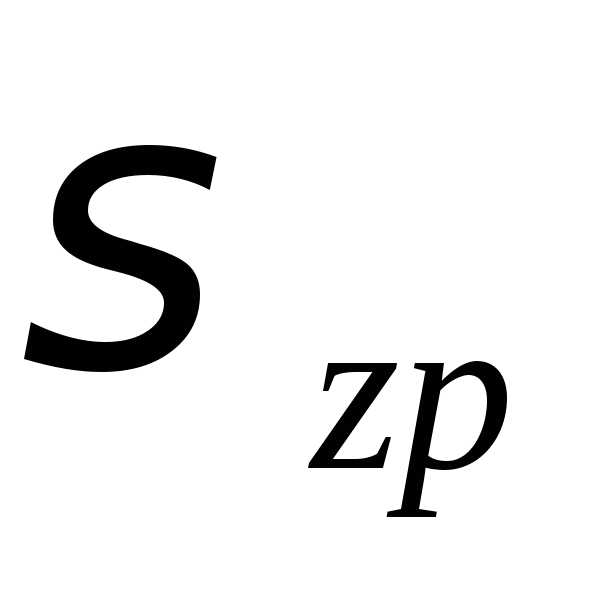
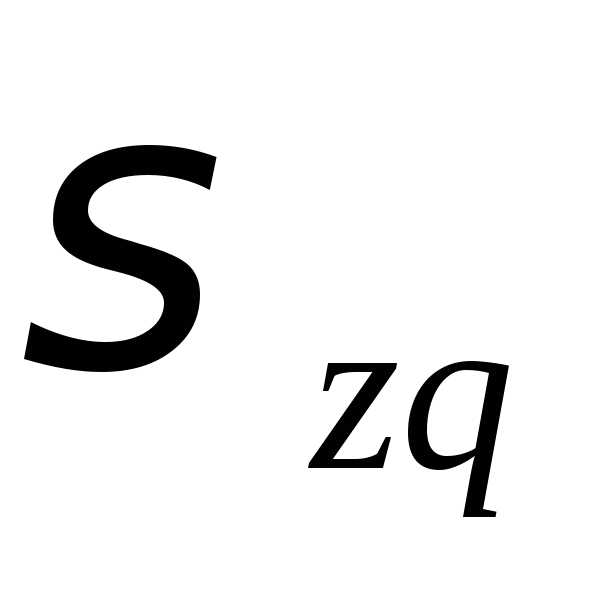
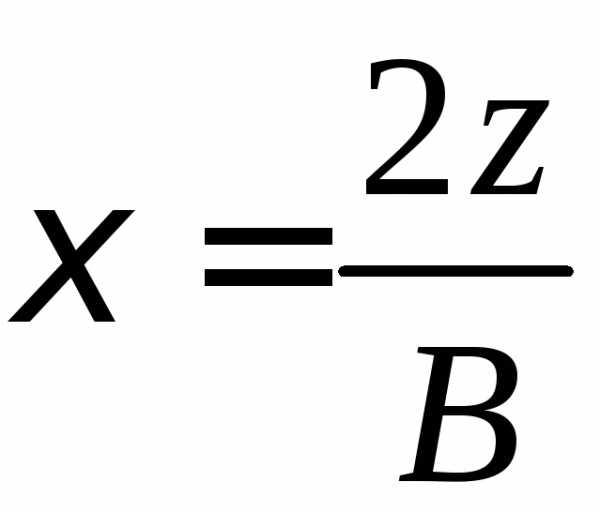
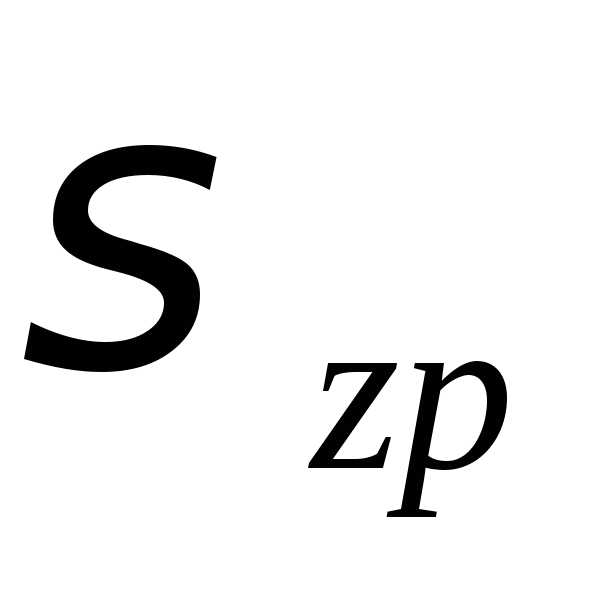 ,
кПа
,
кПа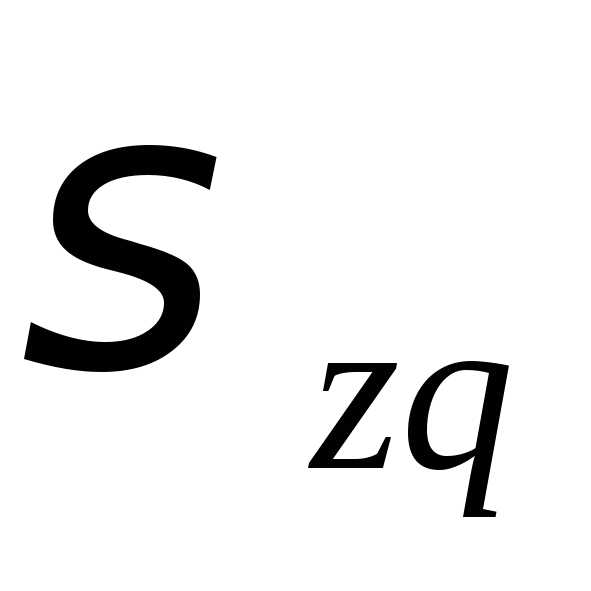 ,
кПа
,
кПа