Решение показательного неравенства с разными основаниями
В этой статье я покажу как решать показательное неравенство вида
Решим неравенство:
Запишем неравенство в таком виде:
Разделим обе части неравенства на 3:
Теперь возьмем от обеих частей неравенства логарифм по основанию 3. Мы имеем право это сделать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.
Получим:
Перенесем слагаемые, содержащие неизвестное влево, а не содержащие — вправо:
Разделим обе части неравенства на , предварительно исследовав знак этого выражения.
Т.к. ,
Получим:
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Показательные неравенства. Как решать показательные неравенства?
\(4^{x}\geq32\)
\(5^{2x-1}-5^{2x-3}≤4,8\)
\((\sqrt{7})^{2x+2}-50(\sqrt{7})^{x}+7>0\)
Как решать показательные неравенства?
Нужно стремиться свести неравенство к виду: \(a^{f(x)}\) \(˅\) \(a^{g(x)}\) (\(˅\) означает любой из знаков сравнения) – это позволяет избавиться от оснований и сделать переход к виду \(f(x) ˅ g(x)\).
Примеры:
| \(4^{x}≥32\) | \((0,5)^{2x}>0,125\) |
| \(2^{2x}≥2^5\) | \((0,5)^{2x}>(0,5)^3\) |
| \(2x≥5\) | \(2x<3\) |
| \(x≥2,5\) | \(x<1,5\) |
Но есть одна важная тонкость в переходе в показательных неравенствах:
\(-\) если основание степени больше \(1\), то знак неравенства должен оставаться прежним,
\(-\) если же основание — число большее \(0\), но меньшее \(1\) (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
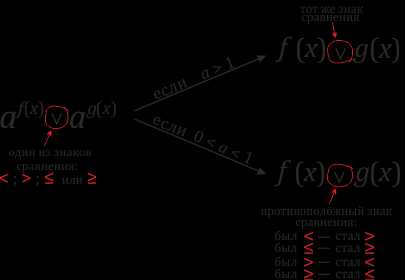
\(2^{x+1}\) \(≥\) \(2^3 ⇒ x+1\) \(≥\) \(3\)
\(0,5^{4x+3}\) \(≤\) \(0,5^{6x-1} ⇒ 4x+3\) \(≥\) \(6x-1\)
Важно! Есть два требования для перехода в показательных неравенствах:
\(-\) число в основании степени слева и справа должно быть одинаковым;
\(-\) степени слева и справа должны быть «чистыми», то есть не должно быть никаких коэффициентов, умножений, делений и т.д.
Например:
|
1) \(3^{x+2}>5^{8-x}\) |
Переход к \(x+2> 8-x \) невозможен, так как в основаниях разные числа |
|
2) \(7^{x}+7^{3x}<7^{2x}\) |
Переход к \(x+3x<2x\) невозможен, так как степени не «чистые» (слева есть сумма) |
|
3) \(2^{5-x}≥-2^{7x}\) |
Переход к \(5-x≥7x\) невозможен, так как степени не «чистые» (перед степенью справа стоит минус) |
Пример. Решить показательное неравенство: \(2^{x}+2^{x+2}\leq 20\)
Решение:
|
\(2^{x}+2^{x+2}\leq 20\) |
Сразу переход делать нельзя, сумма в левой части не дает. Поэтому используем свойства степеней и преобразуем \(2^{x+2}=2^{x} \cdot 2^2=4 \cdot 2^x\) |
|
|
\(2^{x}+4 \cdot 2^{x}\leq 20\) |
Теперь \(2^x\) и \(4 \cdot 2^{x}\) – подобные слагаемые, можно их сложить |
|
|
\(5 \cdot 2^x≤20\) \(| ∶5\) |
Делим обе части неравенства на \(5\) |
|
|
\(2^x≤4\) |
Представляем четверку как \(2^2\) |
|
|
\(2^x≤2^2\) |
|
Вот теперь делаем переход: избавляемся от оснований, не меняя знак сравнения, т.к. основание \(2>1\) |
|
\(x≤2\) |
|
Пример. Решить показательное неравенство: \(4^{2x}-5 \cdot 4^{x}+4< 0\)
Решение:
|
\(4^{2x}-5 \cdot 4^{x}+4< 0\) |
Перед нами типичное показательно-квадратное неравенство. Преобразуем по свойству степеней \(4^{2x}=(4^x)^2\), чтобы на следующем шаге сделать замену. |
|
|
\((4^{x})^2-5 \cdot 4^{x}+4< 0\) |
Делаем замену переменных |
|
|
\(t=4^x\) |
Записываем неравенство в новом виде |
|
|
\(t^2-5t+4<0\) |
Раскладываем на множители правую часть |
|
|
\((t-1)(t-4)<0\) |
|
Решаем неравенство с помощью метода интервалов |
|
|
|
Записываем промежуточное решение в виде системы и делаем обратную замену |
|
\(\begin{cases}t>1\\t<4\end{cases} \Leftrightarrow \begin{cases}4^x>1\\4^x<4\end{cases}\) |
|
Решаем показательные неравенства |
|
\(\begin{cases}4^x>4^0\\4^x<4^1\end{cases} \Leftrightarrow \begin{cases}x>0\\x<1\end{cases}\) |
|
Записываем ответ |
Решение показательных неравенств с разными основаниями
А что делать, если невозможно привести левую и правую часть неравенства к степеням с одинаковыми основаниями (т.е. к виду \(a^{f(x)} ˅ a^{g(x)})\) ? Тогда на сцену выходит его величество логарифм. По основному логарифмическому тождеству — \(c=a^{\log_{a}{c}}\) , а значит любое положительное число можно представить в виде степени с любым основанием: \(5=2^{\log_{2}{5}}\) ; \(0,1=200^{\log_{200}{0,1}}\) и т.д.
Пример: Решить показательное неравенство:
|
\(0,2^{-7x+4}≥4\) |
Заменим \(4\) на \(0,2^{\log_{0,2}{4}}\) |
|
|
\(0,2^{-7x+4}≥0,2^{\log_{0,2}{4}}\) |
Избавимся от оснований с переменой знака т.к. \(0,2<1\) |
|
|
\(-7x+4≤\log_{0,2}{4}\) |
\(\log_{0,2}{4}\) – число некрасивое, но все-таки число, т.е. перед нами обычное линейное неравенство. |
|
|
\(-7x≤\log_{0,2}{4}-4\) |
Поделим обе части на \(-7\) |
|
|
\(x≥\) \(\frac{4-\log_{0,2}{4}}{7}\) |
Ответ: \(x∈\)\([\frac{4-\log_{0,2}{4}}{7}\)\(;∞)\)
Знаю, выглядит не очень, но ответ не выбирают.
Особые виды показательных неравенств
Решим неравенство \(5^x<-5\). Подумайте, каким должен быть икс, чтобы \(5^x\) превратилось в \(-5\)? Наверно, вы подумали о минус единице? Давайте проверим эту гипотезу: \(5^{-1}=\frac{1}{5}\) – не подходит.
На самом деле, никакая степень не превратит положительное число в отрицательное. Почему? Потому что показателе степени говорит лишь о том сколько раз умножается само на себя основание. А основание – положительно, и произведение положительных чисел – всегда положительно.
Таким образом, никакой \(x\) не сделает \(5^x\) отрицательным. То же самое можно сказать про \(2^x\), \(3^x\), \(4^x\), \(6^x\) и т.д.
Если \(a\) – положительно, то \(a^x>0\) при любых \(x\)
Поэтому у показательного неравенства \(5^x<-5\) нет решений.
Рассмотрим обратное неравенство: \(5^x>-5\).
\(5^x\) – всегда больше нуля, и, уж тем более, оно будет больше \(-5\). Значит, решением неравенства \(5^x>-5\) будет любое число: \(x∈(-∞;∞)\).
Смотрите также:
Показательные уравнения
Логарифмические уравнения
Равносильные преобразования неравенств
Логарифмические неравенства
cos-cos.ru
Как решать показательные неравенства | Логарифмы
Рассмотрим, как решать показательные неравенства, содержащих степени с разными основаниями. Решение таких неравенств аналогично решению соответствующих показательных уравнений.
Группируем степени с одинаковыми основаниями. Удобнее для этого развести их по разные стороны неравенства:
Из каждой пары степеней выносим за скобки общий множитель — степень с меньшим показателем. Вынести за скобки общий множитель- значит, каждое слагаемое разделить на этот множитель. При делении степеней с одинаковыми основаниями основание оставляем прежним, а показатели вычитаем:
Делить можно сразу на 20 (20=4∙5), но практика показывает, что деление в два этапа позволяет избежать возможных ошибок:
Так как основание 2/5<1, показательная функция
убывает, поэтому знак неравенства между показателями степеней изменяется на противоположный:
Квадратичное неравенство решим методом интервалов. Нули функции, стоящей в левой части неравенства — x1=-1; x2=2. Отмечаем их на числовой прямой.
Для проверки знака возьмем нуль: 0²-0-2=-2, в промежуток, которому принадлежит нуль, ставим «-«. Остальные знаки расставляем в шахматном порядке. Так как решаем неравенство, в котором левая часть меньше нуля, выбираем промежуток со знаком «-«.
Ответ: x ∈ (-1; 2).
Вариант неравенств такого вида — все степени имеют одинаковые основания, но отличаются коэффициентами при x в показателях.
В левой части выносим за скобки степень с наименьшим показателем
Пришли к показательному неравенству простейшего вида. Так как основание 7>1, функция
возрастает, знак неравенства между показателями не изменяется:
Чтобы решить это неравенство методом интервалов перенесем все слагаемые в левую часть и приведём дроби к наименьшему общему знаменателю:
Полученные точки отмечаем на числовой прямой (с учётом ОДЗ x≠0). Для проверки знака возьмём x=2:
в промежуток, которому принадлежит 2, ставим знак «+», остальные знаки чередуем в шахматном порядке:
Ответ:
www.logarifmy.ru
Как решать С3. Урок 3. ЕГЭ по математике 2014. Показательные неравенства — решения.егэцентр.рф
Начнем с основ: разберем, например, как решать неравенство `a^x > a^b`, где `a` и `b` — фиксированные числа, а `x` — переменная.
В общем виде решение такого неравенства будет следующим.
Теоретическая часть, как решать простейшее показательное неравенство
Если `a>1`, то решение — `x > b`, если `0<a<1`, то решение — `x<b`. Эту фразу можно оформить в виде системы неравенств:
$$\left[ \begin{array}{l}\left\{\begin{array}{l} a>1,\\ x>b; \end{array} \right. \\ \left\{\begin{array}{l} a<1,\\x < b. \end{array} \right.\end{array}\right.$$
Чтобы лучше запомнить эту, казалось бы, сложную систему, давайте поймем, откуда она взялась. (Если это вам не очень интересно, то можете пропустить и сразу перейти к решениям неравенств ЕГЭ)
Посмотрим, как ведет себя функция `f(x) = a^x`. В случае, если `a>1`, то в чем большую степень мы его возводим, тем большее число получаем (попробуйте возвести `2` в степени `1, 2, 3, \ldots`). Если `0<a<1`, то чем больше показатель степени — тем меньше будет результат (попробуйте так же возвести `\frac{1}{2}` в несколько разных степеней).
На графике функции при `a>1` это будет выглядеть так:
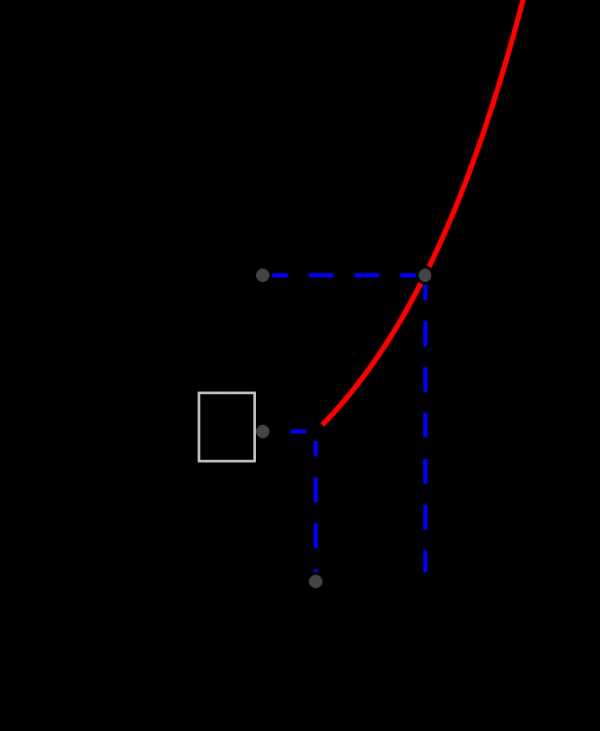
Видно, что чтобы значение `a^x` было больше (лежало выше), чем `a^b`, нужно взять `x` правее, чем `b`. Красным показано решение неравенства.
При `a<1` получаем такую картину:
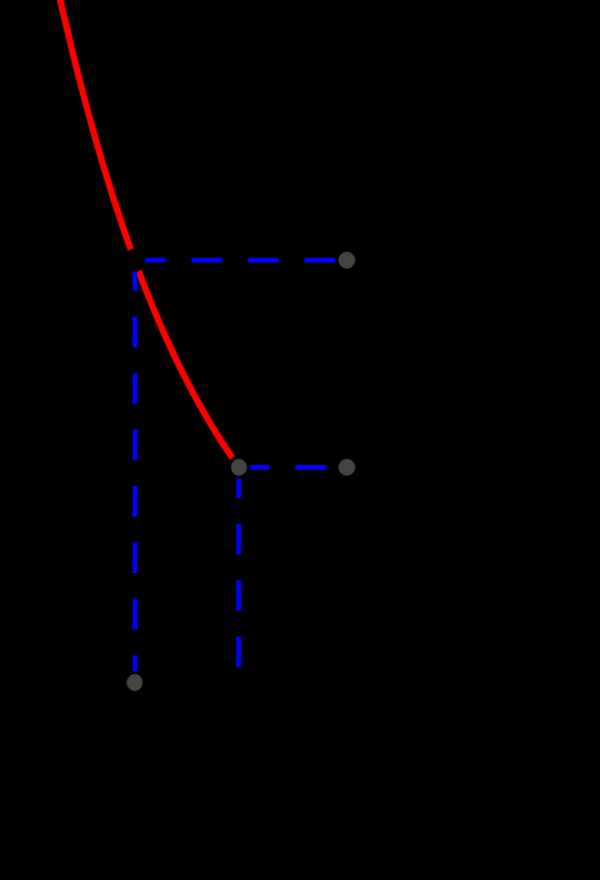
Аналогично: чтобы значение `a^x` было больше (лежало выше), чем `a^b`, нужно взять `x` левее, чем `b`. Красным показано решение неравенства.
Таким образом, наша задача при решении показательных неравенств — привести их к виду простейших показательных неравенств и представить левую и правую часть в виде степеней с одинаковым основанием.
Закончим на этом о простейших показательных неравенствах.
Решение показательных неравенств. Метод замены переменной
Основной способ решения неравенств ЕГЭ, которые содержат показательную функцию, — замена этой функции на новую переменную.
Разберем такой пример:
$$4^{2x} — 5·4^x + 4 \geqslant 0.$$
Выполним замену `4^x= t`.
Используя свойства степеней, получим:
$$t^2 — 5t +4 \geqslant 0.$$
Такое неравенство мы решали в первом уроке про метод интервалов. Разложив на скобки, получим:
$$(t — 4)(t-1) \geqslant 0.$$
На оси решение отмечено красным, концы отрезка также удовлетворяют неравенству. Вернемся к замене:
$$\left[\begin{array}{l}4^x \leqslant 1, \\ 4^x \geqslant 4; \end{array} \right.$$
Представим `1` и `4` в виде степеней с основанием `4`:
$$\left[\begin{array}{l}4^x \leqslant 4^0, \\ 4^x \geqslant 4^1; \end{array} \right.$$
$$\left[\begin{array}{l}x \leqslant 0, \\ x \geqslant 1; \end{array} \right.$$
Ответ получен. Двигаемся дальше.
Второй пример. Решение показательного неравенства, степени с разными основаниями
$$64·9^x — 84 · 12^x + 27·16^x \leqslant 0.$$
Для начала нужно разобраться, что мы будем заменять на `t`. Для этого приведем все степени с разными основаниями к одинаковым.
Заметим, что `9=3^2, 12 = 3·4, 16 = 4^2`. Расписав эти числа таким образом, получим:
$$64·3^{2x} — 84 · 3^x · 4^x + 27·4^{2x} \leqslant 0.$$
Левая часть неравенства очень похожа на однородное тригонометрическое выражение второй степени. Только вместо синусов и косинусов у нас `3^x` и `4^x`. Давайте поступим по аналогии с тригонометрией: поделим на `4^x` (слава богу, любая показательная функция, всегда строго больше нуля).
$$64· \frac{3^{2x}}{4^{2x}} — 84 · \frac{3^x}{4^x} + 27\leqslant 0.$$
Замена `t= \dfrac{3^x}{4^x}`.
$$64·t^2 — 84 · t + 27\leqslant 0.$$
Отсюда получим `t_1 = \frac{9}{16}, t_2 = \frac{3}{4}`.
Получили решение `\frac{9}{16} \leqslant t \leqslant \frac{3}{4}`. Обратная замена.
$$\frac{9}{16} \leqslant \left(\frac{3}{4}\right)^x \leqslant \frac{3}{4},$$
$$\left(\frac{3}{4}\right)^2 \leqslant \left(\frac{3}{4}\right)^x \leqslant \frac{3}{4}.$$
Поскольку основание степени меньше единицы, то избавившись от него, перевернем знаки неравенств:
$$2 \geqslant x \geqslant 1.$$
Приведем к привычному виду.
$$1 \leqslant x \leqslant 2.$$
Ответ получен. Разберем последнее неравенство в этом уроке.
Третий пример. Решение показательного неравенства
$$\frac{2^{1-x} — 2^x +1}{2^x -1 }\leqslant 0.$$
Все степени в этом неравенстве с основанием `2`. Две из них уже имеют удобны для замены на `t` вид `2^x`. Представим `2^{1-x} = 2 · \frac{1}{2^x}`. И выполним замену `2^x = t`.
$$\frac{2· \frac{1}{t} — t +1}{t-1 }\leqslant 0.$$
Приведем все слагаемые в числителе к общему знаменателю.
$$\left(\frac{2-t^2 +t }{t}\right) / (t-1)\leqslant 0,$$
$$\frac{-t^2 +t +2}{t·(t-1)}\leqslant 0,$$
$$\frac{-(t-2)(t+1)}{t·(t-1)}\leqslant 0,$$
Отрицательным `t` быть не может, поскольку это показательная функция. Значит, нам остается только два интервала: `(0,1) \cup [2,∞)`. Выполним обратную замену.
$$\left[\begin{array}{l} 0<2^x <1, \\2^x>2;\end{array} \right.$$
$$\left[\begin{array}{l} x <0, \\ x>1;\end{array} \right.$$
Ответ получен.
Задания для тренировки
Решите неравенства:
- `5^{x^2+6x+8}>1`,
- `2^{x+1}+2^{-x}-3\leqslant 0`,
- `5^{2x+1}+6^{x+1}>30+15^x·10^x`,
- `\dfrac{2·81^x +3^x — 87}{81^x — 3} \geqslant 2.`
На этом все. Если объяснение понятное, то ставьте лайки, а если остались вопросы, оставляйте их в комментариях.
Как обычно, видео с этим материалом прилагается.
xn--e1aajtm3cwc.xn--c1adb6aplz9c.xn--p1ai
Показательные неравенства. Методическая разработка
Дополнительные сочиненияНа данном уроке мы рассмотрим различные показательные неравенства и научимся их решать, основываясь на методике решения простейших показательных неравенств
1. Определение и свойства показательной функции
Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция – это функция вида , где основание степени и Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.
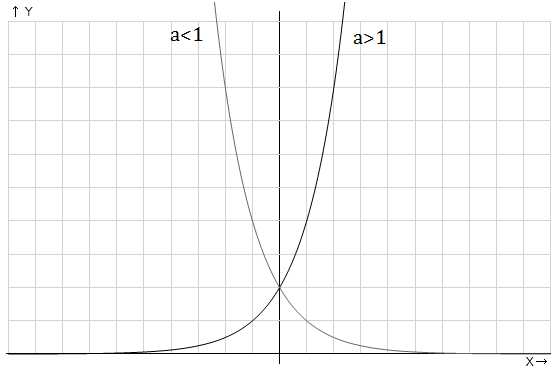
Рис. 1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции:
Область определения: ;
Область значений: ;
Функция монотонна, при возрастает, при убывает.
Монотонная функция принимает каждое свое значение при единственном значении аргумента.
При , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (). При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию ().
2. Простейшие показательные неравенства, методика решения, пример
На основании вышесказанного приведем методику решения простейших показательных неравенств:
Методика решения неравенств:
Уравнять основания степеней;
Сравнить показатели, сохранив или изменив на противоположный знак неравенства.
Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.
Пример 1:
Преобразуем правую часть согласно свойствам степени:
Основание степени больше единицы, значит, знак неравенства сохраняется:
Пример 2:
Преобразуем правую часть согласно свойствам степени:
Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:
Для решения квадратного неравенства решим соответствующее квадратное уравнение:
По теореме Виета находим корни:
Ветви параболы направлены вверх.
Таким образом, имеем решение неравенства:
Пример 3:
Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:
Основание степени больше единицы, знак неравенства не меняется, получаем:
Напомним методику решения таких неравенств.
Рассматриваем дробно-рациональную функцию:
Находим область определения:
Находим корни функции:
Функция имеет единственный корень,
Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:
Рис. 2. Интервалы знакопостоянства
Таким образом, получили ответ.
Ответ:
3. Решение типовых показательных неравенств
Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.Пример 4:
Одно из свойств показательной функции – она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:
Основание степени больше единицы, знак неравенства сохраняется.
Ответ:
Проиллюстрируем решение:
На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства.
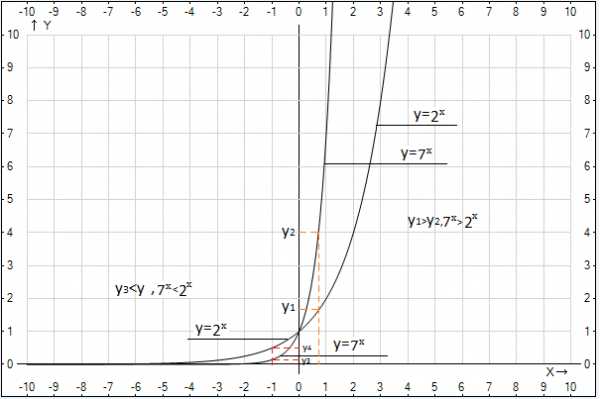
Рис. 3. Иллюстрация к примеру 4
Пример 5:
Преобразуем заданное неравенство согласно свойствам степени:
Приведем подобные члены:
Разделим обе части на :
Теперь продолжаем решать аналогично примеру 4, разделим обе части на :
Основание степени больше единицы, знак неравенства сохраняется:
Ответ:
4. Графическое решение показательных неравенств
Пример 6 – решить неравенство графически:
Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.
Функция – экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Функция – линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ()
Несложно заметить, что корнем данной системы является :
Таким образом, графики функций пересекаются в точке с аргументом, равным единице.
Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ: (рисунок 6.4)
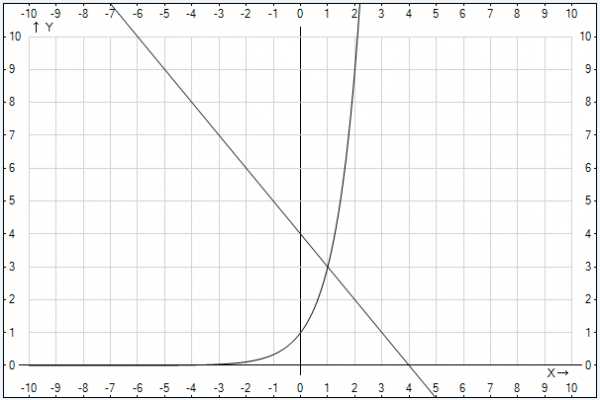
Рис. 4. Иллюстрация к примеру 6
Итак, мы рассмотрели решение различных типовых показательных неравенств. Далее перейдем к рассмотрению более сложных показательных неравенств.
Список литературы
Мордкович А. Г. Алгебра и начала математического анализа. – М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. – М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интерне
Math. md . Mathematics-repetition. com . Diffur. kemsu. ru .
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 472, 473;
2. Решить неравенство:
3. Решить неравенство:
dp-adilet.kz
11 класс. Алгебра. Показательная и логарифмическая функции. Показательные уравнения и неравенства. — Показательные неравенства.
Комментарии преподавателя
Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция – это функция вида , где основание степени и Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.
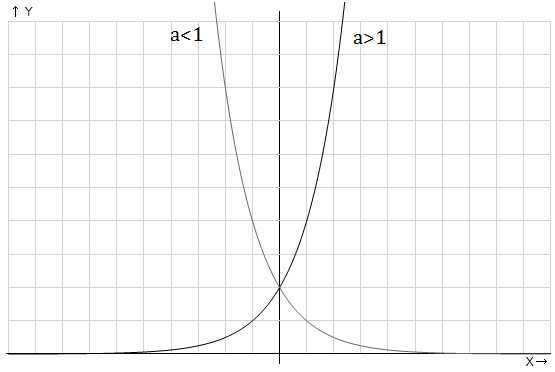
Рис. 1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции:
Область определения: ;
Область значений: ;
Функция монотонна, при возрастает, при убывает.
Монотонная функция принимает каждое свое значение при единственном значении аргумента.
При , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (). При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию ().
На основании вышесказанного приведем методику решения простейших показательных неравенств:
Методика решения неравенств:
Уравнять основания степеней;
Сравнить показатели, сохранив или изменив на противоположный знак неравенства.
Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.
Пример 1:
Преобразуем правую часть согласно свойствам степени:
Основание степени больше единицы, значит, знак неравенства сохраняется:
Пример 2:
Преобразуем правую часть согласно свойствам степени:
Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:
Для решения квадратного неравенства решим соответствующее квадратное уравнение:
По теореме Виета находим корни:
Ветви параболы направлены вверх.
Таким образом, имеем решение неравенства:
Пример 3:
Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:
Основание степени больше единицы, знак неравенства не меняется, получаем:
Напомним методику решения таких неравенств.
Рассматриваем дробно-рациональную функцию:
Находим область определения:
Находим корни функции:
Функция имеет единственный корень,
Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:
Рис. 2. Интервалы знакопостоянства
Таким образом, получили ответ.
Ответ:
Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.
Пример 4:
Одно из свойств показательной функции – она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:
Основание степени больше единицы, знак неравенства сохраняется.
Ответ:
Проиллюстрируем решение:
На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства.
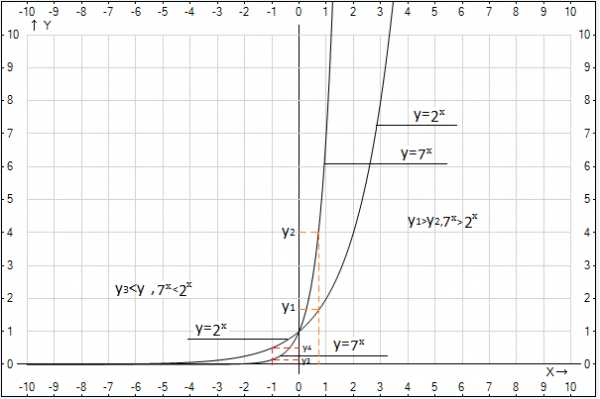
Рис. 3. Иллюстрация к примеру 4
Пример 5:
Преобразуем заданное неравенство согласно свойствам степени:
Приведем подобные члены:
Разделим обе части на :
Теперь продолжаем решать аналогично примеру 4, разделим обе части на :
Основание степени больше единицы, знак неравенства сохраняется:
Ответ:
Пример 6 – решить неравенство графически:
Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.
Функция – экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Функция – линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.
Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ()
Несложно заметить, что корнем данной системы является
www.kursoteka.ru
Методы решения показательных и логарифмических неравенств
Методы решения показательных уравнений.
Показательным уравнением называется уравнение, содержащее переменную в показателе степени (к тому же, переменная может быть и в основании степени).
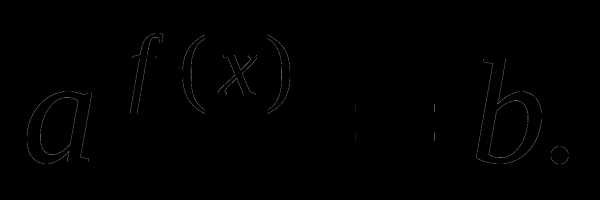
Для успешного решения показательных уравнений необходимо:
— безошибочно решать простейшие показательные уравнения.
— не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
уравнений.
— знать методы решения задач. Для этого:
определить тип уравнения;
вспомнить соответствующий этому типу метод решения задачи.
Тип
Метод
Три разных основания степеней
Разложение оснований на множители и сведение к двум основаниям степени
Тип
Метод
Два разных основания степеней-
разные показатели
Основания степеней –
степени одного числа
Приведение к одинаковым показателям степеней
Приведение к одинаковым основаниям степеней
Тип
Метод
Два разных основания степеней-
одинаковые показатели
Одинаковые основания степеней — разные показатели
Деление на меньшее основание в степени уравнения
Приведение к одинаковым показателям степеней
Тип
Метод
Одинаковые основания степеней — одинаковые показатели степеней
Замена переменной
Тип
Метод
Произведение степеней
Приведение к одному основанию степени
Тип
Метод
Простейшие показательные уравнения
Логарифмирование
ОТВЕТ
Методы решения показательных неравенств.
Показательным неравенством называется неравенство, содержащее переменную в показателе степени (к тому же, переменная может быть и в основании степени).
Для успешного решения показательных неравенств необходимо:
— безошибочно решать простейшие показательные неравенства.
— не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» решений, а тем более, — не терять решений неравенств.
— чётко, подробно и без ошибок проделывать математические преобразования
неравенств.
— знать методы решения задач. Для этого:
определить тип неравенств;
вспомнить соответствующий этому типу метод решения задачи.
Тип
Метод
Три разных основания степеней
Разложение оснований на множители и сведение к двум основаниям степени
Тип
Метод
Два разных основания степеней-
разные показатели
Основания степеней –
степени одного числа
Приведение к одинаковым показателям степеней
Приведение к одинаковым основаниям степеней
Тип
Метод
Два разных основания степеней-
одинаковые показатели
Одинаковые основания степеней — разные показатели
Деление на меньшее основание в степени уравнения
Приведение к одинаковым показателям степеней
Тип
Метод
Одинаковые основания степеней — одинаковые показатели степеней
Замена переменной
Тип
Метод
Произведение степеней
Приведение к одному основанию степени
Тип
Метод
Простейшие показательные неравенства
Логарифмирование и использование монотонности показательной функции
ОТВЕТ
Методы решения логарифмических уравнений.
Логарифмическим уравнением называется уравнение, содержащее переменную под знаком логарифма и/или в основании логарифма.
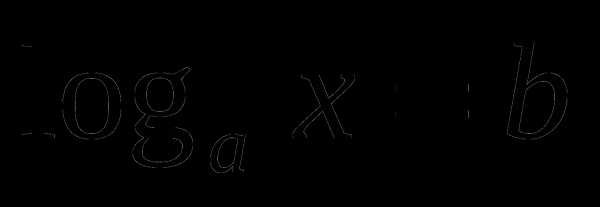 , a>0, a
, a>0, a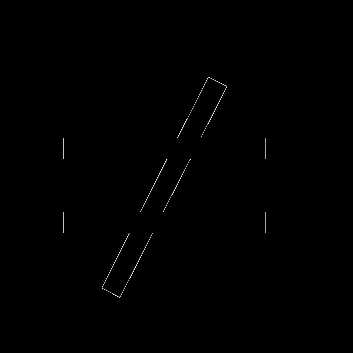 1, x>0.
1, x>0.
Для успешного решения логарифмических уравнений необходимо:
— безошибочно решать простейшие логарифмические уравнения.
— не только активно знать все логарифмические тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
уравнений.
— знать методы решения задач. Для этого:
определить тип уравнения;
вспомнить соответствующий этому типу метод решения задачи.
Тип
Метод
Разные основания логарифмов
Приведение к одинаковым основаниям логарифмов
Тип
Метод
Одинаковые основания логарифмов — разные выражения под логарифмами
Приведение к одинаковым выражениям под логарифмами
Тип
Метод
Одинаковые основания логарифмов – одинаковые выражения под логарифмами
Замена переменной
Тип
Метод
Сумма логарифмов
Сворачивание в один логарифм
Тип
Метод
Простейшие логарифмические уравнения
Потенцирование
ОТВЕТ
Необходимо всегда помнить, что логарифм определён при выполнении трёх условий:
— выражение под логарифмом больше нуля;
— основание логарифма больше нуля
— основание логарифма не равно единице.
Методы решения логарифмических неравенств.
Логарифмическим неравенством называется неравенство, содержащее переменную под знаком логарифма и/или в основании логарифма.
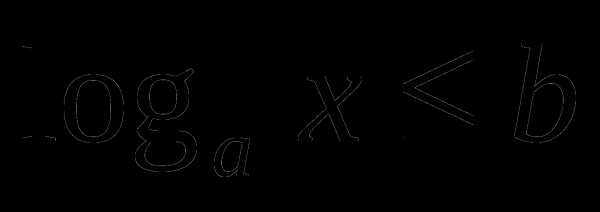 , a>0, a
, a>0, a 1, x>0.
1, x>0.
Для успешного решения логарифмических неравенств необходимо:
— безошибочно решать простейшие логарифмические неравенства.
— не только активно знать все логарифмические тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать «посторонних» корней, а тем более, — не терять решений уравнения.
— чётко, подробно и без ошибок проделывать математические преобразования
уравнений.
— знать методы решения задач. Для этого:
определить тип неравенства;
вспомнить соответствующий этому типу метод решения задачи.
Тип
Метод
Разные основания логарифмов
Приведение к одинаковым основаниям логарифмов
Тип
Метод
Одинаковые основания логарифмов — разные выражения под логарифмами
Приведение к одинаковым выражениям под логарифмами
Тип
Метод
Одинаковые основания логарифмов – одинаковые выражения под логарифмами
Замена переменной
Тип
Метод
Сумма логарифмов
Сворачивание в один логарифм
Тип
Метод
Простейшие логарифмические уравнения
Потенцирование и использование монотонности логарифмической функции
ОТВЕТ
Необходимо всегда помнить, что логарифм определён при выполнении трёх условий:
— выражение под логарифмом больше нуля;
— основание логарифма больше нуля
— основание логарифма не равно единице.
infourok.ru
