.Подготовка к олимпиадам по математике в начальных классах
Выступление на секции учителей начальных классов
Тема: .Подготовка к олимпиадам
по математике в начальных классах
Учитель начальных классов МБОУ СОШ №2:
Федянина Н.Л.
Август 2017год
В последние годы проводится много различных математических олимпиад. Кроме традиционных олимпиад, проводятся также дистанционные, устные, заочные, нестандартные и другие виды олимпиад. Математические олимпиады не только дают ценные материалы для суждения о степени математической подготовленности учащихся и выявляют наиболее одаренных и подготовленных молодых людей в области математики, но и стимулируют углубленное изучение предмета.
Основная цель школьных олимпиад:
выявление талантливых ребят,
развитие творческих способностей и интереса к научно-исследовательской деятельности у обучающихся,
создание необходимых условий для поддержки одаренных детей,
распространение научных знаний среди молодежи.
Олимпиады готовят учащихся к жизни в современных условиях, в условиях конкуренции. Победы учащихся на олимпиадах международного и всероссийского уровней являются достаточным основанием для зачисления в вуз на льготных условиях.
Олимпиадные задачи по математике -это задачи повышенной трудности, нестандартные по формулировке или по методам их решения.
При таком подходе к определению в их число попадут как нестандартные задачи использующие необычные идеи и специальные методы решения, так и стандартные задачи, но допускающие более быстрое, оригинальное решение.
В настоящее время издано большое количество сборников с описанием олимпиадных заданий: Русанов В.Н. «Математические олимпиады младших школьников», Королёва Е.В. «Предметные олимпиады в начальной школе», Белицкая Н.Г. «Школьные олимпиады. Начальная школа», Ю.А. Дробышев «Математические олимпиады –как средство развития исследовательских способностей обучающихся» и другие..
После анализа литературы, содержащей олимпиадные задания можно выделить следующие их типы.
Пример задачи или задания
Задачи
На «сообразительность» (на смекалку)
На столе в корзине лежало 7 груш. Рядом поставили пустую корзину. Как ты думаешь, больше стало груш на столе? Почему?
У собаки 2 правые лапы, 2 левые лапы, 2 лапы впереди и 2 лапы сзади. Сколько лап у собаки?
На «рассуждение»
Оля моложе Димы, а Дима моложе Коли. Кто моложе: Оля или Коля?
На «перебор» (комбинаторные)
На день рождения к Оле пришли 9 учеников первого класса – мальчиков и девочек. Сколько могло быть среди гостей мальчиков и сколько девочек?
Задачи – шутки
Коля свой дневник с двойками закопал на глубину 2 метра, а Толя закопал свой дневник на глубину 6 метров. На сколько метров глубже закопал свой дневник с двойками Толя?
Задачи на планирование действий
Коротышки из Цветочного города решили объехать на автомобиле озеро. Это озеро имеет форму круга и его можно объехать на машине за 5 дней. Однако бак автомобиля вмещает горючего лишь на один день пути, и ещё можно увести на автомобиле горючего на два дня. Коротышки в месте, показанном точкой А, основали базу с горючим и продуктами. Можно организовывать хранение запасов и в других местах берега озера.
Каким образом Знайка организовал путешествие? Сколько времени потребуется на подготовку путешествия и его проведение?
Задачи в стихах
Взял иголку Ежик в лапки,
Стал он шить зверятам шапки.
Пять — для маленьких зайчат,А четыре — для волчат.
Ежик шапки шьет толково.
Сколько шапок у портного?
(Девять.)
Арифметические задания
Установление зависимости между компонентами арифметических действий
Что произойдёт с суммой, если одно слагаемое увеличить на 72, а второе уменьшить на 12
Восстановление пропущенных знаков действий и цифр.
873*
**67
9*03
Поиск рациональных способ вычислений.
Найди более легкий способ вычислений
1+2+3+4+5+6+7+8+9
Геометрические задания
На знание геометрических фигур и понятий
Какие из данных фигур являются ломаными? Обведи их.
О Z S
Какие геометрические фигуры здесь нарисованы? Сколько их?
На конструирование
На переконструирование
Из спичек составили фигуру. Убери 4 спички так, чтобы осталось 5 одинаковых квадратов.
На знание единиц измерения
Спутник Земли делает один оборот за 1 час 40 минут. Однако другой оборот он совершает за 100 минут. Как это объяснить?
На пространственное воображение
Квадратный лист бумаги сложили пополам, затем ещё раз пополам и от полученного квадратика отрезали маленький уголок. Затем лист бумаги развернули. Что не могло получиться?
Логические задания
На нахождение пропущенной фигуры или числа в ряду
5,15,30 6,18,36 4,?,?
7 9 11 5 6
14 18 22 10 ?На продолжение ряда фигур или чисел
Установи правило, по которому составлен данный ряд чисел, и продолжи его, записав ещё 3 числа:
Какими будут 2 следующих знака? Обведи правильный ответ.
40 а 100 рона
Впишите в пустые кружки числа от 4 до 9, чтобы их сумма в каждом из пяти рядов (двух вертикальных, одном горизонтальном и двух наклонных) была одинакова. Все цифры в задании разные.
Ответ: сумма 18.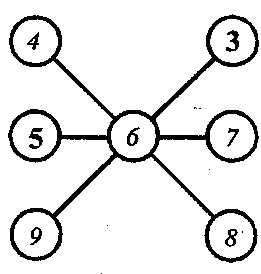
Занимательный квадрат.
Расставьте квадратах такие числа, чтобы в сумме во
всех клетках по всем направлениям было 9.
Алгебраические задания
Реши уравнение
12х-4х+13=61
Как добиться успешного участия школьника в математической олимпиаде? Тренироваться, тренироваться и ещё раз тренироваться, — скажете вы. И это правильно. Но ведь прежде необходимо увлечь детей математикой. А как это сделать?
Можно выделить несколько этапов
1 этап: Прежде всего, необходимо просто отыскать таких детей, разглядеть среди множества учеников несколько «звездочек», восприимчивых к новой информации, не боящихся трудностей, умеющих находить нетривиальные способы решения поставленных перед ними задач.
2 этап: Разработка личностно — ориентированного подхода к обучению одаренных, способных детей.
3 этап: Развитие в способных учащихся психологию лидера, осторожно чтобы это не привело к появлению «звездной болезни». Но и не стесняться показывать свои способности, не бояться выражать свои мысли, хотя бы потому, что они нестандартны и не имеют аналогов.
Для успеха в конкурсной математике, конечно, нужно решать задачи. Успех связан не только со способностями, но и со знанием классических олимпиадных задач.
Начиная с 1 класса в начале каждого урока можно включать в устный счет хотя бы одну задачу, требующую нестандартного подхода при своем решении. В младших классах это может быть задача со сказочным сюжетом, с нестандартными вычислениями, но требующие умения размышлять, анализировать задания, направленные на развитие сообразительности и логического мышления. Можно назвать этот этап урока «Утренней сказкой» или «Разминкой».
Рассмотрим варианты заданий, используемых на уроках математики для развития познавательного интереса к предмету.
1.Различные занимательные задания для отработки арифметических навыков сложения и вычитания во время индивидуальной работы у доски либо на карточках представлены в работе Е.П. Фефиловой, Е.А.Поторочиной (30 )
Математические бусы
Заселяем домики
Весёлые человечки
2. Отработка арифметических навыков сложения и вычитания во время фронтальной работы.
3. Игры.
Дети по цепочке воспроизводят ряд чисел от 0 до 10 через одно. Называние чисел сначала идёт в прямом, затем в обратном направлении.
1
9
-2
+2
Эстафета проводится между двумя командами по 5 человек.
Выходят к доске 2 ребёнка; они прибавляют 2 к числу в окошечке и пишут ответ на ступеньку выше, затем мел передаётся вторым членам команды. Побеждает та команда, которая первой придёт к флажку.
4. Логические упражнения.Большое количество разнообразных логических упражнений предлагается в учебниках Т.К. Жикалкиной, Н.Б.Истоминой, Л.Г.Петерсон, И.И. Аргинской, С.И. Волковой и Н.Н.Столяровой. Вот некоторые из них:
Разгадай правило, продолжи ряд (чисел или геометрических фигур).
Поиск девятого
?
Вставь число.
1 2 3 4 5
2 4 8 10
5. Геометрические задания. Истомина Н.Б. и Шадрина И.В. являются авторами тетрадей «Наглядная геометрия». Выполнение заданий, предложенных в этой тетради, способствует формированию у учащихся представлений о форме предметов, их взаимном расположении и расположении на плоскости; развивает пространственное мышление младших школьников. Эту тетрадь можно использовать, работая с детьми и по другим учебникам математики для начальной школы.
Задания на конструирование и переконструирование из счётных палочек. Такого вида задания встречаются у многих авторов учебников по математике для начальных классов.
— Составьте фигуру из палочек
— Переложите 4 палочки так, чтобы получилось 4 треугольника.
-Задания на нахождение и пересчёт геометрических фигур на чертеже.
Сколько на чертеже треугольников? (задание из учебника Т.К.Жикалкиной)
6. Задачи
На рассуждение.
На сообразительность
Комбинаторные. Задачи такого вида встречаются в учебниках С.И.Волковой, Н.Н. Столяровой, Т.К. Жикалкиной. Выпущены тетради с печатной основой « Учимся решать комбинаторные задачи» автор Н.Б.Истомина. Выполнение заданий, предложенных в тетради, способствует формированию у учащихся приёмов умственной деятельности (анализ, синтез, сравнение), развивает такие качества мышления, как гибкость и критичность, расширяет представление младших школьников о способах моделирования при решении текстовых задач.
7.Математические кроссворды. Этот интересный вид работы предлагает Т.К.Жикалкина. В заданиях прослеживаются межпредметные связи с уроками литературы и окружающего мира.
Методические подходы подготовки учащихся к олимпиадам могут быть различными.? На основе собственного опыта могу предложить условия подготовки к олимпиадам.
Условия подготовки к олимпиадам:
1. Отбор учащихся, выявляющих общие и определенные способности по предмету. Идеальным контингентом для подготовки являются высокомотивированные к освоению математики учащиеся, высокий уровень их как общих, так и специфических способностей, высокая работоспособность в выполнении заданий (умение работать с различными источниками знаний, умение осуществлять многовариантные решения поставленных проблем). Отбор осуществляю в ходе наблюдения на уроках, организации исследовательской деятельности, проведения внеклассных мероприятий. Я веду отбор и привлекаю к участию в олимпиадах учащихся с 1 класса. И уже к 4-му классу имею резерв из 4-5 учащихся, способных защищать честь школы на муниципальном этапе олимпиады. Одновременно с выявлением школьников интересующихся математикой и формированием этого интереса, должно происходить создание творческой группы, команды школьников готовящихся к олимпиадам. Несмотря на то, что основной формой подготовки школьников к олимпиаде является индивидуальная работа, наличие такой команды имеет большое значение. Она позволяет реализовать взаимопомощь, передачу опыта участия в олимпиадах, психологическую подготовку новых участников.
2. Подготовка к олимпиаде через внеурочные занятия. Организация развивающей среды, стимулирующей любознательность и обеспечение её удовлетворения, осуществляется через внеурочную деятельность: различные конкурсы, кружки, факультативы, посещение библиотек.
3. Использование творческих заданий повышенного уровня на уроках. Как правило, участники олимпиад всегда на уроках получают индивидуальные задания олимпиадного уровня сложности, это касается и домашних заданий. Кропотливая работа будет результативна, если отношения между учителем и учениками будут партнерским. Превосходство учителя выражается лишь в уровне знаний, умений и его способности передать их ученику.
Принципы при подготовке к олимпиаде:
При подготовке учащихся к олимпиаде я придерживаюсь нескольких принципов:
1.Максимальная самостоятельность – предоставление возможности самостоятельного решения заданий. Самые прочные знания это те, которые добываются собственными усилиями, в процессе работы с литературой при решении различных заданий. Данный принцип, предоставляя возможность самостоятельности учащегося, предполагает тактичный контроль со стороны учителя, коллективный разбор и анализ нерешенных заданий, подведение итогов при решении задач.
2. Активность знаний:
Олимпиадные задания составляются так, что весь запас знаний находится в активном применении. Они составляются с учётом всех предыдущих знаний, в соответствии с требованиями стандарта образования и знаниями, полученными в настоящий момент. При подготовке к олимпиадам постоянно происходит углубление, уточнение и расширение запаса знаний. Исходя из этого, следует, что разбор олимпиадных заданий прошлых лет является эффективной формой подготовки учащихся для успешного участия в олимпиадах.
3. Принцип опережающего уровня сложности:
Для успешного участия в олимпиаде необходимо вести подготовку по заданиям высокого уровня сложности. В этом заключается суть принципа опережающего уровня сложности, эффективность которого подтверждается результатами выступлений на олимпиаде. В психологическом плане реализация этого принципа придает уверенность учащемуся, раскрепощает его и дает возможность успешно реализоваться.
4. Анализ результатов прошедших олимпиад:
При анализе прошедших олимпиад вскрываются упущения, недостатки, находки, не учтённые в предыдущей деятельности, как учителя, так и ученика. Этот принцип обязателен для учителя, так как он положительно повлияет на качество подготовки к олимпиаде. Но он также необходим для учащихся, так как способствует повышению прочности знаний и умений, развивает умение анализировать не только успехи, но и недостатки.
5.Индивидуальный подход:
Индивидуальная программа подготовки к олимпиаде для каждого учащегося, отражающая его специфическую траекторию движения от незнания к знанию, от неумения решать сложные задачи к творческим навыкам выбора способа их решения.
6. Психологический принцип:
Считаю необходимым воспитать в олимпиадниках чувство здоровой амбициозности, стремления к победе. Победитель всегда обладает бойцовскими качествами. Это важно для взрослой жизни! Нужно увидеть задатки в ребёнке и вырастить эти качества. Научить верить в свои силы, внушить, что он способен побеждать. Однако важно подчеркнуть, что победителями все не бывают. Не надо волноваться, в олимпиаде принимают участие такие же ребята, как и вы. И все находятся в равных условиях, результат зависит только от тебя. Все победить не могут. Не нужно расстраиваться, а нужно работать, работать и работать! Неприемлем принцип «административного давления» с целью удержать ученика, заставить его участвовать в олимпиаде по предмету. Это не принесет должного результата. Сам учитель должен быть образцом для ребёнка. Должен постоянно расти в профессиональном смысле, быть интересным ребятам, пользоваться авторитетом, не считаться с личным временем для дела. Тогда ученик стремится не подвести своего учителя. Подготовка олимпиадников возможна (успешная) лишь в случае постоянного тандема учитель-ученик-родитель. Подготовку к олимпиадам можно проводить и на уроках.
Работа на уроке:
1.Решение олимпиадных задач, связанных с темой урока:
На уроке всегда можно найти место задачам, развивающим ученика, причем в любом классе, по любой теме. Если выполнять действия по порядку, на это потребуется много времени. А время на олимпиадах очень ценно. Поэтому ученик, нашедший быстрое решение заданий, сэкономит время на решение других задач. При решении текстовых задач можно предлагать учащимся задачи, которые были на олимпиадах различного уровня.
2.Ребусы, анаграммы, криптограммы, софизмы на уроке.
Для развития интереса к решению нестандартных задач в программу урочных занятий нужно включать рассмотрение занимательных задач, ребусов, задач-шуток, анаграмм и криптограмм, софизмов, задач прикладного характера.
3.Творческие и олимпиадные домашние задания:
Один из путей подготовки к олимпиадам — задания на дом типа: составь задачу, аналогичную составленной в классе, придумайте ребусы по теме, составьте кроссворд (анаграмму, софизм и т.д.), придумайте задачу-сказку по теме и т.п. В качестве домашнего задания можно предложить домашние олимпиады, используя олимпиадные задачи прошлых лет. (Рекомендации учащимся: пользоваться дополнительной литературой, вести поиск решения задач, решать их самостоятельно).
4.Внеклассная работа:
Каждый учитель под внеклассной работой понимает необязательные систематические занятия учащихся с преподавателем во внеурочное время. Внеклассная работа может осуществляться в самых разнообразных видах и формах. Можно выделить следующие три вида внеклассной работы.
Индивидуальная работа — такая работа, когда учитель принимает решение о выборе методики в каждой конкретной ситуации, в зависимости от способностей и знаний ученика.
Групповая работа — систематическая работа, проводимая с достаточно постоянным коллективом учащихся — факультативы, кружки. В процессе таких занятий происходит расширение и углубление знаний, развитие интереса учащихся к предмету, развитие их предметных способностей. Процесс обучения строится как совместная исследовательская деятельность учащихся.
Массовая работа — эпизодическая работа, проводимая с большим детским коллективом: научно — практические конференции, предметные недели, конкурсы, соревнования и разного вида олимпиады.
5.Применение ИКТ в современном учебном процессе:
Использование информационно коммуникационных технологий во внеклассной работе дает возможность для повышения мотивации обучения, индивидуальной активности, формирования информационной компетенции, свободы творчества, интерактивности обучения. Использование информационно-компьютерных технологий способствуют реализации принципа индивидуализации обучения, столь необходимого для одаренных учащихся, при подготовке к олимпиадам. При подготовке к олимпиадам необходимо предоставлять ученикам возможность пользоваться передовыми информационными технологиями. Ведь учитель сегодня должен не просто учить, а учить учиться. В работе можно опираться на интернет источники, позволяющие разнообразить теоретический материал и практические задания. Учащимся рекомендовать сайты для использования, содержащие теоретический материал по разнообразным темам, олимпиадные задачи с подробным решением, игры, конкурсы по математике.
С 1 класса учащиеся моего класса активно участвуют и занимают призовые места пока в дистанционных и заочных олимпиадах и конкурсах . Таких как « Олимпиада Плюс», Блиц-турнир «Математический сундучок», международная олимпиада «Осень -2016» проекта «Инфоурок».
Опыт моей работы позволяет сделать следующие выводы о необходимых условиях подготовки учащихся к олимпиадам:
Повышение интереса учащихся к углубленному изучению предметов.
Создание оптимальных условий для выявления одаренных школьников, их интеллектуального развития и профессиональной ориентации;
Пропаганда научных знаний и развитие у школьников интереса к научной деятельности;
Развитие у учащихся логического мышления, умения интегрировать знания и применять их для решения нестандартных задач;
infourok.ru
Репетитор по олимпиадной математике
Укажите ваш часовой пояс:Выберите из списка(UTC-12:00) Линия перемены дат(UTC-11:00) Время в формате UTC -11(UTC-10:00) Алеутские острова(UTC-10:00) Гавайи(UTC-09:30) Маркизские острова(UTC-09:00) Аляска(UTC-09:00) Время в формате UTC -09(UTC-08:00) Нижняя Калифорния(UTC-08:00) Время в формате UTC -08(UTC-08:00) Тихоокеанское время (США и Канада)(UTC-07:00) Аризона(UTC-07:00) Ла-Пас, Мазатлан, Чихуахуа(UTC-07:00) Горное время (США и Канада)(UTC-06:00) Центральная Америка(UTC-06:00) Центральное время (США и Канада)(UTC-06:00) о. Пасхи(UTC-06:00) Гвадалахара, Мехико, Монтеррей(UTC-06:00) Саскачеван(UTC-05:00) Богота, Кито, Лима, Рио-Бранко(UTC-05:00) Четумаль(UTC-05:00) Восточное время (США и Канада)(UTC-05:00) Гаити(UTC-05:00) Гавана(UTC-05:00) Индиана (восток)(UTC-04:00) Острова Теркс и Кайкос(UTC-04:00) Асунсьон(UTC-04:00) Атлантическое время (Канада)(UTC-04:30) Каракас(UTC-04:00) Куяба(UTC-04:00) Джорджтаун, Ла-Пас, Манаус, Сан-Хуан(UTC-04:00) Сантьяго(UTC-03:30) Ньюфаундленд(UTC-03:00) Арагуаяна(UTC-03:00) Бразилия(UTC-03:00) Кайенна, Форталеза(UTC-03:00) Буэнос-Айрес(UTC-03:00) Гренландия(UTC-03:00) Монтевидео(UTC-03:00) Пунта-Аренас(UTC-03:00) Сен-Пьер и Микелон(UTC-03:00) Сальвадор(UTC-02:00) Время в формате UTC -02(UTC-02:00) Среднеатлантическое время — старое(UTC-01:00) Азорские о-ва(UTC-01:00) О-ва Зеленого Мыса(UTC) Время в формате UTC(UTC) Касабланка(UTC) Дублин, Лиссабон, Лондон, Эдинбург(UTC) Монровия, Рейкьявик(UTC+01:00) Амстердам, Берлин, Берн, Вена, Рим, Стокгольм(UTC+01:00) Белград, Братислава, Будапешт, Любляна, Прага(UTC+01:00) Брюссель, Копенгаген, Мадрид, Париж(UTC+01:00) Сан-Томе и Принсипи(UTC+01:00) Варшава, Загреб, Сараево, Скопье(UTC+01:00) Западная Центральная Африка(UTC+02:00) Амман(UTC+02:00) Афины, Бухарест(UTC+02:00) Бейрут(UTC+02:00) Каир(UTC+02:00) Восточная Европа(UTC+02:00) Дамаск(UTC+02:00) Сектор Газа, Хеврон(UTC+02:00) Хараре, Претория(UTC+02:00) Вильнюс, Киев, Рига, София, Таллин, Хельсинки(UTC+02:00) Иерусалим(UTC+02:00) Калининград (RTZ 1)(UTC+02:00) Khartoum(UTC+02:00) Триполи(UTC+01:00) Виндхук(UTC+03:00) Багдад(UTC+02:00) Стамбул(UTC+03:00) Кувейт, Эр-Рияд(UTC+03:00) Минск(UTC+03:00) Волгоград, Москва, Санкт-Петербург (RTZ 2)(UTC+03:00) Найроби(UTC+03:30) Тегеран(UTC+04:00) Абу-Даби, Мускат(UTC+04:00) Астрахань, Ульяновск(UTC+04:00) Баку(UTC+04:00) Ижевск, Самара (RTZ 3)(UTC+04:00) Порт-Луи(UTC+04:00) Саратов(UTC+04:00) Тбилиси(UTC+04:00) Ереван(UTC+04:30) Кабул(UTC+05:00) Ашхабад, Ташкент(UTC+05:00) Екатеринбург (RTZ 4)(UTC+05:00) Исламабад, Карачи(UTC+05:30) Колката, Мумбаи, Нью-Дели, Ченнай(UTC+05:30) Шри-Джаявардене-пура-Котте(UTC+05:45) Катманду(UTC+06:00) Астана(UTC+06:00) Дакка(UTC+06:00) Омск(UTC+06:30) Янгон(UTC+07:00) Бангкок, Джакарта, Ханой(UTC+07:00) Барнаул, Горно-Алтайск(UTC+07:00) Ховд(UTC+07:00) Красноярск (RTZ 6)(UTC+06:00) Новосибирск (RTZ 5)(UTC+07:00) Томск(UTC+08:00) Гонконг, Пекин, Урумчи, Чунцин(UTC+08:00) Иркутск (RTZ 7)(UTC+08:00) Куала-Лумпур, Сингапур(UTC+08:00) Перт(UTC+08:00) Тайбэй(UTC+08:00) Улан-Батор(UTC+08:30) Пхеньян(UTC+08:45) Юкла(UTC+09:00) Чита(UTC+09:00) Осака, Саппоро, Токио(UTC+09:00) Сеул(UTC+09:00) Якутск (RTZ 8)(UTC+09:30) Аделаида(UTC+09:30) Дарвин(UTC+10:00) Брисбен(UTC+10:00) Канберра, Мельбурн, Сидней(UTC+10:00) Гуам, Порт-Морсби(UTC+10:00) Хобарт(UTC+10:00) Владивосток, Магадан (RTZ 9)(UTC+10:30) Лорд-Хау(UTC+11:00) Остров Бугенвиль(UTC+11:00) Чокурдах (RTZ 10)(UTC+10:00) Магадан(UTC+11:00) Остров Норфолк(UTC+11:00) Сахалин(UTC+11:00) Соломоновы о-ва, Нов. Каледония(UTC+12:00) Анадырь, Петропавловск-Камчатский (RTZ 11)(UTC+12:00) Веллингтон, Окленд(UTC+12:00) Время в формате UTC +12(UTC+12:00) Фиджи(UTC+12:00) Петропавловск-Камчатский — устаревшее(UTC+12:45) Чатем(UTC+13:00) Время в формате UTC +13(UTC+13:00) Нукуалофа(UTC+13:00) Самоа(UTC+14:00) О-в Киритимати
www.tutoronline.ru
|
Математика. Районные олимпиады. 6—11 классы / Агаханов Н.X., Подлипский О.К. — М. : Просвещение, 2010. Скачать |
|

|
Математика. Областные олимпиады. 8—11 классы / Н. X. Агаханов, И. И. Богданов, П. А. Кожевников и др. — М. : Просвещение, 2010. Скачать |

|
Математика. Всероссийские олимпиады. Вып. 1 / Н. X. Агаханов, И. И. Богданов, П. А. Кожевников и др. — М. : Просвещение, 2008. Скачать |

|
Математика. Всероссийские олимпиады. Вып. 2 / Н. X. Агаханов, О. К. Подлипский — М. : Просвещение, 2009. Скачать |
|
Математика. Международные олимпиады / Н. X. Агаханов, П. А. Кожевников, Д. А. Терешин. — М. : Просвещение, 2010. Скачать |
|

|
Ленинградские математические кружки / Генкин С.А., Итенберг И.В., Фомин Д.В. — Киров, «Аса», 1994. Скачать |
|
Сборник олимпиадных задач по математике. / Горбачев Н.В. — М.: МЦНМО, 2004. Скачать |
|
|
Математические олимпиады в школе. 5-11 классы. 8-е изд., испр. и доп. / Фарков А.В. — М.: Айрис-пресс, 2009. Скачать |
|
|
Московские математические олимпиады 1993—2005 г. / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. Скачать |
|
|
1001 олимпиадная и занимательная задачи по математике. 3-е изд. / Балаян Э.Н. — Ростов н/Д : Феникс, 2008. Скачать |
ermolovskiy.ru
Материалы для подготовки к олимпиаде по математике
Математическое образование в общеобразовательной школе в первую очередь направлено на усвоение учениками алгоритмов решения стандартных задач. Но при работе с одаренными учениками придется иметь дело с задачами, при решении которых традиционных способов недостаточно.
Относительно математических способностей учеников в образовательной среде «ходят» достаточно разные мысли. Некоторые говорят, что для развязывания олимпиадных задач необходимы исключительные способности, другие утверждают, что для этого необходимо иметь особенную, «математическую память» для запоминания формул и способов решения. Невозможно отрицать то, что есть ученики с сильно выраженными наклонностями к той или другой умственной деятельности, но иногда, найдя таких учеников, мы не замечаем рядом тех, у кого такие способности «скрыты» по тем или другим причинам. Мы, учителя, лишь помогаем нашим ученикам развиваться, достигать лучших результатов. Главное задание учебы — учить учеников мыслить.
Логические задачи
Не будем давать определения логической задачи, ведь любая задача требует четких и правильных рассуждений во время ее решения. Но рассмотренные задачи будем относить к логическим, часто они имеют интересный сюжет, а их решение сводится к построению последовательных нескольких «очевидных» выводов. Все трудности решения логической задачи и заключаются в нахождении такой «цепочки» простых рассуждений и выводов.
Задачи на переливание
Задачу на переливание называют задачей Пуассона, это знаменитый французский математик, механик и физик. Когда он был еще молодым и колебался в выборе жизненного пути, приятель, показал ему несколько задач, которые сам не смог решать. Пуассон быстро развязал все. Но особенно ему понравилась задача о двух сосудах: «Кое-кто имеет 12 пинт виноградного сока(пинта это 0,568л) и хочет подарить половину вторую, но у него лишь два пустых сосуда: одна — 8, вторая — 5 пинт. Каким образом налить в больший сосуд 6 пинт»?. «Эта задача определила мою судьбу, — говорил Пуассон. — Я решил, что обязательно стану математиком».
Задачи на переливание помогают развивать логическое мышление, пространственное воображение, выдержку, настойчивость в нахождении оптимального решения. Традиционно в задачах на переливание сосуда не имеют делений, то есть переливать можно лишь до тех пор, пока сосуд, в который наливаем, не заполнится до конца, или пока вовсе не опустеет сосуд, из которого переливаем. Просто так остановиться на середине или разлить содержимое сосуда на две равных части тоже не выйдет.
При использовании олимпиад них задач на переливание нужное средство для развития зрительной памяти, потому что поиск правильного хода решения требует контроль нескольких параметров емкостей. Если в одном из них находится вещество, то вместе с объемом налитого нужно помнить еще об объеме пустой части. А это уже целых два параметра.
Чтобы упростить счет всех возможностей по изменению состояния лучшие занести данные об объемах каждой емкости в специальную таблицу. В каждую колонку занести состояние всех емкостей после каждого измерения. От ученика требуется возможность внимательно следить за их параметрами, во избежание повторений. Если перечислить все возможные варианты, ни повторяясь, то среди них обязательно найдется искомая величина.
Задача 1 . Как с помощью 3-литрового и 5-литрового ведер набрать 1 литр воды? В нашем распоряжении есть водопроводный кран и раковина, куда можно выливать воду.
Решение.
Решение этой задачи можно записать в виде таблицы. Сначала оба ведра пустые. Наполняем 3-литровое ведро и выливаем воду из него в 5-литровое. Опять наполняем 3-литровое ведро и выливаем ее в 5-литровое, пока оно не наполнится. В
3-литровом ведре останется 1 литр воды.
| 3 литры | 0 | 3 | 0 | 3 | 1 |
| 5 литров | 0 | 0 | 3 | 3 | 5 |
Задача 2 . Имеем две емкости 5 и 7 л. Как с помощью емкостей отмерять 6 л воды из крана?
Решение.
Сложим таблицу решения :
| 7 л | 7 | 2 | 2 | 0 | 77 | 4 | 4 | 0 | 7 | 6 |
| 5 л | 0 | 5 | 0 | 2 | 2 | 5 | 0 | 4 | 4 | 5 |
Задача 3 . Имеем три емкости: 9 л, 5 л, 3 л. Первая наполнена водой, а другие две пустые. Как с помощью этих емкостей отмерять 1 л воды? Как отмерять 4 л воды?
Решение:
| 3 л | 0 | 3 | 3 | 4 |
| 5 л | 0 | 0 | 5 | 5 |
| 9 л | 9 | 6 | 1 | 0 |
Задача 4 . В трех кучках лежат 22, 14 и 12 орехов. С помощью трех переложений уравняйте количество орехов в кучках.
Решение: Поскольку орехов всего 48, то в каждой кучке должно очутиться по 16. Переводить из одной кучки в другую можно столько орехов, сколько их есть в куче, в которую перекладывают. Схематически переложение можно показать так:
(22,14,12) — (8,28,12) — (8,16,24) — (16,16,16).
Задача 5. Как отмерять 4л воды с помощью банок вместимостью 3л и 5л?
Решение
| банки | Переливание | |||||||
| 5л | 0л | 3л | 3л | 5л | 0л | 1л | 1л | 4л |
| 3л | 3л | 0л | 3л | 1л | 1л | 0л | 3л | 0л |
Задача 6. Как с помощью двух бидонов вместимостью 4л и 5л налить в ведро 3л воды, если объем ведра не меньше чем 3л?
Решение.
| Сосуды | Переливание | ||||
| 5л | 0л | 4л | 4л | 5л | 5л |
| 4л | 4л | 0л | 4л | 3л | 0л |
| Не меньше чем 3л | 0л | 0л | 0л | 0л | 3л |
Задада 7 Рядом с лабораторией протекает бурная река. Как с помощью двух сосудов объемом 3 и 5 литров отмерять ровно 4 литра речной воды?
Решение
| Шаг | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3л | 0 | 0 | 3 | 0 | 2 | 2 | 3 |
| 5л | 0 | 5 | 2 | 2 | 0 | 5 | 4 |
| река |
4 литра могут поместиться лишь в 5-литровый сосуд. Они могут быть получены после доливания 1 литра до 3, 2 литров до 2, 3 литров до 1, или путем отливания от 5 литров 1 литра. Чтобы можно было отлить, ровно 1 литр, нужно, чтобы в сосуде назначения было свободное место, ровно для 1 литра, то есть, чтобы в 3-литровом сосуде перед этим были 2 литра. Разницу объемов сосудов легко получить: 2 литра выходят, если набрать полный 5-литровый сосуд и отлить из нее в пустой 3-литровый сосуд. После этого их надо перелить в 3-литровый сосуд, загодя опорожнив ее обратно в реку.
Задача 8. У большого алхимика есть нерастворимая колба, в которой содержится 12 миллилитров серной кислоты, а также две нерастворимых мензурки объемом 5 и 7 миллилитров. Как ему получить две порции по 6 миллилитров серной кислоты, необходимых для опыта? (Кислота растворит любую другую посуду в лаборатории.)
Решение
| шаг | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 12 мл | 12 | 5 | 5 | 10 | 10 | 3 | 3 | 8 | 8 | 1 | 1 | 6 |
| 5мл | 0 | 0 | 5 | 0 | 2 | 2 | 5 | 0 | 4 | 4 | 5 | 0 |
| 7 мл | 0 | 7 | 2 | 2 | 0 | 7 | 4 | 4 | 0 | 7 | 6 | 6 |
Задача 9 Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По пути нарвал букет цветов, чтобы подарить пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меду, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л»! Винни-Пух долго думал, но все-таки смог развязать задачку. Как он это сделал?
Решение
| шаг | 1 | 2 | 3 | 4 | 5 | 6 |
| 5л | 5 | 2 | 2 | 0 | 5 | 4 |
| 3л | 0 | 3 | 0 | 2 | 2 | 3 |
Или
| шаг | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 5л | 0 | 3 | 3 | 5 | 0 | 1 | 1 | 4 |
| 3л | 3 | 0 | 3 | 1 | 1 | 0 | 3 | 0 |
Задача 10. Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: одна — вместимостью в 8 л, а другая — вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
Решение
| Шаг | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12л | 12 | 4 | 4 | 9 | 9 | 1 | 1 | 6 |
| 8л | 0 | 8 | 3 | 3 | 0 | 8 | 6 | 6 |
| 5л | 0 | 0 | 5 | 0 | 3 | 3 | 5 | 0 |
Задачи на соответствии между множествами
В каждой из этих задач нужно установить такие соответствия между двумя или тремя множествами, чтобы они удовлетворяли приведенные условия. Обычно задачи на соответствии между множествами решают с помощью таблиц, в строках и столбцах которых записывают элементы поданных множеств, а в соответствующих ячейках ставят знаки « -» или «+» в зависимости от того, выполняется или нет и или другое условие.
Задача 1. В бутылку, стакан, крынку и банку налито молоко, лимонад, квас и вода. Известно, что вода и молоко — не в бутылке, сосуд с лимонадом стоит между крынкой и сосудом с квасом, в банке — не лимонад и не вода, стакан стоит около банки и сосуды с молоком. В который из сосудов налит каждый из напитков?
Решение.
Нужно установить соответствие между двумя множествами — сосудов и напитков. Сложим таблицу:
| Бутылка | Стакан | Крынка | Банка | |
| Молоко | ||||
| Лимонад | ||||
| Квас | ||||
| Вода |
За условием вода и молоко — не в бутылке, а в банке — не лимонад и не вода. Следовательно, в соответствующие ячейки ставим знаки «-» :
| Бутылка | Стакан | Крынка | Банка | |
| Молоко | — | |||
| Лимонад | — | |||
| Квас | ||||
| Вода | — | — |
Поскольку сосуд с лимонадом стоит между крынкой и сосудом с квасом, то в крынке — не лимонад и не квас. Поскольку стакан стоит около банки и сосуды с молоком, то в стакане и в банке — не молоко. Ставим знаки «-» в соответствующей ячейки таблицы :
| Бутылка | Стакан | Крынка | Банка | |
| Молоко | — | — | — | |
| Лимонад | — | — | ||
| Квас | — | |||
| Вода | — | — |
Теперь очевидно, что в крынке — молоко, а в банке — квас. Тогда в крынку не может быть налитой воды, а квас не может быть налитым ни в бутылку, ни в стакан:
| Бутылка | Стакан | Крынка | Банка | |
| Молоко | — | — | — | |
| Лимонад | — | — | ||
| Квас | — | — | — | |
| Вода | — | — | — |
Расставив знаки «+» и «-» в соответствующие ячейки таблицы, делаем вывод, что в бутылке налит лимонад, тогда в стакане — вода.
| Бутылка | Стакан | Крынка | Банка | |
| Молоко | — | — | + | — |
| Лимонад | + | — | — | — |
| Квас | — | — | — | + |
| Вода | — | + | — | — |
Ответ: в бутылке — лимонад, в стакане — вода, в крынке — молоко, в банке — квас.
Задача 2. В гонках участвовали три гонщика: Иваненко, Петренко, Сидоренко. Они выступали на красном, желтом и белом автомобилях. Гонщик на красном автомобиле пришел к финишу раньше, чем Сидоренко. Гонщик на желтом автомобиле пришел к финишу не первым. Гонщик на белом автомобиле перегнал Петренка, хотя Петренко был не последним. Кто на каком автомобиле выступал?
Решение.
Нужно установить соответствие между двумя множествами — фамилиями гонщиков и цветами автомобилей. Поскольку гонщик на красном автомобиле пришел к финишу раньше, чем Сидоренко, то Сидоренко выступал не на красном автомобиле. Дальше из условия задачи делаем вывод, что Петренко пришел к финишу вторым. Поскольку Сидоренко не был первым, потому что за условием гонщик на красном автомобиле пришел к финишу раньше, чем Сидоренко, то первым пришел к финишу Иваненко, и он был на белом автомобиле, потому что за условием гонщик на белом автомобиле перегнал Петренка. Сложим таблицу и ставим «+» и «-» в соответствующих ячейках:
| Красный | Желтый | Белый | |
| Иваненко | — | — | + |
| Петренко | — | ||
| Сидоренко | — | — |
Теперь очевидно, что на красном автомобиле выступал Петренко, а Сидоренко выступал на желтом автомобиле:
| Красный | Желтый | Белый | |
| Иваненко | — | — | + |
| Петренко | + | — | — |
| Сидоренко | — | + | — |
Ответ: Иваненко выступал на белом автомобиле, Петренко — на красном, Сидоренко — на желтом.
Задача 3. В соревнованиях по бегу на 100м участвовали четверо друзей: Котиков, Маслов, Зайцев и Чижов. Один из них брюнет, второй, — блондин, третий, — шатен, четвертый, — рыжий. Котикову удалось перегнать рыжего, однако Маслов прибежал впереди Котикова. Зайцев прибежал раньше Чижова, но позже шатена. Маслов не шатен. Кто какое место занял?
Решение.
Нужно установить соответствие между множеством фамилий и множеством мест.
Поскольку Котикову удалось перегнать рыжего, то Котиков не мог занять последнее место. Поскольку Маслов прибежал впереди Котикова, а тот не на последнем месте, то маслов не мог занять ни третье, ни четвертое место. Поскольку Зайцев прибежал раньше Чижова, то Зайцев также не мог занять последнее место. Следовательно, последнее место занял Чижов. Сложим таблицу и ставим в соответствующие ячейки знаки «+» и «-»:
| 1 место | 2 место | 3 место | 4 место | |
| Котиков | — | |||
| Маслов | — | — | ||
| Зайцев | — | |||
| Чижов | — | — | — | + |
Поскольку Зайцев прибежал позже, по крайней мере, за шатена, то он не мог занять первое место. Поскольку Маслов не шатен, то Зайцев прибежал позже Котикова. За условием Маслов прибежал впереди Котикова. Следовательно, первое место занял Маслов:
| 1 место | 2 место | 3 место | 4 место | |
| Котиков | — | — | ||
| Маслов | + | — | — | — |
| Зайцев | — | — | ||
| Чижов | — | — | — | + |
Поскольку Зайцев прибежал позже за Котикова, то Котиков занял второе место, а Зайцев — третье:
| 1 место | 2 место | 3 место |
kopilkaurokov.ru
Видеолекции для подготовки к окружному этапу
Видеолекции для подготовки к окружному этапу | Главная02.12.2014
Скоро (7 декабря) пройдет окружной этап Всероссийской олимпиады по математике.
Возможно, вы захотите к нему поготовиться.
В этом вам могут помочь условия и решения задач прошлых лет, которые доступны здесь.
Также предлагаем цикл видеолекций, записанных специально для подготовки к окружному этапу.
Лекции записаны студентами и аспирантами механико-математического факультета МГУ, которые в настоящее время ведут различные математические кружки, а в прошлом сами побеждали на математических олимпиадах самого высокого уровня.
Будем рады отзывам (см. контакты на сайте).
Удачи на олимпиадах!
Лекции, записанные в 2014 году:
- «Комбинаторика: задачи «можно ли? и «оценка+пример».» Погудин Глеб Александрович, 43 минуты — лекция предназначена для 10 класса, но может быть полезна 8, 9 и 11 классам.
- «Алгебра: различные методы решения задач.» Меньщиков Андрей Борисович, 44 минуты — лекция предназначена для 10 класса, но может быть полезна 9 и 11 классам.
- «Геометрия: задачи на вписанные углы.» Ивлев Фёдор Алексеевич, 56 минут — лекция предназначена для 10 класса, но может быть полезна 9 и 11 классам.
- «Комбинаторика: задачи «оценка+пример.» Брагин Владимир Алексеевич, 40 минут — лекция предназначена для 9 класса, но может быть полезна 8, 10 и 11 классам.
- «Геометрия: теоремы Чевы и Менелая.» Кушнир Андрей Юрьевич, 62 минуты — лекция предназначена для 9 класса, но может быть полезна 10 и 11 классам.
- «Алгебра: задачи на делимость.» Гусев Антон Сергеевич, 52 минут — лекция предназначена для 9 класса, но может быть полезна 8, 10 и 11 классам.
Лекции, записанные в 2013 году
math.mosolymp.ru
Как и где готовиться к олимпиадам по математике и физике
Как извлечь максимум пользы из участия в олимпиадах, с чего начать подготовку, где взять материалы и кое-что еще. Рассказывает трехкратный победитель всероссийской олимпиады школьников.Михаил Кипнис
Среди школьников распространено заблуждение, что необязательно готовиться, чтобы участвовать в олимпиадах. Эту точку зрения невольно поддерживают и сами организаторы, когда объявляют, что для участия в их состязании не нужны углубленные знания.
Как показывает опыт, это утверждение справедливо только для начальных этапов соревнований. Например, в школьном этапе всероссийской олимпиады действительно можно успешно выступить и без дополнительной подготовки. То же относится и к отборочным турам некоторых олимпиад. Но далеко не всегда необходимые на олимпиаде знания совпадают со школьной программой. А иногда задание на известную тему из школьной программы кажется сложным из-за необычной формулировки, за которой скрывается знакомый материал.
Изучите задания прошедших олимпиад
Попробуйте решить задания выбранной олимпиады за прошлые годы. Они опубликованы в разделе «Задания» на страницах олимпиад или в специальных подборках. Это полезная тренировка, а начинающие олимпиадники поймут, с чем им предстоит столкнуться.
Сравните свои решения с ключами. Разберите задания сами или с преподавателем, который объяснит неясные моменты. Ведь в успехе школьника кроме него заинтересована и школа, так как это повышает ее престиж.
Так или иначе, даже без постановки перед собой высоких целей, изучение заданий прошлых лет — это доступный и действенный способ подготовки к олимпиаде. А интересные задания пробуждают любопытство и желание попробовать себя в деле.
Пользуйтесь материалами для подготовки
Посмотрите рекомендации тренеров сборной Москвы по самоподготовке. Каждому предмету здесь посвящен отдельный раздел, в котором собраны списки учебной и научной литературы, пособий, справочников, академических статей, подобранных специально для заинтересованных школьников. Самостоятельно восполнить пробелы в теоретических знаниях поможет чтение этих материалов.
Готовиться можно и по видеоурокам, включающим лекции, разборы заданий, семинарские занятия для школьников и учителей. Организаторы некоторых олимпиад выкладывают на сайтах видеоразборы заданий, которые проводят сами составители или члены жюри.
Посещайте занятия
Не стоит ограничиваться только самоподготовкой, хотя и нельзя недооценивать ее значение. Занятия с опытными преподавателями все-таки остаются одним из лучших способов подготовки к олимпиадам. Ищите учителя, который заинтересован в успехе школьника. Он может вести кружок или дополнительные занятия по подготовке к олимпиадам.
Помимо курса по предмету, на таких кружках предлагают полезные раздаточные материалы, понятные разборы заданий прошлых лет и подборки новых.
Участвуйте в разных олимпиадах
Более 700 олимпиад для школьников в вашем регионе
Даже выбрав главной целью одну олимпиаду, не стоит отказываться от других. Участие в них в таком случае станет не потерей времени, а дополнительной тренировкой. Умение работать с разными типами заданий и опыт поведения на туре, концентрация, планирование времени — это те элементы подготовки, которые даже регулярные занятия не могут полноценно компенсировать.
Привлекайте друзей
Совместная подготовка проходит продуктивнее и веселее. Бывалые олимпиадники охотно делятся опытом с начинающими, общение с ними приносит полезную «инсайдерскую» информацию об устройстве и «внутренней кухне» олимпиадной жизни и становится началом приятных знакомств. Олимпиадное движение — одно из самых дружных в школьном мире. Главное помнить, что ровесники — не «прямые» конкуренты, и задания устроены таким образом, что успех — это результат победы «над собой» и над заданиями, а не над сверстниками. Участвуйте и добивайтесь успехов вместе.
Репетитор по математике и физике. Краснообск
igor-steps.livejournal.com
Задания и решения олимпиад из Перечня для подготовки
Мы пополнили копилку заданий и решений олимпиад из Перечня
Каждый год на нашем сайте публикуются материалы олимпиад прошедшего года. Для многих соревнований доступны задания и решения за несколько лет. При подготовке можно сначала прочитать условия и решить задачи самостоятельно, а потом посмотреть ответы.
Задания отборочных и заключительных этапов олимпиад из Перечня доступны в разделе подготовки на страницах олимпиад. В верхнем меню нужно будет выбрать класс и год. Можно зайти и по прямым ссылкам на задания 2016/17 учебного года:
- олимпиады 1 уровня в 2017/18 учебном году;
- олимпиады 2 уровня в 2017/18 учебном году;
- олимпиады 3 уровня в 2017/18 учебном году.
1 уровень
Московская олимпиада школьников
Московская математическая олимпиада
Московская олимпиада школьников по информатике
Московская олимпиада школьников по физике
Московская олимпиада школьников по химии
Московская традиционная олимпиада по лингвистике
Турнир городов
Олимпиада «Покори Воробьёвы горы!»
Олимпиада «Покори Воробьёвы горы!» по биологии
Олимпиада «Покори Воробьевы горы!» по иностранным языкам
Олимпиада «Покори Воробьевы горы!» по истории
Олимпиада «Покори Воробьевы горы!» по литературе
Олимпиада «Покори Воробьевы горы!» по математике
Олимпиада «Покори Воробьевы горы!» по обществознанию
Олимпиада «Покори Воробьевы горы!» по физике
Открытая олимпиада школьников по программированию
Межрегиональная олимпиада школьников «Высшая проба»
Межрегиональная олимпиада школьников «Высшая проба» по дизайну
Межрегиональная олимпиада школьников «Высшая проба» по журналистике
Межрегиональная олимпиада школьников «Высшая проба» по иностранным языкам
Межрегиональная олимпиада школьников «Высшая проба» по истории
Межрегиональная олимпиада школьников «Высшая проба» по математике
Межрегиональная олимпиада школьников «Высшая проба» по обществознанию
Межрегиональная олимпиада школьников «Высшая проба» по праву
Межрегиональная олимпиада школьников «Высшая проба» по русскому языку
Межрегиональная олимпиада школьников «Высшая проба» по экономике
Всероссийская олимпиада школьников «Нанотехнологии — прорыв в будущее!»
Олимпиада школьников «Ломоносов»
Олимпиада школьников «Ломоносов» по биологии
Олимпиада школьников «Ломоносов» по географии
Олимпиада школьников «Ломоносов» по журналистике
Олимпиада школьников «Ломоносов» по иностранным языкам
Олимпиада школьников «Ломоносов» по информатике
Олимпиада школьников «Ломоносов» по истории
Олимпиада школьников «Ломоносов» по истории российской государственности
Олимпиада школьников «Ломоносов» по литературе
Олимпиада школьников «Ломоносов» по математике
Олимпиада школьников «Ломоносов» по обществознанию
Олимпиада школьников «Ломоносов» по праву
Олимпиада школьников «Ломоносов» по русскому языку
Олимпиада школьников «Ломоносов» по философии
Олимпиада школьников «Ломоносов» по химии
Олимпиада школьников «Ломоносов» по международным отношениям и глобалистике
Олимпиада школьников «Физтех» по физике
Отраслевая физико-математическая олимпиада школьников «Росатом» по физике
Межрегиональная олимпиада школьников по математике и криптографии
Олимпиада школьников по праву Московской государственной юридической академии имени О.Е. Кутафина
Открытая олимпиада школьников «Информационные технологии»
Олимпиада школьников Санкт-Петербургского государственного университета
Олимпиада школьников Санкт-Петербургского государственного университета по биологии
Олимпиада школьников Санкт-Петербургского государственного университета по географии
Олимпиада школьников Санкт-Петербургского государственного университета по истории
Олимпиада школьников Санкт-Петербургского государственного университета по математике
Олимпиада школьников Санкт-Петербургского государственного университета по обществознанию
Олимпиада школьников Санкт-Петербургского государственного университета по праву
Олимпиада «Юные таланты»
Олимпиада «Юные таланты» по географии
Олимпиада «Юные таланты» по химии
Всесибирская олимпиада школьников
Всесибирская олимпиада школьников по физике
Всесибирская олимпиада школьников по химии
Олимпиада школьников по информатике и программированию
Межрегиональная экономическая олимпиада школьников имени Н. Д. Кондратьева
Санкт-Петербургская олимпиада школьников по математике
Санкт-Петербургская астрономическая олимпиада
Телевизионная гуманитарная олимпиада школьников «Умницы и умники»
Олимпиада по комплексу предметов «Культура и искусство»
Олимпиада по комплексу предметов «Культура и искусство» по академическому рисунку, живописи, композиции, истории искусства и культуры
Олимпиада по комплексу предметов «Культура и искусство» по техническому рисунку и декоративной композиции
Строгановская олимпиада по рисунку, живописи и скульптуре
2 уровень
Турнир имени М. В. Ломоносова
Московская олимпиада школьников
Московская астрономическая олимпиада
Московская олимпиада школьников по географии
Московская олимпиада школьников по изобразительному искусству
Московская олимпиада школьников по истории
Московская олимпиада школьников по обществознанию
Московская олимпиада школьников по праву
Московская олимпиада школьников по филологии
Московская олимпиада школьников по экономике
Интернет-олимпиада школьников по физике
Объединенная межвузовская математическая олимпиада
Олимпиада школьников «Ломоносов»
Олимпиада школьников «Ломоносов» по геологии
Олимпиада школьников «Ломоносов» по механике и математическому моделированию
Олимпиада школьников «Ломоносов» по политологии
Олимпиада школьников «Ломоносов» по физике
Олимпиада школьников «Ломоносов» по экологии
Олимпиада школьников «Физтех» по математике
Открытая олимпиада школьников по математике
Межрегиональная олимпиада школьников «Евразийская лингвистическая олимпиада»
Олимпиада Курчатов
Олимпиада Курчатов по математике
Олимпиада Курчатов по физике
Отраслевая физико-математическая олимпиада школьников «Росатом» по математике
Олимпиада РАНХиГС
Олимпиада РАНХиГС по английскому языку
Олимпиада РАНХиГС по обществознанию
Олимпиада МГИМО(У) МИД России для школьников
Олимпиада Юношеской математической школы СПбГУ
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений (иностранные языки)
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений (математика)
Межрегиональная олимпиада школьников по математике «САММАТ»
Олимпиада школьников Санкт-Петербургского государственного университета
Олимпиада школьников Санкт-Петербургского государственного университета по журналистике
Олимпиада школьников Санкт-Петербургского государственного университета по медицине
Олимпиада школьников Санкт-Петербургского государственного университета по социологии
Олимпиада школьников Санкт-Петербургского государственного университета по филологии
Олимпиада школьников Санкт-Петербургского государственного университета по химии
Олимпиада школьников Санкт-Петербургского государственного университета по экономике
Городская открытая олимпиада школьников по физике
Герценовская олимпиада школьников
Герценовская олимпиада школьников по географии
Герценовская олимпиада школьников по иностранным языкам
Межрегиональная олимпиада школьников «Высшая проба»
Межрегиональная олимпиада школьников «Высшая проба» по востоковедению
Межрегиональная олимпиада школьников «Высшая проба» по восточным языкам
Межрегиональная олимпиада школьников «Высшая проба» по информатике
Межрегиональная олимпиада школьников «Высшая проба» по истории мировых цивилизаций
Межрегиональная олимпиада школьников «Высшая проба» по политологии
Межрегиональная олимпиада школьников «Высшая проба» по социологии
Межрегиональная олимпиада школьников «Высшая проба» по филологии
Межрегиональная олимпиада школьников «Высшая проба» по философии
Олимпиада по программированию для школьников «ТехноКубок»
Олимпиада школьников «Государственный аудит»
Межрегиональная олимпиада по праву «Фемида»
Олимпиада школьников «Учитель школы будущего» по иностранным языкам
Междисциплинарная олимпиада школьников имени В. И. Вернадского по истории и обществознанию
Олимпиада по информатике и компьютерной безопасности
Инженерная олимпиада школьников
Олимпиада школьников «Россия в электронном мире»
Олимпиада школьников «Россия в электронном мире» по истории
Олимпиада школьников «Россия в электронном мире» по обществознанию
Открытая олимпиада Университета Иннополис по информатике
Плехановская олимпиада школьников по английскому языку
Открытая межвузовская открытая олимпиада школьников «Будущее Сибири» по химии
Олимпиада школьников «Основы православной культуры»
Санкт-Петербургская олимпиада школьников по химии
Олимпиада РГГУ для школьников по русскому языку
Межрегиональный экономический фестиваль школьников «Сибириада. Шаг в мечту!»
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки»
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по биологии
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по русскому языку
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по химии
Межрегиональная предметная олимпиада Казанского федерального университета по химии
Северо-Восточная олимпиада школьников по химии
Межрегиональная олимпиада МПГУ для школьников по географии
Олимпиада «Покори Воробьевы горы!» по журналистике
Всероссийская Толстовская олимпиада школьников по истории
Олимпиада школьников «Робофест» по физике
Всесибирская олимпиада школьников
Всесибирская олимпиада школьников по информатике
Всесибирская олимпиада школьников по математике
Межрегиональная олимпиада школьников имени В. Е. Татлина
Всероссийская олимпиада учащихся музыкальных училищ и колледжей
Всероссийская олимпиада учащихся музыкальных училищ и колледжей по предмету «Инструменты народного оркестра»
Всероссийская олимпиада учащихся музыкальных училищ и колледжей по предмету «Хоровое дирижирование»
3 уровень
Открытая всероссийская интеллектуальная олимпиада «Наше наследие»
Объединенная международная математическая олимпиада «Формула Единства» / «Третье тысячелетие»
Олимпиада школьников Санкт-Петербургского государственного университета
Олимпиада школьников Санкт-Петербургского государственного университета «Инженерные системы»
Олимпиада школьников Санкт-Петербургского государственного университета по информатике
Олимпиада школьников Санкт-Петербургского государственного университета по физике
Межрегиональная химическая олимпиада школьников имени академика П. Д. Саркисова
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений (обществознание)
Межрегиональная олимпиада школьников на базе ведомственных образовательных учреждений (физика)
Межрегиональная олимпиада школьников «Высшая проба»
Межрегиональная олимпиада школьников «Высшая проба» по психологии
Межрегиональная олимпиада школьников «Высшая проба» по физике
Межрегиональная олимпиада школьников «Высшая проба» по электронике
Олимпиада Национальной технологической инициативы
Олимпиада школьников «Шаг в будущее»
Олимпиада школьников «Шаг в будущее» по инженерному делу
Олимпиада школьников «Шаг в будущее» по информатике
Олимпиада школьников «Шаг в будущее» по математике
Олимпиада школьников «Шаг в будущее» по физике
Университетская олимпиада школьников «Бельчонок»
Университетская олимпиада школьников «Бельчонок» по информатике
Университетская олимпиада школьников «Бельчонок» по математике
Олимпиада по дискретной математике и теоретической информатике
Южно-Российская межрегиональная олимпиада школьников «Архитектура и искусство»
Всероссийский химический турнир школьников
Всероссийская Сеченовская олимпиада школьников по химии
Всесибирская олимпиада школьников по биологии
Герценовская олимпиада школьников по биологии
Олимпиада школьников «Будущее с нами»
Олимпиада школьников «Надежда энергетики» по физике
Открытая олимпиада школьников по программированию «Когнитивные технологии»
Многопрофильная инженерная олимпиада «Звезда»
Многопрофильная инженерная олимпиада «Звезда» по естественным наукам
Многопрофильная инженерная олимпиада «Звезда» по истории
Многопрофильная инженерная олимпиада «Звезда» по обществознанию
Открытая химическая олимпиада
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки»
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по истории
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по математике
Межрегиональная олимпиада школьников «Будущие исследователи — будущее науки» по физике
Олимпиада школьников «Ломоносов»
Олимпиада школьников «Ломоносов» по инженерным наукам
Олимпиада школьников «Ломоносов» по робототехнике
Олимпиада школьников «Надежда энергетики» по математике
Открытая олимпиада Университета Иннополис по математике
Физико-математическая олимпиада «Phystech.International»
Всероссийская олимпиада «Миссия выполнима. Твое призвание — финансист!»
Всероссийская олимпиада «Миссия выполнима. Твое призвание — финансист!» по математике
Всероссийская олимпиада «Миссия выполнима. Твое призвание — финансист!» по обществознанию
Всероссийская олимпиада «Миссия выполнима. Твое призвание — финансист!» по экономике
Олимпиада РГГУ для школьников по истории
Олимпиада школьников «Кодекс знаний»
Многопрофильная олимпиада УрФУ для школьников «Изумруд»
Многопрофильная олимпиада УрФУ для школьников «Изумруд» по обществознанию
Многопрофильная олимпиада УрФУ для школьников «Изумруд» по русскому языку
Олимпиада «Океан знаний»
Олимпиада «Океан знаний» по истории
Олимпиада «Океан знаний» по обществознанию
Олимпиада «Океан знаний» по русскому языку
Олимпиада «Юные таланты» по геологии
Олимпиада ГУУ по обществознанию «Турнир будущих управленцев»
Олимпиада РАНХиГС
Олимпиада РАНХиГС по журналистике
Олимпиада РАНХиГС по истории
Олимпиада РАНХиГС по политологии
Олимпиада РАНХиГС по экономике
Олимпиада школьников «В начале было Слово…»
Поволжская открытая олимпиада школьников «Будущее медицины»
Межрегиональная транспортная олимпиада школьников «Паруса надежды» по технике и технологии
Олимпиада «Покори Воробьевы горы!» по географии
Открытая региональная межвузовская олимпиада вузов Томской области
Открытая региональная межвузовская олимпиада вузов Томской области по географии
Открытая региональная межвузовская олимпиада вузов Томской области по истории
Открытая региональная межвузовская олимпиада вузов Томской области по литературе
Открытая региональная межвузовская олимпиада вузов Томской области по русскому языку
Открытая региональная межвузовская олимпиада вузов Томской области по физике
Всероссийский конкурс научных работ школьников «Юниор»
Всероссийский конкурс научных работ школьников «Юниор» по естественным наукам
Всероссийский конкурс научных работ школьников «Юниор» по инженерным наукам
Многопрофильная олимпиада «Аксиос»
Многопрофильная олимпиада «Аксиос» по литературе
Многопрофильная олимпиада «Аксиос» по обществознанию
Олимпиада школьников «Гранит науки» по естественным наукам
Плехановская олимпиада школьников по экономике
Всероссийская Толстовская олимпиада школьников
Всероссийская Толстовская олимпиада школьников по литературе
Всероссийская Толстовская олимпиада школьников по обществознанию
Открытая олимпиада по экономике НОЦ ВолНЦ РАН
Олимпиада Северо-кавказского федерального университета «45 параллель» по географии
Сибирская межрегиональная олимпиада школьников «Архитектурно-дизайнерское творчество»
«Учись строить будущее» («Строительная олимпиада») МГСУ по архитектурной графике
Региональный конкурс школьников Челябинского университетского образовательного округа
Региональный конкурс школьников Челябинского университетского образовательного округа по иностранным языкам
Региональный конкурс школьников Челябинского университетского образовательного округа по обществознанию
Межвузовская олимпиада школьников по педагогике «Первый успех»
Всероссийская олимпиада учащихся музыкальных училищ и колледжей
Всероссийская олимпиада учащихся музыкальных училищ и колледжей по предмету «Музыкальная педагогика и исполнительство (фортепиано)»
Всероссийская олимпиада учащихся музыкальных училищ и колледжей по предмету «Струнные инструменты»
Всероссийская олимпиада учащихся музыкальных училищ и колледжей по предмету «Теория и история музыки»
Международная олимпиада школьников «Искусство графики»
olimpiada.ru
