Сайт учителей математики и информатики Цумадинского р.
1.1 Методические рекомендации по проведению школьного и муниципального этапов всероссийской олимпиады школьников 2018/2019 учебном году по математике
1.2. Рекомендации по проведению школьного и муниципального этапов ВсОШ 2017/18 год
(посмотрите тематику заданий , примерно такие могут быть в этом году )
2. «Задания по подготовке к олимпиаде по математике».( Автор: Гасанов Камиль Набиевич, Казбековский район, Дылымская гимназия , учитель математики.)
Скачать 8 класс, 9 класс, 10-11 класс.
3.Всероссийская олимпиада школьников 2007-2008 учебного года (школьный этап) решения
4. 2010-2011 учебный год. Задания (5 класс, 6 класс) муниципальной олимпиады школьников среди обучающихся 5-6 классов(
5. 2011-2012 учебный год. Задания (5 класс, 6 класс) муниципальной олимпиады школьников среди обучающихся 5-6 классов(решения 5 класс, 6 класс)
Задания и решения муниципального уровня по математике 7 класс, 8 класс, 9 класс, 8-9 классы.( Взял с сайта инфоурок АРЕЩЕНКО ЕЛЕНА АЛЕКСАНДРОВНА)
6.Олимпиада по математике Муниципальный этап 2013–2014 уч. г. Задачи с указаниями и решениями
7. Муниципальный этап Всероссийской олимпиады школьников по математике в 2014 – 2015 учебном году Ответы и решения
8. Задания олимпиады за 2015/2016 учебный год
9. ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ. 2016—2017 уч. г.
10
. задания и решения 5 класс олимпиада по математике 1 вариантзадания 5 класс , задания 5 класс(2) ,
11. Сайт для подготовки к олимпиаде
13. исследовательская работа «Некоторые методы решения олимпиадных задач» АВТОР: Чернышева Любовь
14. способы решения олимпиадных заданий по математике
15. Задачи математических олимпиад
16. Основные методы и приёмы решения олимпиадных математических задач
18. Московская математическая олимпиада.
19. Устные математические олимпиады.
21. Конкурсные задачи по математике: справочник и методы решения.
22. Международная математическая олимпиада.
23. Всероссийская олимпиада школьников по математике (книга).
24. МетаШкола.
25. Сайт для подготовки к олимпиаде по математике
26. задания районной олимпиады по математике среди 5 -классников . 16.10.2018
27. Задания Всероссийской олимпиады по математике последних лет
САЙТ ОЛИМПИАДА .РУ
( ЗАДАНИЯ И ОТВЕТЫ ШКОЛЬНОГО И МУНИЦИПАЛЬНОГО ЭТАПОВ ПО РЕГИОНАМ РФ)
Математика | Подготовка к олимпиаде 2017 | Занятие 1
Математика | Подготовка к олимпиаде 2017 | Занятие 2
Математика | Подготовка к олимпиаде 2017 | Задача «Сумма квадратов»
matematik-05.ucoz.net
Как я выиграл Всероссийскую олимпиаду школьников — 2017 — Учёба.ру

Соня Белопольская,
ученица 11 класса лицея № 1535,
победитель Всероссийской олимпиады школьников — 2017 по истории
«Я учусь в лицее № 1535. У нас в школе очень сильные учителя по истории, нас много заставляют учить и еще больше — думать, поэтому многие знания, которые помогли мне в ходе олимпиады, были получены на школьных уроках.
Муниципальный, региональный и заключительный этапы олимпиады не так сильно отличаются друг от друга, хотя уровень сложности возрастает. Так, например, на заключительном этапе простых знаний из учебников не хватит: нужны также другие навыки, скажем, логика, умение сопоставлять информацию, знания основ географии и искусства.
Заключительный тур проходил в Архангельске, и это была, наверное, одна из самых насыщенных недель в моей жизни. Нужно было и готовиться к турам, и не волноваться об уже написанных, и еще успеть посмотреть город. Так как я больше всего волновалась за письменный тур (проект и эссе), то мне было легче, поскольку мы написали их в первый день. Перед тестовой частью ничего не повторяла, хотя привезла с собой учебники, да и интернет был, но решила лучше выспаться. Не пожалела — все равно ничего из того, что я хотела повторить, так и не появилось в заданиях. Перед устным туром нам объявили результаты предыдущих туров, я уже знала, что стану призером, и спокойно отправилась на выступление. Там практически не волновалась: осознание, что я получу диплом, дало возможность расслабиться и просто говорить в свое удовольствие. Видимо, это повлияло на результат: баллы мне поставили высокие, и их оказалось достаточно, чтобы я стала победителем.
Задания в этом году были очень интересные: особенно проект, где надо было порассуждать на тему сознания людей Средневековья на основе анализа „Повести временных лет”. И, конечно, мне понравился тест, хотя вначале показался очень сложным: например, нужно было определить школы иконописи и расположить их на карте.
Чтобы выиграть „Всерос”, обязательно нужно иметь сильный характер — в этом году многие в этом убедились. Важно никогда не сдаваться, всегда уверенно идти к своей цели, что бы вокруг ни говорили. Еще важно научиться не нервничать, собираться в сложной ситуации и выкладываться по максимуму. И, конечно, необходимо много работать, не обращая внимания на все отвлекающие факторы: забыть про соцсети, долгий сон по выходным и (приходится признать!) другие уроки. Хотя порой стоит и отвлекаться: например, я иногда гуляла с друзьями или учила английский, просто чтобы не „перегореть” и все-таки дойти до конца.
Я несколько лет мечтала стать дипломатом, поэтому выбрала МГИМО. Что касается ближайших планов, я точно не собираюсь отвлекаться от учебы — за этот год у меня немного забылся английский, да и остальные предметы отошли на второй план, поэтому их нужно подтянуть. Кроме того, в мире множество интересных вещей — начиная от ядерной физики и заканчивая творчеством импрессионистов, поэтому я собираюсь узнать много нового. А еще участвовать в различных волонтерских проектах, ездить в детские лагеря вожатой или преподавать».

Мария Дмитриева,
ученица 11 класса лицея «Вторая школа»,
победитель Всероссийской олимпиады школьников — 2017 по математике
«Я учусь в лицее „Вторая школа“, где математика — профильный предмет, но олимпиадам уделяется не очень много внимания. В этом году школьный и муниципальный туры олимпиады я пропустила (они скучные), так как являюсь победителем „Всероса“ прошлого года. А вот на региональный этап сходила, там интересные задачи.
В качестве подготовки к олимпиаде в первой половине этого учебного года я съездила на сборы по математике, плюс ходила на кружок в Центре педагогического мастерства, но только изредка, так как было много других жизненных задач, в первую очередь учеба в Независимом московском университете, где готовят математиков. Полгода перед финалом олимпиадной математикой я почти не занималась.
Могу сказать, что на школьном и муниципальном этапах задания очень простые, думать не нужно, на региональном — несложные, но мозгом приходится пользоваться, на заключительном — довольно трудные, хотя в большинстве своем решаемые.
Финал олимпиады проходил в Калининграде. Организаторы подготовили для нас неожиданные задания, думаю, что условия задач второго дня не понравились никому из участников. Я волновалась, но не очень: моей задачей было не выиграть, а лишь не провалиться, не слишком опуститься на фоне результата прошлого года. Это мне и помогло стать победителем. Я очень рада, что моя олимпиадная карьера завершилась на такой ноте.
Учиться я буду на математическом факультете Высшей школы экономики, потому что сейчас это лучший матфак в стране. В ближайших планах — сдать сессию в НМУ, разобраться с платьем на выпускной и найти подработку на лето. Могу рассказать, что поеду ассистентом на летние московские сборы по математике и на летнюю школу „Современная математика“».

Дарья Комлева,
ученица 11 класса школы № 2097,
победитель Всероссийской олимпиады школьников — 2017 по русскому языку
«Интерес к русскому языку у меня появился в 5 классе, во многом благодаря замечательным учителям. Сейчас у меня очень сильная учительница русского языка и литературы, она сама связана с олимпиадным движением и помогала мне готовиться к олимпиадам. В качестве подготовки, прежде всего, я очень много читала, проделывала задания самостоятельно, чтобы развивать свои навыки и узнавать новое. Часто решала различные задания олимпиады прошлых лет, чтобы привыкнуть к формату. Не могу не сказать, что много знаний и опыта мне дали выездные учебные лагеря. С 9 по 11 классы я ездила на семинары осенью и весной, где самые лучшие преподаватели читали нам лекции и давали полезные задания. В этом лагере занимались и другие ребята из команды Москвы по русскому языку.
У меня большой опыт участия в олимпиадах школьников. В 9 классе я дошла до регионального этапа, пройдя все предыдущие. В 10 классе я решила писать сразу региональный этап, результат был удачный, прошла на заключительный тур и весной поехала в Курск. Там выступила не очень успешно, что сильно подстегнуло меня стараться еще сильнее, развиваться и изучать новое, чтобы выиграть эту олимпиаду. В 11 классе я снова писала только региональный этап и успешно прошла на финал, который на этот раз проходил в Смоленске.
Заключительный этап состоял из двух туров: на первом предлагались традиционные девять заданий на разные разделы языка, последним заданием был перевод древнерусского текста со множеством маленьких заданий к нему. Второй тур изначально был для всех загадкой. Никто не знает, что его ожидает, пока не окажется на самом туре. Итак, на втором туре у 10-11 классов сначала была проведена лекция по определенному материалу, а затем мы писали комплексный анализ (синтаксис, фонетика, морфология) по потрясающему произведению И. Бродского „Подражание сатирам, сочиненным Кантемиром”. Мне очень понравился этот тур, я получила огромное удовольствие от чтения предложенного текста и его исследования. Задания были очень объемные, но я смогла сделать довольно много. Финал был для меня непростым психологически. Я понимала, что это 11 класс, а значит „Всерос-2017” — мой последний шанс выиграть.
На следующее утро после показа работ в моей гостинице вывесили список с баллами участников. Когда я увидела, что у меня максимальный балл среди 11 классов, меня охватил жуткий шок. Я не понимала, как такое вообще возможно. Честно говоря, я надеялась быть в списке хотя бы призеров, но стать абсолютным победителем, это невероятно!
С конца 10 класса я уже точно знала, что хочу учиться в НИУ ВШЭ на направлении „Медиакоммуникации”. Я в восторге от учебной программы этой специальности и хочу, чтобы в будущем моя жизнь была связана с медиаиндустрией. Но я никогда не перестану интересоваться и изучать филологию и лингвистику».

Георгий Булгаков,
ученик 11 класса лицея № 1547,
победитель Всероссийской олимпиады школьников — 2017 по экономике
«Я учусь в лицее № 1547, в физмат-классе, поэтому такого предмета, как экономика, у меня нет, и к олимпиадам я готовлюсь самостоятельно. Я считаю, что школьный и муниципальный этап можно выиграть почти без подготовки, задания там в основном несложные, а вот к региональному и заключительному этапу уже стоит готовиться. Лучше всего съездить в какую-нибудь выездную школу, их сейчас довольно много, но можно просто дома прорешивать задания прошлых лет, смотреть решения задач, которые не смог решить, и запоминать приемы, которые там используются.
Задания в этом году были интересные: почти не было „шаблонных“, к которым можно легко подготовиться. Большинство задач были математическими, однако были и две задачи на понимание макроэкономических моделей. Многие сильно волнуются, попав на соревнования такого уровня, однако с опытом это проходит. За четыре года участия в олимпиадах я научился концентрироваться только на решении задач во время тура и совершенно не думать о результате. Когда стал одним из победителей, мне, конечно, было приятно, однако я ожидал такого результата и поэтому какой-то особенной радости не ощутил.
Олимпиада по экономике — одна из самых легких среди всероссийских олимпиад школьников, я уверен, что любой при желании может стать там призером или даже победителем. Однако сложность и нестандартность заданий с каждым годом растет, и когда олимпиада в этом плане приблизится к олимпиадам по физике или математике, тогда без какой-то врожденной одаренности, гениальности или таланта выиграть будет намного сложней. Поступать я буду на мехмат МГУ или на матфак НИУ ВШЭ — как наука математика мне кажется намного более красивой и интересной, чем экономика».

Дарья Деревцова,
ученица 11 класса лицея № 1535,
победитель Всероссийской олимпиады школьников — 2017 по русскому языку
«Я учусь в лицее № 1535 в физико-математическом классе, поэтому многие мои одноклассники не воспринимают русский язык как серьезный предмет. Но надо отдать должное нашей учительнице: Вера Вадимовна Антонова является великолепным педагогом, который может привить любовь к родному языку даже в техническом классе.
Во Всероссийской олимпиаде школьников я начала участвовать с 8 класса. На протяжении трех лет я доходила до регионального этапа, становилась призером, но не набирала необходимое количество баллов, чтобы пройти на финал. В этом году я пропустила школьный и муниципальный этапы и пошла сразу на региональный. Быстро написав олимпиаду, я была уверена, что не пройду дальше, как и в предыдущие годы, так как не готовилась к ней. Нам присылали книги, которые можно было почитать, выдавали материалы об истории языка, словарях, известных филологах и лингвистах, но я даже не пыталась это выучить. Именно поэтому считаю выход на заключительный этап счастливой случайностью.
Финал проходил в Смоленске. Как обычно, два тура — два дня. Первый тур состоит из 9 заданий, затрагивает все разделы, начиная с фонетики, синтаксиса, морфологии и заканчивая языковой игрой и старославянским. Каждое задание включает нескольких пунктов, где надо показать как теоретические знания, так и практические. Второй тур начинается с лекции. У нас она была об особенностях литературного языка начала XVIII века и творчестве Кантемира как представителя данной эпохи. В качестве задания нам дали комплексный анализ текста Иосифа Бродского „Подражание сатирам, сочиненным Кантемиром”. Вопросы, объединенные в несколько блоков, проверяли наше умение определять синтаксические функции слов, находить архаические конструкции и сопоставлять их с аналогичными современными, работать с устаревшими орфоэпическими нормами, распознавать трансформированные фразеологизмы.
После написания туров и вплоть до награждения волнение не покидало, а когда я услышала свое имя и уже стояла на сцене с дипломом, то перед глазами пронеслись все эти напряженные дни, и пришло осознание, что затраченные усилия и время были не бессмысленными и дали отличные результаты».

Валерий Мыльцев,
ученик 11 класса гимназии № 1507,
победитель Всероссийской олимпиады школьников — 2017 по истории
«В этом году я поучаствовал во всех четырех этапах олимпиады, чтобы оценить задания и немного потренироваться. Школьный и муниципальный туры, как обычно, сложности не представляли, и пройти их можно было и с базовыми знаниями истории России и логикой, поэтому к ним я практически не готовился, тем более что по результатам прошлого года проходил сразу на региональный, с которым уже пришлось попотеть. Этот этап был наиболее сложным, во многом потому, что для одиннадцатых классов сделали очень высокие проходные баллы. Сам я еле-еле прошел на заключительный этап, отбив несколько баллов на апелляции.
Мне повезло, и я еще с лета попал на курсы по подготовке к олимпиадам в Центре педагогического мастерства. Там же с сентября проходил обучение перед региональным этапом. Кроме того, я по несколько часов в день занимался дома и осилил немалое количество учебников и разных справочных материалов.
Финал в этом году проходил в Архангельске, поэтому перед ним много учил историю Поморья. Организаторы, особенно составители исторического проекта, посвященного предсказаниям Древней Руси, меня сильно удивили, и я не угадал ни одного задания. Немного расстроили темы эссе, потому что среди них не было темы по второй половине XIX века, которую я в основном и готовил. Не помню, когда я испытывал столько невероятных эмоций, как во время вручения дипломов рядом с другими победителями на сцене. И не менее здорово было получать поздравления от моих друзей и знакомых, которых оказалось значительно больше, чем я ожидал.
Гением для победы в олимпиаде быть совсем не обязательно. Она, как мне кажется, рассчитана на обыкновенных школьников, интересующихся предметом за рамками программы. Однако сказать, что победить могут все, нельзя: я знаю достаточно много ребят, которые не смогли пройти через региональный этап, особенно сложный в Москве из-за большой конкуренции. Увы, я уже в 11 классе и не смогу больше участвовать в подобных олимпиадах, хотя с удовольствием попробовал бы себя в смежных дисциплинах, например, обществознании или МХК. Поступать я буду, скорее всего, на „Международные отношения” в МГИМО. Летом хотел бы отдохнуть перед университетом и возобновить занятия спортом, отложенные из-за учебы».
www.ucheba.ru
Как научиться решать олимпиадные задачи по математике, если я перехожу в 10 класс и до этого не имел серьезных успехов? Или для этого нужно быть гением?
Для начала надо определиться, какого уровня мастерства в решении олимпиадных задач вы хотите достичь. Всё определяется задачами, которые вы перед собой ставите, аналогично, как и в любом другом виде спорта: между человеком, иногда делающим зарядку, и профессиональным спортсменом есть большая разница.
Олимпиадные задания, да и сами олимпиады, могут быть разными как по форме, так и по содержанию. Задачи начальных этапов Всероссийской олимпиады школьников, некоторых интернет-олимпиад обычно не несут значительной спортивной составляющей и направлены на развитие интереса к математике. К таким олимпиадам вполне можно подготовиться самостоятельно, вопросы составлены так, чтобы на большую часть из них мог ответить твёрдый хорошист или отличник по математике. Можно ограничиваться только таким уровнем олимпиад для поддержания себя в тонусе, подготовки к последним задачам профильного варианта единого государственного экзамена по математике и некоторым «вузовским» олимпиадам.
Для последующего роста уровня достижений уже не обойтись без наставника. Начиная с некоторого момента может сложиться ощущение, что есть некоторая черта, ниже которой задачи охотно решаются, а вот прыгнуть выше уже не удаётся (обычно эта черта проходит примерно по региональному этапу ВОШ). Преодолеть эту черту без наставника, разбирающегося в олимпиадной математике, очень сложно. Хорошим первым наставником может стать обычный школьный учитель из вашей школы, потом можно искать кого-то ещё. Возможно, придутся по душе заочные курсы и консультации по подготовке к олимпиадам, благо, в эпоху интернета их найти несложно.
В любом случае, при подготовке к олимпиадам любого уровня будет полезно порешать задачи, особенно удачной идеей будет просмотреть задачи прошлых лет того мероприятия, в котором вы собираетесь принять участие. Несмотря на кажущуюся необъятность количества всех возможных задач, можно выделить несколько традиционных идей, которые используются при решении. Это связано как с «модой» на задания определённого типа, так и с тем, что задания одной олимпиады каждый год придумывает примерно одна и та же группа людей. Так что чем больше новых задач вы решите при подготовке к олимпиаде, тем больше вероятность, что на самом конкурсе попадётся что-то, что вы легко решите.
thequestion.ru
Московская математическая олимпиада
Московская математическая олимпиада (ММО, она же — Московская олимпиада школьников по математике) проводится в марте среди учеников 8–11 классов. Это самая престижная из математических олимпиад в Москве (наряду с финальным устным туром Турнира городов и отчасти региональным этапом Всеросса). Чтобы получить диплом ММО, нужно иметь хорошие математические способности и серьёзно заниматься математикой.
Путь многих успешных олимпиадников начинается классе в пятом-шестом — с математических кружков и участия в Математическом празднике, который проводится в МГУ.
Задачи ММО требуют высокой математической культуры и известного олимпиадного профессионализма. Например, уже задачи восьмого класса ММО резко отличаются по сложности от задач Матпраздника (то есть, скачок в сложности при переходе от седьмого класса Матпраздника к восьмому классу ММО является куда более ощутимым, чем при переходе от шестого класса Матпраздника к седьмому). Соответственно, в 9, 10 и 11 классах задачи ММО становятся всё сложнее и сложнее. Поэтому если вы мечтаете о дипломе ММО, то попадать в эту «струю» нужно по возможности раньше (желательно уже в начальной школе участвовать в олимпиадах, а в четвёртом или пятом классе начинать готовиться к Матпразднику).
Одиннадцатиклассникам (которым наличие диплома ММО особенно важно для поступления) следует иметь в виду, что для них ММО проходит в два дня. В первый день предлагается шесть задач, во второй — пять. При определении победителей и призёров работает правило произведения (сравните его с правилом суммы на МОШ по физике):
Вычисляется произведение P числа задач, решённых в первый и во второй день.
При этом задача считается решённой, если за неё поставлен «плюс», «плюс с точкой» или «плюс-минус». Границы призёров в последние годы таковы:
P2018 = P2015 = 6; P2017 = P2016 = P2014 = P2013 = 4; P2012 = 3.
В соответствии с правилом произведения, в 2018 году школьник, решивший пять задач в первый день и одну задачу — во второй, остался без диплома; а тот, кто решил две задачи в первый день, и три — во второй, получил диплом III степени (оба случая имели место в действительности).
В качестве очевидного следствия правила произведения отметим также, что нулевой результат в один из дней (при любом результате другого дня) лишает вас шансов на диплом. (В этом смысле правило суммы на МОШ по физике более лояльно: оно позволяет стать призёром по итогам, например, второго тура при сколь угодно плохо написанном первом.)
Московская математическая олимпиада состоится 17 марта 2019 года. Второй день для 11-классников — 23 марта. Регистрация участников — в ЕСР.
Московская математическая олимпиада в Перечне РСОШ имеет первый уровень.
Задачи ММО последних лет
| 8 класс |
18,
17,
16,
15,
14 13, 12, 11, 10, 09 |
| 9 класс |
18,
17,
16,
15,
14 13, 12, 11, 10, 09 |
| 10 класс |
18,
17,
16,
15,
14 13, 12, 11, 10, 09 |
| 11 класс |
18,
17,
16,
15,
14 13, 12, 11, 10, 09 |
mathus.ru
|
Математика. Районные олимпиады. 6—11 классы / Агаханов Н.X., Подлипский О.К. — М. : Просвещение, 2010. Скачать |
|

|
Математика. Областные олимпиады. 8—11 классы / Н. X. Агаханов, И. И. Богданов, П. А. Кожевников и др. — М. : Просвещение, 2010. Скачать |

|
Математика. Всероссийские олимпиады. Вып. 1 / Н. X. Агаханов, И. И. Богданов, П. А. Кожевников и др. — М. : Просвещение, 2008. Скачать |

|
Математика. Всероссийские олимпиады. Вып. 2 / Н. X. Агаханов, О. К. Подлипский — М. : Просвещение, 2009. Скачать |
|
Математика. Международные олимпиады / Н. X. Агаханов, П. А. Кожевников, Д. А. Терешин. — М. : Просвещение, 2010. Скачать |
|

|
Ленинградские математические кружки / Генкин С.А., Итенберг И.В., Фомин Д.В. — Киров, «Аса», 1994. Скачать |
|
Сборник олимпиадных задач по математике. / Горбачев Н.В. — М.: МЦНМО, 2004. Скачать |
|
|
Математические олимпиады в школе. 5-11 классы. 8-е изд., испр. и доп. / Фарков А.В. — М.: Айрис-пресс, 2009. Скачать |
|
|
Московские математические олимпиады 1993—2005 г. / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. Скачать |
|
|
1001 олимпиадная и занимательная задачи по математике. 3-е изд. / Балаян Э.Н. — Ростов н/Д : Феникс, 2008. Скачать |
ermolovskiy.ru
Персональный сайт — Подготовка к олимпиадам

Методические рекомендации по проведению школьного и муниципального этапов всероссийской олимпиады школьников в 2018/2019 учебном году по математике
скачать
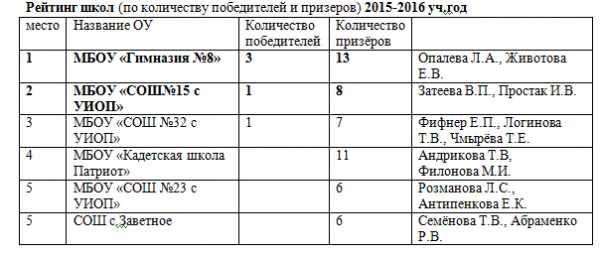
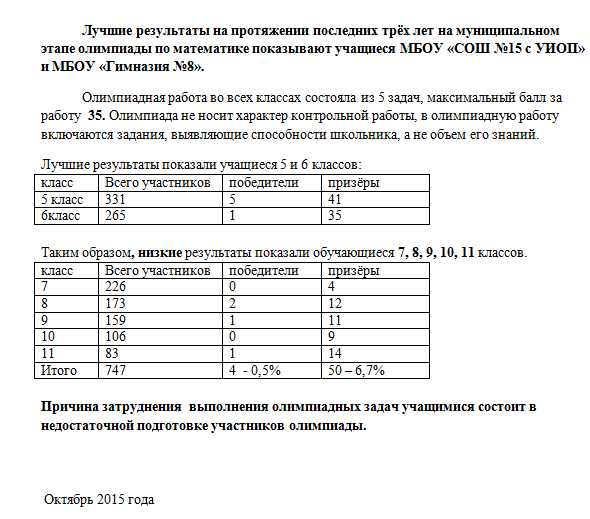
Итоги школьного этапа всероссийской олимпиады школьников по математике в 2015-2016 уч.году
Школьный этап олимпиады по математике был проведён в соответствии с порядком проведения школьного этапа и по олимпиадным заданиям, разработанными предметно-методической комиссией муниципального уровня, с учётом методических рекомендаций центральной предметно-методической комиссии Олимпиады.
Всего в олимпиаде по математике приняли участие 1340 школьников 5- 11 классов из 51 ОУ ЭМР (не участвовали сельские школы: СОШ с.ЗелёныйДол, ООШ с.Калинино, ООШ с.Подстепное, ООШ с.Степное, ООШ с.Старицкое, ООШ с.Титоренко).
(В 2014 году — 1957 школьников)
Победителями признаны 10 школьников -0,7% (5 класс- 5, 6 класс-1, 8 класс -2,
9 класс -1, 11 класс-1) (В 2014 году победителей-131, призёров – 336)
Победители: Гимназия №8 -3 чел., по 1 победителю: СОШ №4, СОШ№15, СОШ №32, МЭЛ, СОШ п.им.К.Маркса, СОШ п.Придорожный, СОШ с.Шумейка.
Призерами признаны 126 школьников – 9,4%
Наибольшее количество призёров:
Гимназия № 8- 13 школьников,
Кадетская школа «Патриот» -11,
СОШ №15 -8,
СОШ №32 -7
СОШ №23 и СОШ с.Заветное по 6 чел.,
СОШ №1, СОШ №21 по 5 чел..
СОШ п.Анисовский, СОШ с.Берёзовка, СОШ п.Бурный по 4 чел.,
СОШ №9, ООШ №14, СОШ с.Кирово, СОШ с.Красный Яр, СОШ п.Новопушкинское, СОШ п.Придорожный, СОШ с.Шумейка, СОШ с.Узморье по 3 призёра,
СОШ №4, СОШ№12, СОШ №18, СОШ №19, ООШ №26, СОШ №30, СОШ №33, СОШ №42, МЭЛ, СОШ с.Воскресенка, СОШ с.Генеральское по 2 призёра.
По одному призёру: ООШ №3, СОШ №1,6, СОШ №24, ООШ №29, СОШ №31, СОШ п.им.К.Маркса, ООШ п.Прибрежный.
Таким образом, только 10% участников школьного этапа стали победителями и призёрами.
15 ноября на базе МБОУ «СОШ №9» прошёл муниципальный этап всероссийской олимпиады школьников по математике среди учащихся 7- 11 классов. В олимпиаде приняли участие 124 школьника из 29 образовательных учреждений Энгельсского муниципального района. По итогам олимпиады победителями признаны 6 школьников, призёрами – 18.
Победители:
1.Зизевский Иван- 7 класс МБОУ «СОШ №9»,
2.Колесниченко Евгения –8 класс МБОУ «Гимназия №8»,
3.Ревзин Леонид – 9 класс МБОУ «Гимназия №8»,
4.Иванов Владимир -9 класс МБОУ «СОШ №12»,
5.Теплотинский Роман -10 класс МБОУ «СОШ №15 с УИОП»,
6.Куликова Дарья – 11 класс МБОУ «СОШ №24».
Призёры:
1.Захарчук София – 7 класс МБОУ «СОШ №32»,
2.Торманова Дарья – 7 класс МБОУ «СОШ №9»,
3.Цыгановский Михаил – 7 класс МБОУ «СОШ №20,
4.Мазур Анна – 8 класс МБОУ «СОШ №15 с УИОП»,
5. Трубенко Ксения -8 класс МБОУ «СОШ с. Заветное»,
6.Гончаров Михаил – 8 класс МБОУ «СОШ №32»,
7. Анциферова Юлия – 8 класс МБОУ «СОШ №15»,
8.Дитяткин Данил – 8 класс МБОУ «СОШ №23»,
9.Баженов Георги – 8 класс МБОУ «Гимназия №8»,
10.Гамаюнова Виктория – 9 класс МБОУ «СОШ №32»,
11.Конониренко Анастасия – 9 класс МБОУ «Гимназия №8»,
12.Ермилов Андрей – 9 класс МБОУ «СОШ №4»,
13.Витулев Арсений – 10 класс МБОУ «СОШ №32 с УИОП»,
14.Шевяков Дмитрий — 10 класс МБОУ «СОШ №15 с УИОП»,
15.Каплина Екатерина – 10 класс МБОУ «СОШ №1»,
16.Ефимовский Кирилл – 10 класс МБОУ «СОШ с.Красный Яр»,
17.Щербаков Антон – 11 класс МБОУ «СОШ №33»,
18.Голованова Ирина – 11 класс МБОУ «СОШ №23».
Поздравляем победителей и призёров муниципального этапа олимпиады по математике!!! Благодарим всех участников муниципального этапа всероссийской олимпиады школьников.
Подготовка к олимпиадам
Муниципальный этап Всероссийской олимпиады 2014 8 класс
Муниципальный этап Всероссийской олимпиады 2014 9 класс
Муниципальный этап Всероссийской олимпиады 2014 10 класс
Муниципальный этап Всероссийской олимпиады 2014 11 класс
Материалы для проведения регионального этапа
XL ВСЕРОССИЙСКОЙ МАТЕМАТИЧЕСКОЙ
ОЛИМПИАДЫ ШКОЛЬНИКОВ 2013- 2014
9-11 9-11
Материалы для проведения регионального этапа
XL ВСЕРОССИЙСКОЙ МАТЕМАТИЧЕСКОЙ
ОЛИМПИАДЫ ШКОЛЬНИКОВ 2012-2013
9 — 11
rmomat.ucoz.ru
