Вычисление длин, площадей и объемов
В этом разделе будут представлены формулы расчета площади, поверхности, окружности и объема для простых двух- и трехмерных форм.
Площадь и периметр квадрата
Площадь квадрата рассчитывается как квадрат длины одной из его сторон. Следующая формула вычисляет площадь квадрата, сторона которого находится в ячейке с именем сторона:
=сторона^2
Чтобы вычислить периметр квадрата, умножьте длину одной из его сторон на 4. Следующая формула вычисляет периметр квадрата, сторона которого находится в ячейке с именем сторона:
=сторона*4
Площадь и периметр прямоугольника
Площадь прямоугольника рассчитывается путем умножения его высоты на основание. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=высота*основание
Периметр прямоугольника можно вычислить путем сложения его удвоенной высоты и удвоенного основания. Следующая формула возвращает площадь прямоугольника, используя ячейки с именами высота и основание:
=(высота*2)+(основание*2)
Площадь круга и длина окружности
Площадь круга рассчитывается как произведение квадрата радиуса на величину π. Следующая формула возвращает площадь круга. Ячейка с именем
=ПИ()*(радиус^2)
Радиус окружности равен половине ее диаметра.
Чтобы вычислить длину окружности, необходимо умножить диаметр окружности на величину π. Следующая формула рассчитывает длину окружности, используя ячейку с именем диаметр.
=диаметр*ПИ()
Диаметр окружности равен радиусу окружности, умноженному на 2.
Площадь трапеции
Для вычисления площади трапеции необходимо сложить две параллельные стороны, умножить их сумму на высоту и разделить на 2. Следующая формула вычисляет площадь трапеции, используя ячейки с именами сторона1, сторона2 и высота:
=((сторона1+сторона2)*высота)/2
Площадь треугольника
Площадь треугольника представляет собой сумму основания и высоты треугольника, деленную на два. Следующая формула рассчитывает площадь треугольника, используя ячейки с именами основание и высота:
=(основание*высота)/2
Площадь поверхности и объем шара
Чтобы вычислить площадь поверхности шара, нужно умножить квадрат радиуса на число π, а затем полученное произведение умножить на 4. Следующая формула возвращает площадь поверхности шара, радиус которого находится в ячейке с именем радиус:
=ПИ()*(радиус^2)*4
Объем шара – это произведение радиуса, возведенного в третью степень, на 4π, которое затем делится на 3. Следующая формула возвращает объем шара, радиус которого находится в ячейке с именем радиус:
=((радиус^3)*(4*ПИ()))/3
Площадь поверхности и объем куба
Площадь поверхности куба определяется путем умножения квадрата его стороны на 6. Следующая формула вычисляет площадь поверхности куба, используя ячейку с именем сторона, которая содержит длину стороны куба:
=(сторона^2)*6
Объем куба – это возведенная в третью степень длина его стороны. Следующая формула возвращает объем куба, используя ячейку с именем сторона:
=сторона^3
Площадь поверхности и объем конуса
Следующая формула вычисляет площадь поверхности конуса (включая площадь основания). В формуле используются ячейки радиус и высота.
=ПИ()*радиус*(КОРЕНЬ(высота^2+радиус^2)+радиус))
Объем конуса вычисляется путем умножения квадрата радиуса основания на число π и высоту, затем произведение делится на три. Следующая формула вычисляет объем конуса, используя ячейки с именами радиус и высота:
=(ПИ()*(радиус^2)*высота)/3
Объем цилиндра
Чтобы вычислить объем цилиндра, необходимо умножить квадрат радиуса основания цилиндра на число π и высоту. Следующая формула рассчитывает объем цилиндра, используя ячейки с именами радиус и высота:
=(ПИ()*(радиус^2)*высота)
Объем пирамиды
Чтобы вычислить объем пирамиды, необходимо определить площадь ее основания, а затем умножить ее на высоту и разделить на 3. Представленная ниже формула вычисляет объем пирамиды, используя для расчетов ячейки с именами ширина (ширина основания), длина (длина основания) и высота (высота пирамиды).
=(ширина*длина*высота)/3
В начало
Полезное
wordex999.ru
вычислить объем тела вращения онлайн калькулятор
Расчет площади и объема геометрических фигур
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон. Другое определение: цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
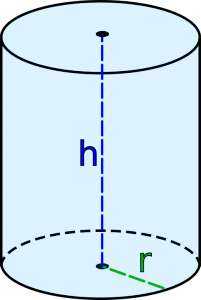
объем цилиндра формула
Если вы хотите знать, как вычислить объем цилиндра,то все, что вам нужно сделать — найти высоту (h) и радиус (r) и и подставить их в формулу:
Если внимательно посмотреть на эту формулу, то можно заметить, что {\pi r^2} — это формула площади круга, а в нашем случае — площадь основания.
Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Произвести расчет объема цилиндра вам поможет наш калькулятор онлайн. Просто введите указанные параметры цилиндра и получите его объем.
Ваша оценка
[Оценок: 168 Средняя: 3.4]
Объем цилиндра Автор mnogof средний рейтинг 3.4/5 — 168 рейтинги пользователей
Просмотров страницы: 45 055
Объем цилиндра формула (через радиус основания и высоту)
{V=\pi r^2 h}, где
r — радиус основания цилиндра,
h — высота цилиндра
Объем цилиндра формула (через площадь основания и высоту)
{V=S h}, где
S — площадь основания цилиндра,
h — высота цилиндра
Объем цилиндра калькулятор онлайн
Как найти объём тела вращения с помощью интеграла
С помощью определённого интеграла можно вычислять не только площади плоских фигур, но и объёмы тел, образованных вращением этих фигур вокруг осей координат.
Тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y= f(x), имеет объём
.
(1)
Аналогично объём v тела, полученного вращением вокруг оси ординат (Oy) криволинейной трапеции выражается формулой
. (2)
При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.
Пример 1.
Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, ограниченной гиперболой , осью абсцисс и прямыми , .
Решение. Объём тела вращения найдём по формуле (1), в которой , а пределы интегрирования a = 1, b = 4:
Пример 2.
Найти объём шара радиуса R.
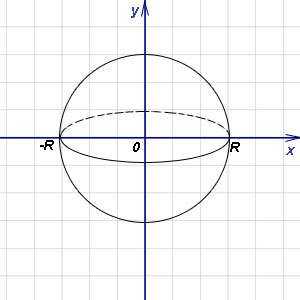
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция запишется в виде , а пределами интегрирования служат -R и R. Следовательно,
Нет времени вникать в решение?
Можно заказать работу!
Пример 3. Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, заключённой между параболами и .
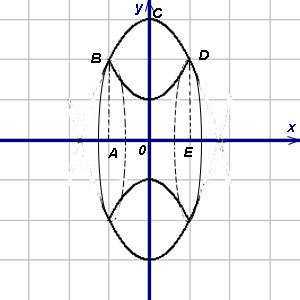
Решение.
Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси абсцисс криволинейных трапеций ABCDE и ABFDE. Объёмы этих тел найдём по формуле (1), в которой пределы интегрирования равны и — абсциссам точек B и D пересечения парабол. Теперь можем найти объём тела:
Пример 4.
Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга ().
Форму тора имеет, например, баранка).
Решение. Пусть круг вращается вокруг оси Ox (рис.
Формулы площадей и объёмов геометрических фигур
20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.
Уравнение окружности LBCD имеет вид
причём уравнение кривой BCD
а уравнение кривой BLD
Используя разность объёмов тел, получаем для объёма тора v выражение
Пример 5.
Найти объём тела, образованного вращением вокруг оси ординат (Oy) фигуры, ограниченной линиями и .
Решение.
Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси ординат треугольника OBA и криволинейной трапеции OnBA.
Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат и — ординаты точек O и B пересечения параболы и прямой.
Таким образом, получаем объём тела:
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Метод интегрирования по частям
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Площадь плоской фигуры с помощью интеграла
Несобственные интегралы
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
Лучшая кроватка в математике. Качественный. Ничего лишнего.
Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объем тела или емкости судна определяется его формой и линейными размерами.
Объем куба
Объем куба равна кубу длины ее лица.
Формула Куб
где — объем куба,
— длина куба.
Область призмы
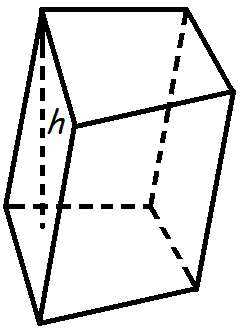
Область призмы равна произведению поверхности дна призмы на высоту.
Формула объема призмы
где — степень призмы,
так
— основание призмы,
час
— высота призмы.
Объем паралелепипедов
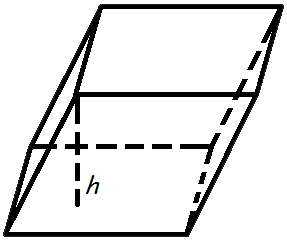
Объем паралелепипедов равна произведению поверхности основания относительно высоты.
Объем формулы паралелепипеда
где — объем паралелепипедов,
так
— базовая площадь,
час
— высота высота.
Объем прямоугольного параллелепипеда
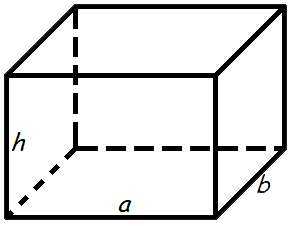
Объем прямоугольного параллелепипеда это то же самое, что и произведение его длины, ширины и высоты.
Формула для объема прямоугольного параллелепипеда
где — объем прямоугольного параллелепипеда,
— длина,
б
— ширина
час
— высота.
Объем пирамиды
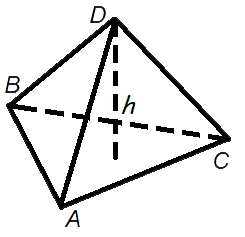
Объем пирамиды составляет одну треть продукта в базовой области по высоте.
Формула объема пирамиды
где — объем пирамиды,
так
— основание основания пирамиды,
час
— длина пирамиды.
Объем правильного тетраэдра
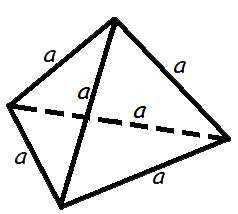
Формула для объема правильного тетраэдра
vipstylelife.ru
Формулы площадей и объемов многогранников
Цилиндрической поверхностью называется поверхность, образуемая прямой, сохраняющей одно и тоже направление и пересекающей направляющую линию. Цилиндр — круговой если в основании его лежит круг. См. также Площадь поверхности цилиндраОбъем всякого цилиндра равен произведению площади основания на высоту:
(r — радиус цилиндра, h — высота цилиндра)Объем круглого конуса равен одной трети произведения площади основания S на высоту H:
| 1. |
|
Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS)
| 1. |
|
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипед имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
(H — высота параллелепипеда, a,b,c — ребра параллелепипеда)Прямоугольный параллелепипед, все грани которого — квадраты, называется кубом. Все ребра куба равны. Объем куба равен кубу его ребра: Объем шара, формула
gtchulkova.blogspot.com
Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара
 Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Ты нашел то, что искал? Поделись с друзьями!
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.
(ведь , ).
Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.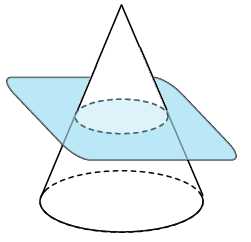
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Объём и площадь поверхности
Объём и площадь поверхности.Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар). Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины» «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма, правильная призма, правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Перейдем к практике.
1. Одна из самых распространенных задач в части B — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького.
Получаем: 754 71.
А как быть с площадью поверхности?
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна 110. А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна 55 25. А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна 25! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна 110. Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали. Ответ: 110.
А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму». Правильный ответ: 96.
Следующий тип задач — когда одно объемное тело вписано в другое.
3. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна 4, высота равна 1, объем равен 4.
4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 4. Найдите объем цилиндра, описанного около этой призмы. В ответ запишите V/π.
Очевидно, высота цилиндра равна боковому ребру призмы, то есть 4. Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна 10. Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ:100.
5. В прямоугольный параллелепипед вписан шар радиуса 1. Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: 8.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице:
be.convdocs.org
Как найти площадь и объем шара
Шаром называют уйма всех точек в пространстве, простирающемся от точки-центра на расстоянии определенного радиуса R. Радиус в свою очередь – это отрезок, соединяющий центр шара с всякий точкой его поверхности.

Вам понадобится
- — формула поверхности площади шара;
- — формула объема шара;
- — навыки арифметического счета.
Инструкция
1. В повседневной жизни нередко появляется надобность вычислить площадь шаровой поверхности либо его части, дабы рассчитать, скажем, расход материала. Вычислив объем шара , вы можете через удельный вес рассчитать массу вещества, составляющего содержимое сферы. Для того дабы обнаружить площадь и объем шара , довольно знать его радиус либо диаметр. По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
2. Скажем, диаметр футбольного мяча, согласно каждым требованиям ФИФА, должен быть в пределах 21,8—22,2 см. Усредните для простоты счета до 22 см. Следственно, радиус (R) будет равен (22:2) – 11 см. Чай увлекательно узнать, какова площадь поверхности футбольного мяча?

3. Возьмите формулу площади поверхности шара : Sшара = 4ттR2Подставьте в приведенную формулу значение радиуса футбольного мяча – 11 см.S = 4 x 3.14 x 11х11 .
4. Позже проведения несложных математических действий вы получаете итог: 1519.76. Таким образом, площадь поверхности футбольного мяча составляет 1 519.76 квадратных сантиметров.
5. Сейчас рассчитайте объем мяча. Берите формулу расчета объема шара : V = 4/3ттR3Подставляйте вновь же значение радиуса футбольного мяча – 11 см.V = 4/3 x 3.14 x 11 х 11 х 11.
6. Позже подсчетов, скажем, на калькуляторе вы получаете: 5576.89.Оказывается, объем воздуха в футбольном мяче составляет 5 576.89 кубических сантиметров.
Шар — это простейшая объемная геометрическая фигура, для указания размеров которой довольно каждого одного параметра. Границы этой фигуры принято называть сферой. Объем пространства, ограничиваемого сферой, дозволено вычислить как с поддержкой соответствующих тригонометрических формул, так и подручными средствами.

Инструкция
1. Используйте классическую формулу объема (V) сферы, если из условий знаменит ее радиус (r) — возведите радиус в третью степень, умножьте на число Пи, а итог увеличьте еще на треть. Записать эту формулу дозволено так: V=4*?*r?/3.
2. Если есть вероятность измерить диаметр (d) сферы, то поделите его напополам и используйте как радиус в формуле из предыдущего шага. Либо обнаружьте одну шестую часть от возведенного в куб диаметра, умноженного на число Пи: V=?*d?/6.
3. Если вестим объем (v) цилиндра, в тот, что вписана сфера, то для нахождения ее объема определите, чему равны две трети от вестимого объема цилиндра: V=?*v.
4. Если вестима средняя плотность (p) материала, из которого состоит сфера, и ее масса (m), то этого тоже довольно для определения объема — поделите второе на первое: V=m/p.
5. Воспользуйтесь какими-нибудь мерными емкостями в качестве подручных средств для измерения объема сосуда сферической формы. Скажем, наполните его водой, измеряя с подмогой мерной емкости число заливаемой жидкости. Полученное значение в литрах переведите в кубические метры — эта единица принята в интернациональной системе СИ для измерения объема. В качестве показателя перевода из литров в кубометры используйте число 1000, потому что один литр приравнен к одному кубическому дециметру, а их в всякий кубический метр вмещается ровно тысяча штук.
6. Используйте правило измерения, противоположный описанному в предыдущем шаге, если тело в форме сферы невозможно наполнить жидкостью, но дозволено погрузить в нее. Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.
Видео по теме
Ремонт, переезд, покраска объекта – все это затребует вычисления площади. Не проступок припомнить школьную программу.
Инструкция
1. Припомним, что такое площадь. Площадь — это мера плоской фигуры по отношению к стандартной фигуре. Либо правильная величина, численное значение которой владеет следующими свойствами:• Если фигуру дозволено разбить на части, которые будут являться примитивными фигурами, то площадь такой фигуры будет равна сумме площадей ее частей• Площадь квадрата со стороной, которая равна единице измерения, равна единице• Равные фигуры владеют равными площадямиИз этих правил следует, что площадь это не определенная величина, то есть площадь дает только условную колляцию какой-нибудь фигуре. Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
2. Пример: Возьмем фигуру – прямоугольник, такой, в котором квадратный сантиметр укладывается в шесть раз. Тогда площадь такого прямоугольника будет равняться – 6 см2. Если взять больше трудную фигуру, скажем, трапецию, то получится что: Если трапеция такой величины, что квадратный сантиметр укладывается в нее только два раза, а третья часть не влезает целиком и остается маленький треугольник. Дабы измерить площадь этого оставшегося треугольника необходимо применить к нему доли квадратного сантиметра, дозволено взять миллиметр. Правда, данный метод для трудных фигур не дюже комфортный. Следственно для вычисления площади различных фигур существуют разные формулы. Если надобно вычислить площадь определенной фигуры, то дозволено взять учебник по геометрии и припомнить материал, тот, что когда-то проходили в школе.Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2
Видео по теме
Все планеты ясной системы имеют форму шара . Помимо того, шарообразную либо близкую к таковой форму имеют и многие объекты, сделанные человеком, включая детали технических устройств. Шар, как и всякое тело вращения, имеет ось, которая совпадает с диаметром. Впрочем это не исключительное главное качество шара . Ниже рассмотрены основные свойства этой геометрической фигуры и метод нахождения ее площади.

Инструкция
1. Если взять полукруг либо круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром именуется тело, ограниченное сферой. Сфера представляет собой оболочку шара , и ее сечением является окружность. От шара она отличается тем, что является полой. Ось как у шара , так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара именуется отрезок, проложенный от его центра до всякий внешней точки. В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения — круги различной площади.
2. Шар и сфера — взаимозаменяемые тела, в различие от конуса, невзирая на то, что конус также является телом вращения. Сферические поверхности неизменно в своем сечении образуют окружность, самостоятельно от того, как именно она вращается — по горизонтали либо по вертикали. Коническая же поверхность получается лишь при вращении треугольника по его оси, перпендикулярной основанию. Следственно конус, в различие от шара , и не считается взаимозаменяемым телом вращения.
3. Самый огромный из допустимых кругов получается при сечении шара плоскостью, проходящей через центр О. Все круги, которые проходят через центр О, пересекаются между собой в одном диаметре. Радиус неизменно равен половине диаметра. Через две точки A и B, располагающиеся в любом месте поверхности шара , может проходить безграничное число кругов либо окружностей. Именно по этой причине через полюса Земли может быть проведено неограниченное число меридианов.
4. При нахождении площади шара рассматривается, раньше каждого, площадь сферической поверхности.Площадь шара , а вернее, сферы, образующей его поверхность, может быть рассчитана на основании площади круга с тем же радиусом R. От того что площадь круга есть произведение полуокружности на радиус, его дозволено рассчитать дальнейшим образом:S = ?R^2Так как через центр шара проходят четыре основных огромных круга, то, соответственно площадь шара (сферы) равна:S = 4 ?R^2
5. Данная формула может быть пригодна в том случае, если вестим либо диаметр, либо радиус шара либо сферы. Впрочем, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь поверхности шара в полтора раза поменьше полной поверхности цилиндра:S = 2/3 S цил., где S цил. —площадь полной поверхности цилиндра.
Видео по теме
Шаром называют простейшую объемную фигуру геометрически положительной формы, все точки пространства внутри границ которой удалены от ее центра на расстояние, не превышающее радиуса. Поверхность, образуемая большинством максимально удаленных от центра точек, именуется сферой. Для количественного выражения меры пространства, заключенного внутри сферы, предуготовлен параметр, тот, что именуется объемом шара.

Инструкция
1. Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость — мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах — миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра.
2. Если знаменит материал, из которого изготовлен шар, и плотность этого материала дозволено узнать, скажем, из справочника, то определить объем дозволено взвесив данный предмет. Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.
3. Если радиус шара вестим из условий задачи либо его дозволено измерить, то для вычисления объема дозволено применять соответствующую математическую формулу. Умножьте учетверенное число Пи на третью степень радиуса, а полученный итог поделите на тройку: V=4*?*r?/3. Скажем, при радиусе в 40см объем шара составит 4*3,14*40?/3 = 267946,67см? ? 0,268м?.
4. Измерить диаметр почаще бывает проще, чем радиус. В этом случае нет необходимости разделять его напополам для применения с формулой из предыдущего шага — класснее упростить саму формулу. В соответствии с преобразованной формулой умножьте число Пи на диаметр в третьей степени, а итог поделите на шестерку: V=?*d?/6. Скажем, шар диаметром в 50см должен иметь объем в 3,14*50?/6 = 65416,67см? ? 0,654м?.
Задачи на вычисление площади круга зачастую встречаются в школьном курсе геометрии. Дабы обнаружить площадь круга, нужно знать длину диаметра либо радиуса окружности, в которую он заключен.

Вам понадобится
- — длина диаметра окружности.
Инструкция
1. Окружность — фигура на плоскости, состоящая из множества точек, удалённых на одинаковое расстояние от другой точки, называемой центром. Круг — плоская геометрическая фигура, представляет собой уйма точек, заключённых в окружность, которая является рубежом круга. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через её центр. Радиус — это отрезок, соединяющий точку на окружности и с её центром. ? — число «пи», математическая константа, непрерывная величина. Она показывает отношение длины окружности к длине её диаметра . Вычислить точное значение числа ? невозможно. В геометрии пользуются примерным значением этого числа: ? ? 3,14

2. Площадь круга равна произведению квадрата радиуса на число и вычисляется по формуле: S=?R^2, где S — площадь круга, R — длина радиуса окружности.
3. Из определения радиуса следует, что он равен половине диаметра . Следственно, формула приобретает вид: S=?(D/2)^2, где D — длина диаметра окружности. Подставьте в формулу значение диаметра , вычислите площадь круга.
4. Площадь круга измеряется в единицах площади — мм2, см2, м2 и т.п. В каких единицах выражается полученная вами площадь круга, зависит от того, в каких единицах был дан диаметр окружности.
5. Если вам нужно вычислить площадь кольца, воспользуйтесь формулой: S=?(R-r)^2, где R, r — радиусы внешней и внутренней окружностей кольца соответственно.
Полезный совет
Существует Интернациональный день числа «пи», тот, что отмечается 14 марта. Точное время наступления триумфальной даты — 1 час 59 минут 26 секунд, согласно цифрам числа — 3,1415926…
Видео по теме
Обратите внимание!
Увлекательно: объем шара с диаметром, превышающим в три раза диаметр иного шара, огромнее суммарного объема 3 таких шаров в 9 раз.
Полезный совет
Дабы развить у детей увлечение к математическим вычислениям, предлагайте в качестве примеров для расчета окружающие предметы: мяч, арбуз, клубок бабушкиной пряжи. Это наглядно и потому увлекательно.
jprosto.ru
