Перевод чисел в различные системы счисления с решением | Онлайн калькулятор
Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».
Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Получить запись
=
Выполнено переводов: 758195
Также может быть интересно: Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·103+9·102+2·101+1·100. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·103+2·102+3·101+4·100+5·10-1+6·10-2+7·10-3.
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 10011.11012 = 1·24+0·23+0·22+1·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 16+2+1+0.5+0.25+0.0625 = 19.812510
Ответ: 10011.11012 = 19.812510
2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125 = 3727.1757812510
Ответ:
E8F.2D16 = 3727.1757812510
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
3. Перевести число 27310 в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·82+2·81+1·80 = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.
27310 = 4218
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0.5·2 = 1.0 (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
0.12510 = 0.0012
programforyou.ru
Перевод из десятичной системы счисления в другие
|
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа |
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Перевод в десятичную систему счисления
Перевод целых чисел из системы счисления с основанием q (недесятичной системы) в десятичную систему счисления выполняется по правилу: если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. Рассмотрим примеры:
1123 = 1 · 32
+ 1 · 31 + 2 · 30 = 9 + 3 + 2 = 14101011012 = 1 · 25 + 0 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20 = 32 + 0 + 8 + 4 + 1 = 4510
15FС16 = 1 · 163 + 5 · 162 + 15(F) · 161 + 12(С) · 160 = 4096 + 1280 + 240 + 12 = 562810
Развернутая форма числа
Развернутая форма записи числа – это запись в виде разрядных слагаемых, записанных с помощью степени соответствующего разряда и основания степени=10.
Рассмотрим примеры:
3247810 = 3·10000 + 2·1000 + 4·100 + 7·10 + 8 =
= 3·104 + 2·103 + 4·102 + 7·101 + 8·100
1123
= 1·10
1011012 = 1·105 + 0·104 + 1·103 + 1·102 + 0·101 + 1·100
15FC16 = 1·103 + 5·102 + F·102 + C·100
Арифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
С л о ж е н и е
Таблицы сложения легко составить, используя Правило Счета.
|
Сложение в двоичной системе |
Сложение в восьмеричной системе
|
|
Сложение в двоичной системе
|
Сложение в восьмеричной системе
|
Сложение в шестнадцатеричной системе
 При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.
При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
|
Шестнадцатеричная: F16+616 |
Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2.81 + 5.80 = 16 + 5 = 21, 1516 = 1.161 + 5.160 = 16+5 = 21. |
Пример 2. Сложим числа 15, 7 и 3.
|
Шестнадцатеричная: F16+716+316
|
Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3.81 + 1.80 = 24 + 1 = 25, 1916 = 1.161 + 9.160 = 16+9 = 25. |
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25;
311,28 = 3.82 + 1.81 + 1.80 + 2.8-1 = 201,25 ;
C9,416 = 12.161 + 9.160 + 4.16-1 = 201,25 .
studfiles.net
Перевод чисел из десятичной системы счисления — Циклопедия
Перевод чисел из десятичной системы счисления — это преобразование чисел десятичной системы счисления в числа другой системы счисления.
Сначала производится последовательное деление столбиком исходного числа и получаемых (от предыдущих делений) частных (больших или равных основанию) на основание новой системы счисления и записываются остатки от делений. Деление продолжается до тех пор, пока частное не станет меньше основания. Затем выписываются цифры в новой системе счисления вместо (полученных в десятичной системе счисления) последнего частного и остатков от делений в обратном (получению) порядке. Полученное число является записью исходного числа в новой системе счисления.
[править] Примеры перевода чисел из десятичной системы счисления
[править] Перевод 10→2
143910=101100111112
[править] Перевод 10→3
143910=12220223
[править] Перевод 10→4
143910=1121334
[править] Перевод 10→5
143910=212245
[править] Перевод 10→6
143910=103556
[править] Перевод 10→7
143910=41247
[править] Перевод 10→8
143910=26378
[править] Перевод 10→9
143910=18689
[править] Перевод 10→10
143910=143910
[править] Перевод 10→11
143910=109911
[править] Перевод 10→12
143910=9BB12
[править] Перевод 10→13
143910=86913
[править] Перевод 10→14
143910=74B14
[править] Перевод 10→15
143910=65E15
[править] Перевод 10→16
143910=59F16
[править] Другие алгоритмы:
cyclowiki.org
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
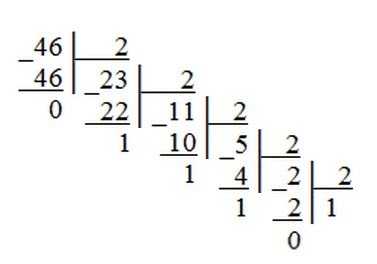
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
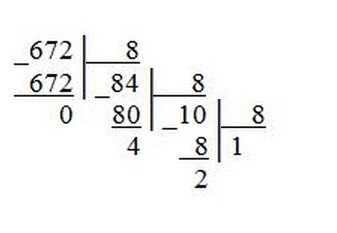
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Перевод числа из одной системы счисления в другую — Мои статьи — Каталог статей
С.С. Лебедев
ст. преподаватель кафедры ЕНТД КФ АГТУ
А.В. Бабкина
студентка химико-технологического факультета
Е.А. Колмогорцев
студент математического факультета КФ ПГУ
Перевод числа из одной системы счисления в другую
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
Количество p различных цифр, употребляемых в системе счисления*, определяет название системы и называется основанием системы счисления – «p».Для человека привычной является десятичная система счисления, т.е. система счисления, основанная на алфавите из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Это связано с тем, что человек учится считать на предметах которые он может увидеть, взять, …, т.е. реально ощутить. И одним из этих предметов являются его собственные пальцы, которых как раз 10.
Естественно, что основание системы счисления может быть любым, а значит, система счисления может быть не только десятичной, например, в современной вычислительной технике применяется двоичная система счисления, основанная всего на двух цифрах: 0 и 1. Это объясняется тем, что электронные устройства могут находиться только в двух устойчивых состояниях: «есть ток», «нет тока». А закодировать в числовой форме эти состояния (для создания программ, управляющих ЭВМ) удобнее всего с помощью именно двоичной системы счисления: 1 – «есть ток», 0 – «нет тока».
Кроме двух перечисленных, достаточно распространены восьмеричная (0, 1, 2, 3, 4, 5, 6, 7) и шестнадцатеричная (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F) системы счисления.
Но человеку, как уже было сказано выше, удобнее оперировать с десятичной системой счисления, и как следствие, требуются способы перевода чисел из одной системы счисления в другую.
Далее мы рассмотрим эти способы.
Перевод чисел в десятичную систему
Осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
Перевести 10101101.1012 в 10-ю систему счисления. Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы, к которой относится число, будем указывать в виде нижнего индекса.
10101101.1012 = 1*27+ 0*26+ 1*25+ 0*24+ 1*23+ 1*22+ 0*21+ 1*20+ 1*2-1+ 0*2-2+ 1*2-3 = 173.62510
Перевод целых десятичных чисел в недесятичную систему счисления (алгоритм Евклида)
Метод перевода числа из десятичной системы счисления в недесятичную с использованием алгоритма Евклида заключается в следующем**:-
Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления.
-
Последовательно выполнять деления данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя.
-
Полученные остатки, являющиеся цифрами числа в новой системе счисления, перевести в соответствие с алфавитом новой системы счисления.
-
Составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример.
Перевести 2510 в 2-ю систему счисления
Результат: 2510 = 110012
Данный способ изучается в школе, однако при этом учитель иногда сталкивается с проблемой. У некоторых учеников сложился устойчивый стереотип: прекращать деление необходимо тогда, когда частное равно 1. Для таких школьников непонятно, почему необходимо прекращать деление, если частное, например, 3. Чтобы преодолеть эту проблему, учителю приходится тратить дополнительное время на повторное объяснение уже пройденного материала.
Следует отметить, что на вопрос ученика «Почему?» учитель нередко отвечает: «Дальнейшее деление невозможно». Такое заявление является, мягко говоря, абсурдным с точки зрения математики.
Вторая проблема, которую выделяем мы, заключается в следующем: почему необходимо брать одно частное и все остатки от деления?
Методически более правильно будет объяснение, основанное на делении числа до тех пор, пока частное не станет равно нулю. Делить с остатком, в том числе и когда частное равно нулю, школьники умеют еще с начальной школы.
Тогда на вопрос: «Почему прекращаем деление?» – можно ответить, что дальнейшее деление бессмысленно, т.к. все время будет получаться нуль в частном и в остатке от деления. И все полученные остатки, записанные в обратном порядке, будут являться значащими цифрами числа в новой системе счисления. Даже если кто-то из учеников предположит, что мы будем делить нулевое частное еще несколько раз, то может ли это повлиять на правильность результата? Конечно же, нет, т.к. появляющиеся нули будут попадать в начало числа, т.е. будут незначащими. Так, приведенный выше пример можно оформить следующим образом:
А сам алгоритм можно трактовать так:
-
Разделить с остатком исходное число, записанное в десятичной системе счисления и по правилам десятичной системы счисления, на основание новой системы счисления.
-
Если частное больше нуля, то повторить п.1 для частного.
-
Все остатки от деления, записанные в обратном порядке, будут являться значащими цифрами числа в новой системе счисления.
Перевод правильных дробей из десятичной системы счисления в недесятичную
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 0.312510 в 8-ю систему счисления.
Результат: 0.312510 = 0.248
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 0.6510 в 2-ю систему счисления (точность 6 знаков)
Результат: 0.6510 ≈ 0.10(1001)2
В заключение приведем довольно любопытную теорему. Известно, что при переводе десятичной дроби в другую систему счисления количество значащих цифр после запятой может меняться. Например, 0,12510 = 0,18 или 0,539062510=0,8А16.
В этом контексте встает вопрос о максимальном количестве значащих цифр после запятой при переводе десятичной дроби в другую систему счисления.
Теорема. Пусть имеется десятичная дробь, имеющая k значащих цифр после запятой, т.е. . Если данную дробь перевести в любую другую отличную от десятичной систему счисления, то количество значащих цифр после запятой конечной дроби в новой системе счисления будет определяться соотношением: .Покажем справедливость теоремы для числа с одной значащей цифрой после запятой в десятичной дроби (k = 1; (0,x1)10, х1 <> 0) при переводе в двоичную систему счисления (z = 2).
Используем метод перевода по частям (умножением) для перевода дробной части числа из десятичной системы счисления в двоичную.
Для любых ai, принадлежащих множеству {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}, т.к. это множество является алфавитом десятичной системы счисления.
Количество ai вместе с x1 соответствует количеству символов десятичного алфавита. Допустим, что все символы алфавита встречаются среди {аi, x1} хотя бы раз, тогда существует i, такой, что, начиная с аi все последующие элементы должны равняться нулю. Если учесть предположение, что все символы алфавита встречаются хотя бы раз, то i = 9 (a9 = 0), тогда число в двоичной системе счисления будет записано как (0.y1y2y3y4y5y6y7y8y9)2. Таким образом, количество значащих цифр после запятой в двоичной системе счисления будет равно 9 или t = 101-1.
Если в ноль обратится элемент, индекс которого, меньше 9, то получаем t < 101-1. Объединим это неравенство с полученным ранее равенством, получаем: t ≤ 101-1.
Допустим, что не один из {аi, x1} не равен нулю, тогда существуют i, j такие, что a i = aj. Тогда дальнейшее умножение приведет к повторяющейся последовательности ai, т.е. полученная дробь в двоичной системе счисления является периодической, что выходит за рамки данной теоремы.
——
* Здесь и далее имеются в виду только позиционные системы счисления. ** Информатика. Задачник-практику в 2т. / под ред. И.Г. Семакина, Е.К. Хеннера: Том 1. – М.: Бином. Лаборатория Знаний, 2002. – 304с.: ил. – С. 32.www.xn--90acbfcbabb9aw0dl.xn--p1ai
Перевод чисел из одной системы счисления в другую
Разделы: Информатика
Цели урока:
- повторить изученный материал по теме система счисления ;
- научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот;
- освоить принципы перевода чисел из одной системы в другую;
- развивать логическое мышление.
Ход урока
Вначале урока краткое повторение и проверка домашнего задания..
Вопросы:
— В каком виде представлена числовая информация в памяти компьютера?
— Для чего используются системы счисления?
— Какие виды систем счисления вы знаете? Привести свои примеры.
— Чем отличаются позиционные системы от непозиционных?.
Цель нашего урока научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот. Но в начале мы рассмотрим, как можно
представить любое целое неотрицательное чисело:
В позиционных системах значение записи целого числа определяется по следующему правилу: пусть a na n-1a n-2…a 1a 0 — запись числа A, а i – цифры, тогда
A = a n·pn+a n-1·pn-1 +a n-2·pn-2+…+a 1·p1+ a0·p0 (1),
где p — целое число большее 1, которое называется основанием системы счисления
Для того, чтобы при заданном p любое неотрицательное целое число можно было бы записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.
Пример:
1) Десятичная система
p = 10
цифры: 0,1,2,3,4,5,6,7,8,9
число 5735 = 5·103+7·102+3·101+8·100
2) Троичная система
p = 3
цифры: 0,1,2
число 2013 = 2·32+0·31+1·30
Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.
Представление отрицательных и дробных чисел:
Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘. Для отделения целой части числа от дробной используется запятая. Значение записи a na n-1a n-2…a 1a 0, a -1 a -2…a m-2 a m-1a m числа A определяется по формуле, являющейся обобщением формулы (1):
A = an·pn+a n-1·p n-1+a n-2·p n-2+…+a1·p1+a0·p0+a-1·p-1+a -2·p-2+…+am-2·p–(m–2)+am–1·p–(m–1)+amp–m (2),
Пример:
75,6 = 7·101+5·100+6·10–1
–2,3145 = –(2·50+3·5–1+1·5–2+4·5–3)
Перевод чисел из произвольной системы счисления в десятичную:
Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.
Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.
Перевод чисел из десятичной системы счисления в произвольную.
Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором. Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что 23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·81+7·80+4·8–1 =27,48. Понятно, что не всегда ответ столь очевиден. В общем случае применяется способ перевода отдельно целой и дробной частей числа.
Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):
1. Найдем частное и остаток от деления числа на p. Остаток будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.
2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.
Замечание 1. Цифры ai в записи числа нумеруются справа налево.
Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.
Пример:
Перевести число 165 в семеричную систему счисления.
165:7 = 23 (остаток 4) => a0 = 4
23:7 = 3 (остаток 2) => a1 = 2
3:7 = 0 (остаток 3) => a2 = 3
Выпишем результат: a2a1a0, т.е. 3247.
Выполнив проверку по формуле (1), убедимся в правильности перевода:
3247=3·72+2·71+4·70=3·49+2·7+4 = 147+14+4 = 165.
Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):
1. Умножим дробную часть числа на p.
2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.
Замечание 1. Цифры am в записи числа располагаются слева направо в порядке возрастания абсолютного значения m.
Замечание 2. Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.
Пример 1:
Перевести число 0,625 в двоичную систему счисления.
0,625·2 = 1,25 (целая часть 1) => a-1 =1
0,25·2 = 0,5 (целая часть 0) => a-2 = 0
0,5·2 = 1,00 (целая часть 1) => a-3 = 1
Итак, 0,62510 = 0,1012
Выполнив проверку по формуле (2), убедимся в правильности перевода:
0,1012=1·2-1+0·2-2+1·2-3=1/2+1/8 = 0,5+0,125 = 0,625.
Пример 2:
Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.
0,165·4 = 0,66 (целая часть 0) => a-1=0
0,66·4 = 2,64 (целая часть 2) => a-2= 2
0,64·4 = 2,56 (целая часть 2) => a-3= 2
0,56·4 = 2,24 (целая часть 2) => a-4= 2
Итак, 0,16510 ” 0,02224
Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:
0,02224 = 0·4-1+2·4-2+2·4-3+2·4-4= 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625
|0,1640625–0,165| = 0,00094 < 4–4 = 0,00390625
Перевод чисел из одной произвольной системы в другую
В этом случае сначала следует выполнить перевод числа в десятичную систему, а затем из десятичной в требуемую.
Особым способом выполняется перевод чисел для систем с кратными основаниями.
Пусть p и q – основания двух систем счисления. Будем называть эти системы системами счисления с кратными основаниями, если p = qn или q = pn, где n – натуральное число. Так, например, системы счисления с основаниями 2 и 8 являются системами счисления с кратными основаниями.
Пусть p = qn и требуется перевести число из системы счисления с основанием q в систему счисления с основанием p. Разобьем целую и дробную части записи числа на группы по n последовательно записанных цифр влево и вправо от запятой. Если количество цифр в записи целой части числа не кратно n, то надо дописать слева соответствующее количество нулей. Если количество цифр в записи дробной части числа не кратно n, то нули дописываются справа. Каждая такая группа цифр числа в старой системе счисления будет соответствовать одной цифре числа в новой системе счисления.
Пример:
Переведем 1100001,1112 в четверичную систему счисления.
Дописав нули и выделив пары цифр, получим 01100001,11102.
Теперь выполним перевод отдельно каждой пары цифр, пользуясь пунктом Перевод чисел из одной произвольной системы в другую.
012=110=14
102=210=24
002=010=04
012=110=14
112=310=34
102=210=24
Итак, 1100001,1112 = 01100001,11102 = 1201,324.
Пусть теперь требуется выполнить перевод из системы с большим основанием q, в систему с меньшим основанием p, т.е. q = pn. В этом случае одной цифре числа в старой системе счисления соответствует n цифр числа в новой системе счисления.
Пример: Выполним проверку предыдущего перевода числа.
1201,324 = 1100001,11102=1100001,1112
В шестнадцатеричной системе есть цифры с числовыми значениями 10,11,12, 13,14,15. Для их обозначения используют первые шесть букв латинского алфавита A, B, C, D, E, F.
Приведем таблицу чисел от 0 до 16, записанных в системах счисления с основаниями 10, 2, 8 и 16.
| Число в десятичной системе счисления | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| В восьмеричной | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 |
| В двоичной | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 |
| В шестнадцатеричной | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
Для записи шестнадцатеричных цифр можно использовать также строчные латинские буквы a-f.
Пример: Переведем число 110101001010101010100,112 в шестнадцатеричную систему счисления.
Воспользуемся кратностью оснований систем счисления (16=24). Сгруппируем цифры по четыре, дописав, слева и справа нужное количество нулей
000110101001010101010100,11002
и, сверяясь с таблицей, получим: 1A9554,C16
Вывод:
В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.
А человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр. Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.
Записываем задание на дом:
а) Запишите дату рождения всех членов вашей семьи в различных системах счисления.
б) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
а) 1001111110111,0112 ;
б) 1110101011,10111012
xn--i1abbnckbmcl9fb.xn--p1ai
Перевод из одной системы счисления в другую
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число X в позиционной системе с основанием s может быть представлено в виде полинома:
где s — база системы счисления, — цифры, допустимые в данной системе счисления . Последовательность образует целую часть X, а последовательность — дробную часть X.
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления представляет собой целую степень двойки: — для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением (запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа). Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад), то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или шестнадцатеричной цифрой (см. таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Соответствие между цифрами в различных системах счисления| DEC | BIN | OCT | HEX | BCD |
| 0 | 0000 | 0 | 0 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 |
| 3 | 0011 | 3 | 3 | 0011 |
| 4 | 0100 | 4 | 4 | 0100 |
| 5 | 0101 | 5 | 5 | 0101 |
| 6 | 0110 | 6 | 6 | 0110 |
| 7 | 0111 | 7 | 7 | 0111 |
| 8 | 1000 | 10 | 8 | 1000 |
| 9 | 1001 | 11 | 9 | 1001 |
| 10 | 1010 | 12 | A | 0001 0000 |
| 11 | 1011 | 13 | B | 0001 0001 |
| 12 | 1100 | 14 | C | 0001 0010 |
| 13 | 1101 | 15 | D | 0001 0011 |
| 14 | 1110 | 16 | E | 0001 0100 |
| 15 | 1111 | 17 | F | 0001 0101 |
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Пусть X — число в системе счисления с основанием s, которое требуется представить в системе с основанием h. Удобно различать два случая.
В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае () удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа в произвольной позиционной системе. Пусть число в исходной системе счисления s имеет вид . Требуется получить запись числа в системе счисления с основанием h:
.
Для нахождения значений разделим этот многочлен на h:
.
Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:
.
Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.
Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы.
Решение:

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Перевод правильных дробей
Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра может быть найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0, если же оно больше или равно 1, то цифра равна целой части произведения. Следующая цифра справа определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется .
Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
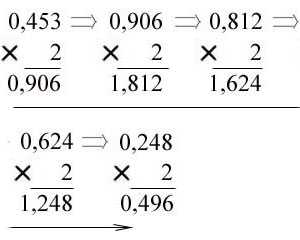
Ответ:
** В восьмеричную систему:
Ответ:
*** В шестнадцатеричную систему:

Ответ: так как , то
Поделиться с друзьями
function-x.ru
