Ответы по олимпиаде по физике – Олимпиадные задания (физика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»

Олимпиада по физике 7, 8 классы

Муниципальный этап всероссийской олимпиады школьников по физике

2016-17 учебный год

7 класс

1. Решение

Выразим расстояние: S=6V_вел. Найдем соотношение между скоростями:

S/V_вел +S/V_пеш = 18 мин; V_пеш = V_вел /2; t= 4 S/ V_пеш = 48 мин.

Критерии оценивания:

Выражено расстояние через скорость — 2 б

Выражено соотношение между скоростями — 2б

Выражено соотношение для времени — 2б

Приведён числовой ответ — 2б.

 2. Решение

Выполним перевод скоростей : 36 км/ч = 10 м/с; 54 км/ч = 15м/с. Если мысленно превратить три стороны квадрата в прямую линию, то получается что велосипедисты едут навстречу друг другу по прямой линии. В этом случае время до их первой встречи определяется, как расстояние (равное 3 сторонам квадрата) деленное на их суммарную (относительную) скорость

t₁ = = = 180 с = 3 мин (1)

Для нахождения интервала времени ∆t, необходимого для расчета времени второй встречи сформулируем задачу: эти велосипедисты после первой встречи начинают движение со своими скоростями в противоположным направлениях и до второй встречи проходят четыре стороны квадрата. Следовательно,

∆t = = = 240 с = 4 мин (2),

Тогда t₂ = t₁ + ∆t =7 мин (3)

Очевидно, что t₃ отличается от t₂ на тот же самый интервал ∆t, т.к. от момента второй встречи все повторяется, как и после первой, т.е.

t₃ = t₂ + ∆t = 7 мин + 4 мин = 11 мин(4 )

ОТВЕТ: t₁ = 3мин, t₂ = 7 мин, t₃ = 11 мин.

Критерии оценивания:

1	Правильно выполнен перевод единиц измерения скоростей	1 балл
2	Получено выражение (1) и вычислено время t1	3 балла
3	Получено выражение (3) и вычислено время t2	2 балла
4	Получено выражение (4) и вычислено время t3	2 балла

3. Решение

Пусть — масса каждой из частей бруска, и — их плотности. Тогда части бруска имеют объемы и , а весь брусок массу и объем . Средняя плотность бруска

.

Отсюда находим плотности частей бруска:

кг/м³, кг/м³.

Критерии оценивания:

1. Определено, что средняя плотность бруска есть – 1 балл.

2. Определены объемы каждой части бруска и – 2 балла.

3. Определен весь объем бруска – 2 балла.

4. Выражена средняя плотность бруска через – 1 балла.

5. Найдена плотность каждого бруска – по 2 балла.

4. Решение

Расход воды из горячего крана составляет (10 л)/(100 с) = 0,1 л/с, а из холодного крана (3 л)/(24 с) = 0,125 л/с . Следовательно, общий расход воды равен 0,1 л/с + 0,125 л/с = 0,225 л/с . Поэтому кастрюля емкостью 4,5 литра наполнится водой за время (4,5 л)/(0,225 л/с) = 20 с.

ОТВЕТ: кастрюля наполнится водой за 20 с.

Критерии оценивания:

1	Вычислен расход воды из горячего крана	1 балл
2	Вычислен расход воды из холодного крана	2 балла
3	Вычислен общий расход воды	2 балла
4	Вычислено время наполнения кастрюли	3 балла

5.

Критерии оценивания:

Рассмотрен ряд из пяти кубиков – 1 балл

Найдена длина ряда кубиков – 2 балла

Найдена длина ребра одного кубика – 2 балла

Найден объём большого куба – 3 балла.

Максимальное количество баллов – 40.

Муниципальный этап всероссийской олимпиады школьников по физике

2016-17 учебный год

8 класс

1. Решение

На систему, состоящую из поплавка и грузила, действуют направленные вниз силы тяжести (приложена к поплавку) и (приложена к грузилу), а также направленные вверх силы Архимеда (приложена к поплавку) и (приложена к грузилу). В равновесии сумма сил, действующих на систему равна нулю:

.

Отсюда

г.

Критерии оценивания:

1. Нарисован рисунок с приложенными к каждому телу силами – 1 балл.

2. Записана сумма сил, действующих на поплавок (с учетом силы натяжения со стороны лески) – 1 балл.

3. Записана сумма сил, действующих на грузило (с учетом силы натяжения со стороны лески) – 1 балл.

4. Исключена сила натяжения и записано условие равновесия системы – 2 балла.

5. Получено конечное выражение для массы грузила – 2 балла.

6. Получено числовое значение – 1 балл.

2. Решение

Выразим высоту налитой жидкости:

h₁=m₁/ (ρ_в*S), где S – площадь сечения сосуда. Гидростатическое давление:

p₁ = ρ_вgh₁.

Изменение давления Δp= ρ_вgh₂, где

h₂= m₂/ (ρ₂*S), так как V_ш = V_в.

Тогда в процентах р₁ – 100%

Δp — х %

Получаем ответ на 2,2%

Критерии оценивания:

Уравнение для давления — 2 балла.

Выражена высота налитой жидкости — 2балла.

Выражено выражение для изменения h — 2балла.

Получено соотношение в % — 2балла.

3.

Критерии оценивания:

Найдено время заполнения бассейна одним насосом – 2 балла.

Найдено время заполнения 2/3 бассейна одним насосом – 2 балла.

Найдено время заполнения 1/3 бассейна тремя насосами – 2 балла.

Найдено время заполнения всего бассейна – 2 балла.

4. Решение

Найдем количество теплоты, необходимое для нагревания льда от -20 до 0⁰С. : 840 Дж.

Найдем количество теплоты, необходимое для охлаждения воды от 20 до 0⁰С: -8400 Дж.

Найдем количество теплоты, необходимое для плавления льда: 6640 Дж.

Баланс количества теплоты в сторону нагревания воды: ΔQ=8400-6680-840= =920Дж.

Тогда установится температура: Δt= 920/(0,12*4200) = 1,8⁰С.

Критерии оценивания:

Перевод единиц — 1 балл.

Записана формула количества теплоты для нагревания льда – 1 балл.

Записана формула количества теплоты для плавления льда – 1 балл.

Записана формула количества теплоты для охлаждения воды – 1 балл.

Вычислена разность количества теплоты — 1балл.

Количество теплоты на нагревание общей массы воды – 2 балла.

Приведён числовой ответ -1 балл.

5.

Критерии оценивания:

Введена мощность чайника – 2 балла.

Уравнение теплового баланса в случае со льдом – 2 балла.

Уравнение теплового баланса в случае с водой – 2 балла.

Найдено значение массы чайника – 2 балла.

 

multiurok.ru

Олимпиада по физике 7-11 классов с решениями

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

7 класс

1. На графике показана зависимость пути, пройденного телом от времени. Какой из графиков соответствует зависимости скорости этого тела от времени?

2. Из пункта A в пункт B выехал автомобиль «Волга» со скоростью 90 км/ч. В то же время навстречу ему из пункта B выехал автомобиль «Жигули». В 12 часов дня машины проехали мимо друг друга. В 12:49 «Волга» прибыла в пункт

B, а ещё через 51 минуту «Жигули» прибыли в A. Вычислите скорость «Жигулей».

3. Материальная точка движется по окружности радиусом R=2 м с постоянной по модулю скоростью, совершая полный оборот за 4 с. Определите среднюю скорость по перемещению за первые 3 с движения

4. Тело движется так, что скорости его в течение каждого из n равных промежутков времени равны соответственно V₁ ,V₂, V₃, …..V_n. Какова средняя скорость тела?

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

8 класс

1. К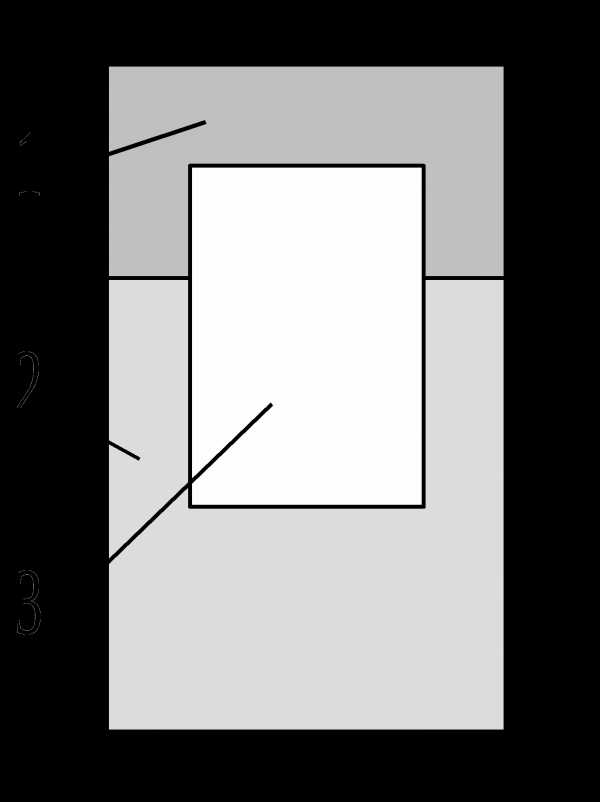убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей ₁ и ₂. Найти плотность материала кубика 

   3.

2. Междугородный автобус прошел 80 км за 1 час. Двигатель развивал мощность 70 кВт при КПД 25%. Сколько дизельного топлива (плотность 800 кг/м³, удельная теплота сгорания 42 10⁶ Дж/кг) сэкономил водитель, если норма расхода горючего 40 л на 100 км пути?

3. Человек переправляется на лодке из пункта А в пункт В, находящийся на кратчайшем расстоянии от А на другом берегу. Скорость лодки относительно воды 2,5 м/c, скорость течения реки 1,5 м/c. Какое минимальное время потребуется ему для переправы, если ширина реки равна 800 м?

4. Тело проходит одинаковые участки пути с постоянными в пределах участка скоростями V₁ , V₂ , V₃, ….. V_n .Определите среднюю скорость на всем пути.

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

9 класс

1. Полый шарик из алюминия находясь в воде, растягивает пружину динамометра с силой 0.24 Н, а в бензине с силой 0,33 Н. Найти объем полости. Плотности алюминия, воды и бензина соответственно  =2,7 10³ кг/м³,  _в = 10³ кг/м³ и  _Б =0,7 10³ кг/м³. Выталкивающей силой воздуха пренебречь. Ускорение свободного падения g = 10 м/c².

2. На наклонном дне сосуда, наполненного водой, покоится на маленьких подставках алюминиевый кубик с ребром a = 10 см. Определите суммарную силу трения между кубиком и подставками. Угол наклона дна сосуда к горизонту  = 30°, плотности алюминия и воды соответственно _a =  2,7 • 10³ кг/м³,  _в = 10³ кг/м³. Ускорение свободного падения g = 10 м/c².

3. Камень, брошенный под углом  30⁰ к горизонту, дважды был на одной высоте h; спустя время t₁ = 3 c и время t₂ = 5 c после начала движения. Найти начальную скорость тела. Ускорение свободного падения Земли равно 9,81 м/c².

4. Ускорение свободного падения на поверхности Солнца 264,6 м/c², а радиус Солнца в 108 раз больше радиуса Земли. Определите отношение плотностей Земли и Солнца. Ускорение свободного падения Земли равно 9,81 м/c².

5. Для измерения температуры 66 г воды в нее погрузили термометр, имеющий теплоемкость С_Т= 1,9 Дж/К, который показывал температуру в помещении t₂=17,8⁰С. Какова действительная температура воды, если термометр показывает 32,4 ⁰С. Теплоемкость воды с=4,2 кДж/K?

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

10 класс

1. Пузырек воздуха поднимается со дна водоема, имеющего глубину H . Найти зависимость радиуса пузырька воздуха от глубины его положения в текущий момент времени, если его объем на глубине H равен V.

2. За время t₁ = 40 c в цепи состоящей из трех одинаковых проводников соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты Q. За какое время выделится такое же количество теплоты, если проводники соединить последовательно?

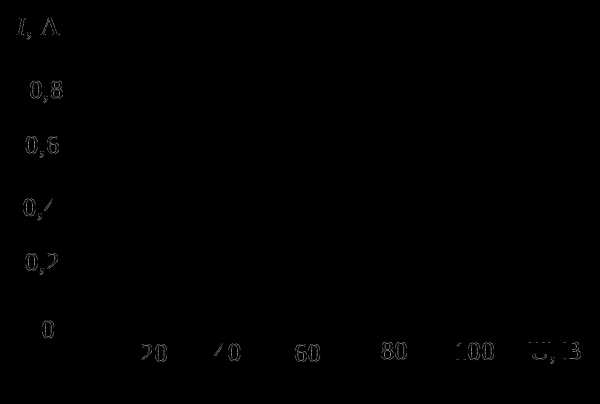
3. Можно ли две лампы накаливания мощностью 60 Вт и 100 Вт, рассчитанные на напряжение 110 В, включить последовательно в сеть напряжением 220 В, если допустимо превышение напряжения на каждой лампе не более 10% от номинального? Вольтамперная характеристика (зависимость силы тока в лампе от приложенного напряжения) показана на рисунке.

4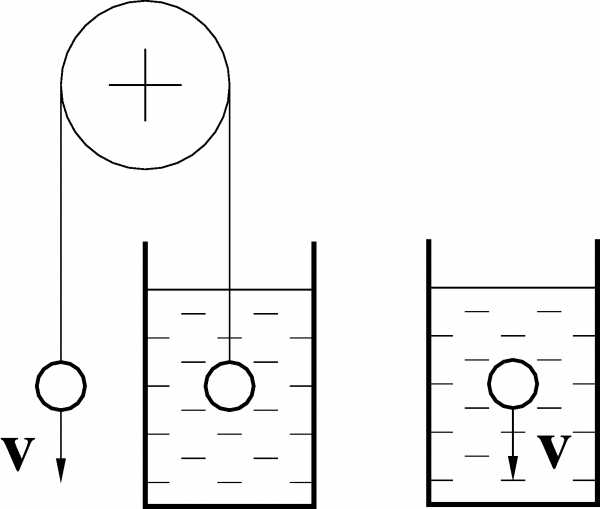. Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ₀, поднимается с установившейся скоростью v. Определить отношение ρ/ρ₀, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.

5. Спортсмены бегут с одинаковыми скоростями v колонной длины l₀ . Навстречу бежит тренер со скоростью u (u

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

11 класс

1. Колесо радиуса R катится без проскальзывания с постоянной скоростью центра колеса v. С верхней точки обода колеса срывается камешек. Через какое время колесо наедет на этот камешек? Радиус колеса R, ускорение свободного падения g.

2. Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В тот момент, когда муравей находится в точке А на расстоянии l₁ = 1 м от центра муравейника его скорость v₁= 2 см/с. За какое время муравей добежит от точки А до точки В, которая находится на расстоянии l₂ = 2 м от центра муравейника?

3. Какой максимальный объём воды плотностью ρ₁ = 1,0 г/см³ можно налить в H-образную несимметричную трубку с открытыми верхними концами, частично заполненную маслом плотностью ρ₂ = 0,75 г/см³? Площадь горизонтального сечения вертикальных частей трубки равна S. Объёмом горизонтальной части трубки можно пренебречь. Вертикальные размеры трубки и высота столба масла приведены на рисунке (высоту h считать заданной).

Примечание. Затыкать открытые концы трубки, наклонять её или выливать из неё масло запрещено.

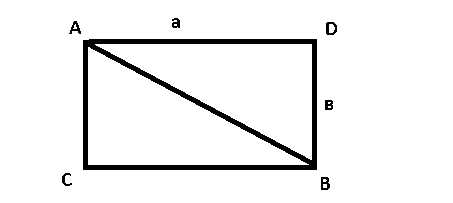
4. Чему равно сопротивление проволочного каркаса в виде прямоугольника со сторонами а и в и диагональю, если ток течет от точки А к точке В? Сопротивление единицы длины провода .

6. Движение материальной точки описывается уравнением х(t)=0,2 sin(3,14t), где х выражается в метрах, t – в секундах. Определите путь, пройденный точкой за 10 с движения.

Возможные решения

7 класс

2. На графике показана зависимость пути, пройденного телом от времени. Какой из графиков соответствует зависимости скорости этого тела от времени?

Решение: Правильный ответ Г.

2. Из пункта A в пункт B выехал автомобиль «Волга» со скоростью 90 км/ч. В то же время навстречу ему из пункта B выехал автомобиль «Жигули». В 12 часов дня машины проехали мимо друг друга. В 12:49 «Волга» прибыла в пункт B, а ещё через 51 минуту «Жигули» прибыли в A. Вычислите скорость «Жигулей».

Решение: Волга» проехала путь от пункта A до места встречи с «Жигулями» за время t_x, а «Жигули» этот же участок проехали за t₁ = 100 минут. В свою очередь, «Жигули» проехали путь от пункта B до места встречи с «Волгой» за время t_x, а «Волга» этот же участок проехала за t₂ = 49 минут. Запишем эти факты в виде уравнений:

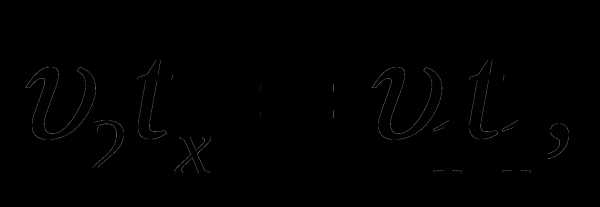
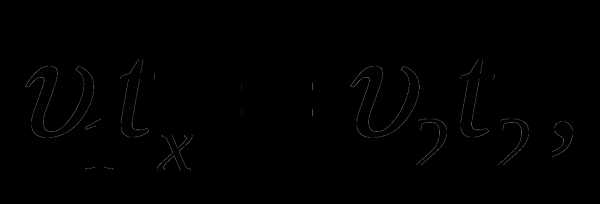
где υ₁ – скорость «Жигулей», а υ₂ – скорость «Волги». Поделив почленно одно уравнение на другое, получим:

.

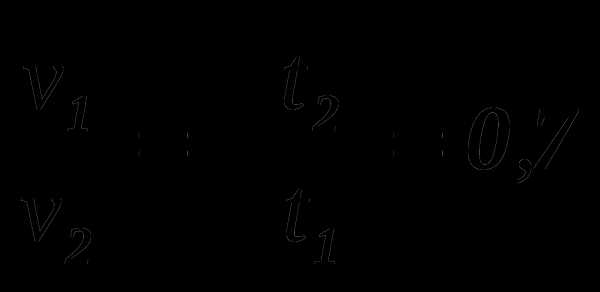Отсюда υ₁ = 0,7υ₂ = 63 км/ч.

3. Материальная точка движется по окружности радиусом R=2 м с постоянной по модулю скоростью, совершая полный оборот за 4 с. Определите среднюю скорость по перемещению за первые 3 с движения

Решение: Перемещение материальной точки за 3 с составляет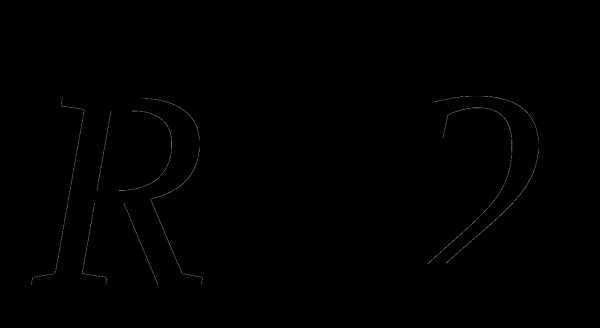

Средняя скорость по перемещению равна 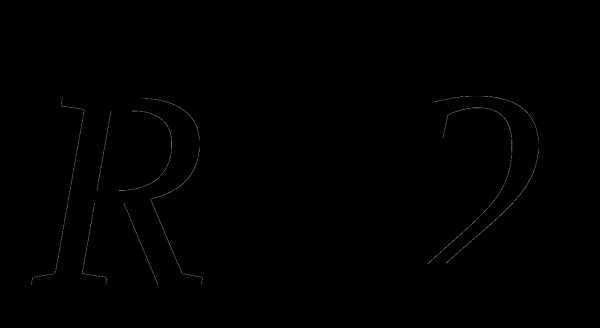/3

4. Тело движется так, что скорости его в течение каждого из n равных промежутков времени равны соответственно V₁ ,V₂, V₃, …..V_n. Какова средняя скорость тела?

Решение: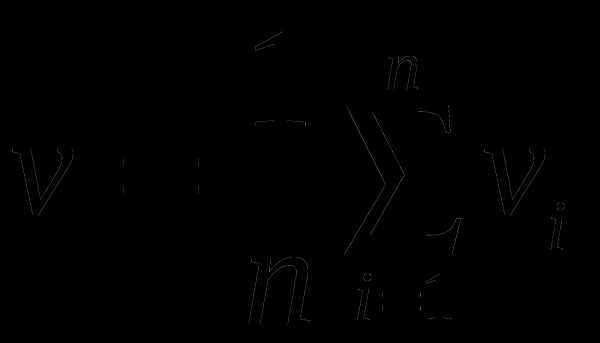

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

Возможные решения

8 класс

2. Кубик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей ₁ и ₂. Найти плотность материала кубика _3.

Решение: F₁ mg =F₁+F₂ F₂

₃ gV = ₁ gV 2/3 +₂ gV 1/3

mg ₃ = ₁2/3 +₂1/3

₃ = (2₁ + ₂)/3

2. Междугородный автобус прошел 80 км за 1 час. Двигатель развивал мощность 70 кВт при КПД 25%. Сколько дизельного топлива (плотность 800 кг/м³, удельная теплота сгорания 42 10⁶ Дж/кг) сэкономил водитель, если норма расхода горючего 40 л на 100 км пути?

Решение: КПД = A/Q =Nt/rm = Nt/rV

V= Nt/rКПД

Вычисления: V= 0,03 м³; из пропорции 80/100 = x/40 определяем норму расхода горючего на 80 км х = 32 (литра)

V=32-30=2 (литра)

3. Человек переправляется на лодке из пункта А в пункт В, находящийся на кратчайшем расстоянии от А на другом берегу. Скорость лодки относительно воды 2,5 м/c, скорость течения реки 1,5 м/c. Какое минимальное время потребуется ему для переправы, если ширина реки равна 800 м?

Решение: Для переправы за минимальное время необходимо, чтобы вектор результирующей скорости v был направлен перпендикулярно берегу

4. Тело проходит одинаковые участки пути с постоянными в пределах участка скоростями V₁ , V₂ , V₃, ….. V_n .Определите среднюю скорость на всем пути.

Решение: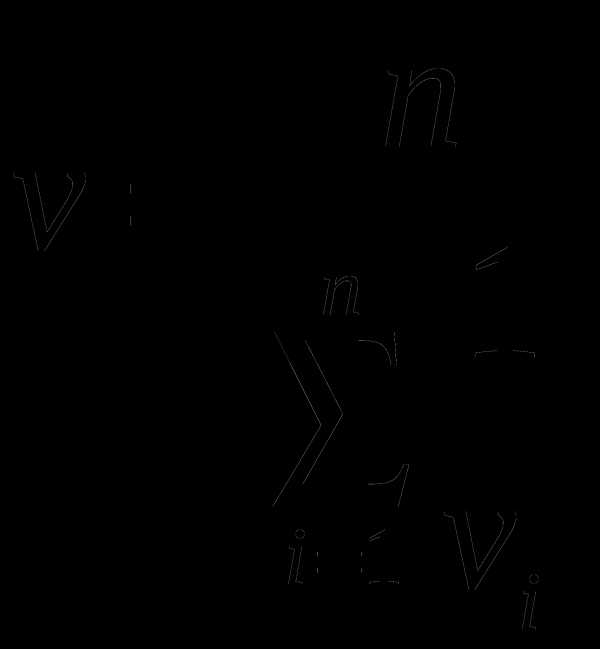

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

Возможные решения

9 класс

7. Полый шарик из алюминия находясь в воде, растягивает пружину динамометра с силой 0.24 Н, а в бензине с силой 0,33 Н. Найти объем полости. Плотности алюминия, воды и бензина соответственно  =2,7 10³ кг/м³, _в = 10³ кг/м³ и _Б =0,7 10³ кг/м³. Выталкивающей силой воздуха пренебречь. Ускорение свободного падения g = 10 м/c².

Решение:

8. На наклонном дне сосуда, наполненного водой, покоится на маленьких подставках алюминиевый кубик с ребром a = 10 см. Определите суммарную силу трения между кубиком и подставками. Угол наклона дна сосуда к горизонту  = 30°, плотности алюминия и воды соответственно _a =  2,7 • 10³ кг/м³,  _в = 10³ кг/м³. Ускорение свободного падения g = 10 м/c².

Решение: Кубик находится в равновесии под действием трех сил: силы тяжести mg, архимедовой силы F_A и силы реакции со стороны подставок, которую, в свою очередь, удобно разложить на две составляющие: нормальную к наклонному дну составляющую силы реакции N и силу трения о подставки F_тр.

Отметим, что наличие подставок, на которых покоится кубик, играет в задаче важную роль, т.к. именно благодаря им вода окружает кубик со всех сторон, и для определения силы, с которой вода действует на него, можно воспользоваться законом Архимеда. Если бы кубик лежал непосредственно на дне сосуда и вода под него не подтекала, то результирующая поверхностных сил давления воды на кубик не выталкивала бы его наверх, а наоборот, еще сильнее прижимала бы ко дну. В нашем случае на кубик действует выталкивающая сила F_A = a³g, направленная вверх.

Проектируя все силы на координатную ось, параллельную дну сосуда, запишем условие равновесия кубика в виде: F_тр = (mg – F_A) sin.

Учитывая, что масса кубика m = _aa³, получаем ответ: F_тр =(_a – _в)a³g sin = 8,5 (Н).

9. Камень, брошенный под углом  30⁰ к горизонту, дважды был на одной высоте h; спустя время t₁ = 3 c и время t₂ = 5 c после начала движения. Найти начальную скорость тела. Ускорение свободного падения Земли равно 9,81 м/c².

Решение: Движение тела в вертикальном направлении описывается уравнением:

Отсюда при y = h получим;

Используя свойства корней квадратного уравнения, согласно которым

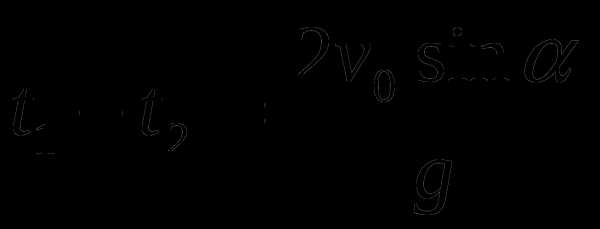получим

10. Ускорение свободного падения на поверхности Солнца 264,6 м/c², а радиус Солнца в 108 раз больше радиуса Земли. Определите отношение плотностей Земли и Солнца. Ускорение свободного падения Земли равно 9,81 м/c².

Решение: Применим закон всемирного тяготения для определения g

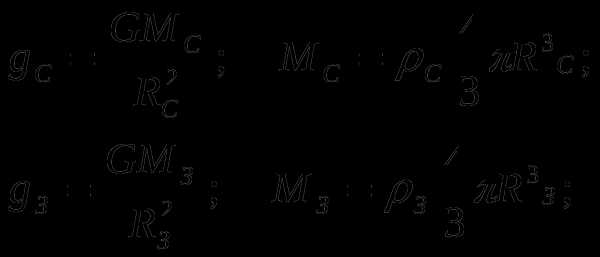
11. Для измерения температуры 66 г воды в нее погрузили термометр, имеющий теплоемкость С_Т= 1,9 Дж/К, который показывал температуру в помещении t₂=17,8⁰С. Какова действительная температура воды, если термометр показывает 32,4 ⁰С. Теплоемкость воды с=4,2 кДж/K?

Решение: Термометр при погружении его в воду получил количество теплоты .

Это количество теплоты отдано ему водой; следовательно .

Отсюда

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап

Возможные решения

10 класс

1. Пузырек воздуха поднимается со дна водоема, имеющего глубину H . Найти зависимость радиуса пузырька воздуха от глубины его положения в текущий момент времени, если его объем на глубине H равен V.

Решение: Давление на дне водоема: на глубине h:

Объем пузырька на глубине h: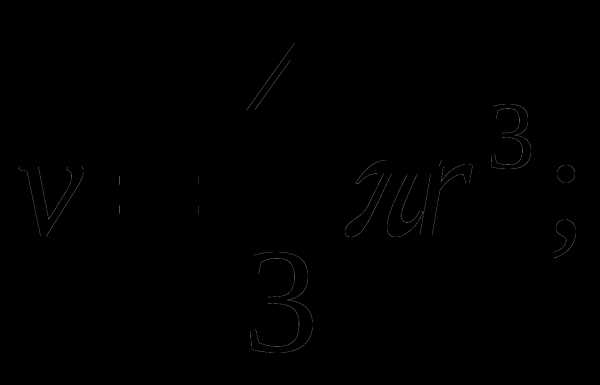

Отсюда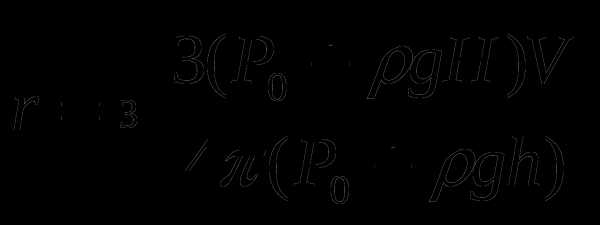

2. За время t₁ = 40 c в цепи состоящей из трех одинаковых проводников соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты Q. За какое время выделится такое же количество теплоты, если проводники соединить последовательно?

Решение:

3. Можно ли две лампы накаливания мощностью 60 Вт и 100 Вт, рассчитанные на напряжение 110 В, включить последовательно в сеть напряжением 220 В, если допустимо превышение напряжения на каждой лампе не более 10% от номинального? Вольтамперная характеристика (зависимость силы тока в лампе от приложенного напряжения) показана на рисунке.

Решение: При номинальном напряжении U_н=110 В ток, текущий через лампу мощностью Р₁= 60 Вт равен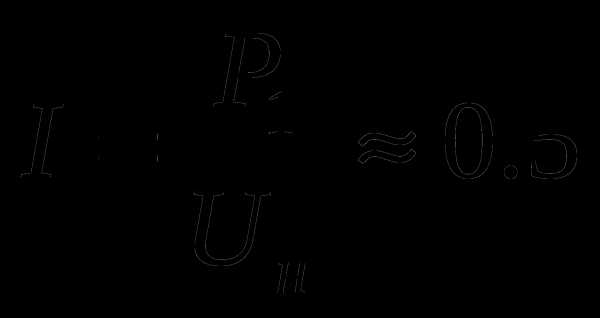А. При последовательном соединении ламп такой же ток пойдет через лампу мощностью Р₂= 100 Вт. Согласно вольтамперной характеристике этой лампы, при токе 0,5 А напряжение на этой лампе должно быть В. Следовательно, при последовательном соединении двух ламп напряжение на лампе мощностью 60 Вт достигает номинального уже при напряжении в сети 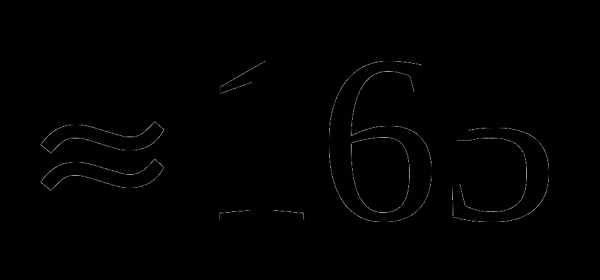В. Поэтому при напряжении в сети 220 В напряжение на этой лампе будет превышать номинальное больше, чем на 10%, и лампа перегорит.

4. Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ₀, поднимается с установившейся скоростью v. Определить отношение ρ/ρ₀, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.

Решение: Силы сопротивления движению шаров из-за равенства их установившихся скоростей одинаковы в обоих случаях, хотя и направлены в противоположные стороны.

Запишем динамическое уравнение движения в проекциях на ось оу, направленную вертикально вверх, для первого и второго случаев (движения системы тел и падения одного шарика в жидкости, соответственно):

T – mg = 0

T + F_A – mg – F_c = 0

F_A – mg + F_c = 0 ,

где mg –модуль силы тяжести, Т – модуль силы натяжения нити, F_A – модуль выталкивающей силы, F_c — модуль силы сопротивления.

Решая систему уравнений, получим, .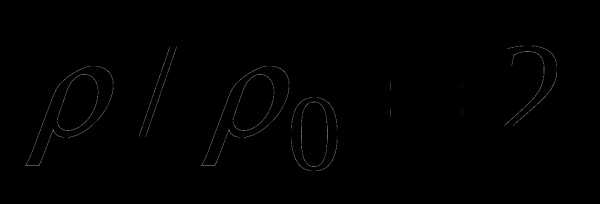

5. Спортсмены бегут с одинаковыми скоростями v колонной длины l₀ . Навстречу бежит тренер со скоростью u (u

Решение: Время, в течение которого все спортсмены, начиная с первого и кончая последним в колонне, повстречаются с тренером, равно

.

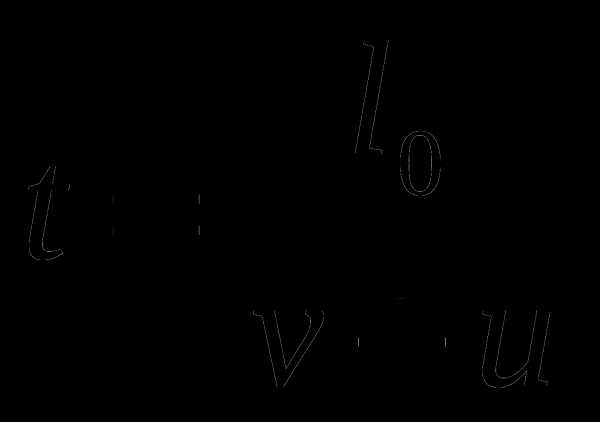В тот момент, когда последний спортсмен поравняется с тренером, первый будет находиться от него на расстоянии

.

Такова и будет длина колонны, когда все спортсмены развернутся.

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область.

Муниципальный этап

Возможные решения

11 класс

1. Колесо радиуса R катится без проскальзывания с постоянной скоростью центра колеса v. С верхней точки обода колеса срывается камешек. Через какое время колесо наедет на этот камешек? Радиус колеса R, ускорение свободного падения g.

Решение: Если ось колеса движется со скоростью v, без проскальзывания, то скорость нижней точки равна 0, а верхней, как и горизонтальная скорость камушка, равна 2v.

Время падения камушка

Время движения оси по горизонтали в два раза больше.

Значит, наезд произойдет через .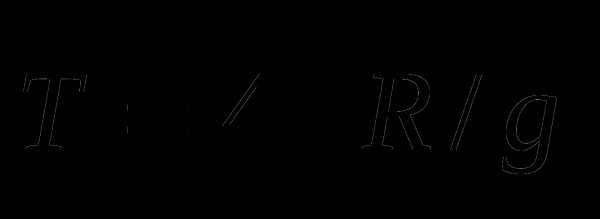

2. Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В тот момент, когда муравей находится в точке А на расстоянии l₁ = 1 м от центра муравейника его скорость v₁= 2 см/с. За какое время муравей добежит от точки А до точки В, которая находится на расстоянии l₂ = 2 м от центра муравейника?

Решение: Скорость муравья меняется со временем не по линейному закону. Поэтому средняя скорость на разных участках пути различна, и пользоваться для решения известными формулами для средней скорости мы не можем. Разобьем путь муравья от точки А до точки В на малые участки, проходимые за одинаковые промежутки времени . Тогда

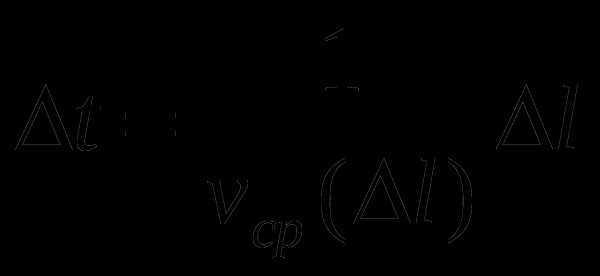, где 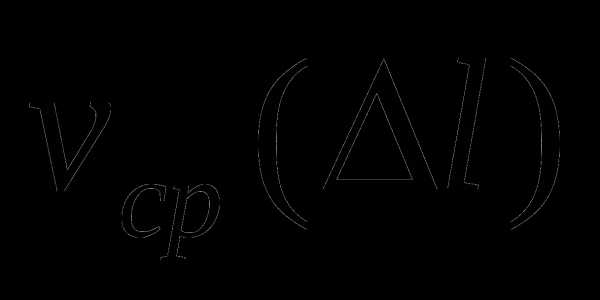— средняя скорость на данном отрезке .

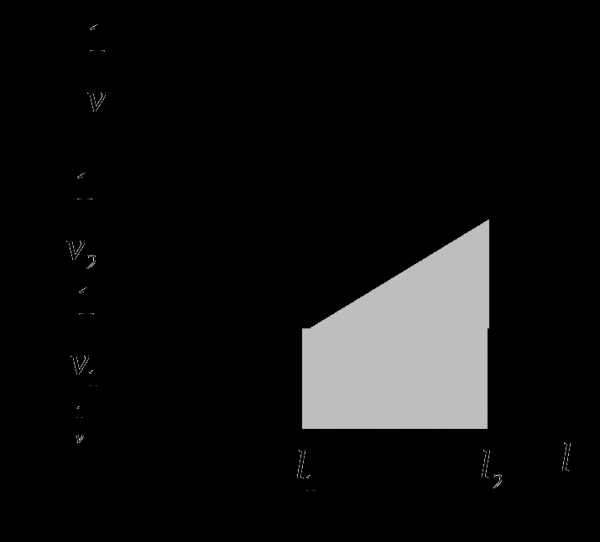Построим график зависимости величины 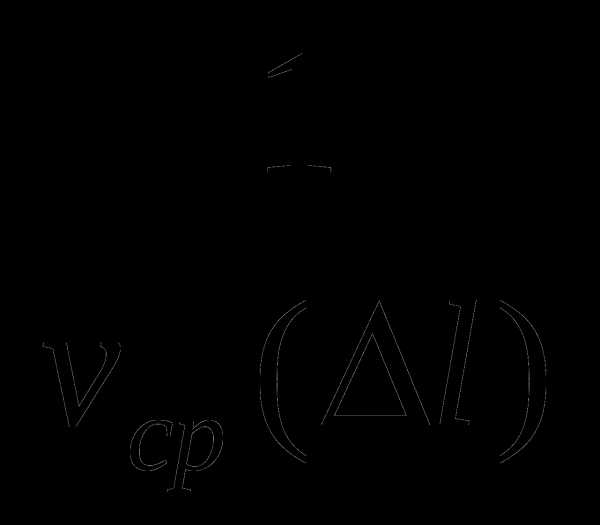от (см. рисунок). Искомое время численно равно заштрихованной на рисунке площади:

.

Учитывая, что 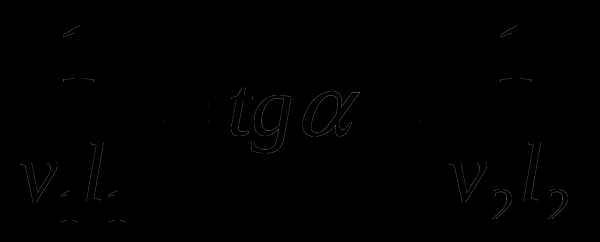, найдем соотношение между обратными величинами скоростей: 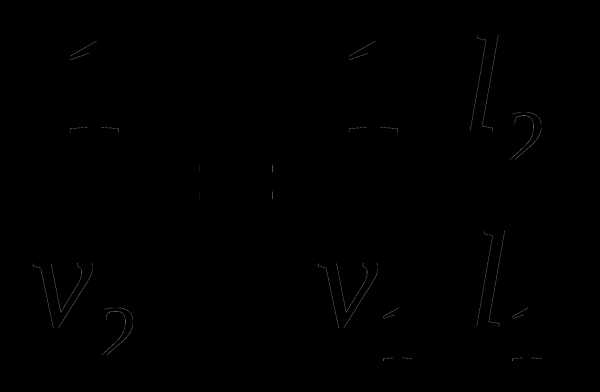. Подставляя полученное равенство в последнее выражение для , получим: .

После подстановки, найдем значение с.

3. Какой максимальный объём воды плотностью ρ₁ = 1,0 г/см³ можно налить в H-образную несимметричную трубку с открытыми верхними концами, частично заполненную маслом плотностью ρ₂ = 0,75 г/см³? Площадь горизонтального сечения вертикальных частей трубки равна S. Объёмом горизонтальной части трубки можно пренебречь. Вертикальные размеры трубки и высота столба масла приведены на рисунке (высоту h считать заданной).

Примечание. Затыкать открытые концы трубки, наклонять её или выливать из неё масло запрещено.

Решение: Важно, чтобы в коротком колене осталось как можно меньше масла. Тогда в высокой трубке можно будет создать столб максимальной высоты, превышающей 4h на х. Для этого начнём наливать воду в правое колено. Так будет продолжаться до тех пор, пока уровень воды не достигнет 2h в правом колене, а уровень масла, соответственно, – 3h в левом. Дальнейшее вытеснение масла невозможно, так как граница раздела масло-вода в правом колене станет выше соединительной трубки, и в левое колено начнёт поступать вода. Процесс добавления воды придётся прекратить, когда верхняя граница масла в правом колене достигнет верха колена. Условие равенства давлений на уровне соединительной трубки даёт:

откуда x = (ρ₁ — ρ₂)h/ρ₂. Окончательно, высота столба воды, который удалось налить (4h + х), а, следовательно, максимальный объем воды будет 4,33hS.

4. Чему равно сопротивление проволочного каркаса в виде прямоугольника со сторонами а и в и диагональю, если ток течет от точки А к точке В? Сопротивление единицы длины провода .

Решение:

R

5. Движение материальной точки описывается уравнением х(t)=0,2 sin(3,14t), где х выражается в метрах, t – в секундах. Определите путь, пройденный точкой за 10 с движения.

Решение: Движение описывается уравнением:

;

отсюда Т=1 с За время 10 с точка совершит 10 полных колебаний. За время одного полного колебания точка проходит путь равный 4 амплитудам.

Полный путь равен 10x 4x 0,2 = 8 м

infourok.ru

Всероссийская олимпиада по физике 10 класс с ответами

            №1

Один  мотоциклист проехал половину пути со скоростью v1, а другую половину пути со скоростью v2. Другой мотоциклист этот же путь проехал половину времени со скоростью v1, а другую половину времени со скоростью v2. Определите отношение средних скоростей мотоциклистов.

Этапы решения	Решение	Баллы
1	Средняя скорость движения мотоциклистов на всем пути равна vср=s/t,где s – весь путь, t-все время движения.	1
2	Для первого мотоциклиста : vср’=s/(t1+t2)=s/(s/2v2+s/2v2)=s/s/2(1/v1+1/v2)=2/(1/v1+1/v2)=2v1*v2/(v2+v1)	3
3	Для второго мотоциклиста : vср’’=s/t=(s1+s2)/t=v1*t/2+v2*t/2=(t/2*(v1+v2))/r=(v1+v2)/2 vcр’’= (v1++v2)/2	4
4	Отношение средних скоростей будет равна: Vcр’’/vcр’=(v1+v2)/2/2v1*v2/(v1+v2)=(v1+v2)(v1+v2)/4v1*v2=(v1+v2)2/4v1+v2	2
	Итого	10

                                                                                                 №2
Шарик с плотностью р, меньшей,чем у воды,падает с высоты Н в воду. Сила сопротивления в воде составляет1/3 веса шарика.Пренебрегая силой сопротивления воздуха, определите, на какую глубину шарик погрузится в воду. Плотность воды р0.

 

 

                                     Решение:                                             Fт                                                           

Дано:                                                   H                                                                                                                                                                                

 р0-плотность воды

р-плотность шарика                                                        Fсопр

Н-высота падения                                                            Fа                     h

F сопр=1/3р                                                                        Fтяж

Найти:

h-глубину погружения

                                                                     

Этапы решения	Решение	Баллы
1	В воздухе на шарик действует только сила тяжести Fт=mg, а в воде на шарик действует кроме силы тяжести еще архимедова сила и сила сопротивления воды.	1
2	В воде шарик имеет отрицательное ускорение,т.к. движение равнозамедленное: -ma=Ft-(Fc+Fa),т.к. Ft=mg,Fc=1/3mg, Fa=p0gV Имеем: -ma=mg-mg/3-p0gV(1)	3
3	Конечная скорость шарика в воздухе равна его начальной скорости в воде: Н= v02/2g          v02=2gH; в воде: а=v02/2h a=2gH/2h=gH/h	3
4	Подставляя значения а в уравнение(1): -m*gH/h=mg-mg/3-p0gm/p -H/h=1-1/3-p0/p H/h=p0/p-2/3 H=3Hp/(3p0-2p)	3
	Итого	10

                                                                  №3

Гиря массой m, подвешенная на пружине жесткостью k, совершает колебания амплитудой А.Определить максимальное значение импульса гири в процессе колебания.

                                                    Решение

Дано:

m-масса гири

k-жесткость пружины

А-амплитуда колебания

Этапы решения	Решение	Баллы
1	При колебаниях пружины потенциальная энергия деформированной пружины превращается в кинетическую энергию движения гири Ep=Ek	2
2	Максимальная потенциальная энергия будет равна: Ep=kA2/2,а в положении равновесия потенциальная энергия будет равна нулю. При этом, кинетическая энергия будет максимальной,т.к. скорость груза небольшая: Ek=mv2/2	3
3	На основании закона сохранения энергии,имеем: kA2/2=mv2/2 kA2= mv2 v=    kA2/m v=A    k/m	3
4	Импульс гири при прохождении положения равновесия будет максимальным: Р=mv P=mA     k/m	2
	Итого	10

                                                                  №4

Определить,до какой минимальной температуры надо нагреть стальной шарик,чтобы он,будучи положен на лед,полностью в него погрузился.Температура льда O0С,удельная теплоемкость стали С,плотность стали р0,плотность льда р,удельная теплота плавления льда λ.

.
Решение

Дано:

t0= O0С
C -удельная теплоемкость стали

р0- плотность стали

p- плотность льда

λ- удельная теплота плавления льда

Этапы решения	Решение	Баллы
1	Количество теплоты,которое выделяет стальной шарик при охлаждении до O0С будет равно количеству теплоты,которое необходимо для расплавления льда в объеме шарика: Qш =Qп	2
2	Следовательно, Qш=m0C(t-t0),где m0— масса шарика. Так как m0=p0V,то Qш= p0VС(t-t0)-количество теплоты,отданное шариком при его охлаждении.	3
3	Количество теплоты,полученное льдом в процессе плавления : Qп= λm,где m-масса расплавленного льда, m=pV Qп=λ pV	3
4	Уравнение теплового баланса: Р0VC(t-t0)= λ pV Решая,получим:t=λ p/ p0С+ t0	2
	Итого	10

                           

                                                      №5

Определить,сколько витков никелиновой проволоки надо навить на фарфоровый цилиндр диаметром d, чтобы сделать кипятильник,в котором за время t закипела бы вода массой m,взятая при температуре t1.Напряжение в сети U.Диаметр проволоки d0, а к  полезного действия кипятильника принять равным 50%. Удельное сопротивление никелина р,удельная теплоемкость воды С.

Дано:

d- диаметр цилиндра

t- время нагрева до кипения

m-масса воды
t1-начальная температура воды

t2-конечная температура воды

С- удельная теплоемкость воды

р- удельное сопротивление никелина

d0-диаметр проволоки

n=50%
U-напряжение в сети
Найти: N

Этапы решения	Решение	Баллы
1	Количество теплоты,необходимое для нагревания воды: Q1=Cmt Количество теплоты ,выделяемое кипятильником за время t: Q2=U2/R*t Cопротивление нагревательного элемента кипятильника: R=pl/s,где l-длина проволоки,s-площадь поперечного сечения	1
2	Коэффициент полезного действия кипятильника: n=Q1/Q2*100% 50%= Q1/Q2*100% 5 Q2=10 Q1 Q2=2 Q1 U2/R*t=2cmt U2s/pl*t=2cm(t2-t1)	3
3	Определим длину проволоки: U2st=pl2cm(t2-t1) l= U2st/2pcm(t2-t1),где s=пr2=пd02/4 тогда l= U2 пd02t/8pcm(t2-t1)	3
4	Длина одного витка проволоки : l1=пd Число витков найдем ,разделив длину проволоки на длину одного витка: N=l/ l1= U2 пd02t/8pcm(t2-t1)пd= U2d02t/8pcm(t2-t1)пd	3
	Итого	10

shkolnaya-olimpiada.ru

Инфофизика : олимпиадные задания по физике

Школьный этап

Вариант задания олимпиады памяти И.В.Савельева для 7 класса по физике с ответами и решениями 1. Первый час автомобиль ехал по дороге со скоростью 40 км/час, следующий час – со скоростью 60 км/час. Найти среднюю скорость автомобиля на всем пути и на второй половине пути. 2. Буратино массой 40 кг сделан из дерева, его плотность 0,8 г/см³. Утонет ли Буратино в воде, если к его ногам привязать кусок стального рельса массы 20 кг? Считать, что плотность стали в 10 раз больше плотности воды. 3. Школьный динамометр тянут в разные стороны, приложив к его корпусу (первый крючок) и к пружине (второй крючок) одинаковые по величине силы 1 Н.Движется ли динамометр? Что показывает при этом динамометр? 4. В одной комнате находится три лампы. Каждая из них включается одним из трех выключателей, расположенных в соседней комнате. Для того, чтобы определить, какая лампа включается каким выключателем, потребуется дважды сходить из одной комнаты в другую. А можно ли это сделать за один раз, используя знания физики?

Муниципальный  этап Всероссийской олимпиады школьников  по физике.             

   7 класс. 2011-2012 учебный год Сосуд объемом V = 1 л заполнен на три четверти водой. Когда в него погрузили кусок меди, уровень воды поднялся и часть ее, объемом V0 = 100 мл, вылилась через край. Найдите массу куска меди. Плотность меди ρ = 8,9 г/см3. На соревнованиях по плаванию два пловца стартуют одновременно. Первый проплывает длину бассейна за 1,5 минуты, а второй — за 70 секунд. Достигнув противоположного края бассейна, каждый пловец разворачивается и плывет в другую сторону. Через какое время после старта второй пловец поравняется с первым, обойдя его на один «круг»?

К трем одинаковым динамометрам, соединенным так, как показано на рисунке, подвешен груз. Показания верхнего и нижнего динамометров 90 Н и 30 Н соответственно. Определите показания среднего динамометра.

Почему при резком торможении передним колесом велосипеда есть опасность перелететь через руль? Вариант задания олимпиады памяти И.В.Савельева для 8 класса по физике с ответами и решениями 1. Первую четверть пути по прямой жук прополз со скоростью V, оставшуюся часть пути – со скоростью 2V. Найти среднюю скорость жука на всем пути и отдельно на первой половине пути. 2. Школьник находится на горизонтальной поверхности. На него действуют горизонтально направленные силы. На север (там кофе и булочки) сила 20 Н. На Запад (там спортивная площадка) сила 30 Н. На восток (в школу) сила 10 Н. И еще действует сила трения. Школьник неподвижен. Определите величину и направление силы трения. 3. Автобус проехал мимо остановки, двигаясь со скоростью 2 м/с. Пассажир в течение 4 секунд стоял и ругался, а потом побежал догонять автобус. Начальная скорость пассажира равна 1 м/с. Ускорение его постоянно и равно 0,2 м/с². Через какое время после начала движения пассажир догонит автобус? 4. Буратино массой 40 кг сделан из дерева, его плотность 0,8 г/см³. Утонет ли Буратино в воде, если к его ногам привязать кусок стального рельса массы 20 кг? Считать, что плотность стали в 10 раз больше плотности воды. 5. Вдали от всех других тел, в глубинах космоса, движется летающая тарелка. Её скорость в некоторый момент времени равна V₀. Пилот хочет произвести маневр, в результате которого скорость будет направлена перпендикулярно начальному направлению (под углом 90 градусов) и останется такой же по величине как до маневра. Ускорение корабля не должно превышать заданной величины а₀. Найдите минимальное время маневра. Ответы. Муниципальный  этап Всероссийской олимпиады школьников  по физике.                 8 класс. 2011-2012 учебный год И уличный, и медицинский ртутные термометры имеют почти одинаковые размеры (около 10-15 см в длину). Почему же уличным термометром можно измерять температуры от -30°C до +50°C, а медицинским — только от 35°C до 42°C? В результате измерения КПД двигателя получился равным 20%. Впоследствии оказалось, что во время измерения 5% топлива вытекало через трещину в топливном шланге. Какой результат измерения КПД получится после устранения неисправности? Вода массой m = 3,6 кг, оставленная в пустом холодильнике, за T = 1 час охладилась от температуры t₁ = 10°C до температуры t₂ = 0°C. При этом холодильник отдавал в окружающее пространство тепло с мощностью P = 300 Вт. Какую мощность потребляет холодильник от сети? Удельная теплоемкость воды c = 4200 Дж/(кг·°C). В сосуде находится вода при температуре t₀ = 0°C. От этого сосуда отводят тепло с помощью двух металлических стержней, торцы которых находятся в дне сосуда. Сначала тепло отводят через один стержень с мощностью P₁ = 1 кДж/с, а спустя T = 1 мин начинают одновременно отводить и через второй стержень, с такой же по величине мощностью P₂ = 1 кДж/с. Дно сосуда покрыто антиобледенительным составом, поэтому весь образовавшийся лед всплывает на поверхность. Постройте график зависимости массы образовавшегося льда от времени. Удельная теплота плавления льда l = 330 кДж/кг.
Вариант задания олимпиады памяти И.В.Савельева для 9 класса по физике с ответами и решениями 1. Первую четверть пути по прямой жук прополз со скоростью V, оставшуюся часть пути – со скоростью 2V. Найти среднюю скорость жука на всем пути и отдельно на первой половине пути. 2. С поверхности земли бросают вверх камень, через t=2 секунды еще один камень из той же точки с той же скоростью. Найдите эту скорость, если удар произошел на высоте H=10 метров. 3. В нижней точке сферической ямы радиуса R=5 м находится маленькое тело. Ему ударом сообщают горизонтальную скорость V=5 м/с. Его полное ускорение сразу после начала движения оказалось равным а=8 м/с². Определите коэффициент трения μ. 4. В легкий тонкостенный сосуд, содержащий m₁= 500 г воды при начальной температуре t₁=+90˚С, доливают еще m₂= 400 г воды при температуре t₂=+60˚С и m₃= 300 г воды при температуре t₃=+20˚С. Пренебрегая теплообменом с окружающей средой, определите установившуюся температуру. 5. На гладкой горизонтальной поверхности находятся два тела с массами m и m/2 . К телам прикреплены невесомые блоки и они связаны невесомой и нерастяжимой нитью так, как показано на рисунке. К концу нити прикладывают постоянную силу F . Найти ускорение конца нити.
Ответы.

Муниципальный  этап Всероссийской олимпиады школьников  по физике.        9 класс. 2011-2012 учебный год

 

Задача 1.

В один из двух одинаковых сосудов налито в два раза больше воды, чем в другой. Сосуды закрыты одинаковыми поршнями, плотно прилегающими к стенкам и поверхности воды, и подвешены за эти поршни к плечам рычага. Трение между поршнями и стенками отсутствует. Система находится в равновесии, а поршни — на одном уровне. В стенках сосудов на одном уровне проделывают маленькие отверстия и соединяют сосуды легкой тонкой трубкой. В какую сторону потечет вода по трубке?

Задача 2.

Кузьма бежал по кругу с постоянной скоростью. В точке A он встретил Матвея, который бежал с постоянным ускорением по диаметру AB. Скорость Матвея в момент встречи была равна скорости Кузьмы. Кузьма, не изменяя скорости, пробежал полкруга и встретился с Матвеем в точке B, куда тот как раз успел добежать. Определите отношение ускорений Кузьмы и Матвея.

Задача 3.

Сосуд наполнен до краев водой массой M = 20 кг с температурой t₁ = 10 °C. В него аккуратно опускают кусок льда массой m = 2,1 кг, имеющий температуру t₀ = 0 °C. Какая температура установится в сосуде? Удельная теплоемкость воды c = 4200 Дж/(кг·°C), удельная теплота плавления льда l = 330 кДж/кг. Тепловыми потерями пренебречь.

Задача 4.

В результате измерения КПД двигателя получился равным 20%. Впоследствии оказалось, что во время измерения 5% топлива вытекало через трещину в топливном шланге. Какой результат измерения КПД получится после устранения неисправности?

 

Задача 5.

К источнику постоянного напряжения 200 В подключена схема из четырех резисторов, как показано на рисунке. На двух резисторах выделяется мощность 50 Вт, на других двух — 100 Вт. Как изменятся эти мощности, если замкнуть ключ К?


Ответы

САЙТ «Школьная физика»

infofizika555.blogspot.com

Примеры школьных олимпиад по физике

Ключевые слова: задания олимпиадного уровня, решение, физика, олимпиады школьников, литература для подготовки.

Объект разработки и исследования: содержательная часть общеобразовательного предмета физика для участников предметных олимпиад школьников по биологии.

Цель работы: применение собственного многолетнего опыта проведения олимпиад школьников для развития творческого потенциала, улучшения качества подготовки школьников по физике, повышения конкурентоспособности школьников при продолжении образования медико-биологического профиля.

Методология проведения работы: анализ опыта проведения олимпиад по общеобразовательному предмету физика в РНИМУ им. Н.И. Пирогова, разработка на основании имеющихся данных научно-образовательного материала для обучающихся средних общеобразовательных учебных заведений, обладающего достаточной степенью информативности и творческим компонентом, разработка заданий для самоподготовки учащихся и абитуриентов, и использования в аудиторной работе со школьниками.

Область применения: предлагаемый научно-образовательный материал по физике адресован школьникам и абитуриентам, желающим улучшить свою подготовку по физике, расширить область познаний в широком спектре, а также готовящимся к участию в олимпиадах, сдаче ЕГЭ и вступительных испытаний в вузах.

Степень внедрения: олимпиадные задания повышенного уровня, представленные в научно-образовательном материале, и аналогичные успешно применяются с 2008 года при проведении предметных олимпиад школьников в РНИМУ им. Н.И. Пирогова, в т.ч. и входящих в ежегодный Перечень олимпиад школьников. В олимпиадах участвовали обучающиеся общеобразовательных учебных заведений московского региона, в т.ч. и учащиеся профильных классов медико-биологического профиля.

Настоящие методические указания написаны для помощи лицам, принимающим участие в олимпиадах по физике «Трудитесь и побеждайте» и «Шаг в будущее», которые проводятся в РНИМУ им. Н.И.Пирогова с 2008 года. Составителями методических указаний являются сотрудники кафедры медицинской и биологической физики Университета: профессор А.Г. Максина и доцент Б.А. Дайняк.

Участникам олимпиад предлагаются варианты, содержащие до 10 задач. Решение задач обязательно содержит элемент творчества, хотя и подразумевается использование известных методических приемов. Несомненным творческим элементом является осмысливание описанных в задаче процессов, подбор соответствующих физических законов, необходимых для решения конкретной задачи. Особенно это касается задач, где необходимо применять знание законов физики из различных разделов. Иногда задача может иметь несколько вариантов решения.

Необходимые методические материалы, которые могут помочь будущим абитуриентам и участникам олимпиад широко представлены на сайте http://www.alleng.ru/edu/phys2.htm4. Рекомендуем также недавно вышедшее пособие, написанное в соавторстве с сотрудниками кафедр Университета: Н.А. Константинова, Б.А. Дайняк, В.М. Кортукова. Физика. Задачи и решения. Пособие для поступающих в ВУЗы.- Москва, Высшая школа, 2008 г., с. 446.

Участие в олимпиадах предполагает достаточно высокий уровень знаний предмета и определенные навыки решения задач. Тем не менее, мы хотим напомнить некоторые общие положения.

При подготовке всегда следует стремиться решить как можно больше задач. При решении задач следует придерживаться следующих общих рекомендаций:

1. Все задачи, независимо от способа заданий исходных данных, следует решать в общем виде в буквенных обозначениях. При такой форме решения остается ясной последовательность применения физических законов, используемых в процессе решения, а сами выкладки позволяют при необходимости проверить любую часть решения и исключить возможные ошибки. Получив ответ, его можно проанализировать, установить характер и пределы изменения искомой величины в функции величин, через которые она выражена. Кроме того, и это, пожалуй, главное, указанный способ решения позволяет отработать методику и приемы решения задач по каждому разделу курса.
2. Ознакомившись с условием задачи, никогда не следует заострять внимание на искомой величине и тем более пытаться сразу найти ее. Необходимо помнить, что ближайшая цель решения состоит в том, чтобы свести задачу от физической к математической, записав ее в виде формул.
3. Чтобы хорошо понять условие задачи, необходимо сделать схематический чертеж, поясняющий ее сущность, и на чертеже, хотя бы условно, указать все величины, характеризующие данное явление. Если при этом окажется, что для полного описания процесса надо использовать величины, не фигурирующие в условии, их нужно ввести самим, т.к. в большинстве случаев без них невозможно найти связь между искомыми и заданными величинами. Следует помнить, что почти во всех случаях чертеж сильно упрощает и поиск, и само решение задачи.
4. Сделав чертеж, следует еще раз прочитать условие задачи и отметить, какие из величин заданы, и какие требуется найти. Все известные величины – их числовые значения и наименования – записываются обычно в колонку.
5. Далее с помощью физических законов и формул необходимо установить математическую связь между всеми величинами, введенными в решение при символическом описании рассматриваемого явления. В результате получится одно или несколько математических уравнений, включающих в себя как заданные, так и неизвестные величины. Таким образом, физическая задача сведется к математической.
6. Решение системы уравнений желательно начинать с исключения тех неизвестных величин, которые не требуется находить по условию задачи, и следить за тем, чтобы при каждом алгебраическом действии число неизвестных уменьшалось.
7. Получив ответ в общем виде и проанализировав его, можно приступать к числовым расчетам. Прежде всего, при этом необходимо выбрать единицы, в которых решено проводить вычисления. Предпочтение отдается Международной системе единиц (СИ). Если величины, входящие в расчетную формулу, даны в разных единицах, их следует выразить в единицах системы, принятой для решения. В тех случаях, когда в числитель и знаменатель расчетной формулы входят однородные величины одной степени, их можно подставлять в любых одинаковых единицах; единицы этих величин сокращаются и на размерность искомой величины не влияют.
8. Подставив в расчетную формулу единицы величин вместо их обозначений, проводят с ними действия с тем, чтобы убедится, что результат получается в единицах искомой величины, принятой в системе. Несоблюдение этого условия проверки решения (оно необходимо, но недостаточно) свидетельствует об ошибке, допущенной в ходе решения. Установив наименование искомой величины, можно приступать к действиям с числами. Если есть полная уверенность в правильности решения, единицы величин в расчетную формулу не подставляют. Проводя арифметические расчеты, следует помнить, что числовые значения являются приближенными. Поэтому нужно пользоваться правилами приближенных вычислений. Получив числовой ответ, желательно, если возможно, оценить, насколько он верен. Иногда такая оценка позволяет установить ошибочность полученного результата.
9. Некоторые задачи могут иметь несколько вариантов решения. Все эти варианты должны быть рассмотрены, иначе решение будет оценено, как неполное.

Ниже приведены задачи с решениями, которые в разные годы предлагались на олимпиадах по физике «Трудитесь и побеждайте» и «Шаг в будущее». Задачи сгруппированы по темам «Механика», «Молекулярная физика» и т.д.

obrazbase.ru

Олимпиада по физике

 

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СВЕРДЛОВСКОЙ ОБЛАСТИ

«ПЕРВОУРАЛЬСКИЙ ПОЛИТЕХНИКУМ»

Методическая разработка

«Олимпиада по физике»

Подготовила:

преподаватель

Кузнецова Алина Валентиновна,

1 к.к.

2016

СОДЕРЖАНИЕ.

стр.

Пояснительная записка…………………………………………………………………3

Текст заданий для I курса………………………………………………………………5

Текст заданий для II курса………………………………………………………………6

Протокол оценки качества выполнения заданий……………………………………..7

Ответы на задания………………………………………………………………………8

Пояснительная записка.

Общие положения

Настоящие материалы представляют собой задания для проведения очной олимпиады по физике для учащихся I и II курса, критерии и принципы оценки качества выполнения заданий.

Целью олимпиады по физике является вовлечение учащихся в полезную досуговую деятельность.

Задачи олимпиады:

создать условия для развития учебной мотивации учащихся;

создать условия для расширения знаний по физике;

выявить обучающихся с ярко выраженными способностями к освоению физики;

поощрить саморазвитие обучающихся.

Источником разработки заданий являются:

• Рымкевич А.П. Физика. Задачник. 10-11 кл. Пособие для общеобразоват. учреждений.- М.: Дрофа, 2013

  Касьянов В.А. Физика 10 кл. Учебник для общеобразовательных учреждений- М: Дрофа, 2003

  Касьянов В.А. Физика 11 кл. Учебник для общеобразовательных учреждений- М: Дрофа, 2004

  Яворский Б.М., Селезнёв Ю.А., Справочное руководство по физике для поступающих в вузы и для самообразования- М.: Наука, 1989

  В. П. Демкович, Л. П. Демкович Сборник задач по физике. Для 8 – 10 классов средней школы. Пособие для учащихся. –М.: Просвещение, 1981

Задания подобраны в соответствии с содержанием образовательной деятельности, определенным рабочей программой по учебной дисциплине, с учетом освоенных на учебных занятиях к моменту проведения олимпиады блоков содержания.

Блоки содержания рабочей программы, вынесенные на олимпиаду:

Задания к очной олимпиаде актуализируют знания учащимися следующих тем рабочей программы:

Механическое движение и его виды.

Относительность механического движения.

Прямолинейное равноускоренное движение.

Задания к очной олимпиаде формируют следующие базовые компетенции:

Базовые компетенции	Универсальные учебные действия
Социальные	Перевод информации из одной формы в другую
Аналитические	Выделение и исследование причинно-следственных связей
Творческие	Представление оригинального решения
Самосовершенствования	Оценка полученного результата, представление вывода

Критерии и принципы оценки качества выполнения заданий.

Критериями оценки качества выполнения олимпиадных заданий являются:

форма представления задач;

анализ условия, установление причинно-следственных отношений, математические расчёты;

оценка полученного результата.

оригинальность решения.

Оценка качества выполнения заданий определяется в соответствии с протоколом.

Принцип выявления победителей:

1 место присваивается учащимся, набравшим не менее 8 баллов;

2 место присваивается учащимся, набравшим не менее 7 баллов;

3 место присваивается учащимся, набравшим не менее 6 баллов.

Олимпиада по физике

(очный тур)

I курс

Уважаемые студенты ППТ!

Перед Вами задания очного тура олимпиады по физике. Прочитайте внимательно задания. Постарайтесь ответить на поставленные перед Вами вопросы максимально правильно и полно. Оформление ответов свободное, в произвольном порядке, в письменном виде. В конце каждого задания в скобках указано максимальное количество баллов, которые можно заработать, выполнив это задание. Максимальное количество баллов за выполнение всей работы – 10. Оценивается правильность, полнота ответа, а также оригинальность Вашего мышления.

Успеха!

1 Вариант

1) Из окна движущегося вагона выпал предмет. Какова траектория предмета для пассажира, стоящего у окна вагона, и для человека, стоящего у полотна дороги? (2 балла)

2) По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский длиной 120 м со скоростью 102 км/ч. Какова относительная скорость движения поездов, если они движутся в одном направлении? В течение какого времени один поезд проходит мимо другого? (5 баллов)

3) Каков период вращения секундной, минутной и часовой стрелки часов? Какова частота вращения? (3 балла)

2 Вариант

1) На рисунке помещён кадр из диафильма по сказке Г.Х. Андерсена «Дюймовочка». Объясните физическую несостоятельность текста под кадром. (2 балла)

2) По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский длиной 120 м со скоростью 102 км/ч. Какова относительная скорость движения поездов, если они движутся в противоположных направлениях? В течение какого времени один поезд проходит мимо другого? (5 баллов)

3) Каков период вращения Земли вокруг Солнца? Какова частота вращения? (3 балла)

Олимпиада по физике

(очный тур)

II курс

Уважаемые студенты ППТ!

Перед Вами задания очного тура олимпиады по физике. Прочитайте внимательно задания. Постарайтесь ответить на поставленные перед Вами вопросы максимально правильно и полно. Оформление ответов свободное, в произвольном порядке, в письменном виде. В конце каждого задания в скобках указано максимальное количество баллов, которые можно заработать, выполнив это задание. Максимальное количество баллов за выполнение всей работы – 10. Оценивается правильность, полнота ответа, а также оригинальность Вашего мышления.

Успеха!

1 Вариант.

Для чего к корпусу бензовоза прикреплена цепь, конец которой тянется по земле? (2 балла)

Кусок неизолированной проволоки сложили вдвое. Как изменилось сопротивление проволоки? Ответ поясните. (3 балла)

Направление тока в обмотке дугообразного электромагнита показано стрелками на рисунке. Определить полюсы сердечника. Ответ поясните. (5баллов)

2 Вариант.

На текстильных фабриках нередко нити прилипают к гребням чесальных машин, путаются и рвутся. Для борьбы с этим явлением в цехах искусственно создаётся повышенная влажность. Объясните физическую сущность этой меры. (3 балла)

Почему спирали электронагревательных приборов делают из материала с большим удельным сопротивлением? (2 балла)

Пометить знаками «+» и «-» полюсы источника тока, питающего соленоид, чтобы наблюдалось указанное на рисунке взаимодействие. Ответ поясните. (5баллов)

Протокол оценки качества выполнения олимпиадных заданий.

I курс

№ п/п	Список участников (группа)	Задание 1	Задание 2	Задание 3	Сумма баллов	Место
1.
2.
3.

Ответы на задания.

I курс.

1вариант.

П

V

1. редмет, который выпал из окна движущегося поезда, продолжает двигаться со скоростью поезда. Следовательно, для пассажира поезда, стоящего у окна вагона, траектория предмета будет отвесная линия, а для человека, стоящего у полотна дороги, траектория будет парабола.

    

Относительная скорость поездов, которые движутся в одном направлении, равна разности их скоростей, т.е. 102 – 48 = 54 км/ч или 15 м/с. Чтобы найти время, в течение которого один поезд проходит мимо другого, нужно сложить длины поездов и разделить на их относительную скорость: (630 + 120)/ 15 = 50 с.

Период вращения (время одного оборота) секундной стрелки 1мин. или 60 с, минутной – 1 час или 60 мин., или 3600с, часовой 12 ч. или 43200 с. Чтобы найти частоту вращения, нужно разделить 1 на период. Следовательно, частота вращения секундной стрелки 1/60 = 0, 017 Гц, минутной – 1/3600 = 0,00028 Гц, часовой – 1/43200 =0,000023 Гц.

2 вариант.

Лист кувшинки плыл по течению, следовательно, его скорость равна скорости течения. Скорость жабы равна её скорости в стоячей воде и скорости течения. Поэтому, она догонит кувшинку через такое же время, как и в стоячей воде.

Относительная скорость поездов, которые движутся в одном направлении, равна сумме их скоростей, т.е. 102 + 48 = 150 км/ч или 41,7 м/с. Чтобы найти время, в течение которого один поезд проходит мимо другого, нужно сложить длины поездов и разделить на их относительную скорость: (630 + 120)/ 41,7 =18,7с.

Период вращения (время одного оборота) Земли вокруг Солнца 1 год = 365 сут. = 8760 ч. = 31536000с. Чтобы найти частоту вращения, нужно разделить 1 на период. Следовательно, частота вращения земли вокруг Солнца 1/31536000 = 0,00000003 Гц.

II курс.

1вариант.

Цепь к корпусу бензовоза крепится для заземления.

Если кусок неизолированной проволоки сложить вдвое, то её длина уменьшится вдвое, а площадь поперечного сечения увеличится вдвое. Следовательно, сопротивление проволоки увеличится в четыре раза.

По правилу буравчика линии магнитной индукции выходят из полюса слева на рисунке, а входят в полюс справа. Следовательно левый полюс северный, а правый южный.

2 вариант.

При высокой влажности на нитях не накапливается статический заряд, следовательно, они меньше прилипают к гребням, меньше путаются и рвутся.

При большом удельном сопротивлении увеличивается количество теплоты, отдаваемое спиралью, при прохождении по ней тока.

Южный полюс стрелки будет притягиваться к северному полюсу электромагнита. Магнитные линии выходят из северного полюса, следовательно, по правилу буравчика ток в катушке течёт против часовой стрелки. Следовательно, левый контакт «-», а правый «+».

xn--j1ahfl.xn--p1ai

Школьный этап областной олимпиады по физике

Разделы: Физика, Внеклассная работа

---

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к олимпиадным заданиям по физике

Вариант олимпиадной работы для учащихся 7-8 классов.

Структура работы.

Вариант работы состоит из двух частей и включает 13 заданий.

Часть 1 содержит 10 заданий с выбором ответа. К каждому заданию приводится четыре варианта ответа, из которых только один правильный.

Часть 2 содержит три задачи открытого типа, для которых необходимо привести развернутый ответ.

Оценивание отдельных заданий и работы в целом (7-8 класс).

Задание с выбором ответа считается выполненным, если выбранный участником Олимпиады номер ответа совпадает с верным ответом. Каждое задание части 1 оценивается в 3 балла.

Задания 11-13 оцениваются в 10 баллов каждое, если в задаче приведено развернутое верное решение и получено числовое значение (там, где необходимы расчеты).

Таким образом, максимальный балл за работу составляет 60 баллов.

Условия проведения олимпиады.

На выполнение работы учащимся 7-8 классов отводится 1 астрономический час, учащимся 9-11 классов — 2 астрономических часа.

Для выполнения заданий Олимпиады каждому участнику выдаются чистые двойные листы в клетку (для чистовика и для черновика), а также распечатанный текст заданий.

Участники олимпиады в 7-8 классах вписывают номера правильных ответов к заданиям 1-10 в таблицу, приведенную в тексте работы. К заданиям 11-13 необходимо привести развернутое решение на листочке.

При выполнении заданий допускается использование непрограммируемого калькулятора.

По окончании работы учащиеся сдают на проверку распечатанные тексты заданий с заполненной таблицей и листы (чистовики и черновики) с решениями заданий открытого типа.

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai