Основные формулы тригонометрии таблица – .

Тригонометрические формулы

© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016

(1)	Основное тригонометрическое тождество	sin2(α) + cos2(α) = 1
(2)	Основное тождество через тангенс и косинус	1 + tg2(α) = 1/cos2(α)
(3)	Основное тождество через котангенс и синус	1 + ctg2(α) = 1/sin2(α)
(4)	Соотношение между тангенсом и котангенсом	tg(α)ctg(α) = 1
(5)	Синус двойного угла	sin(2α) = 2sin(α)cos(α)
(6)	Косинус двойного угла	cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α)
(7)	Тангенс двойного угла	tg(2α) =   2tg(α) 1 – tg2(α)
(8)	Котангенс двойного угла	ctg(2α) = ctg2(α) – 1   2ctg(α)
(9)	Синус тройного угла	sin(3α) = 3sin(α)cos2(α) – sin3(α)
(10)	Косинус тройного угла	cos(3α) = cos3(α) – 3cos(α)sin2(α)
(11)	Косинус суммы/разности	cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β)
(12)	Синус суммы/разности	sin(α±β) = sin(α)cos(β) ± cos(α)sin(β)
(13)	Тангенс суммы/разности	tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β))
(14)	Котангенс суммы/разности	ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β))
(15)	Произведение синусов	sin(α)sin(β) = ½(cos(α–β) – cos(α+β))
(16)	Произведение косинусов	cos(α)cos(β) = ½(cos(α+β) + cos(α–β))
(17)	Произведение синуса на косинус	sin(α)cos(β) = ½(sin(α+β) + sin(α–β))
(18)	Сумма/разность синусов	sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β))
(19)	Сумма косинусов	cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β))
(20)	Разность косинусов	cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β))
(21)	Сумма/разность тангенсов	tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β)
(22)	Формула понижения степени синуса	sin2(α) = ½(1 – cos(2α))
(23)	Формула понижения степени косинуса	cos2(α) = ½(1 + cos(2α))
(24)	Сумма/разность синуса и косинуса	sin(α) ± cos(α) = &sqrt;2sin(α±π/4)
(25)	Сумма/разность синуса и косинуса с коэффициентами	Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²)))
(26)	Основное соотношение арксинуса и арккосинуса	arcsin(x) + arccos(x) = π/2
(27)	Основное соотношение арктангенса и арккотангенса	arctg(x) + arcctg(x) = π/2

scolaire.ru

Тригонометрические формулы — шпаргалка

Здесь можно найти тригонометрические формулы в удобном виде. А тригонометрические формулы приведения можно посмотреть на другой странице.

Основные тригонометрические тождества

— математические выражения для тригонометрических функций, выполняемые при каждом значении аргумента.

 

• sin² α + cos² α = 1
• tg α · ctg α = 1
• tg α = sin α ÷ cos α
• ctg α = cos α ÷ sin α
• 1 + tg² α = 1 ÷ cos² α
• 1 + ctg² α = 1 ÷ sin² α

 

Формулы сложения

 

• sin (α + β) = sin α · cos β + sin β · cos α
• sin (α — β) = sin α · cos β — sin β · cos α
• cos (α + β) = cos α · cos β — sin α · sin β
• cos (α — β) = cos α · cos β + sin α · sin β
• tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
• tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
• ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
• ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)

https://uchim.org/matematika/trigonometricheskie-formuly — uchim.org

 

Формулы двойного угла

 

• cos 2α = cos² α — sin² α
• cos 2α = 2cos² α — 1
• cos 2α = 1 — 2sin² α
• sin 2α = 2sin α · cos α
• tg 2α = (2tg α) ÷ (1 — tg² α)
• ctg 2α = (ctg² α — 1) ÷ (2ctg α)

 

Формулы тройного угла

 

• sin 3α = 3sin α — 4sin³ α
• cos 3α = 4cos³ α — 3cos α
• tg 3α = (3tg α — tg³ α) ÷ (1 — 3tg² α)
• ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)

 

Формулы понижения степени

 

• sin² α = (1 — cos 2α) ÷ 2
• sin³ α = (3sin α — sin 3α) ÷ 4
• cos² α = (1 + cos 2α) ÷ 2
• cos³ α = (3cos α + cos 3α) ÷ 4
• sin² α · cos² α = (1 — cos 4α) ÷ 8
• sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32

 

Переход от произведения к сумме

 

• sin α · cos β = ½ (sin (α + β) + sin (α — β))
• sin α · sin β = ½ (cos (α — β) — cos (α + β))
• cos α · cos β = ½ (cos (α — β) + cos (α + β))

Мы перечислили довольно много тригонометрических формул, но если чего-то не хватает, пишите.

Всё для учебы » Математика в школе » Тригонометрические формулы — шпаргалка

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Ссылка: https://uchim.org/matematika/trigonometricheskie-formuly

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Тригонометрические формулы / Блог :: Бингоскул

• Блог
• →
• Тригонометрические формулы

Формулы тригонометрии, необходимые для ЕГЭ 2019

Представлены таблицы основных тригонометрических формул, которых достаточно для решения задач тригонометрии.

 

Формулы приведения в  тригонометрии

 

Значения тригонометрических функций
α	радианы	0	\frac{\pi}{6}	\frac{\pi}{4}	\frac{\pi}{3}	\frac{\pi}{2}	\pi	\frac{3\pi}{2}	2\pi
	градусы	0°	30°	45°	60°	90°	180°	270°	360°
sin α		0	\frac{1}{2}	\frac{\sqrt{2}}{2}	\frac{\sqrt{3}}{2}	1	0	-1	0
cos α		1	\frac{\sqrt{3}}{2}	\frac{\sqrt{2}}{2}	\frac{1}{2}	0	-1	0	1
tg α		0	\frac{\sqrt{3}}{3}	1	\sqrt{3}	—	0	—	0
сtg α		—	\sqrt{3}	1	\frac{\sqrt{3}}{3}	0	—	0	—

 

Основное тригонометрическое тождество:

• \sin^2 x+ \cos^2 x = 1
• \tg x= \frac{\sin x}{\cos x}
• \ctg x= \frac{\cos x}{\sin x}
• \tg x \ctg x = 1
• \tg^{2} x + 1 = \frac{1}{\cos^{2} x}
• \ctg^{2} x + 1 = \frac{1}{\sin^{2} x}

 

 

Формулы тригонометрических функций суммы и разности углов

• \sin(\alpha \pm\beta) = \sin\alpha\cos\beta \pm\cos\alpha\sin\beta
• \cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp\sin\alpha\sin\beta
• tg(\alpha \pm \beta) = \frac{tg\alpha \pm tg\beta}{1 \mp tg\alpha * tg\beta}

 

Тригонометрические функции двойного и тройного угла

• \sin(2\alpha) = 2\sin\alpha\cos\alpha
• \cos(2\alpha) = \cos^2\alpha — \sin^2\alpha, \cos(2\alpha) =1 — 2\sin^2\alpha, \cos(2\alpha) =2\cos^2\alpha -1
• \tg 2\alpha = \frac{2\cdot \tg \alpha}{1 — \tg^{2} \alpha}
• \ctg 2\alpha = \frac{\ctg^{2} \alpha — 1}{2 \cdot \ctg \alpha}
• \sin3\alpha = 3\sin\alpha \cos^{2}\alpha -\sin^{3}\alpha
• \sin3\alpha = 3\sin\alpha — 4\sin^{3}\alpha
• \cos3\alpha = \cos^{3}\alpha — 3\sin^{2}\alpha\cos\alpha
• \cos3\alpha = -3\cos\alpha + 4\cos^{3}\alpha
• \tg 3\alpha = \frac{3\cdot \tg \alpha — \tg^3 \alpha}{1 — 3\tg^{2} \alpha}
• \ctg 3\alpha = \frac{\ctg^{3} \alpha -3 \ctg \alpha}{3 \cdot^2 \ctg \alpha — 1}

 

Преобразование суммы в произведение:

• 2 \cos\alpha\cos\beta = \cos(\alpha + \beta) + \cos(\alpha — \beta)
• 2 \sin\alpha\sin\beta = \cos(\alpha — \beta) — \cos(\alpha + \beta)
• 2 \sin\alpha\cos\beta = \sin(\alpha + \beta) + \sin(\alpha — \beta)

 

Формулы понижения степени

• \sin^{2}\alpha=\frac{1-\cos2\alpha}{2}
• \cos^{2}\alpha=\frac{1+\cos2\alpha}{2}
• \sin^{3}\alpha=\frac{3\sin\alpha-\sin3\alpha}{4}
• \cos^{3}\alpha=\frac{3\cos\alpha-\cos3\alpha}{4}

 

---

 

 

Смотри также: Основные формулы по математике

 

Решай с разбором:

bingoschool.ru

Основные тригонометрические формулы

В самом начале этой статьи мы с Вами рассмотрели понятие тригонометрических функций. Основное назначение их назначение – это изучение основ тригонометрии и исследование периодических процессов. И тригонометрический круг мы не зря рисовали, потому что в большинстве случаев тригонометрические функции определяются, как отношение сторон треугольника или его определенных отрезков в единичной окружности. Так же я упоминал о неоспоримо огромном значении тригонометрии в современной жизни. Но наука не стоит на месте, в результате мы можем значительно расширить область применения тригонометрии и перенести ее положения на вещественные, а иногда и на комплексные числа.

Формулы тригонометрии бывают нескольких видов. Рассмотрим их по порядку.

1. Соотношения тригонометрических функций одного и того же угла

Здесь мы подошли к рассмотрению такого понятия как основные тригонометрические тождества.

Тригонометрическое тождество — это равенство, которое состоит из тригонометрических соотношений и которое выполняется для всех значений величин углов, которые входят в него.

Рассмотрим наиболее важные тригонометрические тождества и их доказательства:

Первое тождество вытекает из самого определения тангенс.

Возьмем прямоугольный треугольник, в котором имеется острый угол х при вершине А.



Для доказательства тождеств необходимо воспользоваться теоремой Пифагора:

(ВС) ² + (АС) ² = (АВ) ²

Теперь разделим на (АВ) ² обе части равенства и припомнив определения sin и cos угла, мы получаем второе тождество:

(ВС) ²/(AB) ² + (AC) ²/(AB) ² = 1

sin x = (BC)/(AB)

cos x = (AC)/(AB)

sin² x + cos² x = 1

Для доказательства третьего и четвертого тождеств воспользуемся предыдущим доказательством.

Для этого обе части второго тождества разделим на cos² x:

sin²

x/ cos² x + cos² x/ cos² x = 1/ cos² x

sin² x/ cos² x + 1 = 1/ cos² x

Исходя из первого тождества tg x = sin х /cos x получаем третье:

1 + tg² x = 1/cos² x

Теперь разделим второе тождество на sin² x:

sin² x/ sin² x + cos² x/ sin² x = 1/ sin² x

1+ cos² x/ sin² x = 1/ sin² x

cos² x/ sin² x есть не что иное, как 1/tg² x, поэтому получаем четвертое тождество:

1 + 1/tg² x = 1/sin² x

Пришла пора вспомнить теорему о сумме внутренних углов треугольника, которая гласит, что сумма углов треугольника = 180⁰. Получается, что при вершине В треугольника находится угол, величина которого 180⁰ – 90⁰ – х = 90⁰ – х.



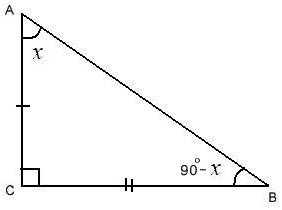
Опять вспомним определения для sin и cos и получаем пятое и шестое тождества:

sin x = (BC)/(AB)

cos(90⁰– x ) = (BC)/(AB)

cos(90⁰– x ) = sin x

Теперь выполним следующее:

cos x = (AC)/(AB)

sin(90⁰– x ) = (AC)/(AB)

sin(90⁰– x ) = cos x

Как видите – здесь все элементарно.

Существуют и другие тождества, которые используются при решении математических тождеств, я приведу их просто в виде справочной информации, потому как все они проистекают из вышерассмотренных.



2. Выражения тригонометрических функций друг через друга

   (выбор знака перед корнем определяется тем, в какой из четвертей круга расположен угол ?)

3. Далее следуют формулы сложения и вычитания углов:



4. Формулы двойных, тройных и половинных углов.

   Замечу, что все они проистекают из предыдущих формул.

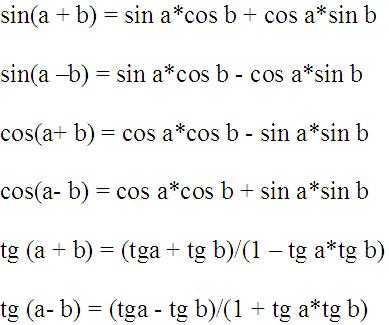
sin 2х =2sin х*cos х

cos 2х =cos²х -sin²х =1-2sin²х =2cos²х -1

tg 2x = 2tgx/(1 — tg² x)

сtg 2x = (сtg² x — 1) /2сtg x

sin3х =3sin х — 4sin³х

cos3х =4cos³х — 3cos х

tg 3x = (3tgx – tg³ x) /(1 — 3tg² x)

сtg 3x = (сtg³x – 3сtg x) /(3сtg² x — 1)

5. Формулы преобразования тригонометрических выражений:

Когда-то, будучи школьником, я с удовольствием применял эти формулы для решения различного рода задач, как то упростить выражение или решить уравнение. Главное разглядеть — куда и какую формулу необходимо применить, и тогда многоярусная конструкция превращается в обычное числовое выражение. Очень полезная штука для развития логического мышления!




---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

reshit.ru

Основные формулы тригонометрии

Тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Их всего четыре:

• Синус \( \displaystyle sin\left( x \right) \)
• Косинус \( \displaystyle cos\left( x \right) \)
• Тангенс \( \displaystyle tg\left( x \right) \)
• Котангенс \( \displaystyle ctg\left( x \right) \)

Существует два способа решения тригонометрических уравнений:

Первый способ — с использованием формул.

\( \displaystyle A \)	\( \displaystyle a \)	\( \displaystyle -1 \)	\( \displaystyle 0 \)	\( \displaystyle 1 \)
\( \displaystyle \sin x=A \)	\( \displaystyle {{\left( -1 \right)}^{n}}\arcsin \alpha +\pi n \)	\( \displaystyle -\dfrac{\pi }{2}+2\pi n \)	\( \displaystyle \pi n \)	\( \displaystyle \dfrac{\pi }{2}+2\pi n \)
\( \displaystyle \cos x=A \)	\( \displaystyle \pm \arccos \alpha +2\pi n \)	\( \displaystyle \pi +2\pi n \)	\( \displaystyle \dfrac{\pi }{2}+\pi n \)	\( \displaystyle 2\pi n \)
\( \displaystyle tgx=A \)	\( \displaystyle arctg\alpha +\pi n \)	\( \displaystyle -\dfrac{\pi }{4}+\pi n \)	\( \displaystyle \pi n \)	\( \displaystyle \dfrac{\pi }{4}+\pi n \)
\( \displaystyle ctgx=A \)	\( \displaystyle arcctg\alpha +\pi n \)	\( \displaystyle \dfrac{3\pi }{4}+\pi n \)	\( \displaystyle \dfrac{\pi }{2}+\pi n \)	\( \displaystyle \dfrac{\pi }{4}+\pi n \)

Второй способ — через тригонометрическую окружность.

Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.



Основные формулы Тригонометрии:

Основное тригонометрическое тождество (нужно его помнить, даже если тебя разбудили среди ночи и спросили!)

\[ \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1 \]

---

Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)

\[ \displaystyle tg\ \alpha =\dfrac{sin\ \alpha }{cos\ \alpha } \]

---

Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)

\[ \displaystyle ctg\ \alpha =\dfrac{cos\ \alpha }{sin\ \alpha }=\dfrac{1}{tg\ \alpha } \]

---

Синус суммы и разности:

\[ \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \]

---

Косинус суммы и разности:

\[ \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \]

---

Тангенс суммы и разности:

\[ \displaystyle tg\left( \alpha \pm \beta \right)=\dfrac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta } \]

Формулы понижения степени:

Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.

\[ \displaystyle si{{n}^{2}}\alpha =\dfrac{1-cos2\alpha }{2} \]

\[ \displaystyle co{{s}^{2}}\alpha =\dfrac{1+cos2\alpha }{2} \]

\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]

\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]

\[ \displaystyle t{{g}^{2}}\alpha =\dfrac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \dfrac{\pi }{2}+\pi n,n\in Z \]

\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]

\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]

Из данных формул можно в частности вывести формулы тройного угла:

\[ \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \]

\[ \displaystyle cos3a=4co{{s}^{3}}a-3cosa \]

\[ \displaystyle tg3\alpha =\dfrac{3tg\alpha -t{{g}^{3}}\alpha }{1-3t{{g}^{2}}\alpha } \]

\[ \displaystyle ctg3\alpha =\dfrac{3ctg\alpha -ct{{g}^{3}}\alpha }{1-3ct{{g}^{2}}\alpha } \]

Формулы преобразования суммы функций

Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.

\[ \displaystyle sin\alpha \pm sin\beta =2sin\dfrac{\alpha \pm \beta }{2}cos\dfrac{\alpha \mp \beta }{2} \]

\[ \displaystyle cos\alpha +cos\beta =2cos\dfrac{\alpha +\beta }{2}cos\dfrac{\alpha -\beta }{2} \]

\[ \displaystyle cos\alpha -cos\beta =-2sin\dfrac{\alpha +\beta }{2}sin\dfrac{\alpha -\beta }{2} \]

\[ \displaystyle tg\alpha \pm tg\beta =\dfrac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta } \]

\[ \displaystyle ctg\alpha \pm ctg\beta =\dfrac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta } \]

Формулы преобразования произведений функций

\[ \displaystyle sin\alpha sin\beta =\dfrac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2} \]

\[ \displaystyle sin\alpha cos\beta =\dfrac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2} \]

\[ \displaystyle cos\alpha cos\beta =\dfrac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2} \]

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Источник

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Основные тригонометрические формулы

В этой статье представлен оптимальный набор тригонометрических формул, которые необходимо знать. Все остальные тригонометрические формулы выводятся из них путем несложных преобразований.

 

1. Основное тригонометрическое тождество:

 

2. Формулы, позволяющие выразить тригонометрические функции одного аргумента одну через другую.

3. Тригонометрические формулы суммы  и разности аргументов.

 

4. Тригонометрические функции двойного аргумента:

 

5. Формулы понижения степени:

 

6. Тригонометрические функции половинного аргумента:

 

7.  Формулы универсальной подстановки:

 

8. Преобразование суммы или разности тригонометрических функций в произведение

 

9. Преобразование произведения тригонометрических функций в сумму или разность.

 

10. Преобразование выражения   к виду

,

где ,

 

Скачать таблицу формулы тригонометрии

формулы тригонометрии (2)

 

И.В. Фельдман, репетитор по математике.


ege-ok.ru