Счетчик слов / калькулятор подсчета слов
Это бесплатный онлайн-калькулятор, который подсчитает вам количество слов в вашем тексте. Писатели, создающие новые шедевры; ученики, работающие над рефератами; труженики клавиатуры и просто любопытствующие! Вы можете смело воспользоваться этой программой для подсчета слов в вашем тексте. Наш онлайн-калькулятор пригодится для создания базы данных, грамматического исследования, переводов, составления словарей, копирайтинга и так далее.
Для начала подсчета просто введите или вставьте текст в соответствующее поле. По завершении: на кнопку «Подсчитать слова», и результат немедленно появится. Вы сможете очистить поле для ввода текста, нажав на кнопку «Сброс».
Максимальный объем диссертации обычно составляет от 3000 до 8000 слов. Объем резюме не должен превышать 600 слов. Чтобы избежать превышения, старайтесь писать одно слово вместо целой фразы, не поддавайтесь многословию, тщательно выбирайте между причастными и деепричастными оборотами. Самый важный совет здесь: не сдавайте работу в день завершения, а проверьте её на следующий день.
Обратите внимание на количество слов
Сколько слов в этом романе?
Читателям нравятся интересные статьи. Именно поэтому авторы стараются подбирать слова с такой целью, чтобы из них формировался текст, интересный для целевой аудитории. Чтобы текст получился убедительным и привлекательным, следует подбирать слова на основе четких фактов и цифр. Вот почему так важно качество и количество слов. В целом, чем меньше слов, тем лучше статья. Романы и повести состоят из слов, а бестселлерами становятся те книги, которые состоят из правильных слов. Авторы смогли бы рассказать сотни историй о психологическом блоке, мешающем облечь образы в правильные слова. Создание бестселлера требует спокойного и упорядоченного подхода, а также сильной целеустремленности. Романы обычно состоят из 60-80 тысяч слов, но известные писатели могут позволить себе превысить этот лимит. Короткие романы, известные как новеллы, состоят из 20-40 тысяч слов. Короткие истории – из 2500 слов, но могут расшириться и до 20 тысяч слов. Дипломные работы и диссертации очень важны, но написать их бывает достаточно трудно из-за отсутствия четкого плана. Слова в диссертации должны быть уникальными и понятными целевой аудитории. Писатели формируют лаконичный, прямой и простой стиль, чтобы обращаться непосредственно к каждому читателю, зажигать и вдохновлять его.
Подсчет слов
Продавцам платят за объем продаж. Рыбакам – за вес рыбы. Писателям – за количество слов. Неудивительно, что авторы тщательно следят за этим фактором. Редакторы журналов также устанавливают ограничения на объем публикуемых статей.
www.skolkoslov.com
Счетчик подсчета количества символов, знаков,букв, слов в тексте онлайн
Приветствую Вас уважаемые друзья на страницах сайта advertseo-helper.ru!
Находясь на этой странице, Вам 100% понадобилось узнать количество символов/знаков/букв в вашем тексте и не только, посредством какого-нибудь онлайн сервиса.
Я очень рад что Вы нашли именно эту страничку, потому что я уверен — тут Вы найдете весь нужный функционал для обработки текста в онлайн режиме, а именно:
— Подсчет абзацев в тексте.
— Подсчет количества символов / знаков / букв в тексте с пробелом и без.
— Также, эта онлайн программа для определения количества символов / знаков / букв, подскажет и покажет, где в своем тексте Вы допустили орфографические ошибки.
Обратите внимание на то что Вам не нужно каждый раз при вставке своего текста в поле, нажимать на какие-нибудь дополнительные кнопки, для того что бы программа смогла показать Вам результаты. А это, я считаю одним из главных преимуществ этого сервиса перед остальными ресурсами, так же как и то, что при редактировании текста, Вы сразу же можете увидеть результаты, и опять же, без нажатия какой либо кнопки.
Если Вы хотите узнать количество символов / знаков / букв в статье или проверить количество символов в одной строке, Вам нужно: Скопировать свой текст и вставить его в поле выше и в правой колонке, Вам мгновенно показываются результаты. ВСЕ! Как Вы заметили, все очень просто и интуитивно понятно.
Я уверен что, уходя, Вы точно решили свою проблему, некоторые из Вас сохраняют даже страничку в закладки и возвращаются снова и снова.
Конечно же существуют и другие способы подсчета букв в тексте — онлайн и оффлайн — это всякого рода программы, Microsoft Word и т.д, но они не такие удобные, для получения результатов нужно нажимать кнопки, если нужно редактировать текст — результаты не показываются в момент редактирования и т.д.
Думаю, Вы уже сами попробовали свои тексты на определение количества знаков и сами убедились в этом.
В конце, хочу выразить ОГРОМНУЮ БЛАГОДАРНОСТЬ тем, кто делится этой страничкой путем НАЖАТИЯ НА СОЦИАЛЬНЫЕ КНОПКИ!
Спасибо Всем друзья, Желаю Вам Здоровья!
PS: не забудьте сохранить страничку, что бы не потерять ее!
advertseo-helper.ru
Подсчет количества слов в тексте
Может получиться так, что в поисках необходимого ответа на разные вопросы люди одновременно оказываются на одном и том же интернет-ресурсе. И этому не нужно удивляться. Скажем, одного интересует, как посчитать количество слов в тексте? А другой хочет узнать, как изменить размер фотографии?И тот, и другой выйдут на указанный сервис вполне закономерно, поскольку именно на нем есть масса самых разных и часто востребованных бесплатных приложений. И многие предпочитают «делать остановку» именно на этом сайте, чтобы не запутаться в «мировой паутине».
Это означает, что среди пользователей сервиса найдутся самые разные люди. Скажем, те, кто с помощью специального приложения хотят определить расстояние между городами или узнать, как изменить размер изображения, фотографии. Или те, кто желают узнать, как скачать видео с youtube или как установить почтовый индекс по адресу?
Эти и многие другие полезные приложения можно найти именно здесь. Они очень просты в использовании. Ко всему нет необходимости в загрузке файлов, установке и последующем обновлении. За них не придется платить. Да и никакой регистрации на сайте не предусмотрено.
Как ресурс помогает работать с текстом
Про каждое приложение мы говорить сейчас не будет. Зато подробно остановимся на том приложении, которое помогает подсчитать количество слов в тексте онлайн. Понятно, что это приложение, возможно, не столь часто востребовано. Например, по сравнению с приложением, которое помогает обрезать фотографию.
Однако не нужно думать, что тех, кто работает с текстами и кто нуждается в точном подсчете слов в нем, совсем уж мало. Достаточно сказать, что в эту группу входят многие журналисты, писатели, копирайтеры, рерайтеры, блогеры, переводчики, оптимизаторы и заказчики статей, как и многие другие.
И у них, тем более работающих дистанционно, доходы зависят от того, сколько ими будет написано. А это означает, что для того же журналиста очень важно, чтобы получить честно заработанный гонорар, нужно получить и точную статистику по каждому написанному слову, по каждому символу. Причем, как с пробелами, так и без них.
А ведь при наличии сервиса это не так уж и сложно. Достаточно только ввести текст в соответствующее поле, и подсчет количества слов в тексте будет готов. Причем моментально.
Иногда тот же журналист пишет статью, имея конкретную задачу в том, что он не должен превысить установленный объем в знаках. В противном случае при верстке газеты статья не поместится на площадях газетной полосы, которые для нее отвели заранее. И тогда придется текст сокращать.
Может быть и по-другому. Если автор написал меньше, чем было запланировано, то на газетной полосе появятся белые пятна, а это допускать нельзя.
И если у тебя на вооружении есть нужный сервис, то этой проблемы можно будет избежать. Ведь сервис определяет количество слов в тексте без малейших погрешностей. И не нужно будет для этого самому пользователю тыкать пальцами в монитор. И тем более считать каждое слово вручную.
Мудрить не надо. Для тех, у кого работа так или иначе связана с подготовкой текста, данное приложение на сайте станет тем самым важным и необходимым инструментом.
Отзывы
Другие сервисы
ru.inettools.net
Определитель что это? Значение слова Определитель
Значение слова Определитель по Ефремовой:
2. Книга, служащая для справок при определении чего-л.
Значение слова Определитель по Ожегову:
Определитель — Книга для справок при определении чего-нибудь Spec
Определитель То, что определяет, выражает собой что-нибудь Lib
Определитель в Энциклопедическом словаре:
Определитель — (детерминант) — составленное по определенному правилу из n2чисел математическое выражение, применяемое при решении и исследованиисистем алгебраических уравнений 1-й степени. Число n называется порядкомопределителя. Так, определитель 2-го порядка, составленный из четырехчисел a1, b1, a2, b2, обозначается:и равен a1b2-b1a2.
Значение слова Определитель по словарю Ушакова:
ОПРЕДЕЛИТЕЛЬ
определителя, м. (книжн.). 1. То, что определяет, выражает собою что-н. 2. Книга, служащая для справок при определении чего-н. (науч.). Определитель растений. Определитель грибов. 3. Выражение, составляемое из коэффициентов системы уравнений 1-й степени с несколькими неизвестными для упрощения вычисления корней уравнений (мат.).
Значение слова Определитель по словарю Брокгауза и Ефрона:
Определитель (Determinant). — Решая два уравнения первой степени с двумя неизвестными: а 1 х + b1 у = c1, а 2 х + b2 у = c2, получаем следующие выражения для x и у: x = (c1b2— c2b1)/(a1b2 — a2b1), y = (a1c2 — a2c1)/(a1b2 — a2b1). Подобным же образом, решая три уравнения первой степени с тремя неизвестными, получим выражение последних в виде отношений многочленов, составленных из постоянных, входящих в уравнения. Например, многочлен, стоящий в знаменателях, будет: a1b2c3
Определение слова «Определитель» по БСЭ:
Определитель — детерминант, особого рода математическое выражение, встречающееся в различных областях математики. Пусть дана Матрица порядка n, т. е. квадратная таблица, составленная из nІ элементов (чисел, функций и т. п.):
| (1) |
(каждый элемент матрицы снабжён двумя индексами: первый указывает номер строки, второй — номер столбца, на пересечении которых находится этот элемент). Определителем матрицы (1) называется многочлен, каждый член которого является произведением n элементов матрицы (1), причём из каждой строки и каждого столбца матрицы в произведение входит лишь один сомножитель, т. е. многочлен вида
| &sum. ± a1&alpha. a2&beta. … an&gamma.. | (2) |
В этой формуле &alpha., &beta., …, &gamma. есть произвольная перестановка чисел 1, 2, …, n. Перед членом берётся знак +, если перестановка &alpha., &beta., …, &gamma. чётная, и знак — , если эта перестановка нечётная. [Перестановку называют чётной, если в ней содержится чётное число нарушений порядка (или инверсий), т. е. случаев, когда большее число стоит впереди меньшего, и нечётной — в противоположном случае. так, например, перестановка 51243 — нечётная, т. к. в ней имеется 5 инверсий 51, 52, 54, 53, 43.] Суммирование производится по всем перестановкам &alpha., &beta., …, &gamma. чисел 1, 2, …, n.
Число различных перестановок n символов равно n! = 1·2·3·…·n. поэтому О. содержит n! членов, из которых Ѕn! берётся со знаком + и Ѕn! со знаком -. Число n называется порядком О.
О., составленный из элементов матрицы (1), записывают в виде:
| (3) |
(или, сокращённо, в виде |aik|). Для О. 2-го и 3-го порядков имеем формулы:
| a11 | a12 | = a11a22 &minus. a12a21, | ||
| a21 | a22 |
| a11 | a12 | a13 | = a11a22a33 + a12a23a31 + a13a21a32 &minus. a11a23a32 &minus. a12a21a33 &minus. a13a22a31. | ||
| a21 | a22 | a23 | |||
| a31 | a32 | a33 |
О. 2-го и 3-го порядков допускают простое геометрическое истолкование:
равен площади параллелограмма, построенного на векторах a1 = (x1, y1) и a2 = (х2.у2), а
равен объёму параллелепипеда, построенного на векторах a1 = (x1, y1, z1), a2 = (x2, у2, z2) и а3 = (х3, y3, z3) (системы координат предполагаются прямоугольными).
Теория О. возникла в связи с задачей решения систем алгебраических уравнений 1-й степени (линейные уравнения). В наиболее важном случае, когда число уравнений равно числу неизвестных, такая система может быть записана в виде:
| (4) |
Эта система имеет одно определённое решение, если О. |aik|, составленный из коэффициентов при неизвестных, не равен нулю. тогда неизвестное xm (m = 1, 2, …, n) равно дроби, у которой в знаменателе стоит О.|aik|, а в числителе — О., получаемый из |aik| заменой элементов m-го столбца (т. е. коэффициентов при хm) числами b1, b2, …, bn. Так, в случае системы двух уравнений с двумя неизвестными
| a11 x1 + | a12 x2 | = b1, | ||
| a21 x1 + | a22 x2 | = b2, |
решение даётся формулами
Если b1 = b2 =…, = bn = 0, то систему (4) называется однородной системой линейных уравнений. Однородная система имеет отличные от нуля решения, только если |aik| = 0. Связь теории О. с теорией линейных уравнений позволила применить теорию О. к решению большого числа задач аналитической геометрии. Многие формулы аналитической геометрии удобно записывать при помощи О.. например, уравнение плоскости, проходящей через точки с координатами (x1, y1, z1), (x2, y2, z2), (х3, y3, z3), может быть записано в виде:
| x | y | z | 1 | = 0. | |||||
| x1 | y1 | z1 | 1 | ||||||
| x2 | y2 | z2 | 1 | ||||||
| x3 | y3 | z3 | 1 |
О. обладают рядом важных свойств, которые, в частности, облегчают их вычисление. Простейшие из этих свойств следующие:
1) O. не изменяется, если в нём строки и столбцы поменять местами:
| = |
| . |
2) О. меняет знак, если в нём поменять местами две строки (или два столбца). так, например:
| = &minus. |
| . |
3) О. равен нулю, если в нём элементы двух строк (или двух столбцов) соответственно пропорциональны. так, например:
| a11 | a12 | a13 | ka11 | = 0. | ||
| a21 | a22 | a23 | ka24 | |||
| a31 | a32 | a33 | ka34 | |||
| a41 | a42 | a43 | ka44 |
4) общий множитель всех элементов строки (или столбца) О. можно вынести за знак О.. так, например:
| = k |
| . |
5) если каждый элемент какого-нибудь столбца (строки) О. есть сумма двух слагаемых, то О. равен сумме двух О., причём в одном из них соответствующий столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же столбцы (строки) — те же, что и в данном О.. так, например:
| a11 | a12 | k1+l1 | = | a11 | a12 | k1 | + | a11 | a12 | l1 | . | ||||||
| a21 | a22 | k2+l2 | a21 | a22 | k2 | a21 | a22 | l2 | |||||||||
| a31 | a32 | k3+l3 | a31 | a32 | k3 | a31 | a32 | l3 |
6) О. не изменяется, если к элементам одной строки (столбца) прибавить элементы другой строки (другого столбца), умноженные на произвольный множитель. так, например:
| a11 | a12 | a13 | a14 | = | a11 | a12 | a13+ka11 | a14 | . | ||||
| a21 | a22 | a23 | a24 | a21 | a22 | a23+ka21 | a24 | ||||||
| a31 | a32 | a33 | a34 | a31 | a32 | a33+ka31 | a34 | ||||||
| a41 | a42 | a43 | a44 | a41 | a42 | a43+ka41 | a44 |
7) О. может быть разложен по элементам какой-либо строки или какого-либо столбца. Разложение О. (3) по элементам i-й строки имеет следующий вид:
| a11 | a12 | … | a1n | = ai1Ai1 + ai2Ai2 + … + ainAin. | ||
| a21 | a22 | … | a2n | |||
| … | … | … | … | |||
| ai1 | ai2 | … | ain | |||
| … | … | … | … | |||
| an1 | an2 | … | ann |
Коэффициент Aik, стоящий при элементе aik в этом разложении, называется алгебраическим дополнением элемента aik. Алгебраическое дополнение может быть вычислено по формуле: Aik = (-1)i+kDik, где Dik — минор (подопределитель, субдетерминант), дополнительный к элементу aik, то есть О. порядка n-1, получающийся из данного О. посредством вычёркивания строки и столбца, на пересечении которых находится элемент aik. Например, разложение О. 3-го порядка по элементам второго столбца имеет следующий вид:
| = &minus.a12 | + a22 | &minus.a32 | . |
Посредством разложения по элементам строки или столбца вычисление О. n-го порядка приводится к вычислению n определителей (n — 1)-го порядка. Так, вычисление О. 5-го порядка приводится к вычислению пяти О. 4-го порядка. вычисление каждого из этих О. 4-го порядка можно, в свою очередь, привести к вычислению четырёх О. 3-го порядка (формула для вычисления О. 3-го порядка приведена выше). Однако, за исключением простейших случаев, этот метод вычисления О. практически применим лишь для О. сравнительно небольших порядков. Для вычисления О. большого порядка разработаны различные, практически более удобные методы (для вычисления О. n-го порядка приходится выполнять примерно nі арифметических операций).
Отметим ещё правило умножения двух О. n-го порядка: произведение двух О. n-го порядка может быть представлено в виде О. того же n-го порядка, в котором элемент, принадлежащий i-й строке и k-му столбцу, получается, если каждый элемент i-й строки первого множителя умножить на соответствующий элемент k-го столбца второго множителя и все эти произведения сложить. иными словами, произведение О. двух матриц равно О. произведения этих матриц.
В математическом анализе О. систематически используются после работ немецкого математика К. Якоби (2-я четверть 19 в.), исследовавшего О., элементы которых являются не числами, а функциями одного или нескольких переменных. Из таких О. наибольший интерес представляет определитель Якоби (Якобиан)
| &part.&fnof.1 &part.x1 | &part.&fnof.1 &part.x2 | … | &part.&fnof.1 &part.xn | . | ||
| &part.&fnof.2 &part.x1 | &part.&fnof.2 &part.x2 | … | &part.&fnof.2 &part.xn | |||
| … | … | … | … | |||
| &part.&fnof.n &part.x1 | &part.&fnof.n &part.x2 | … | &part.&fnof.n &part.xn |
Определитель Якоби равен коэффициенту искажения объёмов при переходе от переменных х1, x2, …, хn к переменным
y1 = &fnof.1(x1, …, xn),
y2 = &fnof.2(x1, …, xn),
………………….
yn = &fnof.n(x1, …, xn).
Тождественное равенство в некоторой области этого О. нулю является необходимым и достаточным условием зависимости функций f1(x1, …, xn), f2(x1, …, xn), …, fn(x1, …, xn).
Во 2-й половине 19 в. возникла теория О. бесконечного порядка. Бесконечными О. называются выражения вида:
| (5) |
(односторонний бесконечный О.) и
| … | … | … | … | … | … | … | ||
| … | a&minus.2,&minus.2 | a&minus.2,&minus.1 | a&minus.2,0 | a&minus.2,1 | a&minus.2,2 | … | ||
| … | a&minus.1,&minus.2 | a&minus.1,&minus.1 | a&minus.1,0 | a&minus.1,1 | a&minus.1,2 | … | ||
| … | a0,&minus.2 | a0,&minus.1 | a0,0 | a0,1 | a0,2 | … | ||
| … | a1,&minus.2 | a1,&minus.1 | a1,0 | a1,1 | a1,2 | … | ||
| … | … | … | … | … | … | … |
(двусторонний бесконечный О.). Бесконечный О. (5) есть предел, к которому стремится О.
| a11 | a12 | … | a1n | ||
| a21 | a22 | … | a2n | ||
| … | … | … | … | ||
| an1 | an2 | … | ann |
при бесконечном возрастании числа n. Если этот предел существует, то О. (5) называется сходящимся, в противном случае — расходящимся. Исследование двустороннего бесконечного О. иногда можно привести к исследованию некоторого одностороннего бесконечного О.
Теория О. конечного порядка создана в основном во 2-й половине 18 в. и 1-й половине 19 в. (работами швейцарского математика Г. Крамера, французских математиков А. Вандермонда, П. Лапласа, О. Коши, немецких математиков К. Гаусса и К. Якоби). Термин
«О.» («детерминант») принадлежит К. Гауссу, современное обозначение — английскому математику А. Кэли.
Лит. см. при статьях Линейная алгебра, Матрица.
Расскажите вашим друзьям что такое — Определитель. Поделитесь этим на своей странице.

xn—-7sbbh7akdldfh0ai3n.xn--p1ai
Значение слова Определитель в 10 словарях (Даль, Ожегов, Ефремова и др.)
Поделиться:ОПРЕДЕЛИТЕЛЬ, -я, м. 1. Устройство для определения чего-н., а также вообще то, с помощью чего можно что-н. точно определить, установить. Телефон с определителем номера. О. ритма. 2. Книга для справок при определении чего-н. (спец.). О. растений.
Ударение: определи́тель м.
- То, что определяет собою что-л.
- Книга, служащая для справок при определении чего-л.
ОПРЕДЕЛИ́ТЕЛЬ, определителя, ·муж. (·книж. ).
1. То, что определяет, выражает собою что-нибудь.
2. Книга, служащая для справок при определении чего-нибудь (научн.). Определитель растений. Определитель грибов.
3. Выражение, составляемое из коэффициентов системы уравнений 1-й степени с несколькими неизвестными для упрощения вычисления корней уравнений (мат.).
опознаватель, гессиан, минор, детерминант
(детерминант) , составленное по определенному правилу из n2 чисел математическое выражение, применяемое при решении и исследовании систем алгебраических уравнений 1-й степени. Число n называется порядком определителя. Так, определитель 2-го порядка, составленный из четырех чисел a1, b1, a2, b2, обозначается:и равен a1b2-b1a2.
автоопределитель, гессиан, детерминант, минор, опознаватель, пылеопределитель
определи́тель,
определи́тели,
определи́теля,
определи́телей,
определи́телю,
определи́телям,
определи́тель,
определи́тели,
определи́телем,
определи́телями,
определи́теле,
определи́телях
glosum.ru
Автоматические определители языков мира — MrTranslate.ru
Иногда мы сталкиваемся с текстом на незнакомом нам языке. Стандартные способы определения языка не помогают. Как узнать, на каком языке он написан? В этом вам помогут автоматические определители языков.
Как работает определитель языка (guesser)
Автоматический определитель языка называют иногда guesser. Он позволяет по введенным нескольким словам определить язык, на котором они написаны. Технически, определение языка реализуется при помощи словаря.Введенный текст разбивается на слова, и они сравниваются со словами из базы определителя. В результате подсчитывается количество совпадений слов разных языков, и выводится отчет в виде названия одного языка или списка языков, которые были признаны наиболее подходящими.
Однако, работа автоматического определителя языка не так проста: система должна учитывать лексические особенности языков, правила построения предложений, различия в диалектах, и другие особенности.
Поэтому, сервисы автоматического определения языка предоставляются обычно разработчиками систем машинного перевода. Результат определения языка не может быть 100% точным. Обычно определитель языка также сообщает, с какой вероятностью ему удалось определить язык.
Чем больше символов текста вы укажете, тем более точным будет определение.
Автоматический определитель языка от Xerox
Определитель языка от Xerox основан на экспериментальных разработках компании. Кроме определения языка система также также распознает кодировку. Эффективность определения языка этой системой — высокая.Автоматический определитель языка Talenknobbel
Как повысить правильность определения языка
При использовании систем автоматического определения языка текста необходимо знать некоторые особенности:- Используйте не менее 20-ти слов (чем больше, тем лучше).
- Проверяйте текст на ошибки перед определением языка.
- Вводите в определитель ту часть текста, которая позволит эффективнее определить язык (например, слова с наличием нестандартных букв, надстрочных и подстрочных символов, и т.д.).
- Для более точного результата воспользуйтесь несколькими сервисами.
Автоматический определитель языка TextCat
Определитель языка TextCat — реализация алгоритма классификации текста (W. B. Trenkle и J. M. Trenkle, «N-Gram-Based Text Categorization»), который был представлен на третьем ежегодном симпозиуме по технологиям анализа документов и поиска информации, проходившем в Лас-Вегасе в апреле 1994 года. Определитель поддерживает 69 языков.Автоматический определитель языка Verbix
Определитель языка создан независимой некоммерческой организацией Verbix, основной деятельностью которой является сохранение языкового разнообразия на нашей планете.Автоматический определитель языка Translated Labs
Определитель языка разработан исследовательским центром Translated Labs (T-Labs), который занимается изучением семантики языков и разработкой языковых моделей для создания автоматизированных комплексов по работе с информацией: поисковых систем, систем анализа данных, систем машинного перевода.Определитель языка Полиглот 3000
| Разработчик: | Likasoft |
| Тип лицензии: | Freeware |
| Требования: | 95/98/NT/ME/2000/XP/Vista |
 Полиглот 3000 — это уникальный автоматический определитель языка, предназначенный для быстрого и корректного ответа на вопрос: «На каком языке написан текст?».
Программа распознает более 400 языков, быстро и качественно определяет язык введенного текста, имеет многоязычный интерфейс.
Программа бесплатна, и будет полезна всем, кто постоянно сталкивается с иностранными языками или часто задает вопрос «Какой это язык?».
Подробнее о Полиглот 3000 →
Полиглот 3000 — это уникальный автоматический определитель языка, предназначенный для быстрого и корректного ответа на вопрос: «На каком языке написан текст?».
Программа распознает более 400 языков, быстро и качественно определяет язык введенного текста, имеет многоязычный интерфейс.
Программа бесплатна, и будет полезна всем, кто постоянно сталкивается с иностранными языками или часто задает вопрос «Какой это язык?».
Подробнее о Полиглот 3000 →
Как определить язык текста?
Если вы столкнулись с текстом на незнакомом вам языке, и если у вас возник вопрос «Какой это язык?», можно попробовать определить его самостоятельно. Это не так уж и сложно. В каждом языке есть свои определенные особенности, которые помогают его распознать: набор знаков, подстрочных и надстрочных символов, направление письма, и пр. Наверняка вы без труда сможете распознать основные языки.Вы также можете просто воспользоваться одним из автоматических определителей языка. В этом случае от вас вообще не требуется никаких усилий, достаточно просто вставить текст в определитель.
Определить, на каком языке написан текст, может потребоваться, например, для того, чтобы воспользоваться онлайн-переводчиком. Некоторые переводчики умеют самостоятельно определять язык, но большая часть из них требуют указания языка вручную.
mrtranslate.ru
Расширение Juisy — выделяем главные мысли в тексте — Вся правда о Chrome и Chromium
Представляем очередной авторский обзор расширения в рамках нашей акции.
Наверняка у многих было так: открыв статью, смотришь на ее длину и откладываешь прочтение на потом. А дело в том, что автор замаскировал свою главную мысль за огромным количеством незначимых слов. В итоге статья так и остается непрочитанной. Поэтому мы и придумали Juisy — расширение для Google Chrome, которое помогает читать только самую суть.
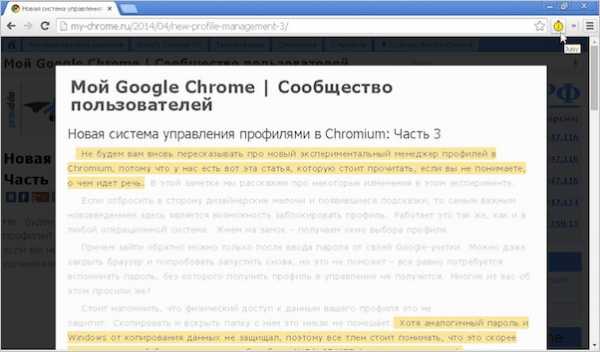
Мы хотели создать решение, которое позволило бы быстрее читать, не откладывая на потом и не умножая количество вкладок в браузере. В основе работы Juisy — технология анализа текста, определяющая наиболее «тяжелые» по смыслу фрагменты.
Мы знаем, что решения, подобные нашему, уже существуют. Но они имеют два серьезных минуса. К сожалению, большинство из них хорошо работает только с английским языком. И второй существенный недостаток — они очень сложны для решения повседневных задач. То есть требуется выделить нужный текст, скопировать его, зайти на сайт, вставить текст в форму, нажать кнопку… Поэтому мы сделали расширение для браузера — чтобы сокращать любой текст на любой странице.
Основная сложность при разработке была связана с автоматизацией определения контента на сайте. Вы сами хорошо представляете, сколько сайтов в сети, все они разные, а многие из них еще и пытаются как-то особенно выделиться. Формально «достать» текст с web-страницы легко, но, например, выделить текст, относящийся только к статье, — уже нетривиальная задача. При этом качество выявления контента играет ключевую роль в качестве работы алгоритма. «Мусор» с сайтов (меню, реклама и так далее) нам не нужен.
Возможно, мы совершили ошибку, пытаясь создать универсальный граббер контента. В ближайшем будущем постараемся для каждого сайта писать специализированные анализаторы контента, начнем с самых популярных. Конечно, все мы покрывать не собираемся, но думаем заточить наш граббер, по крайней мере, под 1000 сайтов рунета.
Сердце дополнения — это наш сервис, который анализирует текст и определяет, что, на его взгляд, вам стоит прочесть. Мы используем комплексные технологии анализа естественного языка. Пока мы не можем похвастаться, что сервис работает безупречно. Но наша команда каждый день работает над ним, делая его умнее.
На нашем сайте вы можете посмотреть, как работает эта технология. Либо установить расширение из Chrome Web Store.
Мы будем очень рады любым вопросам, замечаниям и предложениям. Ждем их на [email protected] или здесь в комментариях.
today 21.04.2014
my-chrome.ru
