Олимпиада по физике 9 класс, задания с ответами
Чтобы подготовиться к олимпиаде по физике ученикам 9 класса нужно серьезно отнестись к подготовке. Для этого мы предлагаем использовать задания, собранные на этой странице. Учителя физики смогут использовать их на уроках для проведения пробной олимпиады. Мы собрали тесты и задачи, которые помогут ученикам закрепить свои знания.
Внизу страницы указаны ответы и решения, благодаря чему эти задания можно использовать и без помощи учителя. Сверившись с ответами и решениями, ученики смогут оценить, насколько успешно они решили олимпиадные задания по физике для 9 класса.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Тестовые задания
1. Благодаря какому явлению распространяется запах духов?
А) Диффузии
Б) Конвекции
В) Электризации
Г) Ионизации
2. К астрономическим телам не относятся:
А) Звёзды
Б) Планеты
Г) Аметисты
3. За 2 часа автомобиль проехал 120 км. Чему равна скорость автомобиля?
А) 240 км/ч
Б) 60 км/ч
В) 122 км/ч
Г) 118 км/ч
4. Каждый из участков пути АВ, ВС и СД автомобиль проезжает за 1 мин. На каком участке скорость наибольшая, на какой наименьшая?
А) АВ и ВС
Б) СД и ВС
В) АВ и СД
Г) АС и ВС
5. Чему равен объем сосуда, в котором помещается 8 кг керосина? Плотность керосина 800 кг/м3.
А) 100 м3
Б) 0,01 м3
В) 10 м3
Г) 0,1 м3
6. Каким прибором измеряют силу тяжести?
А) Манометром
Б) Спектрометром
В) Динамометром
Г) Ареометром
7. Одинакова ли плотность воздуха во всех точках высотного здания?
А) Плотность больше в подвальных помещения
Б) Плотность одинакова во всех точках
В) Плотность больше на верхнем этаже
Г) Плотность больше в центре здания
8. Вычислите давление, которое оказывает керосин на дно бака
площадью 5 м2. Масса керосина в баке 500 кг.
Б) 100 Па
В) 980 Н
Г) 980 Па
9. В каких из нижеприведенных примеров тело совершает
механическую работу?
А) Трос натянут под действием силы тяжести
Б) Человек стоит с сумкой в руках
В) Космический корабль, отключив двигатель, движется в
космическом пространстве
Г) Человек поднимается на второй этаж
10. Чему равна работа, совершаемая при поднятии ящика
массой 4 кг на высоту 2,5 м?
А) 98 Н
Б) 98 Па
В) 9,8 Дж
Г) 98 Дж
Д) 980 Дж
Открытые вопросы
Вопрос 1
Теплоизолированный сосуд до краев наполнили водой при температуре t0 = 20 °С. В него опустили алюминиевую деталь, нагретую до температуры t = 100 °С. После установления теплового равновесия температура воды в сосуде стала t1 = 30,3 °С. Затем этот же эксперимент провели с двумя такими же деталями. В этом случае после установления в сосуде теплового равновесия температура воды стала t2 = 42,6 °С. Чему равна удельная теплоемкость с алюминия? Плотность воды ρ0 = 1000 кг/м3, ее удельная теплоемкость с0 = 4200 Дж/(кг · °С). Плотность алюминия ρ = 2700 кг/м3.
Вопрос 2
На зимней дороге при температуре снега t1 = –10 ºC автомобиль в течение 1 мин
буксует, развивая мощность 12 кВт. Сколько снега растает при буксировании автомобиля, если считать, что вся энергия, выделившаяся при буксировании, идет на нагревание и плавление снега? Удельная теплоёмкость льда с = 2100 Дж/(кг ·ºC), удельная теплота плавления льда λ = 33·104 Дж/кг.
Вопрос 3
Сообщающиеся сосуды состоят из двух одинаковых трубок (U-образная трубка).
Трубки частично заполнили водой. На сколько повысится уровень воды в левой трубке, если в правую налить столько керосина, что он образует столб высотой 30 см?
Плотность керосина 900 кг/м3, плотность воды 1000 кг/м3.
Вопрос 4
Мяч объёмом V и массой m всплыл на поверхность воды с глубины Н. Чему равна механическая работа, совершённая при всплывании мяча? Трением пренебречь. Плотность воды ρо считать известной.
Вопрос 5
В плотно закрытом полиэтиленовом пакете с молоком, хранящемся при постоянной температуре, масса вещества остается неизменной. Почему со временем пакет увеличивается в объеме?
Ответы на тесты
| Тестовое задание | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | А | Г | Б | Б | Б |
| Тестовое задание | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | В | А | Г | Г | Г |
Ответы на открытые вопросы
Ответ на вопрос 1:
Пусть m – масса детали, V – объём сосуда, тогда уравнения теплового баланса
при опускании одной и двух деталей соответственно имеют вид cm(t — t1) = c0 ρ0(V – (m/ρ))∙ (t1 — t0) (*) 2cm(t — t2) = c0 ρ0(V – (2m/ρ))(t2 — t0) (**) Делим соотношение(*) на (t1 — t0), а соотношение (**) на (t2 — t0) и , вычитая соотношение (**) из (*), получаем
с ≈ 922 Дж/(кг∙°С).
Ответ на вопрос 2:
На зимней дороге при температуре снега t1 = –10 ºC автомобиль в течение 1 мин
буксует, развивая мощность 12 кВт. Сколько снега растает при буксировании автомобиля, если считать, что вся энергия, выделившаяся при буксировании, идет на нагревание и плавление снега? Удельная теплоёмкость льда с = 2100 Дж/(кг ·ºC), удельная теплота плавления льда λ = 33·104 Дж/кг.
Ответ на вопрос 3:
Предположим, что в левой трубке уровень воды повысился на h. Тогда в
правой трубке уровень воды будет ниже, чем в левой, на 2h.
ρк gH = ρв g2h. → h = 12 см.
Ответ на вопрос 4:
А = (ρо gV – mg)∙H = (ρоV – m)∙gH
Ответ на вопрос 5:
В результате деятельности молочных бактерий образуются газы. Число молекул газа в пакете увеличивается, число их соударений с внутренней стороной стенки пакета начинает превышать число соударений молекул воздуха с внешней стороной стенки пакета. Стенка приходит в движение, увеличивается объем. Давления по обе стороны стенки пакета выравниваются. Дальнейшее увеличение объема ограничено упругими свойствами пакета.
Скачайте задания, заполнив форму!
После того как укажете данные, кнопка скачивания станет активной
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Олимпиадные задания с ответами по физике 9 класс
Решения и критерии оценки
Олимпиадной работы по физике 9 класс
2013 – 2014 учебный год
Всего 89 баллов.
Задача 1. 16 баллов.
Решение:
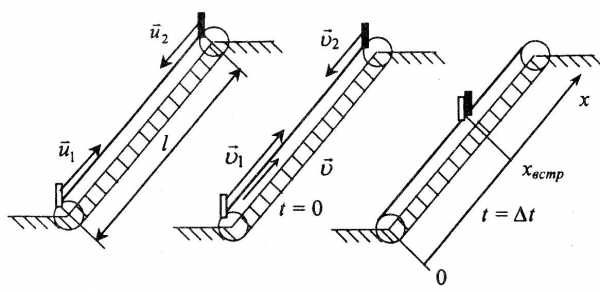
График в условии необычный, но очень удобный для нахождения времени путешествия.
Время Δt прохождения малого отрезка Δх со скоростью υ легко найти: Δt = Δx· 1/υ. Это произведение равно площади под графиком величины 1 /υ как раз над кусочком Δх (малость Δх нужна для того, чтобы можно было считать скорость прохождения этого кусочка неизменной). Полное же время t равно площади под всем графиком от х = 0 до х = 30 м. Площадь эту можно приближенно найти по графику, например — по клеточкам. В нашем случае, учитывая половинки и четвертушки клеток, получаем всего 9 клеток. Одна клетка соответствует Δх- 5 м и 1/υ =10 с/м, т.е. времени Δ t = 50 с. Тогда полное (искомое) время t = 9 · 50 с = 450 с.
Критерии:
Умение работы с графиком (нахождение перемещения по графику скорости) 4 балла,
Умение чтения графика (работа с осями) 4 балла,
Сделаны правильные выводы 4 балла,
Верный математический расчет 4 балла.
Задача 2. 22 балла.
Решение:
Мячик подскакивает на меньшую высоту из-за того, что часть энергии деформации переходит в тепло. Будем считать, что доля переходящей в тепло энергии остается неизменной при различных скоростях мячика перед ударом.
Решим задачу в системе отсчета, которая движется вместе с ракеткой вверх со скоростью u (именно эту скорость необходимо найти). В этой системе мячик на высоте Н имеет скорость u . Тогда максимальное значение энергии деформации составляет
W = mgН + mu2 /2, где m — масса мячика. В тепло перешла 1/10 часть этой энергии, поэтому получаем 9/10 (mgН + ) = mgН. 0,9mgH + =
= mgH, mgH — 0,9mgH, 0,1 mgH, 0,9m=0,2mgH, 0,9=0,2gH,
=/ 3=/ 3 = 1 м/с . Ответ : =1 м/с
Критерии:
Верно выбраны процессы происходящие с мячом 4 балла,
Правильно выбрана система координат 4 балла,
Верно записано уравнение 5 баллов,
Верно произведены математические выводы 5 баллов,
Правильный расчет 4 балла.
Задача 3. 10 баллов.
Решение:
Рядом с серединой длинного магнита стрелка располагается вдоль линий магнитной индукции поля прямого длинного магнита. Если магнит разрезать посередине и половинки развести, то на половинках разреза появятся полюса, противоположные полюсам на дальних концах половинок магнита (получить однополюсной магнит принципиально невозможно). Поэтому стрелка, притягиваемая новыми торцами, которые ближе к ней и сильнее на нее влияют, перевернется.
Критерии:
Понимание характеристик магнитного поля 5 баллов,
Верный ответ 5 баллов.
Задача 4. 16 баллов.
Решение:
Чтобы освещенность центрального светлого пятна на стенке оставалась неизменной, необходимо, чтобы точечный источник света находился в фокусе собирающей линзы, то есть длина пружинки при движении тележки должна быть равна f – фокусному расстоянию линзы. См рис. Поскольку f < , пружинка будет сжата, и сила упругости F ynp = k (—f), действующая на оправу со стороны сжатой пружинки, будет направлена вправо. Следовательно, ускорение оправы, а значит, и тележки, направлено к стенке, а величина его определяется из уравнения движения оправы mα = k (—f).
. Ответ: α = 0,1 м/с2
Критерии:
Понимание условия задачи 4 балла,
Выбор необходимого закона 4 балла,
Запись равнодействующей силы 4 балла,
Верный математический расчет 4 балла.
Задача 5. 25 баллов.
Решение:
Обозначим через 
сопротивление любого из участков AE, EC, CF,
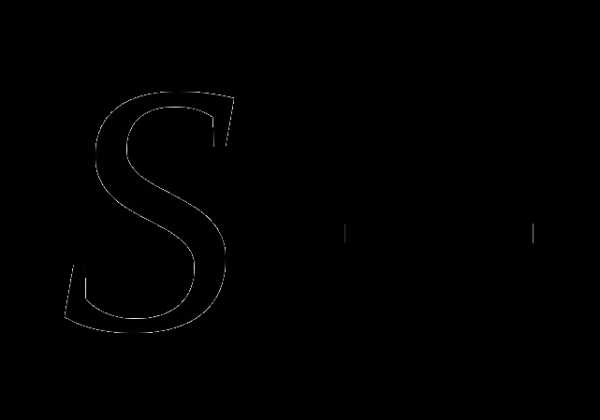площадь сечения любого из участков AE, EC, CF, FB, то площадь сечения участка EF будет 
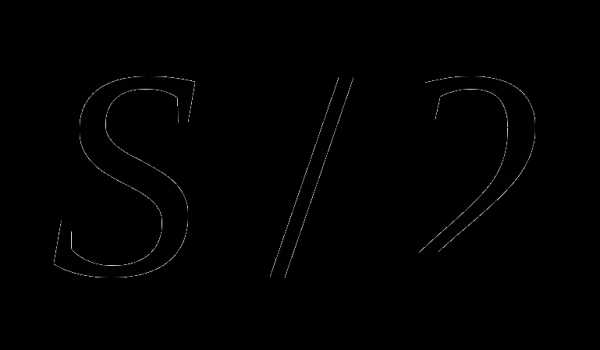. Тогда R равно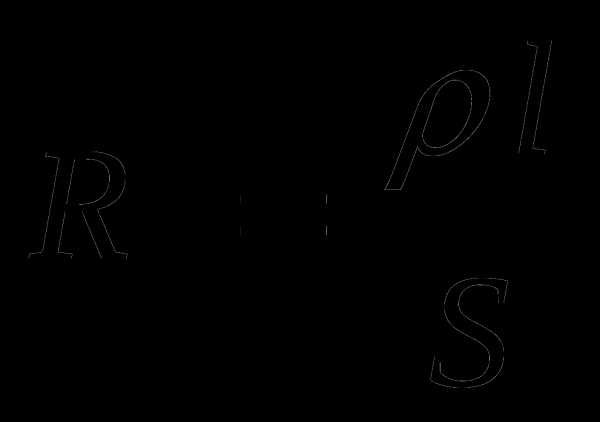 
а для R1 получим
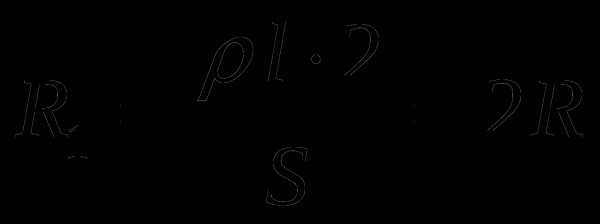
Тогда схема, эквивалентная нашему соединению представлена на рисунке :
Сопротивление среднего участка равно , а общее сопротивление цепи 
, поэтому падение напряжения на этом участке, а следовательно, и на перемычке будет
В
Критерии:
Верное распределение участков цепи 4 балла,
Верное нахождение сопротивления участков 4 балла,
Верная формула для расчета сопротивлений 2 балла,
Правильная эквивалентная формула 6 баллов,
Верный расчет сопротивления участка 5 баллов,
Верный математический расчет 4 балла.
infourok.ru
Подготовка к олимпиадам по физике: 9 класс, равноускоренное движение
Продолжаем готовиться к олимпиадам. В этой статье, ориентированной на школьников 9 класса, предложены задачи на равноускоренное движение. При этом предполагается, что вы знакомы уже с основными формулами и законами такого движения.
Задача 1. Двигаясь равноускоренно из состояния покоя, тело проходит некоторое расстояние. Найдите отношение средней скорости тела на второй и первой половине времени движения.
Графически:
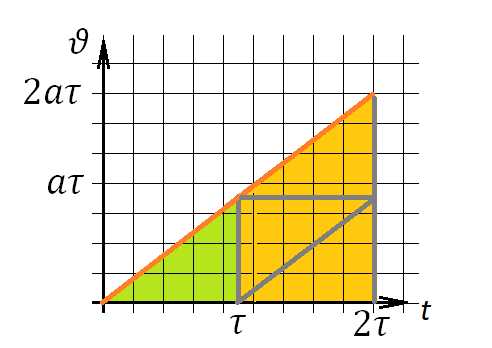
Рисунок 1
Аналитически, первый способ:
Аналитически, второй способ:
Путь может быть определен как
Где – конечная скорость.
Тогда
Ответ: 3.
Задача 2. Двигаясь равноускоренно из состояния покоя, тело проходит некоторое расстояние. Найдите отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути.
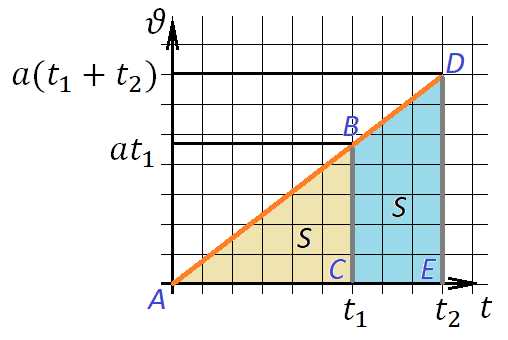
Рисунок 2
Через скорости:
Для первого участка
Для полного пути:
Теперь подставим (1) в (2):
Через подобие: треугольник подобен . Их площади отличаются вдвое, следовательно, коэффициент подобия равен , откуда
Ответ: .
Задача 3. С вершины гладкой горки вдоль наклонной плоскости длиной толкнули со скоростью брусок. Через некоторое время он достиг основания горки. Затем тот же брусок пустили со скоростью вдоль наклонной горки длиной , и он скатился за время . Во сколько раз время скатывания с этой горки больше времени ?
По закону сохранения энергии скорости обоих брусков в конце спуска одинаковы: так как начальная кинетическая энергия одна и та же, и потенциальная – также.
Для участка :
Для участка :
Разделим одно на другое, и получим:
Задача 4. Тело, пущенное вверх вдоль наклонной плоскости со скоростью 1,5 м/с, вернулось обратно со скоростью 1 м/с. Найти среднюю скорость тела на всем пути. Вверх и вниз тело двигалось с постоянными ускорениями.
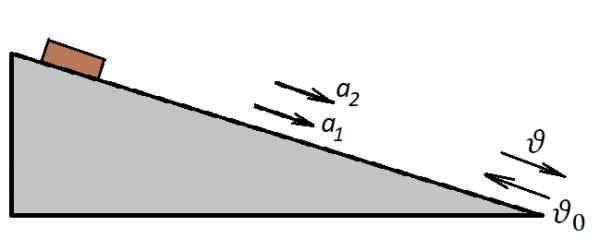
Рисунок 3
Пусть эти ускорения равны и . Путь, пройденный бруском, одинаков: и туда, и обратно, обозначим его . Тогда средняя скорость равна
Площадь зеленого треугольника равна
Площадь желтого:
Откуда
Определяем среднюю скорость:
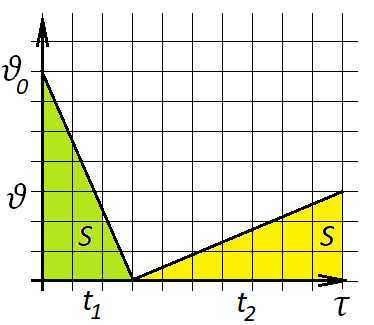
Рисунок 4
Решим эту задачу иначе: на первом участке средняя скорость равна , а на втором (рисунок 4). Остается найти среднюю скорость на всем пути, ответ будет таким же.
Ответ: м/с.
Задача 5. Отходящий от станции поезд на первом километре пути увеличил свою скорость на 10 м/с, а на втором – на 5 м/с. На каком километре среднее ускорение поезда было больше?
Рисунок 5
Обозначим участки пути , их длина – километр. Тогда для первого участка
А на втором
Приравняем:
Ответ: на втором километре.
Задача 6. Реактивный самолет летит по прямой со скоростью км/ч. С некоторого момента самолет движется с ускорением в течение с и в последнюю секунду проходит путь м. Определить ускорение и конечную cкорость самолета.
Переведем скорость самолета в м/с: м/с.
Определим путь, пройденный самолетом за 9 с:
А за все 10 с равноускоренного движения самолет пройдет
Разница, очевидно, составляет 295 м:
Или
Ответ: м/с, м/с.
Задача 7. Поезд трогается с места и равноускоренно проходит мимо неподвижного пассажира. При этом первый вагон прошел мимо него за время , а последний за время . За какое время мимо пассажира прошел весь поезд, если первоначально пассажир стоял у головы поезда?
Пусть длина вагона . Тогда длина первого вагона
До момента, когда последний вагон поравняется с наблюдателем, пройдет время . За это время будет набрана скорость . Тогда длина последнего вагона равна
Приравняем:
Ответ:
Задача 8. Точка начинает двигаться со скоростью м/с и движется равнозамедленно с ускорением м/с2. Определить, какой путь пройдет точка за время с и с.
Ответ: 24 и 16 м.
Решили? Точно? Мы нашли перемещение! А просят найти путь! Между тем, можно заметить, что произойдет остановка. Давайте определим, где.
Путь, пройденный телом будет равен (туда и обратно, но обратно не дошли до точки старта расстояние, равное перемещению)
Вот теперь верно. Ответ: 26 и 34 м.
easy-physic.ru
Олимпиада по физике школьный тур 9 класс 2015-2016 уч г с решениями
Решение школьного этапа всероссийской олимпиады
школьников по физике в 2015 — 2016 учебном году
9 класс.
1. Старшеклассник Вася поехал на мопеде за
мороженым в киоск, который находится на расстоянии
1,1 км от его дома на противоположной стороне той же
улицы. График зависимости скорости его мопеда от
времени показан на рисунке. Однако оказалось, что в
бензобаке мало бензина. Сколько метров Вася шёл
пешком до киоска после того, как бензин кончился и
мопед остановился?
Решение 1. Так как скорость мопеда меняет знак, значит в процессе движения мопед менял
направление движения – разворачивался. Расстояние, пройденное мопедом до разворота (площадь под графиком) – 2400 м, после разворота – 1200 м. Значит, Вася не доехал до киоска 100 м.
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).
5-6
Найдено решение одного из двух возможных случаев (путь мопеда до разворота или путь мопеда после разворота)
5
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
2.Моток медной проволоки сечением 2 мм 2 имеет массу 17,8 кг. Как, не разматывая моток, определить длину проволоки? Чему она равна? Плотность меди 8,9 г/см3
Решение 2.
m=p*V=p*S*L L=m/p*s
Выразим массу в граммах: m=17800г
Площадь поперечного сечения в см3: S=0,02 см2.
Подставим: L=17800г/8,9 г/см3*0,02 см2=100000см=1000м
Ответ: L=1000м
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).
5-6
Записана формула массы, формула объема проволоки через длину и площадь сечения.
5
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
3. В сосуде, из которого быстро откачивают воздух, находится вода массой 
г при температуре t = 0°C. В результате интенсивного испарения происходит замораживание воды. Какая часть первоначальной массы воды обратилась в лед? Удельная теплота парообразования воды 
=2,3*106Дж/кг; удельная теплота плавления льда 
=3,4*105Дж/кг
Решение № 3
Энергия, необходимая для образования пара, может быть получена за счет энергии, выделившейся при замораживании воды.
Пусть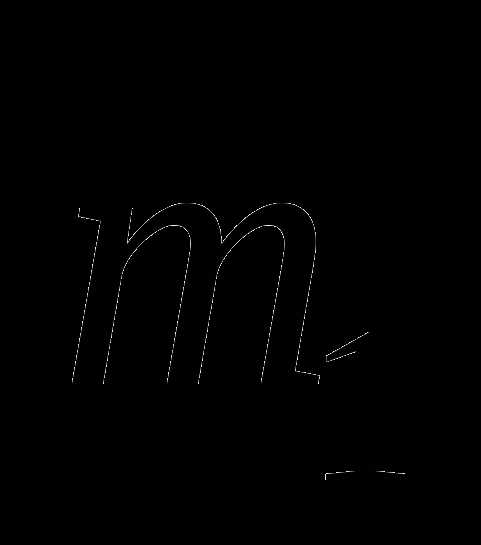 
— масса образовавшегося льда, а 
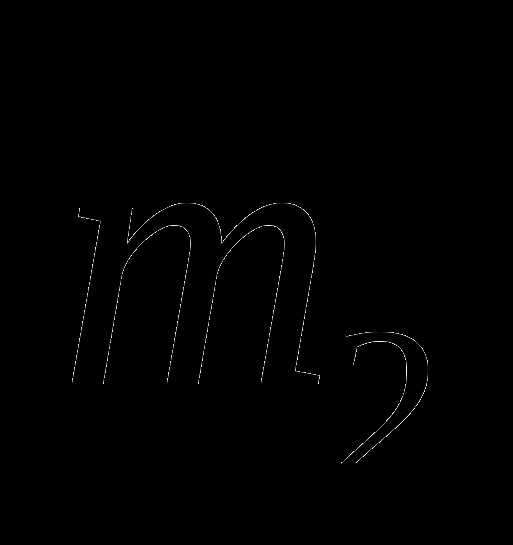— масса пара, тогда масса воды до замерзания
= +.
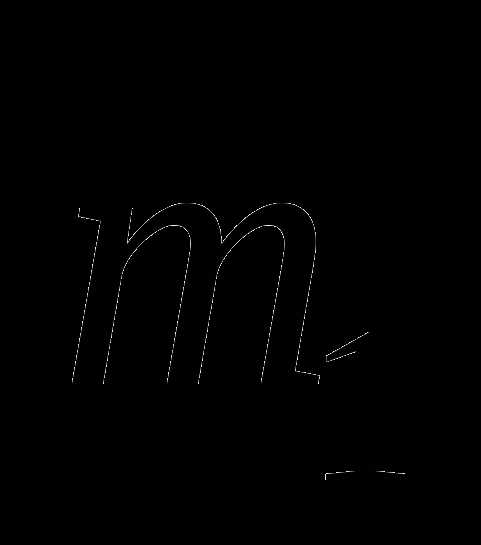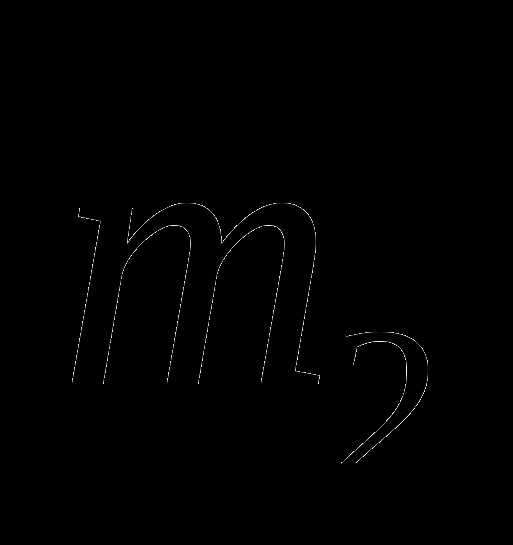При кристаллизации воды массой 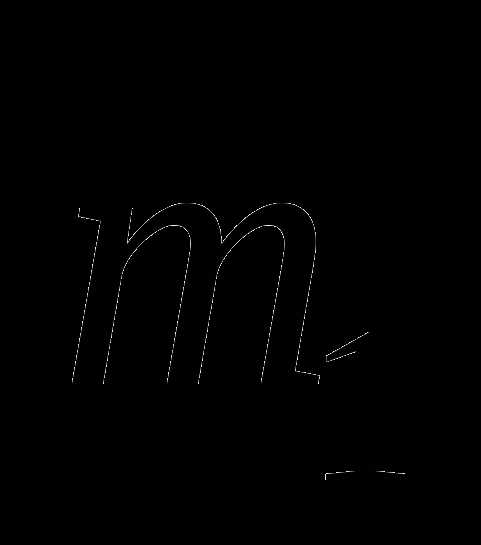выделяется количество теплоты, равное .
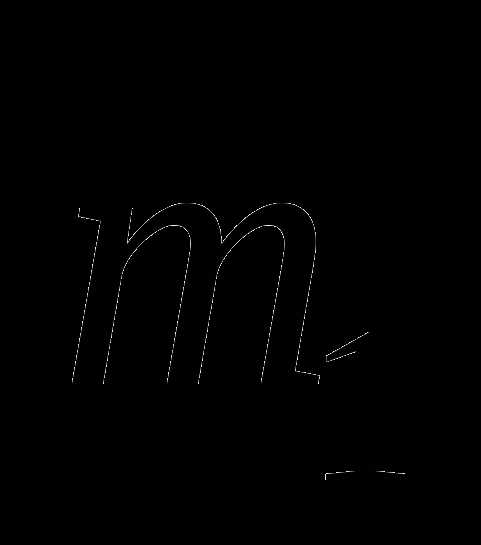Для испарения воды массой 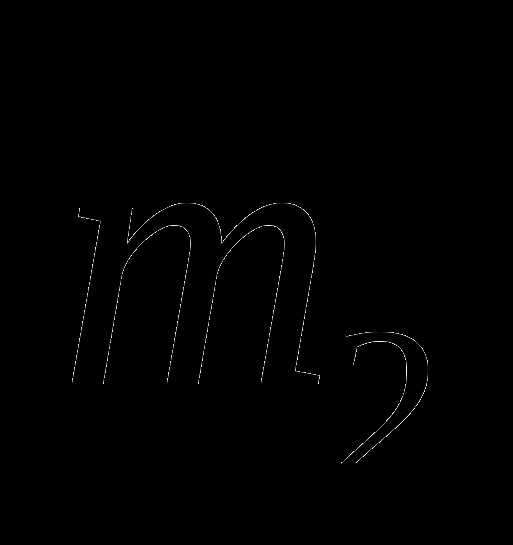требуется количество теплоты, равное .
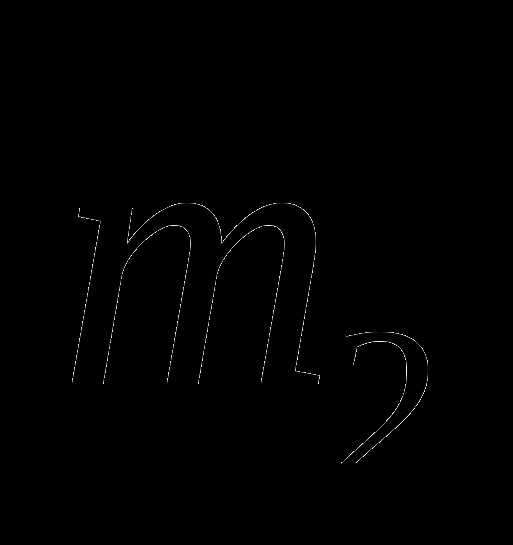В соответствии с законом сохранения энергии можно записать:
.=.
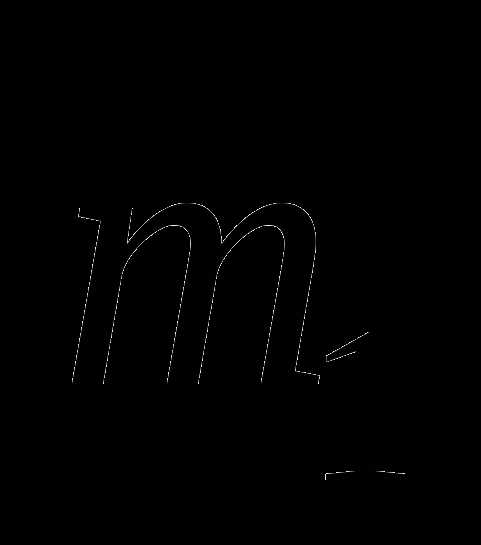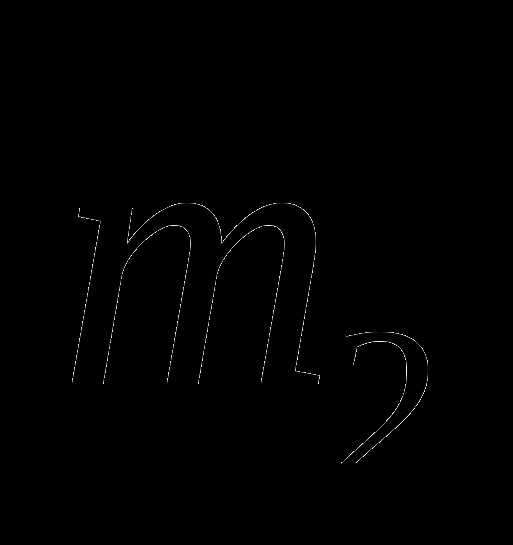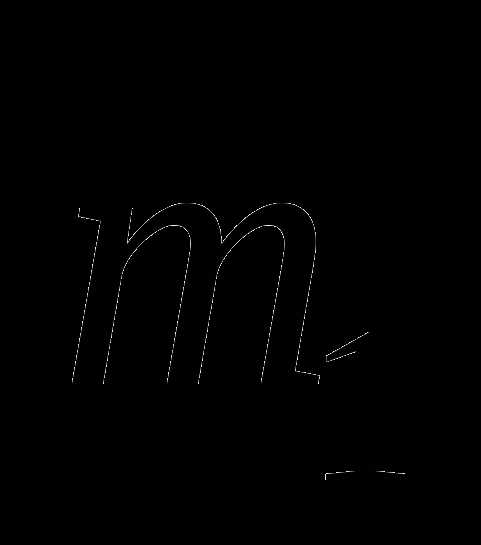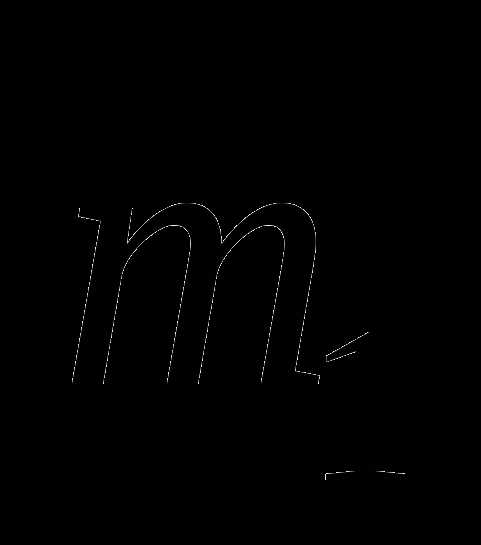.=(—), Откуда: , что составляет 87% первоначальной массы воды.
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).
5-6
Записан закон сохранения энергии, записано количество теплоты при кристаллизации, количество теплоты при парообразовании: за каждую формулу 2 балла
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
4. Электроплитка с двумя одинаковыми спиралями позволяет получить три степени нагрева в зависимости от порядка и характера включения спиралей. Начертите схемы включения. Сравните количества теплоты, полученные от плитки за одно и то же время.
Решение № 4
Спирали можно комбинировать следующим образом:
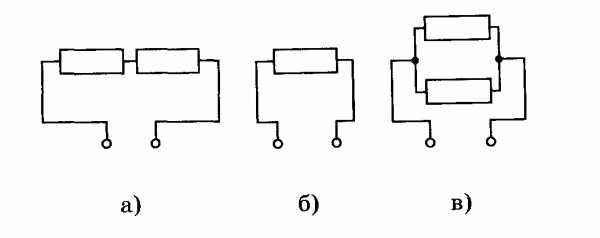
Количество теплоты, полученное от плитки :
для схемы а)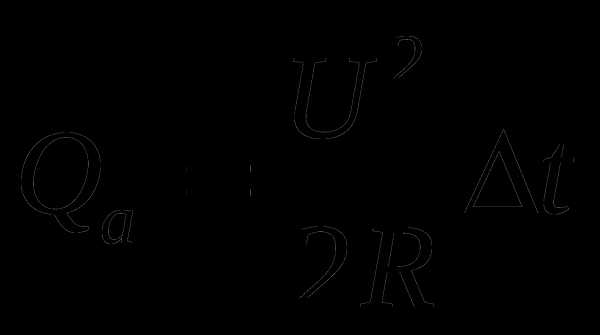 
, для схемы б) 
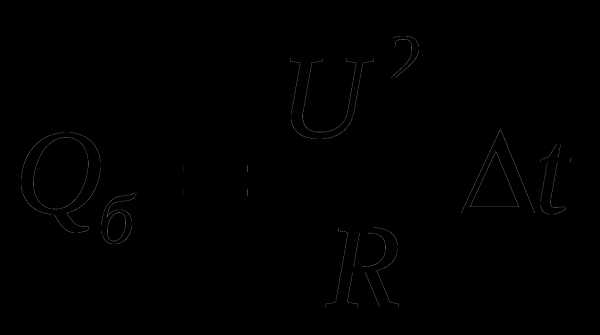, для схемы в) 
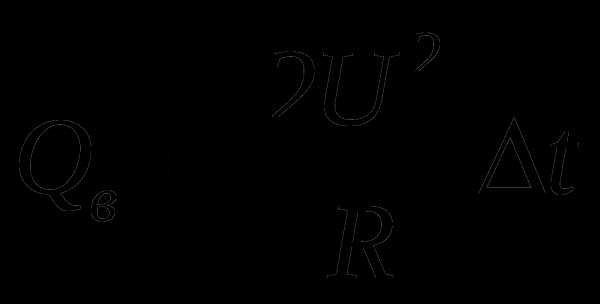. Таким образом: .
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Начерчены все три схемы
3
Найдено решение одного из трех возможных случаев.
2
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
infourok.ru
Физика 9 класс, муниципальный (второй) этап, г. Москва, 2016 год
Задача 1
Массивная горизонтальная плита движется вниз с постоянной скоростью V = 4 м/с. Над плитой на нити неподвижно относительно земли висит мячик. В тот момент, когда расстояние между плитой и мячиком было равно h = 1 м, нить оборвалась.
- Через какое время после обрыва нити мячик догонит плиту?
- На какое максимальное расстояние от плиты удалится мячик после абсолютно упругого отскока?
- Через какое время после первого удара о плиту мячик во второй раз догонит её? Ускорение свободного падения принять равным g = 10 м/с2.
Возможное решение
Направим ось x вниз, совместив начало координат с начальным положением мячика. Тогда законы движения для мячика и плиты, соответственно, запишутся в виде: x1 = g∙t2/2, x2 = h + V∙t.
К моменту времени t1 , когда мячик догонит плиту, их координаты будут равны, значит,
К этому моменту скорость мячика будет равна u =gt1 = 10 м/с. После абсолютно упругого отскока от движущейся плиты у мячика будет скорость u – 2V = 2 м/с, направленная вверх.
Перейдём в систему отсчёта, связанную с плитой. В этой системе отсчёта скорость мячика сразу после абсолютно упругого отскока от плиты равна V′ = 6 м/с и направлена вверх. Тогда максимальное расстояние, на которое удалится мячик от плиты после отскока, равно
Второй раз после первого удара мячик догонит плиту через время
Ответ: t2 = 1,2 с
Критерии оценивания
| Правильно записан закон движения мячика | 1 балл |
| Правильно записан закон движения плиты | 1 балл |
| Найдено время, через которое мячик первый раз догонит плиту (1) | 2 балла |
| Найдено максимальное расстояние, на которое удалится мячик от плиты после отскока (2) | 3 балла |
| Найдено время t2 (3) | 3 балла |
Задача 2
Два кубика, связанные натянутой нитью, находятся в воде (см. рисунок 2.1).
Рисунок 2.1
Верхний кубик со стороной a = 10 см плавает, погрузившись в воду на три четверти своего объёма. Нижний кубик касается дна (вода под него подтекает). Сторона нижнего кубика равна a/2, а его плотность в 2 раза больше, чем у верхнего. Определите, при каких значениях плотности материала верхнего кубика возможно такое состояние системы. Плотность воды ρ0 = 1000 кг/м3, ускорение свободного падения можно принять равным g = 10 м/с2.
Возможное решение
Пусть объём нижнего кубика V, тогда объём верхнего 8V, и в воду погружена его часть объёмом 6V . При малой плотности верхнего кубика система отрывается от дна и нарушается условие сохранения контакта нижнего кубика с дном. Минимально возможное значение плотности ρ1 верхнего кубика соответствует обращению в ноль силы реакции опоры, действующей на нижний кубик (N = 0). Из условия равновесия для всей системы в этом случае следует: ρ0g∙6V + ρ0gV = ρ1g∙8V + 2ρ1gV. Отсюда ρ1 =(7/10)∙ρ0 = 700 кг/м3
При максимально возможной плотности верхнего кубика ρ2 он плавает при объёме погружённой части 6V, не натягивая нить (T=0). Условие плавания верхнего кубика в этом случае имеет вид:
ρ0g∙6V = ρ2g∙8V, откуда
ρ2 = ¾ ∙ρ0 = 750 кг/м3
Окончательно, чтобы выполнялись требования условия задачи, плотность верхнего кубика должна лежать в диапазоне 700 кг/м3 < ρ < 750 кг/м3
Критерии оценивания
| Проведён анализ возможного поведения системы при граничных значениях плотностей | 1 балл |
| Записано условие плавания всей системы в случае N = 0 | 1 балл |
| Получено выражение для минимальной плотности верхнего кубика | 2 балла |
| Найдено численное значение минимальной плотности верхнего кубика | 1 балл |
| Записано условие плавания верхнего кубика в случае T = 0 | 1 балл |
| Получено выражение для максимальной плотности верхнего кубика | 2 балла |
| Найдено численное значение максимальной плотности верхнего кубика | 1 балл |
| Явно указан диапазон допустимых плотностей верхнего кубика | 1 балл |
Задача 3
Система состоит из однородного рычага, однородной рейки и груза массой m = 0,6 кг, соединённых лёгкими нитями, переброшенными через невесомые блоки. При какой массе M рычага возможно равновесие системы? Трения в системе нет. Участки нитей, не лежащие на блоках, вертикальны.
Рисунок 3.1
Возможное решение
Изобразим на рисунке 3.2 силы, действующие на отдельные элементы системы. Из правила моментов для рейки, записанного относительно её центра, следует, что силы натяжения действующих на неё нитей одинаковы – обозначим их модули через T.
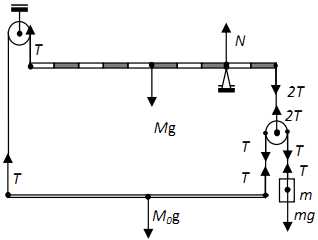
Рисунок 3.2
Из условия равновесия невесомого подвижного блока можно найти силу натяжения нити, действующую на правый конец рычага, – её модуль равен 2T. Тогда из правила моментов для рычага, записанного относительно точки его опоры, получим: T∙8L + 2T∙2L = 3Mg∙L. Отсюда, с учётом условия равновесия груза mg = T, получим: M = 4m = 2,4 кг.
Ответ: M = 2,4 кг.
Критерии оценивания
| Обосновано равенство сил натяжения нитей, действующих на рейку | 2 балла |
| Применено условие невесомости блока | 1 балл |
| Применено условие равновесия груза | 1 балл |
| Записано правило моментов для рычага | 3 балла |
| Получено выражение для массы рычага | 2 балла |
| Получен численный ответ для массы рычага | 1 балл |
Задача 4
Медный кубик со стороной a, брошенный в калориметр с водой, нагрел её от температуры t1 = 20 ⁰С до температуры t2 = 25 ⁰С. Если бы вместо этого кубика в воду бросили медный кубик со стороной 2а и с той же начальной температурой, то вода нагрелась бы до температуры t3 = 44 ⁰С. Какова начальная температура медного кубика? Что больше – масса воды в калориметре или масса медного кубика со стороной a? Потерями теплоты и теплоёмкостью калориметра можно пренебречь. Удельная теплоёмкость меди cм = 380 Дж/(кг·⁰С), удельная теплоёмкость воды св = 4200 Дж/(кг·⁰С).
Возможное решение
Пусть t – начальная температура медного кубика, mв – масса воды, mм – масса кубика со стороной a, тогда 8mм – масса кубика со стороной 2a. Уравнения теплового баланса для первого и второго случаев, соответственно, запишутся в виде:
cмmм(t – t2) = cвmв(t2 – t1),
8cмmм(t – t3) = cвmв(t3 – t1).
Решая данную систему уравнений, получаем:
Из первого уравнения найдём отношение масс медного кубика со стороной a и
воды:
Следовательно, масса кубика больше массы воды.
Критерии оценивания
| Записано уравнение теплового баланса для первого случая | 3 балла |
| Записано уравнение теплового баланса для второго случая | 3 балла |
| Использована связь между массами кубиков | 1 балл |
| Найдена начальная температура медного кубика | 2 балла |
| Показано, что масса кубика со стороной a больше массы воды | 1 балл |
Задача 5
Электрическая цепь представляет собой проволочную сетку состоящую из звеньев, имеющих одинаковые сопротивления R Одно звено заменено на вольтметр, сопротивление которого тоже равно R. К сетке подключён источник напряжения U0 = 10 В так, как показано на рисунке 5.1. Найдите показание вольтметра.
Рисунок 5.1
Возможное решение
Изобразим схематически токи, текущие в звеньях сетки, учитывая её симметрию и закон Ома для участка цепи. Согласно этому закону, силы тока в параллельных звеньях, находящихся под одинаковым напряжением, обратно пропорциональны сопротивлениям этих звеньев. При изображении токов также нужно учитывать закон сохранения электрического заряда для узлов сетки – сумма токов, втекающих в узел, должна быть равна сумме токов, вытекающих из узла. Кроме того, заметим, что в силу симметрии схемы токи через средние вертикальные проводники не текут.
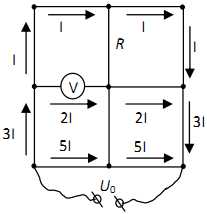
Рисунок 5.2
Если через верхние звенья течёт ток силой I, то через вольтметр течёт ток силой 2I (так как ток I течёт через звенья с общим сопротивлением 4R, а ток 2I – через вольтметр и звено с общим сопротивлением 2R). Ток силой 3I течёт через участок цепи с общим сопротивлением 10R/3 – этот участок включает в себя все элементы, кроме двух нижних горизонтальных звеньев. Это означает, что через два нижних горизонтальных звена с суммарным сопротивлением 2R течёт ток силой 5I. Напряжение на этих двух нижних звеньях равно U0 = 10∙I∙R. Для вольтметра можно записать: UV = 2∙I∙R. Отсюда UV = U0/5 = 2В.
Ответ: UV = 2В.
Критерии оценивания
| Указано на отсутствие протекания токов через средние вертикальные проводники | 1 балл |
| Найдена связь между током, текущим через вольтметр, и токами в других частях цепи | 3 балла |
| Установлена связь между напряжением источника и током, текущим в какой-либо части цепи (например, в нижней ветви) | 2 балла |
| Установлена связь между показанием вольтметра и током, текущим через него | 1 балл |
| Получено выражение для связи напряжения источника и показания вольтметра | 2 балла |
| Получен численный ответ для показания вольтметра | 1 балл |
При решении с помощью построения эквивалентной схемы:
| Указано на отсутствие протекания токов через средние вертикальные проводники | 1 балл |
| Правильно составлена эквивалентная схема | 2 балла |
| Правильно определено полное сопротивление электрической цепи | 3 балла |
| Правильно определён ток, текущий через источник напряжения | 1 балл |
| Определён ток, текущий через вольтметр | 2 балла |
| Получен численный ответ для показания вольтметра | 1 балл |
Общие рекомендации по оцениванию работы
- За каждое верно выполненное действие баллы складываются.
- При арифметической ошибке (в том числе ошибке при переводе единиц измерения) оценка снижается на 1 балл.
- Максимум за 1 задание – 10 баллов.
- Всего за работу – 50 баллов.
olimpiadnye-zadanija.ru
Олимпиада (окт 2015, физика) 9 классы — задачи и ответы
1. Решила баба Яга съесть Иванушку-дурачка. Затопила она печь с КПД 20% и поставила с помощью нечистой силы на огонь огромный медный котелок массой 10 кг, в котором было 80 литров воды, так, чтобы Иванушка полностью поместился в кипящую воду. Сколько березовых дров понадобится, чтобы хотя бы нагреть воду до кипения? Начальная температура воды 20°С. Удельная теплота сгорания березовых дров 1•107 Дж/кг, удельная теплоемкость воды 4200 Дж/(кг•°С), удельная теплоемкость меди 400 Дж/(кг•°С).
Ответ выразите в килограммах, округлив до десятых.
Ответ: 13,6
2. Лягушонок, Цыпленок, Мышонок, Муравей и Жучок построили кораблик из сказочной ореховой скорлупки m = 5 г. Объем скорлупки при полном погружении в воду (так, чтобы вода не заливалась через скорлупку внутрь) 20 см3. Какая общая масса должна быть у строителей кораблика, чтобы он не утонул? Плотность воды 1000 кг/м3.
Ответ выразить в граммах.
Ответ: 15
3. Леший массой 50 кг и Кикимора болотная массой 40 кг решили покачаться на бревне массой 60 кг и длиной 3 м. В какой точке, считая от Лешего, им надо подпереть бревно, чтобы они могли оба находиться в воздухе одновременно сохраняя равновесие?
Ответ выразить в метрах.
Ответ: 1,4
4. Решил Наф-Наф провести к себе в домик свет. Сначала он решил подключиться к напряжению 110 В, но потом подумал и решил, что при постоянной мощности, в целях экономии на потерях, надо подключаться к 220 В. Во сколько раз мощность потерь станет меньше?
Ответ: 4
5. Петух, убегая от лисы к своему домику, сначала бежал равноускоренно, а затем равномерно со скоростью 18 км/ч. Если расстояние до спасительного домика было 400 м, а бежал он 90 с, то с каким ускорением ему надо было бежать в начале, чтобы убежать от лисы?
Ответ выразите в см/с2.
Ответ: 25
www.olymp344.ru
Школьная олимпиада по физике 9, 10 классы
Просмотр содержимого документа
«Олим9Р»
9 класс
Задача 1.
Два человека одновременно вступают на эскалатор с противоположных сторон и движутся навстречу друг другу с одинаковыми скоростями относительно эскалатора u = 2 м/с. На каком расстоянии от входа на эскалатор они встретятся? Длина эскалатора l = 100 м, скорость эскалатора относительно земли v = 1,5 м/с.
Решение
1. Выполнение рисунка и определение скоростей в системе отсчёта «Земля».
СО «Эскалатор» СО «Земля» Момент встречи
2. Запись уравнений координат и определение координаты точки встречи.
3. Расчёт.
= 87,5 м.
Задача 2.
Мальчик вращает камень, привязанный к верёвке длиной l = 0,8 м, в вертикальной плоскости с частотой ν = 4 с-1. В тот момент, когда верёвка была расположена горизонтально, она оборвалась. На какую высоту h взлетит камень? Сопротивление воздуха не учитывать.
Решение
Поскольку камень, оторвавшись, летит вверх, значит, в момент обрыва верёвки его линейная скорость направлена вверх по касательной к окружности, по которой он двигался до того, как оторвался. Это линейная скорость v0 является начальной скоростью его равнозамедленного движения вверх с ускорением свободного падения, взятым со знаком «минус». В высшей точке взлёта камня на высоту h его конечная скорость становится равной нулю. Поскольку речь идёт о начальной и конечной скоростях камня, его ускорении и высоте взлёта, то для решения задачи удобно воспользоваться формулой
Линейную скорость камня определим через частоту, поскольку частота вращения камня ν нам известна, а радиус окружности R, по которой он движется, равен длине верёвки l : v0 = 2πRν, где R = l, поэтому v0 = 2πlν. (2)
Подставив (2) в (1), мы решим задачу в общем виде:
Произведём вычисления:
Задача 3.
В воду массой 1 кг при 20 0С брошен комок мокрого снега массой 250 г. Когда весь снег растаял, общая температура стала равной 5 0С. Определите количество воды в комке снега. Удельная теплота плавления снега 334 кДж/кг, удельная теплоёмкость воды 4200 Дж/(кг ∙ 0С).
Решение
Так как снег мокрый, то температура смеси «снег + вода (в комке снега)» будет иметь температуру 0 0С в течение всего процесса плавления снега.
Тогда:
Задача 4.
Два студента (не физики) А и В, живущие в соседних комнатах общежития, решили сэкономить, соединив свои потолочные светильники последовательно. Они договорились, что установят лампочки по 100 Вт в своих комнатах и будут оплачивать равные доли счёта за электричество. Однако каждый решил попробовать получить лучшее освещение за счёт другого: студент А установил лампочку в 200 Вт, а студент В – лампочку в 50 Вт. Какой студент впоследствии провалит экзамены за очередной семестр? Кто выиграет в освещённости комнаты, а кто – в оплате? Считать время работы ламп одинаковым, сопротивление ламп постоянным.
Решение
Просмотр содержимого документа
«Олимп10»
Просмотр содержимого документа
«Олимп10Р»
10 класс
Задача 1.
Два автомобиля движутся с постоянными скоростями по двум взаимно перпендикулярным улицам. Скорость первого автомобиля в два раза превышает скорость второго, которая равна v2 = 36 км/ч. В тот момент, когда второй автомобиль находился на перекрёстке, первый был от него на расстоянии l = 200 м. Через какой промежуток времени после этого расстояние между автомобилями станет наименьшим?
Решение
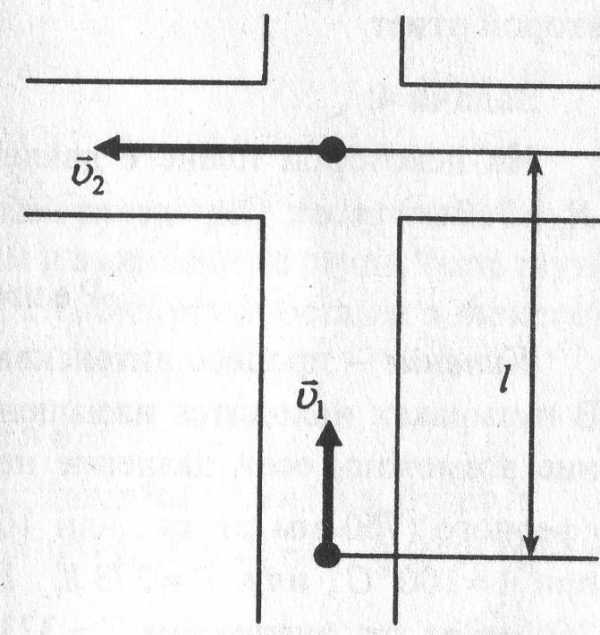
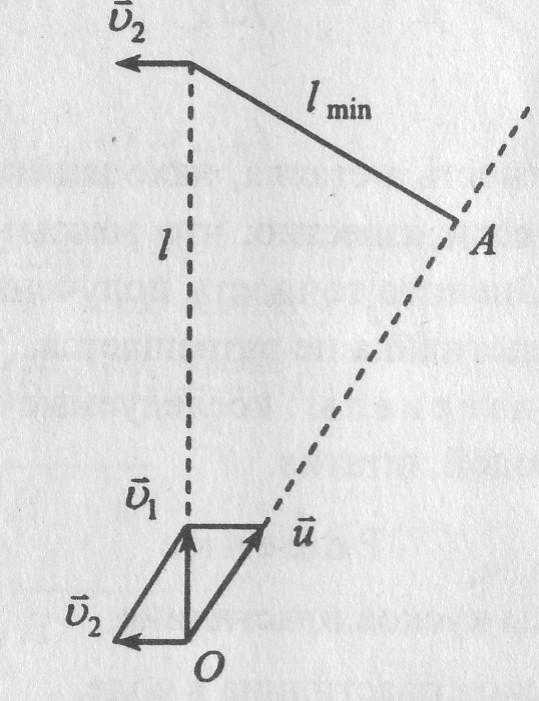
Задача 2.
В сосуде с водой плавает металлическая чашка. Как изменится уровень воды в сосуде, если, наклонив чашку, потопить её в воде? Почему?
Решение
Уровень воды в сосуде уменьшится. Это можно доказать следующим образом.
Уровень воды зависит от объёма подводной части. Когда чашка утонет, объём подводной части уменьшится.
Обозначим:
V1 – объём подводной части чашки;
V2 – объём надводной части чашки;
Vв – объём воздуха внутри чашки, погружённой в воду.
Условие плавания:
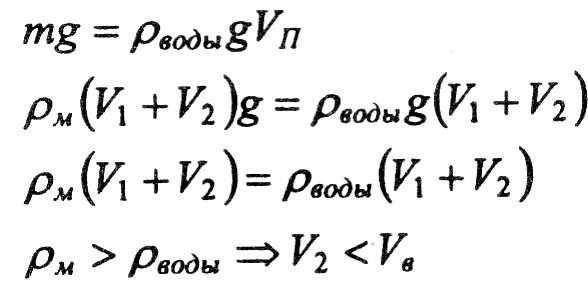
Задача 3.
Ящик с песком массой M = 10 кг стоит на гладкой горизонтальной плоскости. Он соединён с вертикальной стеной пружиной, жёсткость которой k = 200 Н/м. На сколько сожмётся пружина, если пуля, летящая горизонтально со скорость v = 500 м/с, попадёт в ящик и застрянет в нём? Масса пули m = 0,01 кг.
Решение
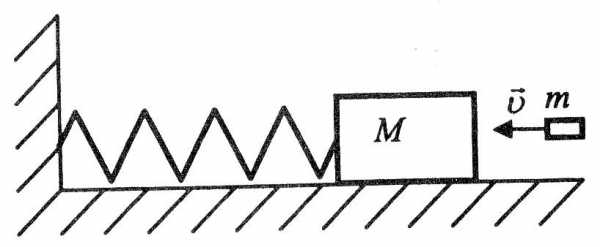
Задача 4.
Электрическим кипятильником мощностью W = 500 Вт нагревают воду в кастрюле. За две минуты температура воды увеличилась от 85 0С до 90 0С. Затем кипятильник выключили, и за одну минуту температура воды упала на один градус. Сколько воды находится в кастрюле? Удельная теплоёмкость воды равна 4200 Дж/(кг∙ 0С).
Решение
Задача 5.
Летом при температуре в помещении t1 = 27 0C промышленный морозильник при работе на полную мощность поддерживал в камере температуру t2 = — 23 0С. Зимой температура в помещении упала до значения t3 = 7 0С. Из-за отказа реле агрегат вновь заработал на полную мощность. Какой при этом стала температура tx в камере? Считайте агрегат идеальной машиной.
Решение
Просмотр содержимого документа
«Олимп9»
multiurok.ru
