Объем и площадь – Площадь поверхности и объем геометрических тел. Прямые призмы. Правильные пирамиды. Круговые цилиндры. Круговые конусы. Шар и его части. Примерно 8 класс (14 лет)

Все формулы объема геометрических тел

Все формулы объема геометрических тел

Все формулы объема геометрических тел

---

 

 

 

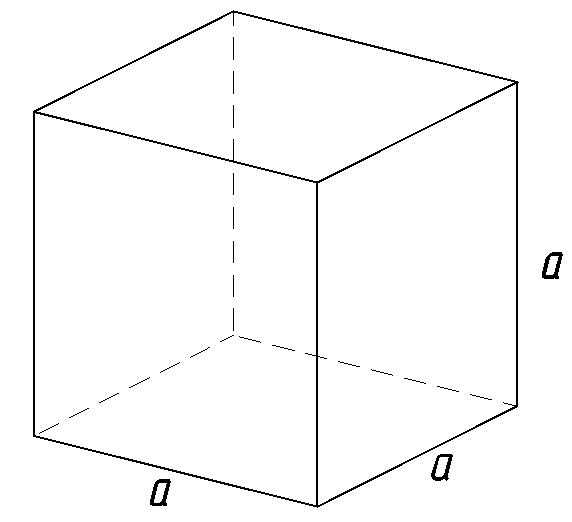
a — сторона куба

 

 

 

Формула объема куба, (V ):

 

---

---

 

 

 

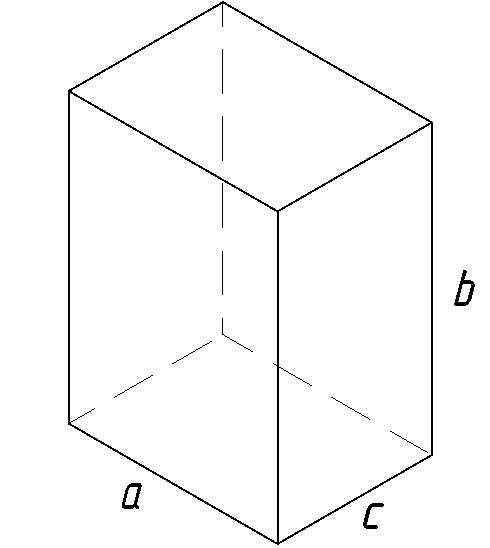
a, b, c— стороны параллелепипеда

 

 

 

Формула объема параллелепипеда, (V):

 

---

 

 

R— радиус шара

π ≈ 3,14

 

 

 

Объем шара, (V):

 

---

---

 

h— высота шарового слоя

R— радиус нижнего основания

r— радиус верхнего основания

π ≈ 3,14

 

 

Объем шарового слоя, (V):

 

---

---

 

 

h — высота сегмента

R — радиус шара

π ≈ 3,14

 

 

Объем шарового сектора, (V):

---

---

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R — радиус шара

h — высота сегмента

π ≈ 3,14

 

 

 

Объем шарового сегмента, (V):

 

 

 

---

---

 

h— высота цилиндра

r— радиус основания

π ≈ 3,14

 

 

 

Объем цилиндра, (V):

 

 

 

---

---

 

 

H-

высота конуса

R- радиус основания

π ≈ 3,14

 

Объем конуса, (V):

 

 

---

---

 

R- радиус нижнего основания

r- радиус верхнего основания

h- высота конуса

π ≈ 3,14

 

Объем усеченного конуса,  (V ):

---

---

 

 

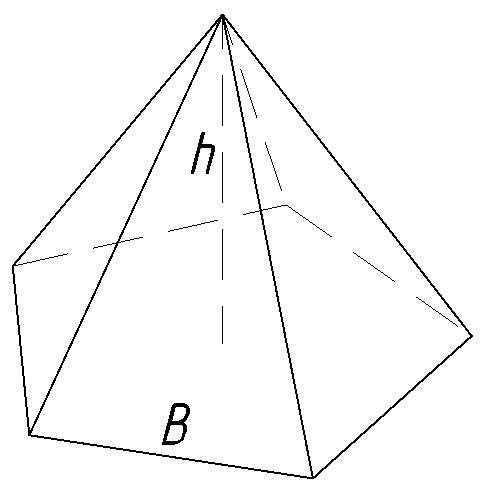
h — высота пирамиды

S — площадь основания ABCDE

 

 

 

Объем пирамиды, (V):

 

---

---

 

h — высота пирамиды

S_ниж — площадь нижнего основания, ABCDE

S_верх — площадь верхнего основания, abcde

 

 

Объем усеченной пирамиды, (V):

 

---

---

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

 

 

Объем правильной пирамиды, (V):

 

---

---

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

h — высота пирамиды

a — сторона основания

 

 

 

Объем правильной треугольной пирамиды, (V):

 

---

---

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

h — высота пирамиды

a — сторона основания

 

 

 

Объем правильной четырехугольной пирамиды, (V):

 

 

---

---

 

Правильный тетраэдр- пирамида у которой все грани, равносторонние треугольники.

а -ребро тетраэдра

 

 

 

 

Объем правильного тетраэдра (V):

 

 

---

---

© 2016 Все права защищены.

При использовании материалов сайта ссылка на источник обязательна.

zdesformula.ru

Формулы объема геометрических фигур.

Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба

где

V

— объем куба,

a

— длина грани куба.

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы

где

V

— объем призмы,

S_o

— площадь основания призмы,

h

— высота призмы.

Объем параллелепипеда

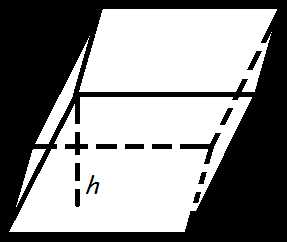
Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда

где

V

— объем параллелепипеда,

S_o

— площадь основания,

h

— длина высоты.

Объем прямоугольного параллелепипеда

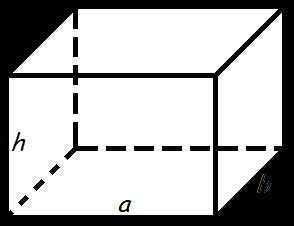
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда

где

V

— объем прямоугольного параллелепипеда,

a

— длина,

b

— ширина,

h

— высота.

Объем пирамиды

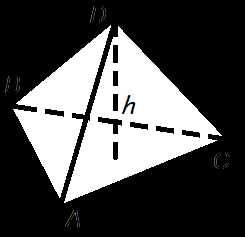
Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды

где

V

— объем пирамиды,

S_o

— площадь основания пирамиды,

h

— длина высоты пирамиды.

Объем правильного тетраэдра

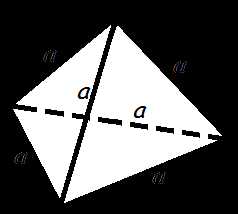
Формула объема правильного тетраэдра

где

V

— объем правильного тетраэдра,

a

— длина ребра правильного тетраэдра.

Объем цилиндра

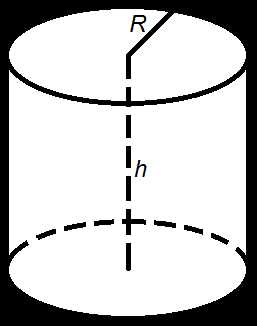
Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра
• V =

  π R

  ²

  h

• V =

  S_o h

где

V

— объем цилиндра,

S_o

— площадь основания цилиндра,

R

— радиус цилиндра,

h

— высота цилиндра,

π = 3.141592

.

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса

где

V

— объем конуса,

S_o

— площадь основания конуса,

R

— радиус основания конуса,

h

— высота конуса,

π = 3.141592

.

Объем шара

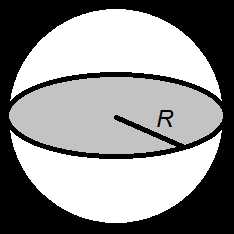
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.

Формула объема шара

где

V

— объем шара,

R

— радиус шара,

π = 3.141592

.

Добавить комментарий

o-math.com

Объем и площадь шарового слоя и шарового пояса.

Объем и площадь шарового слоя и шарового пояса.

Объем шара равен 4/3π³ , а площадь сферы равна 4πr².

Шаровой слой — это часть шара между двумя параллельными плоскостями. На рисунке выше PQRS — шаровой слой.

 

Шаровой пояс — это сферическая поверхность шарового слоя.

Площадь шарового пояса на рисунке выше S=2 πhr;

Объем шарового слоя V=(πh/6)*(h²+3r₁²+3r₂²)

 

 

 

 

Пример1. Определение объема шарового слоя шара.

Определить объем шарового слоя шара с диаметром 50 см, если верхний и нижний диаметры слоя есть 25 и 40 см, а его высота 7,2 см.

Решение:

Как было сказано выше, объем шарового слоя

V=(πh/6)*(h²+3r₁²+3r₂²),

где h=7,2 см, r₁= 25/2=12,5 см, r₂=40/2=20 см

Следовательно, объем шарового слоя равен

V=(7,2π/6)*(7,2²+3*12,5²+3*20²)=6483,18 см² .

 

Пример 2. Определение площади шарового пояса.

Определить площадь шарового пояса из предыдущего примера.

Решение:

Площадь шарового пояса S=2πrh (как было определено выше), где радиус сферы r=50/2=25 см, а h=7,2 см.

Следовательно, площадь шарового пояса равна

S=2π*25*7,2=1130,4 см²

 

Пример 3. Определение объема заполнения сферического резервуара по уровню.

Сферический резервуар наполнен жидкостью до высоты 30 см. Определить объем жидкости в резервуаре (1л=1000 см³), если его внутренний диаметр равен 40 см.

Жидкость представлена в виде заштрихованной области в показанном на рис. ниже сечении.

Объем жидкости включает полусферу и шаровой пояс высотой 6 см.

Следовательно, объем жидкости есть V=(2/3)*πr³+(πh/6)*(h²+ 3r₁²+3r₂²), где

r₂=40/2=20 см и r₁=(20²-6²)^1/2=19,1 см

Объем жидкости V=2/3 π *20³+(6π)/6*(6²+3*19,1²+3*20²)=24064,22 см³

Поскольку 1 литр =1000 см³, то количество литров жидкости равно

24064,22/1000=24,06422 л.

tehtab.ru

Площади и объемы

Площади

История нахождения площадей фигур начинается еще с древнего Вавилона. Уже тогда вычисляли площади прямоугольника, а древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.

В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.

Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.

Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.

Формула площади прямоугольника

Рассмотрим фигуру (рис. 1), которая состоит из $8$ квадратов со сторонами по $1$ см. Площадь одного квадрата со стороной $1$ см называют сантиметром квадратным и записывают $1\ см^2$.

Площадь данной фигуры (рис. 1) будет равна $8\ см^2$.

Площадь фигуры, которую можно разбить на несколько квадратов со стороной $1\ см$ (например, $p$), будет равна $p\ см^2$.

Другими словами, площадь фигуры будет равна стольким $см^2$, на сколько квадратов со стороной $1\ см$ можно разбить эту фигуру.

Рассмотрим прямоугольник (рис. 2), который состоит из $3$ полос, каждая из которых разбита на $5$ квадратов со стороной $1\ см$. весь прямоугольник состоит из $5\cdot 3=15$ таких квадратов, и его площадь равна $15\ см^2$.

Рисунок 1.

Рисунок 2.

Площадь фигур принято обозначать буквой $S$.

Для нахождения площади прямоугольника нужно его длину умножить на ширину.

Если обозначить буквой $a$ его длину, а буквой $b$ — ширину, то формула площади прямоугольника будет иметь вид:

Определение 1

Фигуры называют равными, если при наложении их одна на другую фигуры совпадут. Равные фигуры имеют равные площади и равные периметры.

Площадь фигуры можно найти как сумму площадей ее частей.

Пример 1

Например, на рисунке $3$ прямоугольник $ABCD$ разбит на две части линией $KLMN$. Площадь одной части равна $12\ см^2$, а другой — $9\ см^2$. Тогда площадь прямоугольника $ABCD$ будет равна $12\ см^2+9\ см^2=21\ см^2$. Найдем площадь прямоугольника по формуле:

\[S=a\cdot b=3\cdot 7=21\ см^2.\]

Как видим, площади, найденные обоими способами, равны.

Рисунок 3.

Рисунок 4.

Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.

Определение 2

Прямоугольник с равными сторонами называется квадратом.

Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:

\[S=a\cdot a=a^2.\]

Отсюда и название квадрат числа $a$.

Пример 2

Например, если сторона квадрата равна $5$ см, то его площадь:

\[S=a^2=5^2\ см^2=25\ см^2.\]

Объемы

С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.

Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.

Объем прямоугольного параллелепипеда

Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.

Рисунок 5.

Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.

Объем измеряется с помощью следующих единиц:

$мм^3$ — миллиметр кубический,

$см^3$ — сантиметр кубический,

$дм^3$ — дециметр кубический,

$м^3$ — метр кубический,

$км^3$ — километр кубический.

Пример 3

Например, сантиметр кубический — это объем куба с ребром $1\ см$ (рис.~6).

Замечание 1

Дециметр кубический еще называют литром.

\[1\ л=1\ дм^3.\]

На рисунке $7$ фигура состоит из $4$ кубиков с ребром $1\ см$. объем такой фигуры равен $4\ см^3$.

Рисунок 6.

Рисунок 7.

Рассмотрим прямоугольный параллелепипед длиной $4$ см, шириной $3$ см и высотой $2$ см (рис. 8, а). Разделим его на $2$ слоя толщиной $1$ см (рис. 8, б).

Разделим каждый из слоев на $3$ столбика длиной $4$ см (рис. 8, в), а каждый столбик — на $4$ кубика с ребром $1$ см (рис. 8, г).

Рисунок 8.

Объем каждого кубика равен $1\ см^3$, объем каждого столбика — $4\cdot 1\ см^3=4\ см^3$, объем каждого слоя — $3\cdot 4\ см^3$. Тогда объем всего прямоугольного параллелепипеда — $2\cdot \left(4\cdot 3\right)\ см^3=24\ см^3$.

Таким образом, для вычисления объема прямоугольного параллелепипеда нужно его длину умножить на ширину и на высоту.

Объем фигуры принято обозначать буквой $V$.

Формула объема прямоугольного параллелепипеда:

Определение 3

Куб — прямоугольный параллелепипед с равными ребрами.

Если ребро куба равно $a$, то формула объема куба будет иметь вид:

\[V=a\cdot a\cdot a=a^3.\]

Отсюда и название куб числа $a$.

spravochnick.ru

Расчет объёмов и площадей поверхностей простых фигур онлайн

Куб

Площадь поверхности, м2

Раcчет

Прямоугольный параллелепипед

Площадь поверхности, м2

Раcчет

Правильная пирамида

Усеченная правильная пирамида

Клин (основание — прямоугольник, боковые грани — равнобедренные треугольники и трапеции)

Усеченный клин (основания — прямоугльники, боковые грани не пересекаются в одной точке)

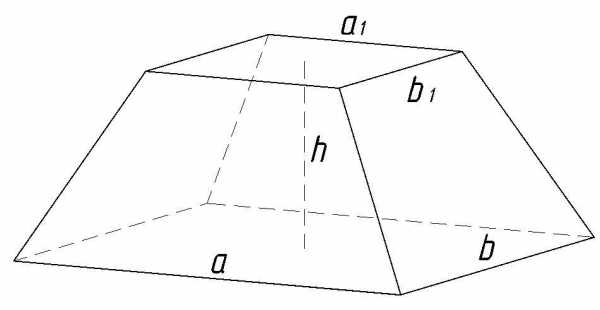
Цилиндр

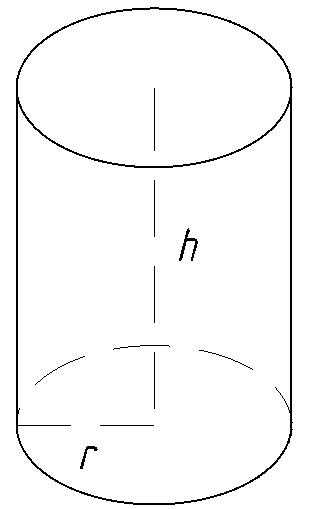
Площадь поверхности, м2

Раcчет

Кососрезанный цилиндр

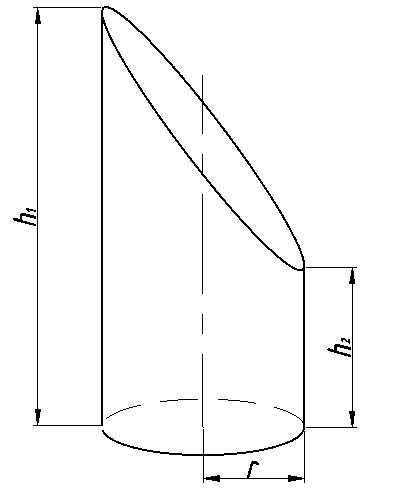
Площадь полной поверхности, м2

Площадь кривой поверхности, м2

Раcчет

Полый цилиндр

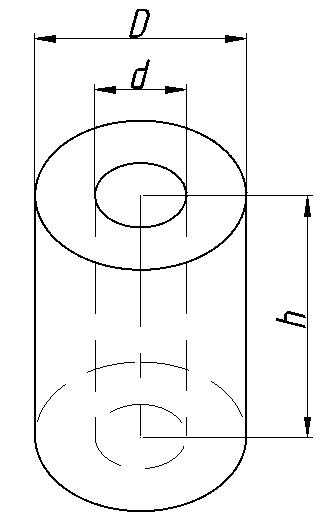
Конус

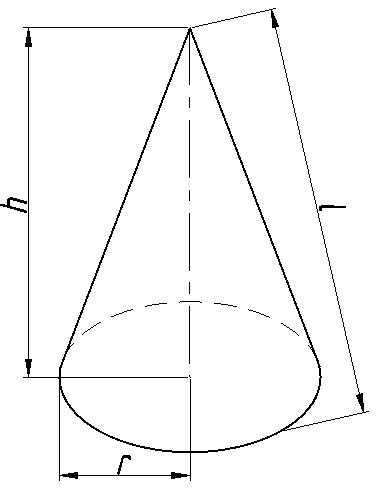
Площадь поверхности, м2

Раcчет

Усечённый конус

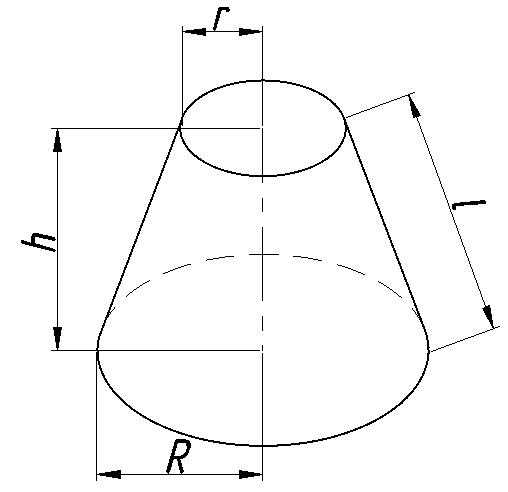
Площадь поверхности, м2

Раcчет

Шар

Площадь поверхности, м2

Раcчет

perekos.net

Шар и его части. Объем, площадь поверхности. |

Рассмотрим понятие таких геометрических тел как шар и его части:

• шаровой сегмент;
• шаровой сектор;
• шаровой слой.

Также представим формулы для вычисления объемов и площадей поверхностей шара и его частей.

Об элементах шара и понятии “сфера” будет опубликовано в отдельной статье.

Шар. 

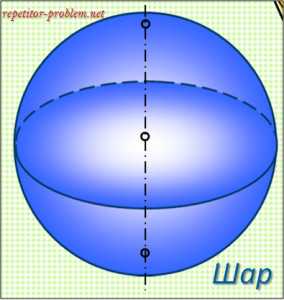Определение.

Шаром называется геометрическое тело, состоящее из точек пространства, находящихся от центра на расстоянии, не больше заданного.

Площадь поверхности шара вычисляется по формуле:

S_пов. = 4*π*R² = π*D² , где R –  радиус шара,   D – диаметр шара.

В школьной программе объем шара представлен одной формулой:

V = 4/3* π*R³ , где R –  радиус шара.

Учитывая, что диаметр шара вдвое больше радиуса шара, имеем формулу объема шара такую:

V = 1/6 * π* D³, где D – диаметр шара.

Но объем шара может быть задан и другими соотношениями . Опишем их ниже.

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара:

V = 1/3 R*S, где R –  радиус шара.

А вот теорема Архимеда:

Объем шара в 1,5 раза меньше объема описанного вокруг него цилиндра, а поверхность шара – в 1,5 раза меньше полной поверхности того же цилиндра.

V = 2/3 * V_ц., где V_ц – объем цилиндра.

S_пов. = 2/3 * S_{пов. ц.} , где S_{пов. ц.} – полная поверхность цилиндра.

Части шара.

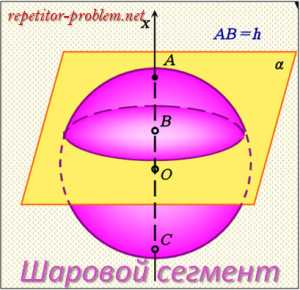Шаровой сегмент.

Определение.

Шаровой сегмент – это  часть шара, отсекаемая от нее плоскостью.

Кривая поверхность шарового сегмента равна произведению его высоты на длину окружности большого круга шара:

S_сегм. = 2πR* h, где R –  радиус шара, h – высота сегмента.

Еще формула площади поверхности сегмента:

S_сегм. = π*(r² + h²), где r – радиус основания сегмента, h – высота сегмента.

Объем шарового сегмента вычисляется по формуле:

V = π* h² *(R – 1/3*h) = 1/6*π*h(h² + 3r²), где r – радиус основания сегмента, h – высота сегмента.

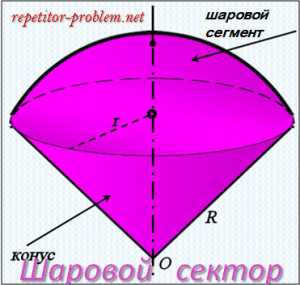Шаровой сектор.

Определение.

Шаровой сектор – часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной – центр шара.

Согласно определению формула площади поверхности шарового сектора выглядит так:

S_{шар. сектор} = S_{бок.конус.} + S_{шар. сегм.}

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезанная сектором часть шаровой поверхности (S), а высота равна радиусу шара (R):

V = 1/3*R*S = 2/3*π*R²*h, где h – высота шарового сегмента, принадлежащая шаровому сектору.

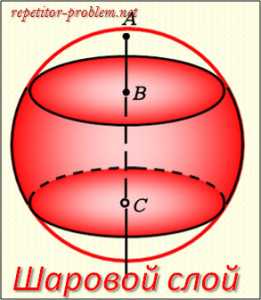Шаровой слой.

Определение.

Часть шара, заключенная между двумя секущими параллельными плоскостями, называется шаровым слоем, а кривая поверхность шарового слоя называется шаровым поясом (или зоной).

S_{шар. слоя} = h*2πR , где R –  радиус шара, h – высота шарового слоя.

Объем шарового слоя:

V = 1/6 * π* h³ +  1/2 * π*(r₁² + r₂²)*h, где r_1, r₂  – радиусы оснований шарового слоя, h – высота шарового слоя.

repetitor-problem.net

Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.

Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.

Представьте себе куб с длиной ребра 1 метр (1 сантиметр, 1 фут, 1 дюйм или 1 «чего Вам угодно»), далее будет метр — для простоты. Объем этого куба равен 1 м³. Каждая сторона имеет площадь1 м² , а вся площадь поверхности этого кубика равна 6 м² — сторон-то шесть. Отношение объема к площади поверхности равно 1:6 = 1/6 (сейчас и далее — без учета размерности).

 
Тепрь представьте себе куб со стороной 3 м.Объем этого куба равен 27 м³ (3х3х3). Каждая сторона имеет площадь 9 м² , а вся площадь поверхности этого кубика равна 54 м². Отношение объема к площади поверхности равно 27:54 = 1/2 = 3/6.

То есть, при росте линейного размера в 3 раза площадь поверхности выросла в 9 раз, но объем вырос в 27 раз. Отношение объема к площади поверхности выросло в 3 раза.

В таблице ниже приведены расчеты для кубов при пошаговом удвоении линейного размера:

Таблица. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.

Линейный размер (м)	Площадь поврхности (м2)	Объем (м3)	Отношение объема к площади поверхности
1	6,00	1,00	0,17
2	24,00	8,00	0,33
4	96,00	64,00	0,67
8	384,00	512,00	1,33
16	1 536,00	4 096,00	2,67
32	6 144,00	32 768,00	5,33
64	24 576,00	262 144,00	10,67
128	98 304,00	2 097 152,00	21,33
256	393 216,00	16 777 216,00	42,67
512	1 572 864,00	134 217 728,00	85,33

При росте линейного размера объем возрастает намного быстрее, чем площадь поверхности тела, посколюку объем пропорционален кубу линейного размера, а площадь — квадрату. Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).

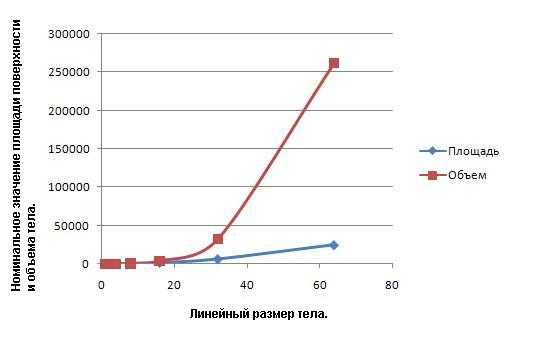
Рисунок. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.

 

Некоторые житейские примеры важности рассматриваемого факта.

1) Теплоотдача пропорциональна площади поверхности. Теплоемкость — объему тела. Из этого факта напрямую следует, что более крупное здание (той же формы) будет дольше отдавать накопленное за световой день тепло (или нагреваться днем) и потребует меньше энергии на единицу полезной площади — ! полезная площадь прямо пропорциональна внутреннему объему ! — на отопление (кондиционирование).

2) Масса (вес) пропорциональна объему опоры. Нагрузка на грунт — площади поверхности. Из этого факта напрямую следует, что для опоры любой формы существует размер, начиная с которого (при сохранении формы) она уйдет в любой грунт.

3) Ребенок имеет совершенно другое соотношение площадь/объем, чем взрослый человек. Поэтому риски переохлаждения или получения теплового удара для ребенка несоизмеримо выше (что, конечно, отчасти компенсируется другой скоростью обменных процессов у детей).

tehtab.ru