Объемы и площади поверхностей усеченных пирамид и конусов.
Объемы и площади поверхностей усеченных пирамид и конусов.Усеченная пирамида или конус — это часть, остающаяся после отсечения вершины плоскостью, параллельной основанию.
Объем усеченной пирамиды или конуса равен объему целой пирамиды или конуса минус объем отсеченной вершины.
Площадь боковой поверхности усеченной пирамиды или конуса равна площади поверхности целой пирамиды или конуса. минус площадь боковой поверхности отсеченной вершины. Если необходимо найти общую площадь усеченной фигуры, тогда площадь двух параллельных оснований добавляется к площади боковой поверхности.
Существует и другой метод определения объема и площади поверхности усеченного конуса:
V=1/3 π h(R2+Rr+r2),
площадь боковой поверхности конуса S=π l(R+r),
общая площадь поверхности
Пример1. Определение площади необходимого для изготовления материала для абажура. (Расчет площади боковой поверхности конуса).
Абажур имеет форму усеченного конуса. Высота абажура равна 50 см, нижний и верхний диаметры — 40 и 20 см соответственно.
Определить с точностью до 3х значащих цифр площадь материала, необходимого для изготовления абажура.
Как было определено выше, площадь боковой поверхности усеченного конуса S=π l(R+r).
Поскольку верхний и нижний диаметры усеченного конуса равны 40 и 20 см, то из рис. выше находим r=10 см, R=20 см и
l=(50 2+102)1/2=50,99 согласно теореме Пифагора,
Следовательно, площадь боковой поверхности конуса равна S=π 50,99(20+10)=4803,258 см2 , т.е. площадь необходимого для изготовления абажура материала равняется 4800 см2 с точностью до 3х значащих цифр, хотя, конечно, сколько на самом деле уйдет материала зависит от кроя.
Пример 2. Определение объема цилидра, увенчанного усеченным конусом.
Башенный охладитель имеет форму цилиндра, увенчанного усеченным конусом, как показано на рис. ниже. Определить объем воздушного пространства в башне, если 40 % объема занято трубами и другими структурами.
Объем цилиндрической части
V=π R2h=π(27/2)2*14=8011,71 м3
Объем усеченного конуса
V=1/3 π h(R2+Rr+r2), где
h=34-14=20 м, R=27/2=13,5 м и r=14/2=7 м.
Т.к. R=27/2=13,5 м и r=14/2=7 м.
Следовательно, объем усеченного конуса
V=1/3 π 20(13,52+13,5*7+72)=6819,03 м3
Общий объем башенного охладителя
Если 40% объема занято, объем воздушного пространства V=0,6*14830,74=8898,44 м3
tehtab.ru
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.Объемы и площади поверхностей правильных тел.
Общая информация об объемах и площадях поверхностей правильных тел приведена в таблице.
Пример 1.Расчет объема прямоугольного бака.
Бак для воды имеет форму прямоугольного параллелепипеда длиной 1 м, шириной 65 см и высотой 30 см. Определить объем бака в м3, см3, литрах
Решение:
Объем прямоугольного параллелепипеда равен l*b*h
а)Vбака=1*0.65*03=0.195 м3
б) 1 м 315000 мм2=315000/100=3150 см2
1 м3=106 см3, значит, 0.195 м3=0.195*106=195000 см3
в) 1 литр=1000 см3, значит 195000 см3=195 л
Пример 2. Расчет объема и площади поверхности трапецеидальной призмы.
Вычислить объем и общую площадь поверхности призмы, показанной на рис.
Тело, показанное на рис. — это трапецеидальная призма.
Так как объем = площадь поперечного сечения * высота, то
V=1/2*(10+5)*4*20=30*20=600 cм3
Так как площадь поверхности вычисляется сложением суммы площадей двух трапеций и суммы площадей четырех прямоугольников, то
S=(2*30)+3(5*20)+(10*20)=560 см2
Пример 3. Расчет объема и общей площади поверхности правильной пирамиды.
Определить объем и общую площадь поверхности правильной пирамиды с квадратным основанием, показанной на рис., если ее высота равна 15 см.
Решение:
Так как объем пирамиды =1/3(площадь основания)*высота, то
V=1/3*(5*5)*15=125 см3
Общая площадь поверхности включает площадь квадратного основания и площади четырех равных треугольников.
Площадь треугольника ADE=1/2*основание*(высота грани).
Высоту грани АС можно найти по теореме Пифагора из треугольника АВС, где АВ=15 см, ВС=1/2*3=1.5 см, и АС2=AB2+BC2=225+2.25=227.25
AC=15.07 cм
Следовательно, площадь треугольника ADE
SADE=1/2*3*15.07=22.605 см2
Общая площадь пирамиды S=(3*3)+4*22.605=99.42 cм2.
Пример 4. Расчет объема и общей площади поверхности конуса.
Определить объем и общую площадь поверхности конуса радиусом 4 см и высотой 10 см.
Объем конуса V=1/3πr2h =1/3*π42*10=167.5см3
Общая площадь поверхности равна сумме площади конической поверхности и площади основания, т.е. S=πrl+πr2
Из рисунка видно, что длину образующей l можно найти по теореме Пифагора.
l2=102+42=116 см
l=10,8 cм
Следовательно, общая площадь поверхности равна
S=π*4*10.8)+(π*42=185.89 cм2
Пример 5. Расчет объема и общей площади поверхности призмы.
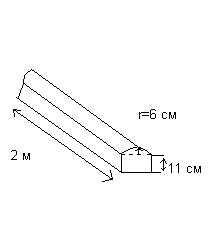
На рис. показан деревянный профиль. Найдем: а) его объем в м3
б) общую площадь его поверхности
Профиль представляет собой призму, поперечное сечение которой состоит из прямоугольника и полукруга. Поскольку радиус полукруга равен 6 см, диаметр равен 12 см.
Тогда размеры прямоугольника 12*11 см
Площадь поперечного сечения S
Поскольку объем деревянной детали равен произведению площади поперечного сечения на длину, то
a) V=188,52*200=37704 см3=37704 см3/106= 0,037704 м3
б) Общая площадь включает два торца (площадь каждого 188,52 см2), три прямоугольника и криволинейную поверхность (которая представляет собой полуцилиндр). Следовательно, общая площадь поверхности
S=(2*188,52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377,04+4400+2400+3768=10945,04 см2=1,094504 м2.
Пример 6. Расчет объема и общей площади поверхности сложного бойлера.
Бойлер состоит из цилиндрической секции длиной 9 м и диаметром 5 м, к одному концу которой присоединена полусферическая секция диаметром 5 м, а к другому концу — коническая секция высотой 3 м и диаметром основания 5 м. Вычислить объем бойлера и общую площадь его поверхности.
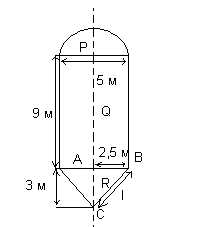
Vполусферы P =2/3*πr3 =2/3*π*2,53 =10,42 π м3
V цилиндра Q = π r2h=π*2,52*9=56,25 π м3
V конуса R =1/3 π r2=1/3*π*2,52*3=6,25π м 3
Общий объем бойлера V= 10,42 π м3+56,25 π м3+6,25π м 3=72,92π=228,97 м 3
S полусферы P. =2*(πr2)=2*π*2,52=12,5π м2
S бок. поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м2 (т.к. этот цилиндр представляет собой трубу без оснований)
Длина образующей конуса l рассчитывается по теореме Пифагора из треугольника ABC;
значит
l=(32+2,52)1/2=3,9 м.
S конуса R. =πrl=π*2,5*3,9=9,75 π м 2
Общая площадь поверхности бойлера
S= 12,5π+45π+9,75 π=67,25π=211,2 м 2
tehtab.ru
Формулы перевода градусов в радианы, длин, площадей и объемов основных геометрических фигур
Во первых, под числом «пи» Администрация Сайта понимает величину близкую к:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… (100 знаков после запятой)
ФОРМУЛЫ ПЕРЕВОДА
Перевод радиан в градусы
Зная, что углу 2 * пи соответствует угол 360 градусов:
Ad = Ar * 180 / пи
Где Ad — угол в градусах, Ar — угол в радианах.
Перевод градусов в радианы
Зная, что углу 360 градусов соответствует угол 2 * пи:
Ar = Ad * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.
ФОРМУЛЫ РАСЧЕТА ДЛИНЫ
Длина окружности
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.
Длина дуги окружности
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах.
Так, для окружности, A = 2*пи (360 градусов), получим L = 2*пи*R.
ФОРМУЛЫ РАСЧЕТА ПЛОЩАДИ
Площадь треугольника.
Формула Герона.
S = (p * (p-a) * (p-b) * (p-c) )1/2.
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.
Площадь круга
S = пи * R2
Где S — площадь круга, R — радиус круга.
Площадь сектора
S = (Ld * R)/2 = (A * R2)/2
Где S — площадь сектора, R — радиус круга, Ld — длина дуги.
Площадь поверхности шара (сферы)
S = 4 * пи * R
Где S — площадь поверхности шара, R — радиус шара.
Площадь боковой поверхности цилиндра
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь полной поверхности цилиндра
S = 2 * пи * R * H + 2 * пи * R2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь боковой поверхности конуса
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Площадь полной поверхности конуса
S = пи * R * L + пи * R2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
ФОРМУЛЫ РАСЧЕТА ОБЪЕМА
Объем шара
V = 4 / 3 * пи * R3
Где V — объем шара, R — радиус шара.
Объем цилиндра (прямого, круглого)
V = пи * R2 *H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Объем конуса (прямого, круглого)
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
tehtab.ru
Как найти объем через площадь
Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.Инструкция
- Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³.
- Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба — 36 см². Вычислите объем.Извлеките квадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.
- Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³ - Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.
completerepair.ru
| Тема: Обобщение и систематизация знаний по теме « Площади и объемы»
5класс 19.12.2011 Цель урока:
Ход урока: I. Организационный момент. 2. Мотивация урока. Я очень хочу, чтобы урок получился интересным, познавательным, чтобы мы вместе повторили и закрепили то, что знаем и постарались открыть новые секреты в нашей удивительной стране «Геометрия». Для этого мы настроимся на урок, так как задания, которые я предложу, требуют внимания, дисциплины, знания математических терминов, свойств, законов и быстрых вычислительных навыков 3. Актуализация прежних знаний в виде математического диктанта:
— является ли куб прямоугольным параллелепипедом
Из истории (выступление ученика) Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей. У римлян мерой земляных участков был югер (от «югум» — «ярмо»). Это участок земли, вспахиваемый за день двумя волами, впряженными в деревянное ярмо. В древней Руси слабо знали основы геометрии и испытывали трудности их приложения к измерению земельных участков неправильной формы. С течением времени для пахотных земель главенствующую роль стала играть четверть — площадь, на которую высевали четверть (меру объема) ржи. 4. Решение задач по теме «Объем и площадь» 1 задание. Устный счет и индивидуальная работа Назвать рёбра, равные АК. Назвать рёбра, выходящие из вершины К. Назвать грань, равную КРМЕ. Назвать грани, которым принадлежит вершина А. Что нужно знать, чтобы вычислить площадь всей поверхности параллелепипеда? Вычислите площадь всей поверхности данного параллелепипеда. Как находится объём прямоугольного параллелепипеда? Вычислите объём данного параллелепипеда Физкультминутка:
Вращение туловищем столько раз, сколько равен периметр прямоугольника. Ответ: 6раз
2 задание. Работа по учебнику. №815, 845 на доске и в тетрадях. На повторение №848г,д.
Сделав необходимые измерения, найти площадь фигур (на моделях). 5.Итоги урока. Д/з. №843,848в, повторить формулы. Рефлексия. С помощью этой формулы можно вычислить: A) Р=(а+в)*2 ——периметр прямоугольника (Да) Б) S = а* а ——площадь квадрата (Да) B) V = а* в* с ——площадь прямоугольника ( Нет) Г) V =а*а*а ——объём куба (Да) Д) S = 4а ——объём параллелепипеда (Нет) |
www.tilimen.org
Как посчитать объем помещения в м3 калькулятор – площадь в метрах кубических
Как посчитать объем помещения
Объем – геометрический термин, позволяющий измерить количественные характеристики жилого и нежилого пространства.
Определить объемы помещения можно, обладая сведениями о его линейных размерах и характеристиками формы. Объем очень тесно переплетается с характеристиками вместимости. Наверняка каждому знакомы такие термины как внутренний объем сосуда или какой-либо тары.
Единица измерения объема классифицируется в соответствии с всемирными стандартами. Существует специальная система измерений – СИ, в соответствии с которой кубический метр, литр или сантиметр выступает метрической единицей объема.
Любое помещение, будь-то жилая комната или производственное помещение – имеет свои характеристики объема. Если рассматривать любое помещение с точки зрения геометрии, то комната сравнима с параллелепипедом. Это шестигранная фигура, в случае с комнатой грани ее – это стены, пол и потолок. Каждая из сторон комнаты – это прямоугольник. Как известно из геометрии, существует формула нахождения объема прямоугольного параллелепипеда. Объем данной фигуры вычисляется посредством умножения трех главных измерений параллелепипеда – длины, ширины и высоты граней. Также вычислить объем помещения можно по более простой формуле – площадь пола умножают на высоту комнаты.
Как узнать объём комнаты
Итак, каким же образом производят вычисления объема конкретной комнаты? Вначале измеряем длину стены, самой длинной в комнате. Затем определяем длину самой короткой стены в комнате. Все эти измерения проводятся на уровне пола, по линии пролегания плинтусов. При измерениях рулеточная лента должна располагаться ровно. Настал черед измерить и высоту потолка. Для этого необходимо провести рулетку от пола до потолка в одном из углов комнаты.
Все измерения необходимо записывать, с точностью до десятых частей. После этого можно приступить непосредственно к вычислению объемов комнаты. Берем длину самой большой стены, умножаем ее на длину самой маленькой стены, затем полученный результат умножаем на высоту комнаты. В итоге получаем необходимые цифры – объем комнаты.
Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.
Объём помещения сложной формы
В том случае, когда комната имеет неправильную форму, нужно исходить снова же, из фигуры параллелепипеда. В данном случае комната будет представлена большим и маленьким объемным телом. Так вот, объем нужно измерить отдельно у большого параллелепипеда, а затем – у маленького. После этого два объема складываются между собой. Бывает, что строение комнаты совершенно нестандартное, могут присутствовать арки и ниши полукруглой формации. В данном случае объемы нужно вычислять по другой формуле – объем цилиндра. Объем цилиндра всегда вычисляется по единой формуле – площадь его основания умножается на высоту цилиндрического тела. Полукруглые конструкции в комнате можно представить частью цилиндра, исходя из этого делаются расчеты полного объема цилиндра, а затем из них отнимается лишняя часть, в соответствии с размерами полукруглой ниши.
Как найти объем помещения
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения. Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Как посчитать объем помещения
Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.
Параллелепипед — это большая фигура, у которой 6 граней. и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.
2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены ,позже определите длину 2-ой стены. Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.
На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать.
Как посчитать объем в м3 бетона калькулятор
На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение умножите на высоту и вы получите требуемый итог.
Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков. тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где. – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.
Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.
Как рассчитать площадь комнаты?
Если комната с четырьмя стенами и имеет стандартную геометрическую фигуру с прямыми углами, тогда необходимо измерить две стенки и умножив полученные две цифры друг на друга мы получим площадь помещения, а для объёма нужно умножить полученный результат на высоту. но это только при правильных геометрических фигурах.
Сложнее находить площадь и размеры, когда форма комнаты неправильного размера, например такого.
Тогда нужно применять все знания геометрии, а именно — разделить комнату на несколько правильных фигур и в соответствии с формулами этих фигур найти их площадь, а потом все результаты сложить вместе, тогда получится общая площадь помещения. Для нахождения высоты необходимо полученный результат общей площади умножить на высоту.
Ещё хуже обстоят дела с нестандартными помещениями с неправильными углами стен и крыши. Тогда придётся переносить все размеры помещения на бумагу, разделять его на правильные фигуры и исходя из каждой фигуры находить её площадь и объём, а потом полученные результаты суммировать.
В площадь помещения не входят выступы окон и прочего, что выше пола, но они входят в расчёт объёма помещения.
Как посчитать площадь помещения
В случае измерения комнаты неправильной формы для более точного подсчета площади рекомендуется разбить ее на прямоугольники. Подсчитав площадь каждого такого участка, можно узнать общую площадь комнаты путем простого суммирования всех полученных результатов.
Если же разбить комнату на прямоугольные участки не представляется возможным, то можно попробовать такие фигуры как треугольник либо сектор круга. Площадь треугольника считается по формуле Герона: S=v**).
Р — полупериметр треугольника, который можно рассчитать таким образом: р=/2
http://denisyakovlev.com
stroyvolga.ru
Объём и площадь поверхности
Объём и площадь поверхности.Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар). Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины» «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма, правильная призма, правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Перейдем к практике.
1. Одна из самых распространенных задач в части B — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького.
Получаем: 754 71.
А как быть с площадью поверхности?
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна 110. А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна 55 25. А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна 25! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна 110. Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали. Ответ: 110.
А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму». Правильный ответ: 96.
Следующий тип задач — когда одно объемное тело вписано в другое.
3. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна 4, высота равна 1, объем равен 4.
4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 4. Найдите объем цилиндра, описанного около этой призмы. В ответ запишите V/π.
Очевидно, высота цилиндра равна боковому ребру призмы, то есть 4. Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна 10. Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ:100.
5. В прямоугольный параллелепипед вписан шар радиуса 1. Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: 8.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице:
flatik.ru
