Мудрая мысльБедствия бывают двух видов: когда не везет тебе и когда везет другим. Амброз Бирс |
|
||
old.edu54.ru
|
|||
uchitel.edu54.ru
|
|||
vospitatel.edu54.ru
8.2. Силы инерции в системах отсчета, движущихся поступательно
Пусть к потолку вагона на нити подвешен шарик массы m. Пока вагон движется равномерно и прямолинейно (или покоится), сила тяжести и сила реакции нити уравновешивают друг друга, и нить
занимает вертикальное положение (рис.
8.6).
уравновешивают друг друга, и нить
занимает вертикальное положение (рис.
8.6).
Вагон начал
двигаться с ускорением
 .
Нить отклонится от вертикали на угол
.
Нить отклонится от вертикали на угол .
С точки зрения наблюдателя, находящегося
в инерциальной системе отсчета (например,
на Земле) результирующая сила
.
С точки зрения наблюдателя, находящегося
в инерциальной системе отсчета (например,
на Земле) результирующая сила
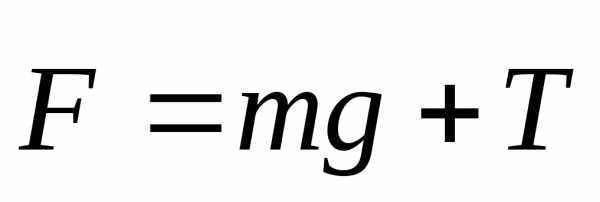
обеспечит
ускорение шарика
 :
:
 .
.
С точки зрения
наблюдателя, находящегося в неинерциальной
системе (в ускоренно движущемся вагоне)
шарик покоится, т.е. сила
 уравновешивается равной и противоположно
направленной ей силой
уравновешивается равной и противоположно
направленной ей силой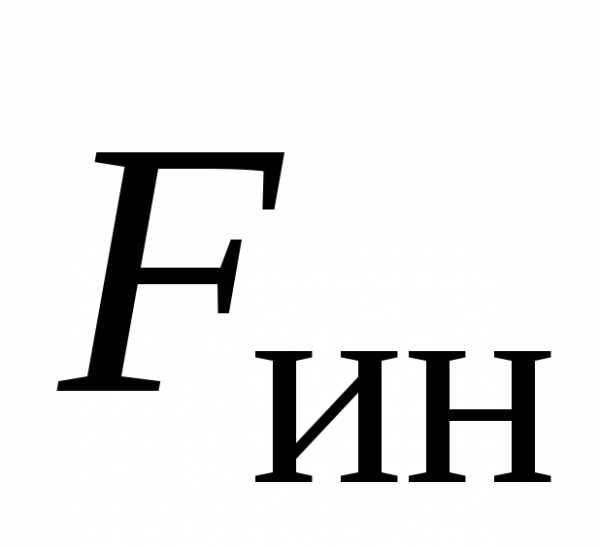 ,
которая является силой инерции.
,
которая является силой инерции.
Рис. 8.6
Таким образом,
(8.7)
– сила инерции, действующая на тело, равна массе этого тела, умноженной, на ускорение системы отсчета и направлена противоположно ускорению.
Действию сил инерции подвергается, например, пассажир: при резком торможении вагона сила инерции бросает его вперед, при ускорении вагона – назад.
8.3. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
Система
отсчета, вращающаяся относительно
инерциальной системы отсчета с угловой
скоростью
 является неинерциальной системой
отсчета.
является неинерциальной системой
отсчета.
Рассмотрим
пример такой неинерциальной системы
отсчета.
На рис. 8.7 изображен
вращающийся с угловой скоростью
 диск, на котором находится тело массойm. Тело относительно
диска покоится.
диск, на котором находится тело массойm. Тело относительно
диска покоится.
Относительно
инерциальной системы отсчета (относительно
точки О,
относительно Земли) тело движется
по окружности и его ускорение равно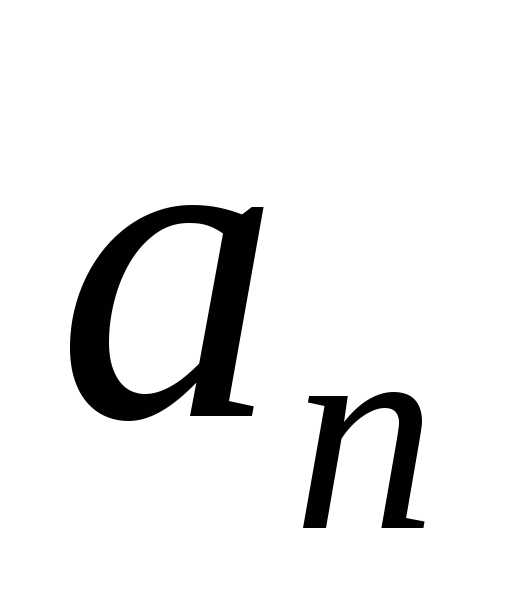
 ,
которое направлено к центру окружности.
,
которое направлено к центру окружности.|
Рис. 8.7 |
|
Уравнение движения тела можно записать в виде: или. Тогда.
Так как тело m покоится относительно диска (неинерциальной системы отсчета), оно вращается вместе с диском, то
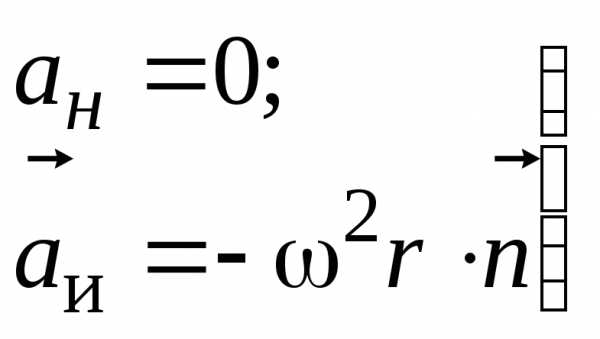
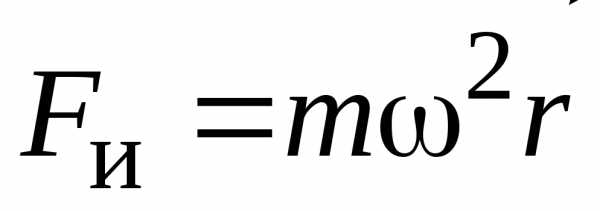 –сила инерции,
действующая на неподвижное относительно
вращающейся системы отсчета тело,
называется центробежной
силой инерции.
Центробежная сила инерции сообщает
телу центробежное ускорение
–сила инерции,
действующая на неподвижное относительно
вращающейся системы отсчета тело,
называется центробежной
силой инерции.
Центробежная сила инерции сообщает
телу центробежное ускорение
 . (8.9)
. (8.9)
Свойства центробежной силы инерции:
1) величина
центробежной силы инерции (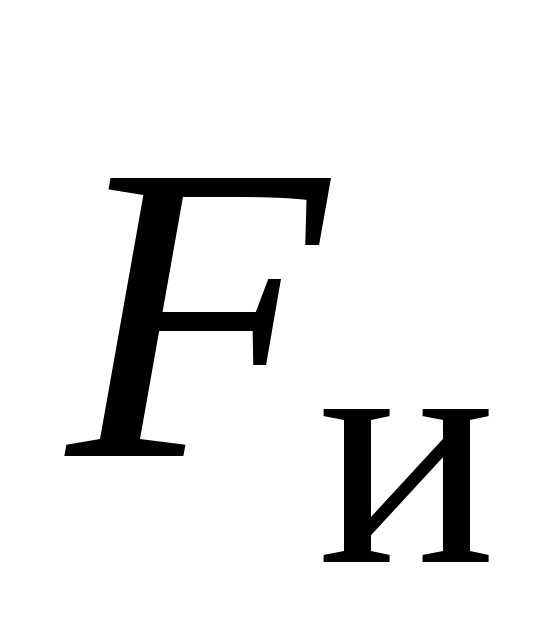 )
зависит от положения тела во вращающейся
системе отсчета;
)
зависит от положения тела во вращающейся
системе отсчета;
2) центробежная сила инерции направлена по радиусу от центра;
3) величина
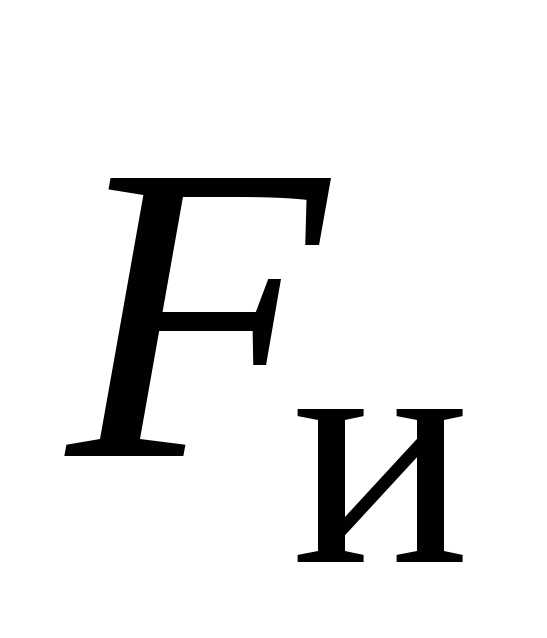
4) силы инерции оказывают на тело такое же действие, что и реальные силы, действующие со стороны других тел. Силы инерции – фиктивные силы. Они могут сообщать телу ускорение или совершать работу по изменению положения относительно неинерциальной системы отсчета.
Покажем, что центробежная сила инерции может совершать работу по перемещению тела. Найдем работу центробежной силы при изменении положения тела относительно точки О от r1 до r2:
или .
Так как , то
,
а при изменении положения от r1 до r2
. (8.10)
Обратите внимание на то, что работа силы инерции не зависит от формы траектории движения тела относительно неинерциальной системы отсчета.
8.4. Силы инерции, действующие на тело, движущееся относительно вращающейся системы отсчета
Е
Рис. 8.8
сли тело движется в неинерциальной системе отсчета, то кроме центробежной силы инерции действует еще одна сила инерции – сила Кориолиса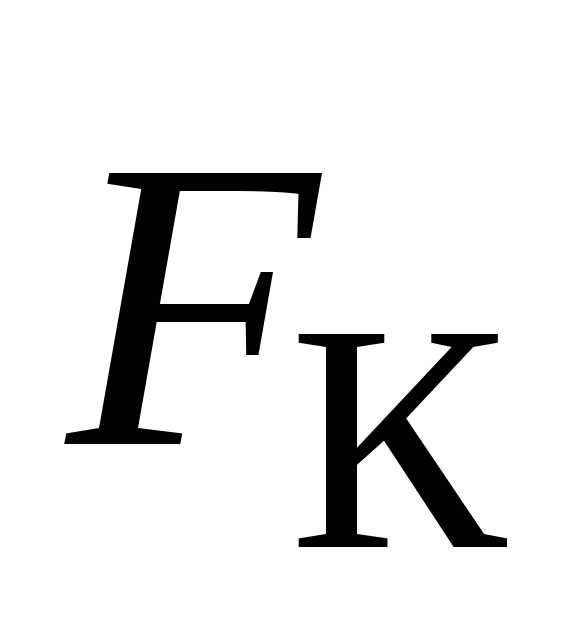 .
Появление силы Кориолиса можно обнаружить
на следующем примере.
.
Появление силы Кориолиса можно обнаружить
на следующем примере.П
Рис. 8.9
усть шарик массыm движется с постоянной скоростью вдоль радиуса диска (рис. 8.8). Если при
этом диск покоится, то шарик попадает
в точкуА.
Если же диск привести во вращение в
направлении, указанном стрелкой, то
шарик покатится по кривой ОВ.
То есть скорость шарика относительно
диска изменит свое направление. Это
значит, что во вращающейся системе
отсчета на шарик действует сила
вдоль радиуса диска (рис. 8.8). Если при
этом диск покоится, то шарик попадает
в точкуА.
Если же диск привести во вращение в
направлении, указанном стрелкой, то
шарик покатится по кривой ОВ.
То есть скорость шарика относительно
диска изменит свое направление. Это
значит, что во вращающейся системе
отсчета на шарик действует сила
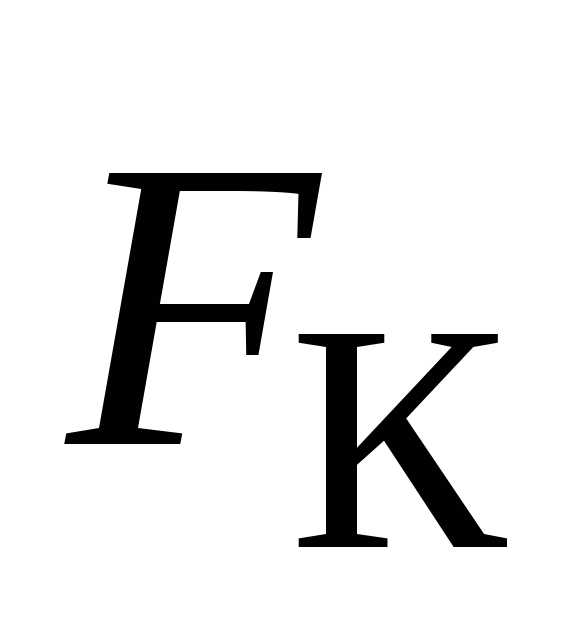 ,
перпендикулярная скорости
,
перпендикулярная скорости .
.Чтобы заставить шарик катится по вращающемуся диску вдоль радиуса, нужно сделать направляющую, например, в виде ребра ОА (рис. 8.9).
При качении шарика
ребро действует на него с некоторой
силой
 .
Относительно диска (вращающейся системы
отсчета) шарик движется равномерно и
прямолинейно. Это можно объяснить тем,
что сила
.
Относительно диска (вращающейся системы
отсчета) шарик движется равномерно и
прямолинейно. Это можно объяснить тем,
что сила уравновешивается приложенной к шарику
силой инерции. Эта сила инерции называется
силой Кориолиса
уравновешивается приложенной к шарику
силой инерции. Эта сила инерции называется
силой Кориолиса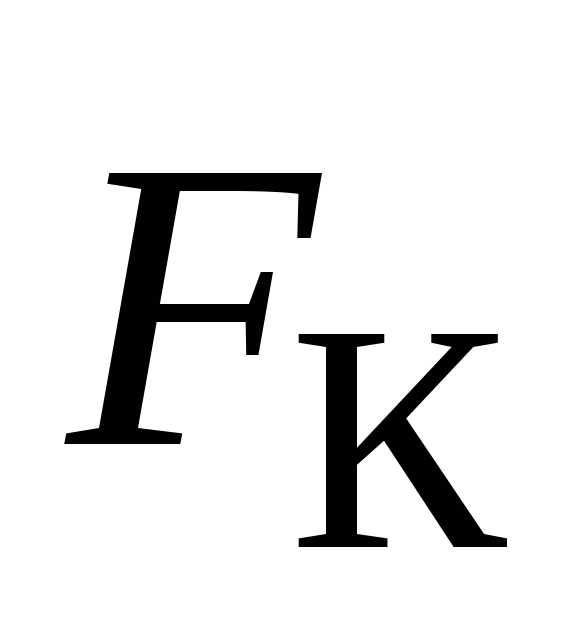 .
Сила Кориолиса возникает, если тело
движется относительно вращающейся
системы отсчета.
.
Сила Кориолиса возникает, если тело
движется относительно вращающейся
системы отсчета.
Рассмотрим пример
(рис. 8.10). На рисунке изображен вращающийся
с угловой скоростью
 диск, по
которому движется тело массой m
со скоростью
диск, по
которому движется тело массой m
со скоростью
 относительно диска.
относительно диска.
|
Рис. 8.10 |
|
Рассмотрим движение точки относительно инерциальной системы отсчета.
Скорость тела относительно инерциальной системы отсчета: , т.к.– это скорость, которую имеет тело, т.к. оно находится на расстоянииr от оси вращающегося с угловой скоростью ω диска. Тело при движении описывает окружность, поэтому согласно второму закону Ньютона можно записать:
(8.11)
Учтем, что
, (8.12)
Тогда
;
, (8.13)
т.к.
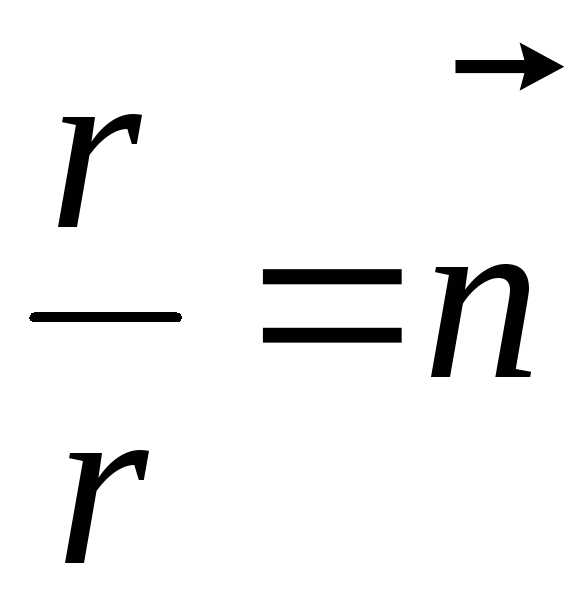 – единичный вектор (орт) радиус-вектора.
– единичный вектор (орт) радиус-вектора.
Тогда движение тела относительно инерциальной системы отсчета можно записать:
. (8.14)
А уравнение движения тела относительно неинерциальной системы отсчета:
. (8.15)
Так как относительно
инерциальной системы отсчета можно
записать второй закон Ньютона в виде:
,
где – реальные силы, действующие на тело
относительно инерциальной системы
отсчета. В неинерциальной вращающейся
системе отсчета на тело действует
центробежная сила инерции,,
которая обусловлена вращением
неинерциальной системы отсчета
относительно инерциальной. Тогда– сила инерции (сила Кориолиса),
обусловленная скоростью движения тела
относительно неинерциальной вращающейся
системы отсчета.
– реальные силы, действующие на тело
относительно инерциальной системы
отсчета. В неинерциальной вращающейся
системе отсчета на тело действует
центробежная сила инерции,,
которая обусловлена вращением
неинерциальной системы отсчета
относительно инерциальной. Тогда– сила инерции (сила Кориолиса),
обусловленная скоростью движения тела
относительно неинерциальной вращающейся
системы отсчета.
Уравнение движения тогда можно записать: .
Таким образом,
если тело (материальная точка) движется
относительно вращающейся (неинерциальной)
системы отсчета со скоростью
 ,
тело кроме центробежной силы инерции
действует ещё сила Кориолиса, равная
,
тело кроме центробежной силы инерции
действует ещё сила Кориолиса, равная
. (8.16)
Свойства силы Кориолиса:
1) величина силы
Кориолиса
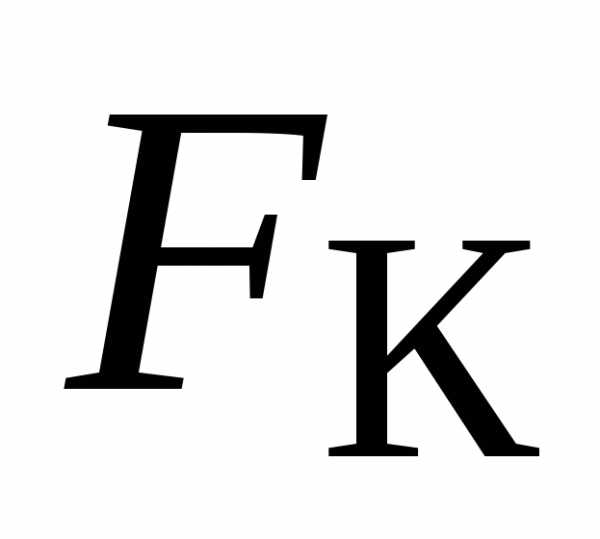 не зависит от положения материальной
точки во вращающейся системе отсчета;
не зависит от положения материальной
точки во вращающейся системе отсчета;
2) сила Кориолиса
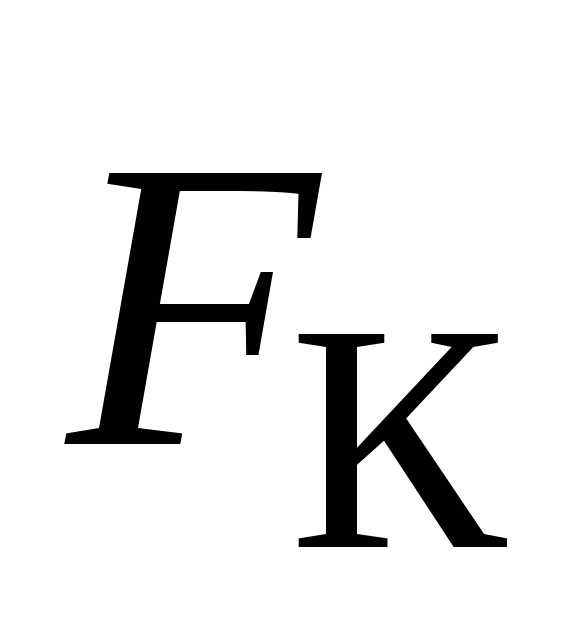 зависит от скорости
зависит от скорости относительно
вращающейся системы отсчета и угловой
скорости вращения системы относительно
инерциальной системы отсчета;
относительно
вращающейся системы отсчета и угловой
скорости вращения системы относительно
инерциальной системы отсчета;
3) сила Кориолиса
всегда направлена перпендикулярно
 скорости
движения тела относительно вращающейся
системы отсчета, т.е.
скорости
движения тела относительно вращающейся
системы отсчета, т.е.
 ,
поэтому сила Кориолиса работы не
совершает. Эта сила называетсягироскопической.
,
поэтому сила Кориолиса работы не
совершает. Эта сила называетсягироскопической.
Вектор
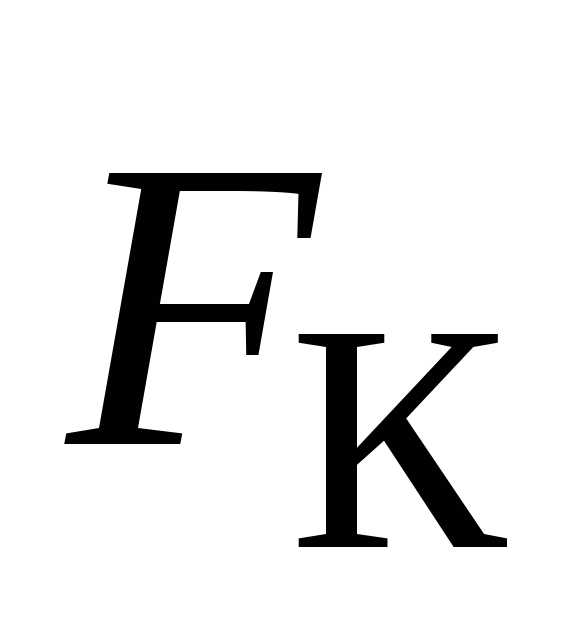 перпендикулярен вектору скорости
перпендикулярен вектору скорости тела и угловой скорости вращения
тела и угловой скорости вращения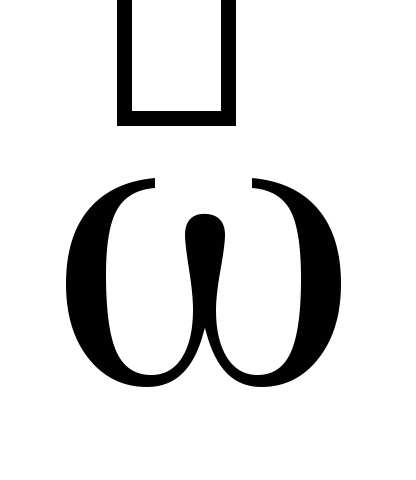 системы отсчета в соответствии с правилом
правого винта.
системы отсчета в соответствии с правилом
правого винта.
Действием сил Кориолиса объясняется ряд наблюдаемых на Земле явлений. Например, если тело движется в северном полушарии на север, то действующая на него сила Кориолиса будет направлена вправо по отношению к направлению движения. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек. За счет действия силы Кориолиса, возникает дополнительная сила бокового давления, с которой поезд действует на рельсы, поэтому правые рельсы железнодорожных путей по движению изнашиваются быстрей, чем левые. Свободно падающее тело отклоняется к востоку и т.д.

Рис. 8.11
Аналогично можно показать, что в южном полушарии сила Кориолиса будет направлена влево по отношению к направлению движения.
studfiles.net

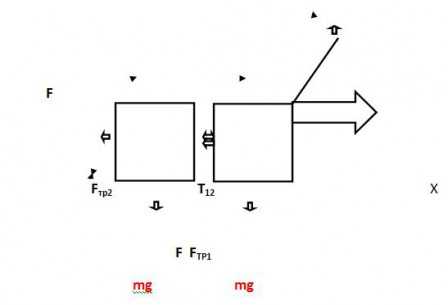
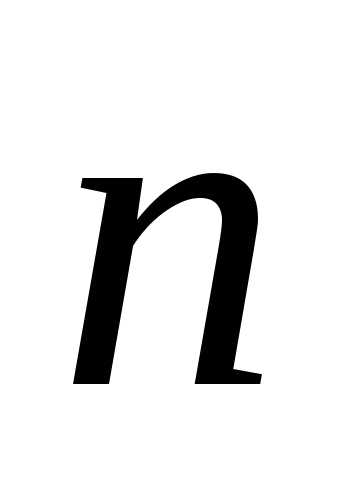 –единичный орт.
–единичный орт. –скорость
движения материальной точки относительно
вращающейся (неинерциальной) системы
отсчета. Направление
–скорость
движения материальной точки относительно
вращающейся (неинерциальной) системы
отсчета. Направление
 произвольное.
произвольное.