Логарифмы в заданиях ЕГЭ
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (3,4 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, —
что, следуя этому методу, мы достигнем цели.
Г.Лейбниц
ТИП УРОКА: Закрепление и совершенствование знаний.
ЦЕЛИ:
- Дидактическая — Повторить и закрепить свойства логарифмов; логарифмические уравнения; закрепить методы решения наибольшего и наименьшего значения функции; совершенствовать применение полученных знаний при решении задач ЕГЭ С1 и С3;
- Развивающая — Развитие логического мышления, памяти, познавательного интереса, продолжить формирование математической речи и графической культуры, вырабатывать умение анализировать;
- Воспитательная — Приучать к эстетическому оформлению записи в тетради, умению общаться, прививать аккуратность.
Оборудование:
классная доска, компьютер, проектор, экран, карточки с заданиями теста, с заданиями для работы всех обучающихся.Формы работы: фронтальная, индивидуальная, коллективная.
ХОД УРОКА
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ
2. ПОСТАНОВКА ЦЕЛИ
3. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- Задания группы В (10 заданий) – проверяется устно;
- Задания С3 из второй части ЕГЭ;
Ответ: - работа личных кабинетов в Интернет (просмотр результатов)
4. АКТУАЛИЗАЦИЯ ЗНАНИЙ
Проанализировать: в каких заданиях ЕГЭ встречаются логарифмы.
(В-7-простейшие логарифмические уравнения
В-11-преобразование логарифмических выражений
В-12- задачи физического содержания, связанные с логарифмами
В-15- нахождение наибольшего и наименьшего значения функции
С-1- тригонометрические уравнения, содержащие логарифм
С-3 – система неравенств, содержащая логарифмическое неравенство)
На данном этапе проводится устная работа, в ходе которой учащиеся не только вспоминают свойства логарифмов, но и выполняют простейшие задания ЕГЭ.
1) Определение логарифма. Какие вы знаете свойства логарифма? (и условия ?)
1. logb b = 1
2. logb 1 = 0, 3. logc (ab) = logc a + logc b.
4. logc (a:b) = logc a – logc b.
5. logc (b k ) = k * logc
6=
7.
8.
2) Какая функция называется логарифмической? D(у) -?
3) Что такое десятичный логарифм? ()
4) Что такое натуральный логарифм? ()
5) Что такое число е?
6) Чему равна производная от ? ()
7) Чему равна производная от натурального логарифма?
5. УСТНАЯ РАБОТА для всех обучающихся
Вычислить устно: (задания В-11)
6. Самостоятельная деятельность учащихся по решению заданий
В-7 с последующей проверкой
Решите уравнения (первые два уравнения проговаривают устно, а остальные решает самостоятельно весь класс и записывает решение в тетрадь):
(Пока ученики работают на месте самостоятельно, к доске выходят 3 ученика и работают по индивидуальным карточкам)
После проверки с места 3-5 уравнений, ребятам предлагается доказать, что уравнение не имеет решения (устно)
7. Решение В-12 — (задачи физического содержания, связанные с логарифмами)
Весь класс решает задачу (у доски 2 человека: 1-й решает вместе с классом, 2-й решает аналогичную задачу самостоятельно)
8. УСТНАЯ РАБОТА (вопросы)
Вспомнить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке и на промежутке.
Работа на доске и в тетради.
(прототип В15 — ЕГЭ)
9. Мини-тест с самоконтролем.
Тест
Ключи к тесту
| №1 | №2 | №3 | №4 | №5 | №6 | |
| Вариант №1 | 250 | 49 | 4 | -8 | 3 | 8 |
| Вариант №2 | 63 | 144 | 13 | -22 | 7 | 3 |
Ребята меняются друг с другом работами и выступают в роли экспертов.
10. Решение заданий С1
Учащиеся выполняют задание, 1 человек работает у доски.
а) Решите уравнение
б) найдите корни уравнения, принадлежащие промежутку (;3)
Подробный разбор предложенного задания на доске.
11.Выступление учащихся в роли экспертов
Ребятам предлагается оценить работу ученика – задание С-1, выполненную на экзаменационном бланке – 0,1,2 баллами (см.презентацию)
12. ДОМАШНЕЕ ЗАДАНИЕ
Учитель поясняет домашнее задание, обращая внимание на то, что аналогичные задания были рассмотрены на уроке. Учащиеся внимательно прослушав пояснения учителя, записывают домашнее задание.
ФИПИ (открытый банк заданий: раздел геометрия, 6-я страница)
uztest.ru (преобразование логарифмов)
С3 – задание второй части ЕГЭ
13. ПОДВЕДЕНИЕ ИТОГОВ
Сегодня на уроке мы повторили свойства логарифмов; логарифмические уравнения; закрепили методы нахождения наибольшего и наименьшего значения функции; рассмотрели задачи физического содержания, связанные с логарифмами; решали задачи С1 и С3, которые предлагаются на ЕГЭ по математике в прототипах В7, В11, В12, В15, С1 и С3.
Выставление оценок.
xn--i1abbnckbmcl9fb.xn--p1ai
| 1. |
Логарифмическое уравнение (определение)
Сложность: лёгкое |
|
| 2. |
Сумма логарифмов (потенцирование)
|
|
| 3. |
Разность логарифмов (потенцирование)
Сложность: лёгкое |
|
| 4. |
Логарифмическое уравнение, сводимое к линейному
Сложность: лёгкое |
|
| 5. |
Логарифмирование (показательное уравнение)
Сложность: лёгкое |
|
| 6. |
Сумма логарифмов
Сложность: лёгкое |
|
| 7. |
Логарифмическое уравнение (неизвестно основание)
Сложность: среднее |
|
| 8. |
Логарифмическое уравнение (произведение равно 0)
Сложность: среднее |
|
| 9. |
Логарифмическое уравнение, разность логарифмов
Сложность: среднее |
|
| 10. |
Логарифмическое уравнение (логарифм в квадрате)
Сложность: среднее |
|
| 11. |
Логарифмическое уравнение (разложение на множители)
Сложность: среднее |
|
| 12. |
Логарифмическое уравнение, сводимое к дробно-рациональному (разность логарифмов)
Сложность: среднее |
|
| 13. |
Логарифмирование (основное логарифмическое тождество)
Сложность: среднее |
|
| 14. |
Логарифмическое уравнение, сводимое к линейному
Сложность: среднее |
|
| 15. |
Логарифмическое уравнение, сводимое к квадратному (основание-натуральное число)
Сложность: среднее |
|
| 16. |
Логарифмическое уравнение, сводимое к квадратному (обыкновенная дробь)
Сложность: среднее |
|
| 17. |
Логарифмическое уравнение, сводимое к квадратному (сумма логарифмов)
Сложность: среднее |
|
| 18. |
Метод введения новой переменной (логарифм частного)
Сложность: среднее |
|
| 19. |
Логарифмическое уравнение, сводимое к алгебраическому (теорема Виета)
Сложность: среднее |
|
| 20. |
Логарифмическое уравнение, сводимое к алгебраическому (дискриминант)
Сложность: среднее |
|
| 21. |
Логарифмическое уравнение (тригонометрия)
Сложность: сложное |
|
| 22. |
Логарифмическое уравнение (новая переменная)
Сложность: среднее |
|
| 23. |
Логарифмическое уравнение, сводимое к дробно-рациональному (десятичный логарифм)
Сложность: сложное |
|
| 24. |
Показательное уравнение (логарифмические корни)
Сложность: сложное |
|
| 25. |
Логарифмическое уравнение (графический способ)
Сложность: сложное |
www.yaklass.ru
Логарифмические уравнения в задаче C1
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
log2x = 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не cодержали, обязательно нужно привести к уравнению вида:
logaf (x) = logag(x)
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
logaf (x) + logag(x) = logaf (x) · g(x)
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
a = logbba
Здесь нужно понимать: когда мы говорим «Любое основание b», то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0 < b ≠ 1
Давайте посмотрим, что происходит в нашем случае:
1 = log2 21 = log2 2
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
logabn = n · logab
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k.
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n), окажется в числителе. А то, что было степенью у основания, ak, отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Вынесение степени из основания логарифма
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
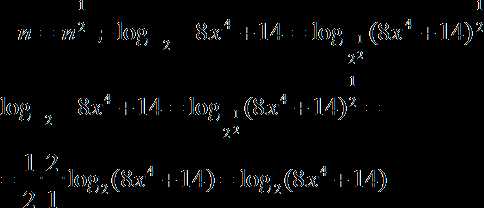
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log2 2(9x2 + 5) = log2 (8x4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x2 + 5) = 8x4 + 14
Давайте раскроем скобки слева. Получим:
18x2 + 10 = 8x4 + 14
Перенесем все из левой части в правую:
8x4 + 14 − 18x2 − 10 = 0
Приведем подобные и получим:
8x4 − 18x2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x4 − 9x2 + 2 = 0
Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x, а x2, потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x2 + 5 (эта функция всегда положительна), либо 8x4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9 < 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
- Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81 < 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b, именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Смотрите также:
- Задача C1: логарифмы и тригонометрия в одном уравнении
- Задача C1: еще одно показательное уравнение
- Пробный ЕГЭ-2011 по математике, вариант №8
- Пробный ЕГЭ 2012. Вариант 2 (без логарифмов)
- Тест: простейшие показательные уравнения (2 вариант)
- Четырехугольная пирамида: как найти координаты вершин
www.berdov.com
№ Логарифмические уравнения — Документ
Тема № 5.3. Логарифмические уравнения
I. Теоретический материал
Основные понятия
Логарифмическое уравнение
Простейшее логарифмическое уравнение
Методы решения логарифмических уравнений
Пусть a – данное
положительное, не равное 1 число, b
– данное действительное число. Тогда
уравнение
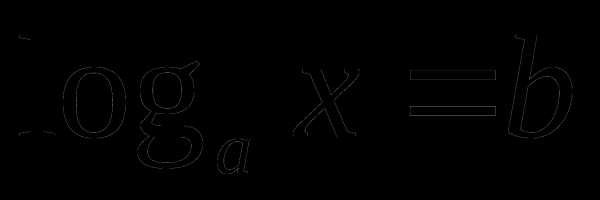 (***)
называют простейшим логарифмическим
уравнением.
(***)
называют простейшим логарифмическим
уравнением.
Например, уравнения
 ,
,
являются простейшими логарифмическими
уравнениями.
,
,
являются простейшими логарифмическими
уравнениями.
По определению логарифма если число удовлетворяет числовому равенству , то число есть , причем это число = единственное. Таким образом, для любого действительного числа b уравнение (***) имеет единственный корень =.
II. Практический материал
Примеры выполнения заданий
Методы решения логарифмических уравнений
Функционально-графический метод
Суть этого метода состоит в использовании свойств показательной функции.
Если невозможно решить уравнение,
используя свойства, тогда используют
графическую иллюстрации функций,
заданных в нем. Рисуем функции в одной
системе координат и ищем точки пересечения.
Координата
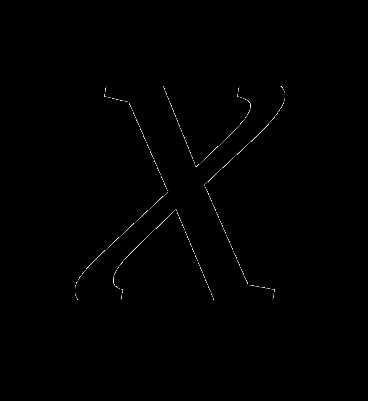 этих
точек и будет решением уравнения.
этих
точек и будет решением уравнения.
Пример 1. Решить уравнение .
Решение. По определению логарифма: , (так как , по определению). Ответ: .
П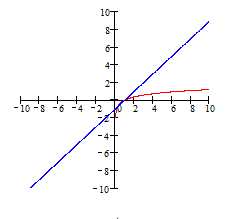 ример
2. Решить уравнение
.
ример
2. Решить уравнение
.
Р
y
x
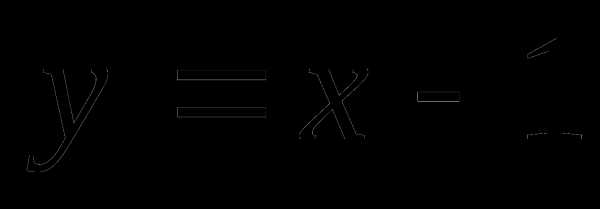
Метод потенцирования
Этот метод основан на следующей теореме.
Теорема. Уравнение равносильно уравнению при ограничениях
Примечание: если основания логарифмических функций разные, то необходимо перейти к одному основанию с помощью свойств логарифмической функции и после применить теорему.
Пример 3. Решить уравнение .
Решение. Так как , , то по теореме ; ; , .
Проверим, удовлетворяют ли корни условию:
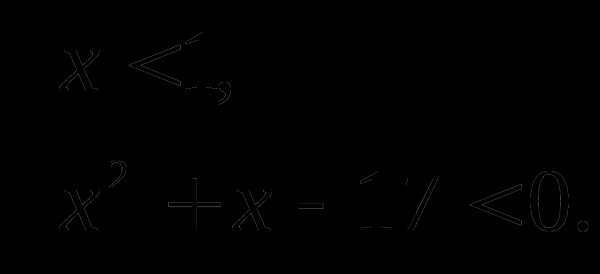
Подходит только первый корень. Следовательно, — корень уравнения .
Метод введения новой переменной
При данном методе логарифмическая функция заменяется на переменную и уравнение преобразуется в алгебраическое. Далее переходим от переменной к логарифмической функции и получаем простейшее логарифмическое уравнение.
Пример 4. Решить уравнение .
Решение. Введем новую переменную 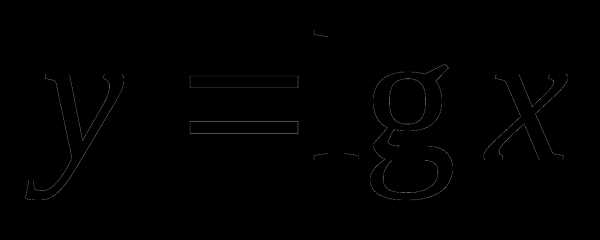 .
Подставляем переменную в исходное
уравнение и получаем следующее квадратное
уравнение:
.
Находим корни:
.
Подставляем переменную в исходное
уравнение и получаем следующее квадратное
уравнение:
.
Находим корни:
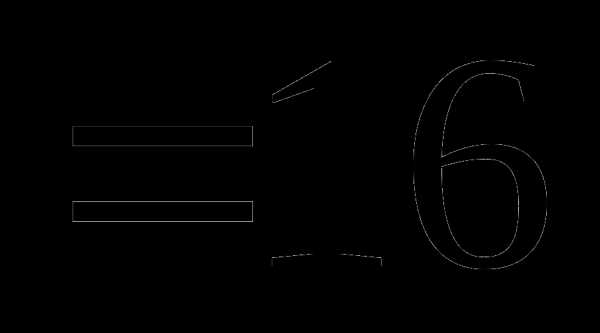 ,
,
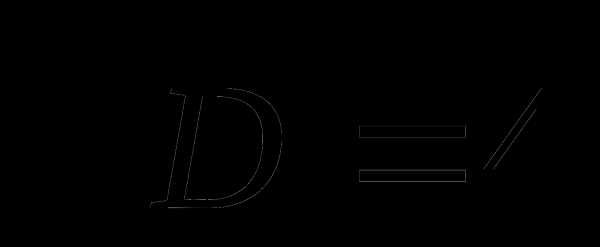 ;
;
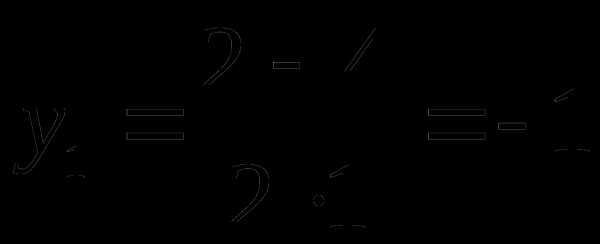 ,
,
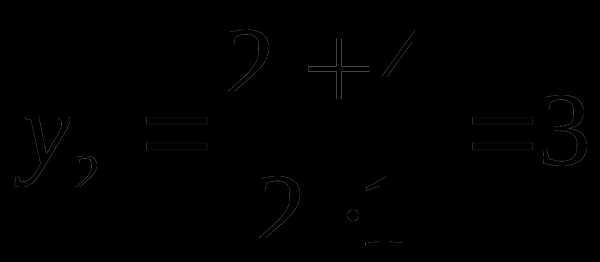 .
Но
.
Но

 ,
,
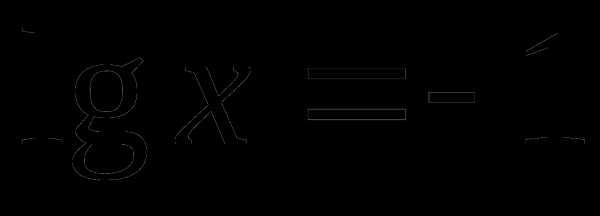 ,
;
,
;
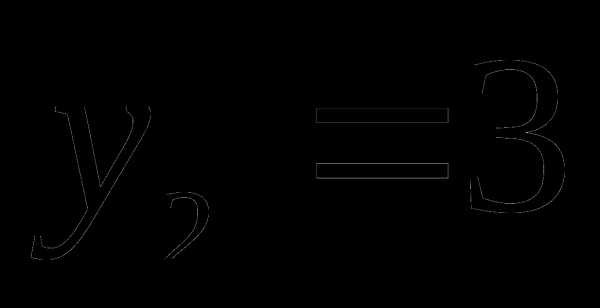 ,
,
 ,
.
Ответ:
,
.
,
.
Ответ:
,
.
Задания для самостоятельной работы
Функционально-графический метод
Задание 1. Решить уравнение
.
Задание 2. Решить уравнение .
Задание 3. Решить уравнение .
Задание 4. Решить уравнение .
Задание 5. Решить уравнение
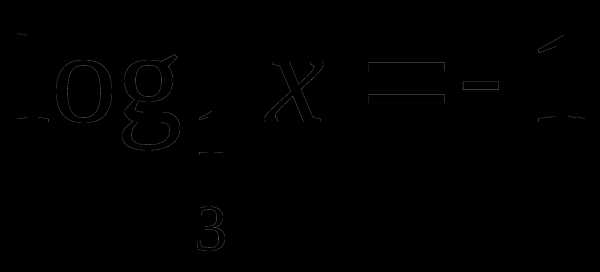 .
.
Задание 6. Решить уравнение .
Метод потенцирования
Задание 7. Решить уравнение .
Задание 8. Решить уравнение .
Задание 9. Решить уравнение .
Задание 10. Решить уравнение .
Задание 11. Решить уравнение .
Задание 12. Решить уравнение
Метод введения новой переменной
Задание 13. Решить уравнение
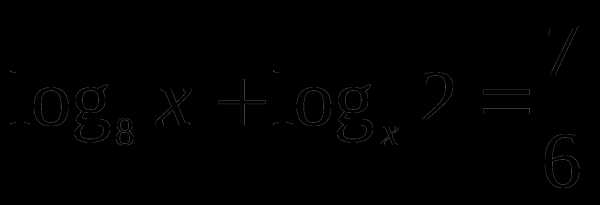 .
.
Задание 14. Решить уравнение
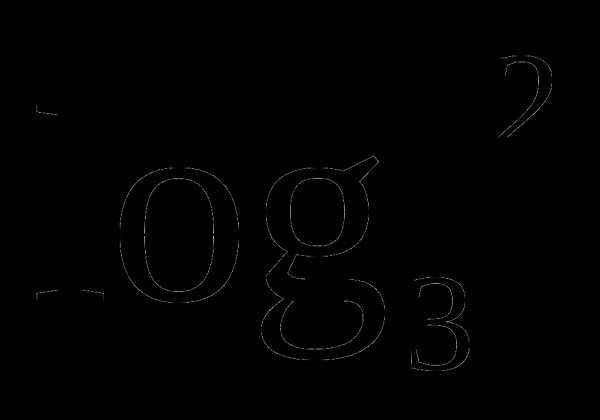

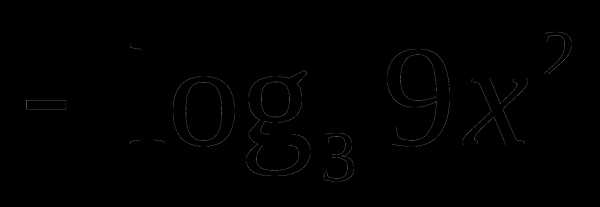 .
.
Задание 15. Решить уравнение .
Задание 16. Решить уравнение .
Задание 17. Решить уравнение
Задание 18. Решить уравнение
gigabaza.ru
Уроки обобщающего повторения по теме «Логарифмическая функция. Решение логарифмических уравнений, неравенств»
Разделы: Математика
В контрольно измерительных материалах ЕГЭ обязательно присутствуют задания по теме «Логарифмическая функция» (задания нам преобразование логарифмических выражений, знания свойств логарифмической функции, решения логарифмических уравнений и неравенств).
Данные уроки проходили в классах, в которых несколько человек плохо справляются с выполнением заданий по данной теме на базовом уровне, основная часть учащихся работают на базовом уровне, есть учащиеся, которые успешно выполняют задания повышенного уровня.
Методическая цель:
- продемонстрировать применение дифференцированного подхода в обучении,
- продемонстрировать закрепление умений и навыков при выполнении тестовых заданий в формате ЕГЭ.
Логарифмическая функция
Цель:
- обобщить теоретические знания свойств логарифмической функции,
- закрепить умения применять знания при выполнении заданий,
- развивать навыки самоконтроля у учащихся.
Оборудование:
- рабочие тетради,
- карточки с заданиями,
- бланки для ответов,
- доска,
- компьютер, мультимедийная установка.
Ход урока
_. Организационный момент.
Приветствие. Сообщение темы (на доске: «Обобщающий урок по теме «Логарифмическая функция»».).
Целеполагание.
Учитель:
Перед нами стоит задача обобщить знания по теме: «Логарифмическая функция».
Каждому предстоит оценить свои знания, скорректировать пробелы, выполнить тестовое задание по своим силам.
Будем на уроке внимательными, активными, с большим желанием выполним предложенную работу. Это поможет нам в подготовке к ЕГЭ.
__. Обобщение теоретического материала.
Предварительно учащимся в домашнем задании требовалось повторить теоретический материал по теме по учебнику А.Н.Колмогорова и др. «Алгебра и начала анализа» для 10 -11 классов п.37 стр.232 «Логарифм и его свойства», п.38 стр.238 «Логарифмическая функция».
1. Математический диктант.
Учитель зачитывает утверждения. Можно использовать экран (с помощью мультимедийной установки). На экране поочередно появляются вопросы.
Учащиеся отвечают так: «да» — V, «нет» — _.
Текст. Предлагаются верные и не верные утверждения.
Верны ли утверждения?
- Логарифмическая функция у = logax определена при любом х.
- Функция у = logx логарифмическая при а>0, а 1, х>0.
- Область определения логарифмической функции множество действительных чисел.
- Область значений логарифмической функции множество действительных чисел.
- Логарифмическая функция является четной функцией.
- Функция у = log3x является возрастающей.
- Функция у = logax при положительном а, но меньшим 1, является возрастающей.
- Логарифмическая функция имеет экстремумы.
- График функции у = logax пересекает ось Ох.
- График логарифмической функции симметричен относительно оси Ох.
- График логарифмической функции расположен в _ и _ V четвертях.
- График логарифмической функции всегда пересекает ось Ох в точке (1,0).
Выполнение данного задания позволит проверить учащимся теоретический материал по теме свойства логарифмической функции.
2. Самопроверка учащимися своих ответов.
На экране появляется графическое изображение верного ответа.
Учащиеся сверяют свои ответы с верными ответами, делают выводы.
Учащимся, которые допустили ошибки, поможет скорректировать знания следующий момент.
3. Обобщение теоретического материала.
На экране появляется слайд, на котором в виде конспекта представлен необходимый теоретический материал.
Учащимся, которые допустили ошибки, предлагается прокомментировать конспект.
Учащиеся анализируют ошибки, делают выводы.
Функция вида у = logax называется логарифмической функцией с
Основанием а ( а>0, а 1)
Учащиеся проговаривают свойства логарифмической функции.
— область определения — множество всех положительных чисел (х>0).
— область значений — множество всех действительных чисел ( -; +).
— непрерывна на всей области определения.
— функция у = logx возрастает на всей области определения, если а>1.
— Функция у = logx убывает на всей области определения, если 0< а>1.
— точка пересечения графика функции у = logax с осью Ох (1,0).
— наибольшего и наименьшего значения функции не существует.
— функция экстремумы не имеет.
— положение точки а относительно1, и значения функции при х=а
Учитель: «Необходимо помнить свойства логарифма. Они помогут при выполнении заданий.»
Учащиеся называют свойства логарифма.
«Приведите пример задания в которых нужно использовать названное вами свойство»
Пример: =k logc a , logaa =1 log223=3 log22=3,
logc(ab)= logca + logb log22= log22 + log2=1+=1=1,2.
logba= =log3 81=4. и т.д.
Учитель после ответов учащихся предлагает еще раз обратить внимание формулы на слайде.
На экране появляется слайд:
___. Закрепление знаний при выполнении тестовых заданий
Учитель: «Применим знания при выполнении тестовых заданий. Вам предлагается три варианта заданий. Каждый может выбрать тот, который ему по силам.
Желаю удачи!»
1. Учащиеся выбирают карточки с заданиями. Приступают к выполнению.
Карточки с вариантами заданий представлены в приложениях.
Задания подобраны с учетом рекомендаций Федерального института педагогических измерений и курса » Система подготовки к ЕГЭ по математике».
2. Самопроверка учащихся.
На экране появляется слайд с таблицей верных ответов. Учащиеся сверяют ответы.
Оценивают свою работу. Делают вывод.
_V. Подведение итогов, рефлексия.
На данном уроке мы обобщили теоретические знания и закрепили навыки, которые необходимы при выполнении проверочной работы, а также понадобятся нам при решении логарифмических уравнений и неравенств.
Продолжите фразу:
- «Сегодня на уроке я повторил:.»
- «Сегодня на уроке я закрепил:.»
- «Для себя я понял:»
Бланки с ответами сдают учителю, каждый получает оценку за урок.
Задания смотрим в Приложении 1.
Решение логарифмических уравнений, неравенств
Цель: обобщить теоретические знания, используемые при решении логарифмических уравнений, неравенств; организовать работу учащихся на уровне, соответствующем уровню уже сформированных знаний и умений.
Ход урока
_. Организационный момент.
Целеполагание. Учитель:
«Продолжаем работу с логарифмической функцией. На предыдущем занятии мы обобщили знания по теме и закрепили их при выполнении тестовых заданий.
(на доске: «Решение логарифмических уравнений и неравенств».)
На этом уроке повторим основные методы решения логарифмических уравнений и неравенств базового и повышенного уровня».
__. Повторение теоретического материала по теме.
Совместная работа учащихся и учителя. Используется мультимедийная установка, презентация » Решение логарифмических уравнений, неравенств».
Фронтальная работа.
Учитель: «Какое уравнение называется простейшим логарифмическим?»
Учащиеся: «Простейшее логарифмическое уравнение — это уравнение вида loga x=b, где a 0, а 1.Имеет единственное решение х= ab.
Учитель: «Запишите пример каждый в своей тетради такого уравнения и его решение.»
Трое учащихся выполняют задание у доски.
Например:
a) log3x=4, x>0, x=81,
b) log2(x+1)=3, x>-1, x+1=8, x=7,
в) loga16=2, а>0, а 1, а=4.
«Логарифмические уравнения и неравенства приводятся к простейшим с помощью формул преобразования логарифмов. Какие это формулы?»
Учащиеся отвечают, учитель и сами учащиеся корректируют не верные ответы.
После этого на экране последовательно появляются нужные формулы.
В данном случае расширяется область определения уравнения, что может привести к появлению посторонних корней!
«Назовем способы решения логарифмических уравнений, приводящим к появлению посторонних корней.»
Способы:
- Решение логарифмических уравнений на основании определения логарифма,
- Метод потенцирования,
- Приведение логарифмического уравнения к квадратному,
- Уравнения, решаемые приведением логарифмов к одному и тому же основанию,
- Уравнения, решаемые логарифмированием его обеих частей,
Также необходимо отметить для учащихся следующее:
Применение формул логарифмирования может привести к потере корней, так как область определения сужается, поэтому в данном случае нужно пользоваться следующими формулами:
Учитель отмечает, что самой распространенной ошибкой является ошибка — учащиеся переходят от логарифмического уравнения к уравнению следствию, а проверку сделать забывают, или не правильно усвоили фразу: » логарифм не определен для отрицательного числа». В дальнейшей работе необходимо уделить особое внимание данным замечаниям.
На доске записано уравнение logf(x)= logg(x), a >0, a 1.
Учащимся предлагается записать алгоритм его решения в своих тетрадях. Один из учащихся записывает на доске.
Запись: logf(x)= logag(x), a >0, a 1.
Равносильно каждой из следующих систем:
1) и
2)
(можно спросить учащихся, какие уравнения называются равносильными)
Учитель: Выполним решение уравнения: log2(4x-8)= log2(3x-5).
Учащийся выходит к доске и записывает решение:
log2(4x-8)= log2(3x-5).
Решение: Уравнение равносильно системе:
Решаем систему и получаем ответ х=3.
Учитель: «Необходимо помнить, что замечания по решению логарифмических уравнений необходимо учитывать и при решении логарифмических неравенств.
Что является главным при решении неравенства?»
Учащиеся: Нужно запомнить — при каком основании «перевернуть» знак неравенства.
Учитель: «Какое свойство логарифмической функции нужно помнить?»
Учащиеся: «Свойство монотонности —
— функция у = logax возрастает на всей области определения, если а>1.
— функция у = logax убывает на всей области определения, если 0< а>1″.
Учащиеся: «Знак меняется на противоположный, если 0< а>1.»
Учитель: «Какие схемы помогают решать логарифмические неравенства?»
Учащиеся записывают в тетради. Для помощи учащимся, не справившимся с заданием, несколько более «сильных» учащихся записывают на доске:
logaf(x)> logag(x), a >0, a 1.
Или logaf(x) >g(x), a >0, a 1. Решаем по определению:
Учитель: «Решим неравенство устно: log2х>5″.
Учащиеся дают ответ:т.к.2>1, х>0, то х>25 , х>32.
Учитель: «Среди заданий ЕГЭ есть такие, которые предлагают для нахождения ответа применение решений логарифмических неравенств.
Например: Найти область определения функции: f(x)=
Предлагаю выполнить решение вместе.
Учащийся выходит к доске и выполняет решение.
f(x)=
выражение, стоящее под знаком корня должно быть 0.
Значит, нам предстоит решить логарифмическое неравенство, поэтому запишем:
{log 0,5(x2-9) +4 0, x2-9>0.
log 0,5(x2-9) -4 ,т.к. функция у=log 0,5t убыв на всей области определения ( 0<0,5<1), переходим к неравенству:
x2-9 0,5-4, x2-9 16, x2-25 0, х,
Ответ. х.
___. Закрепление знаний. Работа в разноуровневых группах.
1. Учащиеся выбирают карточки с заданиями. Приступают к выполнению.
Карточки с вариантами заданий представлены в приложениях.
Задания подобраны с учетом рекомендаций Федерального института педагогических измерений и курса «Система подготовки к ЕГЭ по математике».
Каждый учащийся работает в тетради. Некоторых учащихся можно вызвать к доске
(учащихся, которые решают задания разного уровня) для записи решения и комментариев отдельных уравнений, неравенств. Остальные могут сверить решение, если нужно — исправить ошибки.
2. Самопроверка учащихся.
На экране появляется слайд с таблицей верных ответов. Учащиеся сверяют ответы.
Оценивают свою работу. Делают вывод.
_V. Подведение итогов. Рефлексия.
Учитель обращает внимание на теоретический материал, уравнения, неравенства, предложенные на уроке. Отмечает успешную работу отдельных учащихся.Выставляет оценки.
Продолжите фразу:
- «Сегодня на уроке я повторил:.»
- «Сегодня на уроке я закрепил:.»
- «Для себя я понял:»
В качестве домашнего задания учащиеся получают вариант тематической проверочной работы.
Задания смотрим в Приложении 2.
xn--i1abbnckbmcl9fb.xn--p1ai
Логарифмические уравнения, примеры решений
Найдем ОДЗ:
Решение логарифмического уравнения имеет вид . Применяя это к исходному уравнению, получим
Умножим левую и правую части последнего равенства на , получим:
Полученное показательное уравнение решим методом замены переменной. Введем замену , тогда уравнение примет вид:
Полученное квадратное уравнение можно свернуть по формулам сокращенного умножения в квадрат разности:
Сделаем обратную замену ОДЗ.
ru.solverbook.com
Самостоятельная работа по математике на тему: «Решение логарифмических уравнений».
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №4
г.Рассказово Тамбовская область
Самостоятельная работа по математике.
Тема: «Решение логарифмических уравнений». Задания типаВ5 из открытого банка заданий ЕГЭ(http://mathege.ru/)
Подготовила: учитель математики
МБОУ СОШ №4
Ситникова Н.В
11 класс
Задание типаВ5 в ЕГЭ проверяет умение решать простейшие уравнения. Данная разработка посвящена одному из разделов задания В5 – это решение логарифмических уравнений.
Самостоятельная работа предназначена для проверки уровня знаний, умений и навыков учащихся по данной теме и поможет выпускникам при подготовке к ЕГЭ.
Задачи:
— повторить основные логарифмические свойства;
— научится применять их при решении логарифмических уравнений;
— повысить вычислительную культуру учащихся.
Представленная проверочная работа состоит из 11 вариантов, в каждом из которых по 12 заданий. Задания данной работы соответствуют прототипам заданий В5 из открытого банка заданий ЕГЭ по математике. Данный материал можно использовать при изучении темы: «Простейшие логарифмические уравнения». Для удобства проверки приведены ответы.
Логарифмические уравнения, задания типа В5 из открытого банка заданий ЕГЭ.
1вариант
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Найдите корень уравнения .
Найдите корень уравнения .
2вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10)Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
3вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
4вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
5вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
6вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
7вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
8вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
9вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
10вариант
1)Найдите корень уравнения .
2) Найдите корень уравнения .
3) Найдите корень уравнения .
4) Найдите корень уравнения .
5) Найдите корень уравнения .
6) Найдите корень уравнения .
7) Найдите корень уравнения .
8) Найдите корень уравнения .
9) Найдите корень уравнения .
10) Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11) Найдите корень уравнения .
12) Найдите корень уравнения .
Ответы:
№
1
2
3
4
5
6
7
8
9
10
11
12
1в
-124
21
-7
-12
7
-4,2
1
1,2
0
6
5,5
13,4
2в
-77
72
1
-7
7
-14
-118
-4
-0,7
-3
0
34,5
3в
-33
0
15
3
4
-51
0
-2,75
0
6
0
-0,8
4в
-57
29
-13
5
-11
-1
1
1
1
6
4
59,5
5в
-5
125
14
-4
3
-68
-20
6
1
-2
5,5
115
6в
-21
22
-6
0
26
0
-614
-9
1,5
1
9,5
-1,5
7в
-11
0
1
2
4
-3
-10,5
-0,75
0,8
6
4,4
2
8в
248
28
-1
-14
3
-1
0,2
9
0,4
12
5
171
9в
-24
56
5
-7
5
-2
-21
0,4
8
7
10
22
10в
-508
121
9
-11
16
-15
-0,2
2
-2
-4
2
125,5
infourok.ru
