7 класс геометрия основные теоремы – . 7 —

Смежными углами называют два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой;

filesclub.net

Теория по геометрии 7 класс

Теория по геометрии 7 класс

Основные понятия

Теорема — утверждение, которое доказывается путем рассуждений. Доказательство — сами рассуждения.

Определение — предложение, в котором разъясняется смысл того или иного выражения или названия.

Аксиома или постулат — исходное положение, принимаемое без доказательств и лежащее в основе доказательств истинности других положений (предложение, не требующее доказательств; самоочевидный факт).

Аксиомы геометрии можно разбить на пять групп.

1. Аксиомы принадлежности

1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.

1.2 Через любые две точки можно провести прямую и притом только одну.

1.3 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости и точки, не принадлежащие ей.

2. Аксиомы расположения

2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.

2.2 Прямая разбивает плоскость на две полуплоскости.

2.4 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

3. Аксиомы измерения

3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

4. Аксиомы откладывания.

4.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.

4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с заданной градусной мерой, меньшей  и притом только один.

4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.

5. Аксиома параллельности.

5.1 Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной. (аксиома параллельных прямых).

Начальные геометрические сведения

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой. Сумма смежных углов равна 180º.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Вертикальные углы равны.

Перпендикулярные прямые — это прямые, при пересечении которых образуются четыре прямых угла.

Две прямые, перпендикулярные к третьей прямой, не пересекаются.

Треугольники

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Точки — вершины, отрезки — стороны. Элементы треугольника: углы и стороны.

Периметр треугольника— сумма длин всех сторон.

Если два треугольника равны, то соответственные элементы таких треугольников тоже равны.

Против соответственно равных сторон лежат соответственно равные углы и наоборот, против равных углов лежат соответственно равные стороны.

Признаки равенства треугольников

Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и при том только один.

Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.

Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.

В любом треугольнике:

• медианты пересекаются в одной точке;

• биссектрисы пересекаются в одной точке;

• высоты пересекаются в одной точке.

Равнобедренный треугольник — треугольник, у которого две стороны равны.Равные стороны — боковые стороны, третья сторона — основание.

Свойства:

1.В равнобедренном треугольнике углы при основании равны.

2.В равнобедренном треугольнике высота, проведенная к основанию является биссектрисой и медианой (медиана является высотой и биссектрисой; биссектриса является высотой и медианой).

Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник равнобедренный.

Равносторонний треугольник — треугольник, у которого все стороны равны.

Свойства:

1. В равностороннем треугольнике все углы равны по 60 градусов.

2. В равностороннем треугольнике все медианы — высоты и биссектрисы.

Признак: если в треугольнике все углы равны, то он равносторонний.

В треугольнике: 1) против большей стороны лежит больший угол; 2) против большего угла лежит большая сторона, и наоборот.

Неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон.

Сумма углов треугольника равна .

Внешний угол треугольника — угол, смежный с каким-нибудь внутренним углом треугольника.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Виды треугольников :

Остроугольный — треугольник, у которого все углы острые.

Тупоугольный — треугольник, у которого один угол тупой.

Прямоугольный — треугольник, у которого один угол прямой (сторона, лежащая напротив угла в 90 градусов, называется гипотенузой; стороны, образующие угол в 90 градусов, называются катетами). В прямоугольном треугольнике гипотенуза больше катета.

Свойства:

1. Катет, лежащий напротив угла в равен половине гипотенузы.

2. Сумма острых углов прямоугольного треугольника равна 90°.

3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен .

Окружность — геометрическая фигура, состоящая их всех точек плоскости, равноудаленных от заданной точки, называемой центром окружности.

Радиус — отрезок, соединяющий центр окружности и точку на окружности.

Хорда — отрезок, соединяющий две точки на окружности.

Диаметр — хорда, проходящая через центр окружности.

Дуга окружности — часть окружности, ограниченная двумя точками.

Круг — часть плоскости, ограниченная окружностью.

Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.

Параллельные прямые

Параллельные прямые — две прямые на плоскости, которые не пересекаются (не имеют общих точек).

Углы:

Накрест лежащие

При пересечении двух параллельных прямых секущей накрест лежащие углы равны.

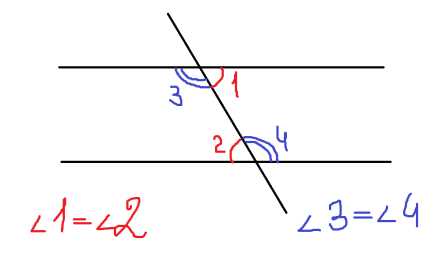
Односторонние

При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180.

Соответственные

При пересечении двух параллельных прямых секущей соответственные углы равны.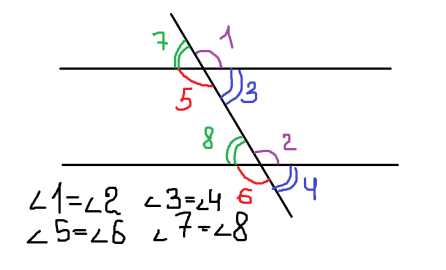

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых третьей накрест лежащие(внутренние или внешние) углы равны, то такие прямые параллельны.

2. Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых третьей сумма односторонних (внутренних или внешних) углов равна , то прямые параллельны.

Аксиома параллельных прямых: Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной.

Следствия из аксиомы параллельных прямых:

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

2.Если две прямые параллельны третьей прямой, то они параллельны.

Теоремы об углах, образованных двумя параллельными прямыми и секущей

1. Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Следствие: Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Расстояние от точки до прямой — это перпендикуляр, проведенный из данной точки к данной прямой. Любая другая прямая, отличная от перпендикуляра, называется наклонной. Любая наклонная больше перпендикуляра. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

infourok.ru

Теоремы по геометрии 7 класс

Т. Свойство смежных углов.

Дано: ∟ АОВ и ∟ ВОС – смежные

_________________________ Доказать: ∟ АОВ + ∟ ВОС = 180⁰

Доказательство:

1. По условию ∟ АОВ и ∟ВОС – смежные, значит ∟ АОВ + ∟ ВОС = ∟ АОС

2. ∟ АОС – развернутый (по определению), значит ∟ АОС = 180⁰

Из первого и второго равенств следует, что: ∟ АОВ + ∟ВОС = 180⁰. Вывод.

Т. Свойство вертикальных углов.

Дано: ∟ АОВ и ∟СОД – вертикальные

Доказать: ∟АОВ = ∟СОД

Доказательство:

1. ∟ АОВ и ∟ ВОС – смежные (по определению), значит ∟АОВ + ∟ ВОС = 180⁰.

∟АОВ = 180⁰ — ∟ ВОС

2. ∟ ВОС и ∟ СОД – смежные (по определению), значит ∟ ВОС + ∟СОД = 180⁰.

∟СОД = 180⁰ — ∟ВОС

Из первого и второго равенств следует, что: ∟ АОВ = ∟СОД (если в двух равенствах правые части равны, то и левые части равны). Вывод.

Т. Первый признак равенства треугольников (по СУС).

Дано: Δ АВС, Δ А₁В₁С_1,

АВ = А₁В₁, АС = А₁С₁, А = А₁

Доказать: Δ АВС = Δ А₁В₁С₁

Доказательство:

1. Наложим Δ АВС на Δ А₁В₁С₁ так: вершину А совместим с вершиной А₁, луч АВ с лучом А₁В_1.

2. По условию ∟А = ∟ А₁, значит луч АС совместится с лучом А₁С₁.

3. По условию отрезок АВ = А₁В_1, значит точка В совместится с точкой В₁,

отрезок АС = А₁С₁, значит точка С совместится с точкой С_1.

_{Значит, весь Δ АВС полностью совместился с Δ А1В1С1, значит Δ АВС =Δ А1В1С1(по опр). Вывод.}

Т. Свойство углов при основании равнобедренного треугольника.

Дано: Δ АВС – равнобедренный с основанием АС

Доказать: ∟ А = ∟ С

Доказательство:

1)Дополнительное построение: проведем биссектрису ВД.

2)Рассмотрим Δ АВД и Δ СВД: а) АВ = ВС (это боковые стороны равнобедренного треугольника),

б) ВД – общая сторона,

в) ∟ АВД = ∟ СВД (так как ВД – биссектриса ∟АВС)

__________________________________________

Значит, Δ АВД = Δ СВД (по СУС), тогда ∟ А = ∟ С, так как в равных треугольниках соответственные элементы равны. Вывод.

Т. Свойство биссектрисы равнобедренного треугольника,

проведенной к основанию.

Дано: Δ АВС – равнобедренный с основанием АС,

ВД – биссектриса

Доказать: 1) ВД – медиана, 2) ВД – высота

Доказательство:

1)Рассмотрим Δ АВД и Δ СВД: а) АВ = ВС (это боковые стороны равнобедренного треугольника),

б) ВД – общая сторона,

в) ∟ АВД = ∟ СВД (так как ВД – биссектриса ∟ АВС)

__________________________________________

Значит, Δ АВД = Δ СВД (по СУС). 2) В равных треугольниках соответствующие элементы равны:

а) АД = ДС, значит ВД – медиана ( по определению),

б) ∟ АДВ = ∟СДВ = 180⁰: 2 = 90⁰ ( так как они смежные ), значит ВД | АС и ВД – высота ( по определению)

Вывод.

Следствия из аксиомы параллельных прямых

Т1

_______________а Дано: а || в, с ∩ в = М

Доказать: с ∩ а

____М___________в

с

Доказательство (методом от противного):

1) Предположим, что с ∩ а, тогда с || а (по определению), в || а (по условию).

2) Получили, что через точку М проходит две прямых: с и в, обе || а.

3) Это противоречит аксиоме параллельных прямых. Значит предположение, что с ∩ а неверно. Тогда с ∩ а. Вывод.

Т 2

______________ а Дано: а || с, в || с

______________ в Доказать: а || в

______________с

Доказательство (методом от противного):

1) Предположим, что а || в, тогда а ∩ в = М. ______________а

2) Получили, что через точку М проходит две прямых: а и в, обе || с.

3) Это противоречит аксиоме параллельных прямых. Значит ______________с

предположение, что а || в неверно. Тогда а || в. Вывод.

Т Сумма углов в треугольнике.

_____________В____а Дано: Δ АВС, обозначим: ∟ А = ∟1, ∟В = ∟2, ∟С = ∟3.

Доказать: ∟1 + ∟2 + ∟3 = 180⁰

А С

Доказательство: 1) Дополнительное построение: через точку В проведем прямую а || АС,

обозначим ∟4 и ∟5.

2) ∟4 + ∟2 + ∟5 = 180⁰, так как они образуют развернутый угол.

3) ∟4 = ∟1, так как это накрест лежащие углы для а || АС и секущей АВ (по свойству)

∟5 = ∟3, так как это накрест лежащие углы для а || АС и секущей ВС (по свойству)

Значит ∟4 + ∟2 + ∟5 = ∟1 + ∟2 + ∟3 = 180⁰. Вывод: ∟А + ∟В + ∟С = 180⁰.

Т Свойство внешнего угла треугольника.

В Дано: Δ АВС, ∟ВСД — внешний

обозначим: ∟ А = ∟1, ∟В = ∟2, ∟АСВ = ∟3, ∟ВСД =4.

Доказать: ∟ВСД = ∟А + ∟В

___________________________

А С Д Доказательство:

1. ∟4 + ∟3 = 180⁰ (смежные), значит ∟4 = 180⁰ — ∟3

2. ∟1 + ∟2 + ∟3 = 180⁰ (по Т о сумме углов в треугольнике), значит ∟1 + ∟2 = 180⁰ — ∟3

3. Если в равенствах правые части одинаковые, то и левые части равны: ∟4 = ∟1 + ∟2 .

Вывод: ∟ВСД = ∟А + ∟В

Т Свойство прямоугольного треугольника с углом 30⁰.

В

Дано: Δ АВС, ∟С = 90⁰, ∟В = 30⁰.

Доказать: АС = ½ АВ

А Д Доказательство:

С

1. ∟А + ∟В = 90⁰ (по свойству прямоугольного Δ), значит ∟А = 90⁰ — ∟В = 90⁰ – 30⁰ = 60⁰

2. Д. п.: приложим к Δ АВС ΔВСД = ΔВСА.

3. В равных треугольниках соответственные элементы равны, значит ∟Д = ∟А = 60⁰, ∟ДВС = ∟АВС = 30⁰. Тогда ∟АВД = 30⁰ + 30⁰ = 60⁰ .

4. Следовательно ΔАВД – равносторонний, значит АВ = ВД = АД (по определению)

АС = СД = ½ АД, но АД = АВ, значит АС = ½ АВ.

(соответст) Вывод.

Т Признак равенства прямоугольных треугольников по гипотенузе и острому

углу.

А А₁Дано: Δ АВС, ΔА₁В₁С₁, ∟С = 90⁰, ∟С₁ = 90⁰

АВ = А₁В₁, ∟А = ∟А₁

С В С₁ В₁Доказать: Δ АВС = Δ А₁В₁С₁

_{Доказательство:}

1. Сумма острых углов в любом треугольнике равна 90⁰, значит

∟А + ∟В = 90⁰, следовательно ∟В = 90⁰ — ∟А

∟А₁ + ∟В_{1 =} 90⁰, следовательно ∟В₁ = 90⁰ — ∟А₁

Если в двух равенствах правые части равны, то и левые части равны, значит ∟В = ∟В₁

2. Тогда Δ АВС = Δ А₁В₁С₁ (по УСУ). Вывод.

infourok.ru

Основные определения и теоремы для подготовки к зачёту по геометрии Л. С. Атанасян 7 класс. PDF

Основные определения и теоремы
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.

Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия»
означает «землемерие»).
В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются
сторонами угла, а точка — вершиной угла.
Угол называется развѐрнутым, если обе его стороны лежат на одной прямой. ( Развѐрнутый угол равен 180°).
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
Угол называется прямым, если он равен 90°.
Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развѐрнутого).
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Вертикальные углы равны.
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех
отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки— сторонами треугольника.
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам
другого треугольника.
Теорема – утверждение, справедливость которого устанавливается путѐм рассуждений. Сами рассуждения называются
доказательством теоремы.
(Т. Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно
равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
(Т. о перпендикуляре к прямой) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и
притом только один.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной
стороны.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны.
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей
противоположную сторону.
(Свойства медианы, биссектрисы и высоты треугольника) В любом треугольнике медианы пересекаются в одной точке;
биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми
сторонами, а третья сторона — основанием равнобедренного треугольника.
Треугольник называется равносторонним, если все его стороны равны.
(Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике углы при основании равны.
(Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике биссектриса, проведенная к основанию,
является медианой и высотой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
(Т. Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
(Т. Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трѐм
сторонам другого треугольника, то такие треугольники равны.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от
данной точки. Данная точка называется центром окружности.
Радиус окружности – отрезок, соединяющий центр окружности с какой-либо еѐ точкой.
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Круг — это часть плоскости, ограниченная окружностью.
Две прямые на плоскости называются параллельными, если они не пересекаются.
При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и
соответственные.
(Т. Признак параллельности двух прямых по накрест лежащим углам) Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые параллельны.
(Т. Признак параллельности двух прямых по соответственным углам) Если при пересечении двух прямых секущей
соответственные углы равны, то прямые параллельны.
(Т. Признак параллельности двух прямых по односторонним углам) Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны.
Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений,
на основе которых доказываются теоремы и строится вся геометрия.
(Аксиома) Через любые две точки проходит прямая, и притом только одна.

44. (Аксиома параллельных прямых) Через точку, не лежащую на данной прямой, проходит только одна прямая,
параллельная данной.
45. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
46. Если две прямые параллельны третьей прямой, то они параллельны.
47. Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).
48. Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а
заключением – условие данной теоремы.
49. (Т.) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
50. (Т.) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
51. (Т.) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
52. (Т. о сумме углов треугольника) Сумма углов треугольника равна 180°.
53. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
54. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
55. Если все три угла треугольника острые, то треугольник называется остроугольным.
56. Если один из углов треугольника тупой, то треугольник называется тупоугольным.
57. Если один из углов треугольника прямой, то треугольник называется прямоугольным.
58. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны,
образующие прямой угол — катетами.
59. (Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший
угол, и обратно, против большего угла лежит большая сторона.
60. В прямоугольном треугольнике гипотенуза больше катета.
61. (Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
62. (Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
63. (Свойство прямоугольного треугольника) Сумма двух острых углов прямоугольного треугольника равна 90°.
64. (Свойство прямоугольного треугольника) Катет прямоугольного треугольника, лежащий против угла в 30°, равен
половине гипотенузы.
65. (Свойство прямоугольного треугольника) Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
66. (Признак равенства прямоугольных треугольников по двум катетам) Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие треугольники равны.
67. (Признак равенства прямоугольных треугольников по катету и острому углу) Если катет и прилежащий к нему острый
угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие
треугольники равны.
68. (Т. Признак равенства прямоугольных треугольников по гипотенузе и острому углу) Если гипотенуза и острый угол
одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники
равны.
69. (Т. Признак равенства прямоугольных треугольников по гипотенузе и катету) Если гипотенуза и катет одного
прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
70. Расстоянием от точки до прямой называется длина перпендикуляра, проведѐнного из этой точки к прямой.
71. (Т. Свойство параллельных прямых) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
72. Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных
прямых до другой прямой.
Чертежи ко всем вопросам!!!

freedocs.xyz