Контрольные работы по математике 11 класс
Инфоурок › Алгебра › Другие методич. материалы › Контрольные работы по математике 11 классВыберите документ из архива для просмотра:
Выбранный для просмотра документ Логарифм нер-ва.doc
Выбранный для просмотра документ Показат и логарифм уравнения.doc
Выбранный для просмотра документ Показат нер-ва.doc
Выбранный для просмотра документ Прост логарифм ур.doc
Выбранный для просмотра документ Прост показат ур.doc
Выбранный для просмотра документ Простейшие иррац ур.doc
Выбранный для просмотра документ Степ с рац показ.doc
Выбранный для просмотра документ Тождест преобр рац выр.doc
Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
Общая информация
Номер материала: ДБ-053930
infourok.ru
|
РАЗРАБОТКИ |
11 классВ категории разработок: 22 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Книга посвящена особому классу задач, который называют «софизмами». Суть их в том, что требуется найти ошибку в заведомо ложном доказательстве. Последнее иногда оказывается довольно сложно. Не случайно с греческого «софизм» можно перевести как хитрая выдумка, уловка. Некоторые софизмы возникли еще в античном мире, скорее всего в результате ошибок в серьезных рассуждениях. Но история происхождения большей их части навсегда останется тайной. Зачем нужны такие задачи? На этот вопрос ответил в предисловии к одной из своих книг известный популяризатор науки, профессор Геттингенского университета немецкий математик Карл Литцман: «Серьезное значение изучения ошибок и софизмов для воспитания математического мышления, как кажется автору, еще недостаточно осознано. Не только учитель должен иметь дело с ошибками, которые делают его ученики; сами учащиеся зачастую научаются большему на примере разъясненной ошибки, чем даже при правильном выполнении по готовым образцам задач и упражнений»
Целевая аудитория: для 11 класса Контрольная работа по теме «Тела вращения». Контрольная работа содержит 4 варианта по пять заданий в каждом. Тексты контрольной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Задания контрольной работы взяты из сборника экзаменационных материалов за курс средней школы (базовый уровень). Создана контрольная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Целевая аудитория: для 11 класса Самостоятельная работа содержит 2 варианта по пять заданий в каждом. Тексты самостоятельной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана самостоятельная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Целевая аудитория: для 11 класса Контрольная работа по теме «Многогранники». Контрольная работа содержит 2 варианта по пять заданий в каждом. Тексты контрольной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана контрольная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Целевая аудитория: для 11 класса Самостоятельная работа по теме «Преобразование графика показательной функции». Самостоятельная работа содержит 2 варианта по пять заданий в каждом. Тексты самостоятельной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана самостоятельная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Целевая аудитория: для 11 класса Целевая аудитория: для 11 класса Самостоятельная работа по теме «Понятие логарифма. Основное логарифмическое тождество». Самостоятельная работа содержит 2 варианта по пять заданий в каждом. Тексты самостоятельной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана самостоятельная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Целевая аудитория: для 11 класса Самостоятельная работа по теме «Показательная функция». Самостоятельная работа содержит 2 варианта по три заданий в каждом. Тексты самостоятельной работы разбиты по трем уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана самостоятельная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы.Самостоятельная работа проводится по итогам пройденного материала соответственной темы. Также материал самостоятельной работы можно использовать как подготовку к централизованному тестированию и для проведения факультативных занятий по математике. Целевая аудитория: для 11 класса Контрольная работа по теме «Конус. Площадь сферы и объем шара». Контрольная работа содержит 5 вариантов по пять заданий в каждом. Тексты контрольной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана контрольная работа в текстовом редакторе Microsoft Word. Для удобства приведены правильные ответы. Контрольную работу можно использовать для проведения самостоятельных работ, для подготовки к сдаче экзаменов, для проведения факультативных курсов. Целевая аудитория: для 11 класса В 10 классе на первом уроке двухурочной контрольной работы учащиеся отвечают на вопросы по теории (письменно и без использования каких-либо дополнительных источников информации). На втором уроке учащиеся получают текст контрольной работы на два варианта и с буквенными данными, а также карточку с индивидуальными числовыми данными, с которыми должны решить задачи своего варианта, а затем ПРОВЕРИТЬ правильность решения по таблицам конечных и промежуточных ответов, разработанных учителем. В случае ошибочного решения учащийся должен на уроке контрольной работы исправить свои ошибки, а только после этого приступать к следующей задаче. В итоге за подобные исправления он получит 0,5 балла. По завершению уроков тематического контроля учитель собирает тетради и выставляет учащимся две оценки: одну — за теорию (ее можно исправить только устно) и вторую — за практику (ее можно исправить, решив задачи противоположного варианта).В 11 классе теория не проверяется, а на каждом из двух уроков тематического контроля учащиеся решают задачи с индивидуальным набором числовых данных, проверяют правильность решения по таблицам конечных и промежуточных ответов и получают одну оценку по итогам двух уроков.примечание: на уроке проверки практических умений и навыков учащиеся могут воспользоваться любыми дополнительными источниками информации, а также консультироваться друг с другом и с учителем. Целевая аудитория: для 11 класса |
Конкурсы Диплом и благодарность каждому участнику! |
www.uchportal.ru
Сборник контрольных работ по математике в 11 классе
Сборник
контрольных работ по математике
11 класс
естественно-математического направления
Авторы: Соколова В.А., Лутченко А.Н.
учителя математики
КГУ «Майская средняя школа Отдела образования
акимата Тарановского района»
2014 г
Пояснительная записка
Сборник содержит полный набор контрольных работ по всему курсу алгебры и началам анализа и геометрии для 11 класса естественно-математического направления : в двух вариантах по каждой теме и итоговые контрольные работы.
Тематика и содержание работ охватывают требования действующих программ по математике для 10-11 классов естественно-математического направления утверждённых приказом Министра образования и науки Республики Казахстан №115 от 3 апреля 2013 года.
Материалы сборника будут полезны учителям и учащимся и их можно использовать при организации тематического и обобщающего контроля, итогового повторения.
Сборник можно применять в школах с различными учебно-методическими планами. Учитель сможет выбирать задания из сборника, которые гармонично впишутся в его индивидуальный творческий процесс.
Содержание
11 класс Алгебра и начала анализа
Контрольная работа по теме «Первообразная и интеграл»
Вариант 1
Найдите общий вид первообразной
для функции:
;
;
f(x)=3 .
Вычислите интеграл
dx;
.
Вычислить площадь фигуры, ограниченной линиями
у=х2-5х+6, у=3-x.
При каких значениях а верно неравенство:
Вариант 2
1.Найдите общий вид первообразной для функции:
1) ;
2) ;
3) f(x)= .
Вычислите интеграл
1) dx;
2).
Вычислить площадь фигуры, ограниченной линиями
у=х2-2x+1, у=3-x.
При каких значениях а верно неравенство:
11 класс Алгебра и начала анализа
Контрольная работа по теме «Применение интеграла»
Вариант 1
Найдите площадь фигуры, ограниченной линиями:
у = 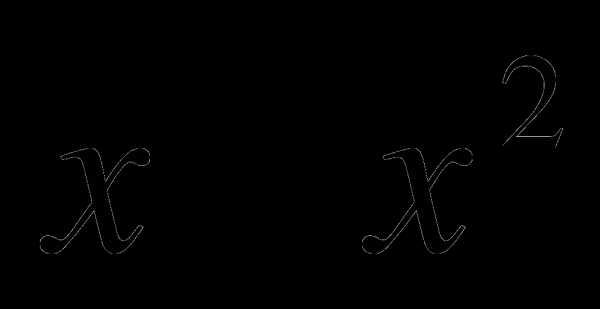 и у =
и у = 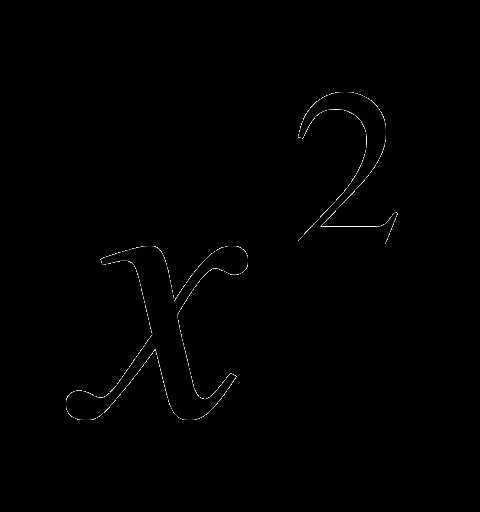 — х
— х
Найти объём тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
у = 1 — х и у = 0.
и у = 0.
Найти площадь фигуры , ограниченной линиями :
у = х + 1; у = 2 и осью ОУ.
+ 1; у = 2 и осью ОУ.
Вариант 2
Найдите площадь фигуры, ограниченной линиями:
у = 2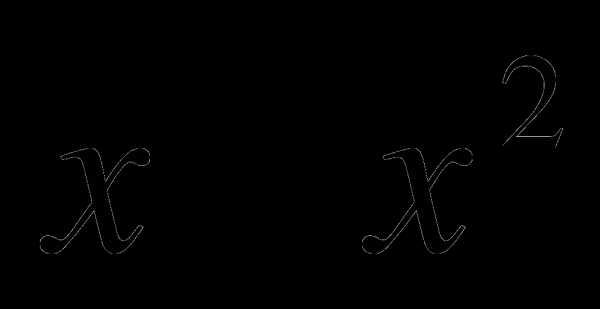 и у =
и у = 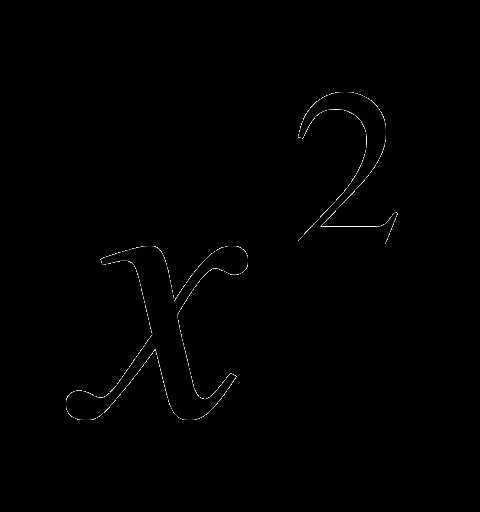
Найти объём тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
у = 2 + х , х= -1, х =1, у = 0.
, х= -1, х =1, у = 0.
Найти площадь фигуры , ограниченной линиями :
у = 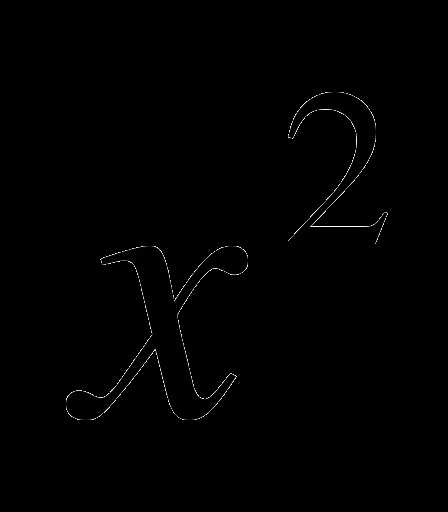 + 4,5 ; у = 4,5
+ 4,5 ; у = 4,5
11 класс Алгебра и начала анализа
Контрольная работа по теме «Преобразование иррациональных выражений»
Вариант 1
Упростите выражение: а)
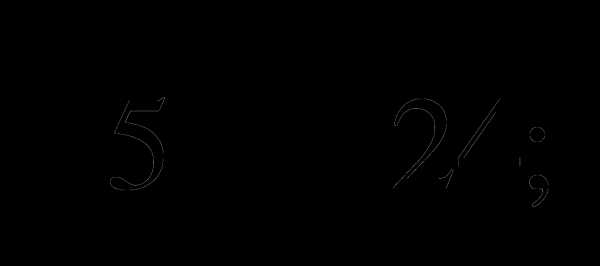 б)
б) 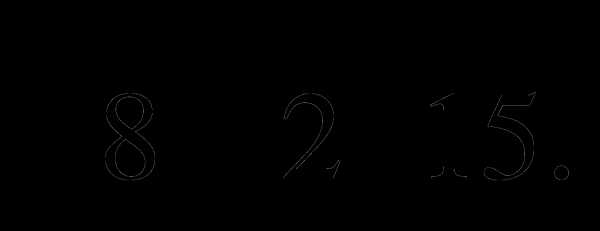
Вычислите:
Сократите дробь: а)
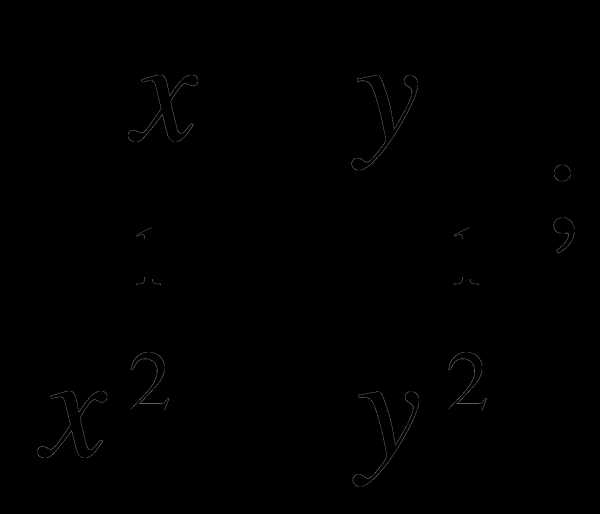 б)
б) 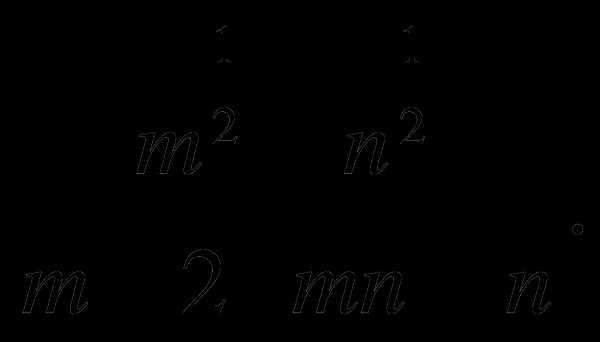
Вынести множитель из-под знака корня:
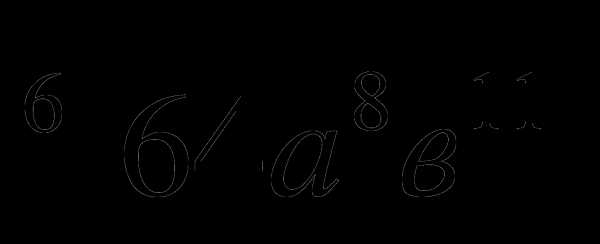
Избавиться от иррациональности в знаменателе дроби:
а)  б)
б)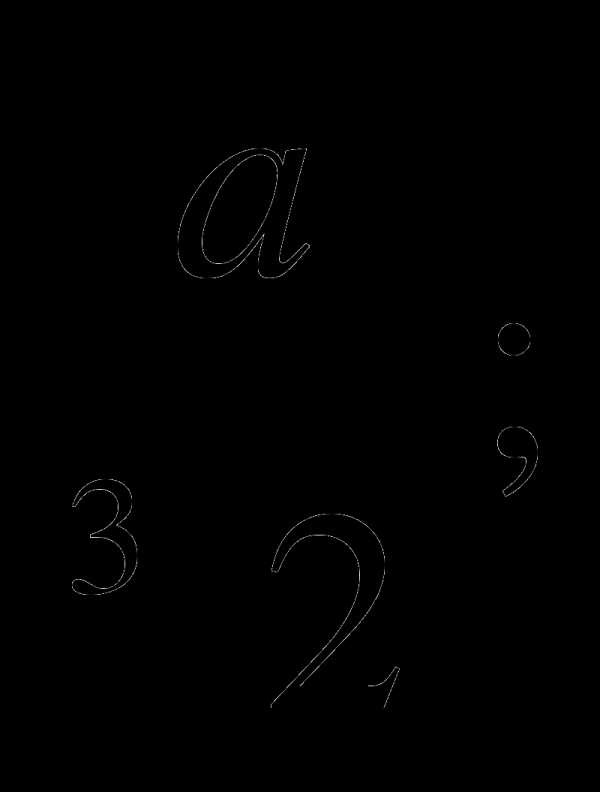 в)
в) 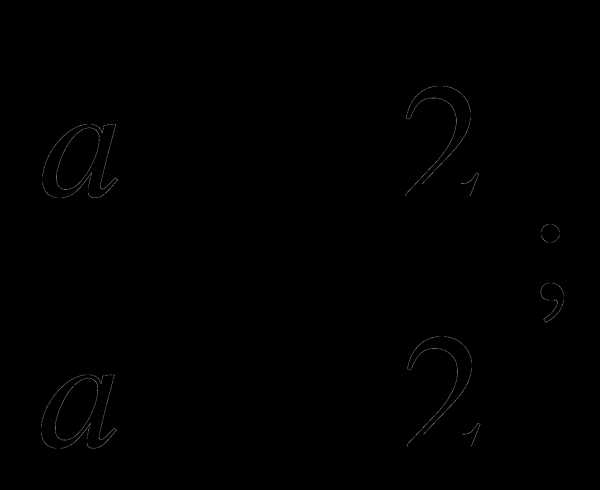 г)
г) 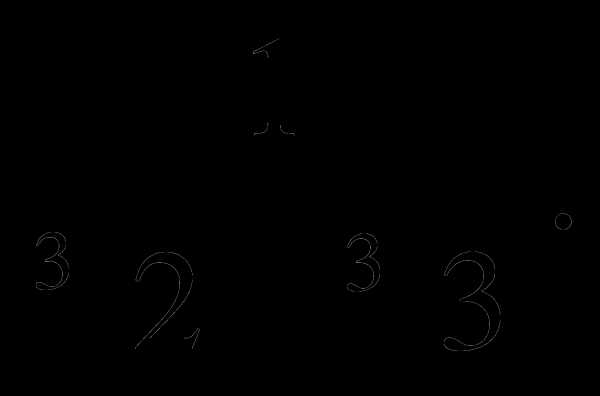
6. Упростите выражение: 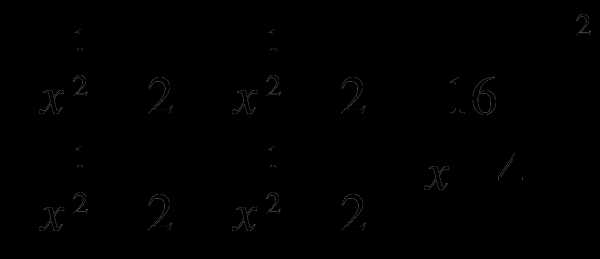
Вариант 2
Упростите выражение: а)
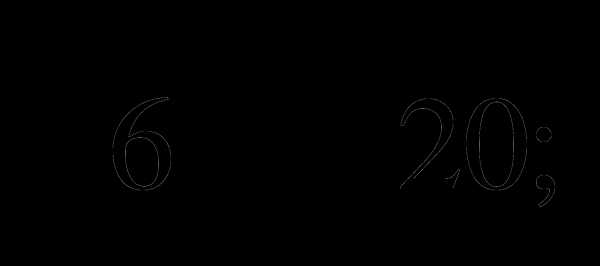 б)
б) 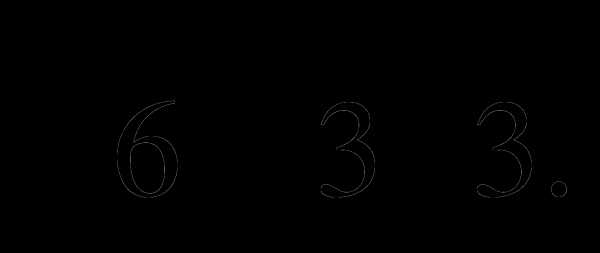
Вычислите:
Сократите дробь: а)
 б)
б) 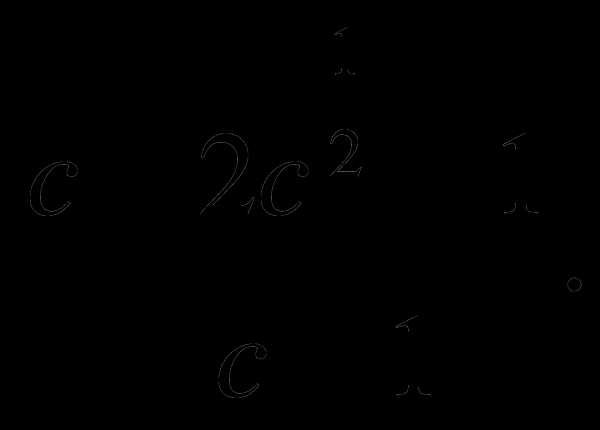
Вынести множитель из-под знака корня:
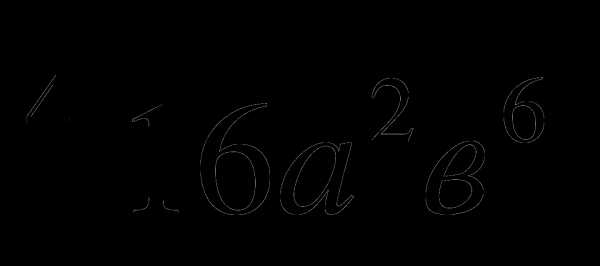
Избавиться от иррациональности в знаменателе дроби:
а)  б)
б) в)
в)  г)
г) 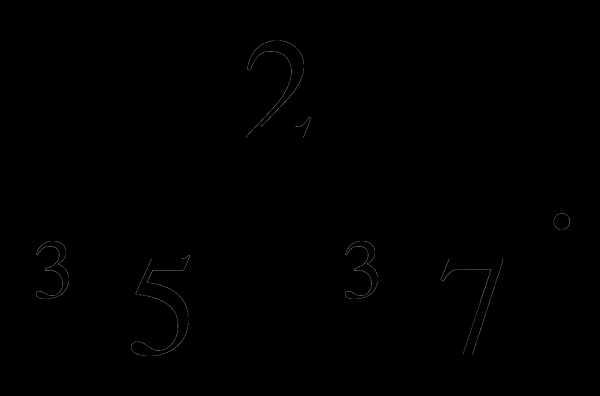
6. Упростите выражение:  .
.
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Решение иррациональных уравнений, неравенств и их систем»
Вариант 1.
Решить уравнения:
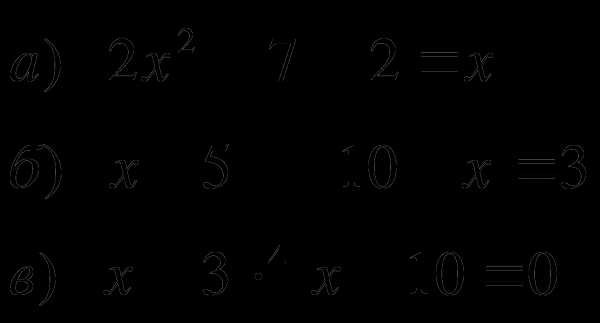
Решить неравенства:
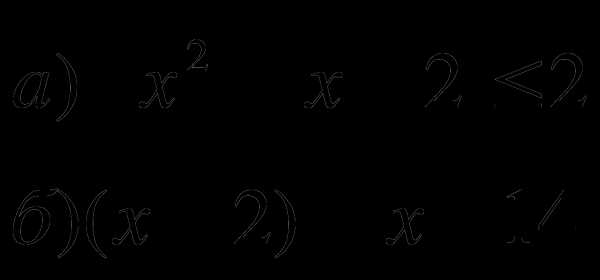
Решить систему уравнений:

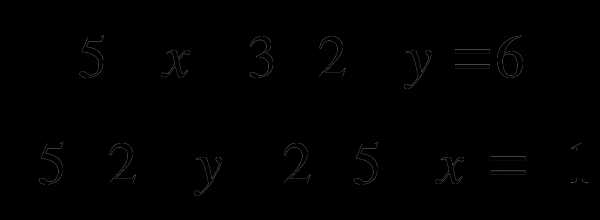
Вариант 2.
1.Решить уравнения:
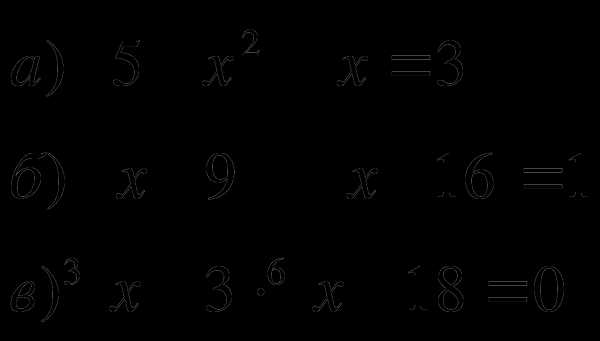
2.Решить неравенства:
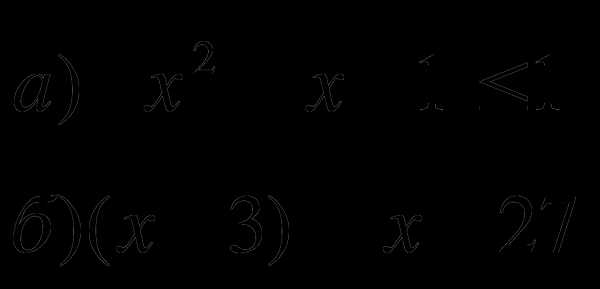
3.Решить систему уравнений:
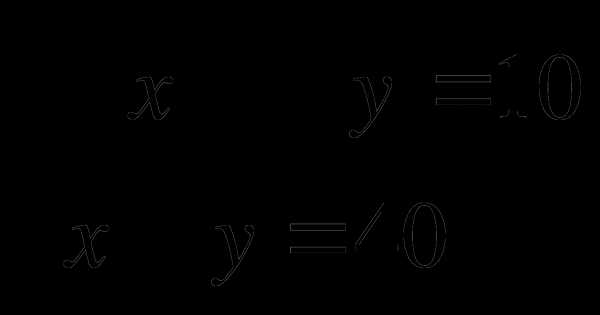
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Дифференцирование и интегрирование степенной функции
с действительным показателем»
Вариант 1
1. Найти производные функции:
a) 
b)
c) 
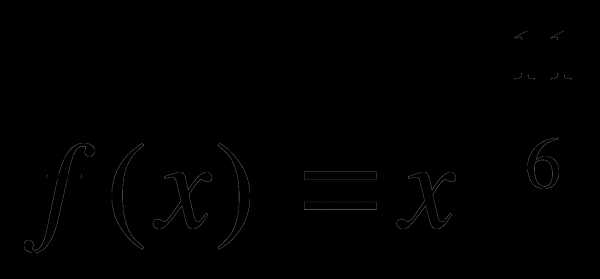
2. Составить уравнение касательной к графику функции 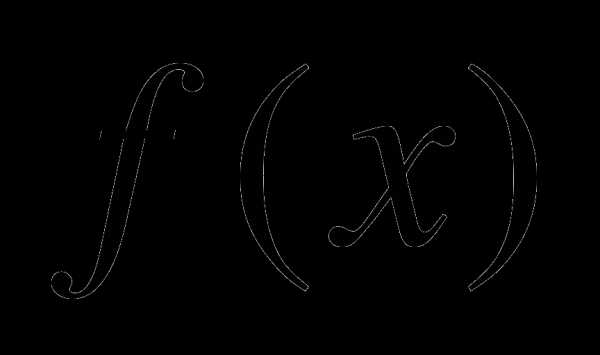 в точке с абсциссой
в точке с абсциссой 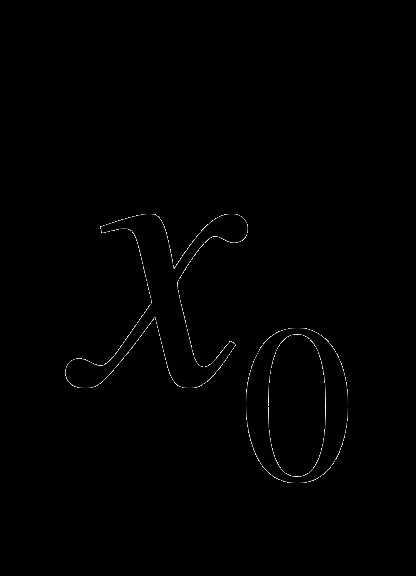 : .
: .
3. Вычислить площадь фигуры, ограниченной линиями:
Вариант 2
1. Найти производные функции:
a) 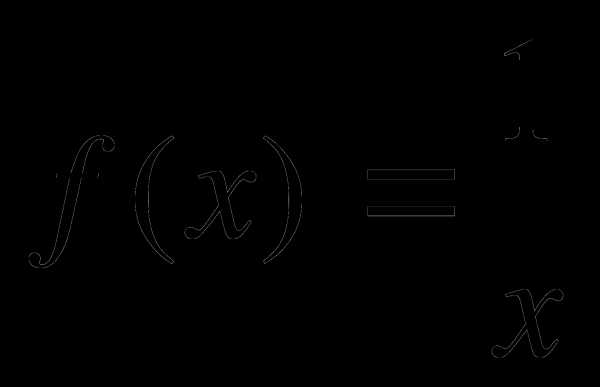
b) 
c) 
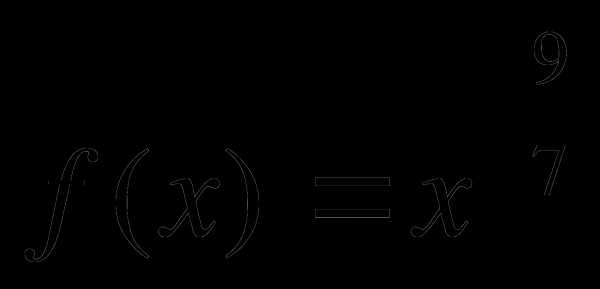
2. Составить уравнение касательной к графику функции 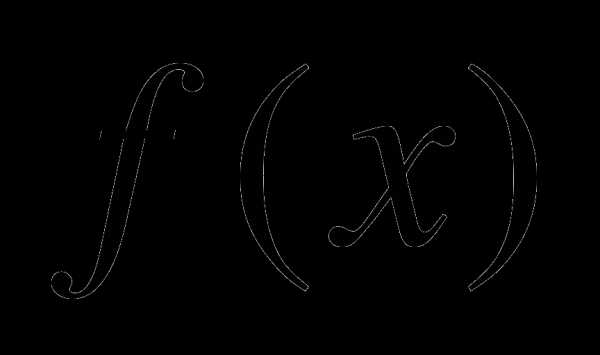 в точке с абсциссой
в точке с абсциссой 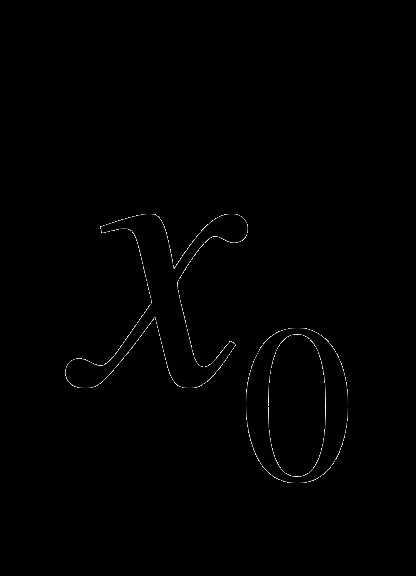 : .
: .
3. Вычислить площадь фигуры, ограниченной линиями:
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Дифференцирование и интегрирование показательной и логарифмической функций»
Вариант 1
Найдите
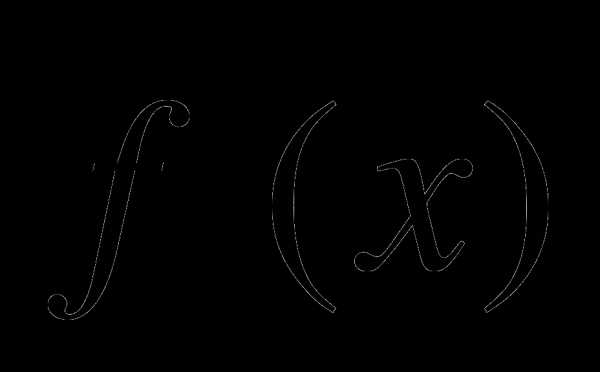 и
и 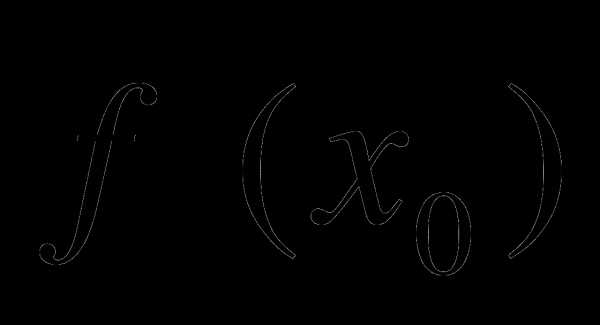 , если
, если
f(x) = 4 lnx, x =2.
=2.
Составьте уравнение касательной к графику функции f(x) = 3
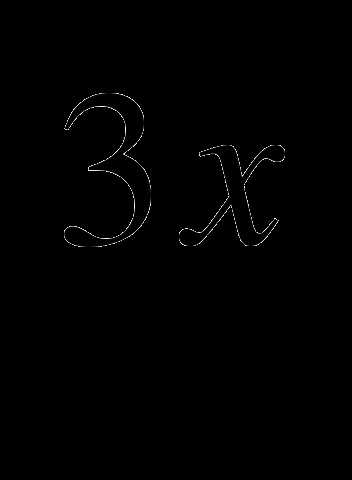 , проведённой через точку пересечения его с осью ординат.
, проведённой через точку пересечения его с осью ординат.
Найдите промежутки возрастания и убывания функции f(x) = 2х е
 .
.
Вычислите площадь фигуры, ограниченной линиями :
у =  , у = 0, у = 2, х = 0, х = 2.
, у = 0, у = 2, х = 0, х = 2.
Вариант 2
Найдите
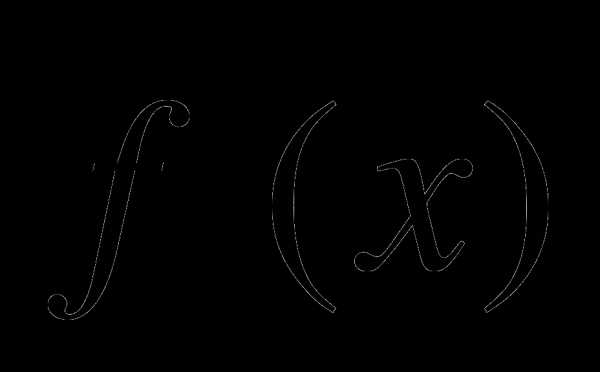 и
и 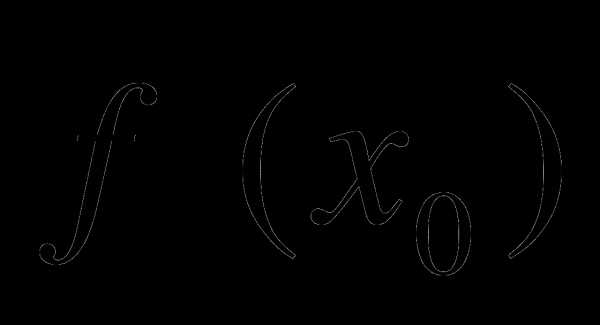 , если
, если
f(x) = 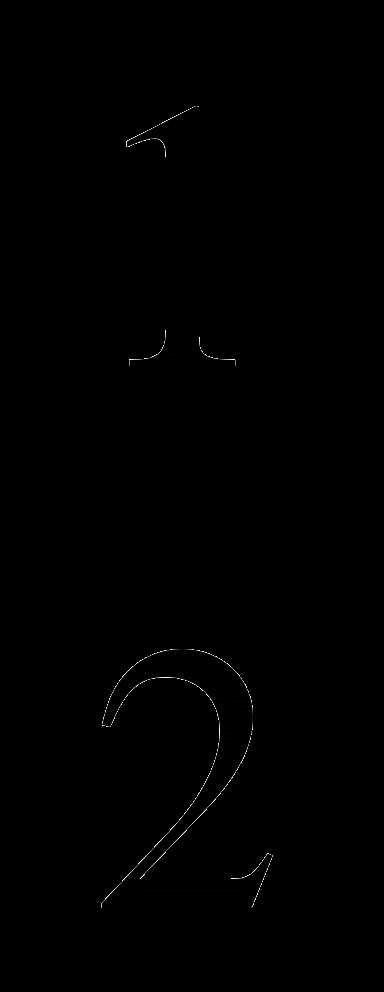 lnx, x
lnx, x =
=  .
.
Составьте уравнение касательной к графику функции f(x) = е
 , проведённой через точку пересечения его с осью ординат.
, проведённой через точку пересечения его с осью ординат.
Найдите промежутки возрастания и убывания функции f(x) =
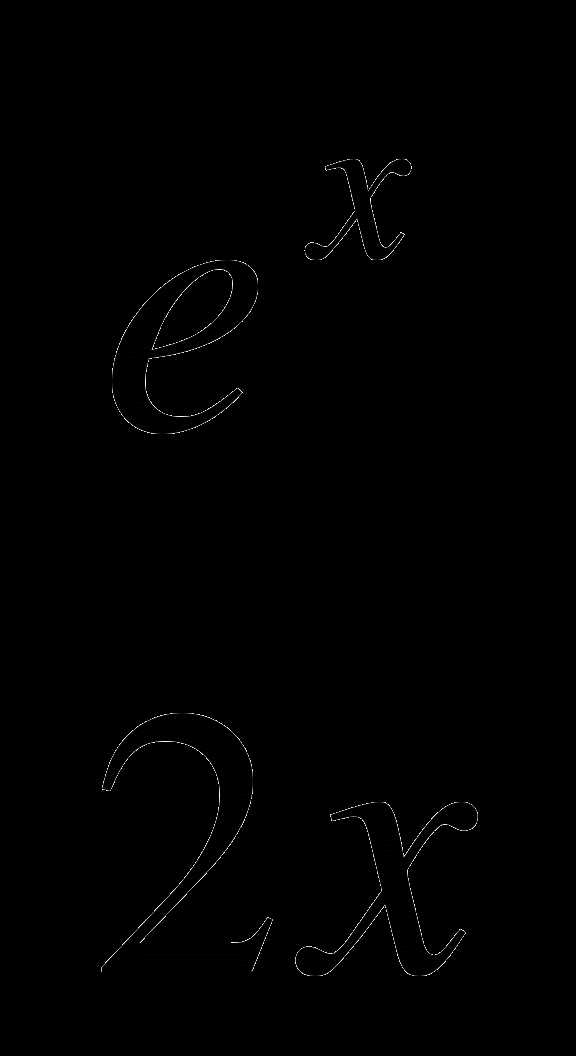 .
.
Вычислите площадь фигуры, ограниченной линиями :
у = 2 , у =
, у =  , х = 1.
, х = 1.
11 класс Алгебра и начала анализа
Контрольная работа по теме «Показательные уравнения и их системы»
Вариант 1
Решить уравнение:
1)
2)
3
Найти сумму квадратов корней уравнения:
Решить систему уравнений:
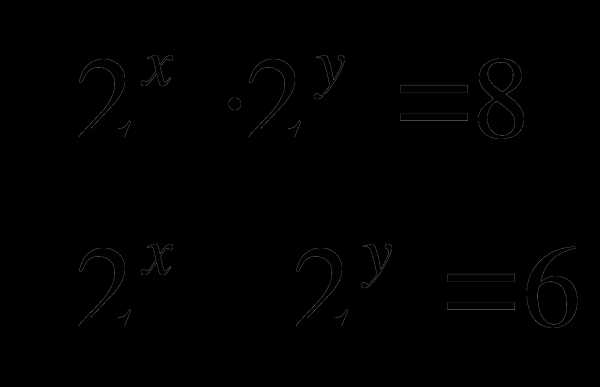
Найти х + 2у, где х и у решения системы уравнений:
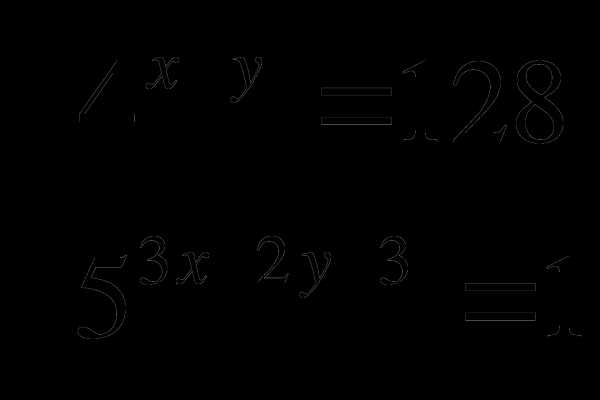
Вариант 2
Решить уравнение:
1)
2) 3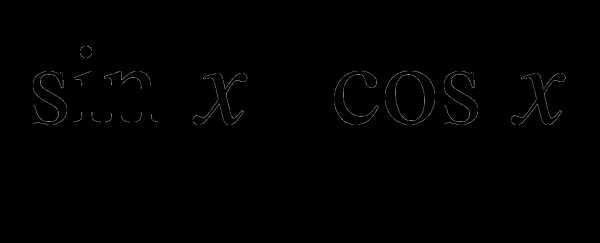 =1
=1
3) 2
2. Найти наибольший корень уравнения:
3. Решить систему уравнений: 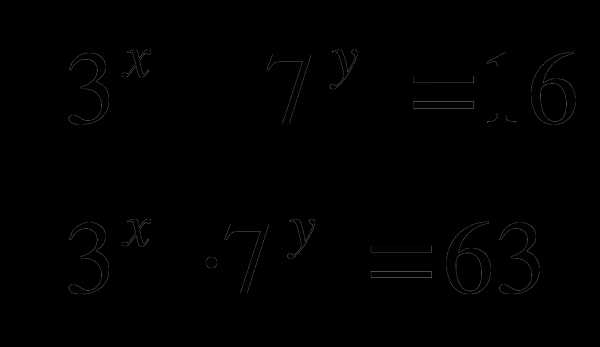
Найти
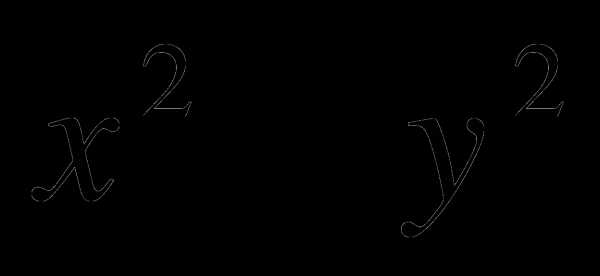 , где х и у решения системы уравнений:
, где х и у решения системы уравнений:
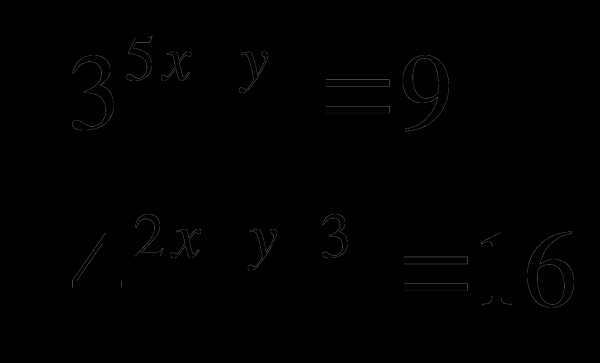
11 класс Алгебра и начала анализа
Контрольная работа по теме «Показательные неравенства и их системы»
Вариант 1
Решить неравенства:
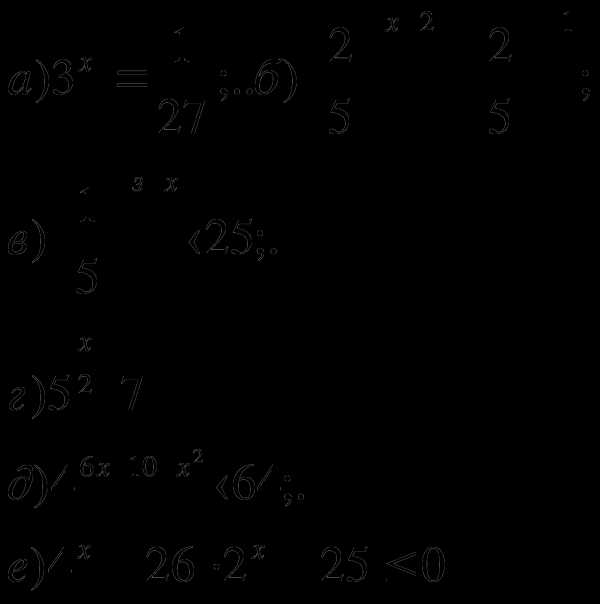
2.Найти длину отрезка, являющегося решением неравенства
3.Найти наименьшее целое решение неравенства:
4. Решить систему неравенств: 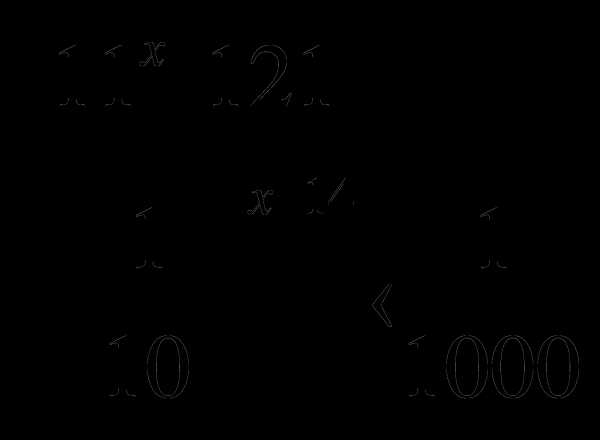
Вариант 2
Решить неравенства:
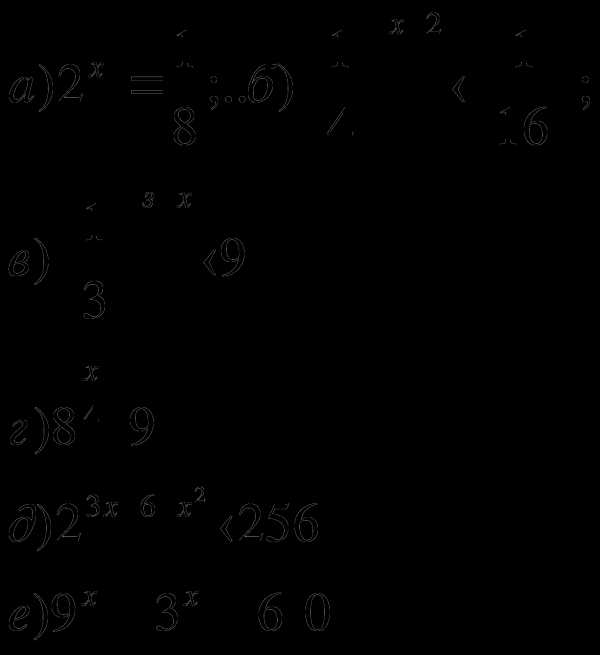
2.Найти длину отрезка, являющегося решением неравенства
3.Найти наименьшее целое решение неравенства:
4. Решить систему неравенств :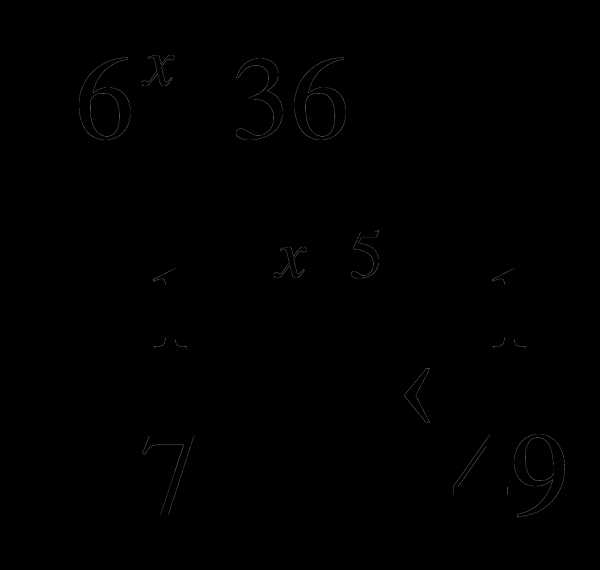
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Логарифмические уравнения, неравенства и их системы»
Вариант 1
1. Решить систему уравнений:
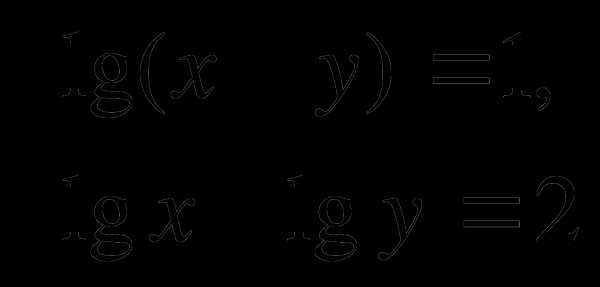
2. Решить уравнение:
3. Решить неравенство:
4.Найти сумму корней уравнения:
*5. Решить систему уравнений:
Вариант 2
1. Решить систему уравнений:
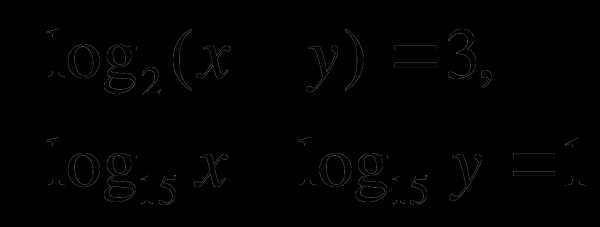
2. Решить уравнение:
3. Решить неравенство:
4.Найти произведение корней уравнения:
*5. Решить систему уравнений:
11 класс Алгебра и начала анализа
Итоговая контрольная работа (2часа)
Вариант 1
Найти сумму 75 первых членов последовательности, общий член которой определяется формулой .
Вычислить:
 .
.Найти область определения функции: .
Найдите общий вид первообразной функции: .
Решить систему уравнений:
Найдите наибольшее и наименьшее значения данных функций на указанных промежутках:
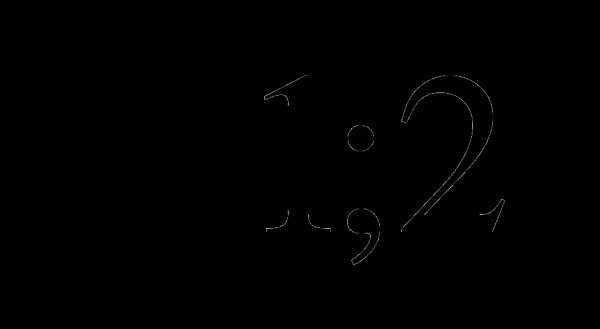
Вариант 2
Найти сумму 10 первых членов последовательности, общий член которой определяется формулой
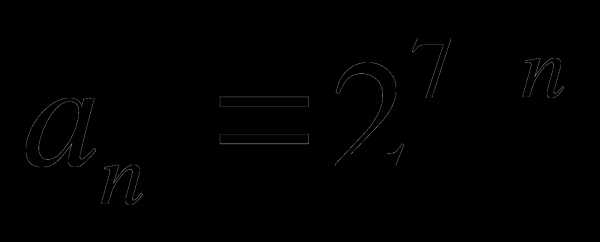 .
.Вычислить:
 .
.Найти область определения функции: .
Найдите общий вид первообразной функции: .
Решить систему уравнений:
Найдите наибольшее и наименьшее значения данных функций на указанных промежутках:
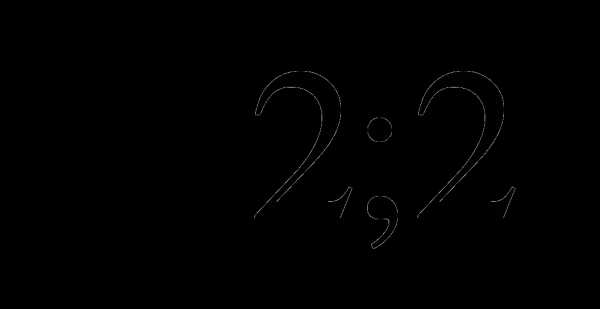
11 класс Геометрия
Контрольная работа по теме «Призма»
Вариант 1
1.Найти сторону основания и высоту правильной четырёхугольной призмы, если площадь полной поверхности равна 140 кв см, а площадь боковой поверхности равна 12 кв см.
2. В прямой треугольной призме стороны основания 10,17,21, а высота призмы 20. Найти площадь полной поверхности призмы.
3.В прямом параллелепипеде стороны основания 4 см и 10 см. Один из углов между сторонами равен 30 градусов. Площадь боковой поверхности равна 160 кв см. Найти площадь полной поверхности.
Вариант 2
1.Найти сторону основания и высоту правильной четырёхугольной призмы, если площадь полной поверхности равна 40 кв см, а площадь боковой поверхности равна 8 кв см.
2. В прямой треугольной призме основание — прямоугольный треугольник с катетами 16см и 12 см. Боковое ребро призмы равно 7см. Найдите площадь полной поверхности призмы.
3. Найдите площадь поверхности прямоугольного параллелепипеда, у которого стороны основания 5м и 12м, а диагональ наклонена к плоскости основания под углом 450.
11 класс Геометрия
Контрольная работа по теме «Пирамида. Усечённая пирамида»
Вариант 1
Основанием пирамиды является прямоугольник со сторонами 18см и 10 см. Основанием высоты пирамиды, равной 12см, является точка пересечения диагоналей прямоугольника. Найти площадь боковой поверхности пирамиды ,площадь полной поверхности пирамиды.
Высота правильной четырёхугольной усечённой пирамиды равна 5см. Стороны оснований – 8см и 6см. Найти боковое ребро пирамиды.
Вариант 2
В правильной четырёхугольной пирамиде сторона основания равна 10м, а высота-12м. Найдите площадь боковой поверхности пирамиды, площадь полной поверхности пирамиды.
Стороны оснований правильной усечённой треугольной пирамиды 12дм и 3дм. Боковое ребро 6дм. Найдите высоту пирамиды.
11 класс Геометрия
Контрольная работа по теме «Конус . Цилиндр. Усечённый конус »
Вариант 1
1.Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости его основания под углом 300. Найдите площадь полной поверхности цилиндра
2.Осевым сечением конуса является прямоугольный треугольник. Расстояние от центра до образующей равно 5 см. Найти площадь боковой поверхности конуса.
3.В усечённом конусе высота равна 24см, а радиусы оснований 3см и 10 см. Вычислите площадь боковой поверхности усечённого конуса.
Вариант 2
1.Угол при вершине осевого сечения конуса равен 1200. Образующая его 16см. Найдите площадь полной поверхности конуса.
2.Площщадь осевого сечения цилиндра равна 40см2. Длина окружности его основания 8π см. Найти площадь боковой поверхности цилиндра.
3.Найдите, чему равна площадь осевого сечения и площадь боковой поверхности усечённого конуса, если радиусы его оснований 3 и 6 см, а высота равна 4 см.
11 класс Геометрия
Контрольная работа по теме «Шар и сфера»
Вариант 1
В шаре радиуса 84мм на расстоянии 30мм от центра проведена секущая плоскость. Найдите площадь сечения.
Шар с центром в точке О касается плоскости в точке В. Точка А лежит в этой плоскости, ОА = 20см, АВ = 16 см. Найдите площадь поверхности шара.
Радиусы шаров 25см и 29см, а расстояние между их центрами 36см. Найдите радиус круга, являющегося пересечением шаров и длину линии, по которой пересекаются поверхности шаров.
Вариант 2
Радиус шара равен 13дм. Секущая плоскость проходит на расстоянии 5дм от центра шара. Найдите площадь сечения.
Точка В лежит на касательной к шару плоскости на расстоянии 17см от центра и 15см от точки касания. Найдите площадь поверхности шара.
Два шара с радиусом 10см расположены так, что расстояние между их центрами равно 12см. Найдите радиус круга, являющегося пересечением шаров и длину линии, по которой пересекаются поверхности шаров.
11 класс Геометрия
Контрольная работа по теме «Объёмы»
Вариант 1
В правильной треугольной призме сторона основания 12 см, а высота 5см. Найдите объём призмы.
Равнобедренный треугольник с основанием 48см и высотой 10 см вращается вокруг основания. Найдите объём тела вращения.
Вариант 2
В правильной четырёхугольной пирамиде высота равна 8 дм, а боковое ребро 10дм. Найдите объём пирамиды.
Стороны прямоугольника 14см и 16см. Найдите объём тела вращения, полученного вращением данного прямоугольника вокруг меньшей стороны..
11 класс Геометрия
Контрольная работа по теме «Комбинации геометрических тел»
Вариант 1
1. Около правильной треугольной пирамиды со стороной основания 6см и высотой 8см описан шар. Найдите радиус шара.
2. Правильная четырёхугольная призма вписана в шар. Найдите высоту призмы, если радиус шара 5 см, а ребро основания призмы 6 см.
3.В конус вписан шар объёмом  см
см . Найти объём конуса, если его высота 9 см.
. Найти объём конуса, если его высота 9 см.
4.Угол между высотой правильной треугольной пирамиды и боковой гранью равен 300. Найти длину стороны основания, если радиус вписанного в пирамиду шара равен 1 см.
Вариант 2
В правильную треугольную пирамиду со стороной основания 6см и высотой 8см вписан шар. Найдите радиус шара.
Длина бокового ребра правильной треугольной пирамиды равна см. Боковое ребро составляет с плоскостью основания угол 600 . Найти радиус описанного около пирамиды шара.
Правильная треугольная призма вписана в шар. Найдите высоту призмы, если радиус шара
 , а ребро основания 2см.
, а ребро основания 2см.
Образующая конуса, вписанного в шар равна 16 см, а радиус шара 10 см. Найдите радиус основания конуса.
11 класс Геометрия
Итоговая контрольная работа
Вариант 1
Правильная четырёхугольная призма вписана в шар. Найдите высоту призмы, если радиус шара 5 см, а ребро основания призмы 6 см.
В конус вписан шар объёмом см3 . Найти объём конуса, если его высота 3 см.
Вариант 2
Длина бокового ребра правильной треугольной пирамиды равна см. Боковое ребро составляет с плоскостью основания угол 600 . Найти радиус описанного около пирамиды шара.
В шар объёмом 36π см3 вписан цилиндр с квадратным сечением. Найдите боковую поверхность цилиндра.
infourok.ru
Контрольная работа по математике для 11 класса
Контрольная работа по математике для 11 класса
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Школьная отметка | |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 |
Вариант 1
Часть I
В1. Найдите значение выражения
logВ2. Найдите остаток от деления многочлена
13 + 67 — 3x + 4 на многочлен P(x) =+5 x +1.В3. На рисунке изображен график первообразной y = F (x) некоторой функции y = f(x), определенной на интервале ( — 16; — 2). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-15; -8].
В4. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
В5. Решите уравнение
= 0,04.В6 Высота конуса равна 30, а длина образующей — 34. Найдите диаметр основания конуса.
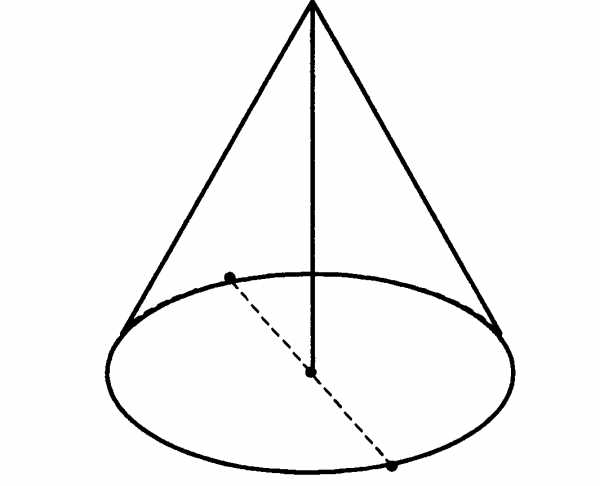
В7. Коэффициент полезного действия некоторого двигателя определяется формулой
. При каком наименьшем значении температура нагревателя ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника = 200 К?В8. Объем цилиндра равен 12см
. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?В9. Два автомобиля отправляются в 420 – километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найти скорость автомобиля, пришедшего к финишу вторым.
В10. Найдите наименьшее значение функции y = (
на отрезке [6; 8].Часть II
С1. Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.
С2. Решите систему неравенств
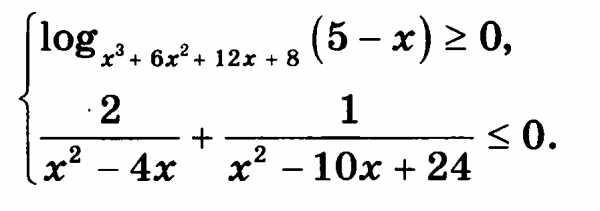
.
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10 заданий. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Школьная отметка | |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 |
Вариант 2
Часть I
В1.
В2. Найдите остаток от деления многочлена
— 11 + x + 7 на многочлен P(x) =+3.В3. На рисунке изображен график первообразной
некоторой функции y = f(x). Одна из первообразных этой функции равна F( x) =
. Найдите площадь заштрихованной фигуры.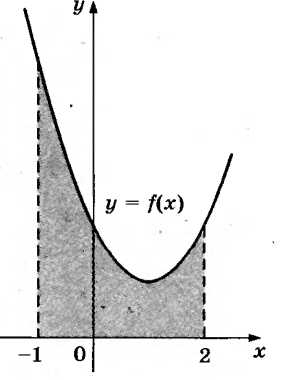
В4. В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
В5. Решите уравнение
= 0,25.В6. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.) Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
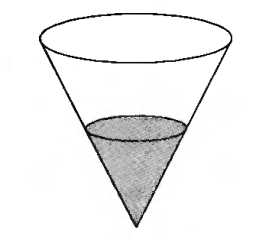
Часть II
С1. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Школьная отметка | |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 |
Вариант 3
Часть I
В1
В2. Найдите остаток от деления многочлена
+ x на многочлен р(x) =+ x + 1В3. На рисунке изображен график некоторой функции у =
Пользуясь рисунком, вычислите определенный интеграл dx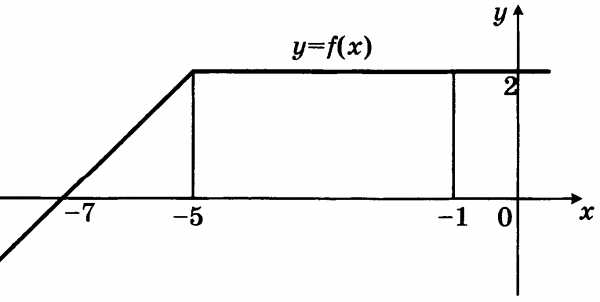
В4. В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям.
В5. Решите уравнение
= 36.В6 Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.

В7. Температуру нагревательного элемента (в градусах Кельвина) в зависимости от времени (вминутах) можно вычислять по формуле Т(t) = Т0 + аt + b t2, где Т0 = 760 К, а = 34 К/мин, b = -0,2 К/мин2. Известно, что при температурах нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время (в минутах) после начала работы нужно отключать прибор.
В8. Площадь боковой поверхности цилиндра равна
, а высота — 8 . Найдите диаметр основания.В9. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
В10. Найдите наимбольшее значение функции
на отрезке [-4,5; 0].Часть II
С1. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите угол между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств
.
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10 заданий. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
Школьная отметка | |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 |
Вариант 4
Часть I
В1. Найдите значение выражения
.В2. Найдите остаток от деления многочлена
— 2 — 5 на многочлен р(x) =– 9х.В3. На рисунке изображён график функции y = F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
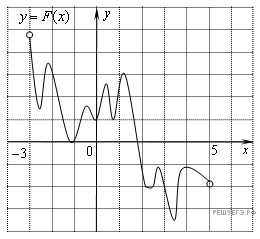
В4.. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из Голландии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Боливии.
В5. Найдите корень уравнения:
.В6. Длина окружности основания цилиндра равна 7. Площадь боковой поверхности равна 105. Найдите высоту цилиндра.
В7 На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:
, где – постоянная, – радиус аппарата в метрах, м3 – плотность воды, а – ускорение свободного падения (считайте Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.В8 Диаметр основания конуса равен 136, а длина образующей — 85 . Найдите высоту конуса.
В9. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
В10. Найдите наименьшее значение функции
на отрезке [0; 2].Часть II
С1. Две параллельные плоскости, находящиеся на расстоянии 12 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 64л. Найдите площадь поверхности шара.
С3. Решите систему неравенств
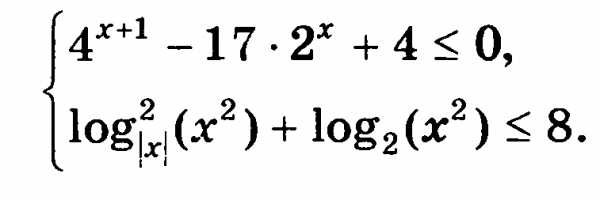
globuss24.ru
Контрольные работы по математике 11 класс
Контрольные работы по алгебре и началам анализа в 11 классе
Контрольная работа № 1 «Тригонометрические функции»
1. Найдите область определения и множество значений функции у = sin2x+1.
2. Выясните, является ли функция у = sin x – tg x четной или нечетной.
3. Сравните числа:
А) sin и ) sin ; Б) cos и cos ; В) sin 2 и cos 2,3
4. Найдите все числа из отрезка [-], для которых выполняется равенство sin x= — .
5. Постройте график функции у = -2 cos (х -.
Контрольная работа № 2 «Производная и ее геометрический смысл»
1. Найдите производную функции: а) 4 х 3 + б) sin х; в) ; г)
2.Найдите значения х, при которых значения производной функции f(x) = -3 равны нулю.
3. Запишите уравнение касательной к графику функции f(x) = 1+4х-sin x в точке с абсциссой х0 = 0.
4. На графике функции f(x)=х3 -3х2+2 найдите все такие точки, в которых касательная, проведенная к графику, параллельна прямой у=3х.
Контрольная работа № 3 «Применение производной к исследованию функции»
Найдите интервалы возрастания и убывания функции у=1+2х2—.
Постройте график функции у=2х2 .
Найдите ромб наибольшей площади,если известно, что сумма его диагоналей равна 10.
Найдите направления выпуклости графика функции у=х+
Контрольная работа № 4 «Интеграл»
1. Докажите, что функция F(x) = ех+х3-cos х является первообразной функции f (x) = 2е2х+3х2+sin х на всей числовой оси.
2. Найдите первообразную F функции f (x) = 3х2+2х-3 , график которой проходит через точку М(1;-2).
3. Вычислите площадь фигуры, ограниченной параболой у=х2+х-6 и осью Ох.
4. Найдите площадь фигуры, ограниченной линиями у=2+4х-х2 и у=х2-2х+2.
5. Найдите площадь фигуры, ограниченной параболой у=х2-12 и касательными к ней, проведенными из точки А (0;3).
Контрольная работа № 5 «Комплексные числа»
На комплексной плоскости постройте точки –i, -2+2i.
Выполните действия: а) i4+i5-2i; б) -.
Решите уравнение 2z2-6z+5=0/
Найдите все аргументы комплексного числа z=-2-2 и запишите его в тригонометрической форме.
Пользуясь формулой Муавра, возведите в степень (1+i)6 и результат запишите в алгебраической форме.
Решите уравнение z3=-27.
Контрольная работа № 6 «Элементы комбинаторики»
Упростите , где n€N, n>4.
Найдите значение выражения +.
Сколько различных трехзначных чисел можно записать с помощью цифр 0,1,2,3 при условии, что цифры в числе могут повторяться?
Сколькими способами можно составить букет из трех цветков, выбирая цветы из девяти имеющихся?
Запишите разложение бинома (1+х)6.
Контрольная работа № 6 «Теория вероятности»
В ящике находится 3 белых, 5 черных, 6 красных шаров. Наугад вынимают один шар. Какова вероятность того, что вынутый шар: а) белый или черный; б) желтый; в) не белый?
Брошены 2 игральные кости. Какова вероятность того, что на одной кости выпало 3 очка, а на другой – четное число очков?
В корзине лежат 5 яблок и 3 апельсина. Наугад дважды из корзины вынимают по одному плоду (не возвращая их в корзину). Какова вероятность того, что вторым было взято яблоко, при условии, что первым был апельсин?
Имеется 13 карт черной масти и 5 карт красной масти. Какова вероятность того, что среди двух карт, вынутых наугад, хотя бы одна будет красной?
Контрольные работы
по геометрии
в 11 классе
Контрольная работа № 1 «Метод координат в пространстве»
Вариант 1
1. Вычислите скалярное произведение векторов и , если , , = 2, = 3, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая а отображается на прямую а1, а плоскость β – на плоскость β1. Докажите, что если а|| β, то b1 || β1.
Контрольная работа №1 «Метод координат в пространстве»
Вариант 2
1. Вычислите скалярное произведение векторов и , если , , = 3, = 2, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
3. При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, и . Докажите, что .
Контрольная работа № 2 «Цилиндр, конус, шар»
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь полной поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 2 «Цилиндр, конус, шар»
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь полной поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 3 «Объемы тел»
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 3 «Объемы тел»
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
infourok.ru
Комплекстная контрольная работа по математике 11 класс
Комплексная контрольная работа по математике в 11 классе.
1 вариант
2 вариант
А1. Вычислите:
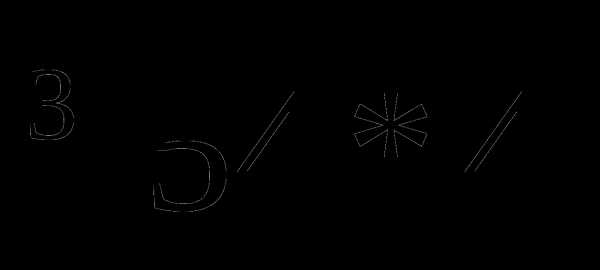
1)24 2)18 3)12 4)6
А1. Вычислите:


1)24 2)18 3012 4)6
А2. Вычислите:
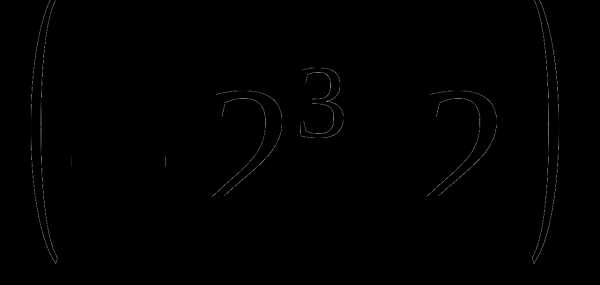

1)-128 2)128 3)-256 4)256
А2. Вычислите:
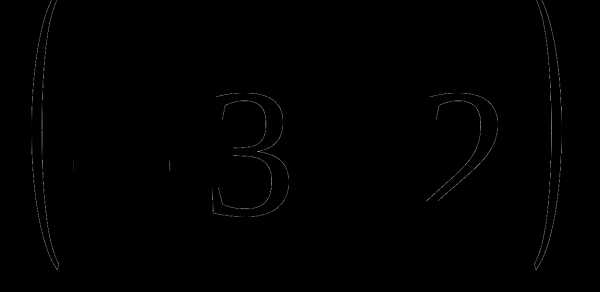

1)162 2)-162 3)324 4)-324
А3. Найдите произведение корней уравнения:
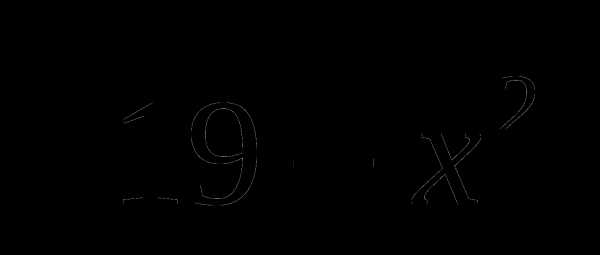 =3
=3
1)9 2)-9 3)-10 4)10
А3. Найдите произведение корней уравнения:
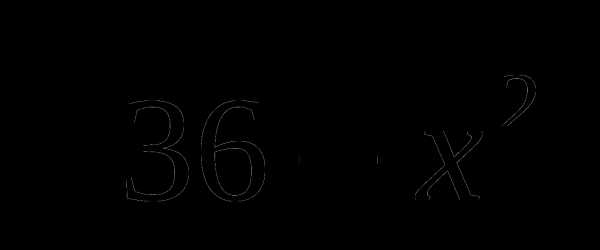 =3
=3
1)25 2)-25 3)27 4)-27
А4. Найдите значение выражения:
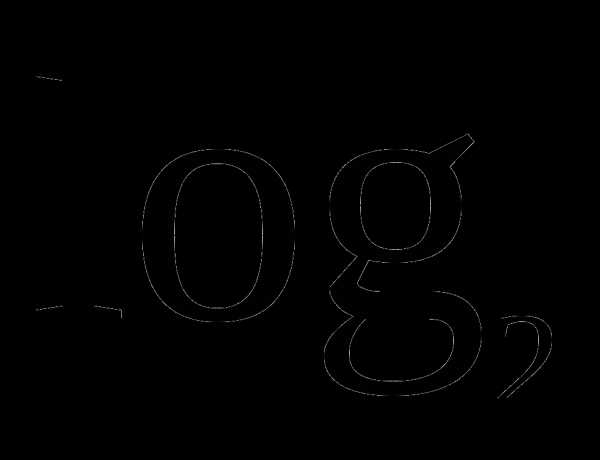 12+
12+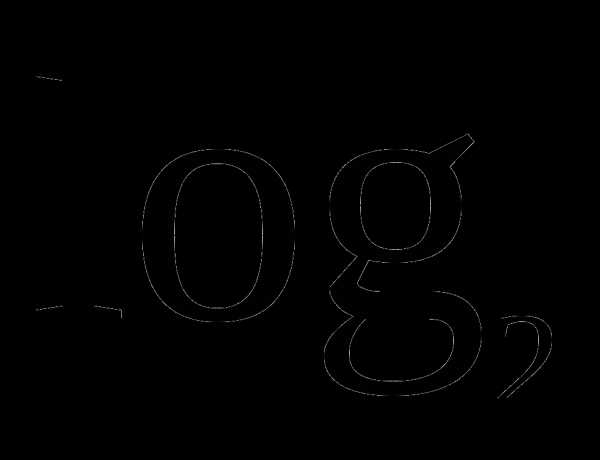 6-
6-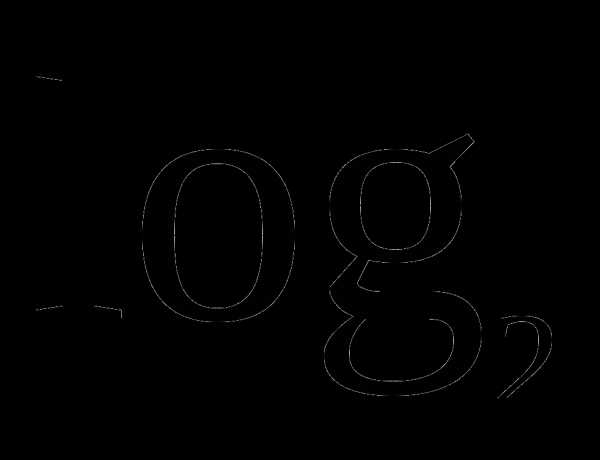 18
18
1)1 2)2 3)3 4)4
А4. Найдите значение выражения:
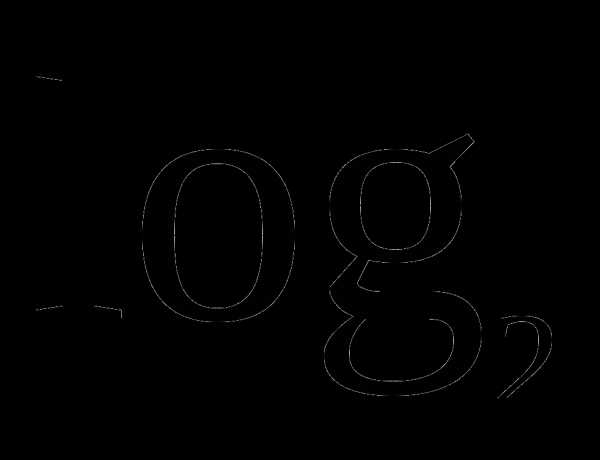 6+
6+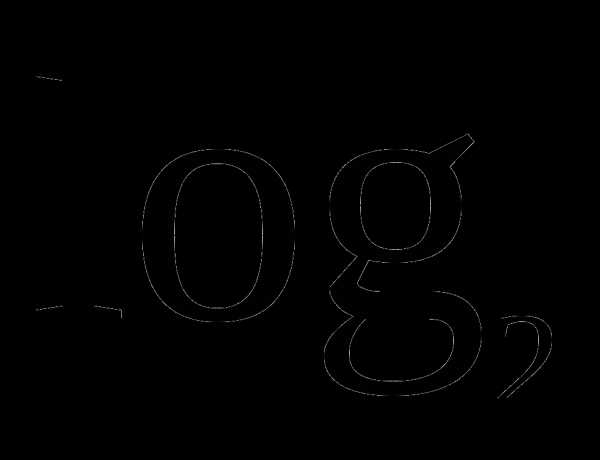 3-
3-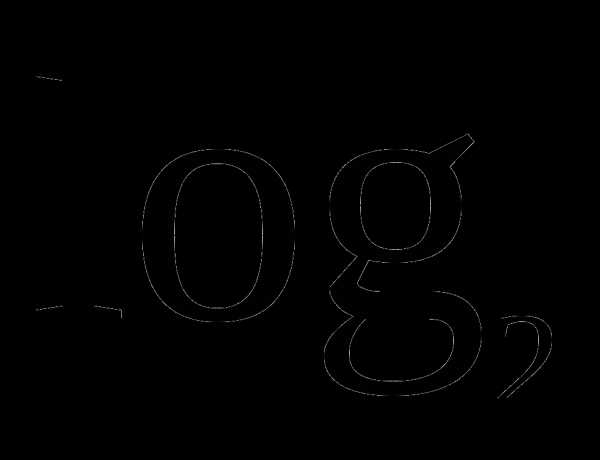 9
9
1)1 2)2 3)3 4)4
А5. Укажите промежуток, содержащий корень уравнения:
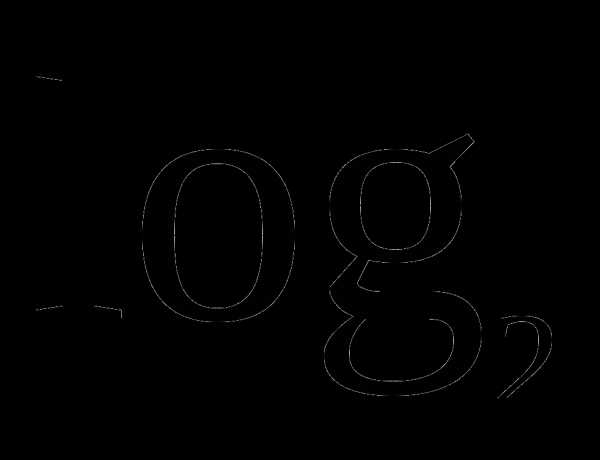 х=-2
х=-2
1) (-5;-1) 2) (-1;0) 3 (0;1) 4) (1;2)
А5. Укажите промежуток, содержащий корень уравнения:
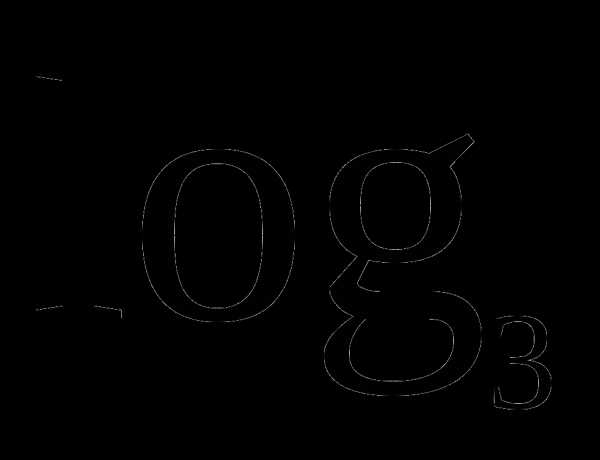 х=-2
х=-2
1) (-10;-1) 2) (-1;0) 3) (0;1) 4) (1;2)
А6. Укажите промежуток, содержащий корень уравнения:
2х=8
1) (0;1) 2) (1;2) 3) (2;3) 4) (3;4)
А6. Укажите промежуток, содержащий корень уравнения:
3х=9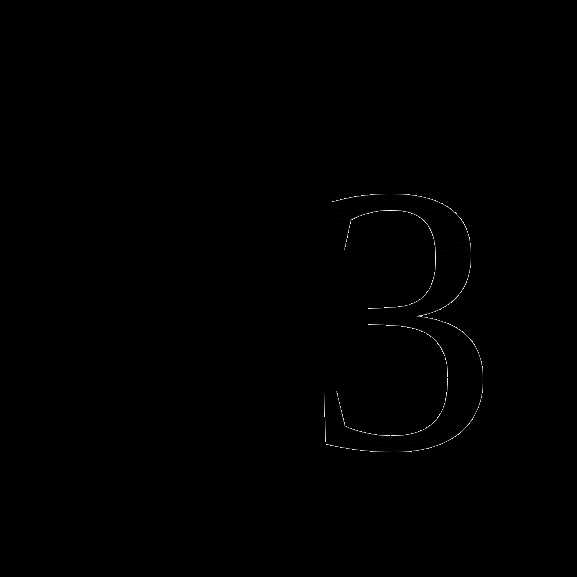
1) (0;1) 2) (1;2) 3) (2;3) 4) (3;4)
В1. Укажите сумму целых решений неравенства:
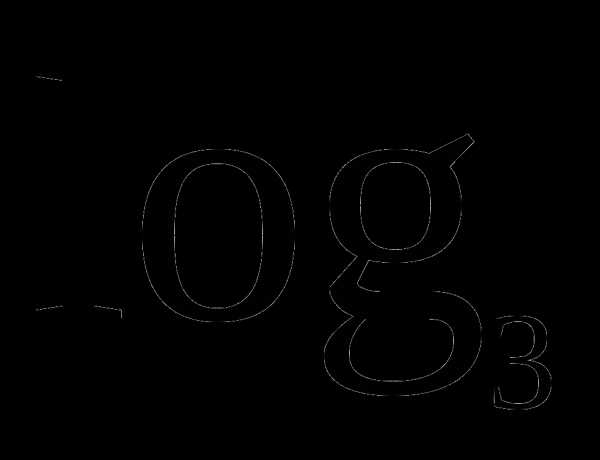 х>
х>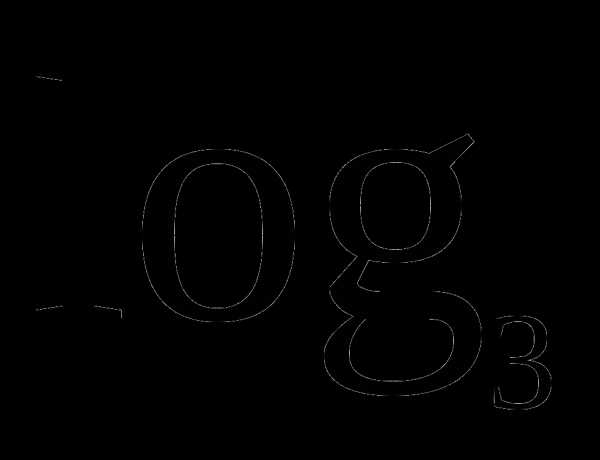 (5-х)
(5-х)
В1. Укажите число целых решений неравенства:
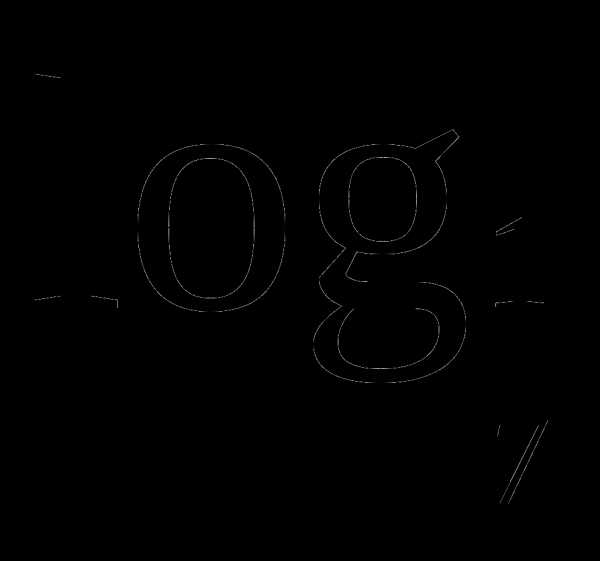 (2х+3)<
(2х+3)< 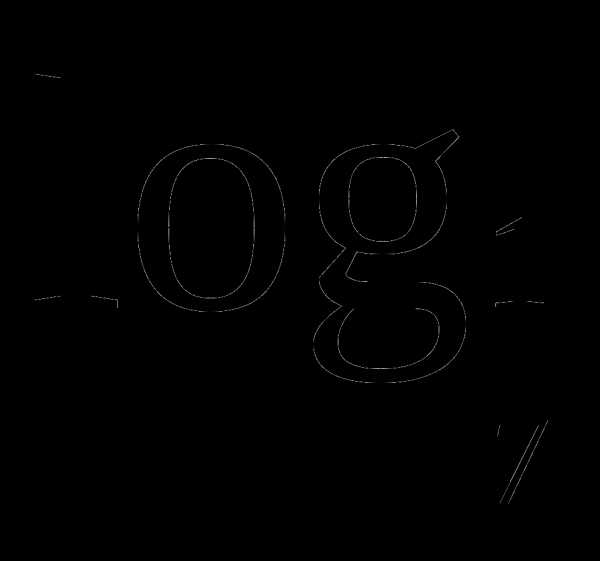 (3х-2)
(3х-2)
В2. Вычислите:
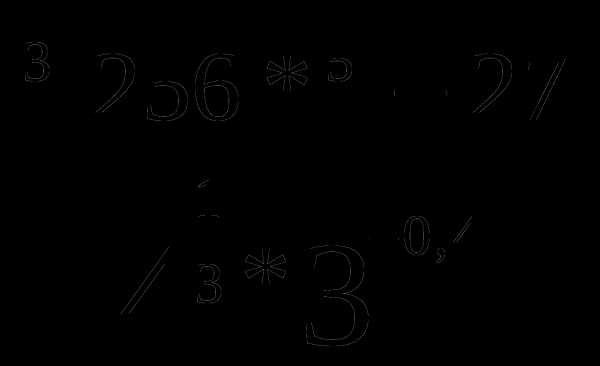
В2. Вычислите:
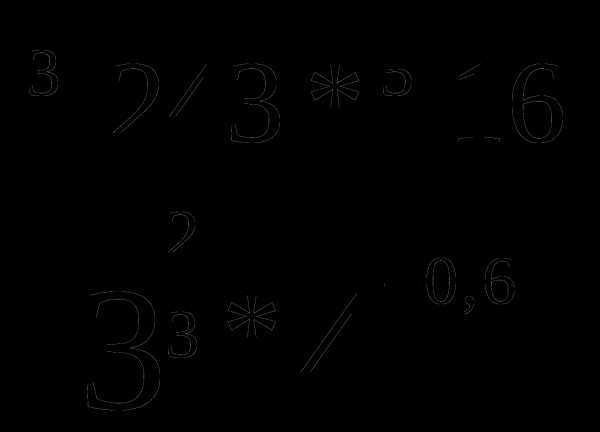
С1. Вычислите:
2*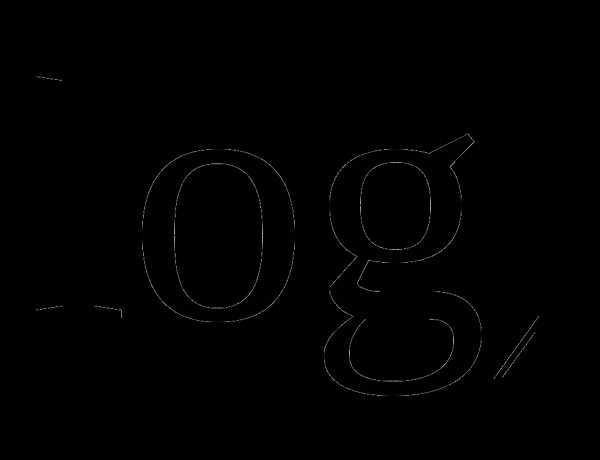 (8(
(8( —
—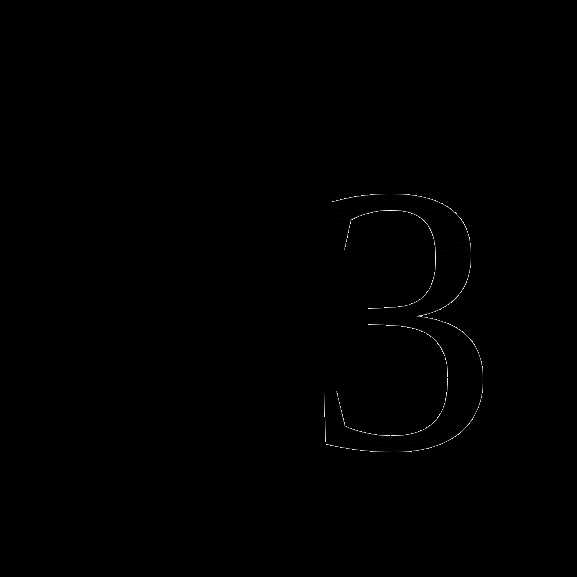 )) +
)) + 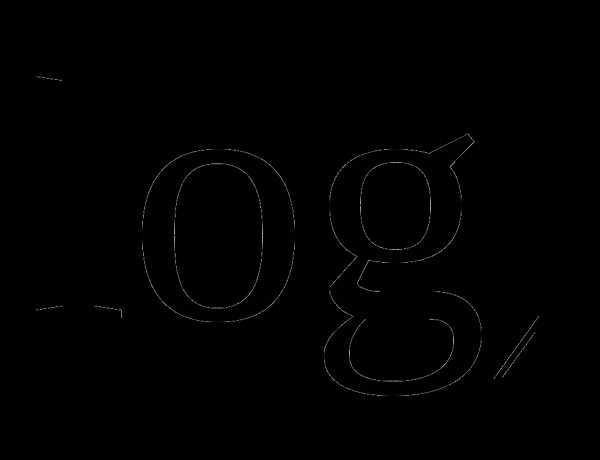 (10+2
(10+2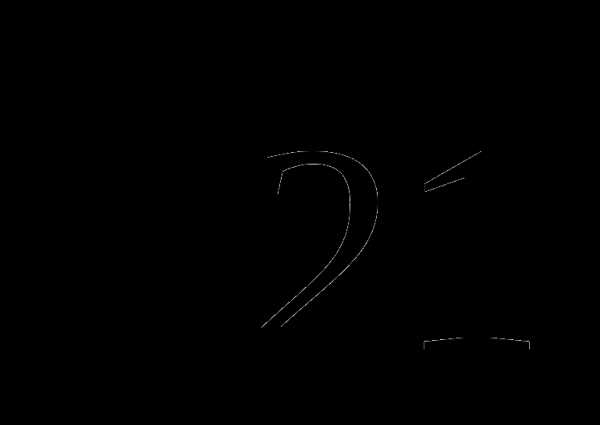 )
)
С1. Вычислите:
2*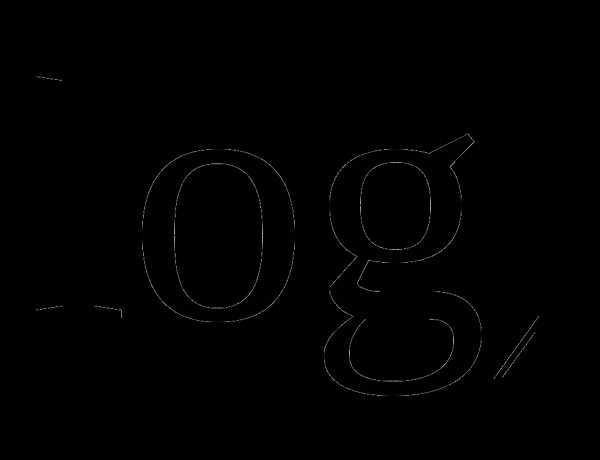 (8(
(8( —
— )) +
)) + 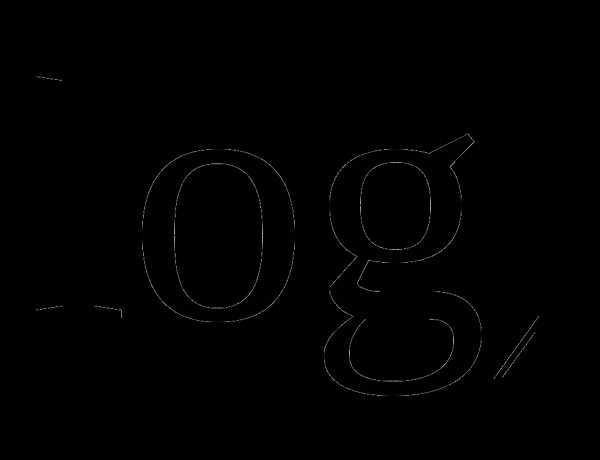 (12+2
(12+2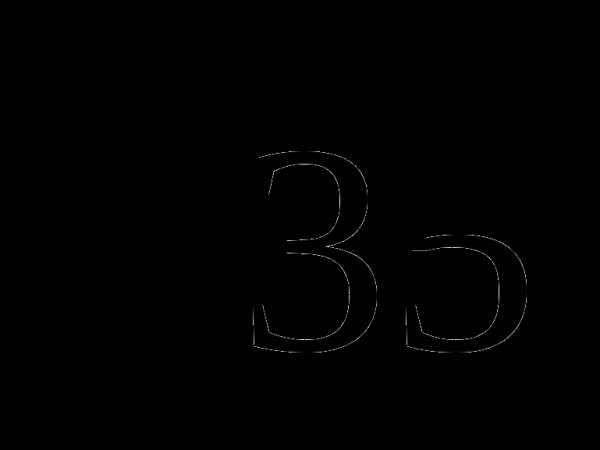 )
)
Спецификация итоговой контрольной работы по математике в 11 классе.
Цель работы:
Проверить знание понятия корня степени n,свойства корня степени n, степени с рациональным показателем; понятие логарифма, свойства логарифмов;
Выявить умения решать иррациональные уравнения, показательные и логарифмические уравнения и неравенства.
Структура контрольной работы.
Документы, определяющие содержание работы:
Закон РФ « Об образовании»
Федеральный компонент государственного образовательного стандарта.
Обязательный минимум содержания среднего общего образования по математике.
Программа по математике.
Структура работы.
Общее число заданий в работе – 9.
Вес заданий распределяется с учетом уровня сложности и времени, необходимого на его выполнения:
6 заданий – 1 балл;
2 задания – 2 балла;
1 задание – 5 баллов.
Распределение заданий по максимальному первичному баллу.
Наименование задания
Число заданий
Максимальный первичный балл
% максимального первичного балла за задание от максимального первичного балла.
Базовый уровень
1…6
6
6
40 %
Повышенный уровень
7,8
2
4
13,3 %
Высокий уровень
9
5
5
33,3 %
Итого:
15
100 %
Распределение заданий работы по уровню сложности
Уровень сложности задания
Число заданий
Максимальный первичный балл
% максимального первичного балла за задание от максимального первичного балла.
Базовый
6
6
Повышенный
2
4
Высокий
1
5
Итого:
9
15
100 %
Распределение заданий работы по содержанию и видам деятельности.
Выполнение работы по математике потребует от обучающихся следующих умений:
Решать иррациональные уравнения;
Решать показательные уравнения и неравенства;
Решать логарифмические уравнения и неравенства;
Находить значения выражений, содержащих степени с рациональными показателями, логарифмы.
Содержательные разделы
Число заданий
Максимальный первичный балл
% максимального первичного балла за задание от максимального первичного балла.
Степени и корни.
3
4
Иррациональные уравнения
1
1
Показательные уравнения и неравенства
1
1
Логарифмические уравнения и неравенства
4
9
Итого:
Система оценивания отдельных заданий и работы в целом.
Уровень сложности
Система оценивания
Базовый (1-6 задания)
Оценивается по шкале от 0 до 1 балла:
За верное выполнение – 1 балл
За неверное выполнение – 0 баллов
Повышенный (7-8 задания)
Оценивается по шкале от 0 до 2 баллов:
За верное выполнение – 2 балла
За одну ошибку – 1 балл
За неверное выполнение – 0 баллов
Высокий (9 задание)
Оценивается по шкале от 0 до 5 баллов:
За верное выполнение – 5 баллов
За одну ошибку – 3 балла
За две ошибки – 1 балл
За неверное выполнение – 0 баллов
Время выполнения работы.
На выполнение работы отводится 45 минут.
infourok.ru
Контрольная работа по математике за 1 полугодие 11 класс
Контрольная работа по математике за 1 полугодие 11 класс Вариант 1 Алгебра 1 часть
- Найдите значение выражения
- Найдите значение выражения
- Найдите корень уравнения ()² =27
- Решите уравнение
- Найдите наименьшее значение х из области определения функции у =
- Найдите наименьшее целое значение функции у = 3+
- Найдите наибольшее значение функции у = 14х – х + 13 на отрезке[10;20]
- Решите уравнение sin( — х ) = — на отрезке [;. Ответ дайте в градусах.
- Решите уравнение 15 + 5х =
- Найдите корень уравнения или произведение корней, если их несколько
6
- А) Решите уравнение
Б)Найдите корни уравнения на отрезке [ −3 ]
2. Решите систему неравенств + 10 ,
.
Геометрия
- Площадь сечения шара плоскостью, проходящей через центр, равна 7. Найдите площадь поверхности шара
- В цилиндр, радиус основания которого равен 5, а высота равна 6, вписана правильная четырехугольная призма. Найдите площадь поверхности этой призмы.
- Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения
- В прямоугольном параллелепипеде известны рёбра Точка принадлежит ребру и делит его в отношении считая от вершины Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки и
Контрольная работа по математике за 1 полугодие 11 класс Вариант 2 Алгебра 1 часть
- Найдите значение выражения
- Найдите значение выражения
- Найдите корень уравнения =
- Решите уравнение
- Найдите наименьшее значение х из области определения функции у =
- Найдите наименьшее целое значение функции у = 5 −
- Найдите наибольшее значение функции у = х − 2,5х + 25 на отрезке[10;20]
- Решите уравнение –х) = − — на отрезке [. Ответ дайте в градусах.
- Решите уравнение х² + 8х + 13 =
- Найдите корень уравнения или произведение корней, если их несколько
х
- А) Решите уравнение ( + = 2
Б)Найдите корни уравнения на отрезке[ 2]
2. Решите систему неравенств +6 ,
.
Геометрия
- Площадь поверхности шара . равна 1. Найдите площадь сечения плоскостью, проходящей через его центр
- Прямоугольный параллелепипед описан около цилиндра, радиус основания, которого равен 4, а высота равна 5.. Найдите площадь поверхности этого параллелепипеда
- Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 6. Найдите расстояние от центра основания конуса до плоскости сечения
- В прямоугольном параллелепипеде известны рёбра: Точка принадлежит ребру и делит его в отношении считая от вершины Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки и
kopilkaurokov.ru
