Примеры решения задач по механике
Задача 1. Движение тела массой 2 кг задано уравнением: , где путь выражен в метрах, время — в секундах. Найти зависимость ускорения от времени. Вычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.
|
Дано: | |
|
| |
|
Найти: |
Решение: Модуль мгновенной скорости находим как производную от пути по времени:
Мгновенное тангенциальное ускорение определяется как производная от модуля скорости по времени:
Среднее ускорение определяется выражением:
После подстановки:
Равнодействующая сила, действующая на тело, определяется по второму закону Ньютона:
Тогда
Ответ: a(t) = 36t, F = 144 H, = 72 H.
Задача 2. По наклонной плоскости, составляющей с горизонтом угол 30º, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.
|
Дано: |
Рис. 1 | |
|
| ||
|
Найти: |
Решение: Покажем на рисунке силы, действующие на каждое тело. Запишем для каждого из тел уравнение движения (второй закон Ньютона):
В проекциях на выбранные оси координат:
Учитывая, что , где, получим систему уравнений:
Вычтем из первого уравнения второе:
Искомое ускорение равно:
Вычислим ускорение а:
Силу натяжения найдем из первого уравнения системы:
Ответ:
Задача 3. Найти линейные ускорения движения центров тяжести шара и диска, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30º. Начальная скорость тел равна нулю.
|
Дано: |
Рис. 2 | |
|
| ||
|
Найти: |
Решение: При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:
(1)
где I — момент инерции тела, m — масса.
Длина наклонной плоскости l связана с высотой соотношением (рис. 2):
(2)
Линейная скорость связана с угловой:
(3)
После подстановки (2) и (3) в (1), получим:
(4)
Так как движение происходит под действием постоянной силы (силы тяжести), то движение тел — равноускоренное. Поэтому:
(5)
и
(6)
Решая совместно (4), (5) и (6), получим:
(7)
Моменты инерции:
|
для шара: | |
|
| |
|
для диска: |
Подставляя выражение для момента инерции в формулу (7), получим:
|
для шара: | |
|
| |
|
для диска: |
Ответ:
2. Электричество и магнетизм
Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Силовой характеристикой электрического поля является напряженность, энергетической — потенциал φ. Следует обратить внимание на связь междуи φ . Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип суперпозиции (задачи 201-220 контрольной работы).
При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца. В контрольной работе это задачи 221- 230. При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Нужно знать этот закон и уметь применять его для расчета вектора магнитной индукции — основной характеристики магнитного поля (в контрольной работе это задачи 231-240). Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле (задачи 241-250).
При изучении явления электромагнитной индукции необходимо усвоить, что механизм возникновения ЭДС индукции имеет электронный характер. Основной закон электромагнитной индукции — это закон Фарадея-Ленца. Согласно этому закону, ЭДС индукции в замкнутом контуре возникает при изменении магнитного потока, сцепленного с контуром. Необходимо знать, как вычисляется магнитный поток, ЭДС индукции, как рассчитывается работа по перемещению замкнутого контура с током в магнитном поле и энергия магнитного поля (в контрольной работе задачи 251-260).
Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
В программе большое внимание уделяется изучению уравнений Максвелла. Эти уравнения могут быть записаны в двух формах: в интегральной и дифференциальной. Уравнения Максвелла удовлетворяют принципу относительности: они инвариантны относительно преобразований Лоренца. Основным следствием теории Максвелла является вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
ФИЗИКА: Задачи на механическую работу
Задачи на механическую работу с решениями
Формулы, используемые на уроках «Задачи на механическую работу».
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила |
F |
H |
F = mg |
Путь |
s |
м |
s = A / F |
Масса |
m |
кг |
m = АТ / (gh) |
Высота |
h |
м |
h = АТ / (mg) |
Работа |
A |
Дж |
A = Fs |
Работа сил тяжести |
Ат |
Дж |
АТ = mgh |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Шар катится по инерции по горизонтальной поверхности. а) Совершается ли при этом работа силой тяжести? б) Совершается ли в этом случае работа какой-либо другой силой?
Решение:
а) Работа силой тяжести не совершается, потому что перемещения в вертикальном направлении (то есть в направлении силы тяжести) не происходит.
б) Работа совершается силой трения, так как шар остановится под действием этой силы.
Задача № 2. Какую работу надо совершить, чтобы положить гантель весом 100 Н на стол высотой 80 см?
Задача № 3. Какая совершается работа при равномерном перемещении ящика на 25 м, если сила трения 450 Н?

Задача № 4. Какую работу совершает сила тяжести при падении камня массой 0,5 кг с высоты 12 м?

Задача № 6. Определите работу, совершенную краном при равномерном подъеме тела массой 3 т на высоту 7 м.

Задача № 7. При равномерном подъеме из шахты нагруженной углем бадьи массой 10,5 т произведена работа 6200 кДж. Какова глубина шахты?

Задача № 8. Давление воды в цилиндре нагнетательного насоса 1200 кПа. Чему равна работа при перемещении поршня площадью 400 см2 на расстояние 50 см.
Теория для решения задач.
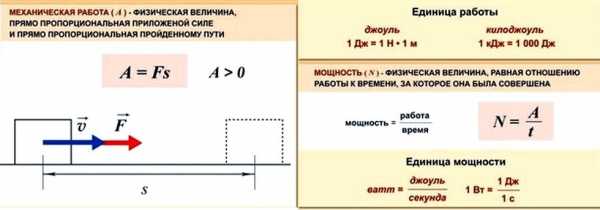

Конспект урока «Задачи на механическую работу с решениями».
Следующая тема: «Задачи на механическую мощность с решениями».
ЗАДАЧИ на механическую работу с решениями
5 (100%) 2 votesuchitel.pro
| 4. Автомобиль проходит первую половину пути со средней скоростью 70 км/ч, а вторую — со средней скоростью 30 км/ч. Определить среднюю скорость на всем пути.
6. При какой максимальной скорости самолеты могут приземляться на посадочную полосу аэродрома длиной 800 м при торможении с ускорением a1= −2,7 м/с2? a2= −5 м/с2? 7. Сигнальная ракета, запущенная вертикально вверх, вспыхнула через 6 с после запуска в наивысшей точке своей траектории. На какую высоту поднялась ракета? С какой начальной скоростью ее запустили? 8. Луна движется вокруг Земли по окружности радиусом 384 000 км с периодом 27 сут 7 ч 43 мин. Какова линейная скорость Луны?
Каково центростремительное ускорение Луны к Земле? Механика. ДинамикаОсновная задача динамики материальной точки состоит в том, чтобы найти законы движения точки, зная приложенные к ней силы, или, наоборот, по известным законам движения определить силы, действующие на материальную точку. Общие правила решения задач по динамике Характерная особенность решения задач механики о движении материальной точки, требующих применения законов Ньютона, состоит в следующем:
—————————————————————————————————- 1. На опускающегося парашютиста действует сила земного притяжения. Объясните, почему он движется равномерно. 2. Почему машинисту подъемного крана запрещается резко поднимать с места тяжелые грузы? 3. Вагонетка массой 500 кг движется под действием силы 100 Н. Определите ее ускорение. 4. Автобус массой 8000 кг едет по горизонтальному шоссе. Какая сила требуется 5. Два человека тянут за веревку в разные стороны с силой 90 Н каждый. Разорвется ли веревка, если она выдерживает натяжение до 120 Н? 6. На самолет, летящий в горизонтальном направлении, действует в направлении полета сила тяги двигателя F = 15000 Н, сила сопротивления воздуха FC = 11000 Н и сила давления бокового ветра FВ = 3000 H, направленная под углом α = 90° к курсу. Найти равнодействующую этих сил. Какие еще силы действуют на самолет в полете и чему равна их равнодействующая? 7. Определите силу, с которой притягиваются друг к другу два корабля массой по 107 кг каждый, находящиеся на расстоянии 500 м друг от друга. 8. Между всеми телами существует взаимное притяжение. Почему же мы наблюдаем притяжение тел к Земле и не замечаем взаимного тяготения окружающих нас предметов друг к другу? 9. Пружину детского пистолета сжали на 3 см. Определите возникшую в ней силу упругости, если жесткость пружины равна 700 Н/м. 10. Какой силой можно сдвинуть ящик массой 60 кг, если коэффициент трения между ним и полом равен 0,27? Сила действует под углом 30° к полу (горизонту). 11. Какую начальную скорость нужно сообщить сигнальной ракете, выпущенной под углом α = 45° к горизонту, чтобы она вспыхнула в наивысшей точке траектории, если запал ракеты горит t = 6 с? 12. Вычислить первую космическую скорость у поверхности Луны, если радиус Луны R= 1760 км, а ускорение свободного падения на Луне составляет 0,17 земного. Механика. Импульс, мощность, энергия1. Пуля массой 10 г, летящая горизонтально со скоростью 400 м/с, ударяется в преграду и останавливается. Чему равен импульс, полученный пулей от преграды? Куда он направлен? 2. Космический корабль массой 4800 кг двигался по орбите со скоростью 8000 м/с. При торможении из него тормозными двигателями было выброшено 500 кг продуктов сгорания со скоростью 800 м/с относительно его корпуса в направлении движения. Определите скорость корабля после торможения. 3. Снаряд, летевший горизонтально со скоростью 480 м/с, разорвался на два осколка равной массы. Один осколок полетел вертикально вверх со скоростью 400 м/с относительно Земли. Определите скорость второго осколка. 4. Охотник, плывя по озеру на легкой надувной лодке, стреляет в уток. Какую скорость приобретает лодка в момент выстрела из двух стволов ружья (дуплетом)? Масса охотника с лодкой и ружьем 80 кг, масса пороха и дроби в одном патроне 40 г, начальная скорость дроби 320 м/с, ствол ружья во время выстрела направлен под углом 60° к горизонту. 5. Стоящий на коньках человек массой 60 кг ловит мяч массой 500 грамм, летящий горизонтально со скоростью 72 км/ч, определите расстояние на которое откатится при этом человек, если коэффициент трения 0,05. Решение: 6. Самолет должен иметь для взлета скорость 25 м/с. Длина пробега по полосе аэродрома составляет 100 м. Какую мощность должны развивать двигатели при взлете, если масса самолета 1000 кг и сопротивление движению равно 200 Н? 7. Футбольный мяч массой 400 г падает на Землю с высоты 6 м и отскакивает на высоту 2,4 м. Какое количество механической энергии мяча превращается в другие виды энергии? 8. Автомобиль массой 5000 кг при движении в горной местности поднялся на высоту 400 м над уровнем моря. Определите потенциальную энергию автомобиля относительно уровня моря. 9. Перед загрузкой в плавильную печь чугунный металлолом измельчают ударами падающего бойка молота массой 6000 кг. Определите полную энергию в нижней точке при падении бойка с высоты 9 м. Сравните ее с полной энергией, которую имеет боек, пройдя при падении 5 м. 10. Самолет массой 1000 кг летит горизонтально на высоте 1200 м со скоростью 50 м/с. При выключенном двигателе самолет планирует и приземляется со скоростью 25 м/с. Определите силу сопротивления воздуха при спуске, считая длину спуска равной 8 км. 11. Достаточна ли мощность электродвигателя токарного станка 1А62 (7,8 кВт) для обработки детали со скоростью резания 5 м/с, если сопротивление металла резанию составляет 600 Н? КПД станка 0,75. 12. Автомобиль, мощность двигателя которого 50 кВт, движется по горизонтальному шоссе. Масса автомобиля 1250 кг. Сопротивление движению равно 1225 Н. Какую максимальную скорость может развить автомобиль? 13. При формировании железнодорожного состава происходят соударения вагонов буферами. Пружины двух буферов вагона сжались при ударе на 10 см каждая. Определите работу сжатия пружин, если коэффициент их жесткости равен 5·106 Н/м.
|
osiktakan.ru
Решение задач по физике (механика)
Цель урока: продолжить формирование умения рассчитывать механическую работу, мощность, КПД простых механизмов, применять законы сохранения при решении качественных и вычислительных задач.
Ход урока 
Проверка домашнего задания методом решения качественных задач
1. Человек толкнул вагонетку. Она пришла в движение по горизонтальному пути. Совершил ли человек работу? ( Да)
2. Когда расходуется меньше энергии при запуске искусственного спутника Земли : вдоль меридиана или вдоль экватора в сторону вращения Земли? ( При запуске вдоль экватора в сторону вращения Земли, так как скорость суточного вращения Земли складывается со скоростью, сообщенной спутнику двигателем ракеты.)
3. На первом и пятом этаже сожгли по 1м3 газа, Потенциальная энергия газа на 5 этаже больше, чем на первом. Будет ли энергия, полученная от сжигания газа на 5 этаже, больше
по сравнению с той, которую получили при сжигании газа на первом этаже? (Энергия от сжигания газа будет одинаковая)
4. Два яблока висят неподалеку друг от друга, но под одним из них яма глубиной 0,5 м. Массы яблок одинаковы и равны 0, 1кг. Сравните потенциальные энергии взаимодействия с Землей для каждого яблока.
(Решаем устно. Считаем, что g=10м/c². Ep1= 3 Дж; Ep2 = 4 Дж
Решение вычислительных задач
Задача. Подъемный кран поднимает груз массой 5 т на высоту 1,5 м . За какое время поднимается груз, если мощность двигателя крана 10 кВт и КПД равен 80%?
η= Ап/ Аз·100%; Ап= m g h; A3= N t; η= m g h·100%/Nt; t = m g h·100% / N·η; t = 5·10³·9.8·15/ 104·0.8 = 94(c)
Задача. Найдите КПД наклонной плоскости длиной 1м и высотой 60 см, если коэффициент трения при движении по ней равен 0,1.
l η= Aп/Аз·100%; Ап= m g h; A3= Fm· l
N Y Запишем уравнение движения тела при условии, что тело движется равномерно и
X Ft прямолинейно, т.е. а=0. F̄m+ mḡ+ F̄np+N̄ = 0. Спроектируем на оси координат:
на ось Ох: Fm- mg sinα – Ftp = 0; на ось Оy Т – mg cosα = 0; N = mg cosα/
Подставим значение N в выражение Ftp= μ N и получим: Ftp= μ m g cosα. Тогда Fm= mg sinα+ μmg cosα = = mg(sinα + μcosα ). A3= Fm= mg (sinα + μcosα)·l; η = mgh / mg(sinα+μcosα) ·l = h / (sinα + μcosα)·l
Найдем значение sinα = h/l; и cosα = √l²-h²/ l; Тогда η = 0,6·100%/ (0,6+0,1√1² -0,6² )·1 = 88%
Задача. С какой скоростью двигался поезд массой 1500 т, если под действием силы сопротивления 150 кН он прошел с момента начала торможения до остановки путь 500 м?
Решение: Атр= mV²/2 – mV₀²/2; так как V=0, то Aтр = mV₀²/2; значит Aтр= – FтрS; тогда mV02/2 = FтрS
Отсюда V₀= √2 Fтр S/ m Вычисляем: V₀²= 2·150·10³·500/ 1500·10³; V₀= 10 м/с
Подводим итоги урока .
Домашнее задание: §52,53, №377 (Р)
home-task.com
Примеры простых задач по механике.
1.За первую секунду движения автомобиль проехал 10 м, за вторую
секунду — 30 м, за третью секунду — 50 м. Каков был характер движения
автомобиля?
1) равномерное
2) равноускоренное
3) равнозамедленное
4) точно сказать нельзя
2. По горизонтальной деревянной доске равномерно тянут брусок массой
120 г с помощью динамометра. Стрелка динамометра показывает 2 Н. Чему
равна сила трения, действующая на брусок?
1) 2 Н 2) 1,2 Н 3) 2,4 Н 4) 0,16 Н
3. Снаряд пружинного пистолета вылетает под углом 60
перемещаясь по параболе, падает вниз. На каком из графиков верно показано
изменение потенциальной энергии снаряда с изменением высоты?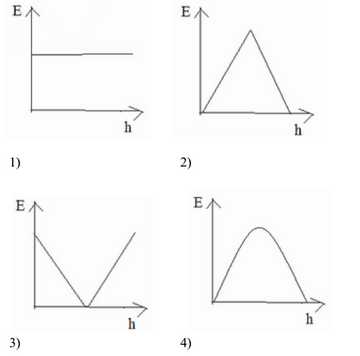
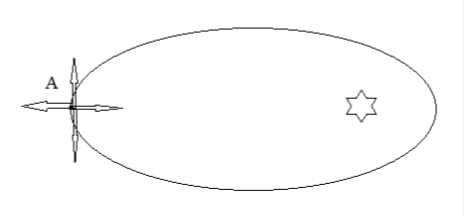
4.Астероиды двигаются вокруг Солнца по эллиптическим орбитам то
приближаясь к Солнцу, то удаляясь от него. Определите направление
ускорения астероида в точке А.
1) влево 2) вправо 3) вверх 4) вниз
5. Мяч подбрасывают вертикально вверх, сообщив ему скорость 15 м/с. На
какой высоте окажется мяч через 2 с после начала движения?
1)50 м 2) 10 м 3) 40 м 4) 30 м
6. С помощью графика определите путь пройденный автомобилем за 8 с.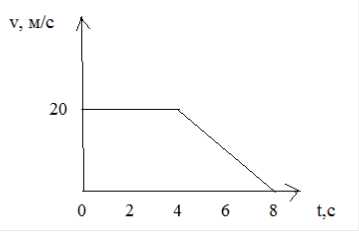
1) 160 м 2)80 м 3) 140 м 4) 120 м
8. На холодильнике висит сувенирный магнит. Сравните силы взаимодействия магнита и холодильника.
1) масса холодильника многократно больше массы магнита, поэтому сила притяжения холодильника больше,
2) холодильник не намагничен, поэтому сила действия магнита больше,
3) одинаковы,
4) силы магнитного взаимодействия сравнивать нельзя.
9. После удара клюшкой шайба движется по льду, но спустя некоторое
время останавливается. Какое из приведенных ниже утверждений правильно
описывает происходящее явление?
1) потенциальная энергия шайбы превращается во внутреннюю энергию,
2) кинетическая энергия шайбы превратилась в потенциальную энергию,
3) кинетическая энергия шайбы превратилась во внутреннюю энергию,
4) потенциальная энергия шайбы превращается в кинетическую энергию.
10. По прямолинейному шоссе с одинаковой начальной скоростью движутся
два автомобиля: один со скоростью 60 км/ч, другой со скоростью 40 км/ч Подъезжая к светофору, они начинают торможение с одинаковым ускорением. Сравните время движения автомобилей до полной остановки и их тормозной путь.
1. одинаковы
2. у первого автомобиля больше тормозной путь и время,
3. у второго автомобиля больше тормозной путь и время,
4. у первого автомобиля больше тормозной путь, но меньше время торможения.
11. После удара ракеткой теннисный мяч летит по параболе, как показано на рис. Куда направлено ускорение мяча в точке А? Сопротивлением воздуха пренебречь.
1)1 2) 2 3) 3 4) 4
12. Какими видами механической энергии обладает пуля после выстрела из ружья вертикально вверх?
1) только кинетической энергией
2) только потенциальной энергией
3) и потенциальной, и кинетической энергией
4) пуля не имеет механической энергии
fizikakkep.ru
Механика (расчетная задача) | ЕГЭ по физике
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt, где x0 — начальная координата тела, Vx — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением
где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести — это сила, с которой все тела притягиваются к Земле:
При неподвижной опоре вес тела равен по модулю силе тяжести:
Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.
где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.
Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей
где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:
где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения
Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность — это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волны
Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины
x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое
колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:
Частота измеряется в с-1. Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле
где l — длина маятника.
Период колебаний груза на пружине определяется по формуле
где k — жёсткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
где v — скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
examer.ru
Механика
Определение 1
Механика — это наука о систематическом механическом движении всех материальных тел, а также взаимодействии, которое происходит при этом между ними.

Рисунок 1. Механика и ее виды. Автор24 — интернет-биржа студенческих работ
Под механикой принято понимать называемое классическое учение, которое базируется на законах механики Ньютона. Научные труды знаменитого физика исследуют движение любых физических тел (кроме атомов и других элементарных частиц) при условии, что скорость подвижности всех объектов намного меньше скорости света. Таким образом, быстрота движение материальных тел, которая близка к скорости света, рассматривают в механике относительности, а внутриатомные процессы и действие элементарных частиц — в квантовой физике.
Под механическим воздействием ученые понимают кардинальное изменение с течением определенного периода времени общего расположения тел или их элементов в пространстве. Например, передвижение небесных тел, постоянные колебания земной коры, морские и воздушные течения, быстрота летательных аппаратов и транспортных средств, деформация основных элементов сооружений, движение газов и другое.
В механике взаимодействия тел считаются логическим результатом изменения всех скоростей точек объектов или их деформации. В этом аспекте, притяжение предметов по закону всемирного тяготения, а также взаимное давление соприкасающихся частиц являются главными показателями деятельности механических явлений.
При исследовании движения материальных объектов физики оперирует рядом понятий, которые демонстрируют те или иные характеристики реальных тел:
- материальная точка — представляет собой пренебрежимо малых размеров предмет, имеющий определенную массу;
- абсолютно твердое тело — объект, где расстояние между двумя любыми точками не меняется, следовательно, этим определением пользуются при деформации тела;
- сплошное изменяемое пространство — применяется, когда необходимо пренебречь молекулярной структурой предмета и изучить движения газов, жидкостей, и деформируемых твердых тел.
История развития механики
Процесс развития и становления механики, так же как и иных естественных наук, напрямую связан с историей эволюции общества и его производительных сил. Технографию механики можно условно разделить на несколько основных периодов, которые отличаются характером проблем и способами их решения.
Замечание 1
Эпоху создания первых обязательных орудий производства и искусственных сооружений следует считать началом накопления необходимого опыта и знаний, которые в дальнейшем помогли ученым открыть главные законы механики.
В то время, когда астрономия и геометрия античного мира представляли уже достаточно развитые научные концепции, положения в сфере механики были практически не изучены и относились к самым элементарным случаям равновесия материальных тел. Ранее всех разделов официально зародилась статика. Этот раздел развивался в тесной взаимосвязи со строительным искусством древних народов.
Основное определения статики – понятие мощности и интенсивности– изначально связывали с мускульным усилием, которое происходит посредством давления предмета на руку.
Приблизительно к середине IV в. до н. э. уже были представлены обществу простейшие законы уравновешивания и сложения сил, приложенных к одному объекту вдоль однородной линии. Задача о рычаге, которая была разработана великим философом Архимедом, вызвала особый интерес у древних мыслителей. Физик установил основные правила разложения и сложения параллельных объектов, дал определение понятия центра тяжести и системы двух грузов, которые были подвешены к одному стержню. Архимеду также принадлежит открытие ключевых законов гидростатики.
Динамические и Кинематические исследования эпохи Возрождения были направлены на точное представление о нестабильном криволинейном движении материальных точек. До этого времени все процессы было принято считать не соответствующими действительности воззрениям Аристотеля, который считал, что для полноценного поддержания равномерного движения тела к необходимо приложить беспрерывно действующую силу.
Основная заслуга правильной формулировки всех известных на сегодняшний день законов динамики принадлежит известному английскому ученому И. Ньютону (1643 – 1727). В своих трактатах, которые были представлены обществу в 1687 г., физик окончательно подвел итог достижениям своих предшественников, указав пути дальнейшего развития механических процессов на столетия вперед.
Задача механики
Замечание 2
Основная задача механики заключается в детализированном описании свойств механического движения тел, то есть установление уравнения движения объектов на основе их характеристик, описывающих перемещение, координаты, длину пройденного пути и динамику развития изучаемых предметов.
Другими словами, если путем составленного закона перемещение материальных тел можно определить положение любой элемента системы в конкретный момент времени, то главная задача механики считается полностью решенной. В зависимости от исследуемых физических величин и способов решения проблем в механики ее разделяют на динамику, кинематику и статику.
Кинематика представляет собой раздел механики, в котором исследуется беспрерывное механическое движение без предоставления его причин. Это направление помогает ответить на вопрос, где в следующий раз окажется материальный объект, если известны только его первоначальные особенности.
Динамика, в первую очередь, занимается изучением закономерностей всех механических движений предметов под непосредственным влиянием приложенных к ним сил. Данный процесс дает ответ на вопрос, почему именно таким образом движется тело.
Определение 2
Статика – особый и значимый раздел механики, который изучает и трактует условия равновесия материальных объектов под действием приложенных к ним явлений.
Основные направления развития механики
Практически все решенные задачи механики отражают технические проблемы определенного времени. В этой среде необходимо выделить группу самых важных процессов динамики, представляющие собой основу современной теории предметных колебаний. Изучая малые движения, можно увидеть, что любое движение физического тела можно представить, как конечный итог наложения друг на друга простых естественных колебаний.
Механика XIX и начала XX столетия подытожила все достижения теоретической механики прошлых веков определив своим положением следующие главные направления в дальнейшем развития:
- расширение общих понятий взаимосвязей и обобщение центральных уравнений динамики нестабильной системы для новых трансформаций;
- правильная формулировка градации принципов динамики и метода сохранения механической энергии;
- создание методов целостного интегрирования уравнений механики.
В середине XIX века был озвучен принцип сохранения энергии: для любой физической концепции возможно выделить коэффициент, называемую интенсивность, равную сумме потенциальной, кинетической и электрической силам, определение которого остается стабильным независимо от происходящих в системе изменений.
Дальнейшая эволюция гипотез малых непостоянных колебаний было тесно взаимосвязана с появлением отдельных серьезных технических проблем.
Замечание 3
Наиболее значимые работы по теории в механической сфере принадлежат известному советскому ученому А. Н. Крылову, деятельность которого была полностью посвящена использованию новых достижений в математике и механике для решения важнейших технических задач.
spravochnick.ru
