Колебания и волны | Формулы и расчеты онлайн
Любые колебания представляют собой движение с переменным ускорением. Отклонение, скорость и ускорение в этом случае являются функциями времени. Для любых колебаний характерна периодичность, т.е. движение повторяется по истечении времени T, называемого длительностью или периодом колебания. Колебания возникают в тех случаях, когда системе способной совершать колебания, сообщается энергия.
Необходимо различать:
Незатухающие колебания
Незатухающие колебания, происходят с постоянной амплитудой Ym. Предполагается, что в данном случае подводимая энергия сохраняется. Приближенно такие условия имеют место при малых потерях энергии и малом времени наблюдения. Для получения действительно незатухающих колебаний необходимо регулярно восполнять теряемую энергию.
Затухающие колебания
Затухающие колебания, постепенно уменьшают свою амплитуду Ym. Без пополнения энергии любые колебания затухают.
Важные характеристики колебаний
| Отклонение | $ y = f(t) $ |
Мгновенное перемещение относительно положения равновесия. |
| Амплитуда | $ Y_m $ |
максимальное отклонение, размах колебаний. |
| Период | $ T = \frac[-1.5]{1}{f} $ |
длительность полного колебания. |
| Частота | $ f = \frac[-1.5]{1}{T} $ |
число колебаний в единицу времени. |
| Угловая Частота | $ ω = 2πf = \frac[-1.5]{2π}{T} $ |
|
| Фаза | $ φ = ωt + φ_0 $ |
|
| Начальная Фаза | $ φ_0 $ |
значение фазы при t=0 (начало колебаний). |
| Время | $ t $ |
Отсчитывается от момента начала колебаний. |
В помощь студенту
Колебания и волны |
стр. 530 |
|---|
www.fxyz.ru
Механические колебания и волны. Формулы ЕГЭ — Репетитор по физике (Краснодар)
Все формулы взяты в строгом соответствии с Федеральным институтом педагогических измерений (ФИПИ)
1.5 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
1.5.1 Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Амплитуда (м) — максимальное отклонение колеблящегося тела от положения равновесия.
Фаза колебаний (рад) — величина, показывающая какая часть периода прошла с момента начала наблюдения колебаний.
Кинематическое описание:
Динамическое описание:
Энергетическое описание (закон сохранения механической энергии):
Связь амплитуды колебаний исходной величины с амплитудами колебаний её скорости и ускорения:
1.5.2 Период (с) — время одного полного колебания (туда-обратно).
Частота колебаний (Гц) — количество колебаний в секунду (величина обратная периоду).
Период малых свободных колебаний математического маятника:
Период свободных колебаний пружинного маятника:
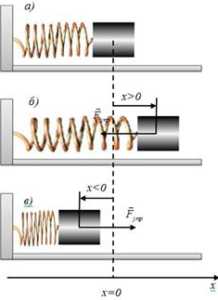
1.5.3 Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.
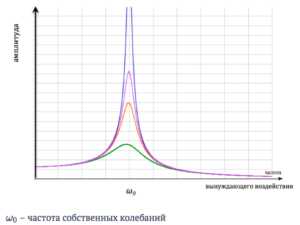
Резонанс — это частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы (увеличение амплитуды при совпадении фаз).
Резонансная кривая — график зависимости амплитуды вынужденных колебаний от частоты вынуждающего воздействия.
1.5.4 Поперечные волны — волны, распространяющиеся в направлении, перпендикулярном к плоскости, в которой происходят колебания частиц среды (в случае упругой волны) или в которой лежат векторы электрического и магнитного поля (для электромагнитной волны).
Продольные волны — волны, распространяющиеся в направлении, в котором происходят колебания частиц среды.
Скорость распространения и длина волны:
Интерференция — наложение двух или нескольких волн.Дифракция — явление огибания волной препятствия, размер которых сопоставим с длиной волны.

1.5.5 Звук — физическое явление, представляющее собой распространение в виде упругих волн механических колебаний в твёрдой, жидкой или газообразной среде (волны, воспринимаемые человеческим ухом).
Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных (скорость звука в сухом воздухе при 20 °C = 343 м/с).
xn--80ancdodk1bn.xn--p1ai
Колебания и волны — Класс!ная физика
ЦОР – мультимедиа. Колебания и волны
Здесь даны ссылки на материалы по физике из «Единой коллекции ЦОР» (файлы в формате swf, можно открыть программой Adobe Flash Player )
!!! Некоторые модели открываются, к сожалению, с задержкой.
Механические колебания
Запомни «Механические колебания» ……….смотреть
Анимация «Маятник Максвелла» ……….смотреть
Крутильный маятник ……….смотреть
Пружинный маятник ……….смотреть
Подборка заданий «Колебаний пружинного и математического маятника» ……….смотреть
Видеоролик «Энергия при колебаниях маятника» ……….смотреть
Интерактивный рисунок «Колебания горизонтального маятника» ……….смотреть
Подборка заданий «Колебаний пружинного и математического маятника» ……….смотреть
Интерактивная задача «Параметры колебаний горизонтального пружинного маятника» ……….смотреть
Слайд-шоу «Что такое отклонение и амплитуда» ……….смотреть
Формула «Понятие частоты колебаний» ……….смотреть
Видеоролик — анимация «Затухающие колебания пружинного маятника» ……….смотреть
Формула «Понятие периода колебаний» ……….смотреть
Анимация «Получение графика гармонических колебаний» ……….смотреть
Интерактивная задача «Параметры колебаний маятника по графику» ……….смотреть
Интерактивный рисунок «График гармонических колебаний» ……….смотреть
Формула «Период колебаний пружинного маятника» ……….смотреть
Интерактивная задача «Параметры колебаний математического маятника» ……….смотреть
Анимация со звуком «Условие возникновения и продолжения колебаний» ……….смотреть
Анимация со звуком «От чего зависит период колебаний математического маятника» ……….смотреть
Формула «Период колебаний математического маятника» ……….смотреть
Анимация «Фаза колебаний» ……….смотреть
Интерактивная модель «Изучение колебаний математического маятника» ……….смотреть
Видеоролик — анимация «Затухающие колебания пружинного маятника» ……….смотреть
Анимация «Резонанс колебаний» ……….смотреть
Видеоролик «Резонанс разрушает мост» ……….смотреть
Рисунок «Резонансная кривая» ……….смотреть
Рисунок «Схема автоколебательной системы» ……….смотреть
Анимация «Работа часового механизма» ……….смотреть
Электромагнитные колебания
Формула «Емкость конденсатора» ……….смотреть
Интерактивный рисунок «Емкость конденсатора» ……….смотреть
Интерактивная задача «Емкость конденсатора» ……….смотреть
Подборка заданий «Емкость и энергия конденсатора» ……….смотреть
Формула «Энергия конденсатора» ……….смотреть
Интерактивная задача «Энергия конденсатора» ……….смотреть
Формула «Энергия магнитного поля» ……….смотреть
Интерактивная задача «Энергия магнитного поля катушки» ……….смотреть
Подборка заданий «Энергия магнитного поля катушки» ……….смотреть
Анимация «Затухающие электрические колебания в контуре» ……….смотреть
Подборка заданий «Свободные электрические колебания в контуре» ……….смотреть
Анимация «Период электрических колебаний в контуре» ……….смотреть
Интерактивная задача «Период электрических колебаний в контуре» ……….смотреть
Формула «Период свободных электрических колебаний в контуре» ……….смотреть
Рисунок «Схема генератора незатухающих электрических колебаний как автоколебательной системы» ……….смотреть
Механические волны
Формула «Длина волны» ……….смотреть
Запомни «Механические волны» ……….смотреть
Рисунок «Длина волны» ……….смотреть
Интерактивная задача «Длина, период и скорость волны» ……….смотреть
Слайд-шоу «Волны в природе и технике» ……….смотреть
Анимация «Образование волн» ……….смотреть
Анимация со звуком «Определение поперечных и продольных волн» ……….смотреть
Видеоролик «Продольные волны» ……….смотреть
Видеоролик — анимация «Поперечные волны» ……….смотреть
Видеоролик «Поперечные волны» ……….смотреть
Слайд — шоу «Измерение скорости звука» ……….смотреть
Слайд — шоу «Образование звука при полете насекомого» ……….смотреть
Интерактивная задача «Скорость звука» ……….смотреть
Видеоролик «Распространение звука в воздухе» ……….смотреть
Слайд — шоу «Что такое акустика» ……….смотреть
Слайд-шоу «Звук и как мы его слышим» ……….смотреть
Анимация «Наблюдение акустического резонанса» ……….смотреть
Видеоролик «Отражение звука» ……….смотреть
Рисунок «Эхолокация» ……….смотреть
Слайд-шоу «Ультразвуковое сканирование» ……….смотреть
Видеоролик «Работа эхолокатора» ……….смотреть
Слайд — шоу «Эхолокация у животных» ……….смотреть
Видеоролик «Дефектоскопия» ……….смотреть
Слайд — шоу «Эхо» ……….смотреть
Рисунок «Микрофон» ……….смотреть
Таблица «Диапазон слышимых звуковых частот. Инфра и ультразвук» ……….смотреть
Видеоролик «Звук от струн гитары» ……….смотреть
Видеоролик «Связь частоты колебаний и длины волны» ……….смотреть
Слайд — шоу «Инфразвук» ……….смотреть
Таблица «Характеристики звука» ……….смотреть
Рисунок «Ухо» ……….смотреть
Слайд — шоу «Тембр» ……….смотреть
Видеоролик — анимация «Принцип действия слухового аппарата человека» ……….смотреть
Электромагнитные волны
Слайд — шоу «Электромагнитные волны» ……….смотреть
Анимация «Электромагнитная волна» ……….смотреть
Анимация «Наблюдение возникновения и распространения электромагнитной волны» ……….смотреть
Таблица «Диапазоны радиоволн» ……….смотреть
Рисунок «Схема радиосвязи» ……….смотреть
Рисунок «Шкала электромагнитных волн» ……….смотреть
Слайд — шоу «Радиоволны» ……….смотреть
Рисунок-плакат «Схема радиосвязи» ……….смотреть
Рисунок — плакат «Схема приемника Попова» ……….смотреть
Интерактивный рисунок «Сборка детекторного радиоприемника» ……….смотреть
Интерактивная задача «Радиолокация объекта» ……….смотреть
Анимация «Радиолокация» ……….смотреть
Рисунок «Радиотелескоп» ……….смотреть
Таблица «Радиоизлучение Вселенной» ……….смотреть
Анимация «Излучение пульсара» ……….смотреть
Электромагнитные колебания в идеальном колебательном контуре ……….смотреть
Устройство радиоприемника ……….смотреть
Характеристики волны при переходе границы раздела сред ……….смотреть
Радиолокация ……….смотреть
class-fizika.ru
Механические колебания (Основные формулы)
Механические колебания
Основные формулы
Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой \(A\), периодом колебаний \(T\), частотой \(\nu\), циклической (круговой) частотой \(\omega\) и фазой колебаний \(\varphi\).
Амплитудой \(A\) называют наибольшее значение колеблющейся величины.
Число полных колебаний в единицу времени называют частотой:
\(\nu=\frac{n}{t}\).
Циклическая (круговая) частота — это число полных колебаний в течении \(2\pi\) с:
\(\omega=\frac{2\pi{n}}{t}=2\pi{\nu}\).
Периодом называю время, в течении которого совершается одно полное колебание:
\(T=\frac{t}{n}=\frac{2\pi}{\omega}=\frac{1}{\nu}\).
Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями
\(x=A\sin(\omega{t}+\varphi_0)\),
\(v=\dot x=A\omega\cos(\omega{t}+\varphi_0)\),
\(a=\ddot x=-A\omega^2\sin(\omega{t}+\varphi_0)=-\omega^2x\).
Здесь \((\omega{t}+\varphi_0)\) — фаза колебаний, а \(\varphi_0\) — начальная фаза.
Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:
\(F=ma=-m{\omega_0}^2x=-kx\)
где \(k=m{\omega_0}^2\) — коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение \(x\), равное единице.
При отсутствии сопротивления среды циклическая частота \(\omega_0\) свободных гармонических колебаний, называемых собственной циклической частотой и период \(T\) равны:
\(\omega_0=\sqrt{\frac{k}{m}}\), \(T=2\pi\sqrt{\frac{m}{k}}\)
Период колебания математического маятника длиной \(l\) равен
\(T=2\pi\sqrt{\frac{l}{g}}\).
Период колебаний физического маятника
\(T=2\pi\sqrt{\frac{I}{mgd}}\),
где \(I\) — момент инерции маятника относительно оси качаний, \(d\) — расстояние от оси его до центра тяжести.
Полная энергия тела, совершающего гармонические колебания, постоянна и равна
\(W=\frac{m\omega^2A^2}{2}\).
Уравнение смещения в затухающих колебаниях при наличии силы сопротивления \(F_s\) пропорциональной скорости (\(F_s=-rv\), где \(r\) — коэффициент сопротивления) имеет вид:
\(x=A_0e^{-\beta{t}}\sin(\omega{t}+\varphi_0)\).
Здесь \(A_0e^{-\beta{t}}\) — убывающая по времени амплитуда смещения; \(\beta\) — коэффициент затухания; \(\omega\) — циклическая частота; \(A_0,\varphi_0\) — начальные амплитуда и фаза, определяются из начальных условий.
Величины \(\beta\) и \(\omega\) выражаются через параметры системы \(r,m,k\) формулами:
\(\beta=\frac{r}{2m}\),
\(\omega=\sqrt{{\omega_0}^2-\beta^2}=\sqrt{\frac{k}{m}-\frac{r^2}{4m^2}}\).
Логарифмический декремент затухания
\(\lambda=\ln(\frac{A_1}{A_2})=\beta{T}\),
где \(A_1,A_2\) — амплитуды двух последовательных колебаний.
Амплитуда вынужденных колебаний
\(A=\frac{h}{\sqrt{({\omega_0}^2-\omega^2)^2+4\beta^2\omega^2}}\),
где \(h\) — есть отношение амплитуды вынуждающей силы к массе тела; \(\omega_0\) — собственная циклическая частота; \(\omega\) — циклическая частота вынуждающей силы.
Резонансная циклическая частота равна
\(\omega_r=\sqrt{{\omega_0}^2-2\beta^2}\).
————-
Источник: sfiz.ru
sfiz.ru
3. Колебания. Волны
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебаний (в контрольной работе это задачи 301-310 для механических колебаний и задачи 311-320 для электромагнитных колебаний).
Нужно уметь представить гармонические колебания в виде вектора и пользоваться графическим методом сложения колебаний, т.е. строить векторную диаграмму (задачи 321-330). Важно представлять себе, что периодические процессы иной формы, чем гармонические, могут быть представлены в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухания (в контрольной работе это задачи 331-340).
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом (в контрольной работе это задачи 341-350).
При изучении темы «Волны» следует обратить внимание на картину мгновенного распределения смещений и скоростей частиц среды в бегущей волне. Здесь вводится понятие длины волны, скорости распространения волны, волнового числа (в контрольной работе это задачи 351-360).
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Основные формулы
|
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; t — время; α — начальная фаза; (ωt+α ) — фаза. | |
|
Связь между периодом и круговой частотой: | |
|
Частота: | |
|
Связь круговой частоты с частотой: | |
|
Периоды собственных колебаний пружинного маятника: где k — жесткость пружины; математического маятника: где l — длина маятника, g — ускорение свободного падения; колебательного контура: где L — индуктивность контура, С — емкость конденсатора. | |
|
Частота собственных колебаний: | |
|
Сложение колебаний одинаковой частоты и направления: амплитуда результирующего колебания где А1 и А2 — амплитуды составляющих колебаний, α1 и α2 — начальные фазы составляющих колебаний; начальная фаза результирующего колебания |
|
|
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов. | |
|
Амплитуда затухающих колебаний: где А0 — амплитуда в начальный момент времени; β — коэффициент затухания; t — время. | |
|
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура. | |
|
Частота затухающих колебаний ω: | |
|
Период затухающих колебаний Т: | |
|
Логарифмический декремент затухания: | |
|
Связь логарифмического декремента χ и коэффициента затухания β: | |
|
Амплитуда вынужденных колебаний где ω — частота вынужденных колебаний, fо — приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: | |
|
Резонансная частота | |
|
Резонансная амплитуда | |
|
Полная энергия колебаний: | |
|
Уравнение плоской волны: где ξ — смещение точек среды с координатой х в момент времени t; k — волновое число: | |
|
Длина волны: где v скорость распространения колебаний в среде, Т — период колебаний. | |
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
studfiles.net
Основные формулы для решения задач по теме «Механические колебания и волны».
Механические колебания
Основные формулы для решения задач.
Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой , периодом колебаний , частотой , циклической (круговой) частотой и фазой колебаний .
Амплитудой называют наибольшее значение колеблющейся величины.
Число полных колебаний в единицу времени называют частотой:
.
Циклическая (круговая) частота — это число полных колебаний в течении с:
.
Периодом называю время, в течении которого совершается одно полное колебание:
.
Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями
,
,
.
Здесь — фаза колебаний, а — начальная фаза.
Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:
где — коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение , равное единице.
При отсутствии сопротивления среды циклическая частота свободных гармонических колебаний, называемых собственной циклической частотой и период равны:
,
Период колебания математического маятника длиной равен
.
Период колебаний физического маятника
,
где — момент инерции маятника относительно оси качаний, — расстояние от оси его до центра тяжести.
Полная энергия тела, совершающего гармонические колебания, постоянна и равна
.
Уравнение смещения в затухающих колебаниях при наличии силы сопротивления пропорциональной скорости (, где — коэффициент сопротивления) имеет вид:
.
Здесь — убывающая по времени амплитуда смещения; — коэффициент затухания; — циклическая частота; — начальные амплитуда и фаза, определяются из начальных условий.
Величины и выражаются через параметры системы формулами:
,
.
Логарифмический декремент затухания
,
где — амплитуды двух последовательных колебаний.
Амплитуда вынужденных колебаний
,
где — есть отношение амплитуды вынуждающей силы к массе тела; — собственная циклическая частота; — циклическая частота вынуждающей силы.
Резонансная циклическая частота равна
.
infourok.ru
4. Механические колебания и волны Основные формулы
Гармонические колебания происходят по закону:
x = A cos(ωt + φ0),
где x – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ0 – начальная фаза, t – время.
Период
колебаний T
=
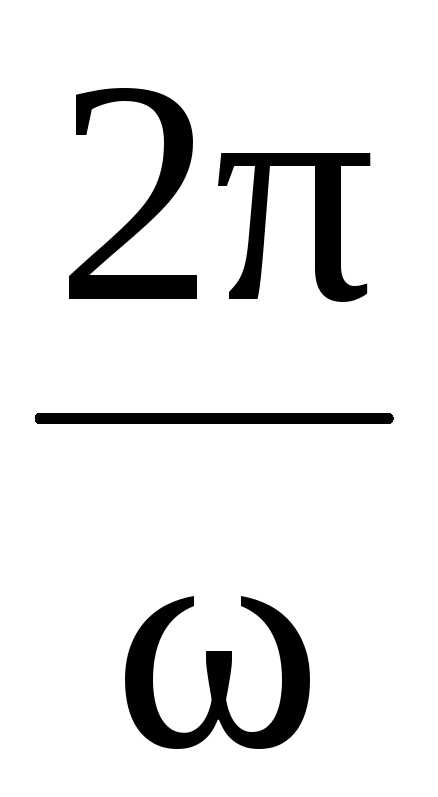 .
.
Скорость колеблющейся частицы:
υ
=
 = – A
ω
sin (ωt
+ φ0),
= – A
ω
sin (ωt
+ φ0),
ускорение
a
=
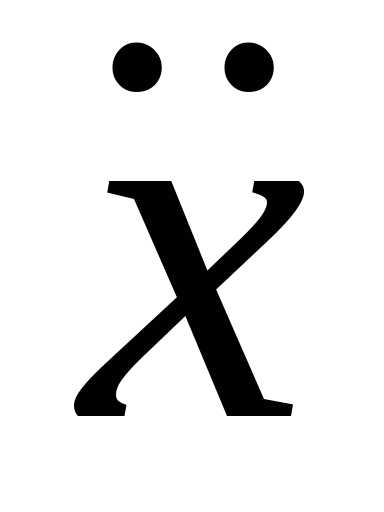 = –
Aω2
cos
(ωt
+ φ0).
= –
Aω2
cos
(ωt
+ φ0).
Кинетическая энергия частицы, совершающей
колебательное движение: Ek
=
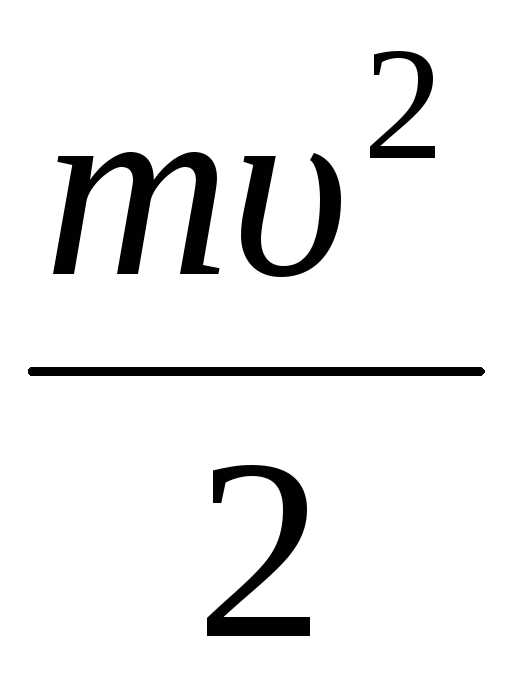 =
=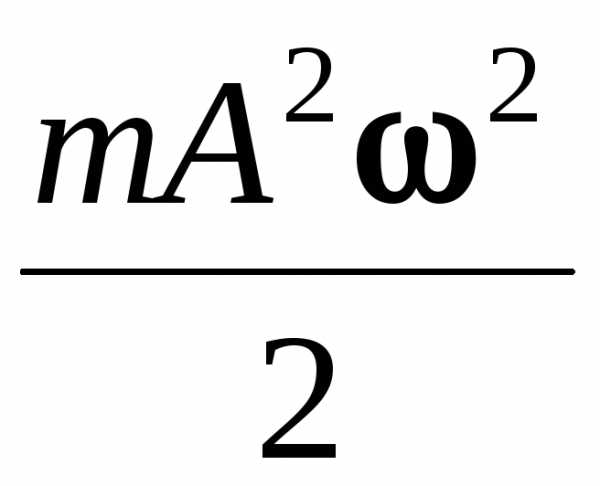 sin2(ωt+ φ0).
sin2(ωt+ φ0).
Потенциальная энергия:
En=
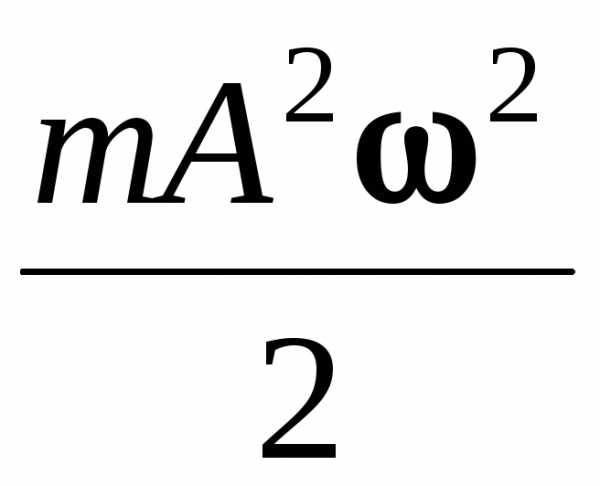 cos2(ωt
+ φ0).
cos2(ωt
+ φ0).
Периоды колебаний маятников
– пружинного
T
=
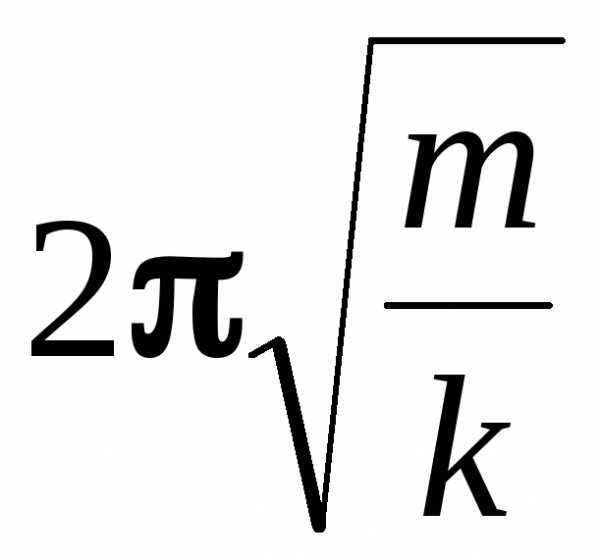 ,
,
где m – масса груза, k – коэффициент жесткости пружины,
– математического
T
=
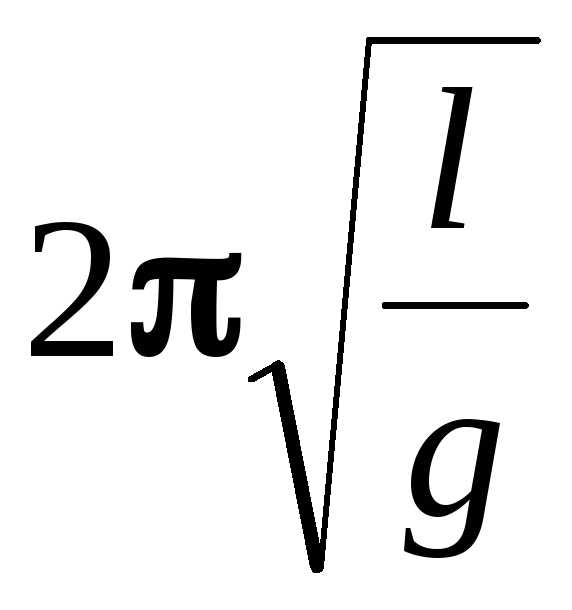 ,
,
где l – длина подвеса, g – ускорение свободного падения,
– физического
T
=
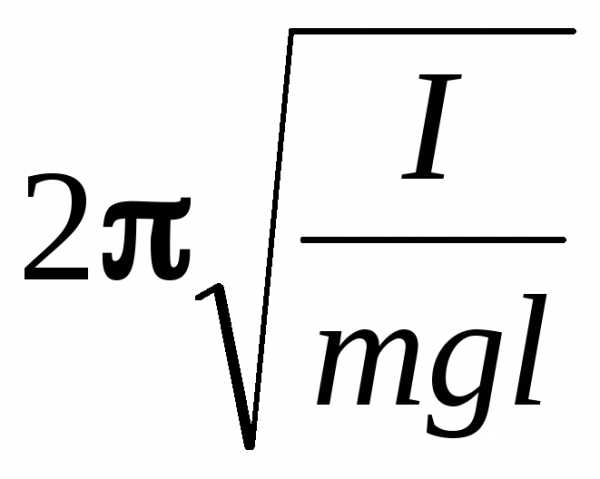 ,
,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса, m – масса маятника, l – расстояние от точки подвеса до центра масс.
Приведенная
длина физического маятника находится
из условия: lnp=
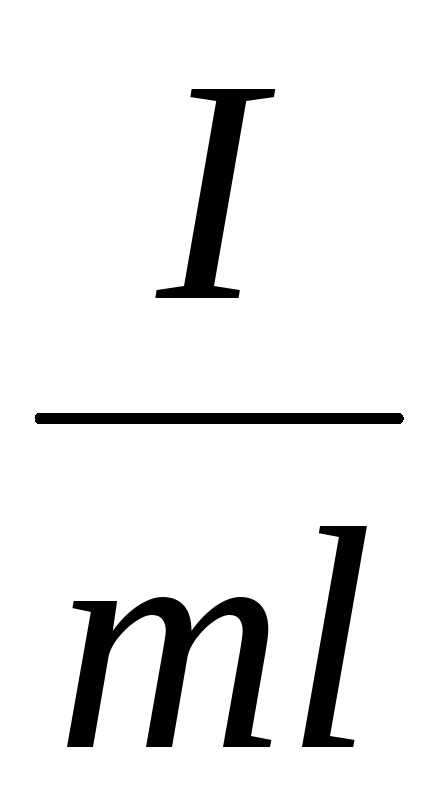 ,
,
обозначения те же, что для физического маятника.
При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:
A = A12 + A22 + 2A1 A2 cos(φ2 – φ1)
и начальной фазой: φ = arctg .
где А1, A2 – амплитуды, φ1, φ2 – начальные фазы складываемых колебаний.
Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:
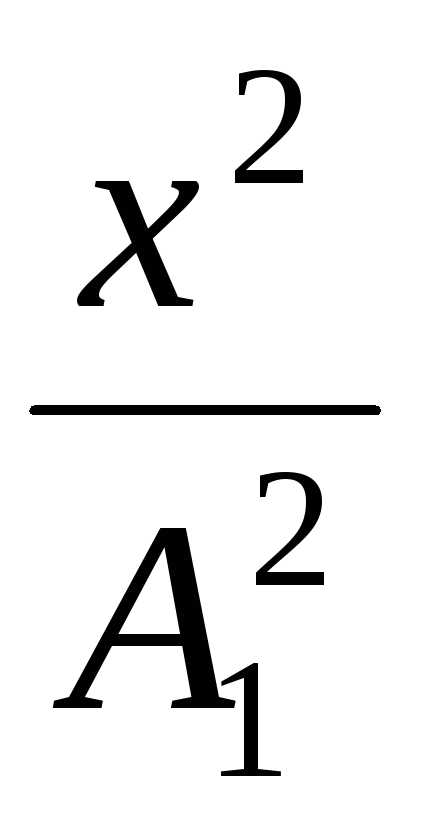 +
+
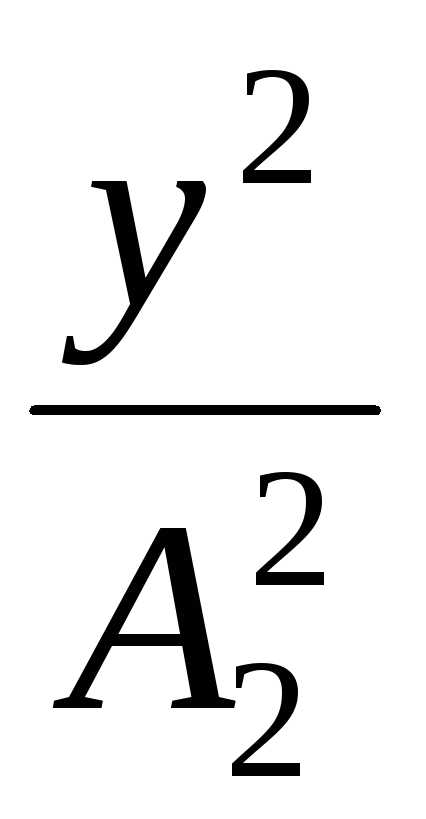 –
–
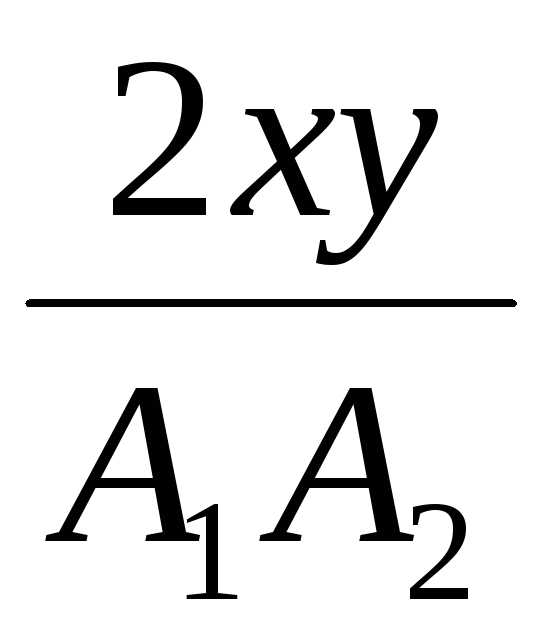 cos
(φ2
– φ1)
= sin2
(φ2
– φ1).
cos
(φ2
– φ1)
= sin2
(φ2
– φ1).
Затухающие колебания происходят по закону:
x = A0 e— βt cos(ωt + φ0),
где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А0 – начальная амплитуда. В момент времени t амплитуда колебаний:
A = A0 e — βt.
Логарифмическим декрементом затухания называют:
λ
= ln
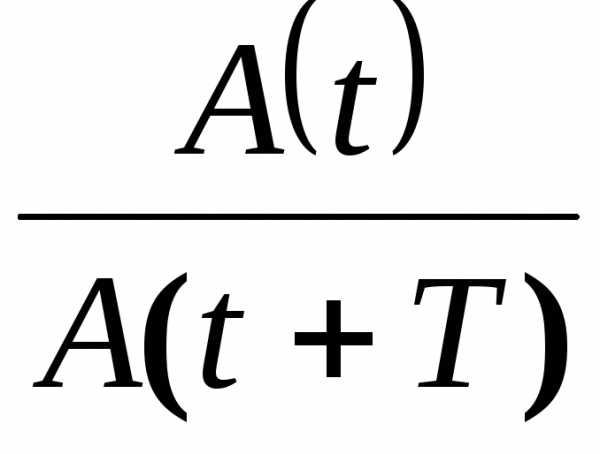 = βT,
= βT,
где
Т
– период колебания: T
=
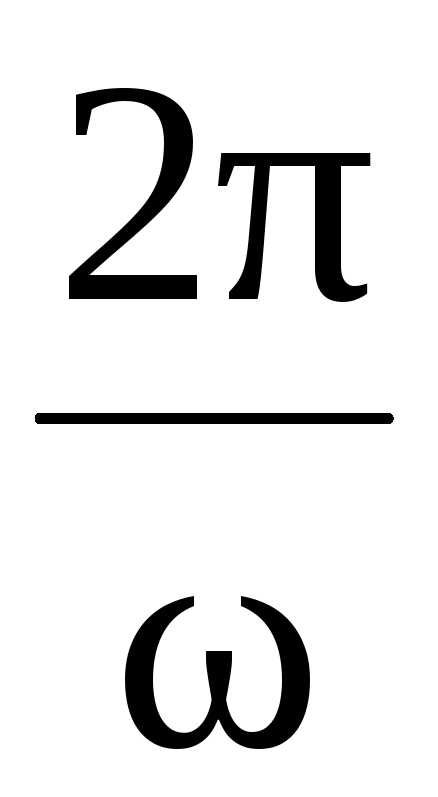 .
.
Добротностью колебательной системы называют:
D
=
 .
.
Уравнение плоской бегущей волны имеет вид:
y
= y0
cos
ω(t
±
 ),
),
где у – смещение колеблющейся величины от положения равновесия, у0 – амплитуда, ω – круговая частота, t – время, х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.
Знак «+» соответствует волне, распространяющейся против оси X, знак «–» соответствует волне, распространяющейся по оси Х.
Длиной волны называют ее пространственный период:
λ = υT,
где υ–скорость распространения волны, T–период распространяющихся колебаний.
Уравнение волны можно записать:
y
= y0
cos
2π
(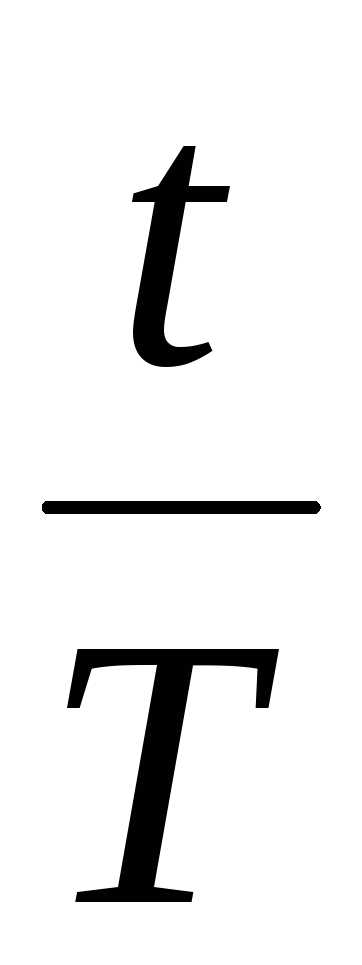 +
+ ).
).
Стоячая волна описывается уравнением:
y
= (2y0
cos
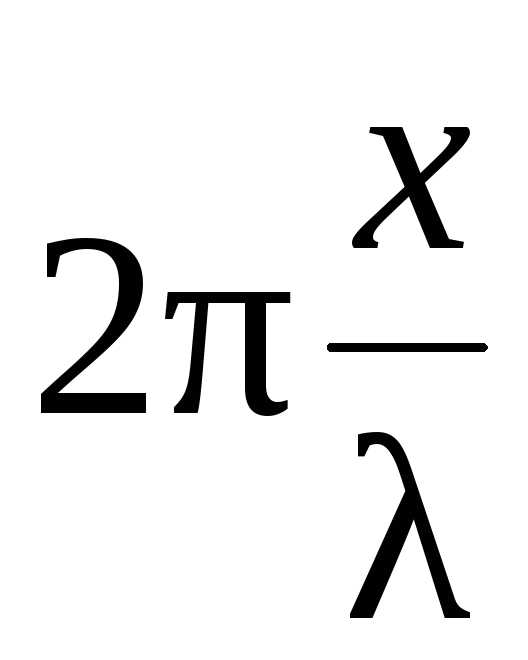 )
cos ωt.
)
cos ωt.
В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,
xп
= n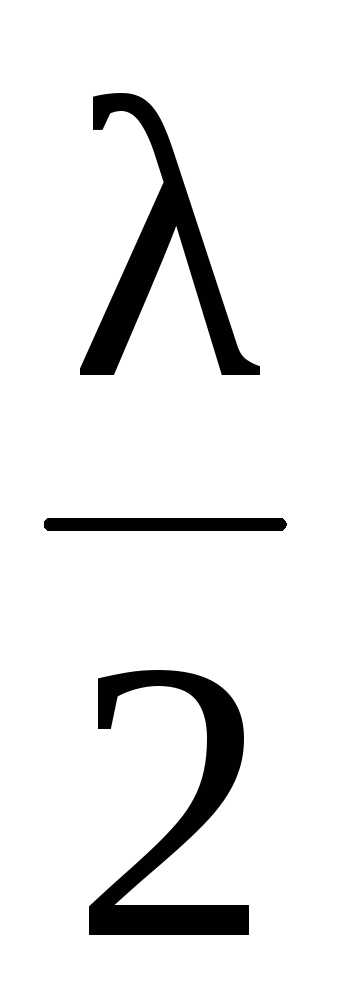 ,
,
точки с нулевой амплитудой – узлами,
xу
=
(n
+
 )
)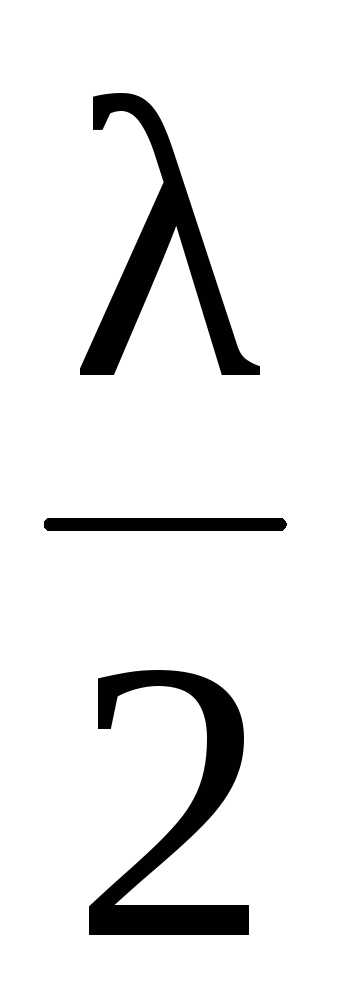 .
.
Примеры решения задач
Задача 20
Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при t=0 и при t = 1,5 с; в) начертить график этого движения.
Решение
Уравнение колебания записывается в виде x = a cos(t + 0).
По
условию известен период колебаний.
Через него можно выразить круговую
частоту
=
 .
Остальные параметры известны:
.
Остальные параметры известны:
а)
x
= 0,05 cos( t
+
t
+
 ).
).
б) Смещение x при t = 0.
x1
= 0,05 cos =
0,05
=
0,05
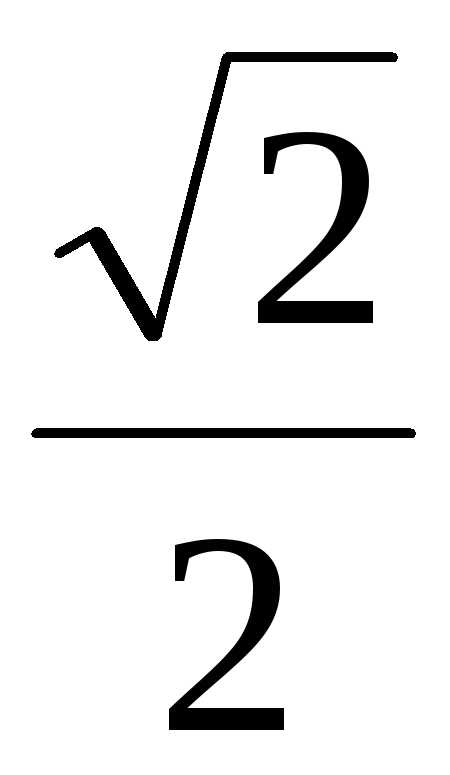 =
0,0355 м.
=
0,0355 м.
При t = 1,5 c
x2
= 0,05 cos( 1,5
+
1,5
+
 )=
0,05 cos
=
– 0,05 м.
)=
0,05 cos
=
– 0,05 м.
в)
график функцииx=0,05cos
( t
+
t
+
 )
выглядит следующим образом:
)
выглядит следующим образом:
Определим положение нескольких точек. Известны х1(0) и х2(1,5), а также период колебаний. Значит, через t = 4 c значение х повторяется, а через t = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .
Задача 21
Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.
Решение
1 способ. Записываем уравнение колебания точки:
x
= 0,05 cos
t,
т.
к.
=
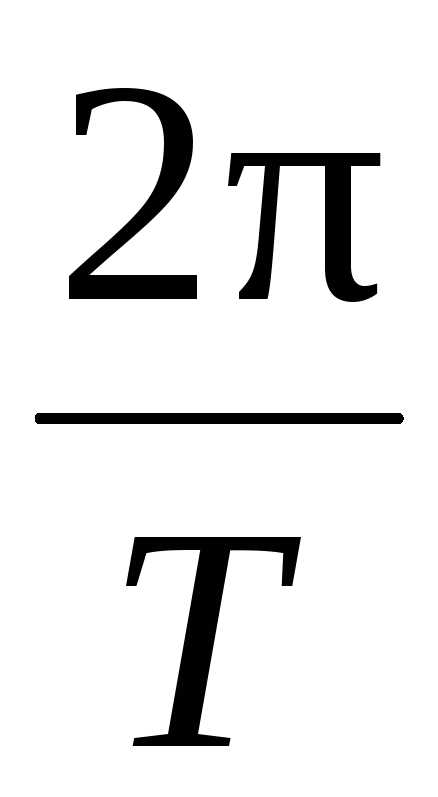 =.
=.
Находим скорость в момент времени t:
υ
=
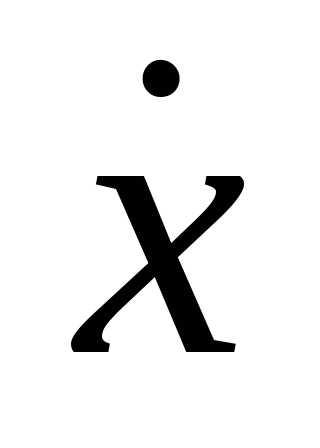 = – 0,05
cos
t.
= – 0,05
cos
t.
Находим момент времени, когда смещение равно 0,025 м:
0,025 = 0,05 cos t1,
отсюда
cos t1
=
 ,
t1
=
,
t1
=
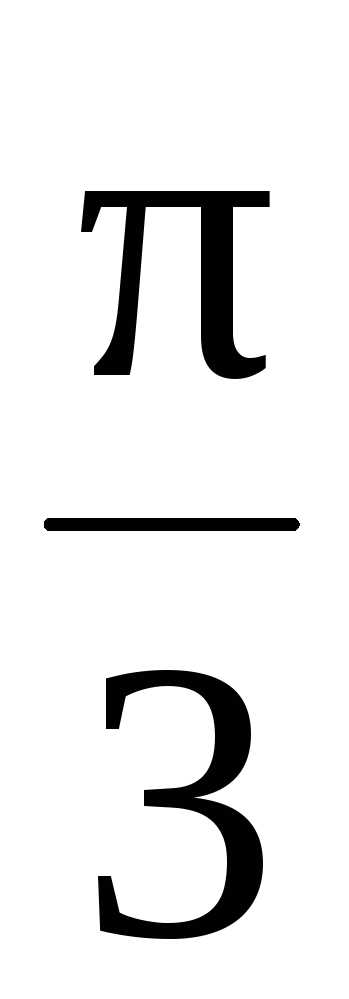 .Подставляем
это значение в выражение для скорости:
.Подставляем
это значение в выражение для скорости:
υ
= – 0,05
sin
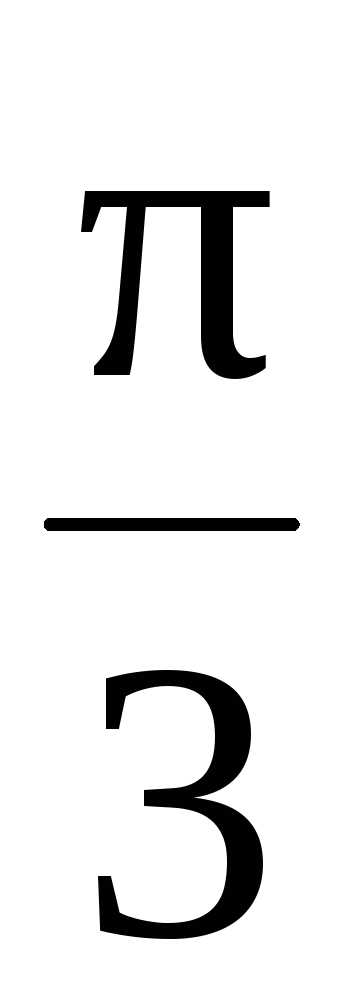 =
–
0,05
=
–
0,05
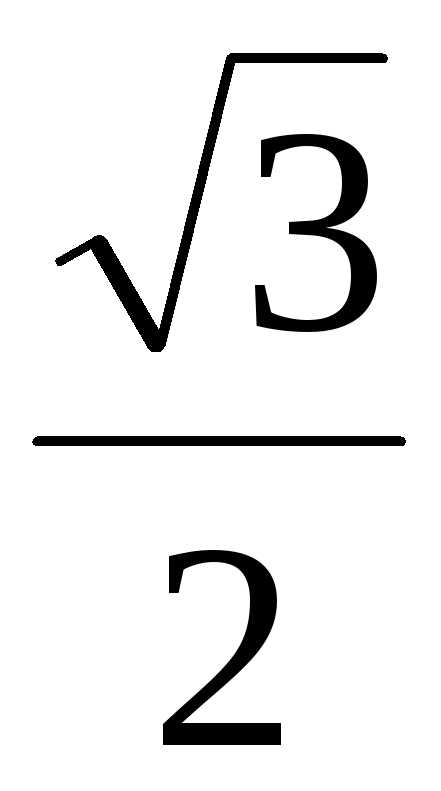 =
0,136 м/c.
=
0,136 м/c.
2 способ. Полная энергия колебательного движения:
E
=
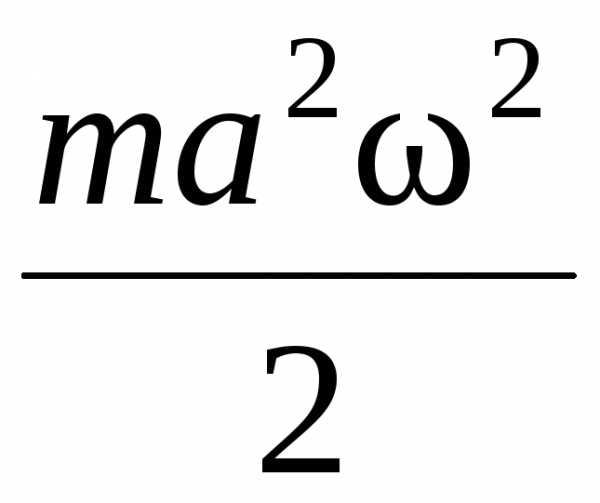 ,
,
где а – амплитуда, – круговая частота, m – масса частицы.
В каждый момент времени она складывается из потенциальной и кинетической энергии точки
Ek=
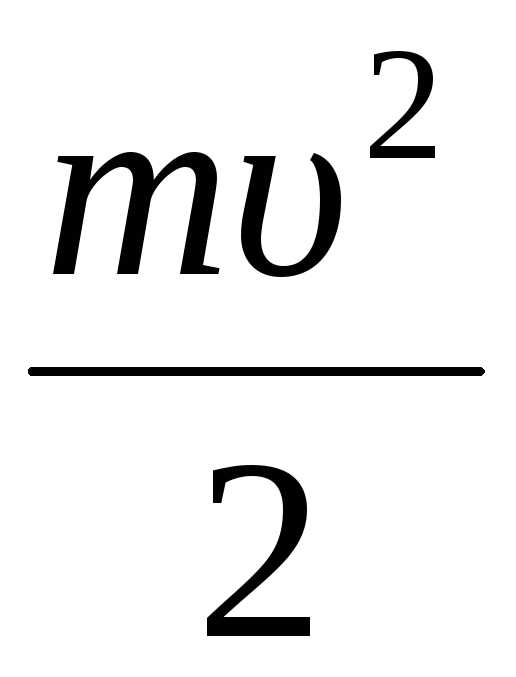 ,
Eп=
,
Eп=
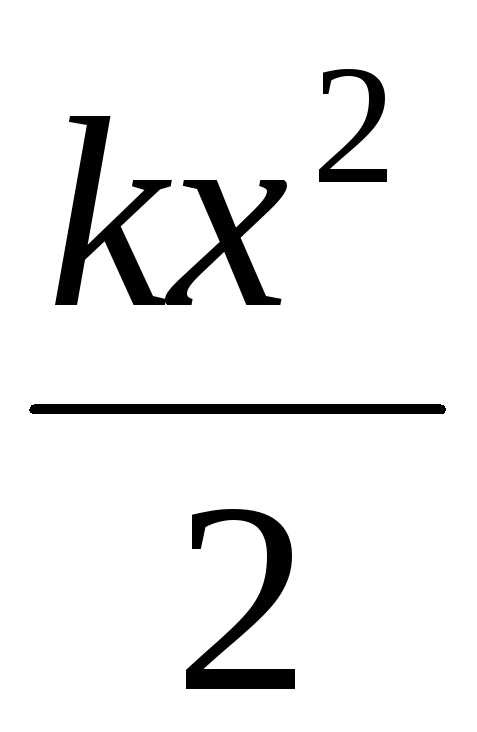 ,
но k
= m2,
значит, Eп
=
,
но k
= m2,
значит, Eп
=
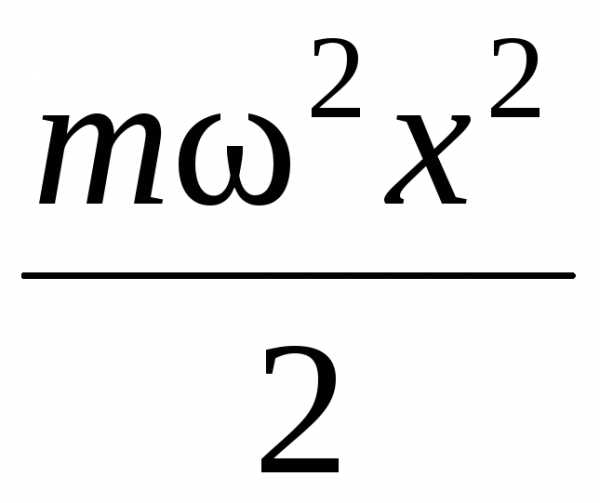 .
.
Запишем закон сохранения энергии:
 =
=
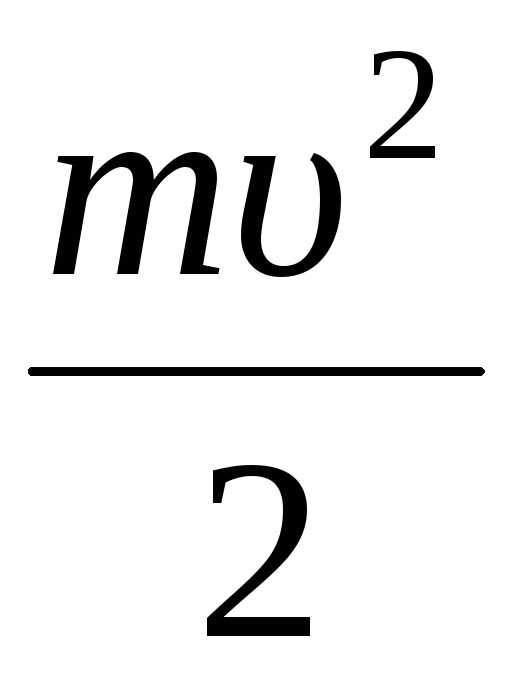 +
+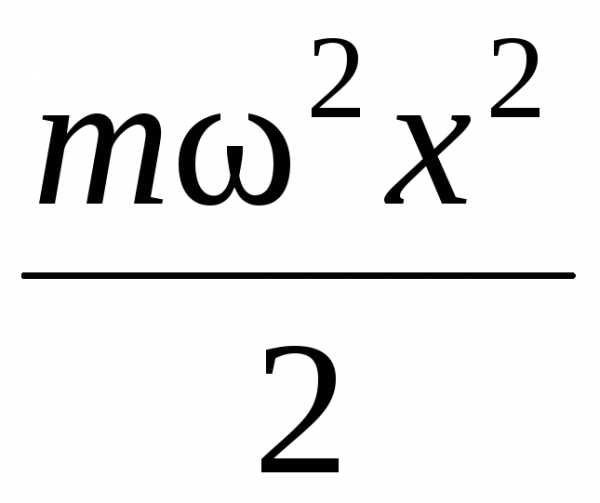 ,
,
отсюда получаем: a22 = υ 2 + 2x2,
υ
=
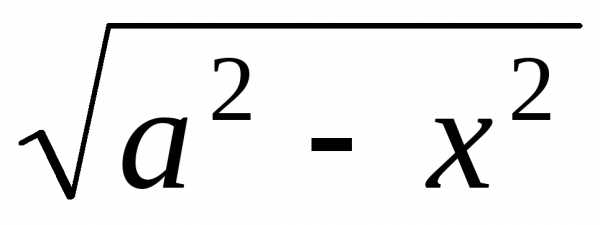 =
=
0,136 м/c.
=
=
0,136 м/c.
Задача 22
Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10-5 Н?
Решение
Полная
энергия точки, совершающей гармонические
колебания, равна:
E
=
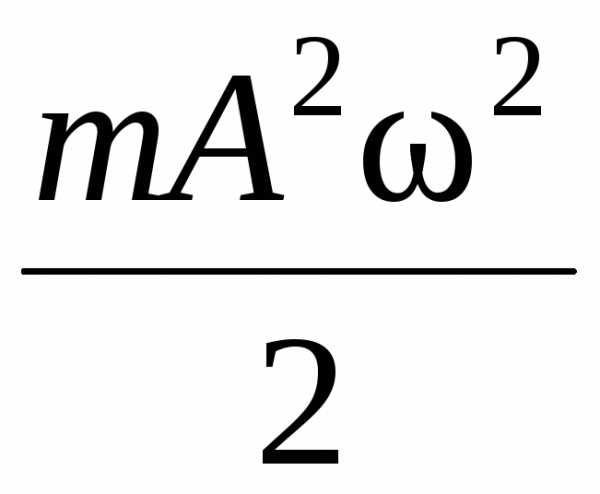 .
(13)
.
(13)
Модуль упругой силы выражается через смещение точек от положения равновесия x следующим образом:
F = k x (14)
В формулу (13) входят масса m и круговая частота , а в (14) – коэффициент жесткости k. Но круговая частота связана с m и k:
2
=
 ,
,
отсюда
k
= m2
и F
= m2x.
Выразив m2
из
соотношения (13) получим:
m2
=
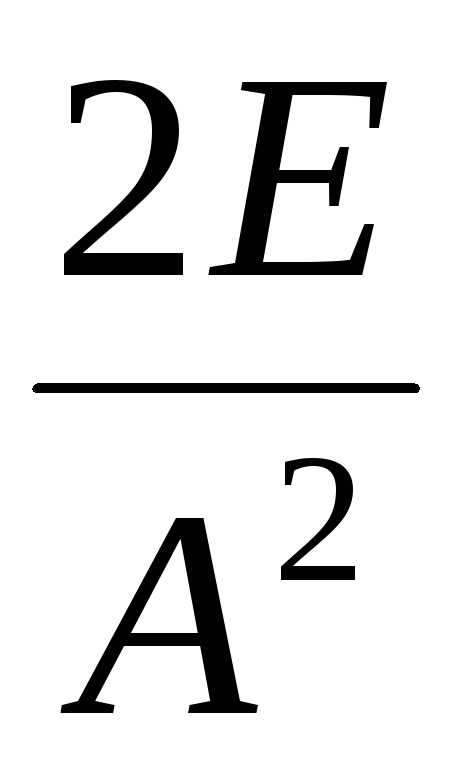 ,
F
=
,
F
=
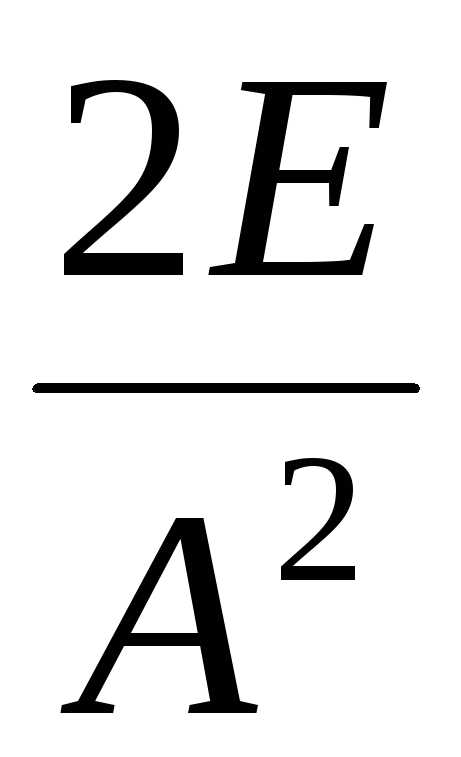 x.
x.
Откуда
и получаем выражение для смещения x:
x
=
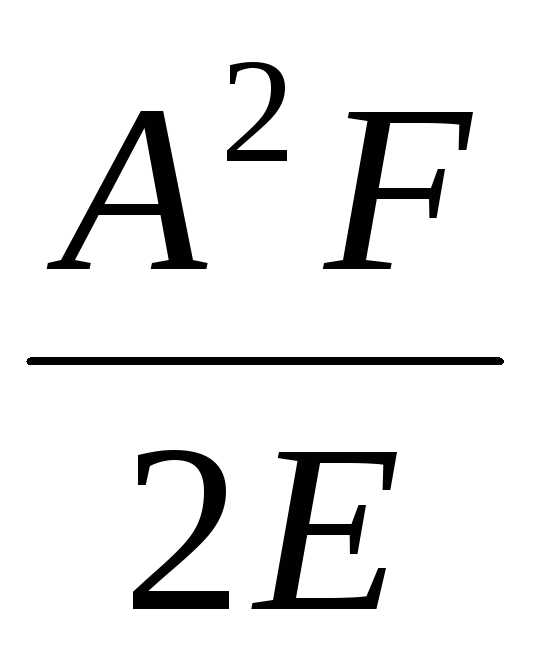 .
.
Подстановка числовых значений дает:
x
=
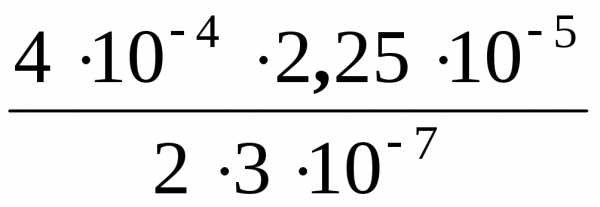 = 1,5∙10-2
м
= 1,5 см.
= 1,5∙10-2
м
= 1,5 см.
Задача 23
Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А1 = 3 см и А2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.
Решение
Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:
A = ,
где А1 и А2 – амплитуды складываемых колебаний, 1 и 2–начальные фазы. По условию начальные фазы одинаковы, значит 2 – 1 = 0, а cos 0 = 1.
Следовательно:
A = == А1+А2 = 7 см.
Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:
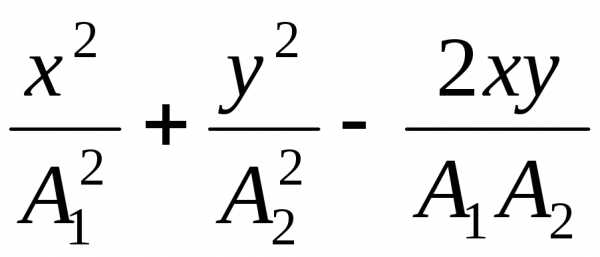 cos(2
–
1)
= sin2(2
–
1).
cos(2
–
1)
= sin2(2
–
1).
Так
как по условию 2
–
1
=
0, cos
0 = 1, sin
0 = 0, то уравнение запишется в виде:
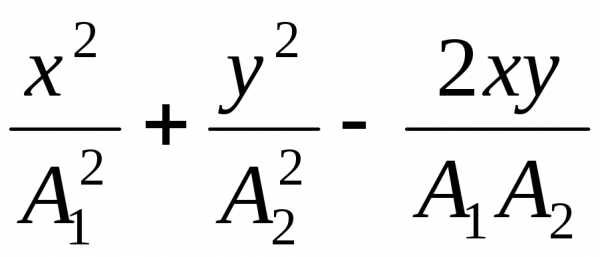 =0,
=0,
или
 =0,
=0,
или
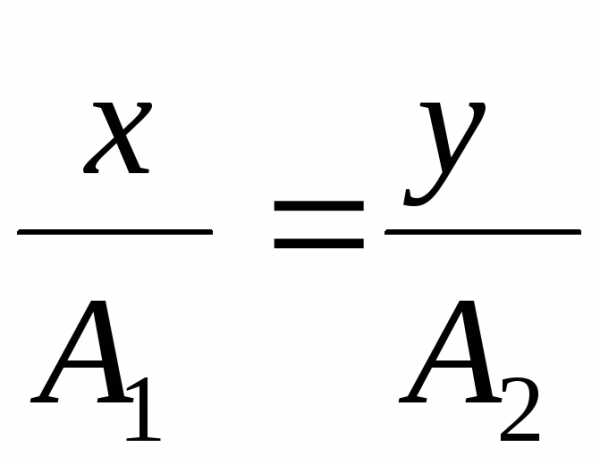 .
.
Полученное
соотношение между x
и у
можно
изобразить на графике. Из графика видно,
что результирующим будет колебание
точки на прямой MN.
Амплитуда этого колебания определится
как:
A
=
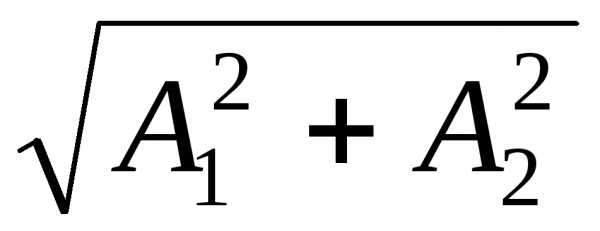 =
5 см.
=
5 см.
Задача 24
Период
затухающих колебаний Т=4
с, логарифмический декремент затухания
= 1,6 , начальная фаза равна нулю. Смещение
точки при t
=
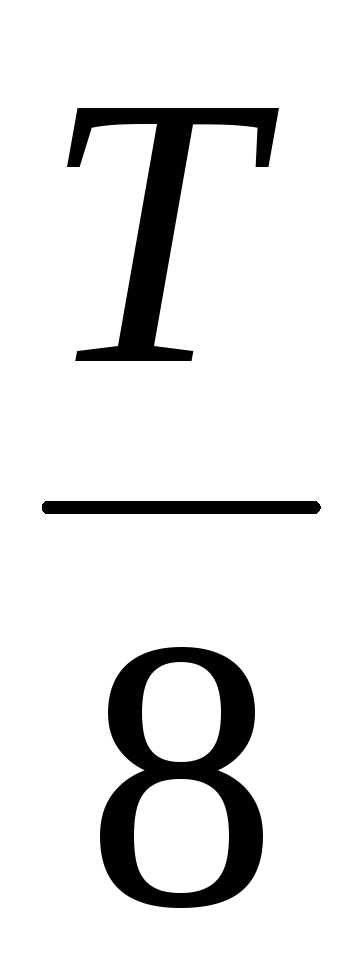 равно 4,5 см. 1) Написать уравнение этого
колебания; 2) Построить график этого
движения для двух периодов.
равно 4,5 см. 1) Написать уравнение этого
колебания; 2) Построить график этого
движения для двух периодов.
Решение
Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:
x
= A0e
—tcos2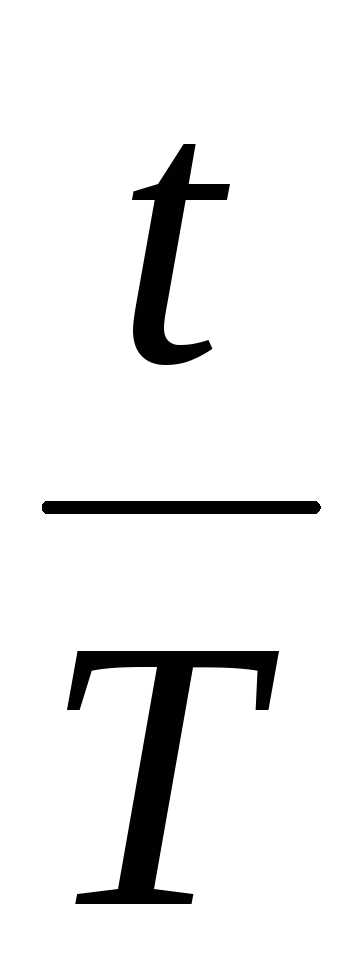 .
.
Для подстановки числовых значений не хватает величин начальной амплитуды А0 и коэффициента затухания .
Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:
= Т.
Таким
образом
=
 =
=
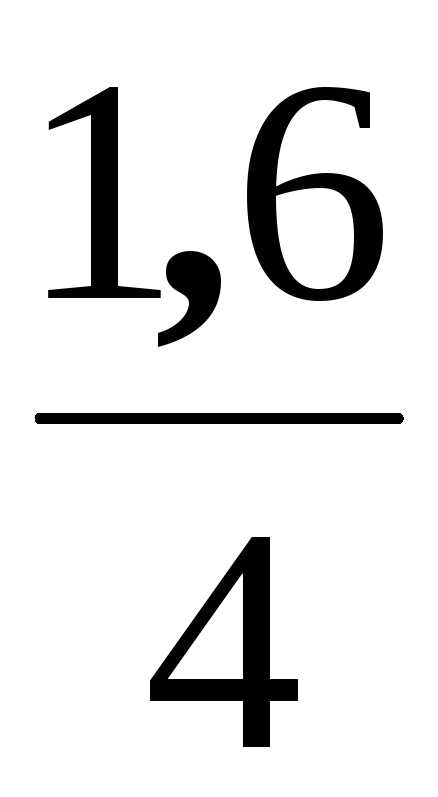 = 0,4 с-1.
= 0,4 с-1.
Начальную амплитуду можно определить, подставив второе условие:
4,5
см
= A0
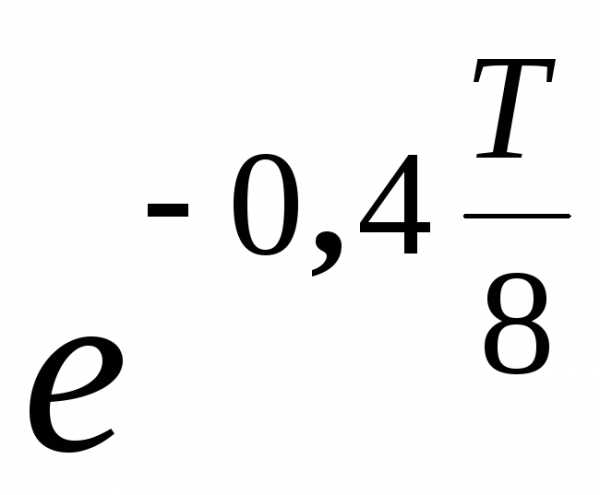 cos
2
cos
2 = A0
= A0
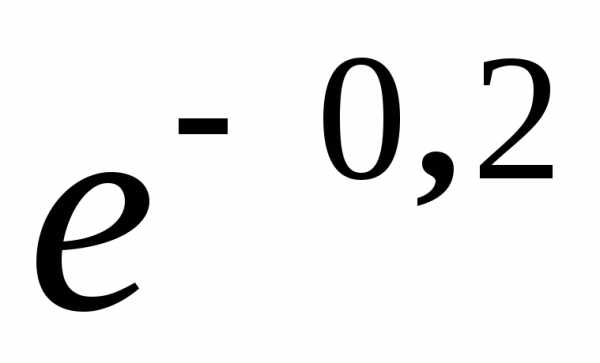 cos
cos
 =A0
=A0
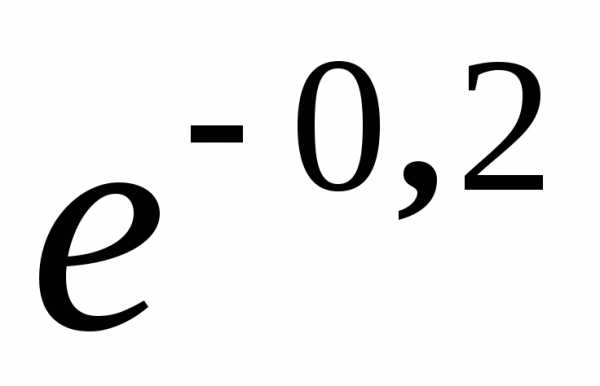
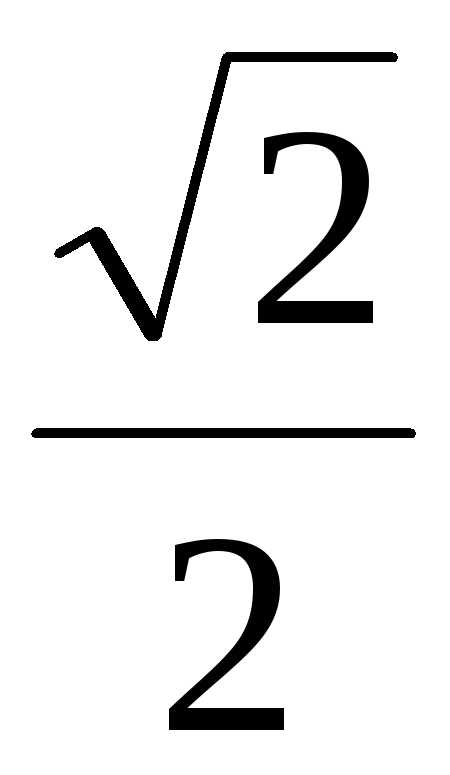 .
.
Отсюда находим:
A0=
4,5∙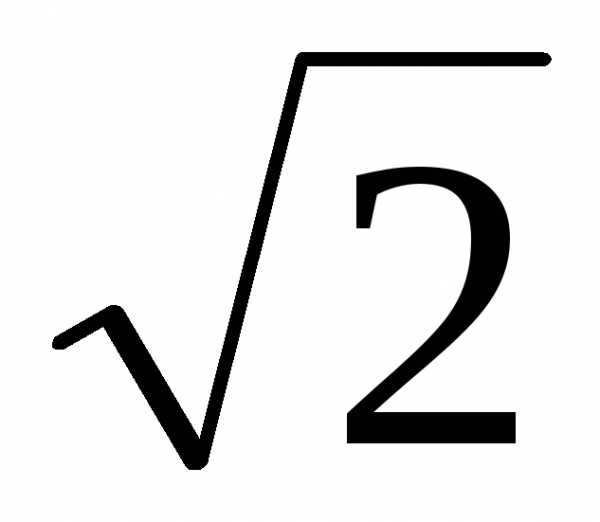
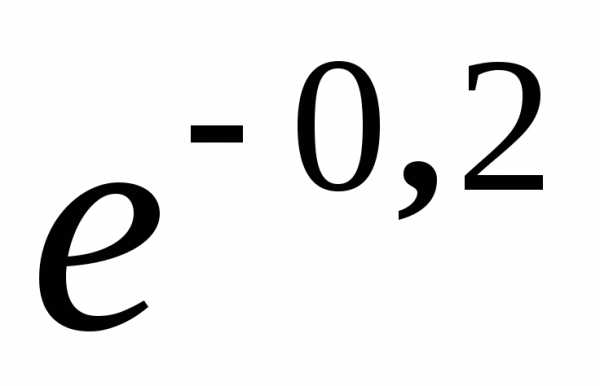 (см)
= 7,75 см.
(см)
= 7,75 см.
Окончательно уравнение движения:
x
= 0,0775
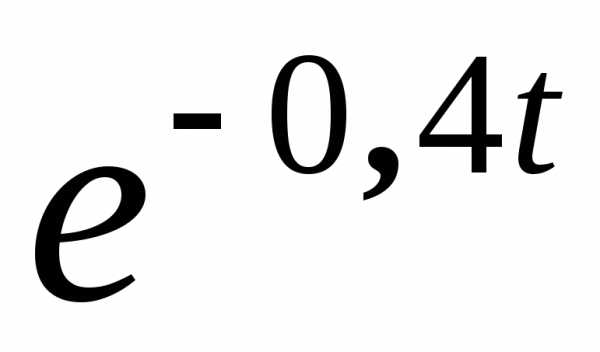 cos
cos t.
t.
Для построения графика сначала рисуем огибающую x = 0,0775
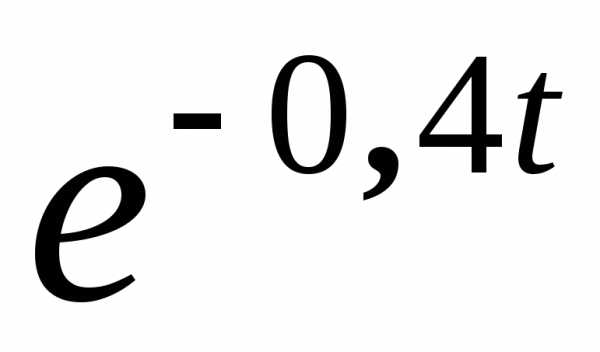 ,
а затем колебательную часть.
,
а затем колебательную часть.

Задача 25
Чему равен логарифмический декремент затухания математического маятника, если за t = 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника l = 1 м.
Решение
Логарифмический декремент затухания можно найти из соотношения: = Т,
где – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:
0
=
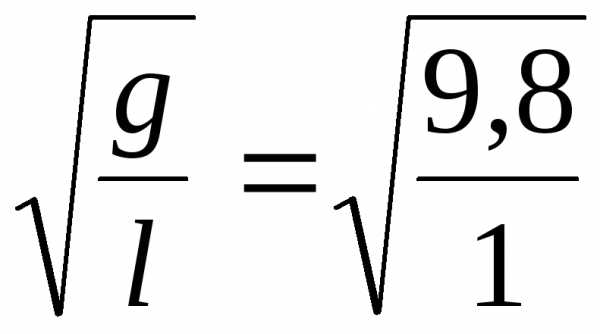 = 3,13 с-1.
= 3,13 с-1.
Коэффициент
затухания колебаний можно определить
из условия:
 A0=
A0
e—t,
A0=
A0
e—t,
t = ln2 = 0,693 ,
=
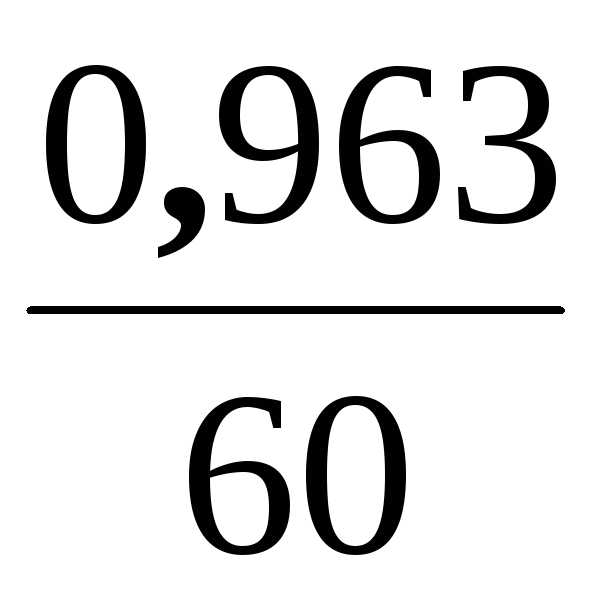 = 0,0116c-1.
= 0,0116c-1.
Поскольку
<< 0,то
в формуле =
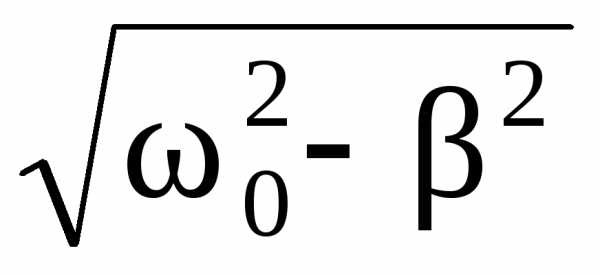 можно пренебречь
по сравнению с 0
ипериод
колебаний определить по формуле:
T
=
можно пренебречь
по сравнению с 0
ипериод
колебаний определить по формуле:
T
=
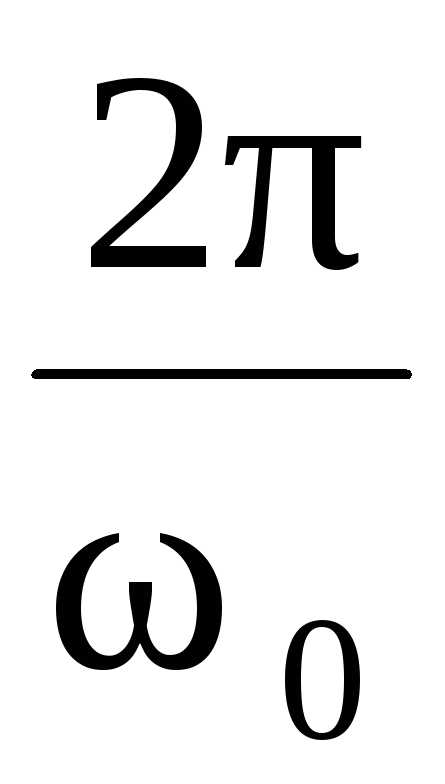 = 2c.
= 2c.
Подставляем и Т в выражение для логарифмического декремента затухания и получаем:
= T = 0,0116 с-1 ∙ 2 с = 0,0232.
Задача 26
Уравнение незатухающихколебанийдано в виде x=4sin600 t см.
Найти смещение от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, через t = 0,01 с после начала колебаний. Скорость распространения колебаний υ = 300 м/с.
Решение
Запишем
уравнение волны, распространяющейся
от данного источника: x
= 0,04 sin
600 (t
–
 ).
).
Находим фазу волны в данный момент времени в данном месте:
t
–
 = 0,01 –
= 0,01 –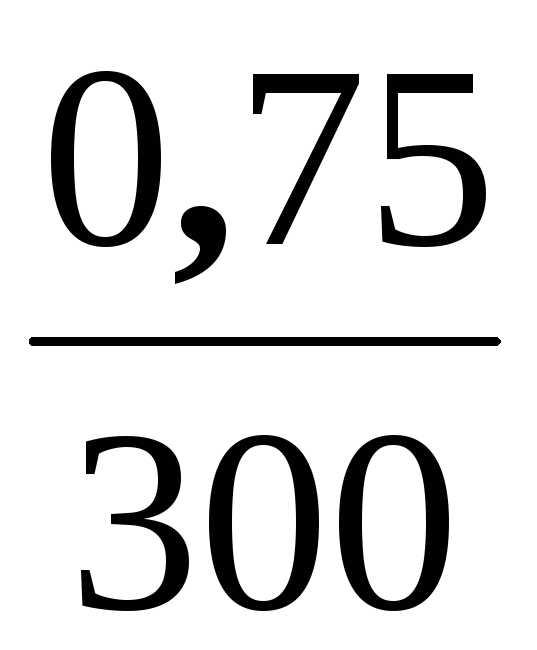 = 0,0075 ,
= 0,0075 ,
600 ∙ 0,0075 = 4,5 ,
sin
4,5
= sin
 = 1.
= 1.
Следовательно, смещение точки x = 0,04 м, т.е. на расстоянии l =75 см от источника в момент времени t = 0,01 c смещение точки максимально.
Список литературы
Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.
Савельев И.В. Сборник вопросов и задач по общей физике. – М.: Наука, 1998.
35
studfiles.net
