Какой вид движения называется вращательным – Дать определение вращательного движения и всех величин, характеризующих данное движение?

xn—-7sbfhivhrke5c.xn--p1ai

Вращательное движение тела. Закон вращательного движения :: SYL.ru

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

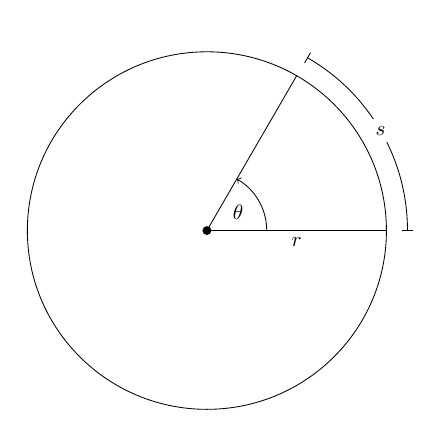
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

φ = φ(t).

Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

ΔS = Δφr.

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

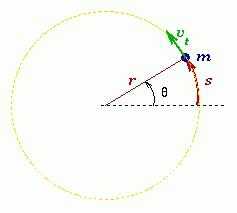
Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

ω = dφ/dt.

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

ω = φ/t.

Согласно предварительной формуле размерность угловой скорости

[ω] = 1 рад/с.

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

ω = 2π/T,

поэтому период вращения определим следующим образом:

T = 2π/ω.

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

ν = 1/T.

Единицы измерения частоты: [ν]= 1/c = 1 c^-1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

ω = 2πν.

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

ε = dω/dt.

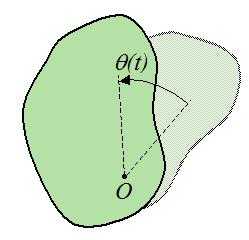
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.

Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).

Связь величин, характеризующих поступательное и вращательное движение

Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением

ΔS = Δφ r.

Тогда линейная скорость материальной точки, выполняющей вращательное движение

υ = ΔS/Δt = Δφr/Δt = ωr.

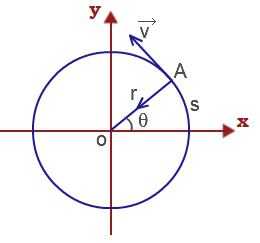
Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:

a = υ²/r = ω²r²/r.

Итак, в скалярном виде

a = ω²r.

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

a = ε r.

Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_iк υ_i правый винт покажет направление вектора L_i).

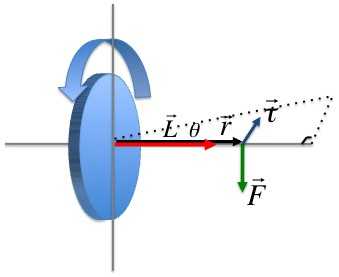
В скалярной форме

L = m_iυ_ir_isin(υ_i,r_i).

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

sin(υ_i,r_i) = 1.

Так что момент импульса материальной точки для вращательного движения примет вид

L = m_iυ_ir_i.

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

M_i = r_iF_isin(r_i, F_i).

Считая, что r_isinα = l_i, M_i = l_iF_i.

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

M = dL/dt.

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

L_i = m_iυ_ir_i.

Если вместо линейной скорости подставить ее выражение через угловую:

υ_i = ωr_i,

то выражение для момента импульса примет вид

L_i = m_ir_i²ω.

Величина I_i = m_ir_i² называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

L_i = I_iω.

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

L = Iω.

Момент силы и момент инерции

Закон вращательного движения гласит:

M = dL/dt.

Известно, что представить момент импульса тела можно через момент инерции:

L = Iω.

Тогда

M = Idω/dt.

Учитывая, что угловое ускорение определяется выражением

ε = dω/dt,

получим формулу для момента силы, представленного через момент инерции:

M = Iε.

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma²,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

www.syl.ru

Вращательное движение твердого тела | Лекции и примеры решения задач механики

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется

φ=φ(t) – уравнение вращательного движения твердого тела.

Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

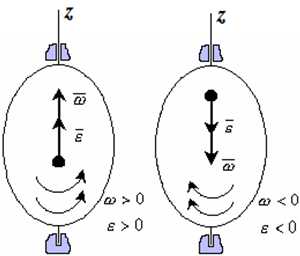
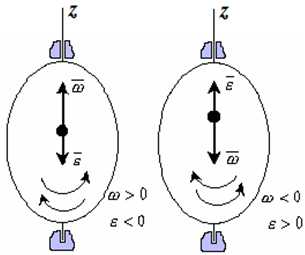
Рис. 1.4

1. Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
   ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.
2. При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz.
3. Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
4. Если ε >0 при
   ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.
5. Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения

   φ=φ₀+ωt

6. Если угловое ускорение ε=const
   , то вращательное движение называется равнопеременным.
   Уравнение равнопеременного вращения и уравнение, выражающее угловую скорость в любой момент времени

   ω=ω₀+εt

   представляют совокупность основных формул вращательного равнопеременного движения тела.

isopromat.ru

Вращательное движение — это… Что такое Вращательное движение?

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам.

Характеристики вращения тела

Кинематические характеристики

Вращение твердого тела, как целого характеризуется углом , измеряющегося в угловых градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).

При равномерном вращении (T оборотов в секунду),

,

• Период вращения — время одного полного оборота. Период вращения T и его частота связаны соотношением .

,

.

Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергии вращения можно записать в виде . В этой формуле момент инерции играет роль массы, а угловая скорость роль обычной скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы .

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

• Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения.  — угловая скорость

См. также

Ссылки

dic.academic.ru

Вращательное движение — это… Что такое Вращательное движение?

или вращение. — Всем хорошо известное равномерное вращение твердого тела вокруг неподвижной оси служит простейшим представителем тех движений предметов, имеющих протяжения, которые называются вращательными движениями; поэтому, прежде чем говорить о вращательных движениях вообще, следует обратить внимание на те качества, которые свойственны равномерному вращению твердых тел вокруг неподвижных осей. При таком вращении все точки твердого тела (за исключением находящихся на оси вращения) описывают окружности, центры которых находятся на оси вращения, а плоскости — перпендикулярны к этой оси. Скорости точек тела направлены по касательным к описываемым ими окружностям и, следовательно, перпендикулярны к кратчайшим расстояниям их от оси. Если наблюдатель станет вдоль по оси, то увидит, что скорости точек будут направлены все слева направо или все справа налево, смотря по тому, как расположится наблюдатель вдоль по оси; если он станет так, чтобы видимое им вращение тела совершалось

dφ/dt (1).

Но так как вращение предполагается равномерным, то этой же самой величине будет равно отношение между углом одного полного оборота вокруг оси (т. е. углом 2π) и временем T, в течение которого совершается полный оборот; оно же равняется отношению между углом 2nπ (если тело делает n оборотов в минуту) и величиной одной минуты. Единица угловой скорости будет та, при которой тело вращается на угол равный единице (т. е. угол в 57°17’44,7″…, у которого длина дуги равна радиусу) в течение единицы времени — одной секунды. Величина единицы угловой скорости выразится

символом 1/(сек.).

Угловая скорость тела, делающего n полных оборотов в минуту, будет равна:

2nπ/60∙(сек) = 0,10471975∙n∙1/(сек.)

а угловая скорость вращения Земли равна:

2π/86164,09∙1/(сек.) = 0,0000729∙1/(сек.)

потому что в звездных сутках содержится 86164,09 секунд среднего времени.

При неравномерном вращении твердого тела вокруг постоянной неподвижной оси угловая скорость выражается также формулой (1), но это уже не постоянная, а изменяющаяся с течением времени величина. Производная от нее по t или производная второго порядка от φ по t называется угловым ускорением при вращении твердого тела вокруг постоянной неподвижной оси. При равномерном или неравномерном вращении твердого тела вокруг постоянной неподвижной оси все точки тела, находящиеся на оси, остаются неподвижными; гораздо сложнее и разнообразнее вращательные движения твердого тела вокруг неподвижной точки, которая одна только остается в покое. Как бы ни было сложно такое движение, одновременные скорости всех точек тела имеют такие величины и направления, как будто бы тело вращалось вокруг некоторой оси, проходящей через неподвижную точку, так что скорости точек тела, находящихся на этой оси, равны нулю, а скорости прочих точек перпендикулярны к плоскостям, проходящим через них и через вышесказанную ось, и пропорциональны кратчайшим расстояниям от этой оси. Эта ось называется мгновенной осью вращения и величина отношений скоростей точек к кратчайшим расстояниям их от мгновенной оси — мгновенной угловой скоростью. Мгновенными называются они потому, что как направление оси, так и величина угловой скорости изменяются с течением времени. Для примера возьмем вращение конуса B вокруг его вершины O, когда этот конус катится без скольжения по другому круговому конусу K, неподвижному.

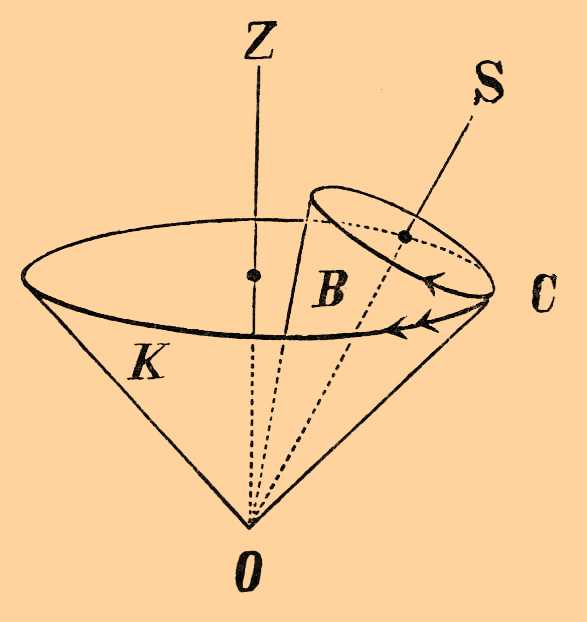
В положении, изображенном на чертеже, мгновенной осью служит производящая OC обоих конусов; если качение происходит в таком направлении, что ось OS симметрии конуса B перемещается слева направо по отношению к оси симметрии OZ конуса K, то мгновенная ось (т. е. место прикосновения поверхностей) будет перемещаться в пространстве по поверхности конуса K в сторону, указанную двойной строкой, и по поверхности конуса B — в сторону, указанную простой стрелкой. Каково бы ни было вращение твердого тела вокруг неподвижной точки, если только это не есть вращение вокруг неподвижной постоянной оси, мгновенная ось вращения изменяет свое положение в пространстве и в теле. Коническая поверхность или пирамида, вычерчиваемая мгновенной осью в пространстве, называется неподвижным аксоидом, а коническая поверхность, вычерчиваемая ею в твердом теле — подвижным аксоидом. При вращении тела подвижный аксоид катится без скольжения по неподвижному. К числу вращений твердого тела относятся: вращения тел по инерции (см. Инерция) и вращения различных гироскопов (см. Гироскоп).

Д. Б.

dic.academic.ru

Вращательное движение | Физика

Расскажу вам о вращательном движении.

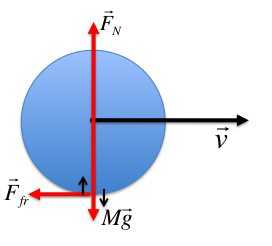
На первый взгляд может даже показаться, что вращательное движение нарушает законы механики.

В чем же нарушение и каких законов? Ну, скажем, закон инерции. Ведь всякое тело, если на него не действуют уравновешенные силы, должно или покоиться, или двигаться равномерно и прямолинейно. Но вот я даю боковой толчок этому глобусу, и он начинает вращаться. Если бы не трение, он, вероятно, вращался бы вечно, как вращается земной шар, никем не подталкиваемый. Как же быть с первым законом Ньютона? Или есть два закона инерции: одни для прямолинейного, а другой для вращательного движения?

Не торопитесь, мы сейчас выясним, в чем тут дело, и убедимся, что беспокоиться за законы Ньютона не приходится.

Вращательное движение отличается от поступательного. Однако есть в них и много общего, и весьма полезно сопоставить эти два вида движения. Много путаницы в головах учащихся происходит оттого, что в курсе физики средней школы не строго разграничивают механику материальной точки и механику материального тела. Скажите, вы помните, что называется поступательным движением?

– Конечно. Движение тела, при котором все его точки движутся одинаково.

– А как вы это понимаете?

– Я понимаю это так, что все точки тела в каждый момент времени имеют одинаковую по модулю и направлению скорость. Все точки описывают одинаковые траектории.

– Вот именно. Поэтому и можно рассматривать поступательное движение тела как движение одной точки, вернее, заменить движение тела движением его центра масс. Если на такое тело (материальную точку) не действуют другие тела, т. е. если оно не испытывает на себе действия неуравновешенных сил, то оно покоится или движется равномерно и прямолинейно.

Вращение тела характеризуют угловой скоростью, показывающей, на какой угол оно повернется за единицу времени. В технике угловую скорость часто выражают числом оборотов в минуту. Если угловая скорость постоянна, то мы говорим, что тело вращается равномерно. Если угловая скорость равномерно возрастает, то вращение называют равноускоренным. Сходство законов поступательного и вращательного движения поразительное. Только буквенные обозначения различны, а формулы получаются совершенно одинаковые. Вот первая параллель: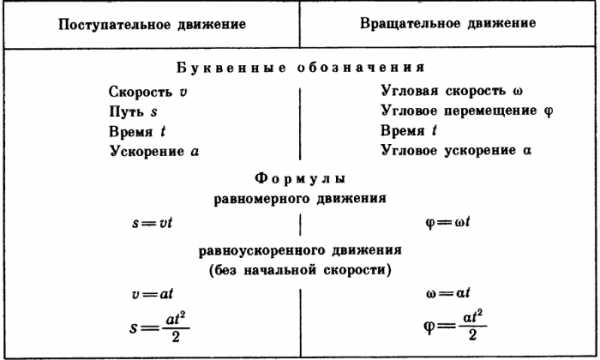

Все задачи по кинематике как вращательного, так и поступательного движения решаются по этим формулам аналогично.

– Это все понятно. Но как же быть с законом Ньютона?

– Не торопитесь, слушайте дальше. Рассмотрим движение одной материальной точки. Если хотите, вы можете представить себе ее как маленький тяжелый шарик. Можно сделать так, чтобы он двигался по окружности? (Катим маленький шарик от шарикоподшипника по столу.)

– Конечно, нет, он катится по прямой.

Можно, конечно, вести шарик по окружности, поддерживая его все время пальцами. Но стоит только убрать руку, как он будет продолжать движение по прямой линии.

– Итак, материальная точка может двигаться по окружности только под действием силы. Я вел шарик рукой, можно было бы привязать к нему веревочку или катить его внутри желобка. Как только прекратится действие силы, шарик начнет двигаться прямолинейно и равномерно.

В твердом теле не одна точка, а множество. Как вы думаете, они (точки) свободны или связаны?

– На них действует сила сцепления.

– Верно. Они-то и удерживают точки на круговой орбите. Не будь этих сил, материальные точки вращающегося тела разлетелись бы, как грязь слетает с вращающихся колес.

Есть еще одно сходство между поступательным и вращательным движением. При поступательном движении все точки тела движутся в данный момент времени с одинаковой линейной скоростью v. Если тело вращается, тоо все точки вращающегося тела движутся с одинаковой угловой скоростью ω.

Например, угловые скорости всех точек вращающейся спицы AB (рис. 59) одинаковы, а линейные различны.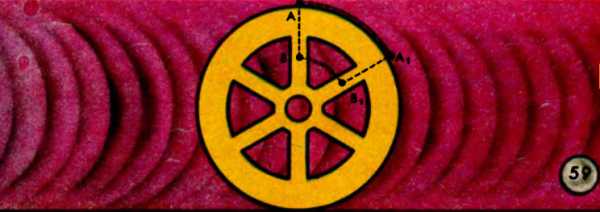

На уроке физики вам говорили. Что равномерное движение точки по окружность есть в то же время движение с ускорением. Это ускорение называется центростремительным ускорением. Оно не характеризует изменение скорости по модулю, а характеризует только изменение направления скорости. Тут нелегко разобраться.

Я бы отстаивал определение равномерного вращательного движения только по угловой скорости. Тогда те параллельные формулы, о которых я говорил, будут всем понятны. Да и в технике, когда речь идет о равномерном вращении маховика или ротора электрического генератора или двигателя, подразумевают постоянной угловую скорость. Постоянное число оборотов якоря генератора обеспечивает постоянное напряжение в сети; постоянное число оборотов маховика обеспечивает плавный ход машины и экономичность ее работы. Это постоянство стараются поддержать, регулируя работу машины.

Теперь проведем параллель динамическую. По второму закону Ньютона ускорение, получаемое телом, вычисляется из формулы a = F/m. При вращении тела изменение угловой скорости будет зависеть от силы. Теперь скажите, все ли равно, где приложить силу при завинчивании, скажем, гайки: к концу рукоятки гаечного ключа или к самой гайке?

Вращающее действие силы, или момент силы, – вот что здесь важно, вот что является аналогом силы поступательного движения. Параллель найдена: силе в поступательном движении соответствует момент силы во вращательном движении. Так продолжим нашу сравнительную табличку.

– Я еще не написал формулу второго закона Ньютона, потому что об этом законе следует сказать подробнее. В формулу закона Ньютона входит масса m. Что она характеризует?

– Инертность тела.

– Правильно. Теперь подумайте, характеризует ли масса инертность вращающегося тела?

– Инертность вращающегося тела характеризуется не массой, а особой величиной, называемой моментом инерции, в которую входит как составная часть и масса. Момент инерции обозначается буквой I. Он зависит от массы тела и распределения этой массы, т. е. от формы тела. Тела различной формы имеют различные моменты инерции.

Простейший случай — движение материальной точки по окружности. Момент инерции такой точки равен произведению массы точки на квадрат расстояние ее от оси вращения, т. е. I = mr². Если массу отнести от оси вращения на расстояние, вдвое большее, то инертность этой массы, или устойчивость вращательного движения, будет больше в четыре раза. Вот почему маховые колеса делают большими. Но слишком увеличивать радиус нельзя. С увеличением радиуса колеса увеличивается линейная скорость точек обода колеса: v = ωr. Учитывая, что центростремительное ускорение есть a = v²/r, получаем отсюда: a = ω²r. Это означает, что с увеличением радиуса колеса растет центростремительное ускорение точек его обода. Создающая это ускорение сила сцепления молекул может оказаться недостаточной для удержания их на круговом пути, и тогда колесо разрушится.

Каждое тело можно представить состоящим из множества точек. Для вычисления момента инерции тела надо суммировать моменты инерции отдельных точек. Эта задача вам пока не под силу. Скажу только, что для диска и сплошного цилиндра, вращающихся вокруг собственной оси, I = ½ mr². В телах такой формы разные точки тела находятся на разных расстояниях от оси вращения, начиная от 0 и до r. Момент инерции тонкого круглого кольца (есть сходство с ободом маховика) I = mr². Обо всем этом вы узнаете из курса теоретической механики, когда будете учиться в техникуме или институте. Сейчас же вы должны понять, что во вращательном движении роль массы играет момент инерции и закон динамики вращательного движения, аналогичный второму закону Ньютона, примет вид: M = Iα. Теперь мы можем закончить сравнительную таблицу, включив в нее формулы для основного уравнения динамики, импульса и кинетической энергии:

phscs.ru

Простейшие движения твердого тела.

Простейшие движения твердого тела