Как перевести из восьмеричной в шестнадцатеричную систему – Перевод чисел из восьмеричной системы счисления в шестнадцатеричную

перевод

Методика перевода чисел в разные системы исчисления

Перевод целых десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системы осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная частного с последнего.

Пример1.

а) Выполнить перевод числа 19 в двоичную систему счисления.

Решение

Таким образом, 19 = 10011₂

б) Перевести 181₁₀->”8” систему счисления

181	8
176	22	8
5	16	2
	6

Результат. 181₁₀->265₈

в) Перевести 622₁₀ — «16» систему счисления

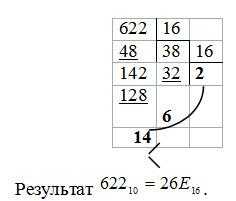
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.

Пример 2.

а) Перевести 10101101.1012 в десятичную систему счисления

10101101.101₂ = 1 2⁷+ 0 2⁶+ 1 2⁵+ 0 2⁴+ 1 2³+ 1 2²+ 0 2¹+ 1 2⁰+ 1 2^-1+ 0 2^-2+ 1 2^-3 =  173.625₁₀

б) Перевести 703.048 в в десятичную систему счисления

703.048 = 7 82+ 0 81+ 3 80+ 0 8-1+ 4 8-2 = 451,062510

в) Перевести B2E.416 в в десятичную систему счисления

B2E.4₁₆ =  11 16²+ 2 16¹+ 14 16⁰+ 4 16^-1 = 2862,25₁₀

 Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.

Для перехода от двоичной к восьмеричной  или шестнадцатеричной системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три ( четыре ) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной ( шестнадцатеричной ) цифрой.

Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.

Арифметические операции

Сложение

Выполняется точно также как и в десятичной системе счисления

Вычитание

Вычитание чисел в 2 и 8 СС выполняется по тем же правилам что и в десятичной. Если вычитаемое больше уменьшаемого, разность определяется между большим и меньшим числом, и перед ней ставится знак минус

Умножение

Операция умножения выполняется точно также как и в десятичной системе счисления

Прямой код

Используется при выполнении умножения и деления чисел, а остальные коды для замены вычитания сложением.

0.011 число положительное

1.011 число отрицательное

При выполнении операции умножения или деления двух двоичных дробей знаковые разряды складываются независимо от дробных частей

Обратный код

Применяется для замены операции вычитания сложением

Для положительных чисел: изображение правильной двоичной дроби одинаково в обратном и прямом коде

Для записи отрицательной правильной двоичной дроби в обратном коде необходимо заменить нули единицами и наоборот, а слева от запятой вместо –0 поставить 1

То есть –0,0101=1,1010

Необходимо учитывать:

• Все цифры слагаемых, включая и цифры знаковых разрядов, расположенных слева от запятой участвуют в сложении как разряды единого числа

• При переполнении, когда слева от запятой в результате сложения появляются две цифры, левая крайняя цифра переносится и складывается с младшим разрядом дробной части, а оставшаяся цифра слева от запятой определяет знак результата

• Если число разрядов дробной части отрицательной правильной двоичной дроби меньше числа разрядов дробной части другого слагаемого, то перед тем как перевести отрицательную дробь в обратный код необходимо дополнить ее справа нулями до равенства разрядов второго слагаемого

Если в знаковом разряде числа аобратном коде стоит 1, то для перехода к обычной записи надо в дробной части единицы заменить нулями, а нули – единицами, а слева от запятой записать –0

Дополнительный код

Так же как и обратный применяется для замены вычитания сложением

При этом: изображение положительной правильной двоичной дроби одинаково в прямом, обратном и дополнительном кодах.

Для перевода отрицательной дроби: Необходимо нули заменить единицами, а 1 нулями. К младшему разряду прибавить единицу, затем слева от запятой поставить 1.

Необходимо помнить:

• Все цифры слагаемых, включая и цифры знаковых разрядов, расположенных слева от запятой участвуют в сложении как разряды единого числа

• При переполнении, когда слева от запятой в результате сложения появляются две цифры, левая крайняя цифра отбрасывается, а оставшаяся цифра слева от запятой определяет знак результата

• числа разрядов дробной части другого слагаемого, то перед тем как перевести отрицательную дробь в обратный код необходимо дополнить ее справа нулями до равенства разрядов второго слагаемого

• если в результате сложения слева от запятой получился 1, то число отрицательное, если 0, то положительное (соответственно переводить ничего не нужно)

studfiles.net

Системы счисления — конспект задач

В мире 10 категории людей — те, которые понимают двоичную систему счисления, и те, которые ее не понимают.

I. Перевод целых чисел из какой-либо системы счисления в десятичную.
Составляется степенной ряд с основанием той системы, из которой число переводится.

a)

b)

c)

Теперь, после того, как мы научились переводить числа в десятичную систему счисления, станет сразу понятным стихотворение:

 Ей было 1100 лет. 
Она в 101 класс ходила. 
В портфеле по 100 книг носила. 
Всё это правда, а не бред. 
Когда пыля десятком ног,
Она шагала по дороге, 
За ней  всегда бежал щенок
С одним хвостом, зато 100-гий,
Она ловила каждый звук
Своими 10-ю ушами, 
И 10 загорелых рук
Портфель и поводок держали.
И 10 тёмно-синих глаз
Оглядывали мир привычно.
Но станет всё совсем обычным,
Когда поймёте наш рассказ.
А. Стариков. «Странная девочка»

II. Перевод целых десятичных чисел в недесятичную систему счисления.

Десятичное число делят на основание той системы, в которую оно переводится, пока не получим частное, меньшее этого основания. Число в новой системе записывается в виде остатков от деления, начиная с последнего.

III. Перевод правильных дробей из десятичной системы счисления в недесятичную.

Дробь надо последовательно умножать на основание той системы, в которую она переводится. Умножаются только дробные части. Дробь в новой системе счисления записывается в виде целых частей произведения, начиная с первого.

IV. Перевод восьмеричного или шестнадцатиричного числа в двоичную систему счисления.

Заменить каждую цифру этого числа соответствующим трёхразрядным двоичным числом (триадой) или четырёхразрядным двоичным числом (тетрадой) (см. таблицу). При этом отбрасываются ненужные нули в страрших и младших разрядах.

V. Перевод из двоичной в восьмеричную или 16 ричную систему

.

Двигаясь от разделительной точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайнюю левую и правую группы. Затем триаду (тетраду) заменяют соответсвующей восьмериной (16 ричной) цифрой. От этого запись числа становится значительно короче.

VI. Перевод из восьмеричной в шестнадцатиричную и обратно.

Через двоичную систему с помощью триад и тетрад.

www.e-ope.ee

Перевод чисел из восьмеричной системы в двоичную и шестнадцатеричную

Алгоритм перевода чисел из одной системы счисления в другую наиболее прост в том случае, когда одно из оснований этих систем является степенью другой, как, например, в случае двоичной и восьмеричной систем счисления. В таком случае алгоритм перевода состоит в простой замене чисел одной системы на равные им числа другой системы счисления (в случае положительных чисел). На начальном этапе удобно и полезно воспользоваться таблицей соответствия, приведенной в Приложении.

Пусть требуется перевести восьмеричное число 2473₈ в двоичное число. Воспользовавшись Таблицей соответствия из Приложения, получим:

2473₈ = 10100111011₂,

поскольку 28 = 010₂, 48 = 100₂, 78 = 111₂… Следует помнить, что восьмеричное число кодируется тремя битами, и выписывать триады нужно полностью. Исключением из этого правила может служить только старшая триада, в которой старший бит (СБ) равен нулю.

Сложнее обстоит дело при переводе чисел из восьмеричной системы в шестнадцатеричную. Обычно вначале переводят восьмеричное число в двоичное, а затем уже в шестнадцатеричное по алгоритму, описанному в разделе Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную. Для рассмотренного выше примера имеем:

2473₈ = 10100111011₂ = 0101 0011 1011₂ = 53B₁₆

Перевод чисел из шестнадцатеричной системы в двоичную и восьмеричную

Алгоритм перевода чисел из шестнадцатеричной системы счисления двоичную крайне прост. Необходимо только заменить каждую цифру шестнадцатеричного числа ее эквивалентом в двоичной системе счисления (в случае положительных чисел). Как и в предыдущих параграфах, удобно и полезно воспользоваться таблицей соответствия, приведенной в Приложении. Отметим только, что каждое шестнадцатеричное число следует заменять двоичным, дополняя его до 4 разрядов (в сторону старших разрядов).

Пусть требуется перевести шестнадцатеричное число F1₁₆ в двоичное число. Воспользовавшись Таблицей соответствия из Приложения, получим:

F1₁₆ = 11110001₂,

поскольку F₁₆ = 1111₂, 1₁₆ = 0001₂. Этот пример иллюстирует тот факт, что следует дополнять младшие разряды до 4 разряда в двоичном числе. Естественно, дополнять старший разряд двоичного числа до 4 старших битов нулями не имеет смысла, другими словами пишут

1F₁₆ = 11111₂, а не 00011111₂

Обычно при переводе чисел из шестнадцатеричной в восьмеричную систему счисления вначале шестнадцатеричное число переводят в двоичное, затем разбивают его на триады, начиная с младшего бита, а потом заменяют триады соответствующими им эквивалентами в восьмеричной системе (аналогично алгоритму, описанному в разделе Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную. Для рассмотренных выше примеров имеем:

1F₁₆ = 11111₂ = 011 111₂ = 37₈

F1₁₆ = 11110001₂ = 011 110 001₂ = 361₈

Непосредственное преобразование чисел из шестнадцатеричной системы счисления в восьмеричную требует выполнения арифметических действий в этой системе счисления. Об этом речь пойдет позже, в IV главе нашего курса. Отмечу только, что программная реализация вышеприведенного алгоритма проще и надежнее, поскольку при выполнениях операций деления неизбежно возникают дробные числа и переполнения разрядной сетки, необходимость округления, и, как следствие, потеря точности, не говоря уже о скорости выполнения компьютером такого типа алгоритмов.

studfiles.net

4.8. Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?

Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1   …  a0  ,  a-1  a-2   …   a—m)q   сводится к вычислению значения многочлена    x10 = an  qn +  an-1  qn-1   +   …   +  a0   q0   +   a-1   q -1   +   a-2   q-2   +     …     +   a-m   q-m     средствами десятичной арифметики.

Примеpы:

4.9. Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:

На этом рисунке использованы следующие обозначения:

• в кружках записаны основания систем счисления;

• стрелки указывают направление перевода;

• номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 4.1.

Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.

Сводная таблица переводов целых чисел Таблица 4.1.

4.10. Как производятся арифметические операции в позиционных системах счисления?

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

С л о ж е н и е

Таблицы сложения легко составить, используя Правило Счета.

Сложение в двоичной системе

Сложение в восьмеричной системе

                 Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Пример 1.Сложим числа 15 и 6 в различных системах счисления.

Шестнадцатеричная:F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2.81+ 5.80= 16 + 5 = 21,  1516= 1.161+ 5.160= 16+5 = 21.

  Пример 2.Сложим числа 15, 7 и 3.

Шестнадцатеричная:F16+716+316

Ответ:5+7+3 = 2510= 110012= 318= 1916.Проверка:110012= 24+ 23+ 20= 16+8+1=25, 318= 3.81+ 1.80= 24 + 1 = 25,  1916= 1.161+ 9.160= 16+9 = 25.

  Пример 3.Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆Проверка. Преобразуем полученные суммы к десятичному виду: 11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25 311,2₈ = 3^.8² + 18¹ + 1^.8⁰ + 2^.8^-1 = 201,25 C9,4₁₆ = 12^.16¹ + 9^.16⁰ + 4^.16^-1 = 201,25

В ы ч и т а н и е

Пример 4. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆Пример 5. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆. Пример 6. Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ — 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆. Проверка. Преобразуем полученные разности к десятичному виду: 10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^-1 = 141,5; 215,4₈ = 2^.8² + 1^.8¹ + 5^.8⁰ + 4^.8^-1 = 141,5; 8D,8₁₆ = 8^.16¹ + D^.16⁰ + 8^.16^-1 = 141,5.

У м н о ж е н и е

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям. Пример 7.Перемножим числа 5 и 6.

Ответ: 5^.6 = 30₁₀ = 11110₂ = 36₈. Проверка. Преобразуем полученные произведения к десятичному виду: 11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30; 36₈ = 38¹ + 68⁰ = 30. Пример 8.Перемножим числа 115 и 51.

Ответ: 115^.51 = 5865₁₀ = 1011011101001₂ = 13351₈. Проверка. Преобразуем полученные произведения к десятичному виду: 1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865; 13351₈ = 1^.8⁴ + 3^.8³ + 3^.8² + 5^.8¹ + 1^.8⁰ = 5865.

Д е л е н и е

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей. Пример 9.Разделим число 30 на число 6.

Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈. Пример 10. Разделим число 5865 на число 115.

Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈. Проверка. Преобразуем полученные частные к десятичному виду: 110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6^.8¹+ 3^.8⁰= 51.Пример 11.Разделим число 35 на число 14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈. Проверка. Преобразуем полученные частные к десятичному виду: 10,1₂ = 2¹ + 2 ^-1 = 2,5; 2,4₈ = 2^.8⁰ + 4^.8^-1 = 2,5.

studfiles.net