Как перевести число из двоичной в восьмеричную – План-конспект урока по информатике и икт (10 класс) на тему: Перевод из двоичной системы в восьмеричную, шестнадцатеричную и обратно | скачать бесплатно

Как перевести число из двоичной системы в восьмеричную и шестнадцатеричную

Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную или четвертичную и наоборот часто требуется для решения задач по теме Системы счисления. Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел. А также можно воспользоваться онлайн калькулятором для перевода чисел из одной системы счисления в другую.

Таблица перевода чисел

Десятичная СС	Двоичная СС	Четвертичная СС	Восьмеричная СС	Шестнадцатеричная СС
1	1	1	1	1
2	10	2	2	2
3	11	3	3	3
4	100	10	4	4
5	101	11	5	5
6	110	12	6	6
7	111	13	7	7
8	1000	20	10	8
9	1001	21	11	9
10	1010	22	12	A
11	1011	23	13	B
12	1100	30	14	C
13	1101	31	15	D
14	1110	32	16	E
15	1111	33	17	F
16	10000	100	20	10

Как перевести число из двоичной системы счисления

Чтобы перевести число из двоичной системы счисления в четвертичную, восьмеричную или шестнадцатеричную систему, нужно воспользоваться алгоритмом перевода:

1. Разбить двоичное число справа налево на группы по 2 (для четвертичной СС), 3 (для восьмеричной СС) или 4 (для шестнадцатеричной СС) цифры. Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
2. Заменить каждую группу цифр на ее аналог в соответствующей системе счисления.

Пример 1:

Перевести число 111100110₂ из двоичной системы в четвертичную.

Решение:

Разбиваем число на группы по 2 цифры справа налево и заменяем каждую группу на аналог в четвертичной системе счисления из таблицы:

111100110₂ = 01 11 10 01 10 = 13212₄

Пример 2:

Перевести число 111100110₂ из двоичной системы в восьмеричную.

Решение:

Разбиваем число на группы по 3 цифры справа налево и заменяем каждую группу на аналог в восьмеричной системе счисления из таблицы:

111100110₂ = 111 100 110 = 746

8

Пример 3:

Перевести число 111100110₂ из двоичной системы в шестнадцатеричную.

Решение:

Разбиваем число на группы по 4 цифры справа налево и заменяем каждую группу на аналог в шестнадцатеричной системе счисления из таблицы:

111100110₂ = 0001 1110 0110 = 1E6₁₆

Как перевести число в двоичную систему счисления

Чтобы перевести число из четвертичной, восьмеричной или шестнадцатеричной системы счисления в двоичную, нужно воспользоваться алгоритмом перевода:

1. Заменить каждую цифру на двоичный аналог, состоящий из 2 (для четвертичной), 3 (для восьмеричной) или 4 (для шестнадцатеричной) цифр. Если нужно, число дополняется нулями слева.
2. Вычеркнуть из числа незначащие нули.

Пример 4:

Перевести число 120323₄ из четвертичной системы в двоичную.

Решение:

Выполняем замену каждой цифры на группу из 2 цифр в двоичной системе счисления:

120323₄ = 01 10 00 11 10 11 = 11000111011₂

Пример 5:

Перевести число 26475030₈ из восьмеричной системы в двоичную.

Решение:

Выполняем замену каждой цифры на группу из 3 цифр в двоичной системе счисления:

26475030₈ = 010 110 100 111 101 000 011 000 = 10110100111101000011000₂

Пример 6:

Перевести число _{2AC0F7416 из шестнадцатеричной системы в двоичную.}

Решение:

Выполняем замену каждой цифры на группу из 4 цифр в двоичной системе счисления:

2AC0F74₁₆ = 0010 1010 1100 0000 1111 0111 0100 = 10101011000000111101110100₂

worksbase.ru

Перевод чисел из двоичной системы счисления в восьмеричную — Циклопедия

Перевод чисел из двоичной системы счисления в восьмеричную и наоборот // Дмитрий Тарасов [6:42] Перевод из двоичной в восьмеричную систему счисления // Никита Вайз (информатик) [7:20]

Перевод чисел из двоичной системы счисления в восьмеричную

— это преобразование чисел двоичной системы счисления в числа восьмеричной системы счисления.

Исходное число двоичной системы счисления разбивается на триады (тройки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) триада может быть неполной, тогда в неё слева добавляется цифра 0 (одна или две). Затем триады заменяются на соответствующие (по таблице триад) цифры восьмеричной системы счисления.

[править] Таблица триад

• Заметим, что возможны другие способы перевода чисел: 2→4→8 и 2→10→8.

[править] Пример перевода 2→8

[править] Другие алгоритмы:

cyclowiki.org

Алгоритмы перевода чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

 

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Перевод чисел между системами счисления, основания которых являются степенями числа 2 (q = 2ⁿ), может производиться по упрощённому алгоритму. Такие алгоритмы могут применяться для перевода чисел между двоичной (q = 2¹), восьмеричной (q = 2³) и шестнадцатеричной (q = 2⁴) системами счисления.

Перевод чисел из двоичной системы счисления в восьмеричную. Для записи двоичных чисел используются две цифры, то есть в каждом разряде числа возможны 2 варианта записи. 2 = 2i . Так как 2 = 21, то i = 1 бит. Каждый разряд двоичного числа содержит 1 бит информации. Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение: 8 = 2i . Так как 8 = 23, то i = 3 бита. Каждый разряд восьмеричного числа содержит 3 бита информации. Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями. Переведем таким способом двоичное число 1010012 в восьмеричное: 101    0012 => 518. Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры: Двоичные триады 000 001 010 011 100 101 110 111 Восьмеричные цифры 0 1 2 3 4 5 6 7 Для перевода дробного двоичного числа (правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями. Далее необходимо триады заменить на восьмеричные числа. Например, преобразуем дробное двоичное число А2 = 0,1101012 в восьмеричную систему счисления: Двоичные триады 110 101 Восьмеричные цифры 6 5 Получаем: А8 = 0,658. Теперь преобразуем число 101 001,110 1012 в восьмеричную систему счисления Вы убедились что это 51,658

Перевод чисел из двоичной системы счисления в шестнадцатеричную. Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи.

16 = 2ⁱ . Так как 16 = 2⁴, то i = 4 бита.

Каждый разряд шестнадцатеричного числа содержит 4 бита информации.

Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.

Затем надо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр.

Переведем целое двоичное число А₂ = 101001₂ в шестнадцатеричное:

Двоичные тетрады	0010	1001
Шестнадцатеричные цифры	2	9

В результате имеем: А₁₆ = 29₁₆.

Переведем дробное двоичное число А₂ =0,110101₂ в шестнадцатеричную систему счисления:

Двоичные тетрады	1101	0100
Шестнадцатеричные цифры	D	4

Получаем: А₁₆ = 0,D4₁₆.

Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.

Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную. Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа — в группу из четырех цифр (тетраду).

Например, преобразуем дробное восьмеричное число А₈ = 0,47₈ в двоичную систему счисления:

Восьмеричные цифры	4	7
Двоичные триады	100	111

Получаем: А₂ = 0,100111₂ .

Переведем целое шестнадцатеричное число А₁₆ = АВ₁₆ в двоичную систему счисления:

Шестнадцатеричные цифры	А	В
Двоичные тетрады	1010	1011

В результате имеем: А₂ = 10101011₂

Значит

1. если необходимо перевести число из из восьмеричной и шестнадцатеричной систем счисления в десятичную нам проще сделать это через двоичную.
   Необходимую для записи  двоичных чисел в развёрнутой форме таблицу степеней двойки удобнее иметь в таком виде:
   

2. если необходимо перевести число из десятичной системы в восьмеричную и шестнадцатеричную, удобней это делать через двоичную систему счисления, используя ту же самую таблицу степеней. Простой способ сделать это показан в скринкасте
   

Списываем и заполняем таблицу используя таблицу соответствия (вертикальная таблица выше)

Записываем в тетрадь разделение двоичных чисел на триады и тетрады.

1. В таблицу записываем только значащие цифры.

2. Разделитель при записи рациональных чисел — запятая.

3. Из восьмеричной системы в шестнадцатеричную переводим через двоичную

4. Из шестнадцатеричной системы в восьмеричную переводим через двоичную
   для этого нам надо по разному разбивать цифры двоичного числа на группы

Bin	Oct	Hex	Сколько нолей дописали разбивая
			На триады	На тетрады
11011,01
100001,1
	1000,4
	3567,2
		3АВ,8
		80,4

Задание

Чертим в тетради такую же таблицу и вписываем в неё исходные данные

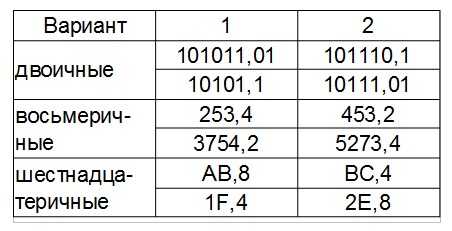
Или

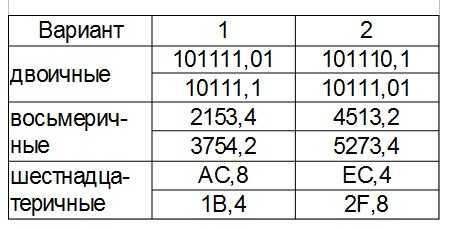
На 5 — переводим свои двоичные числа в десятичные через развёрнутую форму записи

www.oivt.ru

Перевод числа из двоичной системы в восьмеричную систему счисления

Для перевода двоичных чисел в восьмеричные. Нужно, начиная от запятой влево и вправо от нее разбить набор двоичных цифр, изображающих число, на тройки цифр, каждое полученное трехзначное число отдельно перевести в восьмеричную систему счисления; если крайние правая или левая группы цифр не будут полными тройками, их дополняют соответственно справа и слева нулями; затем каждую триаду заменяют соответствующей цифрой восьмеричной системы счисления.

Примеры:

дано двоичное число 1101111011, разбитое на группы по три двоичные цифры, можно записать как 1 101 111 011 и затем после записи каждой группы одной восьмеричной цифрой получить восьмеричное число 1573₈.

1. 1011101,10011 число переводим на восьмеричный,

1 011 101,100 11 → 001 011 101,100 011 → 125,43₈;

Двоичная система счисления	000	001	010	011	100	101	110	111
Восьмеричная система счисления	0	1	2	3	4	5	6	7

Перевод числа из двоичной системы в шестнадцатеричную систему

Для перевода двоичных чисел в шестнадцатеричную систему, нужно, начиная от запятой влево и вправо от нее разбить набор двоичных цифр, изображающих число, на четверки цифр, каждое полученное четырехзначное число отдельно перевести в шестнадцатеричную систему счисления; если крайние правая или левая группы цифр не будут полными четверками, их дополняют соответственно справа и слева нулями; затем заменяют соответствующей цифрой шестнадцатеричной системы счисления.

Двоичное число 1101111011, использованное в предыдущем примере, после разбиения на группы по четыре двоичных цифры, можно записать как 11 0111 1011 и после выражения каждой группы одной шестнадцатиричной цирой получить шестнадцатиричное число 37В.

Пример: 101111,100011 легко перевести на шестнадцатеричную,

10 1111,1000 11 → 0010 1111,1000 1100 → 2F8C₁₆;

Представим в виде таблицы:

Двоичная система счисления	0000	0001	0010	0011	0100	0101	0110	0111
Шестнадцатеричная система счисления	0	1	2	3	4	5	6	7

Двоичная система счисления	1000	1001	1010	1011	1100	1101	1110	1111
Шестнадцатеричная система счисления	8	9	A	B	C	D	E	F

Правила выполнения арифметических операций в двоичной системе

Сложение. Операция сложения выполняется так же, как и в десятичной системе. Переполнение разряда приводит к появлению единицы в следующем разряде:

0+0=0 1+0=1

1+1=10 0+1=1

Пример: Выполним сложение двух двоичных чисел 101+11 (в десятичной системе это 5+3=8).

Сложение лучше выполнять в столбик, добавив недостающие нули.

101

+ 011

Рассмотрим процесс сложения поэтапно.

1. Выполняется сложение в младшем разряде: 1+1=10. В младшем разряде суммы записывается 0,и единица переносится в следующий старший разряд.

2. Суммируются цифры следующего слева разряда и единица переноса: 0+1+1=10. В этом разряде суммы записывается 0, и опять единица переносится в старший разряд.

3. Суммируются цифры третьего слева разряда и единица перенса: 1+0+1=10. В этом разряде записывается 1, и единица переносится в следующий старший разряд и .т.д.

В результате получили: 101

+ 011

1000

Итак, 1000₂=8₁₀

studfiles.net

Системы счисления — Перевод чисел из одной системы счисления в другую

Перевод чисел в десятичную систему счисления

Перевод из двоичной системы в десятичную

Преобразуем двоичное число 1001011 из первого примера

Пример Перевести число 11010101 из двоичной системы в десятичную.

Преобразуем число:

11010101₂= 1 * 2⁷ + 1 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰=128+64+0+16+0+4+0+1=213₁₀

Перевод из восьмеричной системы в десятичную

Преобразуем восьмеричное число 572.

Пример Перевести число 572 из восьмеричной системы в десятичную.

Преобразуем число:

572₈=5 * 8² + 7 * 8¹ + 2 * 8⁰=320+56+2=378₁₀

Перевод из шестнадцатеричной системы в десятичную

Числа в шестнадцатеричной системе состоят из цифр 0-9 и букв A, B, C, D, E, F, таблица соответствия:

десятичная	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
шестнадцатеричная	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Преобразуем шестнадцатеричное число A5C.

Пример Перевести число A5C из шестнадцатеричной системы в десятичную.

Преобразуем число:

A5C₁₆= 10 * 16² + 5 * 16¹ + 12 * 16⁰ =2560+80+12=2652₁₀

calcs.su

Перевод чисел из десятичной системы в восьмеричную

Для перевода чисел из десятичной системы счисления в восьмеричную используют тот же «алгоритм замещения», что и при переводе из десятичной системы счисления в двоичную, только в качестве делителя используют 8, основание восьмеричной системы счисления:

Делим десятичное число А на 8. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит восьмеричного числа.

Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток записывается в разряды восьмеричного числа в направлении от младшего бита к старшему.

Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a меньше 8.

Например, требуется перевести десятичное число 3336 в восьмеричное. В соответствии с приведенным алгоритмом получим: 3336 : 8 = 417

3336 — 3336 = 0, остаток 0 записываем в МБ восьмеричного числа.

417 : 8 = 52

417 — 416 = 1, остаток 1 записываем в следующий после МБ разряд восьмеричного числа.

52 : 8 = 6

52 — 48 = 4, остаток 4 записываем в старший разряд восьмеричного числа.

6 : 8 = 0, остаток 0, записываем 6 в самый старший разряд восьмеричного числа.

Таким образом, искомое восьмеричное число равно 6410₈.

Перевод чисел из десятичной системы в шестнадцатеричную

Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же «алгоритм замещения», что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16, основание шестнадцатеричной системы счисления:

Делим десятичное число А на 16. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит шестнадцатеричного числа.

Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток записывается в разряды шестнадцатеричного числа в направлении от младшего бита к старшему.

Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a меньше 16.

Например, требуется перевести десятичное число 32767 в шестнадцатеричное. В соответствии с приведенным алгоритмом получим: 32767 : 16 = 2047

32767 — 32752 = 15, остаток 15 в виде F записываем в МБ шестнадцатеричного числа.

2047 : 16 = 127

2047 — 2032 = 15, остаток 15 в виде F записываем в следующий после МБ разряд шестнадцатеричного числа.

127 : 16 = 7

127 — 112 = 15, остаток 15 в виде F записываем в старший разряд шестнадцатеричного числа.

7 : 16 = 0, остаток 7 записываем в старший разряд шестнадцатеричного числа.

Таким образом, искомое шестнадцатеричное число равно 7FFF₁₆.

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную

При обработке данных и вычислениях одной из наиболее часто встречающихся задач является перевод чисел из одной системы счисления в другую. Рассмотрим простейшие алгоритмы перевода положительных чисел из двоичной системы в восьмеричную и шестнадцатеричную.

Пусть требуется перевести двоичное число 10101101100110110111100101011001011₂ в восьмеричную систему счисления. Для этого следует разбить это двоичное число на триады, начиная с младшего бита (МБ). Получим:

010 101 101 100 110 110 111 100 101 011 001 011₂

Если старшая триада не заполнена до конца, следует дописать в ее старшие разряды нули, как в нашем случае. После этого необходимо заменить двоичные триады, начиная с младшей, на числа, равные им в восьмеричной системе:

2 5 5 4 6 6 7 4 5 3 1 3₈

Таким образом,

10101101100110110111100101011001011₂=255466745313₈

Аналогично поступаем при переводе чисел из двоичной системы счисления в шестнадцатеричную, но разбиение двоичного числа производим на тетрады. Для примера будем использовать то же двоичное число, что и при переводе в восьмеричную систему счисления:

0101 0110 1100 1101 1011 1100 1010 1100 1011₂

Заменяя двоичные тетрады на их шестнадцатеричные значения, получим искомое шестнадцатеричное число:

10101101100110110111100101011001011₂=56CDBCACB₁₆

Очевидно, что разбиения на триады и тетрады связаны со степенями двойки (для триады, при переводе в восьмеричную систему, 23, а для тетрады, при переводе в шестнадцатеричную, 24)). Сравнительные таблицы соответствия чисел в различных системах счисления можно найти в Приложении.

studfiles.net

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления и наоборот

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления

Двоичная система счисления имеет основание 2 и две цифры: 0 и 1.

Восьмеричная система имеет основание 8 и цифры: 0, 1, …, 7.

Шестнадцатеричная система имеет основание 16 и цифры: 0, 1, …, 9, A, B, C, D, E, F.

Ниже приведена таблица 1 соответствия чисел от 0 до 15 в данных системах счисления.

Таблица 1 Соответствие чисел в разных системах счисления

Десятичная	Шестнадцатеричная	Восьмеричная	Двоичная
	A B C D E F

Для преобразования целого числа Z_p→Z_qв случае q=p^r, где r – целое число, большее единицы, достаточно Z_p разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.

Т.е. для перевода любого целого двоичного числа в восьмеричное (8=2³) необходимо разбить его справа налево на группы по 3 цифры (триады, самая левая группа может содержать менее трех двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент.

Пример 10. Перевести число 11011001 из двоичной системы в восьмеричную.

11011001₍₂₎=11011001=331₍₈₎

т.к. 11₍₂₎=3₍₈₎,

011₍₂₎=3_(8),

001₍₂₎=1₍₈₎.

А перевод целого двоичного числа в шестнадцатеричное (16=2⁴) производится путем разбиения данного числа на группы по 4 цифры (тетрады).

Пример 11. Перевести число 1100011011001 из двоичной системы в шестнадцатеричную.

1100011011001 ₍₂₎=1100011011001=18D9₍₁₆₎

т.к. 1₍₂₎=1₍₁₆₎,

1000₍₂₎=8₍₁₆₎,

1101₍₂₎=D_(16),

1001₍₂₎=9₍₈₎.

Задания.

Перевести следующие числа из двоичной системы счисления в восьмеричную и шестнадцатеричную:

1) 1110101011₍₂₎à?_{(8), (16)}

2) 10101001011₍₂₎à? _{(8), (16)}

3) 11110101101₍₂₎à? _{(8), (16)}

4) 1000010111110₍₂₎à? _{(8), (16)}

5) 101010101₍₂₎à? _{(8), (16)}

6) 1011010101101₍₂₎à? _{(8), (16)}

^{1.3.2 Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную}

Для преобразования целого числа Z_p→Z_q в случае p=q^r, где r – целое число, большее единицы, достаточно каждую цифру числа Z_p заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при этом нулями слева до группы в r цифр.

То есть, перевод восьмеричных и шестнадцатеричных чисел в двоичные производится обратным путем – сопоставлением каждому знаку числа соответствующей триады (тетрады).

Пример 12. Перевести число 331 из восьмеричной системы в двоичную.

331₍₈₎=11011001=11011001.

т.к. 3₍₈₎=11₍₂₎, (первое число не обязательно дополнять до триады)

3₍₈₎=11₍₂₎, а если дополнит до триады, то 011,

1₍₈₎=1₍₂₎, а если дополнить до триады, то 001.

Пример 13. Перевести число 18D9 из шестнадцатеричной системы в двоичную.

18D9 ₍₁₆₎=1100011011001=1100011011001 ₍₁₆₎

т.к. 1₍₁₆₎=1₍₂₎,

8₍₁₆₎=1000₍₂₎,

D₍₁₆₎=1101_(2),

9₍₈₎=1001₍₂₎.

Задания.

Перевести следующие числа из восьмеричной и шестнадцатеричной системы счисления в двоичную:

1) 3A74₍₁₆₎à?₍₂₎ 7) 2A9C₍₁₆₎à?₍₂₎

2) 746₍₈₎à?₍₂₎ 8) 2535₍₈₎à?₍₂₎

3) 7BCD₍₁₆₎à?₍₂₎ 9) 152E₍₁₆₎à?₍₂₎

4) 253₍₈₎à?₍₂₎ 10) 1624₍₈₎à?₍₂₎

5) 1F67₍₁₆₎à?₍₂₎ 11) 7FD₍₁₆₎à?₍₂₎

6) 637₍₈₎à?₍₂₎ 12) 251₍₈₎à?₍₂₎

 

Кодирование чисел. Прямой, обратный и дополнительный коды. Сложение чисел с фиксированной запятой в прямом, обратном и дополнительных кодах

 

 

В современных ЭВМ используется 2 способа представления двоичных чисел – с фиксированной и с плавающей запятой. В формате с фиксированной запятой используется как беззнаковое представление чисел, так и представление чисел со знаком, где знак кодируется двоичной цифрой – обычно плюсу соответствует 0, а минусу – 1. Под код знака обычно отводится старший разряд a₀ двоичного вектора a₀a₁a_2…a_n, называемый знаковым.

Запятая может быть фиксирована после любого разряда двоичного числа, но чаще всего используется 2 формата: целые числа, когда запятая фиксируется после младшего разряда a_n, и дробные числа – запятая фиксируется после a₀.

Мы будем рассматривать дробные числа a₀,a₁a_2…a_n.

Кодирование чисел

Прямой код

Пусть А= a₀,a₁a_2…a_n.Если A>0, то А= 0,a₁a_2…a_n, если же A<0, то А= =1,a₁a_2…a_n.Приведенное кодирование дробных двоичных чисел со знаком принято называть прямым кодом числа и обозначается [A]_d. То есть,

Пример 14.Если A=0,110101, то [A]_d=0,110101.

Если A=-0,101110, то [A]_d=1,101110.

Обратный код

Представление обратного кода определяется следующим соотношением:

Т.е. обратный код положительного числа равен самому числу. Для получения обратного кода отрицательного числа достаточно присвоить знаковому разряду значение 1 и проинвертировать все остальные разряды числа.

Для перехода из обратного кода в прямой осуществляется преобразование т.е. [[A]_i]=[A]_d.

Пример 15.Если A=-0,111000, то [A]_i=1,000111.

Если A=-0,101110, то [A]_i=1,010001.

Дополнительный код

Представление дополнительного кода определяется следующим соотношением:

Дополнительный код положительного числа равен самому числу. Дополнительный код отрицательного числа дополняет исходное число до основания системы счисления. Дополнительный код отрицательного числа образуется в соответствии:

Первый способ.Для преобразования отрицательного числа в дополнительный код следует преобразовать его сначала в обратный код и добавить единицу к младшему разряду обратного кода.

Второй способ: оставить без изменения все младшие нули и одну младшую единицу, остальные разряды проинвертировать.

Пример 16.Если A=-0,111000, то [A]_i=1,000111, а [A]_c=1,001000.

ЕслиA=-0,101110, то[A]_i=1,010001, а[A]_c=1,010010.

Задания.

Перевести следующие числа в прямой, обратный и дополнительный код:

1) 0,0111 6) -0,11110101

2) -0,0111 7) 0,1010110

3) -0,1000 8) -0,1000110

4) -0,0101 9) 0,10100000

5) -0,10100010 10) -0,10111000

studopedya.ru