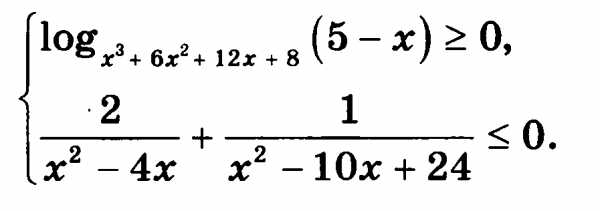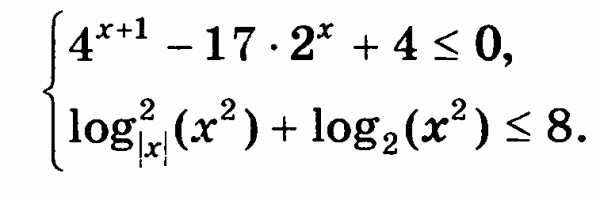Итоговая контрольная работа по математике 11 класс
Спецификация
Контрольно-измерительных материалов для проведения
промежуточной аттестации учащихся 11 класса
по математике
Назначение контрольно-измерительных материалов (далее КИМ) – оценить уровень подготовки по математике учащихся 11 класса МБОУ «СОШ №8»
Документ, определяющий содержание КИМ-рабочая программа учебного предмета «Математика» для учащихся 10-11 классов.
Подходы к отбору содержания, разработке структуры КИМ-содержание заданий разработано по основным темам учебного предмета «Математика»
Структура КИМ
Работа состоит из трех частей
Часть 1(базовый уровень) содержит 6 заданий базового уровня, среди которых задания 1-3 с выбором ответа.
Часть 2 (повышенный уровень) содержит 2 задания с развернутым ответом.
Часть 3 (высокий уровень) содержит 1 задание с развернутым ответом, подразумевающее нахождение наибольшего и наименьшего значения функции на заданном отрезке.
Таблица 1 распределение заданий по частям работы
Количество заданий
Максимальный первичный балл
Процент максимального первичного балла за выполнение заданий данной части от максимального первичного балла за всю работу, равного 100
Тип задания
Часть 1
6
13
52
С выбором ответа
Часть 2
2
7
28
С развернутым ответом
Часть 3
1
5
20
С развернутым ответом
итого
9
25
100
Распределение заданий КИМ по содержанию и видам деятельности
Число заданий
Максимальный балл
1
Тригонометрические формулы
1
2
2
Производная и её геометрический смысл
1
2
3
Тригонометрические функции
1
2
4
Элементы комбинаторики
1
2
5
Производная и её геометрический смысл
1
2
6
Объемы тел
1
3
7
Решение тригонометрических уравнений
1
3
8
Интеграл
1
4
9
Применение производной к исследованию функций
1
итого
9
25
Продолжительность работы 85 минут, 5 минут — организационный момент
Система оценивания выполнения заданий и работы в целом
«2»
«3»
«4»
«5»
баллы
0-12
13-18
19-23
24-25
План варианта КИМ для проведения аттестационной письменной работы
Проверяемые предметные результаты
Уровень сложности задания
Максимальный балл за выполнение задания
1
Синус, косинус, тангенс углов
Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц.
базовый
2
2
Производные некоторых элементарных функций
Использовать определение производной при нахождении производных элементарных функций
базовый
2
3
Область определения и множество значений тригонометрических функций
Находить область определения и область значения тригонометрических функций
базовый
2
4
Комбинаторные задачи
Решать простейшие задачи из теории вероятности
базовый
2
5
Геометрический смысл производной
Применять понятие производной при решении физических задач
базовый
2
6
Объемы тел
Решать задачи на вычисление объемов
базовый
3
7
Решение тригонометрических уравнений
Уметь решать простейшие тригонометрические уравнения
повышенный
8
Наибольшее и наименьшее значения функций
Применять правило нахождения наибольшего и наименьшего значения функции на отрезке и на интервале
повышенный
4
9
Площадь криволинейной трапеции
Изображать криволинейную трапецию, ограниченную заданными кривыми.
Находить площадь криволинейной трапеции
высокий
5
Итоговая контрольная работа по математике для 11 класса
Вариант 1
I уровень. В заданиях 1–3 укажите букву верного ответа.
1.Вычислить
А. 1; Б 0; В. -1. Г. 2
2. Найдите производную функции
А. Б. В. Г.
3. Найдите множество значений функции
А. [–1; 1] Б. В. Г.
4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
5. Тело движется прямолинейно по закону х(t) = 3t4 — 2t3 +1 (x в метрах, t в секундах). Найдите его скорость в момент времени t = 2.
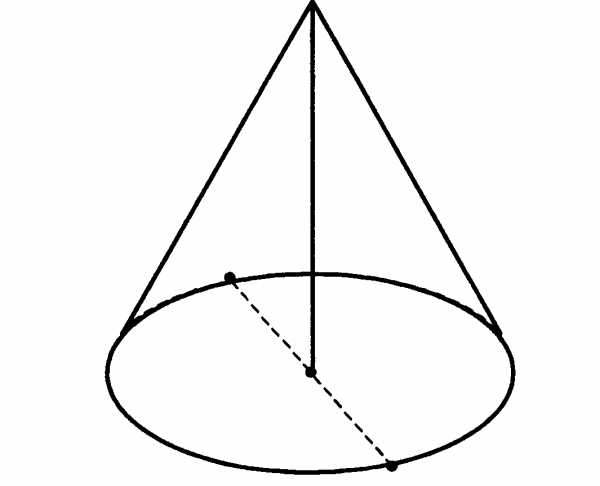
6. Радиус основания конуса равен 4 , высота в два раза больше радиуса. Найдите объем конуса. (π=3)
II уровень
7. Решите уравнение
8. Найдите наименьшее значение функции у= х3 –х2 — 40х + 3 на отрезке
III уровень
9. Вычислить площадь фигуры ограниченной линиями: у = х+3 , у = -х2 +8х -7.
Вариант 2
I уровень. В заданиях 1–3 укажите букву верного ответа.
1. Вычислить
А
2. Найдите производную функции
А. Б. В. Г.
3. Найдите множество значений функции
А. [–1; 1] Б. В. Г.
4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
5. Тело движется прямолинейно по закону х(t) = 2t4 — 3t2 – 5t (x в метрах, t в секундах). Найдите его скорость в момент времени t = 4c
6. Радиус основания цилиндра равен 6, а высота в три раза меньше радиуса. Найдите объем цилиндра. (π=3)
II уровень
7. Решите уравнение
8. Найдите наибольшее значение функции у= х3 +2х2 -4х +4 на отрезке
II
I уровеньВычислить площадь фигуры ограниченной линиями: у = 8х — х2-2, у = х+8.
Ключ
1 вариант
2 вариант
1
А
Б
2
Б
В
3
В
В
4
0,17
0,11
5
72
483
6
128
216
7
x=π+ 2πn
x=π/2+πn
8
-109
12
9
4.5
4,5
Итоговая контрольная работа (11 класс)
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
ОТВЕТЫ
Итоговая контрольная работа
Вариант 1
№1. Найдите значение выражения log
№2. Решите неравенство 32x+3>81
№3. На рисунке изображен график первообразной y = F (x) некоторой функции y = f(x), определенной на интервале ( — 16; — 2). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-15; -8].
№4. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
№5. Решите уравнение = 0,04.
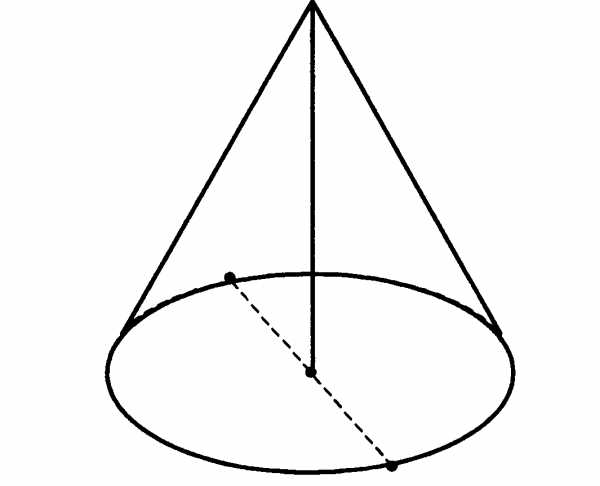
№6. Высота конуса равна 30, а длина образующей — 34. Найдите диаметр основания конуса.
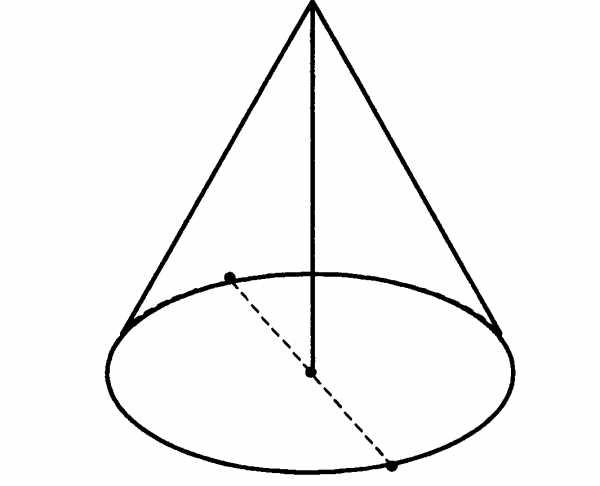
№7. Коэффициент полезного действия некоторого двигателя определяется формулой . При каком наименьшем значении температура нагревателя ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника = 200 К?
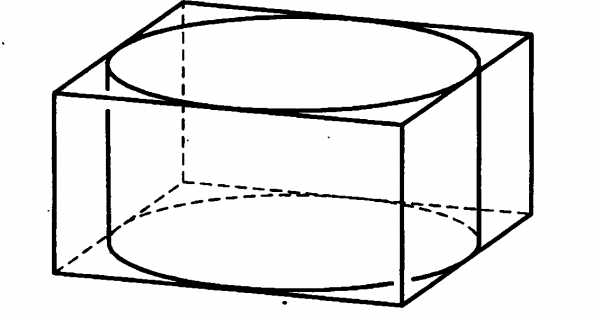
№8. Объем цилиндра равен 12см. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
№9. Два автомобиля отправляются в 420 – километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найти скорость автомобиля, пришедшего к финишу вторым.
№10. Найдите наименьшее значение функции y = ( на отрезке [6; 8].
№11. а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие промежутку
№12. Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.
№13. Решите систему неравенств
.
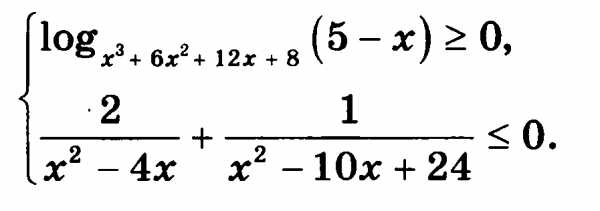
Итоговая контрольная работа
Вариант 2
№1.
№2. Решите неравенство <
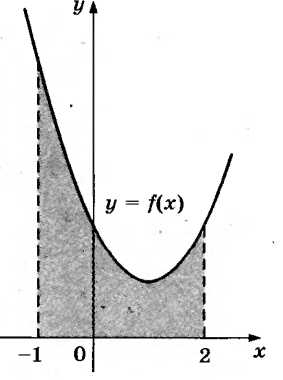
№3. На рисунке изображен график первообразной
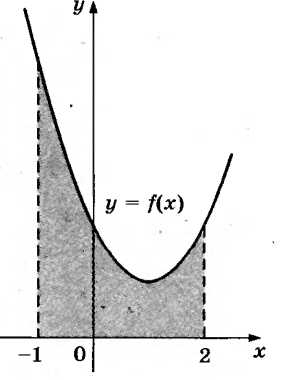
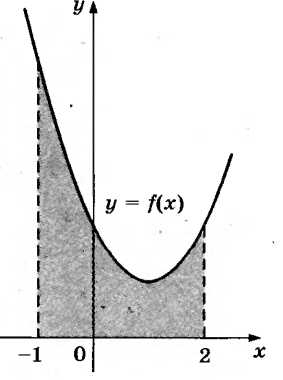
некоторой функции y = f(x). Одна из первообразных этой функции равна F( x) = . Найдите площадь заштрихованной фигуры.
№4. В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
№5. Решите уравнение = 0,25
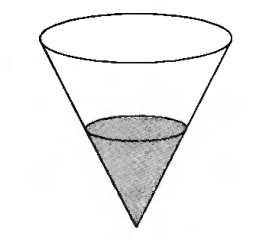
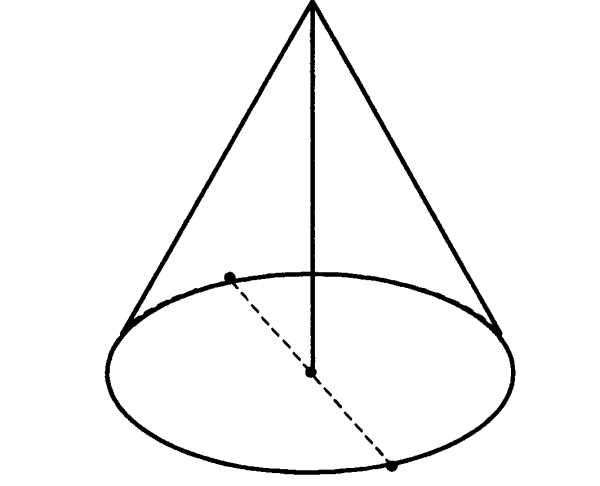
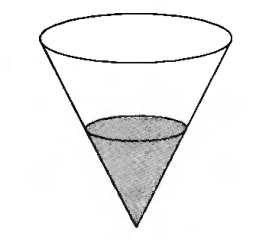
№6. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.) Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
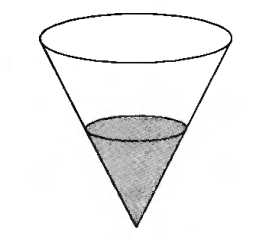№7. Коэффициент полезного действия некоторого двигателя определяется формулой , — температура нагревателя ( в градусах Кельвина) , — температура холодильника ( в градусах Кельвина) При какой температуре нагревателя КПД двигателя будет 45%, если температура холодильника = 275 К? Ответ выразите в градусах Кельвина.
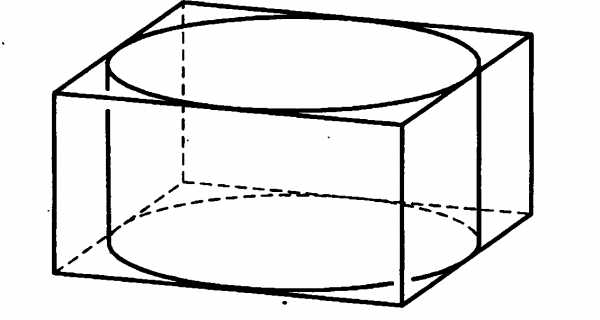
№8. Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объем параллелепипеда.
№9. Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?
№10. Найдите набольшее значение функции y = ( на отрезке [19; 21].
№11. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
№12. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
№13. Решите систему неравенств
Итоговая контрольная работа
Вариант 3
№1.
№2. Решите неравенство
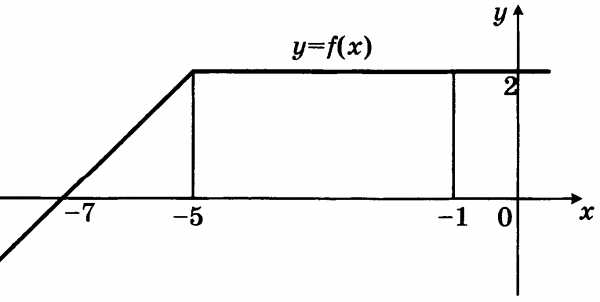
№3. На рисунке изображен график некоторой функции у = Пользуясь рисунком, вычислите определенный интеграл dx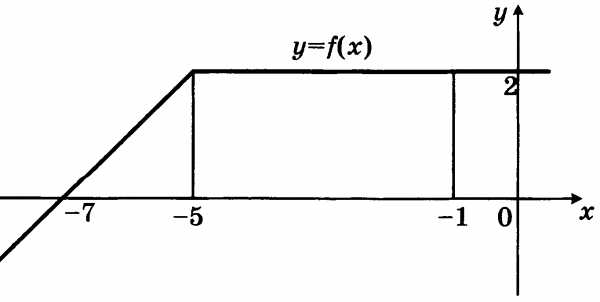 
№4. В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям.
№5. Решите уравнение = 36.
№6 Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
№7. Температуру нагревательного элемента (в градусах Кельвина) в зависимости от времени (вминутах) можно вычислять по формуле Т(t) = Т0 + аt + b t2, где Т0 = 760 К, а = 34 К/мин,
b = -0,2 К/мин2. Известно, что при температурах нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время (в минутах) после начала работы нужно отключать прибор.
№8. Площадь боковой поверхности цилиндра равна , а высота — 8 . Найдите диаметр основания.
№9. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
№10. Найдите наимбольшее значение функции на отрезке [-4,5; 0].
№11.
№12. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите угол между этой плоскостью и плоскостью основания цилиндра.
№13. Решите систему неравенств
.
Итоговая контрольная работа
Вариант 4
№1. Найдите значение выражения .
№2.
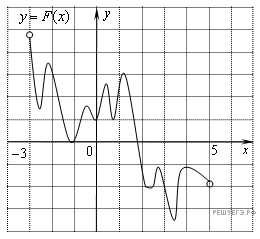
№3. На рисунке изображён график функции y = F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
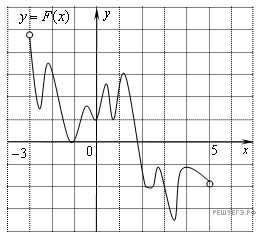
№4. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из Голландии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Боливии.
№5. Найдите корень уравнения:
№6. Длина окружности основания цилиндра равна 7. Площадь боковой поверхности равна 105. Найдите высоту цилиндра.
№7. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где – постоянная, – радиус аппарата в метрах, м3 – плотность воды, а – ускорение свободного падения (считайте Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
№8. Диаметр основания конуса равен 136, а длина образующей — 85 . Найдите высоту конуса.
№9. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
№10. Найдите наименьшее значение функции на отрезке [0; 2].
№11.
№12. Две параллельные плоскости, находящиеся на расстоянии 12 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 64л. Найдите площадь поверхности шара.
№13. Решите систему неравенств
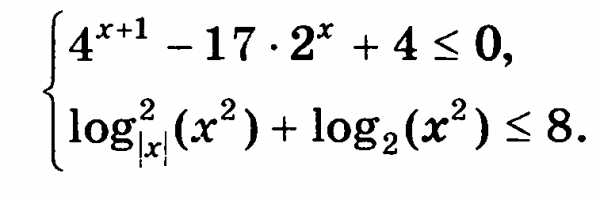
infourok.ru
Школьная отметка | |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 | Школьная отметка |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 | Школьная отметка |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 | Школьная отметка |
0-4 | 2 |
5-8 | 3 |
9-11 | 4 |
12-15 | 5 |
doc4web.ru
Итоговая контрольная работа по математике для 11 класса
Просмотр содержимого документа
«Итоговая контрольная работа по математике для 11 класса»
1 вариант
1.Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2. Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
3. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
4. Найдите точку минимума функции .
5. На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите синус этого угла
6. Решить уравнение: а)
б)
7. Найдите значение выражения
8.Найти , если
Д. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [2π; 7π/2].
2 вариант
Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
3. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (2 ; 13). Найдите точку из отрезка [8 ; 12],
в которой производная функции f(x) равна 0.
4.Найдите наименьшее значение функции на отрезке [− 4; 4].
5. На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите косинус этого угла.
6.Решить уравнение: а)
б)
7. Найдите значение выражения
8. Найти , если
Д. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку (2; 8/3).
multiurok.ru
Итоговая контрольная работа по математике за 1 полугодие в 11 классе (тест)
Итоговая контрольная работа по математике
за 1 полугодие
для учащихся 11 класса
(Учебник: Алгебра и начала математического анализа. 11 класс: учеб. Для общеобразоват. учреждений: базовый и профил. уровни/[Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин]; под ред. А.Б. Жижченко)
1. Укажите наибольшее целое число, принадлежащее множеству значений функции
у=5sinx — 5cosx -1.
1) 0; 2) 4; 3) 6; 4) 9.
2. В параллелепипеде АВСDА1В1С1D1 вершины В(1; 2; -4), С1(0,0,0) и D1(3; 0; 2).
Найдите длину диагонали АС1.
1) 24; 2) 2
; 3) 
4) 12.
3. Площадь полной поверхности тела. Полученного при вращении квадрата с
диагональю 2а вокруг этой диагонали, составляет:
1) 
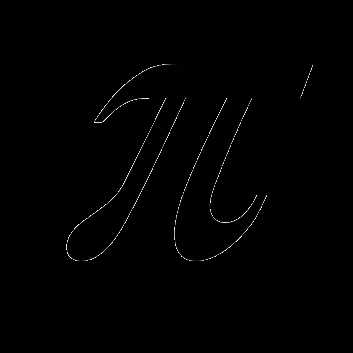а
; 2) 
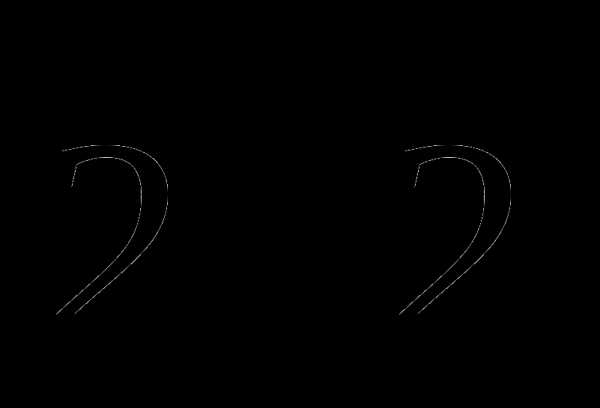
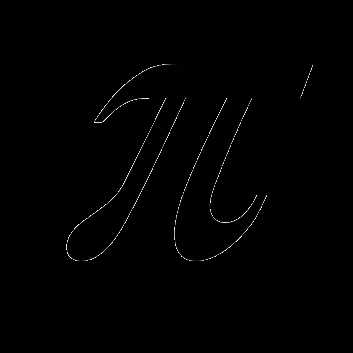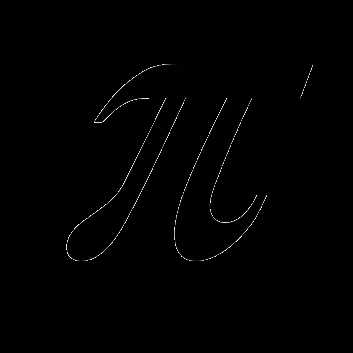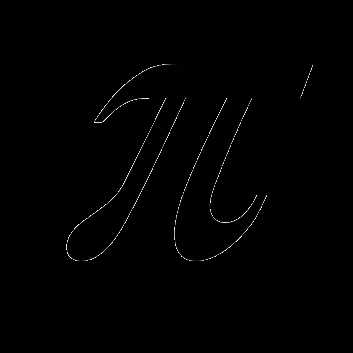а; 3) 2а; 4) 4а.
4. Найдите производную функции у = (х2 – 2)sin x.
1) 2хsin x + 2xcos x; 2) 2хsin x — (x2 – 2)cos x.
3) 2хcos x; 4) 2хsin x + (x2 – 2)cos x.
5. Найдите значение производной функции у =(1-х)3 в точке х0=0.
1) 1; 2) -1; 3) 3; 4) -3.
6. Запишите уравнение касательной к графику функции у = — х2 — 2, параллельной оси
абсцисс.
1) у=0; 2) у=2; 3) у= –2; 4) х= –2.
7. Скалярное произведение векторов 
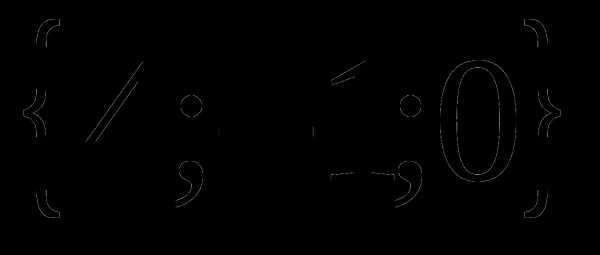и 
равно:
1) 1; 2) –1; 3) 0; 4) 50.
8. Найдите угол наклона касательной к графику функции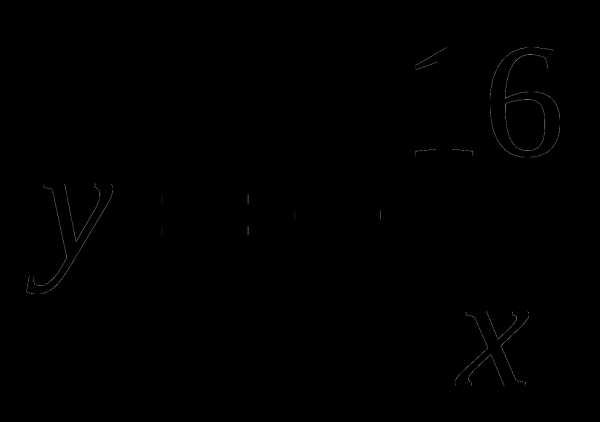 
в точке с
абсциссой х0=4.
1) 00; 2) 450; 3) 1350; 4) — 450.
9. Найдите количество промежутков возрастания функции у=х3-2х2+х-1.
1) 3; 2) 2; 3) 1; 4) 0.
10. Площадь боковой поверхности цилиндра, полученного при вращении
прямоугольника со стороной 3а и гипотенузой 5а вокруг большей стороны,
составляет:
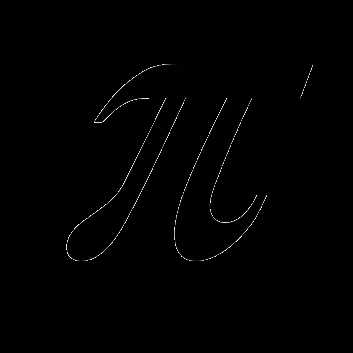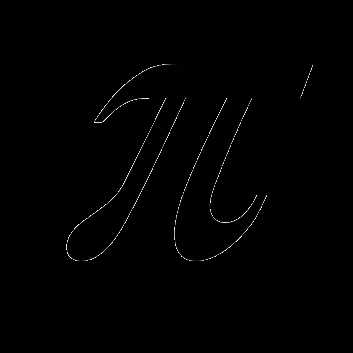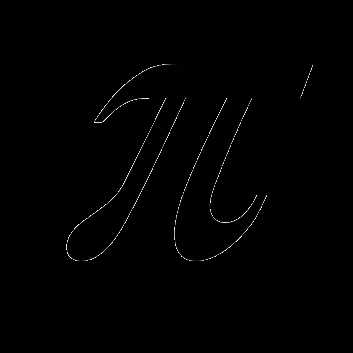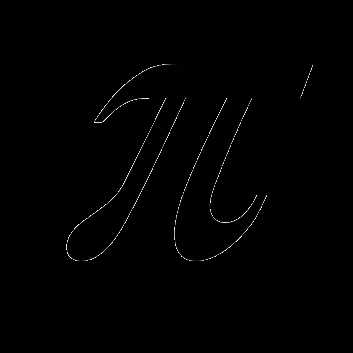1) 2а; 2) 12а; 3) 30а; 4) 24а.
11. Укажите точку минимума функции f(x), если ее производная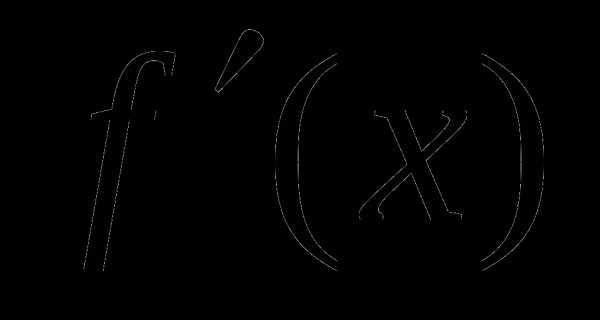 
= (x-3)(7+x).
1) –7; 2) 0; 3) 3; 4) точки минимума нет.
12. Даны точки: А(1;–1;2), В(0;0;0), С(–3; -3; 0). Найдите величину угла АВС.
1) 450;
2) 600;
3) 900;
4) arccos
.
.13. Сравнение значений в примерах а) и б) выполнено верно:
а) tg0,8 >tg 2,8 б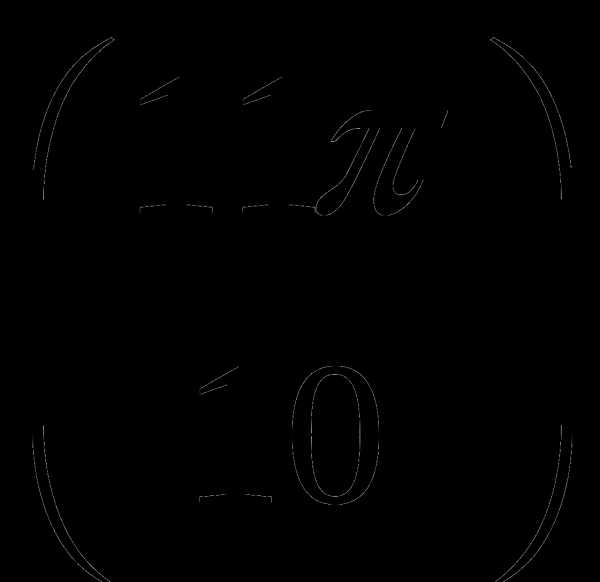) tg 
< tg 
1) только в а) 2) только в б)
3) и в а) и в б) 4) ни в а), ни в б).
14. Дан график производной функции у=f(x). Сколько стационарных точек имеет
сама функция на изображенном промежутке?
1) 1;
2) 2;
3) 3;
4) данных для ответа недостаточно.
www.metod-kopilka.ru
Оценочные материалы для промежуточного контроля успеваемости по математике в 11 классе
Оценочные
материалы для промежуточного контроля успеваемости
по математике
в 11 классе
№
Форма работы
Дата провед
Наименование тем, разделов
Источник
1
Комбинированная контрольная работа
13.05
Первообразная .
Интеграл.
Обобщение понятия степени
Цилиндр, конус, шар
Показательная и логарифмическая функция
Объемы тел
Производная показательной и логарифмической функции
Элементы теории вероятности
Открытый банк задач ЕГЭ по математике www.mathege.ru
Решу ЕГЭ
http://reshuege.ru/
Открытый банк задач ЕГЭ по математике 2015
http://live.mephist.ru/
Итоговая контрольная работа по математике в 11 классе в рамках промежуточной аттестации за 2014-2015 учебный год
СПЕЦИФИКАЦИЯ
диагностической работы по математике для учащихся 11 класса
1. Назначение работы – оценить общеобразовательную подготовку по математике учеников XI класса с целью их подготовки к итоговой аттестации.
2. Документы, определяющие содержание диагностической работы.
Содержание работы определяется на основе следующих документов:
1. Обязательный минимум содержания основного общего образования по предмету
2. Обязательный минимум содержания среднего (полного) общего образования по предмету
3. Федеральный компонент государственного стандарта общего образования. Математика
3. Структура и содержание диагностической работы
Структура работы отвечает ее основной цели – оценить общеобразовательную подготовку выпускников по математике, поэтому содержание контролируемого материала включает темы, изучаемые в 11 по алгебре и начала анализа и геометрии.
4. Распределение заданий диагностической работы по уровню сложности.
В соответствии с принятой структурой и содержанием работы , содержит 8 заданий: В1–В7 и С1, составленных на материале курса алгебры и начал анализа и геометрии 11. Эти задания обеспечивают достаточную полноту проверки овладения материалом этого курса на базовом уровне.
Содержание этих заданий отвечает минимуму содержания средней школы.
5. Время выполнения работы
На выполнение диагностической работы отводится 45 минут
6. Параллельность вариантов
Работа содержит 4 параллельных варианта.
7.Система оценивания выполнения отдельных заданий и работы в целом
Задание части 1 В1-В7 считается выполненным верно, если записан верный ответ. За каждое верно выполненное задание 1 балл.
Задание части 1 С1 считается выполненным верно, если дано полное решение. Оценивается до 3 баллов.
Максимальное количество баллов за работу — 10.
Рекомендации по переводу первичных баллов в отметку:
Отметка «5» соответствует оптимальному уровню и ставится, если общее количество баллов составляет 8-10 баллов
Отметка «4» соответствует удовлетворительному (допустимому) уровню и ставится, если общее количество баллов составляет от 6 до 7.
Отметка «3» соответствует критическому уровню и ставится, если учащийся набрал 4-5 балла.
Отметка «2» соответствует недопустимому уровню и ставится, если учащийся набрал менее 4 баллов.
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 45 мин. . Работа состоит из двух частей. Первая часть содержит 7. К каждому заданию В1-В7 требуется дать краткий ответ. Задание С1 ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В7 оцениваются в 1 балл, С1– 3 балла.
Вариант 1
Часть I
В1. Найдите значение выражения log
В2. На рисунке изображен график первообразной y = F (x) некоторой функции y = f(x), определенной на интервале ( — 16; — 2). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-15; -8].
В3. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
В4. Решите уравнение = 0,04.
В5 Высота конуса равна 30, а длина образующей — 34. Найдите диаметр основания конуса.
В6. Объем цилиндра равен 12см. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
В7. Найдите наименьшее значение функции y = ( на отрезке [6; 8].
Часть II
С1 а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 45 мин. . Работа состоит из двух частей. Первая часть содержит 7. К каждому заданию В1-В7 требуется дать краткий ответ. Задание С1 ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В7 оцениваются в 1 балл, С1– 3 балла.
Вариант 2
Часть I
В1.
В2. На рисунке изображен график первообразной
некоторой функции y = f(x). Одна из первообразных этой функции равна F( x) = . Найдите площадь заштрихованной фигуры.
В3. В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
В4. Решите уравнение = 0,25.
В5. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.) Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
В6. Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объем параллелепипеда.
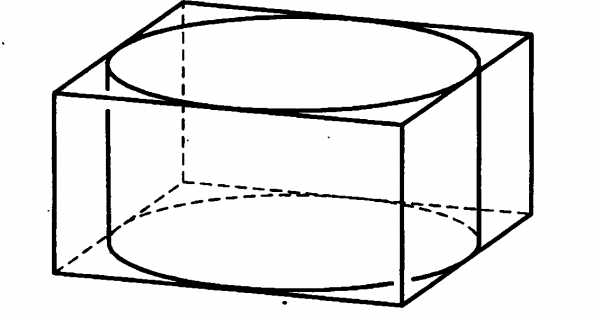
В7. Найдите набольшее значение функции y = ( на отрезке [19; 21].
Часть II
С1 а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 45 мин. . Работа состоит из двух частей. Первая часть содержит 7. К каждому заданию В1-В7 требуется дать краткий ответ. Задание С1 ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В7 оцениваются в 1 балл, С1– 3 балла.
Вариант 3
Часть I
В1
В2. На рисунке изображен график некоторой функции у = Пользуясь рисунком, вычислите определенный интеграл dx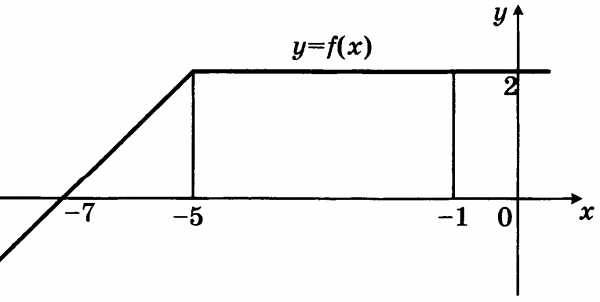 
В3. В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям.
В4. Решите уравнение = 36.
В5 Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
В6. Площадь боковой поверхности цилиндра равна , а высота — 8 . Найдите диаметр основания.
В7. Найдите наимбольшее значение функции на отрезке [-4,5; 0].
Часть II
С1. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
МАТЕМАТИКА, 11 класс
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 45 мин. . Работа состоит из двух частей. Первая часть содержит 7. К каждому заданию В1-В7 требуется дать краткий ответ. Задание С1 ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В7 оцениваются в 1 балл, С1– 3 балла.
Вариант 4
Часть I
В1. Найдите значение выражения .
В2. На рисунке изображён график функции y = F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
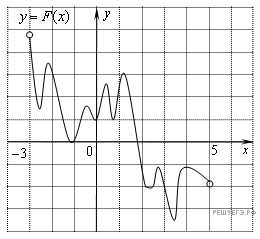
В3.. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из Голландии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Боливии.
В4. Найдите корень уравнения: .
В5. Длина окружности основания цилиндра равна 7. Площадь боковой поверхности равна 105. Найдите высоту цилиндра.
В6 Диаметр основания конуса равен 136, а длина образующей — 85 . Найдите высоту конуса.
В7. Найдите наименьшее значение функции на отрезке [0; 2].
Часть II
С1. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
infourok.ru
МАТЕМАТИКА, 11 класс Итоговая контрольная работа
Documents войти Загрузить ×- No category
Related documents
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ СОЦИАЛЬНЫЙ
Русское лото
Тест по теме тела и поверхности вращения
Макеты тел вращения (цилиндр, конус)
Примерные экзаменационные задания по математике: Вариант 2 Вариант 1
Занятие 24-25. Задачи на нахождение объема тел. Задача 1 Решение. а=в=2r=5,5
Задания по алгебре и началам анализа для 11 класса учащихся… Вопросы теоретические:
Олимпиада «Покори Воробьёвы горы!» по математике 2015 год
Тестовые задания по математике 1-вариант
Маршрутный лист 2
Скачать advertisement StudyDoc © 2018 DMCA / GDPR Пожаловатьсяstudydoc.ru
