Какой газ называется идеальным
1. Какой газ называется идеальным? (Смотри приложение № 1)
Идеальный газ — это газ, удовлетворяющий следующим условиям:
1) собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
2. Какими параметрами характеризуется состояние газа? Дайте молекулярно-кинетическое толкование параметров р,Т.
Состояние данной массы газа m характеризуют параметры: давление p, объём V, температура T.
3. Запишите формулу, связывающую температуры по шкале Кельвина и по шкале Цельсия? Каков физический смысл абсолютного нуля?
Связь между термодинамической температурой T и температурой по стоградусной шкале Цельсия имеет вид T = t + 273,15. При абсолютном нуле энергия молекул равна нулю.
4. Запишите уравнение состояния идеального газа.
5. Какой процесс называется изотермическим? Запишите и сформулируйте закон Бойля-Мариотта и начертите график зависимости давления от объема.
6. Какой процесс называется изохорическим? Запишите и сформулируйте закон Шарля. Начертите график зависимости давления от температуры.
Давление данной массы газа при постоянном объёме изменяется линейно с температурой , при .
Процесс, протекающий при постоянном объёме, называется изохорным.
7. Какой процесс называется изобарическим? Запишите и сформулируйте закон Гей-Люссака. Начертите график зависимости объема от температуры.
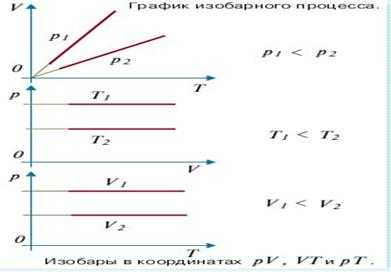
Объём данной массы газа при постоянном давлении изменяется линейно с температурой: , при . Процесс, протекающий при постоянном давлении, называется изобарным.
8. Какой процесс называется адиабатическим? Запишите уравнение Пуассона и представьте его графически. (см. приложение № 2)
Адиабатический процесс – это процесс, протекающий без теплообмена с окружающей средой , следовательно .
Работа в ходе адиабатического расширения осуществляется за счет убыли внутренней энергии.
9. Запишите и сформулируйте первый закон термодинамики. Дайте понятие внутренней энергии, работы, количества тепла.
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход.
ΔU = Q – A
10. Запишите выражение для работы расширения газа. Как ее представить графически на рV диаграмме.
11. Примените первый закон термодинамики ко всем процессам, рассматриваемым в данной лабораторной работе и проанализируйте вытекающие из него следствия.
12. Дайте определение удельной и молярной теплоемкостей и запишите соотношение между ними.
Удельная теплоёмкость вещества – величина равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К .
Молярная теплоёмкость — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К .
С=сM.
13. Выведите уравнение Майера. Какая из теплоемкостей СP или CV больше и почему?
Связь между молярными и теплоёмкостями (уравнения Майера) .
Связь между удельными теплоёмкостями
Степеней свободы число в механике, число независимых между собой возможных перемещений механической системы. Число степеней свободы зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему механических связей. Для свободной частицы число степеней свободы равно 3, для свободного твёрдого тела — 6, для тела, имеющего неподвижную ось вращения, число степеней свободы равно 1 и т.д. Для любой голономной системы (системы с геометрическими связями) число степеней свободы равно числу s независимых между собой координат, определяющих положение системы, и даётся равенством 5 = 3n — к, где n — число частиц системы, k — число геометрических связей. Для неголономной системы число степеней свободы меньше числа координат, определяющих положение системы, на число кинематических связей, не сводящихся к геометрическим (неинтегрируемых). От числа степени свободы зависит число уравнений движения и условий равновесия механической системы.
15. Зная число степеней свободы молекул воздуха, рассчитайте γ и сравните со значением γ, полученным опытным путем.
16. Нарисуйте и поясните на рV диаграмме последовательно все процессы, происходящие с газом.
17. Какова причина изменения температуры воздуха в баллоне при накачивании воздуха в баллон и при выпуске его из баллона?
18. Выведите расчетную формулу для определения отношения теплоемкостей γ.
www.birmaga.ru
Какой газ называется идеальным? Запишите уравнение состояния идеального газа и объясните его.
Какие погрешности возникают при измерениях в Лабораторной работе № 4 «Определение удельной теплоты кристаллизации (плавления) и изменения энтропии при кристаллизации олова»? Объясните их причины.
В нашей лабораторной работе № 4 возникают такие погрешности, как состав олова, комнатная температура, а так же на результат может повлиять долгое нагревание олова. Причины: состав олова может содержать какие-либо примеси, вследствие чего это может повлиять на результат измерений. Так же погрешностью можно назвать комнатную температуру, т.к. каждый раз делая данную лабораторную работу, мы используем разную температуру окружающей среды в лаборатории.
Какие погрешности возникают при измерениях в Лабораторной работе № 4 «Определение удельной теплоты кристаллизации (плавления) и изменения энтропии при кристаллизации олова»? Объясните их причины.
В нашей лабораторной работе № 4 возникают такие погрешности, как состав олова, комнатная температура, а так же на результат может повлиять долгое нагревание олова. Причины: состав олова может содержать какие-либо примеси, вследствие чего это может повлиять на результат измерений. Так же погрешностью можно назвать комнатную температуру, т.к. каждый раз делая данную лабораторную работу, мы используем разную температуру окружающей среды в лаборатории.
Какой газ называется идеальным? Запишите уравнение состояния идеального газа и объясните его.
Идеальный газ- это газ, молекулы которого рассматриваются как материальные точки взаимодействия между собой по законам соударения упругих шаров. Т.е. модели идеального газа пренебрегают собственным объемом молекул и силами взаимодействия между ними. Формула: или PV= . Эта формула дает связь между макропараметрами вещества. f(P,V,T)=0 общий вид уравнения состояния.
Процесс –переход системы из одного состояния в другое.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (PV=RT) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (P, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах P, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.
В случае постоянной массы газа уравнение можно записать в виде: Последнее уравнение называют
29. Сформулируйте первое начало термодинамики в общем, виде и для каждого изопроцесса. Начертите графики изопроцессов в координатах (pV), (pT), (VT).
Первое начало термодинамики- это применение закона сохранение и превращение энергии к явлениям, изучаемым термодинамикой.Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Энергия – это общая количественная мера всех процессов и видов взаимодействия в природе , подчиняющаяся закону сохранения. Энергия имеет определенное значение в любом состоянии системы, поэтому dU явл-ся функцией состояния.Функция состояния- это функция, которая в заданном состоянии системы имеет вполне определенное значение, не зависящее от того, каким путем или способом система в это состояние приведена. Характеризуется полным дифференциалом. Ф-я процесса- функции, значение которой определяется видом процесса, в результате которого система изменила свое состояние. К функциям процесса относятся Работа, Кол-во теплоты.
Первое начало термодинамики:
1) при изобарном процессе(p=const)-Закон Гей-Люссака. При P=const- Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от до равна и определяется площадью прямоугольника.
.
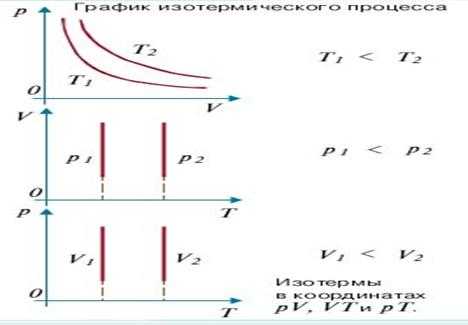
2)При изотермическом процессе — процесс изменения состояния термодинамической системы при постоянной температуре (T=const) PV=const-уравнение Бойля-Мариотта. При T=const — dU=0; Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс.
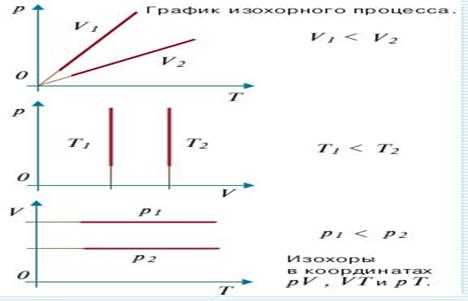
3)При изохорном процессе(V=const)-процесс изменения состояния термодинамической системы при постоянном объёме (V=const). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
При V=const-
cyberpedia.su
какой газ называются идеальным? каковы его параметры?
тебе учебника по физике/химии школьной программы не хватило, бедненькая? тебе прислать?Идеальный газ — математическая модель газа, в которой предполагается, что все частицы (молекулы) бесконечно малы (то есть размер молекул много меньше расстояний между ними) , между ними не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги. Модель очень хорошо описывает большинство задач по термодинамике газов, кроме экстремальных температур или давлений. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью является идеальным газом. Более точной моделью является т. н. газ Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.
Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна) .
Классический идеальный газ
Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
объём частицы газа равен нулю (то есть размеры молекул пренебрежимо малы по сравнению со средним расстоянием между ними) ;
импульс передается только при соударениях (то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях) ;
суммарная энергия частиц газа постоянна (то есть нет передачи энергии за счет передачи тепла или излучением)
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия — сумме энергий частиц газа. Свойства идеального газа описываются уравнением Клапейрона — Менделеева p = nkT
где p — давление, n — число частиц газа в единице объёма, k — постоянная Больцмана, T — абсолютная температура.
Распределение частиц классического идеального газа по состояниям описывается распределением Больцмана:
Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми — Дирака и Бозе — Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа. Для любого идеального газа справедливо соотношение Майера
otvet.mail.ru
Какой газ называется идеальным
1. Какой газ называется идеальным? (Смотри приложение № 1)
Идеальный газ — это газ, удовлетворяющий следующим условиям:
1) собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
2. Какими параметрами характеризуется состояние газа? Дайте молекулярно-кинетическое толкование параметров р,Т.
Состояние данной массы газа m характеризуют параметры: давление p, объём V, температура T.
3. Запишите формулу, связывающую температуры по шкале Кельвина и по шкале Цельсия? Каков физический смысл абсолютного нуля?
Связь между термодинамической температурой T и температурой по стоградусной шкале Цельсия имеет вид T = t + 273,15. При абсолютном нуле энергия молекул равна нулю.
4. Запишите уравнение состояния идеального газа.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: , где p — давление, Vμ — молярный объём, T — абсолютная температура, R — универсальная газовая постоянная.
5. Какой процесс называется изотермическим? Запишите и сформулируйте закон Бойля-Мариотта и начертите график зависимости давления от объема.
6. Какой процесс называется изохорическим? Запишите и сформулируйте закон Шарля. Начертите график зависимости давления от температуры.
Давление данной массы газа при постоянном объёме изменяется линейно с температурой , при .
Процесс, протекающий при постоянном объёме, называется изохорным.
7. Какой процесс называется изобарическим? Запишите и сформулируйте закон Гей-Люссака. Начертите график зависимости объема от температуры.
Объём данной массы газа при постоянном давлении изменяется линейно с температурой: , при . Процесс, протекающий при постоянном давлении, называется изобарным.
8. Какой процесс называется адиабатическим? Запишите уравнение Пуассона и представьте его графически. (см. приложение № 2)
Адиабатический процесс – это процесс, протекающий без теплообмена с окружающей средой , следовательно .
Работа в ходе адиабатического расширения осуществляется за счет убыли внутренней энергии.
9. Запишите и сформулируйте первый закон термодинамики. Дайте понятие внутренней энергии, работы, количества тепла.
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход.
ΔU = Q – A
10. Запишите выражение для работы расширения газа. Как ее представить графически на рV диаграмме.
11. Примените первый закон термодинамики ко всем процессам, рассматриваемым в данной лабораторной работе и проанализируйте вытекающие из него следствия.
12. Дайте определение удельной и молярной теплоемкостей и запишите соотношение между ними.
Удельная теплоёмкость вещества – величина равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К .
Молярная теплоёмкость — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К .
С=сM.
13. Выведите уравнение Майера. Какая из теплоемкостей СP или CV больше и почему?
Связь между молярными и теплоёмкостями (уравнения Майера) .
Связь между удельными теплоёмкостями
Степеней свободы число в механике, число независимых между собой возможных перемещений механической системы. Число степеней свободы зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему механических связей. Для свободной частицы число степеней свободы равно 3, для свободного твёрдого тела — 6, для тела, имеющего неподвижную ось вращения, число степеней свободы равно 1 и т.д. Для любой голономной системы (системы с геометрическими связями) число степеней свободы равно числу s независимых между собой координат, определяющих положение системы, и даётся равенством 5 = 3n — к, где n — число частиц системы, k — число геометрических связей. Для неголономной системы число степеней свободы меньше числа координат, определяющих положение системы, на число кинематических связей, не сводящихся к геометрическим (неинтегрируемых). От числа степени свободы зависит число уравнений движения и условий равновесия механической системы.
15. Зная число степеней свободы молекул воздуха, рассчитайте γ и сравните со значением γ, полученным опытным путем.
16. Нарисуйте и поясните на рV диаграмме последовательно все процессы, происходящие с газом.
17. Какова причина изменения температуры воздуха в баллоне при накачивании воздуха в баллон и при выпуске его из баллона?
18. Выведите расчетную формулу для определения отношения теплоемкостей γ.
birmaga.ru
Идеальный газ и его определение :: SYL.ru
Наука физика играет значимую роль в изучении окружающего мира. Поэтому ее понятия и законы начинают проходить еще в школе. Свойства вещества измеряются в разных аспектах. Если рассматривать его агрегатное состояние, то здесь существует особая методика. Идеальный газ — это физическая концепция, которая позволяет оценить свойства и характеристики материала, из которого состоит весь наш мир.
Общее определение
Идеальным газом названа модель, в которой взаимодействием между молекулами принято пренебрегать. Процесс взаимодействия частиц любого вещества друг с другом довольно сложный. 
Когда они подлетают друг к другу вплотную и находятся на очень малом расстоянии, они сильно взаимоотталкиваются. Но на большой удаленности между молекулами действуют относительно небольшие силы притяжения. Если же среднее расстояние, на котором они находятся друг от друга, большое, это положение вещества называют разреженным газом. Взаимодействие таких частиц проявляется как редкие удары молекул. Это происходит, лишь когда они подлетают вплотную друг к другу. В идеальном же газе взаимодействие молекул не учитывается вообще. В идеальном газе количество молекул очень большое. Поэтому вычисления происходят только при помощи статистического метода. Причем следует отметить, что частички вещества в таком случае распределяются в пространстве равномерно. Это самое часто встречающееся состояние идеального газа.
Когда газ можно считать идеальным
Существует несколько факторов, благодаря которым газ называется идеальным. Первым признаком является поведение молекул как абсолютно упругих тел, между ними отсутствуют силы притяжения. При этом газ будет очень разряжен. Расстояние между мельчайшими составляющими вещества будет гораздо больше размеров их самих. В таком случае тепловое равновесие будет достигаться мгновенно по всему объему. Чтобы достичь положения идеального газа в лабораторных условиях, реальный его тип разрежается соответствующим образом. Некоторые вещества в газообразном состоянии даже при комнатной температуре и нормальном атмосферном давлении практически не отличаются от идеального состояния.
Границы применения модели
Иеальный газ рассматривается в зависимости от поставленных задач. Если перед исследователем поставлена задача определить зависимость между температурой, объемом и давлением, то идеальным можно считать такое состояние вещества, при котором у газа наблюдается высокая точность до давлений, измеряемых несколькими десятками атмосфер. Но в случае изучения фазового перехода, например, испарения и конденсации, процесса достижения равновесия в газе, рассматриваемую модель нельзя применять даже при очень маленьком давлении. Давление газа на стенку пробирки происходит при хаотическом ударении молекул о стекло. Когда такие удары часты, организм человека может уловить эти изменения как непрерывное воздействие.
Уравнение идеального газа
Основываясь на главных принципах молекулярно-кинетической теории, было выведено главное уравнение идеального газа.
Работа идеального газа имеет следующее выражение: p = 1/3m0nv2, где p — давление газа идеального, m0 — молекулярная масса, v2 — среднее значение концентрации частиц, квадрат скорости молекул. Если обозначить средний показатель кинетического движения частиц вещества, как Ек = m0n/2, то уравнение будет иметь такой вид: p = 2/3nEk. Молекулы газа, ударяясь о стенки сосуда, вступают с ними во взаимодействие как упругие тела по законам механики. Импульс от таких ударов передается стенкам сосуда.
Температура
Вычислив только давление газа на стенки сосуда, нельзя определить средний показатель кинетической энергии его частиц.
Причем этого нельзя сделать ни для отдельной молекулы, ни для их концентрации. Поэтому для измерения параметров газа необходимо определять еще одну величину. Ею выступает температура, которая также связана с кинетической энергией молекул. Такой показатель выступает скалярной физической величиной. Температура описывает термодинамическое равновесие. В таком состоянии не происходит изменение параметров на микроуровне. Температура измеряется как отклонение от нулевого значения. Она характеризует насыщенность хаотического движения наименьших частиц газа. Она измеряется средним значением их кинетической энергии. Определяется этот показатель при помощи термометров в градусах различных отметок. Существует термодинамическая абсолютная шкала (Кельвина) и эмпирические ее разновидности. Они отличаются начальными точками.
Уравнение положения идеального газа с учетом температуры
Физик Больцман утверждает, что средний показатель кинетической энергии частицы пропорционален абсолютному показателю температуры. Ек = 3/2 кТ, где к = 1,38∙10-23, Т — температура. Работа идеального газа будет равна: Р = NkT/V, где N — количество молекул, V — объем сосуда. Если к этому показателю добавить концентрацию n = N/V, то вышеприведенная формула будет иметь такой вид: p = nkT. Эти два уравнения имеют различные формы записи, но они связывают для идеального газа давление, объем и температуру. Эти вычисления можно применять как к чистым газам, так и к их смесям. В последнем варианте под n нужно понимать все число молекул веществ, их суммарную концентрацию или полное количество молей в веществе.
Три газовых закона
Идеальный газ и его частные законы были открыты экспериментально и лишь потом подтверждены теоретически.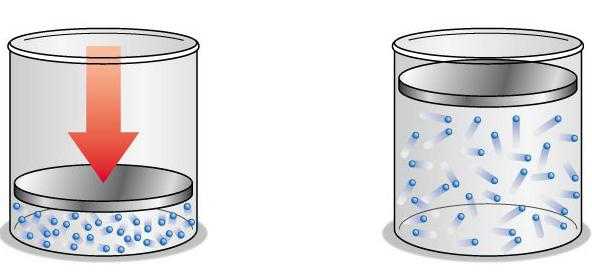 
Первый частный закон гласит, что идеальный газ при постоянной массе и температуре будет иметь обратно пропорциональное давление его объему. Процесс, при котором показатель температуры постоянный, был назван изотермическим. Если же при исследовании постоянным является давление, то объем пропорционален значению абсолютной температуры. Этот закон носит имя Гей-Люссака. Изохорный же процесс происходит при постоянном объеме. При этом давление будет пропорционально абсолютным температуре. Его название — закон Шарля. Это три частных закона поведения идеального газа. Их удалось подтвердить лишь при овладении знаниями о молекулах.
Абсолютная шкала измерения
В абсолютной шкале измерения принято единицей называть Кельвин. Она выбрана исходя из популярной шкалы Цельсия. Один Кельвин соответствует одному градусу по Цельсию. Но в шкале абсолютной за ноль принято значение, при котором давление идеального газа при постоянном объеме будет равно нулю.
Это общепринятая система. Такое значение температуры названо абсолютным нулем. Произведя соответствующие вычисления, можно получить ответ, что значение этого показателя будет составлять -273 градуса по Цельсию. Это подтверждает, что между абсолютной и шкалой Цельсия существует связь. Ее можно выразить в таком уравнении: Т = t + 237. Следует отметить, что достичь абсолютного нуля невозможно. Любой охладительный процесс основан на испарении с поверхности вещества молекул. Приближаясь к абсолютному нулю, поступательное движение частиц так сильно замедляется, что испарение прекращается практически совсем. Но чисто с теоретической точки зрения если бы было реально достичь точки абсолютного нуля, то скорость движения молекул уменьшилась бы настолько, что ее можно было бы назвать отсутствующей вовсе. Тепловое движение молекул прекратилось бы.
Изучив такое понятие, как идеальный газ, можно понять принцип работы любого вещества. Расширив знания в этой области, можно понять свойства и поведение любого газообразного вещества.
www.syl.ru
Идеальный газ — это… Что такое Идеальный газ?
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.
Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).
История
Клапейрон первым сформулировал уравнение идеального газаСуществование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта[1].
В 1802 году Гей-Люссаком был впервые опубликован в открытой печати закон объёмов (называемый в русскоязычной литературе законом Гей-Люссака) [2], однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века. Впоследствии он уточнил свои эксперименты и установил, что при изменении температуры от 0 до 100 °C объём воздуха линейно увеличивается на 0,375. Проведя аналогичные опыты с другими газами, Гей-Люссак установил, что это число одинаково для всех газов, несмотря на общепринятое мнение, что разные газы расширяются при нагревании различным образом.
В 1834 году из комбинации этих законов Клапейрон смог составить уравнение идеального газа[3]. Тот же закон, уже с использованием молекулярно-кинетической теории был сформулирован Августом Крёнигом в 1856 году[4] и Рудольфом Клаузиусом в 1857 году[5].
Классический идеальный газ
Объём идеального газа линейно зависит от температуры при постоянном давленииСвойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
- Диаметр молекулы пренебрежимо мал по сравнению со средним расстоянием между ними () [6][7].
- Импульс передается только при соударениях, то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.
- Суммарная энергия частиц газа постоянна если нет передачи тепла или совершения газом работы.
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия — сумме энергий частиц газа.
По эквивалентной формулировке идеальный газ — такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака[7], то есть:
где — давление, — абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона
- ,
где — универсальная газовая постоянная, — масса, — молярная масса.
или
где — концентрация частиц, — постоянная Больцмана.
Для любого идеального газа справедливо соотношение Майера:
где — универсальная газовая постоянная, — молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.
Применение теории идеального газа
Физический смысл температуры газа
Так как давление молекул газа на стенку определяется по формуле , где — средняя кинетическая энергия поступательного движения молекул газа. Подставив это в уравнение Менделеева — Клапейрона получаем, что температура пропорциональна .
Распределение Больцмана
Распределение скоростей для 106 молекул кислорода при -100, 20, 600 градусах ЦельсияРавновесное распределение частиц классического идеального газа по состояниям следует из уравнения Менделеева — Клапейрона, из которого можно вывести распределение газа в поле потенциальной энергии. Это распределение приводит к распределению Больцмана:
где — среднее число частиц, находящихся в -ом состоянии с энергией , а константа определяется условием нормировки:
где — полное число частиц.
Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми — Дирака и Бозе — Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа.
Адиабатический процесс
C помощью модели идеального газа можно предсказать изменение параметров состояния газа при адиабатическом процессе. Перепишем уравнение в виде:
Продифференцировав обе части, получаем:
Затем, если подставить в это уравнение значение работы и внутренней энергии газа, получим Уравнение Пуассона.
Квантовый идеальный газ
Понижение температуры и увеличение плотности газа может привести к ситуации, когда среднее расстояние между частицами становится соизмеримым с длиной волны де Бройля для этих частиц, что приводит к переходу от классического к квантовому идеальному газу (см. Вырожденный газ). В таком случае поведение газа зависит от спина частиц: в случае полуцелого спина (фермионы) действует статистика Ферми — Дирака (Ферми-газ), в случае целого спина (бозоны) — статистика Бозе — Эйнштейна (Бозе-газ).
Ферми-газ
Для фермионов действует принцип Паули, запрещающий двум тождественным фермионам находиться в одном квантовом состоянии. Вследствие этого при абсолютном нуле температуры импульсы частиц и, соответственно, давление и плотность энергии Ферми-газа отличны от нуля и пропорциональны числу частиц в единице объёма. Существует верхний предел энергии, который могут иметь частицы Ферми-газа при абсолютном нуле (Энергия Ферми ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом.
Особенностью Ферми-газов является крайне слабая зависимость давления от температуры: в нерелятивистском случае давление , в релятивистском — .
Примерами Ферми-газов являются электронный газ в металлах, сильнолегированных и вырожденных полупроводниках, вырожденный газ электронов в белых карликах и вырожденный газ нейтронов в нейтронных звёздах.
Бозе-газ
Распределение скоростей атомов рубидия вблизи абсолютного нуля.Слева — распределение до образования конденсата, в центре — после образования, справа — после испарения газообразной составляющей и появления чистого конденсатаТак как на бозоны могут быть строго тождественны друг другу[8][9] и, соответственно, принцип Паули на них не распространяется, то при снижении температуры Бозе-газа ниже некоторой температуры возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе — Эйнштейна. Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при давление Бозе-газа зависит только от температуры.Этот эффект в 1995 году наблюдался экспериментально, а в 2001 году авторам эксперимента была присуждена Нобелевская премия[10].
Примерами Бозе-газов являются различного рода газы квазичастиц (слабых возбуждений) в твёрдых телах и жидкостях, сверхтекучая компонента гелия II, конденсата Бозе — Эйнштейна куперовских электронных пар при сверхпроводимости. Примером ультрарелятивистского Бозе-газа является фотонный газ[8][9].
См. также
Примечания
- ↑ Кудрявцев, 1956, с. 185—186
- ↑ Gay-Lussac, J. L. Recherches sur la dilatation des gaz et des vapeurs // Annales de chimie. — 1802. — Vol. XLIII. — P. 137.
- ↑ Clapeyron, E. (1834). «Mémoire sur la puissance motrice de la chaleur». Journal de l’École Polytechnique XIV: 153–90. (фр.) Facsimile at the Bibliothèque nationale de France (pp. 153–90).
- ↑ Krönig, A. (1856). «Grundzüge einer Theorie der Gase». Annalen der Physik 99 (10): 315–22. DOI:10.1002/andp.18561751008. Bibcode: 1856AnP…175..315K. (нем.) Facsimile at the Bibliothèque nationale de France (pp. 315–22).
- ↑ Clausius, R. (1857). «Ueber die Art der Bewegung, welche wir Wärme nennen». Annalen der Physik und Chemie 176 (3): 353–79. DOI:10.1002/andp.18571760302. Bibcode: 1857AnP…176..353C. (нем.) Facsimile at the Bibliothèque nationale de France (pp. 353–79).
- ↑ Коган М. Н. Динамика разреженного газа (кинетическая теория. М., 1967)
- ↑ 1 2 Савельев, 2001, с. 24
- ↑ 1 2 Einstein A. (1924). «Quantentheorie des einatomigen idealen Gases». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse 1924: 261—267. (нем.)
- ↑ 1 2 Einstein A. (1925). «Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung». Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse 1925: 3—14. (нем.)
- ↑ Anderson, M. H.; Ensher, J. R.; Matthews, M. R.; Wieman, C. E.; Cornell, E. A. (1995). «Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor». Science 269: 198—201. DOI:10.1126/science.269.5221.198. PMID 17789847. (англ.)
Литература
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9
- П. С. Кудрявцев История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
- V.P.Maslov, Mathematical conception of the gas theory
ushakov.academic.ru
Что такое «идеальный газ» простыми словами?
На этом примере мы можем детально рассмотреть, как математические модели трансформируются в физические модели.
Прежде всего, идеальный газ — это математическая модель газа. И с математической точки зрения, идея очень проста: атомы (или молекулы) этого самого газа «не видят» друг друга. То есть каждая частица воспринимает сосуд как совершенно пустой. Такие частицы могут проходит друг сквозь друга. Из этого следует, например, что все частицы могут собраться в одной пространственной точке.
С другой стороны идеальный газ — это физический термин. А значит, нам надо понять, какая физика отвечает такой математической модели.
а) Итак, во-первых, чтобы атомы «не видели» друг друга надо чтобы между ними не было потенциальных сил взаимодействия, то есть сил зависящих от расстояния между частицами. В терминах энергии это требование звучит так: » потенциальная энергия взаимодействия частиц равна нулю». Такое строгое равенство нулю, это все еще математика, в физике мы можем смягчить это условие, сказав «потенциальная энергия взаимодействия частиц много меньше …». Чего? Энергию можно сравнивать только с энергией, а системе движущихся частиц наибольший вклад дает кинетическая энергия. И вот наше первое условие:
1) Потенциальная энергия взаимодействия частиц газа много меньше их кинетической энергии.
б) В математической модели молекулы представляются математическими точками, то есть без размера. В реальном мире такого требовать мы не можем. Как же нам сформулировать это условие физически? Зачем нам безразмерные молекулы? Для того чтобы они не сталкивались друг с другом. Мы не можем запретить соударение частиц ненулевого размера без ввода в систему сил отталкивания. Но силы отталкивания мы исключили первым пунктом. Тогда нам придется разрешить столкновения в системе, но с наложением 3 условий: редко, быстро и без потерь энергии. И вот еще 3 пункта:
2) Средняя длина свободного пробега частиц (то есть расстояние проходимое между двумя последовательными столкновениями) много больше их размера.
3) Время столкновения пренебрежимо мало.
4) Все столеновения происходят без потерь энергии.
Пункты 3) и 4) мы распространим и на соударение со стенками сосуда. Если все четыре требования выполнены, то мы можем считать наш газ идеальным.
в) Еще одна интересная деталь. Кое-что наши столкновения в систему все же вносят. А именно, изменения скоростей. Причем модуля и направления. Так что какое бы распределение скоростей не было в самом начале, после множества столкновений они уже будут распределены по Максвеллу. По этому, строго говоря, нам надо потребовать, чтобы уже изначально распределение скоростей было таким. Тогда наши столкновения не будут влиять на изначальную физику системы:
5) Частицы в системе имеют случайные скорости, распределенные по закону Максвелла.
В неявном виде мы уже потребовали применимость закон Ньютона в системе (для закона сохранения импульса, например):
6) В системе действуют законы Ньютона.
Последний пункт всегда подразумевается, так что его можно опустить. А предпоследний можно опустить, так как система сама придет к нему, если первые четыре пункта выполнены.
Но! Если вы будете моделировать идеальный газ на компьютере, например, и захотите сделать его математически идеальным, т.е. без столкновений, то вам необходим пункт 5)! Иначе вы не получите правильной физики. И наоборот, если вы будете моделировать физическую систему, т.е. в соотвествии с первыми четырьмя пунктами, то как я писала ранее, через какое-то время система сама придет к пункту 5).
thequestion.ru
