Оптика — Основные формулы
1. Фотометрия и светотехника
1.1 Поток излучения
Φ — поток излучения,
W — энергия излучения,
t — время прохождения энергии излучения.
1.2 Сила света
I — сила света,
Φ — поток излучения,
Ω — телесный угол, через который проходит поток излучения.
1.3 Освещенность
E — освещенность,
Φ — поток излучения,
σ — площадь, через которую проходит поток излучения.
1.4 Яркость источника света
L — яркость источника света,
I — сила света,
σ — площадь видимой светящейся поверхности.
1.5 Коэффициент поглощения
α — коэффициент поглощения,
Φα — световой поток, поглощенный телом,
Φi — световой поток, падающий на тело.
1.6 Коэффициент отражения
ρ — коэффициент отражения,
Φρ — световой поток, отраженный телом,
1.7 Коэффициент пропускания
τ — коэффициент пропускания,
Φτ — световой поток, пропущенный телом,
Φi — световой поток, падающий на тело.
2. Геометрическая оптика
2.1 Относительный показатель преломления
n — относительный показатель преломления для граничащих сред
n2 — абсолютный показатель преломления для второй среды,
n1 — абсолютный показатель преломления для первой среды.
2.2 Закон преломления света
i — угол отражения,
r — угол преломления,
n — относительный показатель преломления для граничащих сред.
2.3 Предельный угол полного внутреннего отражения
iпр — предельный угол полного внутреннего отражения,
n — относительный показатель преломления для граничащих сред.
2.4 Основная формула тонкой линзы
a — расстояние от источника света до линзы,
f — фокусное расстояние линзы.
2.5 Основная формула сферического зеркала
a — расстояние от источника света до зеркала,
a’ — расстояние от зеркала до изображения источника света,
R — радиус кривизны зеркала,
f — фокусное расстояние зеркала.
2.6 Линейное увеличение
β — линейное увеличение линзы или зеркала,
h — высота источника света,
h’ — высота изображения источника света,
a — расстояние от источника света до линзы или зеркала,
a’ — расстояние от линзы или зеркала до изображения источника света.
2.7 Угловое увеличение
γ — угловое увеличение линзы или зеркала,
β — линейное увеличение линзы или зеркала.
2.8 Оптическая сила линзы
D — оптическая сила линзы,
f — фокусное расстояние.
2.9 Светосила линзы
E — светосила линзы,
f — фокусное расстояние.
3. Оптические приборы
3.1 Увеличение лупы
N — увеличение лупы,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние лупы.
3.2 Увеличение микроскопа
N — увеличение микроскопа,
N1 — увеличение окуляра микроскопа,
N2 — увеличение объектива микроскопа,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние системы линз микроскопа: окуляра и объектива.
3.3 Увеличение зрительной (подзорной) трубы
N — увеличение зрительной (подзорной) трубы,
f1 — фокусное расстояние объектива,
f2 — фокусное расстояние окуляра.
fizikazadachi.ru
| № п/п | Наименование параметра | Формула | Обозначения | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.1 | Формула тонкой линзы | a ― расстояние от оптического центра линзы до предмета; b ― расстояние от оптического центра линзы до изображения; f ― фокусное расстояние линзы | |||||||||||||||||||||||||
| 5.2 | Закон преломления | n1 — показатель преломления среды, из которой свет падает на границу раздела; α — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности; n2 — показатель преломления среды, в которую свет попадает, пройдя границу раздела; β — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности | |||||||||||||||||||||||||
| 5.3 | Разность хода лучей, отраженных от тонкой пленки | если n < n1; если n > n1 | n — показатель преломления пленки; n1 — показатель преломления среды; d — толщина пленки; φ — угол падения; слагаемое λ/2 учитывает, что при отражении луча от оптически более плотной среды фаза изменяется на 180° | ||||||||||||||||||||||||
| 5.4 | Радиус k-той зоны Френеля для сферической волны | а ― расстояние диафрагмы с круглым отверстием от точечного источника света, b ― расстояние диафрагмы от экрана, k ― номер зоны Френеля, λ ― длина волны | |||||||||||||||||||||||||
| 5.5 | Радиус k-той зоны Френеля для плоской волны | b ― расстояние диафрагмы от экрана, k ― номер зоны Френеля, λ ― длина волны | |||||||||||||||||||||||||
| 5.6 | Условие главных максимумов интенсивности при дифракции на дифракционной решетке Если свет падает на решётку под углом θ | d ― постоянная решетки; φ ― угол, под которым виден дифракционный максимум; λ ― длина волны; m ― порядок или порядковый номер максимума или порядок спектра | |||||||||||||||||||||||||
| 5.7 | Разрешающая сила дифракционной решетки | Δλ ― наименьшая разность длин волн двух соседних спектральных линий (λ и λ+Δλ), при которой эти линии могут быть видны раздельно в спектре, полученной посредством данной решетки, N ― число штрихов решетки; k ― порядковый номер дифракционного максимума | |||||||||||||||||||||||||
| 5.8 | Угловая дисперсия дифракционной решетки | k ― порядковый номер спектра, d ― постоянная решетки, φ ― угол отклонения луча, λ ― длина волны света | |||||||||||||||||||||||||
| 5.9 | Условие минимумов интенсивности при дифракции на щели | a ― ширина щели, φ ― угол, под которым виден дифракционный минимум, k ― порядок спектра, λ ― длина волны | |||||||||||||||||||||||||
| 5.10 | Условие максимумов интенсивности при дифракции на щели | В центре дифракционной картины также максимум | a ― ширина щели, φ ― угол, под которым виден дифракционный максимум, k ― порядок спектра, λ ― длина волны | ||||||||||||||||||||||||
| 5.11 | Условие главных дифракционных минимумов при дифракции на нескольких щелях Условие главных дифракционных максимумов Условие дополнительных дифракционных минимумов | a ― ширина щели, φ ― угол, под которым виден дифракционный минимум, k ― порядок спектра, λ ― длина волны | |||||||||||||||||||||||||
| 5.12 | Ширина интерференционных полос на экране при дифракции на двух щелях | λ ― длина волны, L ― расстояние от щелей до экрана, d ― расстояние между щелями | |||||||||||||||||||||||||
| 5.13 | Формула Вульфа-Брэгга | d ― расстояние между атомными плоскостями кристалла, θ ― угол скольжения (угол между направлением пучка рентгеновских лучей и гранью кристалла), определяющий направление, в котором имеет место зеркальное отражение излучений (дифракционный максимум), k ― порядок максимума, λ ― длина волны. | |||||||||||||||||||||||||
| 5.14 | Закон Малюса | I ― интенсивность плоскополяризованного света, прошедшего через анализатор; I0 ― интенсивность плоскополяризованного света, падающего на анализатор; α ― угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора. | |||||||||||||||||||||||||
| 5.15 | Закон Брюстера | iБ ― угол падения, при котором отраженная световая волна полностью поляризована; n21 ― относительный показатель преломления. | |||||||||||||||||||||||||
| 5.16 | Энергия фотона | h = 6,63∙10−34 Дж∙с ― постоянная Планка, с = 3∙108 м/с ― скорость света в вакууме, λ ― длина волны | |||||||||||||||||||||||||
| 5.17 | Работа выхода из металла | h = 6,63∙10−34 Дж∙с ― постоянная Планка, с = 3∙108 м/с ― скорость света в вакууме, λ0 ― длина волны, соответствующая красной границе фотоэффекта | |||||||||||||||||||||||||
| 5.18 | Формула Эйнштейна для фотоэффекта | или | m ― масса электрона, А ― работа выхода; v ― скорость электрона, рэ ― импульс электрона | ||||||||||||||||||||||||
| 5.19 | «Красная граница» фотоэффекта для данного металла | λ0 ― максимальная длина волны излучения; ν0 — минимальная частота, при которой фотоэффект еще возможен | |||||||||||||||||||||||||
| 5.20 | Масса фотона | h = 6,63∙10−34 Дж∙с ― постоянная Планка, с ― скорость света в вакууме, hν ― энергия фотона | |||||||||||||||||||||||||
| 5.21 | Импульс фотона | h = 6,63∙10−34 Дж∙с ― постоянная Планка, λ ― длина волны | |||||||||||||||||||||||||
| 5.22 | Радиус светлых колец Ньютона в отраженном свете | вывод формулы | k ― номер кольца, λ ― длина волны падающего света, R ― радиус кривизны линзы, n ― показатель преломления среды, заполняющей пространство между пластинкой и линзой | ||||||||||||||||||||||||
| 5.23 | Расстояние между двумя соседними максимумами (или минимумами) в опыте Юнга | Главный максимум, соответствующий m = 0, проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д. Между минимумами m-го порядка находится 2m интервалов Δx, т. е. | |||||||||||||||||||||||||
| 5.24 | Зеркала Френеля Ширина b полос интерференции на экране | l ― расстояние от изображения источника света до экрана, d ― расстояние между двумя изображениями источника света, λ ― длина волны света | |||||||||||||||||||||||||
| 5.25 | Сериальная формула, определяющая длину волны λ света, излучаемого или поглощаемого атомом водорода при переходе электрона с одной орбиты на другую Энергия фотона Длины волн спектральных линий водородоподобных атомов всех серий определяются формулой |
| R = 1,097∙107 м−1 ― постоянная Ридберга; с ― скорость света в вакууме; Z ― число протонов в ядре | ||||||||||||||||||||||||
| 5.26 | Радиус стационарной орбиты с номером n | ε0 ― электрическая постоянная; h ― постоянная Планка; m ― масса электрона; e ― заряд электрона | |||||||||||||||||||||||||
| 5.27 | Изменение длины волны Δλ фотона при рассеянии его на электроне на угол θ (эффект Комптона) | m ― масса электрона отдачи; λ и λ’ ― длины волн; c ― скорость света в вакууме; h ― постоянная Планка | |||||||||||||||||||||||||
| 5.28 | Длина волны де Бройля для движущейся частицы а) в классическом приближении (v << с; р = m0v) в релятивистском случае (скорость v частицы сравнима со скоростью с света в вакууме | h ― постоянная Планка, p ― импульс частицы, m0 ― масса покоя частицы, T ― кинетическая энергия частицы | |||||||||||||||||||||||||
| 5.29 | Давление, производимое светом при нормальном падении | Ее ― облученность поверхности; с ― скорость света в вакууме; w ― объемная плотность энергии излучения; ρ ― коэффициент отражения | |||||||||||||||||||||||||
| 5.30 | Закон Стефана-Больцмана | Re ― излучательная способность абсолютно черного тела; Т ― термодинамическая температура; σ ― постоянная Стефана-Больцмана (σ = 5,67∙10−8 Вт/(м2∙К4)) | |||||||||||||||||||||||||
| 5.31 | Излучательная (лучеиспускательная) способность серого тела | аТ ― коэффициент черноты (коэффициент излучения) серого тела; Т ― термодинамическая температура; σ ― постоянная Стефана-Больцмана (σ = 5,67∙10−8 Вт/(м2∙К4)) | |||||||||||||||||||||||||
| 5.32 | Закон смещения Вина | λm ― длина волны, на которую приходится максимум энергии излучения; b ― постоянная закона смещения Вина (b = 2,90∙10−3 м∙К) | |||||||||||||||||||||||||
| 5.33 | Формула Планка | ― спектральная плотность излучательности (энергетической светимости) абсолютно черного тела; λ ― длина волны; с ― скорость света в вакууме; k ― постоянная Больцмана; Т ― термодинамическая температура; h ― постоянная Планка | |||||||||||||||||||||||||
| 5.34 | Зависимость максимальной спектральной плотности энергетической светимости черного тела от температуры | С ― постоянная [С = 1,30∙10−5 Вт/(м3∙К5)], T ― термодинамическая температура | |||||||||||||||||||||||||
| 5.35 | Формула Рэлея-Джинса для спектральной плотности энергетической светимости черного тела | ν ― частота излучения, с ― скорость света в вакууме, k ― постоянная Больцмана, T ― термодинамическая температура | |||||||||||||||||||||||||
| 5.36 | Связь радиационной Тp и истинной Т температур | аТ ― поглощательная способность серого тела | |||||||||||||||||||||||||
| 5.37 | Эффект Доплера в релятивистском случае | ν ― частота электромагнитного излучения, воспринимаемого наблюдателем; ν0 ― собственная частота электромагнитного излучения, испускаемого неподвижным источником; β = v/c ― скорость источника электромагнитного излучения относительно наблюдателя; с ― скорость распространения электромагнитного излучения в вакууме; θ ― угол между вектором v и направлением наблюдения, измеренный в системе отсчета, связанной с наблюдателем | |||||||||||||||||||||||||
| 5.38 | Угол поворота φ плоскости поляризации оптически активными веществами: в твердых телах в чистых жидкостях в растворах | φ = αdφ = [α]ρdφ = [α]Сd | α — постоянная вращения; d — длина пути, пройденного светом в оптически активном веществе; [α] — удельное вращение; ρ — плотность жидкости; С — массовая концентрация оптически активного вещества в растворе | ||||||||||||||||||||||||
| 5.39 | Давление света | Ее ― облученность поверхности; с ― скорость электромагнитного излучения в вакууме; ρ ― коэффициент отражения | |||||||||||||||||||||||||
| 5.40 | Сила света точечного источника | Единица измерения силы света ― кандела (кд) | Ф ― световой поток (энергия световых волн, переносимая в единицу времени) | ||||||||||||||||||||||||
| 5.41 | Телесный угол ― отношение площади ΔS поверхности шарового сегмента к квадрату радиуса r сферы | Единица измерения силы света ― стерадиан (стер) | |||||||||||||||||||||||||
| 5.42 | Световой поток | Единица измерения светового потока ― люмен (лм) | I ― cила света точечного источника; ΔΩ ― телесный угол | ||||||||||||||||||||||||
| 5.43 | Яркость источника света ― отношение силы света I источника в определенном направлении к проекции S светящейся поверхности на площадь, перпендикулярную к этому направлению | Единица яркости ― нит (нт) | |||||||||||||||||||||||||
| 5.44 | Освещенность ― световой поток, падающий на единицу площади освещаемой поверхности | ||||||||||||||||||||||||||
| 5.45 | Закон освещенности от точечного источника света | Единица освещенности ― 1 лк (люкс) | I ― cила света точечного источника; r ― расстояние от источника света до освещаемой поверхности; α ― угол падения света |
reshenie-zadach.com.ua
Оптика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Световые волны
К оглавлению…
Свет – это электромагнитные волны, длины волн которых лежат для среднего глаза человека в пределах от 400 до 760 нм. В этих пределах свет называется видимым. Свет с наибольшей длиной волны кажется нам красным, а с наименьшей – фиолетовым. Запомнить чередование цветов спектра легко с помощью поговорки «Каждый Охотник Желает Знать, Где Сидит Фазан». Первые буквы слов поговорки соответствуют первым буквам основных цветов спектра в порядке убывания длины волны (и соответственно возрастания частоты): «Красный – Оранжевый – Желтый – Зеленый – Голубой – Синий – Ф
Электромагнитные волны (и, в частности, световые волны, или просто свет) – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Световые волны, как и любые другие электромагнитные волны, распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:
где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м. Скорость света в вакууме (где ε = μ = 1) постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорость света в вакууме является одной из фундаментальных физических постоянных. Если свет распространяется в какой-либо среде, то скорость его распространения также выражается следующим соотношением:
где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:
- Свет переносит энергию. При распространении световых волн возникает поток электромагнитной энергии.
- Световые волны испускаются в виде отдельных квантов электромагнитного излучения (фотонов) атомами или молекулами.
Кроме света существуют и другие виды электромагнитных волн. Далее они перечислены по уменьшению длины волны (и соответственно, по возрастанию частоты):
- Радиоволны;
- Инфракрасное излучение;
- Видимый свет;
- Ультрафиолетовое излучение;
- Рентгеновское излучение;
- Гамма-излучение.
Интерференция
К оглавлению…
Интерференция – одно из ярких проявлений волновой природы света. Оно связано с перераспределением световой энергии в пространстве при наложении так называемых когерентных волн, то есть волн, имеющих одинаковые частоты и постоянную разность фаз. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра.
Для расчета интерференции используется понятие оптической длины пути. Пусть свет прошел расстояние L в среде с показанием преломления n. Тогда его оптическая длина пути рассчитывается по формуле:
Для интерференции необходимо наложение хотя бы двух лучей. Для них вычисляется оптическая разность хода (разность оптических длин) по следующей формуле:
Именно эта величина и определяет, что получится при интерференции: минимум или максимум. Запомните следующее: интерференционный максимум (светлая полоса) наблюдается в тех точках пространства, в которых выполняется следующее условие:
Разность фаз колебаний при этом составляет:
При m = 0 наблюдается максимум нулевого порядка, при m = ±1 максимум первого порядка и так далее. Интерференционный минимум (темная полоса) наблюдается при выполнении следующего условия:
Разность фаз колебаний при этом составляет:
При первом нечетном числе (единица) будет минимум первого порядка, при втором (тройка) минимум второго порядка и т.д. Минимума нулевого порядка не бывает.
Дифракция. Дифракционная решетка
К оглавлению…
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий, размеры которых сопоставимы с длиной волны света (огибание светом препятствий). Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени (то есть быть там, где его быть не должно). Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50–100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки.
При нормальном падении света на дифракционную решетку в некоторых направлениях (помимо того, в котором изначально падал свет) наблюдаются максимумы. Для того, чтобы наблюдался интерференционный максимум, должно выполняться следующее условие:
Законы геометрической оптики
К оглавлению…
Геометрическая оптика – это раздел физики, в котором не учитываются волновые свойства света. Основные законы геометрической оптики были известны задолго до установления физической природы света.
Оптически однородная среда — это среда, во всем объеме которой показатель преломления остаётся неизменным.
Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Этот закон приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны (в этом случае наблюдается дифракция).
На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде.
Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α. Заметьте, что все углы в оптике измеряются от перпендикуляра к границе раздела двух сред.
Закон преломления света (закон Снеллиуса): падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред, и определяется выражением:
Закон преломления был экспериментально установлен голландским ученым В.Снеллиусом в 1621 году. Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.
Среду с большим значением абсолютного показателя называют оптически более плотной, а с меньшим – менее плотной. При переходе из менее плотной среды в более плотную луч «прижимается» к перпендикуляру, а при переходе из более плотной в менее плотную – «удаляется» от перпендикуляра. Единственный случай, когда луч не преломляется, это если угол падения равен 0 (то есть лучи перпендикулярны границе раздела сред).
При переходе света из оптически более плотной среды в оптически менее плотную n2 < n1 (например, из стекла в воздух) можно наблюдать явление полного внутреннего отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол αпр, который называется предельным углом полного внутреннего отражения. Для угла падения α = αпр, sinβ = 1, так как β = 90°, это значит, что преломленный луч идет вдоль самой границы раздела, при этом, согласно закону Снеллиуса, выполняется следующее условие:
Как только угол падения становиться больше предельного, то преломленный луч уже не просто идет вдоль границы, а он и вовсе не появляется, так как его синус теперь уж должен быть больше единицы, а такого не может быть.
Линзы
К оглавлению…
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
Линзы бывают собирающими и рассеивающими. Если показатель преломления линзы больше, чем окружающей среды, то собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше. Если показатель преломления линзы меньше, чем окружающей среды, то всё наоборот.
Прямая, проходящая через центры кривизны сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз можно приближенно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, симметрично расположенных относительно линзы на главной оптической оси. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначается той же буквой F.
Правила построения хода луча в линзах
К оглавлению…
Формула линзы
К оглавлению…
Основное свойство линз – способность давать изображения предметов. Изображение – это точка пространства, где пересекаются лучи (или их продолжения), испущенные источником после преломления в линзе. Изображения бывают прямыми и перевернутыми, действительными (пересекаются сами лучи) и мнимыми (пересекаются продолжения лучей), увеличенными и уменьшенными.
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей.
Для простоты можно запомнить, что изображение точки будет точкой. Изображение точки, лежащей на главной оптической оси, лежит на главной оптической оси. Изображение отрезка – отрезок. Если отрезок перпендикулярен главной оптической оси, то его изображение перпендикулярно главной оптической оси. А вот если отрезок наклонен к главной оптической оси под некоторым углом, то его изображение будет наклонено уже под некоторым другим углом.
Изображения можно также рассчитать с помощью формулы тонкой линзы. Если кратчайшее расстояние от предмета до линзы обозначить через d, а кратчайшее расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единица измерения оптической силы является 1 диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0. Оптическая сила рассеивающей линзы также отрицательна.
Величины d и f также подчиняются определенному правилу знаков: f > 0 – для действительных изображений; f < 0 – для мнимых изображений. Перед d знак «–» ставится только в том случае, когда на линзу падает сходящийся пучок лучей. Тогда их мысленно продлевают до пересечения за линзой, помещают туда воображаемый источник света, и определяют для него расстояние d.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета. Для линейного увеличения линзы существует формула:
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета и так далее.
educon.by
Оптика волновая (формулы) | База Знаний AWMD Group Wiki
Связь частоты и длины волны света Править
$ \lambda=\frac{V}{\nu} $
Оптическая разность хода волн Править
$ \triangle n=\sum_{1}{l_{i}n_{i}}-\sum_{2}{l_{i}n_{i}}\pm \frac{\lambda_{0}}{2} $
Условия максимумов и минимумов Править
$ \triangle n=(2k+ 1)\frac{\lambda_{0}}{2} $
$ \triangle n= 2k\frac{\lambda_{0}}{2} $
Ширина полосы в опыте Юнга Править
Условия темных и светлых колец Ньютона Править
$ \triangle n=\frac{r^{2}}{R}\pm \frac{\lambda_{0}}{2} $
Оптическая разность хода волн при отражении от тонкой пленки Править
- При угле падения 90
$ \triangle n=2d\cdot n $
- При другом угле падения
$ \triangle n=2dn\sqrt{1-\frac{n_{1}^{2}}{n^{2}}sin(\alpha)}+ (*) $
Ширина полосы при интерференции на клине Править
$ \triangle n=2dn\sqrt{n^{2}-n_{1}^{2}sin^{2}(\alpha)} \pm (*) $
Число зон Френеля при дифракции на круглом отверстии (экране) Править
- Точечный источник света
$ n=\frac{R^{2}(r_{0}+ b)}{r_{0}b\lambda_{0}} $
- Не точечный источник света
$ n=\frac{R^{2}}{b\lambda_{0}} $
Условия минимумов при дифракции на щели Править
$ b\cdot sin(\varphi )=k\lambda_{0} $
Условие главных максимумов при дифракции на щели Править
$ k=\frac{b\cdot sin(\varphi )}{\lambda} $
Дисперсии решетки и ее разрешающая способность Править
$ D=\frac{d\varphi }{d\lambda}=\frac{k}{dcos(\varphi )} $
$ k $ — порядок спектра
- Разрешающая способность
$ R=\frac{\lambda}{\triangle \lambda_{min}}=kn $
Разрешающая способность оптических приборов Править
$ R=\frac{1}{\Psi_{min}} $
$ \Psi _{min}=1.22\frac{\lambda}{D} $
Степень поляризации Править
$ P=\frac{I_{lin.polariz}}{I_{chast.polariz}}=\frac{I_{max}-I_{min}}{I_{max}+ I_{min}} $
Интенсивность света на выходе из поляризатора. Править
$ I=\tau I_{0}cos^{2}(\alpha) $
$ \tau $ — коэффициент пропускания
- При падении естественного света
$ I=\frac{1}{2}\tau I_{est} $
ru.awmdkb.wikia.com
Формулы — Оптика
Основные формулы
• Радиус k—ой.зоны Френеля:
для сферической волны
,
где а —расстояние диафрагмы с круглым отверстием от точечного источника света;b —расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины;k —номер зоны Френеля; λ —длина волны;
для плоской волны
.
• Дифракция света на одной щели при нормальном падении лучей. Условие минимумов интенсивности света
,k=1,2,3,…,
где а —ширина щели; φ— угол дифракции;k —номер минимума;
λ —длина волны.
Условие максимумов интенсивности света
,k=l, 2, 3,…,
где φ’ — приближенное значение угла дифракции.
• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности
dsinφ=±kλ,k=0,1,2,3,…,
где d— период (постоянная) решетки;k —номер главного максимума; φ —угол между нормалью к поверхности решетки и направлением дифрагированных волн.
• Разрешающая сила дифракционной решетки
,
где Δλ— наименьшая разность длин волн двух соседних спектральных линий (λ и λ+Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;N —число штрихов решетки;k —порядковый номер дифракционного максимума.
• Угловая дисперсия дифракционной решетки
,
линейная дисперсия дифракционной решетки
.
Для малых углов дифракции
,
где f— главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны.
• Разрешающая сила объектива телескопа
,
где β — наименьшее угловое расстояние между двумя светлыми точками, при котором изображения этих точек в фокальной плоскости объектива могут быть видны раздельно; D —диаметр объектива; λ —длина волны.
• формула Вульфа — Брэгга
2dsin=kλ,
где d —расстояние между атомными плоскостями кристалла;— угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла), определяющий направление, в котором имеет место зеркальное отражение лучей (дифракционный максимум).
studfiles.net
Законы геометрической оптики — ГЕОМЕТРИЧЕСКАЯ ОПТИКА — ФИЗИКА
ФИЗИКА
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
Законы геометрической оптики
Закон отражения
α = γ
α — угол падения;
γ — угол отражения;
— перпендикуляр к границе раздела двух сред.
Закон преломления
β — угол преломления.
Относительный показатель преломления
n21 — относительный показатель преломления;
υ1,υ2— скорость света в данных средах, [м/c].
Абсолютный показатель преломления
n21 — абсолютный показатель преломления;
с — скорость света в вакууме, c = 2,998 108м/c.
Оптическая плотность среды.
Луч из среды с большей оптической плотностью переходит в среду с меньшей оптической плотностью
n1, n2 — показатели преломления среды каждого.
Оптическая плотность среды.
Луч из среды с меньшей оптической плотностью переходит в среду с большей оптической плотностью
Предельный угол полного отражения
αв — угол падения, при котором наступает полное отражение света.
Построение изображения в плоском зеркале
Изображение предмета в плоском зеркале является мнимым
Построение изображения в вогнутом зеркале
Построение изображения в выпуклом зеркале
Прохождение света сквозь плоскопараллельную пластинку
α — смещение луча.
Прохождение света сквозь треугольную призму
Если нет полного отражения.
При полном отражении. Применяется в перископе
При полном отражении. Применяется в отражателях
При полном отражении. Применяется в биноклях
Собирательная линза
F > 0, d > 0
Рассеивающую линза
F < 0, d > 0
Формула линзы
d — расстояние от линзы до источника, [м];
f — расстояние от линзы до изображения, [м];
F — фокусное расстояние, [м].
Главная оптическая ось
Оптический центр
Побочная оптическая ось
Фокус
Фокусное расстояние
Фокальная плоскость
Увеличение линзы
Г — увеличение линзы;
Н — линейный размер изображения, [м];
h — линейный размер предмета, [м].
Оптическая сила линзы
D — оптическая сила линзы, [дптр].
Изображения действительное f > 0.
Изображения мнимое f < 0.
Луч, проходящий через оптический центр
Луч, параллельный главной оптической оси
Луч, проходящий через фокус
Изображение точки, не лежащей на главной оптической оси
Ход пучка параллельных лучей, что идут вдоль побочной оптической оси
schooled.ru
Формулы геометрической оптики для «чайников»
Все знают или по крайней мере слышали о том, что свет имеет свойство преломляться и отражаться. Но только формулы геометрической и волновой оптики могут объяснить, как, а точнее по какому именно признаку это происходит. И все данное учение основывается на понятии «луча», которое ввел еще Евклид за три века до нашей эры. Так что же такое луч, если говорить научным языком?
Луч — это прямая, вдоль которой движутся световые волны. Как, зачем — на эти вопросы отвечают формулы геометрической оптики, которая является частью волновой оптики. Последняя, как можно было бы предположить, рассматривает лучи как волны.
Формулы геометрической оптики
Закон прямолинейного распространения: луч в однотипной среде имеет свойство распространяться прямолинейно. То есть свет двигается по кратчайшему пути, который существует между двумя точками. Можно даже сказать, что световой луч стремится сэкономить себе время. Этим законом объясняются явления тени и полутени.

К примеру, если источник света сам по себе маленького размера или же находится на таком большом расстояние, что его размеры можно проигнорировать, то световой луч образует четкие тени. Но если источник света большого размера или же находится на очень близком расстоянии, то световой луч образует нечеткие тени и полутени.
Закон независимого распространения
Световые лучи имеют свойство распространяться вне зависимости друг от друга. То есть они никак не повлияют друг на друга, если будут пересекаться или проходить друг через друга в какой-нибудь однородной среде. Лучи будто бы не подозревают о существовании других лучей.
Закон отражения
Представим, что человек направил лазерную указку на зеркало. Разумеется, луч отразится от зеркала и будет распространяться уже в другой среде. Угол между перпендикуляром к зеркалу и первым лучом зовется углом падения, угол между перпендикуляром к зеркалу и вторым лучом — углом отражения. Эти углы равны.
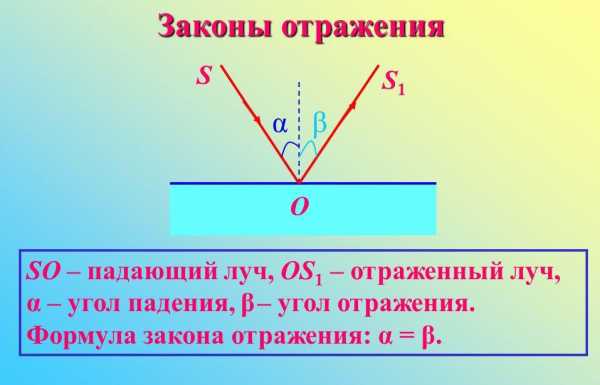
Формулы геометрической оптики раскрывают многие ситуации, о которых никто даже не задумывается. Например, закон отражения объясняет, почему мы можем видеть себя в «прямом» зеркале в точности такими же, какие мы есть, и почему его искривленная поверхность создает иной образ.
Формула:
a — угол падения, b — угол отражения.
a = b
Закон преломления
Луч падения, луч преломления и перпендикуляр к зеркалу расположены в одной плоскости. Если синус падающего угла поделить на синус преломляющегося угла, то получится величина n, которая является постоянной для обеих сред.
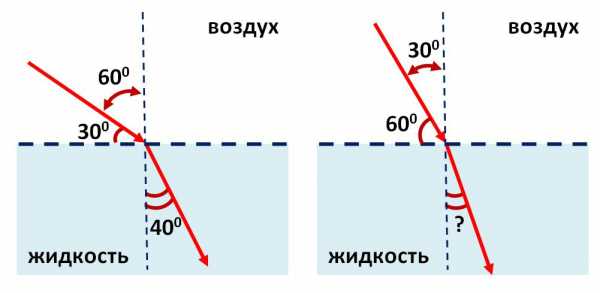
n показывает, под каким углом луч из первой среды переходит во вторую, и как соотносятся составы этих сред.
Формула:
i — падающий угол. r — преломляющийся угол. n21 — показатель преломления.
sin i/sin r = n2/n1 = n21

Закон обратимости света
О чем гласит закон обратимости света? Если луч распространяется по определенно выстроенной траектории в одном направлении, то и в противоположном направлении он повторит тот же маршрут.
Итоги
Формулы геометрической оптики в несколько упрощенном виде объясняют, как работает луч света. В этом нет ничего сложного. Да, формулы и законы геометрической оптики пренебрегают некоторыми свойствами вселенной, но нельзя недооценивать их важность для науки.
fb.ru
