Формулы по математике сложные – Математические формулы

Величайшая формула математики | Математика, которая мне нравится

Без дальнейших церемоний, вот она:

   

Ее обычно называют тождеством Эйлера в честь великого швейцарского математика Леонарда Эйлера (1707 — 1783). Ее можно увидеть на футболках и кофейных кружках, и несколько опросов среди математиков и физиков удостоили ее такого названия, как “величайшее уравнение” (Crease, Robert P., “The greatest equations ever”).

Ощущение красоты и элегантности тождества происходит из того, что оно сочетает в простой форме пять самых важных чисел математических констант: — основание натурального логарифма, — квадратный корень из и . Глядя на него внимательно, большинство людей задумываются о показателе: что значит возвести число в мнимую степень? Терпение, терпение, мы до этого доберемся.

Чтобы объяснить, откуда возникает эта формула, мы должны сначала получить более общую формулу, найденную Эйлером, а затем показать, что наше равенство является всего лишь частным случаем этой формулы. Общая формула удивительна сама по себе и имеет множество замечательных приложений в математике, физике и технике.

Первый шаг в нашем путешествии — понять, что большинство функций в математике может быть представлено в виде бесконечной суммы по степеням аргумента. Это пример:

   

Здесь измеряется в радианах, а не в градусах. Мы можем получить хорошее приближение для конкретного значения , используя только несколько первых членов ряда. Это пример ряда Тейлора, и довольно легко вывести эту формулу, используя математический анализ. Здесь я не предполагаю знание математического анализа, поэтому прошу читателя принять ее на веру.

Соответствующая формула для косинуса:

   

Наконец,

   

Число — константа, равная , и Эйлер был первым, кто признал его фундаментальное значение в математике и вывел последнюю формулу (две предыдущие были найдены Исааком Ньютоном). О числе написаны книги (например, Maor, E. (1994). e, the story of a number. Princeton University Press), можно также прочитать о нем здесь.

Примерно в 1740 году Эйлер посмотрел на эти три формулы, расположенные приблизительно так, как мы их здесь видим. Сразу видно, что каждое слагаемое в третьей формуле также появляется в любой предыдущей. Тем не менее, половина членов в первых равенствах являются отрицательными, в то время как каждый член в последнем положителен. Большинство людей так бы это и оставили, но Эйлер увидел во всем этом закономерность. Он первый сложил первые две формулы:

   

Обратите внимание на последовательность знаков в этом ряду: , она повторяется группами по 4. Эйлер заметил, что эта же последовательность знаков получается, когда мы возводим мнимую единицу в целые степени:

   

Это означало, что можно заменить в последней формуле на и получить:

   

Теперь знаки соответствуют знакам в предыдущей формуле, и новый ряд совпадает с предыдущим, за исключением того, что члены разложения умножаются на . То есть получаем в точности

   

Это удивительный и таинственный результат, он свидетельствует о существовании тесной связи между числом и синусами и косинусами в тригонометрии, хотя было известно только из задач, не связанных с геометрией или треугольниками. Кроме ее элегантности и странности, однако, было бы трудно переоценить важность этой формулы в математике, которая увеличивалась с момента ее открытия. Она появляется везде, и не так давно вышла книга примерно в 400 страниц (Nahin P. Dr. Euler’s Fabulous Formula, 2006), посвященная описанию некоторых приложений этой формулы.

Обратите внимание, что старый вопрос о мнимых показателях в настоящее время решен: для возведения в мнимую степень просто поставьте мнимое число в формулу Эйлера. Если основание – число, отличное от , требуется только ее незначительная модификация.

Теперь вернемся к волшебному равенству. Мы можем подставить в него любое вещественное число , и в результате получим некоторое комплексное число. Один возможный выбор для — это . Вспомним из тригонометрии, что радиан — это 180 градусов. Косинус 180 градусов равен , а синус равен .

Поэтому

   

, или

   

Все это дает понятие о мощи и творческих способностях Леонарда Эйлера, и о том, почему его иногда называют выдающимся умом восемнадцатого века. Я буду еще писать о нем и некоторых его результатах в серии Euler’s Greatest Hits.

Перевод статьи Larry Phillips, The Greatest Formula in Mathematics, http://brightstartutors.com/blog/2010/01/29/the-greatest-formula-in-mathematics.

hijos.ru

Все формулы по математике — Формулы под рукой

Не решается задачка? Наш сайт поможет тебе в учебе, подготовке к сложным экзаменам, контрольным, олимпиадам, сессиям, ЕГЭ.

ФОРМУЛЫ ПО АЛГЕБРЕ

ФОРМУЛЫ ПО ГЕОМЕТРИИ

ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ

Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования. На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели. Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!

Такие примеры вдохновляют, вселяют уверенность, что и каждый из нас может с таким же успехом освежить «хорошо забытое». А там и новый вектор развития появится.

Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!

Быстрее, выше, сильнее!

Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!

Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.

На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».

megaformula.ru

ТОП-50 Важнейших формул по математике — Математика — Теория, тесты, формулы и задачи

Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены 50 важнейших формул по математике.

 

Изучать ТОП-50 Важнейших формул по математике онлайн:

 

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.

 

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

educon.by

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Факт 1.
\(\bullet\) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.

Смежные углы: \(\angle AOB\) и \(\angle BOC\).
Теорема: Сумма смежных углов равна \(180^\circ\): \(\angle AOB+\angle BOC=180^\circ\).

 

Факт 2.
\(\bullet\) Вертикальные углы — два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).

Вертикальные углы: \(\angle 1\) и \(\angle 2\), \(\angle 3\) и \(\angle 4\).
Теорема: Вертикальные углы равны: \(\angle 1=\angle 2\) и \(\angle 3=\angle 4\).

 

Факт 3.
\(\bullet\) Сумма углов \(\angle A, \angle B, \angle C\) треугольника \(ABC\) равна \(180^\circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.

 

Факт 4.
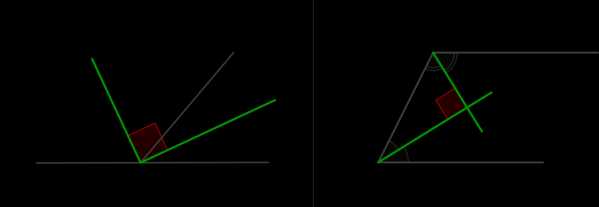
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

 

Факт 5.
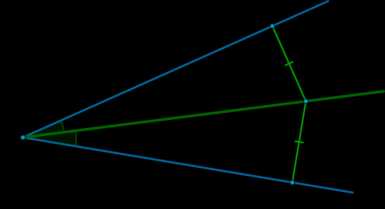
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

 

Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

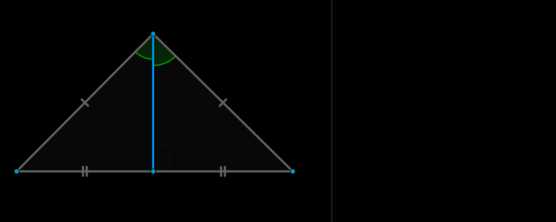
Второе свойство равнобедренного треугольника: углы при основании равны.

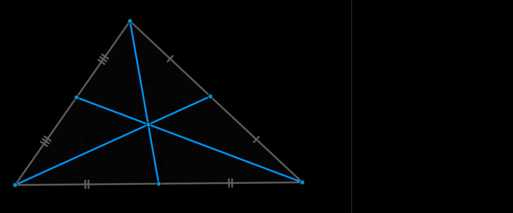
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

 

Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

 

Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.

 

Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

 

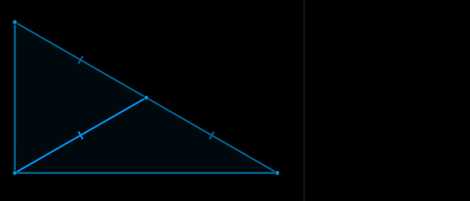
Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

 

Факт 11.
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

shkolkovo.net

Формулы сокращенного умножения: таблица, примеры использования

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

 

Формулы сокращенного умножения. Таблица

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a+b2=a2+2ab+b2
2. формула квадрата разности: a-b2=a2-2ab+b2
3. формула куба суммы: a+b3=a3+3a2b+3ab2+b3
4. формула куба разности: a-b3=a3-3a2b+3ab2-b3
5. формула разности квадратов: a2-b2=a-ba+b
6. формула суммы кубов: a3+b3=a+ba2-ab+b2
7. формула разности кубов: a3-b3=a-ba2+ab+b2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы. 

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умноже

www.zaochnik.com

Что такое формулы и как их понимать? – boeffblog.ru

Изначально, формулы были придуманы математиками для того, чтобы описать простые физические явления. Например формула скорости: скорость = путь/время. Эта формула говорит о том, что если двигаться с одинаковой скоростью, то за определенное время мы пройдем определенное расстояние. То есть она показывает связь между двумя изменяющимися величинами: путь и время. Если же одно и то же расстояние два человека пройдут с разной скоростью, то они потратят на это разное время, и первым финиширует тот, кто шел с большей скоростью.

Таким образом, формулы нужны для более короткой записи (математическими символами или буквами) взаимосвязей между некоторыми величинами (смотрите пример в статье).

Решение заданий с формулами обычно подразумевает нахождение какой-либо величины, зная остальные величины входящие в формулу.

Например: 

Закон Ома выражается формулой: U = I•R, где U – напряжение в Вольтах, I – сила тока в Амперах, R – сопротивление в Омах. Зная, что сила тока равна 2 А, а сопротивление равно 10 Ом, найдите напряжение. 

Все, что требуется в данном задании – подставить вместо букв их значения и посчитать. U = 2 • 10 = 20 В.

Встречаются задания и посложнее. Например: 

Площадь четырехугольника находится по формуле: S = 1/2 d₁d₂ Sinα. Где d₁ и d₂ – диагонали четырехугольника, α – угол между ними. Вычислите Sinα. S = 21,  d₁ = 7, d₂ = 15.

Для начала нужно выразить величину, которую нужно найти (то есть, чтобы эту величину и остальные величины разделял знак равно). Для этого нужно избавиться от лишних величин, стоящих возле Sinα.

Разделим обе части на 1/2 d₁d_2. В результате получим:   =  Sinα.

Теперь осталось подставить числа и посчитать: Sinα =  = 0,4.

 

Из за­ко­на все­мир­но­го тя­го­те­ния F = G  вы­ра­зи­те массу m и най­ди­те её ве­ли­чи­ну (в килограммах), если F = 13,4 Н, r = 5 м, M = 5·10⁹ кг  и гра­ви­та­ци­он­ная по­сто­ян­ная G = 6,7 ·10^-11.

Первым действием разделим обе части на G, чтобы масса была отделена от других величин знаком равно. 

 

Получим:

F : G = m

F : = m

F • = m

= m

Теперь подставляем численные значения и находим наконец-то массу:

= m

m = 1000.

 

Таким образом происходит решение задач на расчет по формулам.

boeffblog.ru

Как запоминать формулы по математике, физике и химии

В школе детей знакомят с новой темой и новой формулой и начинают решать задачи.

Считается, что после многократного применения формула отложится в голове. Если не отложится, то ее просто надо вызубрить.

Однако, некоторые учителя забывают, что объем информации, которую получает ребенок — огромен. И помимо новой формулы по математике, ребенку надо выучить страны и столицы по географии, десяток дат и событий по истории, пару правил по русскому языку, грамматическое правило и десяток слов по английскому и так далее.

В итоге, формулы просто теряются в потоке информации и забываются первыми. Потому что в отличие от другой информации, формулы — совершенно необразные, а порой и непонятные детям.

Мозг решает их первыми забыть.

Что делать, чтобы этого не случилось?

Как запоминать математические, физические и химические формулы — об этом в этой статье.

Приемы которым я вас хочу сейчас обучить, сначала могут показаться ужасно нелепыми. Мы будем использовать технику эффективного обучения «Мнемотехническое выражение»

К нелепостям очень быстро привыкаешь, тем более, что именно благодаря глупостям, смешным моментам обычно бывает легко запомнить сложную для зазубривания информацию.

Например, падежи русского языка легко запомнить с помощью довольно нелепой фразы: Иван родил девчонку, велел тащить пеленку.

Начнем с математики, царицы наук.

Запомним формулу площади круга:

Супермен (S) бегал ровно (=) по всей площади круга за мышью (пи), излучающей радиацию в квадрате (r^2)

Желательно, чтобы в выражении был намек на то, о чем эта формула. Число пи можно сравнить с мышью, ведь мышь пищит.

Эта формула легко выводится логически, однако такие подсказки позволяют вспомнить ее в трудный момент (например, на котрольной).

Запоминим формулу посложнее. Перейдем к интегралу.

Помню, в свое время хохотала над анекдотом:

Встречает мастер своего преподавателя по вышке лет через восемь после окончания вуза, разговорились, вспомнили время былое. Профессор спрашивает:
— Вот я вам читал три года высшую математику, скажи, в жизни тебе мои знания когда-нибудь пригодились?
Студент, подумав:
— А ведь был один случай.
— Очень интересно, расскажи, я его буду на лекциях рассказывать, что высшая математика не такая абстрактная наука и в жизни бывает нужна .
— Шел я как-то по улице, и мне шляпу ветром в лужу сдуло. Так я взял кусок проволоки, загнул его в форме интеграла и шляпу достал

Предлагаю запомнить формулу Ньютона-Лейбница (связь между интегралом и первообразной)

А и Б сидели… на этот раз не на простой трубе, а на интегальной. Рядом с ними был фантастические  f хоромы, окутанные забором (х), в хоромах было что-то драгоценное, и А и Б помечтали. Они все это приравнивали (=) к разнице между Фантастическим имуществом  (b) и фантастическим имуществом (а), ну а по факту фантастическим были только хоромы (х), а а и б лишь наблюдали за этим с трубы.

Подобные размышления над формулами позволяют запомнить их гораздо лучше, нежели простое зазубривание.

По физике запомним формулу закона всемирного тяготения:

Фыркающая сила (F) подошла и поравнялась с гигантским (G) двухъэтажным (дробь) домом, где на втором этаже (числитель) были две мышки (первая и вторая), изучающие с Ньютоном закон тяготения, а на первом этаже (знаменатель) был работник (r) с квадратной головой

По химии выучим формулу процесса спиртового брожения глюкозы (виноградного сахара). Такой процесс происходит во время изготовления вин:

СНОва (С..Н..О..) брожение вина (сопровождаемое двумя шестерками по краям С6 и О6) и их суммой (12) посередине (…Н12…). Ну а после брожения СНачала (СН, но два раза двоечник, потом отличник 2С2Н5) приходит к ОН (..ОН) и прибавляет двойные газы (+2СО2), которые испаряются в воздух

Формула горения ацетилена:

Двоечники Углерод (С) и водород (Н) тождественно равны углероду и водороду (СН) и пяти отличникам (О), получившим двойку.  В результате взаимодейтсвия получим, что углерод получил четверку (4С вместе с молекулой кислорода О2 и так вспотел, что выступили две капли воды 2Н2О)

Такой анализ и творческий подход к запоминанию поможет не только понять формулу, но и придумать свое необычное объяснение. Что запоминается гораздо лучше механического заучивания.

Далее формулы можно нанести на карточки размером с визитную карточку и положить в карман.

С одной стороны написать формулу, с другой — что она обозначает.

В любую удобную минутку можно достать из кармана карточки и гляда на формулу назвать, о чем она. А по обратной стороне карточки можно восстановить историю и вспомнить формулу.

Такие процессы называются — кодирование и декодирование (расшифровка).

Однако, чтобы в совершенстве овладеть этим навыком нужны специальные тренинровки, упражнения и хорошая компания.

Самому бывает очень трудно заставить себя придумать что-то нелепое и научиться использовать в полной мере потенциал своего мозга (ведь нас этому никогда не учили!)

Для таких целей была создана программа Гениальный ребенок. Техники эффективного обучения.

Сегодня на программу повышаются цены. Успейте воспользоваться выгодным предложением!

И уже на тренинге вы научитесь запоминать на автомате:

• Последовательности слов, дел, списки покупок
• Даты, числа, события
• Имена людей
• Изречения великих людей
• Анекдоты, тосты, притчи
• Стихотворения
• Тексты и прозу
• Выучите таблицу Менделеева
• Научитесь запоминать иностранные слова
• Географические названия
• Страны и столицы
• Формулы
• и многое, многое другое

Подобный навык позволяет сократить время на запоминание, силы на вспоминание и является отличным союзником.

Передав этот навык ребенку, вы делегируете процесс обучения ребенку. Вы, как и я, осоводите себя от уроков детей, необходимости что-то учить с ними или объяснять.

Техники эффективного обучения = свобода для родителей

Люди, владеющие суперпамятью не только быстрее легче учатся, добиваются повышения и отличных результатов на работе, но и чувствуют себя счастливее и моложе, легко изучают 2-3 иностранных языка.

Кроме того, тренировка мозга является профилактикой болезни альцгеймера.

Станьте хозяином своей памяти и хозяином своего времени>>>

 

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Понравилось это:

Нравится Загрузка…

Похожее

gladtolearn.ru