Как найти модуль скорости
Как определяется модуль и направление скорость точки при координатном способе задания движения?
Какие способы задания движения точки применяются в кинематике и в чем они состоят? Как определить траекторию при координатном способе задания точки?
Движение точки в пространстве определяется тремя основными способами: векторным, координатным и естественным.
Векторный: выберем некоторый неподвижный центр О и проведём из центра в точку М, движение которой изучаем, радиус-вектор r. При движении точки М радиус-вектор изменяется по величине и направлению.
Каждому моменту времени t соответствует определённое значение r. Следовательно, радиус-вектор однозначно определяет положение точки М.
таким образом, чтобы определить движение точки, нужно задать её радиус-вектор в виде однозначной и непрерывной функции времени r: r=r(t).
Координатный: Если координаты точки заданы как однозначные функции времени: x=x(t), y=y(t), z=z(t), то положение точки М в пространстве известно в каждый момент времени. Эти уравнения определяют закон движение точки и называются уравнениями её движения.
Естественный: этот способ задания движения применяется в том случае, когда траектория точки, относительно выбранной системы отсчёта, известна.
При движении точки М криволинейная координата s будет изменяться с течением времени, то есть: s=s(t). Зная это уравнение, можно определить положение точки в каждый момент времени.
Его называют уравнением движение или законом движения вдоль заданной траектории.
Зададим положение точки в пространстве координатным особом: x=x(t), y=y(t), z=z(t) (*). Чтобы определить положение точки в начальный момент времени (t=0) необходимо в уравнения (*) подставить t=0.
Теперь, для определения траектории точки: s=s(t) воспользуемся формулой длины дуги кривой:или, с учётом того, что дифференцирование производиться по времени, можно переписать так:.
Знак «+» берётся в том случае, когда точка движется в сторону с положительного отсчёта криволинейной координаты s.
Какая зависимость существует между радиус-вектором движущейся точки и вектором скорости этой точки? Как направлен вектор скорости криволинейного движения точки по отношению к её траектории?
Разложим радиус векторпо ортам декартовой системы координат:. Теперь продифференцируем равенство по времени.
В результате получим разложение скорости по ортам:, разложение можно представить так:, где,,- проекции вектора скорости на оси координат.
Таким образом, проекции скорости на неподвижные декартовы оси координат равны первым производным по времени соответствующих координат движущейся точки.
При векторном: Для того, чтобы точно вычислить скорость точки в данный момент времени, необходимо перейти в формулеперейти к пределу при стремлении промежутка времени к нулю, то есть:.
Этот предел представляет собой первую векторную производную по времени от радиус-вектора точки по времени.
Как следует из этих формул, вектор скорости направлен по касательной к траектории точки в сторону её движения.
При координатном: Найдём модуль скорости, зная её проекции:. Для определения направления вектора скорости воспользуемся направляющими косинусами:
,,. В итоге мы всё же прижжем к выводу, что вектор скорости направлен по касательной к траектории.
При естественном:, известно, что. Векторесть единичный вектор касательной к траектории (её орт), направленный в сторону возрастания криволинейной координаты s. Обозначая орт касательнойзапишем начальную формулу так:, домножим левую и правую часть уравнения на единичный вектор:. Перепишет выражение так:. Таким образом, видно, что вектор скорости направлено по касательной к траектории точки.
Как определяется модуль и направление скорость точки при координатном способе задания движения?
,,Таким образом, проекции скорости на неподвижные декартовы оси координат равны первым производным по времени от соответствующих координат движущейся точки. Из равенств следует, что проекции скорости точки на координатные оси равны скорости проекций этой точки на те же оси. Зная проекции вектора скорости точки, найдём его модуль:.
Для определения направления вектора скорости воспользуемся направляющими косинусами:
,,.
Какая зависимость существует между радиус-вектором движущейся точки и вектором ускорения точки? Как направлен вектор ускорения криволинейного движения точки по отношению к её траектории, в какой плоскости он лежит?
, при стремлениик нулю получаем следующий предел:, этот предел называют ускорение точки в данный момент времени. Так как вектор скорости есть первая производная радиус-вектора точки по времени, то:. Таким образом, ускорение точки в данный момент времени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени.
Установим теперь положение вектораотносительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами,и, прибудет поворачиваться вокруг вектора, т.е. вокруг касательной к траектории в точке М, и займёт в пределе определённое предельной положение. Это предельное положение плоскости МАВ называется соприкасающейся плоскостью в точке М траектории.
Вектор среднего ускорениянаправлен так же, как и, т.е. в сторону вогнутости кривой, и всё время находиться в плоскости треугольника МАВ. Предел вектораприесть вектор, который расположен в предельном положении треугольника МАВ, т.е. в соприкасающейся плоскости траектории точки М.
Итак, вектор полного ускорения точки находиться в соприкасающейся плоскости траектории точки М направлен в сторону вогнутости траектории.
Источник: https://megaobuchalka.ru/5/34383.html
модуль скорости — это… Что такое модуль скорости?
- модуль пластичности — Коэфф. пропорц. м ду напряжением и степенью пластич. деформации, определ. по кривым упрочнения. Имеет размерность напряжения. По аналогии с м. упругости различают м. п. 1 го рода (Е ‘) и 2 го рода (G1). При пластич. деформации, когда коэфф.… … Справочник технического переводчика
- Модуль сдвига — Сдвиговая деформация В материаловедении модулем сдвига (обозначается буквой G или μ), называется отношение касательного напряжения к сдвиговой деформации … Википедия
- модуль пластичности — [modulus of plasticity (ductility)] коэффициент пропорциональности между напряжением и степенью пластической деформации, определяемый по кривым упрочнения. Имеет размерность напряжения. По аналогии с модулем упругости различают модуль… … Энциклопедический словарь по металлургии
- Абсолютная относительная и переносная скорости — Скорость (часто обозначается , от англ. velocity или фр. vitesse) векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может… … Википедия
- Вектор скорости — Скорость (часто обозначается , от англ. velocity или фр. vitesse) векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может… … Википедия
- ЦИРКУЛЯЦИЯ СКОРОСТИ — кинематич. характеристика течения жидкости или газа, к рая служит мерой завихренности течения. Ц. с. связана с вращением элементарного объёма жидкости (газа) при его деформации в процессе движения. Если скорости всех жидких ч ц, расположенных на… … Физическая энциклопедия
- Синхронный транспортный модуль — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
- Доплеровский измеритель скорости и сноса — (ДИСС) бортовое радиолокационное устройство, основанное на использовании эффекта Доплера, предназначенное для автоматического непрерывного измерения и индикации составляющих вектора скорости, модуля путевой скорости, угла сноса и координат… … Википедия
- Синхронный транспортный модуль — 3.11 Синхронный транспортный модуль (STM) информационная структура, используемая в СЦИ для поддержки соединений на уровне секции. Состоит из информационной нагрузки и секционного заголовка (SOH), входящих в структуру цикла, который повторяется… … Словарь-справочник терминов нормативно-технической документации
- синхронный транспортный модуль порядка N (системы передачи железнодорожного транспорта) — Информационная структура, используемая для поддержки соединений на уровне секций СЦИ, состоящая из секционного заголовка и информационной нагрузки, организованных в блочную цикличную структуру, которая повторяется каждые 125 мкс. Примечания 1.… … Справочник технического переводчика
- синхронный транспортный модуль порядка N (системы передачи железнодорожного транспорта) — 94 синхронный транспортный модуль порядка N (системы передачи железнодорожного транспорта): Информационная структура, используемая для поддержки соединений на уровне секций СЦИ, состоящая из секционного заголовка и информационной нагрузки,… … Словарь-справочник терминов нормативно-технической документации
Источник: https://geography_russian_kazakh.academic.ru/7417/%D0%BC%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D0%B8
Средний модуль скорости
| Главная | Обратная связь |
| АрхеологияАрхитектураАстрономияАудитБиологияБотаникаБухгалтерский учётВойное делоГенетикаГеографияГеологияДизайнИскусствоИсторияКиноКулинарияКультураЛитератураМатематикаМедицинаМеталлургияМифологияМузыкаПсихологияРелигияСпортСтроительствоТехникаТранспортТуризмУсадьбаФизикаФотографияХимияЭкологияЭлектричествоЭлектроникаЭнергетика | КИНЕМАТИКАДвижение с постоянным ускорением
Свободное падение тел
Средний модуль скорости
|
©2015 studopedya.ru Все права принадлежат авторам размещенных материалов.
Источник: http://studopedya.ru/1-78205.html
Большая Энциклопедия Нефти и Газа
Cтраница 1
Модуль скорости v частицы меняется со временем t по закону vat — — b, где а и Ъ — положительные постоянные. Найти тангенциальное шт и нормальное wn ускорения, а также радиус кривизны R траектории в зависимости от времени. [1]
Модуль скорости 1с, как определено в предыдущей задаче, для данного положения механизма равен 130т; см / сек. [2]
Модуль скорости г в, как мы уже определили, равен 460 см / сек. [3]
Модуль скорости, вообще говоря, не совпадает с производной по времени dr / dt модуля радиуса-вектора частицы. [4]
Модуль скорости v здесь должен быть вычислен по формуле (6.13), а знак берется в соответствии с выбором положительного направления отсчета дуг траектории. [5]
Модуль скорости равен модулю производной от закона движения точки по времени. [6]
Модуль скорости, конечно, остается постоянным и во внешней системе координат, так как модуль вектора — абсолютный скаляр, не зависящий от выбора координатной системы. [7]
Модуль скорости v здесь должен быть вычислен по формуле (6.13), а знак берется в соответствии с выбором положительного направления отсчета дуг траектории. [8]
Модуль скорости т, связанный с изменением энергии активации микрообъема ( т / ( / а, где а. С макроскопической точки зрения т характеризует собой зависимость между установившейся скоростью неупругой деформации и напряжением, соответствующим этой скорости. [9]
Модуль скорости равен модулю производной от закона движения точки по времени. [10]
Модуль скорости т, входящий в уравнение ( 40), представляет собой величину, равную k Т la, где а — константа, связанная с характеристиками микрочастиц, т характеризует зависимость между установившейся скоростью высокоэластической деформации и соответствующим этой скорости напряжением.
Количественная интерпретация этой константы связана с изменением величины максимального напряжения, вызванного увеличением скорости деформирования в е раз.
Модуль скорости практически не зависит от конформации полимерной цепи и от структуры полимера, подразумевая под этим более крупные надмолекулярные образования. [11]
Модуль скорости т, входящий в уравнение ( 40), представляет собой величину, равную kTIa, где а — константа, связанная с характеристиками микрочастиц, т характеризует зависимость между установившейся скоростью высокоэластической деформации и соответствующим этой скорости напряжением.
Количественная интерпретация этой константы связана с изменением величины максимального напряжения, вызванного увеличением скорости деформирования в е раз.
Модуль скорости практически не зависит от конформации полимерной цепи и от структуры полимера, подразумевая под этим более крупные надмолекулярные образования. [12]
| Зависимость параметров труб круглого сечения от наполнения. [13] |
Модуль скорости w имеет ту же единицу измерения, что и скорость; модуль расхода К-ту же единицу измерения, что и расход. [14]
Модуль скорости равен геометрической сумме ее составляющих. [15]
Страницы: 1 2 3 4
Источник: http://www.ngpedia.ru/id160862p1.html
Ускорение
«Класс!ная физика» — на Youtube
«Физика — 10 класс»
Как изменяются показания спидометра в начале движения и при торможении автомобиля?
Какая физическая величина характеризует изменение скорости?
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению.
Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает.
Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26).
Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.
Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).
Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.
Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению.
Пусть в некоторый момент времени t точка занимает положение М и имеет скорость (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М1 и будет иметь скорость 1. Изменение скорости за время Δt1 равно Δ1 = 1 — .
Вычитание вектора можно произвести путём прибавления к вектору 1 вектора (-):
Δ1 = 1 — = 1 + (-).
Согласно правилу сложения векторов вектор изменения скорости Δ1 направлен из начала вектора 1 в конец вектора (-), как это показано на рисунке 1.28.
Поделив вектор Δ1 на промежуток времени Δt1 получим вектор, направленный так же, как и вектор изменения скорости Δ1. Этот вектор называют средним ускорением точки за промежуток времени Δt1. Обозначив его через cр1, запишем:
По аналогии с определением мгновенной скорости определим мгновенное ускорение. Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:
При уменьшении промежутка времени Δt вектор Δ уменьшается по модулю и меняется по направлению (рис. 1.29). Соответственно средние ускорения также меняются по модулю и направлению.
Но при стремлении промежутка времени Δt к нулю отношение изменения скорости к изменению времени стремится к определённому вектору как к своему предельному значению.
В механике эту величину называют ускорением точки в данный момент времени или просто ускорением и обозначают .
Ускорение точки — это предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении Δt к нулю.
Ускорение направлено так, как направлен вектор изменения скорости Δ при стремлении промежутка времени Δt к нулю.
В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории.
В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения точки при прямолинейном и криволинейном движениях.
В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение считается равным векторной сумме двух ускорений — касательного (к) и центростремительного (цс).
Касательное ускорение к характеризует изменение скорости по модулю и направлено по касательной к траектории движения. Центростремительное ускорение цс характеризует изменение скорости по направлению и перпендикулярно касательной, т. е. направлено к центру кривизны траектории в данной точке.
В дальнейшем мы рассмотрим два частных случая: точка движется по прямой и скорость изменяется только по модулю; точка движется равномерно по окружности и скорость изменяется только по направлению.
Единица ускорения.
Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени. Поэтому, обозначив через Δt некоторый произвольный промежуток времени, а через Δ — изменение скорости за этот промежуток, можно записать:
Так как промежуток времени Δt — величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций.
Запишем выражение для модуля ускорения:
Отсюда следует, что: модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.
Если время измерено в секундах, а скорость — в метрах в секунду, то единица ускорения — м/с2 (метр на секунду в квадрате).
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Следующая страница «Движение с постоянным ускорением»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость.
Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
Устали? — Отдыхаем!
Вверх
Источник: http://class-fizika.ru/10_a10.html
Ускорение
| Скачать все статьи раздела КИНЕМАТИКА |
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится.
Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление».
Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где– вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ=-0 (здесь0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость0. В момент времени t2 тело имеет скорость. Согласно правилу вычитания векторов найдём вектор изменения скорости Δ=-0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δпри очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1а направление вектора ускорения совпадает с вектором скорости2.
Если скорость тела по модулю уменьшается, то есть v2 замедление движения, при этом ускорение будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускоренияτ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела.
То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквойn.
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
Источник: http://av-physics.narod.ru/mechanics/acceleration.htm
novpedkolledg2.ru
Как найти модуль скорости
Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько быстро тело передвигается в пространстве. Перемещение предполагает изменение координат.Инструкция
- Введите систему координат, относительно которой вы будете определять направление и модуль скорости. Если в задаче уже задана формула зависимости скорости от времени, вводить систему координат не нужно – предполагается, что она уже есть.
- По имеющейся функции зависимости скорости от времени можно найти значение скорости в любой момент времени t. Пусть, например, v=2t²+5t-3. Если требуется найти модуль скорости в момент времени t=1, просто подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
- Когда задача требует найти скорость в начальный момент времени, подставьте в функцию t=0. Таким же образом можно найти время, подставив известную скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t²+5t-3=0. Отсюда t=[-5±√(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а поскольку время не может быть отрицательным, остается только t=1/2.
- Иногда в задачах уравнение скорости дается в завуалированной форме. Например, в условии сказано, что тело двигалось равноускоренно с отрицательным ускорением -2 м/с², а в начальный момент скорость тела составляла 10 м/с. Отрицательное ускорение означает, что тело равномерно замедлялось. Из этих условий можно составить уравнение для скорости: v=10-2t. С каждой секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, поэтому легко найти общее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд после начала движения тело остановится.
- Помимо прямолинейного движения тела, существует еще и движение тела по окружности. В общем случае оно является криволинейным. Здесь возникает центростремительное ускорение, которое связано с линейной скоростью формулой a(c)=v²/R, где R – радиус. Удобно рассматривать также угловую скорость ω, причем v=ωR.
completerepair.ru
Физические основы механики
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <…> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
Действительно
Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t + и перепишем верхнее соотношение в виде:
Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
Рис. 2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения , , или , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени
С другой стороны, разложение по базису вектора скорости имеет вид
опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть
Модуль вектора скорости равен
Получим ещё одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому
и в пределе (>0)
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени
будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
online.mephi.ru
Найти вектор скорости и ускорения точки, примеры решений
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
artsybashev.ru
Скорость. Ускорение. Равноускоренное прямолинейное движение – FIZI4KA

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.
При неравномерном движении координату тола уже нельзя определить но формуле \( x=x_0+v_xt \), так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.
Средней скоростью \( \vec{v}_{ср} \) неравномерного движения называют физическую величину, равную отношению перемещении \( \vec{s} \) тела ко времени \( t \), за которое оно произошло: \( \vec{v}_{ср}=\frac{s}{t} \).
Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути \( l \) ко времени \( t \), за которое этот путь пройден: \( v_{ср}=\frac{l}{t} \). Эта скорость обычно называется средней путевой скоростью.
2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.
3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.
Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.
Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — \( \vec{s}_1 \) совершено за время \( t_1 \). Средняя скорость движения на этом участке – \( \vec{v}_{ср.1}=\frac{s_1}{t_1} \). Уменьшим перемещение тела. Пусть оно равно \( \vec{s}_2 \), а время движения — \( t_2 \). Тогда средняя скорость за это время: \( \vec{v}_{ср.2}=\frac{s_2}{t_2} \). Еще уменьшим перемещение, средняя скорость на этом участке: \( \vec{v}_{ср.3}=\frac{s_3}{t_3} \).
При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.
Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения (\( \Delta{\vec{s}} \)) к малому промежутку времени \( \Delta{t} \), за которое это перемещение произошло: \( \vec{v}=\frac{\Delta{s}}{\Delta{t}} \).
4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.
Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.
Пусть в начальный момент времени \( t_0=0 \) скорость тела равна \( \vec{v}_0 \). В некоторый момент времени \( t \) она стала равной \( \vec{v} \). Изменение скорости за промежуток времени \( t-t_0=t \) равно \( \vec{v}-\vec{v}_0 \) (рис.18). Изменение скорости за единицу времени равно: \( \frac{\vec{v}-\vec{v}_0}{t} \). Эта величина и есть ускорение тела, она характеризует быстроту изменения скорости \( \vec{a}=\frac{\vec{v}-\vec{v}_0}{t} \).
Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Единица ускорения \( [a]=[v]/[t] \); \( [a] \) = 1 м/с/1 с = 1 м/с2. 1 м/с2 — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.
Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.
6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: \( \vec{v}=\vec{v}_0+\vec{a}t \). Если начальная скорость тела \( v_0=0 \), то \( \vec{v} = \vec{a}t \).
Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: \( v_x = v_{0x} + a_xt \); если\( v_{0x}=0 \), то \( v_x = a_xt \).
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.
График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_{02} \) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_{03} \) и с ускорением, направленным в сторону, противоположную направлению скорости.
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).
График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью \( v_{02} \), с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью \( v_{03} \) : до момента времени \( t_0 \) направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени \( t_0 \) скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.
График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).
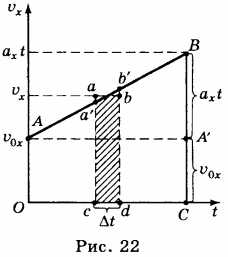
Выделим на графике малый участок \( ab \) и опустим перпендикуляры из точек \( a \) и \( b \) на ось абсцисс. Если промежуток времени \( \Delta{t} \), соответствующий участку \( cd \) на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура \( cabd \) мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку \( cd \).
На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время \( t \) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: \( S_x= \frac{1}{2}(OA+BC)OC \).
Как видно из рисунка, \( OA=v_{0x},BC=v_x,OC=t \). Отсюда следует, что проекция перемещения выражается формулой \( S_x= \frac{1}{2}(v_{0x}+v_x)t \). Так как \( v_x = v_{0x} + a_{xt} \), то \( S_x= \frac{1}{2}(2v_{0x} + a_xt)t \), отсюда \( S_x=v_{0x}t+ \frac{a_xt^2}{2} \). Если начальная скорость равна нулю, то формула имеет вид \( S_x=\frac{at^2}{2} \). Проекция перемещения равна разности координат \( S_x=x-x_0 \), поэтому: \( x-x_0=v_{0x}t+\frac{at^2}{2} \), или \( x=x_{0x}+v_{0x}t+\frac{at^2}{2} \).
Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
11. На практике часто используют формулу или \( v^2_x-v^2_{0x}=2a_xs_x \), или \( v^2-v^2_{0}=2as \).
Если начальная скорость тела равна нулю, то: \( v^2_x=2a_xs_x \).
Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?
2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?
1) 200 м/с2
2) 20 м/с2
3) 2 м/с2
4) 0,5 м/с2
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси \( Оx \). У какого из тел в момент времени \( t_1 \) скорость движения равна нулю?
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси \( Оx \).
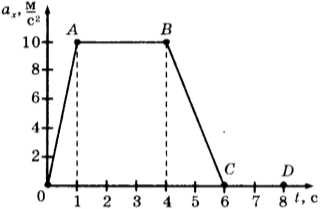
Равноускоренному движению соответствует участок
1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD
5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.
Чему равен путь, пройденный телом за третью секунду?
1) 4 м
2) 4,5 м
3) 5 м
4) 9 м
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.
Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1
2) только 2
3) только 4
4) 3 и 4
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.
1) 1 м/с2
2) -1 м/с2
3) 2 м/с2
4) -2 м/с2
8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?
1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с
9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?
1) 1
2) 2
3) 3
4) 4
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.
1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с
11. Два тела движутся по оси \( Оx \). На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
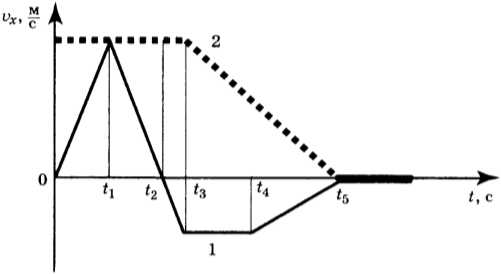
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени \( t_3-t_5 \) тело 2 движется равноускоренно.
2) К моменту времени \( t_2 \) от начала движения тела прошли одинаковые пути.
3) В промежутке времени \( 0-t_3 \) тело 2 находится в покое.
4) В момент времени \( t_5 \) тело 1 останавливается.
5) В промежутке времени \( t_3-t_4 \) ускорение \( a_x \) тела 1 отрицательно.
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени \( t_1 \) тело имело максимальное по модулю ускорение.
4) Момент времени \( t_3 \) соответствует остановке тела.
5) В момент времени \( t_2 \) тело имело максимальное по модулю ускорение.
Часть 2
13. Зависимость координаты от времени для некоторого тела описывается уравнением \( x=12t-t^2 \). В какой момент времени скорость движения равна нулю?
Ответы
Скорость. Ускорение. Равноускоренное прямолинейное движение
5 (100%) 1 votefizi4ka.ru
Кинематика материальной точки
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz:
,
где – единичные векторы (орты) в направлении осей x, y, z.
Скорость точки:
;
.
.
Единичный вектор в направлении касательной к траектории точки:
.
Ускорение точки:
;
;
;
; ;
Тангенциальное (касательное) ускорение:
;
;
.
Нормальное ускорение:
;
;
.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M. Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O. Тогда положение точки M однозначно определяются ее координатами (x, y, z). Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M.
,
где – единичные векторы в направлении осей x, y, z.
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Скорость материальной точки – это производная ее радиус-вектора по времени.
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
Касательная к траектории точки
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Тогда вектор скорости точки можно представить в виде:
.
Далее мы считаем, что если над буквой векторной величины не стоит стрелка, то это обозначает модуль вектора.
Ускорение материальной точки
Ускорение материальной точки – это производная ее скорости по времени.
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают скалярное произведение векторов. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к касательной.
Поскольку , то
(3) .
Тангенциальное (касательное) ускорение
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили:
.
Отсюда видно, что тангенциальное ускорение равно проекции полного ускорения на направление касательной к траектории или, что тоже самое, на направление скорости точки.
Тангенциальное (касательное) ускорение материальной точки – это проекция ее полного ускорения на направление касательной к траектории (или на направление скорости).
Символом мы обозначаем вектор тангенциального ускорения, направленный вдоль касательной к траектории. Тогда – это скалярная величина, равная проекции полного ускорения на направление касательной. Она может быть как положительной, так и отрицательной.
Подставив , имеем:
.
Подставим в формулу:
.
Тогда:
.
То есть тангенциальное ускорение равно производной по времени от модуля скорости точки. Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки. При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль скорости). При уменьшении скорости, тангенциальное ускорение отрицательно (или направлено противоположно скорости).
Радиус кривизны траектории
Теперь исследуем вектор .
Радиус кривизны траектории
Рассмотрим единичный вектор касательной к траектории . Поместим его начало в начало системы координат. Тогда конец вектора будет находиться на сфере единичного радиуса. При движении материальной точки, конец вектора будет перемещаться по этой сфере. То есть он будет вращаться вокруг своего начала. Пусть – мгновенная угловая скорость вращения вектора в момент времени . Тогда его производная – это скорость движения конца вектора. Она направлена перпендикулярно вектору . Применим формулу для вращающегося движения. Модуль вектора:
.
Теперь рассмотрим положение точки для двух близких моментов времени. Пусть в момент времени точка находится в положении , а в момент времени – в положении . Пусть и – единичные векторы, направленные по касательной к траектории в этих точках. Через точки и проведем плоскости, перпендикулярные векторам и . Пусть – это прямая, образованная пересечением этих плоскостей. Из точки опустим перпендикуляр на прямую . Если положения точек и достаточно близки, то движение точки можно рассматривать как вращение по окружности радиуса вокруг оси , которая будет мгновенной осью вращения материальной точки. Поскольку векторы и перпендикулярны плоскостям и , то угол между этими плоскостями равен углу между векторами и . Тогда мгновенная скорость вращения точки вокруг оси равна мгновенной скорости вращения вектора :
.
Здесь – расстояние между точками и .
Таким образом мы нашли модуль производной по времени вектора :
.
Как мы указали ранее, вектор перпендикулярен вектору . Из приведенных рассуждений видно, что он направлен в сторону мгновенного центра кривизны траектории. Такое направление называется главной нормалью.
Нормальное ускорение
Нормальное ускорение
направлено вдоль вектора . Как мы выяснили, этот вектор направлен перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
Пусть – единичный вектор, направленный от материальной точки к мгновенному центру кривизны траектории (вдоль главной нормали). Тогда
;
.
Поскольку оба вектора и имеют одинаковое направление – к центру кривизны траектории, то
.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Нормальное ускорение материальной точки – это проекция ее полного ускорения на направление, перпендикулярное к касательной к траектории.
Подставим . Тогда
.
То есть нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Отсюда можно найти радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Скорость движения в физике
Скорость является одной из основных характеристик механического движения. Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с.
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
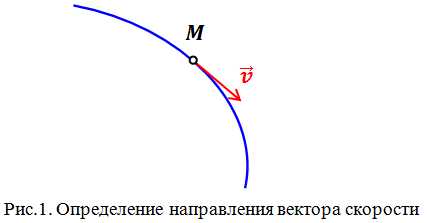
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
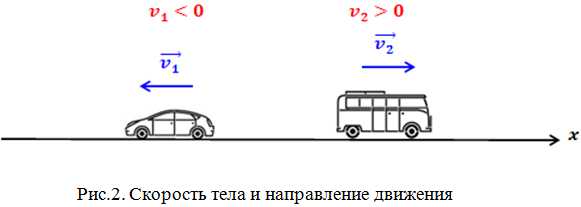
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
В случае неравномерного движения говорят о средней скорости:
Примеры решения задач по теме «Скорость»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
