Число размещений из n элементов по m
Стр 1 из 2Следующая ⇒КОМБИНАТОРИКА
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*…*nk.
Пример 1.Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение:n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n1*n2*n3=6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=…nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk. Такой способ выбора в комбинаторики носит названиевыборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.
Определение 1. Размещением из n элементов по mв комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4.Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
mykonspekts.ru
Лекция 07. Элементы комбинаторики
Лекция 7. Элементы комбинаторики.
Комбинаторика – это раздел математики, изучающий количество комбинаций, которые можно составить из заданного конечного множества попарно различных элементов произвольной природы.
Одно из важных правил комбинаторики – правило умножения:
если объект А
может быть выбран из множества Mn h способами и при каждом выборе объекта
А другой объект В может быть выбран k способами, то объект 
,
состоящий из двух объектов А и В может
быть выбранhk способами.
Конечные подмножества элементов множества Mn называются соединениями.
Если в совокупности соединений подмножества образованы только попарно различными элементами множества Mn, то такие соединения называются соединениями без повторений.
Если в совокупности соединений входят подмножества не только с попарно различными элементами множества M n, но и с одинаковыми, то такие соединения называются соединениями с повторениями.
Различают три основных типа соединений: размещения, перестановки, сочетания.
Определение 7.1. Размещением
из n элементов по m элементов без повторений называется
упорядоченное подмножество попарно
различных m элементов множества Mn (
).
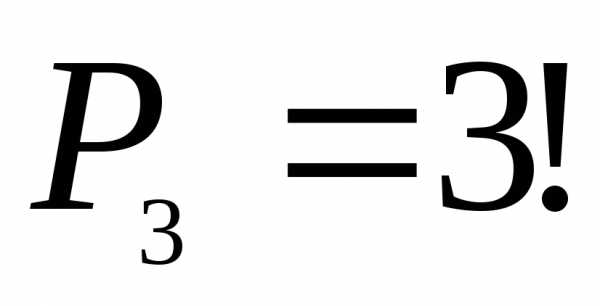Определение 7.2. Перестановкой из n элементов без повторений называется упорядоченное множество всех n элементов множества Mn
Определение 7.3. Сочетанием
из n элементов по m элементов без повторений называется
подмножество из m попарно различных элементов множества Mn без учёта порядка их следования (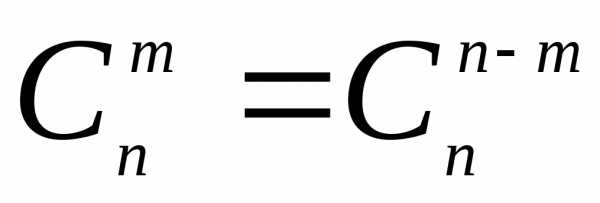
).
Для размещения или сочетания с повторениями требуется лишь условие, чтои, следовательно,m может быть любым натуральным числом, независимым от числа n элементов множества Mn.
В перестановке с повторениями присутствуют все элементы множества Mn, причём указывается, сколько раз повторяются элементы . Число элементов в такой перестановке может быть любым натуральным числом, б ольшим или равным n.
Обозначим символами 
,
,
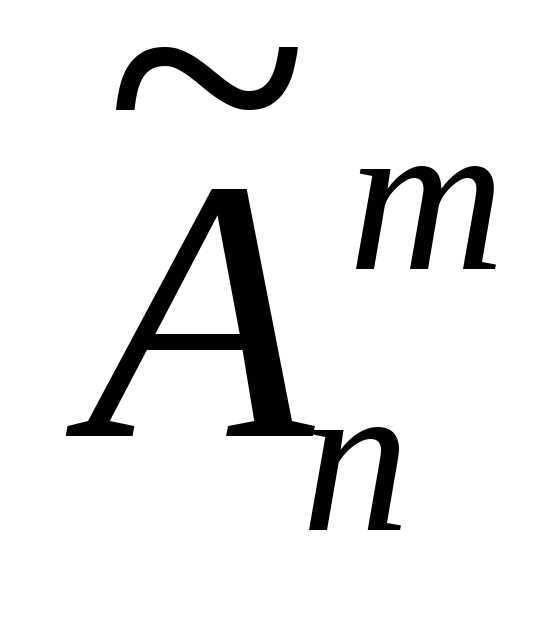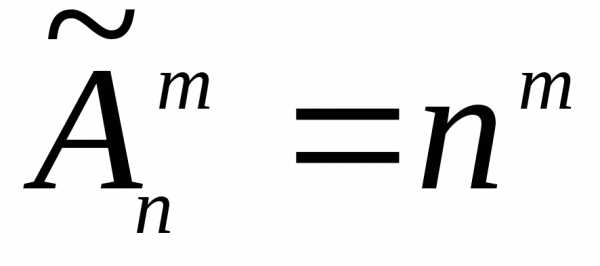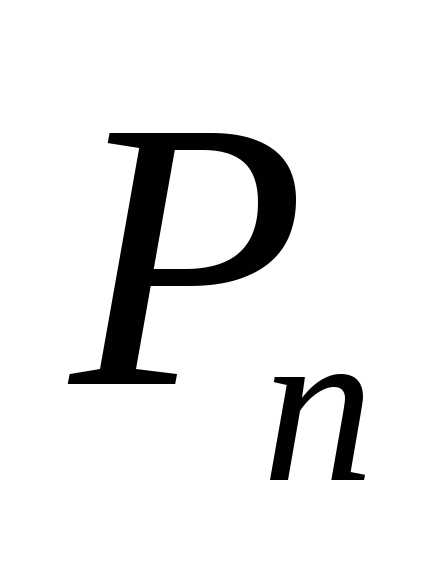число всех размещений, сочетаний без
повторений изn элементов по m элементов и число всех перестановок
без повторений из n элементов (
).
Символы для обозначения числа всех
соединений определённого типа берутся
из начальных букв соответствующих
французских слов: arrangement
– размещение,
combination
– комбинация, сочетание,
permutation
– перестановка.
Символами 
,
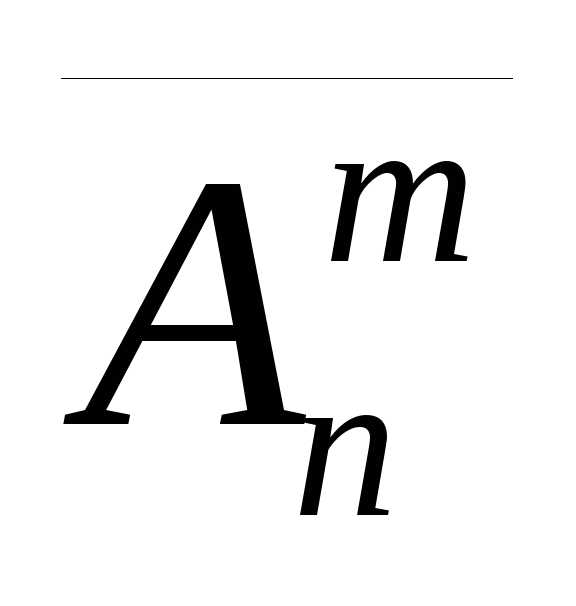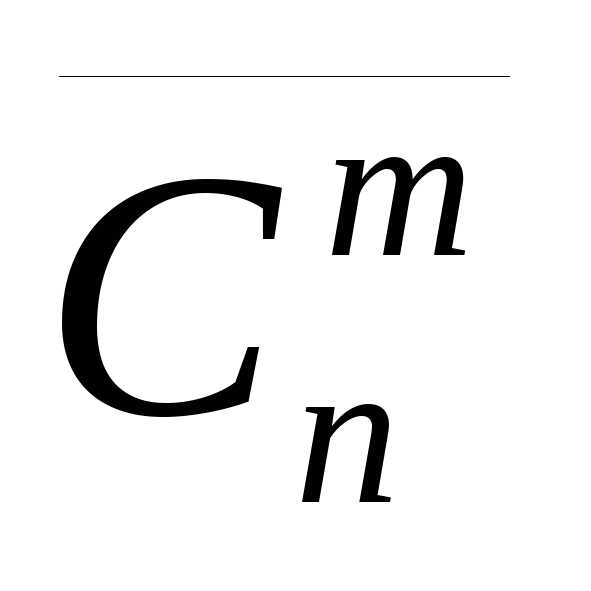
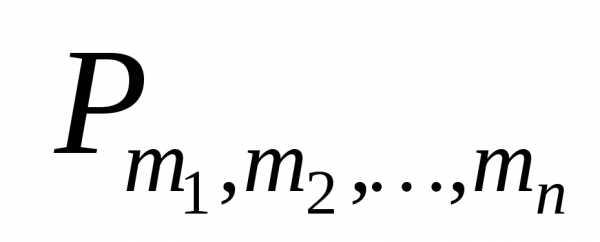обозначим число всех размещений,
сочетаний, перестановок с повторениями
(m, mi – любые натуральные числа). Число mi указывает, что элемент ai повторяется в перестановке mi раз, причем
.Произведение n первых натуральных чисел обозначается символом n! и называется n-факториалом: .
☼ По определению
0!=1 и 
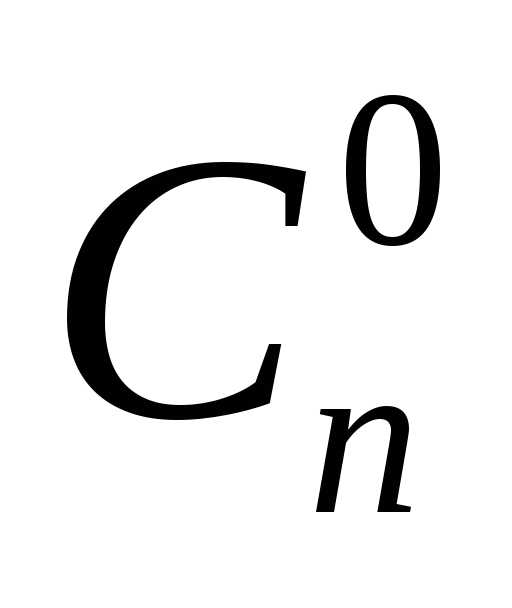=1. ☼
♦ Теорема 7.1. Число размещений без повторений из n элементов по m элементов вычисляется по формуле
, (7.1)
число размещений из n элементов по m элементов с повторениями
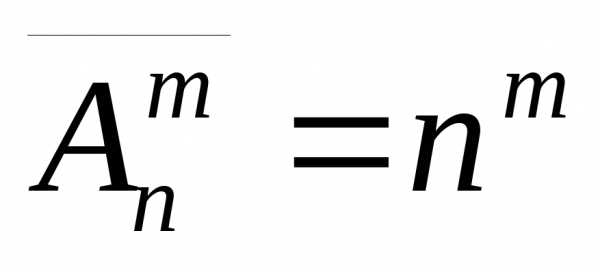
Доказательство. Докажем методом математической индукции формулы (7.1) и (7.2).
1) Для m=1
они справедливы, так как выбор по одному
элементу из множества Mnможно осуществить толькоn способами, а по формулам (7.1) и (7.2)
,
.
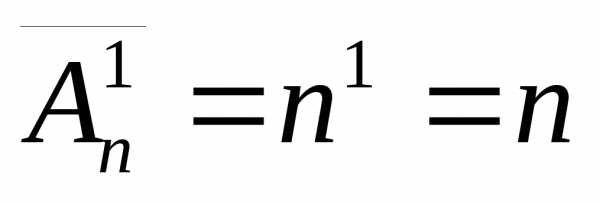2) Пусть эти формулы
справедливы для произвольного
фиксированного натурального числа k,
то есть
,
.
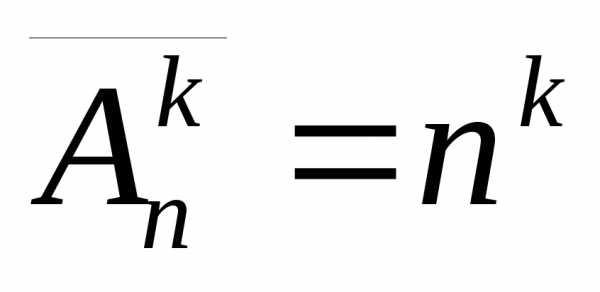По правилу умножения,,
так как в случае подмножества с попарно
различными элементами множестваMn после выбора k элементов из Mn в нём останется n–k элементов, из которых по одному элементу
можно выбрать n–k способами. А в случае размещения с
повторениями (k+1)‑м
элементом может быть любой из
Следствие 1. Так как 
,
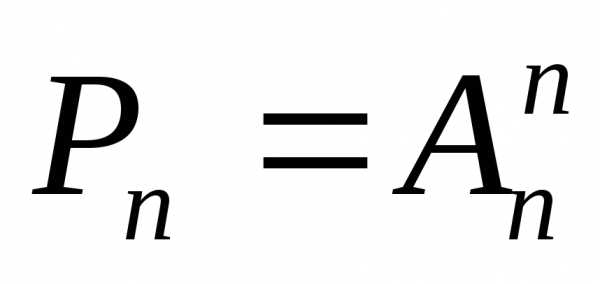то
.
Таким образом, получается формула числа
перестановок:
(7.3)
Формула для перестановок с повторениями такова:
. (7.3а)
Справедливость этой формулы установим следующими рассуждениями: если бы в перестановке все элементов были попарно различными, то таких перестановок было бы . Но, меняя между собой одинаковый элемент ai любыми mi! способами, мы не изменяем самой перестановки. Поэтому в знаменатель надо внести произведение факториалов .
Следствие 2. По правилу умножения . Следовательно,
,
то есть справедлива формула
.
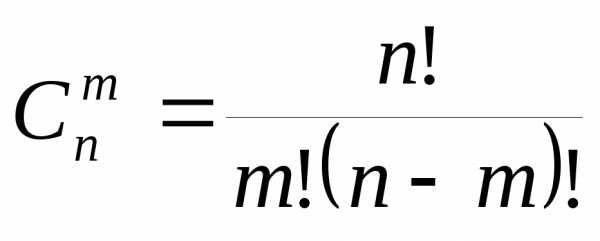(7.4)
♦ Теорема 7.2. Число сочетаний из n элементов по m элементов с повторениями вычисляется по формуле
. (7.5)
Доказательство. Докажем формулу (7.5) методом математической индукции.
1) Для m=1 она справедлива, так как , а выбор по одному элементу из множестваMn можно осуществить только n способами.
2) Пусть формула
(7.5) верна для произвольного фиксированного 
,
то есть 
.
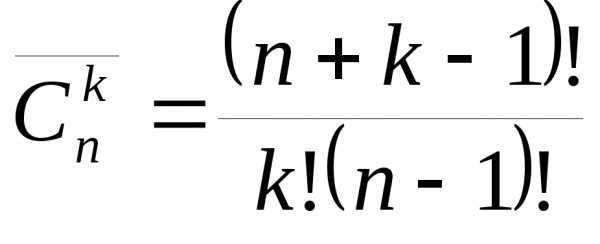Тогда, по правилу умножения,
,
т.к. вставить один элемент, взятый из
Mn,
мы можем n+k способами, добавив к уже выбранным k элементам либо один из них, либо любой
из Mn.
А в знаменателе число k+1
означает, что вставить этот дополнительный
элемент, не изменяя сочетания, мы можем
либо вначале, либо между первым и вторым
и т.д., либо после последнего (то есть k+1
вариантов).
Учитывая, что , убеждаемся, что формула (7.5) справедлива для m=k+1, а значит, она справедлива и для любого натурального числа m. ■
♦ Теорема 7.3. Справедливо правило симметрии
.
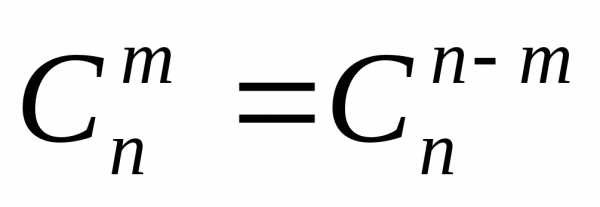(7.6)
Доказательство. . ■
♦ Теорема 7.4. Справедлива формула (правило Паскаля)
. (7.7)
Доказательство. 
. ■
♦ Теорема 7.5. Число всех
подмножеств из n элементов равно 
:
.
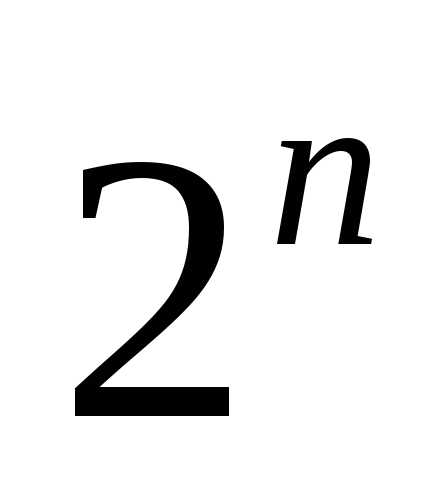Доказательство. Докажем теорему методом математической индукции.
1) При n=1
имеем множество одного элемента 
,
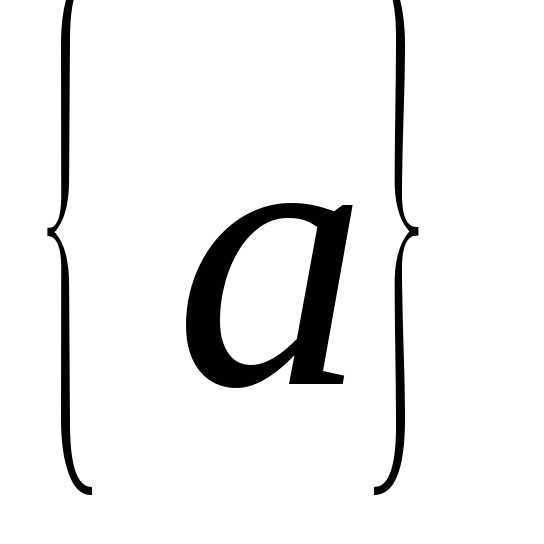которое содержит два подмножества:
пустое множество и само себя.
2) Пусть установлено,
что множество из k элементов содержит ровно 
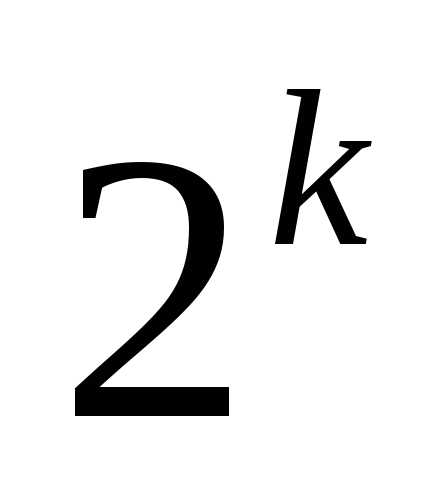подмножеств.
Рассмотрим множество изk+1 элементов. Любое его подмножество В получается одним из двух способов:
а) берётся подмножество В множества ,
в) берётся
подмножество
и присоединяется элемент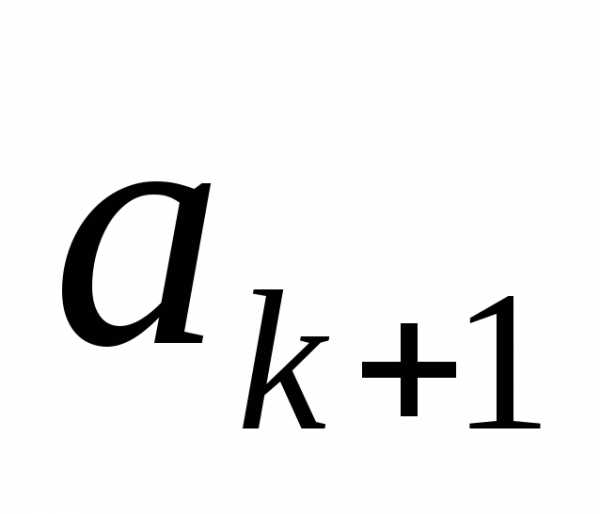
.
Каждым из этих
способов получаем 
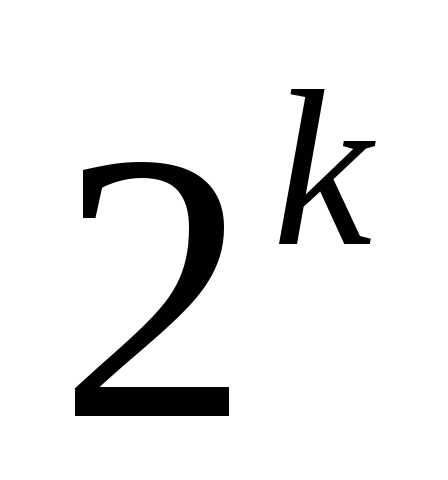подмножеств, а всегоподмножеств множества А. ■
Рассмотрим несколько задач, решение которых осуществляется с использованием доказанных формул.
Пример 7.1. Сколько пятизначных чисел можно составить из цифр 1, 3, 7?
Решение. По формуле (7.2) (размещения с повторениями) находим: .
Пример 7.2. Сколько неподобных членов содержится в многочлене
Решение. По формуле (7.5) (сочетания с повторениями) находим:
Пример 7.3. Сколькими способами можно составить футбольную команду, если её формируют из трёх вратарей и пятнадцати полевых игроков?
Решение. Так как полевых игроков в команде 10 и всего 1 вратарь, то по правилу умножения .
Пример 7.4. Сколько слов, без учёта их смысла, можно составить из букв слова «длинношеее»?
Решение. По формуле (7.3а) (перестановки с повторениями) находим:
.
Пример 7.5. Сколько четырёхзначных чисел можно составить из цифр 0, 1, 5?
Решение. Так
как число не начинается с нуля, то из
числа 
надо вычесть
число 
:
.
Пример 7.6. Сколько шестизначных телефонных номеров можно установить?
Решение. По формуле (7.2) (размещения с повторениями) находим:
.
♦ Теорема 7.6. При любом 
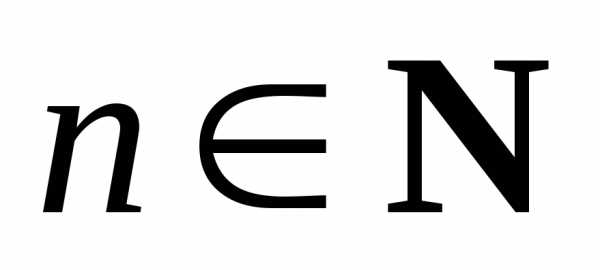справедливо
равенство(бином
Ньютона1)
. (7.8)
Доказательство. Формулу (7.8) докажем методом математической индукции.
1) Проверяем верность
формулы при n=1:
,
так как по формуле (7.4)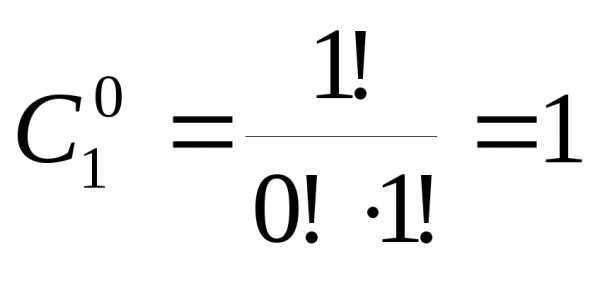
,
.
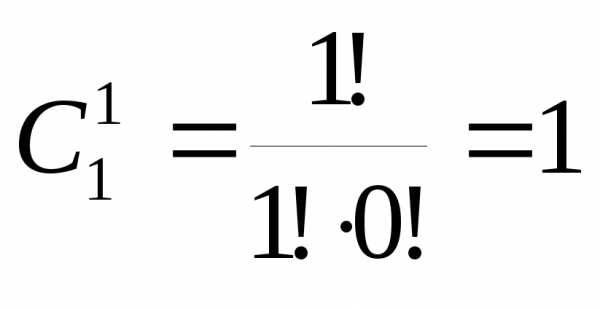Таким образом, приn=1
формула (7.8) верна.
2) Предположим, что формула (7.8) верна для некоторого n. Докажем, что при n+1 имеет место такая же формула, то есть что
. (7.9)
В самом деле,
.
В силу того, что ,,,,, следует формула (7.9). Из 1) и 2) на основании метода математической индукции заключаем, что формула (7.8) верна для любого натурального числаn. ■
Формулу (7.8) обычно коротко записывают так: .
При n=2 и n=3 получаем хорошо знакомые формулы:
;
.
1Ньютон Исаак (1642-1727) – великий английский физик, механик, математик и астроном.
33
studfiles.net
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается Anm и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается Cnm и вычисляется по формуле:
Текст задания:
Задача 1. Сколькими способами можно выбрать 3 дежурных из группы в 20 человек?
Задача 2. Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.
Задача 3. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые начинаются цифрой 3?
Задача 4. Из m книг, стоящих на книжной полке, нужно выбрать k таких, которые не стояли рядом на книжной полке.
Задача 5. Имеется 5 львов и 4 тигра. Необходимо их расставить в ряд, но при этом известно, что тигр не может идти спокойно за тигром.
Задача 6. Сколько перестановок можно сделать из букв слова «Миссисипи»?
Задача 7. Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг?
Задача 8. Сколько экзаменационных комиссий, состоящих из 7 человек, можно составить из 15 преподавателей?
Задача 9. На курсе изучается 5 предметов. Сколькими способами можно составить расписание на субботу, если в этот день должны быть две различные пары?
Задача10. Сколькими способами можно рассадить 8 человек: 1. В один ряд? 2. За круглым столом?
Самостоятельная работа № 22
Тема: Аксиоматическое определение вероятности
Цель: закрепить знания и умения студентов по освоению темы методом решения задач.
Теоритическое обоснование:
Классическое определение вероятности — основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.
Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара.
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу
studfiles.net
Комбинаторика. Основные формулы
Цель занятия: уметь применять основные формулы комбинаторики и знать условия применения этих формул; знать свойства биномиальных коэффициентов и уметь определять разложение бинома при конкретных значениях n.
План занятия:
1. Число размещений.
2. Число перестановок.
3. Число сочетаний.
4. Повторения.
5. Бином Ньютона. Треугольник Паскаля.
Методические указания по изучению темы
Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.
Комбинаторика – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству. Термин «комбинаторика» происходит от латинского слова combina – сочетать, соединять.
Пусть есть некоторое множество из n элементов: x1, x2, x3, …, xn.
Из этого множества можно образовать различные подмножества, то есть выборки, каждая из которых содержит m элементов (0 ≤ m ≤ n). Различают упорядоченные выборки (размещения), перестановки и неупорядоченные выборки (сочетания).
Размещения
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число размещений из n элементов по m элементов обозначают (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:
Понятие факториала
Произведение n натуральных чисел от 1 до n обозначается символом n! (n факториал), то есть
Например, 2!=
3!=
5!=
Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1.
Примеры:
Из последних двух формул следует, что
Пример.
В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки?
Решение: Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда
(вариантов).
Пример.
Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов?
Решение:
(способов).
Пример.
Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными?
Решение:
(телефонных номеров).
Перестановки
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Число всех возможных перестановок из n элементов обозначают Pn (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле:
Пример.
В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега?
Решение:
В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда (вариантов)
Пример.
Сколькими различными способами могут разместиться на скамейке10 человек?
Решение:
(способов)
Пример.
Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов?
Решение:
(способов).
Сочетания
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.
Число сочетаний вычисляют по формуле: (С — первая буква французского слова combinasion).
Пример.
Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?
Решение:
(способов).
Пример.
Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей?
Решение:
(способов).
Другой вид формул числа размещений и числа сочетаний
; , то есть .
Свойства числа сочетаний:
1)
2)
3)
4)
5)
При решении задач комбинаторики используют следующие правила:
Правило суммы.Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.
Правило произведения.Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана n×k способами.
Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.
Размещения с повторениями
Число размещений по m элементов с повторениями из n различных элементов равно nm,то есть
Пример.
Из цифр 1,2,3,4,5 можно составить 53 =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры.
Перестановки с повторениями
Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями
где
Пример.
Сколько различных перестановок букв можно сделать в слове «математика»?
Решение:
Сочетания с повторениями
Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n+m-1) различных элементов по m элементов:
Пример.
Найти число сочетаний с повторениями из четырех элементов a, b, c, d по 3 элемента.
Решение:
Искомое число будет
Бином Ньютона
Для произвольного положительного целого числа n справедлива следующая формула:
.
Это бином Ньютона. Коэффициенты называются биномиальными коэффициентами.
При n = 2 получим формулу ;
При n = 3 получим формулу .
Пример. Определить разложение при n=4.
Решение:
.
Биномиальные коэффициенты обладают рядом свойств:
1. ;
2. ;
3. ;
4. .
Рассмотрим следующий треугольник:
………………………….
Строка под номером n содержит биномиальные коэффициенты разложения . Воспользовавшись свойством , можно заметить, что каждый внутренний элемент треугольника равен сумме двух элементов, расположенных над ним, а боковые элементы треугольника – единицы:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……………………….
Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов.
Решение примеров рекомендуется выполнять в среде табличного процессора MS Excel. При этом надо учитывать некоторую терминологическую путаницу.
В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)
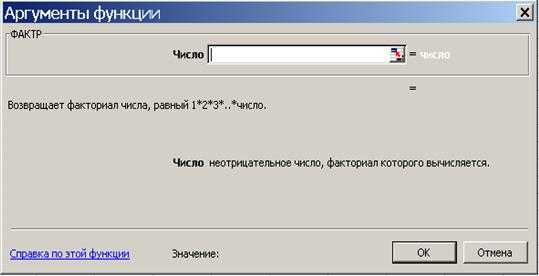
Рис. 1
В Excel считать «перестановки», т.е. размещения, очень удобно, не нужно даже вычислять факториалы (см. рис. №2 и №3): «=ПЕРЕСТ(N;K)». Вместо N и K задаются целые положительные числа, N≥K.
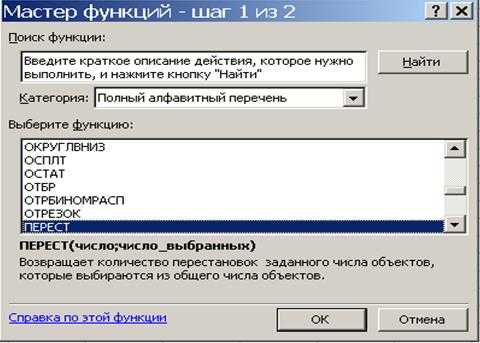
Рис. 2
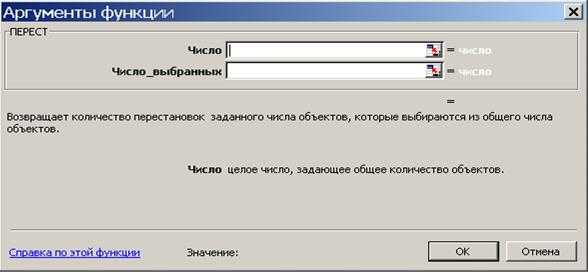
Рис. 3
Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
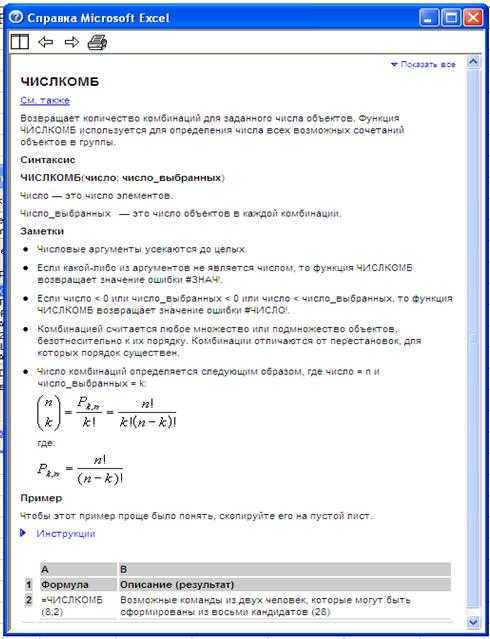
А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)
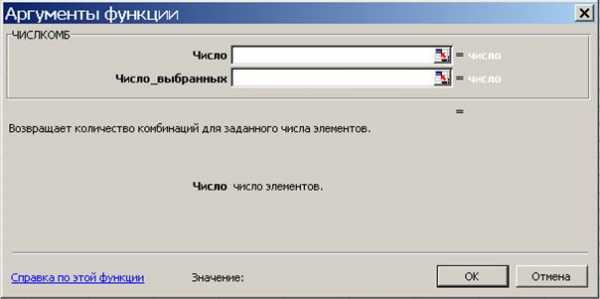
Рис. 4
При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:
Задачи для самостоятельного решения
1. Вычислить:
2. Вычислить:
3. Вычислить:
4. Найти n, если 5Сn3 =
5. Найти n, если
6. Найти n, если
7. Найти n, если
8. Найти n, если , k n
9. Решить уравнение
10. Решить систему
11. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
12. Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?
13. Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?
14. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?
15. Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?
16. Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?
17. В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?
18. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
19. Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?
20. На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?
21. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
22. Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?
23. В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?
24. Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?
25. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
26. В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?
27. Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?
28. В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»?
29. Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?
30. Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?
31. На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.
32. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?
33. Сколько существует различных семизначных телефонных номеров?
34. Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?
35. При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?
36. В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.
37. Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. ( Обмен происходит по одной марке ).
38. У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?
39. Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?
40. Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?
41. В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?
42. Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
43. Определить разложение при n=5.
44. Определить разложение при n=8.
45. Найти член разложения , не содержащий x (то есть содержащий x в нулевой степени).
46. Найти шестой член разложения , если биномиальный коэффициент третьего от конца члена равен 45.
47. В разложении коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени).
48. В разложении бинома найти члены, не содержащие иррациональности.
49. Найти номер того члена разложения , который содержит a и b в одинаковых степенях.
Практическое занятие №2
(интерактивное занятие в малых группах)
Булевы функции
Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные.
План занятия:
1. Основные операции
2. Булевы функции от n переменных
3. Основные эквивалентности
4. Формулы
infopedia.su
Сочетание — Википедия
Материал из Википедии — свободной энциклопедии
В комбинаторике сочетанием из n{\displaystyle n} по k{\displaystyle k} называется набор k{\displaystyle k} элементов, выбранных из данного множества, содержащего n{\displaystyle n} различных элементов.
Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества, k=3{\displaystyle k=3}) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6{\displaystyle n=6}) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать k{\displaystyle k} элементов из множества, содержащего n{\displaystyle n} различных элементов, стоит на пересечении k{\displaystyle k}
ru.wikipedia.org
Комбинаторика. Генератор размещений из N по M.
Следующий калькулятор генерирует все возможные размещения (из n по m) элементов.
Arrangement — процес, когда из множества элементов n выбирают элементы m в определенном порядке.
По данной формуле мы считаем количество всех размещений из n по m.
Anm = n!/(n-m)!
Например для элементов X, Y, Z количество всех возможных размещений из 3 по 2 равно 3!/1! = 6. Все возможные варианты размещения: XY, YX, XZ, ZX, YZ.
При этом, XY и YX — совсем разные размещения.
Также на нашем сайте вы можете увидеть калькулятор всех размещений элементов с повторениями:
http://abcname.com.ua/calc/matematika/generator-placements.html
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
minutes
minutes
minute
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
hour
hours
hours
hours
hours
hours
hours
hours
hours
hours
hours
days
day
day
day
day
days
days
days
days
days
days
days
month
month
month
month
months
months
months
months
months
months
months
year
of the year
of the year
of the year
years
years
years
years
years
years
years
ago
%1 minutes ago
%1 minutes ago
%1 minutesу ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 hour ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 days ago
%1 day ago
%1 day ago
%1 day ago
%1 day ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 month ago
%1 month ago
%1 month ago
%1 month ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 year ago
%1 of the year ago
%1 of the year ago
%1 of the year ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
Комбинаторика. Генератор размещений из N по M без повторений.hostciti.net
Размещения с повторениями — Мегаобучалка
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.
Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.
Число размещений с повторениями из n элементов по m элементов будем обозначать символом (c повт.)
Можно доказать, что оно равно nm.
| (1.3) |
Пример 1.2. Изменим условиепримера 1.1. Правление коммерческого банка выбирает из 10 кандидатов трех человек на три различные должности, Предположим, что один и тот же отобранный из 10 претендентов кандидат, может занять не только одну, но и 2, и даже все 3 различные вакантные должности. Сколько в этом случае возможно комбинаций замещения трех вакантных должностей?
Решение.Как и в предыдущей задаче комбинации замещения вакантных должностей могут отличаться и составом претендентов, и заполняемыми ими вакансиями, т.е. порядком. Следовательно, и в этом случае для ответа на вопрос задачи необходимо рассчитать число размещений. Однако, на этот раз, вакантные должности могут замещаться одним и тем же претендентом, а, значит, здесь речь идет о расчете числа размещений с повторениями.
По условию задачи n = 10, m = 3.
Следовательно:
(с повт.) = 103 = 1000.
Ответ. Можно составить 1000 комбинаций замещения 3 различных вакантных должностей.
Сочетания
Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m в каждом обозначается символом и вычисляется так:
| где , | (1.4) |
или
| где . | (1.5) |
| Свойства сочетаний: |
Пример 1.3. Правление коммерческого банка выбирает из 10 кандидатов трех человек на одинаковые должности (все 10 кандидатов имеют равные шансы). Сколько всевозможных групп по три человека можно составить из 10 кандидатов?
Решение. Состав различных групп должен отличаться, по крайней мере, хотя бы одним кандидатом и порядок выбора кандидата не имеет значения, следовательно, этот вид соединений представляет собой сочетания. По условию задачи n = 10? M = 3. Подставив данные в формулу (1.4.2), получаем
= 10!/3!7! = 120
Ответ. Можно составить 120 групп из 10 человек по 3.
Замечание. Надо уметь отличать сочетания от размещений. Если, например, в группе 25 студентов, и 10 человек из них вышли из аудитории на перерыв. Они стоят вместе и беседуют. Тогдапорядок, в котором они стоят — несущественен. Число всех возможных групп из 25 человек по 10 в этом случае — сочетания. Если же студенты отправились на перерыве в буфет, или в кассу за стипендией, то тогда существенно, в каком порядкеонивстали, то есть кто из них первый, второй и т.д. В этой ситуации при подсчете возможных групп из 25 человек по 10 необходимо составлять размещения.
megaobuchalka.ru
