Размещения с повторениями
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики.
Комбинаторика происходит от латинского слова ”combinatio” соединение.
Группы, составленные из каких-либо предметов, (безразлично каких, например, букв, цветных шаров, кубиков, чисел и т.п.), называются соединениями (комбинациями).
Предметы, из которых состоят соединения, называются элементами.
Различают три типа соединений: перестановки, размещения и сочетания.
Размещения
Размещениями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.
| . | (1.1) |
Понятие факториала
Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть (читается: n факториал).
Например, .
Считается, что 0! = 1.
Используя понятие факториала, формулу (1.1) можно представить так:
| , | (1.2) |
где .
Очевидно, что = n (при m=1) и = 1 (при m=0).
Размещения с повторениями
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m
включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.
Число размещений с повторениями из n элементов по m элементов будем обозначать символом (c повт.)
Можно доказать, что оно равно nm.
| (1.3) |
Сочетания
Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m в каждом обозначается символом и вычисляется так:
| где , | (1.4) |
или
| где . | (1.5) |
| Свойства сочетаний: |
Похожие статьи:
poznayka.org
Генератор размещений элементов с повторениями.
Следующий калькулятор генерирует все возможные варианты размещения с повторениями из заданных элементов и при заданном размере размещения.
Конечные последовательности — так же одно из названий размещений с повторениями.
Размещения с повторениями считаются одинаковыми только когда одни и те же элементы находятся на одинаковых местах.
Давайте рассмотрим пример зазмещения с повторениями трех элементов X, Y, Z:
Пример: Размещения с повторениями из трех элементов A, B, C по два — XX, XY, XZ, YX, YY, YZ, ZX, ZY, ZZ.
Число всех возможных размещений можно высчитать по данной формуле:
An’m = nm
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
minutes
minutes
minute
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
hour
hours
hours
hours
hours
hours
hours
hours
hours
hours
hours
days
day
day
day
day
days
days
days
days
days
days
days
month
month
month
month
months
months
months
months
months
months
months
year
of the year
of the year
of the year
years
years
years
years
years
years
years
ago
%1 minutes ago
%1 minutes ago
%1 minutesу ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 hour ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 days ago
%1 day ago
%1 day ago
%1 day ago
%1 day ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 month ago
%1 month ago
%1 month ago
%1 month ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 year ago
%1 of the year ago
%1 of the year ago
%1 of the year ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
Комбинаторика. Генератор размещений из N по M с повторениями.hostciti.net
Сочетания с повторениями — Мегаобучалка
Тема 1.ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики.
Комбинаторика происходит от латинского слова ”combinatio” соединение.
Группы, составленные из каких-либо предметов, (безразлично каких, например, букв, цветных шаров, кубиков, чисел и т.п.), называются соединениями (комбинациями).
Предметы, из которых состоят соединения, называются элементами.
Различают три типа соединений: перестановки, размещения и сочетания.
Размещения
Размещениями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.
Число размещений из n элементов по m в каждом обычно обозначается символом и вычисляется по формуле (1.1)[1]:
| . | (1.1) |
Понятие факториала
Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть (читается: n факториал).
Например, .
Считается, что 0! = 1.
Используя понятие факториала, формулу (1.1) можно представить так:
| , | (1.2) |
где .
Очевидно, что = n (при m=1) и = 1 (при m=0).
Размещения с повторениями
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.
Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.
Число размещений с повторениями из n элементов по m элементов будем обозначать символом (c повт.)
Можно доказать, что оно равно nm.
| (1.3) |
Сочетания
Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m в каждом обозначается символом и вычисляется так:
| где , | (1.4) |
или
| где . | (1.5) |
| Свойства сочетаний: |
Сочетания с повторениями
Сочетание с повторениями из n элементов по m(m Î n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если, например, два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Число сочетаний с повторениями из n элементов по m будем обозначать символом Формула для вычисления числа сочетаний с повторениями:
| (1.6) |
Замечание: m может быть и больше n.
Перестановки
megaobuchalka.ru
Размещения, перестановки, сочетания
Основные понятия комбинаторики. Множества. Перестановки. Сочетания. Размещения. Разбиения. Понятие алгоритма и сложность алгоритмов.
Два основных правила комбинаторики
Для строгого вывода всех формул используются два основных правила комбинаторики:
Правило умножения (правило «и»). Согласно ему, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару A и B можно выбрать n·m способами.
Это правило обобщается на произвольную длину последовательности.
Правило сложения (правило «или»). Оно утверждает, что, если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n + m способами.
Эти правила нужны и для решения задач.
Понятие факториал также рапространяется на ноль: 0! = 1, так как считается, что пустое множество можно упорядочить единственным способом.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются либо самими элементами, либо порядком элементов.
Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Число размещений из n по m обозначается Anm и определяется по формуле
Anm =n·(n− 1)·(n− 2)·…·(n−m+ 1) =n!/(n − m)!
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при .
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Похожие статьи:
poznayka.org
Формулы комбинаторики
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N.
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4. Число различных перестановок без повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:
Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать способом. С каждым выбором конкретной пятерки можно произвестиперестановок местами. Согласно теореме умножения искомое число способов посадки равно.
Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как
б) Решение очевидно —
в)
 — число выборов занимаемых стульев.
— число выборов занимаемых стульев.
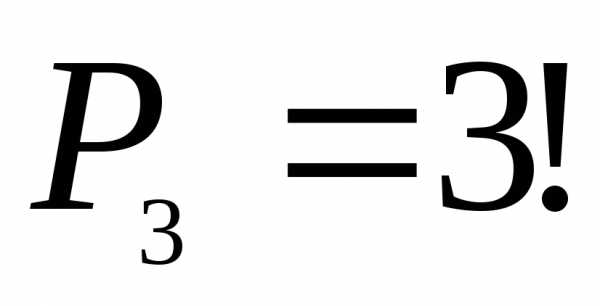 — число размещений
трех человек на трех выбранных стульях.
— число размещений
трех человек на трех выбранных стульях.
Общее число выборов равно .
Не трудно проверить
формулы
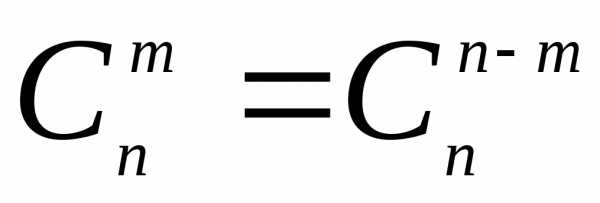 ;
;
;
— число всех подмножеств множества, состоящего из n элементов.
Размещения с повторением
Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N, состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать.
Число
размещений с повторением обозначают
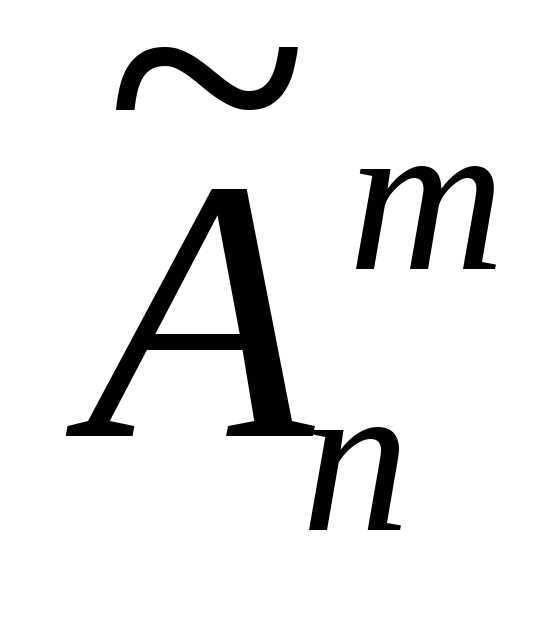 и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
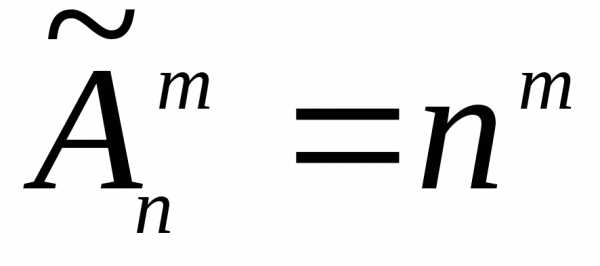
Пример 2. Пусть дано множество из трех букв N = {a, b, c}. Назовем словом любой набор из букв, входящих в это множество. Найдем количество слов длиной 2, которые можно составить из этих букв: .
Замечание: Очевидно, размещения с повторением можно рассматривать и при .
Пример 3. Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?
Ответ:
studfiles.net
Конечные упорядоченные подмножества, содержащие по m элементов, выбранных из n элементов по m элементов основного множества, называются размещениями из n элементов по m элементов.
Число всех возможных размещений из n элементов по m элементов обозначается . Число размещений из n элементов по m можно записать в виде формулы:
Пример: Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день недели должно быть 4 различных урока?
Решение. Число способов равно числу размещений из 7 элементов по 4, т.е. равно А47 =7·6·5·4=840
Число размещений и число перестановок связаны формулой:
Сочетания.
Конечные неупорядоченные множества, содержащие m различных элементов, выбранных из n элементов заданного множества, называются сочетаниями из n элементов по m элементов. Обозначается или
Число различных неупорядоченных множеств, содержащих по m различных элементов, выбранных из элементов, будет вычисляться по формуле: =
Используя формулы для подсчета числа перестановок Рm и числа размещений , получим =
Пример:группу учащихся колледжа должна экзаменовать по математике комиссия, состоящих из 7 человек. Сколькими способами может быть составлена комиссия, если в колледже 14учителей математики?
Решение: используем формулу подсчета числа сочетаний = .
Здесь n=14, а m = 7, тогда = .
Для числа сочетаний справедливы равенства:
= С , С = + С , а также С
.Последнее свойство иногда формулируется в виде следующей теоремы о конечных множествах: Число всех подмножеств множества, состоящего из n элементов, равно 2n.
Контрольные вопросы:
Дайте определение числовой последовательности.
Перечислите способы задания последовательностей.
Какие последовательности называют ограниченными?
Сформулируйте определение предела числовой последовательности.
Сформулируйте необходимые и достаточное условия сходимости последовательности.
Дайте определение предела функции в точке.
Перечислите основные теоремы о пределах функции в точке.
Сформулируйте определение числового ряда.
Какой ряд называется сходящимся, расходящимся?
Сформулируйте необходимое условие сходимости ряда.
Сформулируйте признак Даламбера сходимости рядов.
Какой ряд называют абсолютно сходящимся?
Какой ряд называют условно сходящимся?
Запишите формулу разложения функции в ряд Маклорена.
Понятие множества, элемента множества, подмножества.
Способы обозначения и задания множества.
Понятие равных множеств, пустого множества.
Пересечение множеств. Непересекающиеся множества.
Переместительный и сочетательный законы.
Сумма (объединение) множеств.
Разность множеств. Дополнение до множества.
Прямое произведение множеств.
Эквивалентные множества. Взаимно однозначное соответствие
Сформулируйте определение графа.
Перечислите способы задания графов.
Сформулируйте определение комбинаторики, как раздела математики.
Сформулируйте определение факториала.
Сформулируйте определение перестановок.
Дайте понятие размещения и сочетания.
Домашнее задание
Заполните в рабочей тетради занятие 7. 8, 9, 10
Лекция № 5
.
Тема: Основные понятия теории вероятности и математической статистики
План:
Похожие статьи:
poznayka.org
Элементы комбинаторики
Основные правила комбинаторики.
Комбинаторика— это раздел математики, изучающий способы расположения объектов в соответствии со специальными правилами и методы подсчета числа всех возможных способов. Правило умножения. Если некоторый выбор A можно осуществить m способами, а для каждого из них некоторый другой выбор B можно осуществить n способами, то выбор A и B ( в указанном порядке) можно осуществить m×n способами. Пример 1.На гору ведут 6 дорог. Сколькими способами можно подняться на гору и спуститься с горы, если подъем и спуск должен быть по разным дорогам? Решение. Дорогу на гору можно выбрать 6-ю способами, так как подъем и спуск должны быть по разным дорогам, то выбрать дорогу для спуска можно 5-ю способами. Тогда по правилу умножения число способов выбора дороги для подъема и спуска равно 6×5=30. Правило сложения. Если некоторый выбор A можно осуществить m способами, а выбор B можно осуществить n способами, то выбор A или B можно осуществить m+n способами. Пример 2.В ящике имеется 6 красных карандашей, 5 синих и 3 простых карандаша. Сколькими способами можно выбрать цветной карандаш? Решение. Цветной карандаш — это красный или синий, следовательно, по правилу сложения число способов выбора цветного карандаша равно 6+5=11. Замечание. Данные правила можно обобщить на большее число выборов. Вопрос. Сколько основных правил комбинаторики существует?
2
Перестановки.
Определение 1.Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число от 1 до n, где n — это число элементов данного множества, причем разным элементам поставлены в соответствие разные числа.
Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком. Определение 2. Различные упорядоченные множества, составленные из элементов данного множества, отличающиеся лишь порядком элементов, называются его перестановками. Пример 3.Рассмотрим множество M={a,b,c}. Это множество из трех элементов. Составим его различные перестановки: (a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a). Получили 6 перестановок. Pn — число всех перестановок множества из n элементов.
Pn=n! (1), где
n!=1·2·3·…·n ( читается «н факториал»). Замечание. 0!=1; (n+1)!=n!·(n+1) . Пример 4.Сколько шестизначных чисел, кратных пяти, можно составить из цифр 0,1,2,3,4,5, при условии, что в числе нет одинаковых цифр? Решение. Числа, кратные пяти( делящиеся на пять), оканчиваются либо на 0, либо на 5. Если последняя цифра числа 0, то остальные цифры можно располагать в любом порядке, получим перестановки из пяти элементов, их P5=5!=120. Если на конце 5, то остальные можно расположить P5=120 способами, но среди них не подходят те, которые начинаются на 0, так как это будут не шестизначные числа. а пятизначные, данных чисел P4=4!=24.Тогда требуемых чисел будет 120+120-24=216.
Вопрос.Сколько существует перестановок из шести элементов?
Ваш ответ : 720
верно
Перестановки с повторениями.
Если взять цифры 1, 2, 3, 4, то из них можно составить 24 перестановки. Но если взять четыре цифры 1, 1, 2, 2, то можно получить только следующие различные перестановки: (1,1,2,2),(1,2,1,2),(1,2,2,1),((2,2,1,1),(2,1,2,1),(2,1,1,2), то есть шесть перестановок, их в 4 раза меньше, чем перестановок из четырех различных чисел, так как перестановки, в которых меняются местами одинаковые числа — это не новые перестановки, их 2!·2!=4. Рассмотрим задачу в общем виде:пусть имеется множество из элементов, в котором элементывстречаютсяраз, элементывстречаютсяраз ,…, элементывстречаютсяраз, причем.
Определение 3.Перестановки с повторениями — это перестановки из элементов данного множества, в которых элементы повторяются. — число всех перестановок с повторениями. Число перестановок, не меняющих данную перестановку с повторениями равно, ачисел можно переставлятьспособами, поэтому получаем следующую формулу для вычисления числа перестановок с повторениями:
(2)
Пример 4.Сколькими способами можно расселить 8 студентов по трем комнатам: одноместной, трехместной и четырехместной? Решение. Различныеспособы расселения студентов по комнатам являются перестановками с повторениями, так как внутри, например, трехместной комнаты выбранные студенты могут занимать спальные места по-разному, но эти варианты не будут являться новыми перестановками, поэтому получаем: То есть всего 280 способов расселения студентов.Вопрос. Вычислить
Сочетания.
Пусть некоторое множество содержит n элементов.
Определение 4. Всякое m- элементное подмножество n- элементного множества называется сочетанием из n элементов по m. — число всех сочетаний.
(3)
Пример 5. Для соревнований из 30 спортсменов надо выбрать трех человек. Сколькими способами это можно сделать? Решение. Команда из 3 спортсменов — это подмножество из трех элементов, то есть сочетание из 30 по 3, поэтому количество способов выбора таких команд вычисляется по формуле (3): .
Свойства сочетаний.
1. 2.. Из данных свойств следует, что, тогда, далее,,и так далее. Можно расположить эти числа в виде таблицы:
……………………………………………..
или
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
…………………..
Эта таблица в виде треугольника называется треугольником Паскаля .
Определение 5. Выражение a+b называется биномом.
(4)
Формула (4) называется биномиальной формулой Ньютона, а коэффициенты называются биномиальными коэффициентами. Из данной формулы вытекает следующее свойство числа сочетаний
(5)
Вопрос. .
Сочетания с повторениями
Пусть имеется множество, содержащее n видов элементов, поэтому есть взять какое-то подмножество этого множества, то в нем могут быть одинаковые элементы. Определение 6.Сочетание с повторениями — это m- элементное подмножество множества, содержащего n видов элементов, в котором элементы повторяются. — число всех сочетаний с повторениями из n по m. Состав m- элементного подмножества имеет вид, где. Заменяя каждое из чиселсоответствующим количеством единиц и разделяя единицы нулями, получаем набор, состоящий из m единиц и n-1 нулей. Каждому составу отвечает только одна запись из нулей и единиц, а каждая запись задает только один состав, следовательно, число различных составов равно числу перестановок с повторениями из n-1 нулей и m единиц. Получаем формулу для вычисления всех сочетаний с повторениями.
(5)
Пример 6.В кондитерском магазине продаются пирожные четырех видов: наполеоны, эклеры, песочные и бисквитные. Сколькими способами можно купить 7 пирожных? Решение. Любая покупка — это подмножество, в котором могут быть одинаковые элементы, поэтому это сочетание с повторениями. Число всех возможных покупок находим по формуле (5): .Вопрос. В формуле (5) m может быть больше n.
Размещения
Определение 7. Упорядоченное m — элементное подмножество n- элементного множества называется размещением. — число всех размещений из n элементов по m. Число всех размещений из n по m больше числа всех сочетаний из n по m, так как из каждого подмножества из m элементов с помощью перестановок можно получить m! упорядоченных подмножеств, получаем формулу для числа размещений
(6)
Пример 7. В группе 25 человек. Нужно выбрать актив группы: старосту, заместителя старосты и профорга. Сколькими способами это можно сделать? Решение. Актив группы — это упорядоченное подмножество из трех элементов, так как надо выбрать не только трех человек, но и распределить между ними должности, значит актив группы — это размещение, число всех размещений вычисляем по формуле (6): .Вопрос. Во сколько раз число сочетаний из 20 по 4 меньше числа размещений из 20 по 4?
Размещения с повторениями
Пусть дано множество из n элементов, в котором есть одинаковые элементы, тогда его подмножества тоже могут содержать одинаковые элементы. Определение 8. Упорядоченные m- элементные подмножества n- элементного множества, в которых элементы могут повторяться, называются размещениями с повторениями. — число всех размещений из n по m. В подмножестве из m элементов первый элемент можно выбрать n способами( то есть любой элемент множества) , так как элементы могут повторяться, то второй элемент тоже можно выбрать n способами, аналогично остальные элементы подмножества можно выбрать n способами, если воспользоваться правилом умножения, получим формулу для вычисления числа размещений с повторениями:
(7)
Пример 8. В лифт десятиэтажного дома вошли 5 человек. Каждый из них может выйти на любом этаже, начиная со второго. Сколькими способами они могут это сделать? Решение. Так как каждый человек может выйти на любом этаже, начиная со второго, то этажей для выхода 9. Надо выбрать этажи для возможности выхода каждого человека: для первого человека — можно выбрать любой из девяти этажей, аналогично для остальных пассажиров, тогда по формуле (7): способов.Вопрос. Вычислить .
studfiles.net
