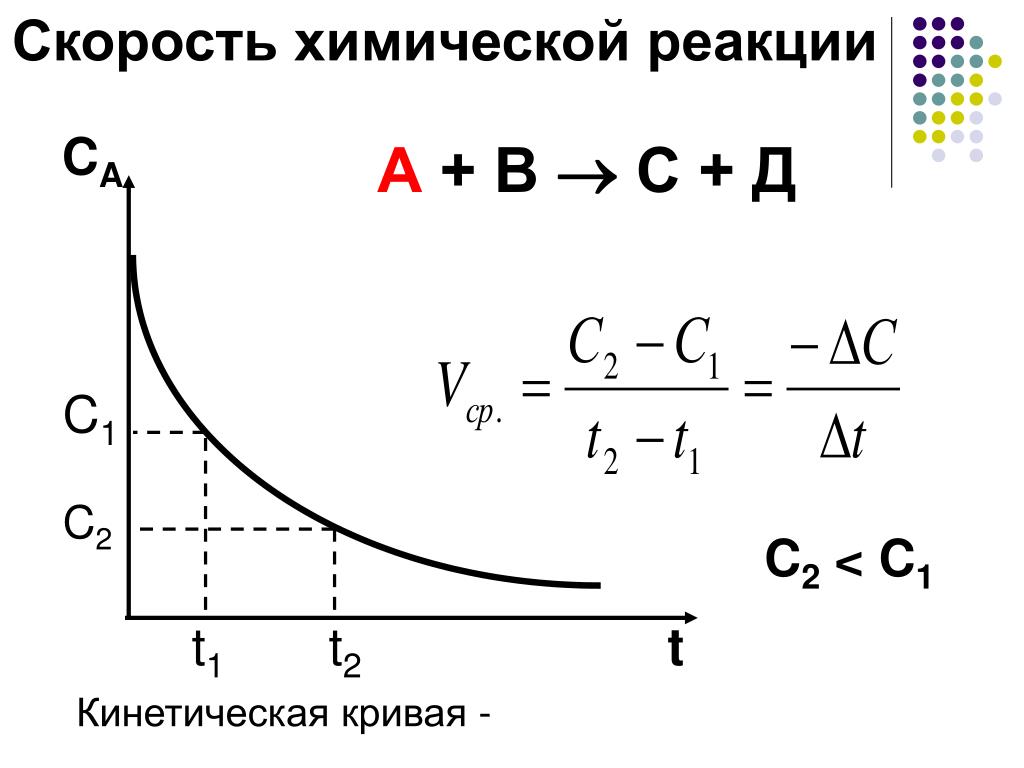
Зависимость скорости реакции от концентрации реагирующих веществ
Зависимость скорости реакций от концентрации реагирующих веществ. Количественно скорость химической реакции принято характеризовать изменением концентрации реагирующих веществ в единицу времени. По существу безразлично, концентрацию какого из реагирующих веществ рассматривать. Концентрации исходных веществ будут уменьшаться, а получаемых — возрастать. [c.463]Основным законом химической кинетики является постулат, выражающий зависимость скорости реакции от концентрации реагирующих веществ скорость реакции в каждый момент времени пропорциональна произведению возведенных в некоторую степень концентраций реагирующих веществ (закон действия масс). Так, для реакции (а) скорость может быть записана [c.320]
Порядок реакции. Порядок химической реакции определяется по более формальному признаку, чем ее молекулярность,— по виду уравнения, выражающего зависимость скорости реакций от концентраций реагирующих веществ.
В пособии по химии написано Зависимость скорости реакции от концентрации реагирующих веществ определяется законом действующих масс скорость химической реакции при постоянной температуре пропорциональна произведению концентраций реагирующих веществ, возведенных в степень их стехиометрических коэффициентов . Найдите ошибки и неточности е определении. [c.119]
Если зависимость скорости реакции от концентрации реагирующих веществ записывается в виде [c.47]
В курсе общей химии рассматривается вывод уравнения константы равновесия кинетическим путем—на основе равенства скоростей прямой и обратной реакций и зависимости скорости реакции от концентрации реагирующих веществ. Таким же путем закон действия масс был выведен Гульдбергом и Вааге (1867). Однако этот путь можно применить лищь для сравнительно простых реакций. В общем же случае следует использовать термодинамический вывод. [c.259]
Таким же путем закон действия масс был выведен Гульдбергом и Вааге (1867). Однако этот путь можно применить лищь для сравнительно простых реакций. В общем же случае следует использовать термодинамический вывод. [c.259]
Для каких реакций можно предсказать зависимость скорости реакции от концентраций реагирующих веществ [c.119]
В формальной кинетике рассматривается зависимость скорости реакции от концентрации реагирующих веществ. Она основана на ряде положений, из которых наиболее важными являются закон химической кинетики, принцип независимости протекания химических реакций в системе и уравнение материального баланса реагентов. Закономерности протекания элементарного химического акта и влияние ИХ на общую скорость процесса в формальной кинетике не рассматриваются.
Таким образом, порядок реакции характеризует формально-кинетическую зависимость скорости реакции от концентрации реагирующих веществ, а молекулярность — элементарный механизм отдельных стадий сложного процесса.
 Эти понятия совпадают только для простых по механизму реакций. [c.18]
Эти понятия совпадают только для простых по механизму реакций. [c.18]Зависимость скорости реакции от концентрации реагирующих веществ подчиняется закону действия масс при постоянной температуре скорость химической реакции пропорциональна произведению концентраций реагирующих веществ. Например, для реакции [c.32]
Зависимость скорости реакции от концентрации реагирующих веществ выражает закон действия масс скорость химической реакции пропорциональна произведению концентраций реагирующих веществ в степенях, равных стехиометрическим коэффициентам, стоящим перед формулами веществ в уравнении химической реакции [c.3]
Кинетическое уравнение характеризует зависимость скорости реакции от концентрации реагирующих веществ и температуры. Выбор формы этого уравнения может быть продиктован или теоретическими соображениями, исходя из некоторой модели, или же кинетическое уравнение является эмпирическим описанием экспериментальных данных. Во всех случаях значение констант уравнения можно определить только опытным путем. Предсказать их теоретически в настоящее время невозможно. [c.58]
Во всех случаях значение констант уравнения можно определить только опытным путем. Предсказать их теоретически в настоящее время невозможно. [c.58]
Скорость реакции зависит от природы системы, концентрации ее компонентов, присутствия в системе катализаторов или ингибиторов, а также от температуры и давления системы. Зависимость скорости реакции от концентрации реагирующих веществ описывается основным законом кинетики-.
Как вытекает из уравнения ЗДМ, для реакции синтеза аммиака повышение давления или концентрации азота и водорода в 2 раза должно вызвать увеличение скорости реакции в 16 раз. Однако наблюдаемое увеличение скорости намного меньше, т. е. реальная зависимость скорости реакции от концентрации реагирующих веществ не подчиняется ЗДМ. Объяснить это можно следующим образом. Когда записывается уравнение ЗДМ для скорости реакции синтеза аммиака исходя из химического уравнения реакции, то предполагается, что взаимодействие происходит в один акт путем одновременного столкновения трех молекул Нг и одной молекулы N2. В действительности же эта реакция протекает через ряд промежуточных стадий, каждая из которых описывается характерным для
[c.112]
В действительности же эта реакция протекает через ряд промежуточных стадий, каждая из которых описывается характерным для
[c.112]
В отличие от молекулярности реакции, порядок реакции определяется по уравнению, выражающему зависимость скорости реакции от концентрации реагирующих веществ. [c.314]
Зависимость скорости реакции от концентраций реагирующих веществ. Необходимым условием того, чтобы между частицами (атомами, молекулами, ионами) исходных веществ произошло химическое взаимодействие, является их столкновение друг с другом (соударение). Точнее говоря, частицы должны сблизиться друг с другом настолько, чтобы атомы одной из них испытывали бы действие электрических полей, создаваемых атомами другой. Только при этом станут возможны те переходы электронов и перегруппировки атомов, в результате которых образуются молекулы новых веществ — продуктов реакции. Поэтому скорость реакции пропорциональна числу соударений, которые претерпевают молекулы реагирующих веществ.
Зависимость вида (11.8) практически всегда выполняется для реакций, протекающих в одну стадию. В гл. 1П показано, что кинетическое уравнение, описывающее зависимость скорости реакции от концентрации реагирующих веществ для такой одностадийной (элементарной) реакции, протекающей по стехиометрическому уравнению [c.44]
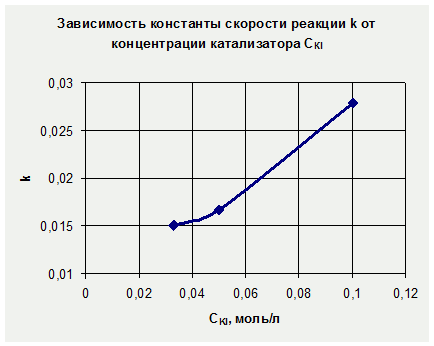
Запись данных опыта. Данные опыта занести в таблицу. Начертить график зависимости скорости реакции от концентрации реагирующих веществ. На оси абсцисс отложить в определенном масштабе относительные концентрации Тиосульфата натрия, на оси ординат —соответствующие им скорости. [c.44]
О характере зависимости скорости реакции от концентрации реагирующих веществ можно судить по значениям константы скорости и порядка реакции. Это очевидно из сравнения кинетических кривых реакций разных порядков, приведенных на рис. П1.3. [c.157]
Зависимость скорости реакции от концентрации реагирующих веществ выражается кинетическим уравнением [c. 59]
59]
Зависимость скорости реакции от концентраций реагирующих веществ выражается законом действия масс скорость химической реакции прямо пропорциональна произведению молярных концентраций реагирующих веществ, взятых в степени, равной стехиомет-рическому коэффициенту данного вещества в уравнении реакции. Для реакции общего вида [c.105]
Таким образом, только в отдельных простейших случаях исходя из химического уравнения реакции можно вывести уравнение ЗДМ, описывающее реальную зависимость скорости реакции от концентрации реагирующих веществ. В большинстве других случаев этого сделать нельзя, так как из хими-уравнения следует только то, какие вещества и в каких мольных соотношениях взаимодействуют. О механизма протекания реакций химические уравнения ничего не говорят, Для вывода уравнения ЗДМ, описывающего реальную зависимость скорости реакции от концентраций реагирующих веществ, необходимо изучить механизм и расшифровать все стадии реакций.  113]
113]
Вторая стадия — самая медленная (лимитирующая). Каков ожидаемый вид зависимости скорости реакции от концентрации реагирующих веществ [c.153]
Закон действия масс первоначально был сформулирован как выражение зависимости скорости реакции от концентрации реагирующих веществ, см. 11.9. [c.120]
Зависимость скорости реакции от концентрации реагирующих веществ [c.111]
Удобнее всего рассмотреть зависимость скорости реакции от концентрации реагирующих веществ для случая, когда все реагирующие вещества находятся в газообразном состоянии. Особенностью таких реакций является то, что химическое взаимодействие протекает во всем объеме реакционной среды. Такие реакции называются гомогенными в отличие от гетерогенных реакций, когда реагирующие вещества находятся в различных агрегатных состояниях и взаимодействие веществ происходит на поверхности одного из них.
Уравнения, показывающие зависимость скорости реакции от концентраций реагирующих веществ, называются кинетическими уравнениями. [c.81]
Чтобы осуществлялось химическое взаимодействие веществ А и В, пх молекулы (частицы) должны столкнуться. Чем больше столкновений, тем быстрее протекает реакция. А число столкновений тем больше, чем выше концентрация реагирующих веществ. Отсюда на основе обширного экспериментального материала сформулирован основной закон химической кинетики, устанавливающий зависимость скорости реакции от концентрации реагирующих веществ скорость химической реакции пропорциональна произведению концентраций реагирующих веществ. Для приведенной выше реакции этот закон выразится уравнением
Во второй половине XIX века были разработаны начала учения о скорости химических реакций — химической кинетике—и учения о равновесиях в химических системах. Вскоре после указанных выше работ Бекетова шведскими учеными Гульд-бергом и Вааге (1867) был открыт закон, количественно выражающий зависимость скорости реакции от концентрации реагирующих веществ и выражающий соотношение между концентрациями веществ, участвующих в реакции при равновесии, — закон действия масс. [c.17]
Вскоре после указанных выше работ Бекетова шведскими учеными Гульд-бергом и Вааге (1867) был открыт закон, количественно выражающий зависимость скорости реакции от концентрации реагирующих веществ и выражающий соотношение между концентрациями веществ, участвующих в реакции при равновесии, — закон действия масс. [c.17]
Характер зависимости скорости реакции от концентрации реагирующих веществ определяется порядком реакции. [c.21]
Зависимость скорости реакции от концентрации реагирующих веществ определяется основным законом химической кинетики скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ. [c.68]
Действительный, экспериментально найденный характер зависимости скорости реакции от концентраций реагирующих веществ и определяет порядок реакции (который лишь для элементарных реакций определяется суммой стехиометрических коэффициентов). В общем случае для реакции [c. 201]
201]
Все данные опыта занесите в таблицу. Сделайте вывод о зависимости скорости реакции от концентрации реагирующих веществ. Как согласуются ваши наблюдения с законом действия масс [c.42]
На первой стадии изучения реакции надо прежде всего определить скорость протекания изучаемой реакции. Эта область кинетических исследований называется формальной кинетикой. Она включает также изучение зависимости скорости реакции от концентрации реагирующих веществ, температуры и давления. [c.111]
Зависимость скорости реакции от концентрации реагирующих веществ выражена в законе действия масс Скорость реакции прямо пропорциональна произведению концентраций реагируюи их веществ [c.78]
Для объяснения зависимости скорости реакции от концентрации реагирующих веществ необходимо знать, сколько молекул (атомов или ионов) реагента одновременно участвует в одном элементарном акте реакции, т. е. молекулярность реакции. Если в элементарном акте участвует одна молекула реагента (как, например, в реакции разложения МзОд = N02 + + N0 4- О2), то это — мономоле к улярная реакция, если две — бимолекулярная, если три — тримоле-кулярная. Может показаться, что для нахождения моле-кулярности реакции достаточно знать коэффициенты в уравнении процесса. Однако сам процесс может складываться из различных элементарных актов, происходящих последовательно или параллельно. В этом случае уравнение химической реакции отражает лишь суммарный эффект этих взаимодействий. [c.171]
Если в элементарном акте участвует одна молекула реагента (как, например, в реакции разложения МзОд = N02 + + N0 4- О2), то это — мономоле к улярная реакция, если две — бимолекулярная, если три — тримоле-кулярная. Может показаться, что для нахождения моле-кулярности реакции достаточно знать коэффициенты в уравнении процесса. Однако сам процесс может складываться из различных элементарных актов, происходящих последовательно или параллельно. В этом случае уравнение химической реакции отражает лишь суммарный эффект этих взаимодействий. [c.171]
Зависимость скорости реакции от концентрации реагирующих веществ можно понять, исходя из представлений молекулярно-кинетической теории. Для этого рассмотрим в качестве примера взаимодействие между двумя газообразными веществами при условии, что их молекулы сталкиваются друг с другом беспрепятственно. Молекулы газов, находясь в непрерывном движении, неизбеж-сталкиваются друг с другом. Взаимодействие между молекулами, очевидно, может происходить только при их столкновении, следовательно, чем чаще будут сталкиваться молекулы, тем быстрее будет протекать химическая реакция. Частота же столкновений молекул прежде всего зависит от числа реагирующих молекул в единице объема, т. е. от концентраций реагирующих веществ. [c.129]
Частота же столкновений молекул прежде всего зависит от числа реагирующих молекул в единице объема, т. е. от концентраций реагирующих веществ. [c.129]
Для химического взаимодействия веществ А и В их молекулы или частицы должны столкнуться. Чем больше столкновений, тем быстрее протекает реакция. А число столкновений тем больше, чем выше концентрация реагирующих веществ. Отсюда на основе обншрного экспериментального материала сформулирован основной закон химической кинетики, устанавливающий зависимость скорости реакции от концентрации реагирующих веществ [c.112]
Для объяснения зависимости скорости реакции от концентрации реагирующих веществ необходимо знать, сколько молекул (атомов или ионов) реагента одновременно участвует ь одном элементарном акте реакции, т. е. молекулярность реакции. Если в элементарном акте участвует одна молекула реагента (как, например, в реакции разложения N205=N02+N0 + 02), то это — мои о молекулярная реакция, если, две — бимолекулярная, если три — тримолекулярн а я. Может показаться, что для [c.129]
Может показаться, что для [c.129]
Считая началом реакции момент сливания растворов реагентов, а концом — момент выделения свободного иода (появление синей окраски), можно установить время течения процесса по секундомеру или метроному. Изменяя концентрацию раствора одного из реагентов (в данном опыте — иодата калия), можно установить зависимость скорости реакции от концентрации реагирующих веществ при посто51нной температуре. [c.40]
Зависимость скорости химических реакций от концентраций реагирующих веществ. Закон действия масс
Скорость реакции зависит от природы реагирующих веществ, их концентрации, температуры и от присутствия в системе катализаторов. В тех случаях, когда для протекания реакции необходимо столкновение двух реагирующих частиц (молекул, атомов), зависимость скорости реакции от концентраций определяется законом действия масс при постоянной температуре скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ. [c.89]
[c.89]
Основным законом химической кинетики является постулат, выражающий зависимость скорости реакции от концентрации реагирующих веществ скорость реакции в каждый момент времени пропорциональна произведению возведенных в некоторую степень концентраций реагирующих веществ (закон действия масс). Так, для реакции (а) скорость может быть записана [c.320]
Химическая кинетика. Скорость химических реакций. Зависимость скорости реакции от природы, поверхности соприкосновения и концентрации реагирующих веществ, температуры реакции и катализаторов. Закон действующих масс для скорости химической реакции. Понятие о катализе. Катализаторы и ингибиторы. [c.26]
В пособии по химии написано Зависимость скорости реакции от концентрации реагирующих веществ определяется законом действующих масс скорость химической реакции при постоянной температуре пропорциональна произведению концентраций реагирующих веществ, возведенных в степень их стехиометрических коэффициентов . Найдите ошибки и неточности е определении. [c.119]
Найдите ошибки и неточности е определении. [c.119]
Зависимость скорости химических реакций от концентрации реагирующих веществ. Закон действия масс [c.314]
Зависимость скорости химической реакции от концентрации определяется законом действия масс скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ. [c.84]
Зависимость скорости химической реакции от концентрации реагирующих веществ при постоянстве других факторов отражена в законе действующих масс скорость реакции при постоянной температуре прямо пропорциональна произведению мольных концентраций реагирующих веществ, взятых в степенях, равных коэффициентам, стоящим перед формулами данных веществ в уравнении реакции. [c.53]
Количественную зависимость скорости химической реакции вывел H.H. Бекетов. Эта зависимость известна под названием закона действующих масс скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций реагирующих веществ.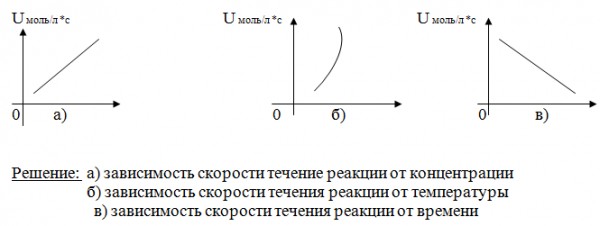 Если, например, проходит реакция [c.35]
Если, например, проходит реакция [c.35]
Количественно зависимость скорости химической реакции от концентрации реагирующих веществ определяется законом действия масс. В наиболее простом случае, когда молекулы двух реагирующих веществ взаи- [c.36]
Соотношения, связывающие концентрации и парциальные давления в выражении констант равновесия Кс и К , так же как и соотношения зависимости скорости химических реакций от концентрации реагирующих веществ, выражают закон действующих масс. Из соотношений следует, что изменение концентрации (или парциального давления) одного вещества, участвующего в реакции, влечет за собой изменение концентраций (или парциальных давлений) остальных веществ. Причем изменение будет таким, что численное значение константы равновесия при данных условиях постоянно. [c.114]
Закон действия масс — соотношение, лежащее в основе химической кинетики.
 Одиако он строго выполняется только в пределах применимости к реагирующим веществам законов идеальных газов. Ои также применим и к реакциям в сильно разбавленных растворах. Для других условий зависимости скорости химических реакций от концентрации приобретают более сложную форму. [c.91]
Одиако он строго выполняется только в пределах применимости к реагирующим веществам законов идеальных газов. Ои также применим и к реакциям в сильно разбавленных растворах. Для других условий зависимости скорости химических реакций от концентрации приобретают более сложную форму. [c.91]Описываемая законом действующих масс зависимость скорости химической реакции от концентраций реагирующих веществ справедлива лишь для реакций, проходящих в гомогенной (однородной) — газовой или жидкой — фазе, и не распространяется на гетерогенную (неоднородную) систему, для которой существенно влияние поверхности соприкосновения реагирующих веществ. Скорость гетерогенной реакции прямо пропорциональна площади поверхности соприкосновения реагирующих веществ. [c.57]
Зависимость скорости реакции от концентрации реагирующих веществ выражает закон действия масс скорость химической реакции пропорциональна произведению концентраций реагирующих веществ в степенях, равных стехиометрическим коэффициентам, стоящим перед формулами веществ в уравнении химической реакции [c. 3]
3]
Константа скорости химического процесса — это параметр, который входит в кинетическое уравнение (IV.6). Константа скорости реакции к является наряду со скоростью реакции одной из основных величин в химической кинетике. Как следует из закона действующих масс (уравнение (VI.4)), константа скорости реакции к показывает, с какой скоростью идет химический процесс при концентрациях реагирующих веществ, равных единице. Зависимость константы скорости реакции к от температуры наиболее часто выражают в виде уравнения Аррениуса [c.65]
Скорость как гомогенной, так и гетерогенной реакции при постоянном давлении и неизменном количестве посторонних примесей зависит от температуры и концентрации реагирующих веществ. Как было показано в 4-2, зависимость скорости химической реакции от концентраций реагирующих веществ выражается законом действующих масс. [c.58]
Зависимость скорости химической реакции от концентрации реагирующих веществ устанавливает закон действующих масс.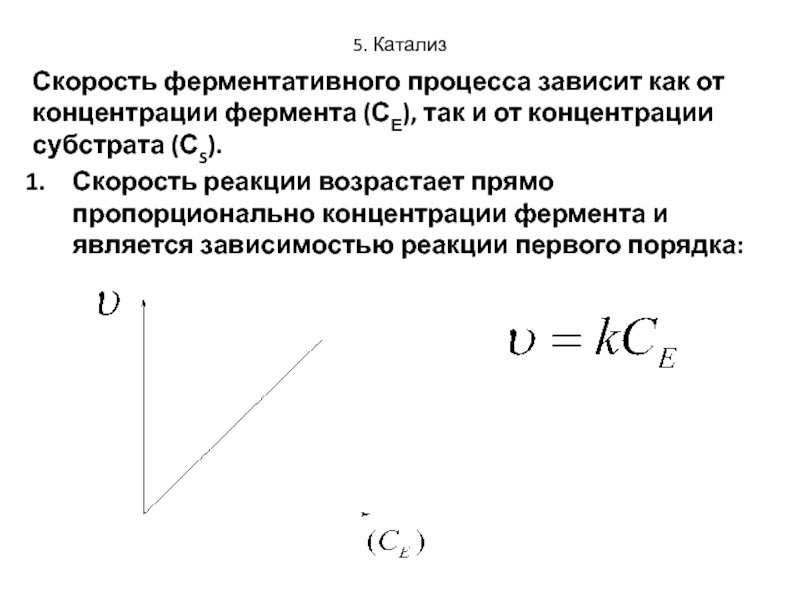 Частная формулировка этого закона была дана Н. Н. Бекетовым в 1865 г. при изучении влияния давления газообразного водорода на скорость вытеснения им металлов из растворов солей. [c.108]
Частная формулировка этого закона была дана Н. Н. Бекетовым в 1865 г. при изучении влияния давления газообразного водорода на скорость вытеснения им металлов из растворов солей. [c.108]
Зависимость скорости химической реакции от концентрации реагирующих веществ выражается законом действия масс скорость химической реакции прямо пропорциональна произведению молярных концентраций реагирующих веществ, взятых в степенях, равных стехиометрическим коэффициентам соответствующих веществ в уравнении реакции. [c.154]
Зависимость скорости химической реакции (v) от произведения концентраций реагирующих веществ выражается законом действия масс [c.398]
Давно замечено, что скорость химической реакции зависит от температуры и первоначальной концентрации реагирующих веществ. В 1867 г. Гульберг и Вааге открыли так называемый закон действия масс, устанавливающий зависимость скорости химической реакции от концентрации. Согласно этому закону, скорость химической реакции прямо пропорциональна концентрации реагирующих веществ. [c.4]
[c.4]
Зависимость скорости реакции от концентрации реагирующих веществ подчиняется закону действия масс при постоянной температуре скорость химической реакции пропорциональна произведению концентраций реагирующих веществ. Например, для реакции [c.32]
Зависимость скорости реакции от концентрации дается законом действующих масс скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ. Для реакции тА+пВ-> ее скорость, согласно закону действующих масс, выражается равенством [c.157]
Развитие представлений о кинетике химических реакций. Классическая кинетика, основываясь на законе действующих масс и на законе распределения Максвелла — Больцмана, создала фундаментальные -количественные зависимости скорости протекания химических реакций от таких основных параметров, как концентрация реагирующих веществ, температура и давление процесса. При этом сохранялось представление о чисто молекулярном механизме протекания реакций, описываемом обычными стехиометрическими уравнениями.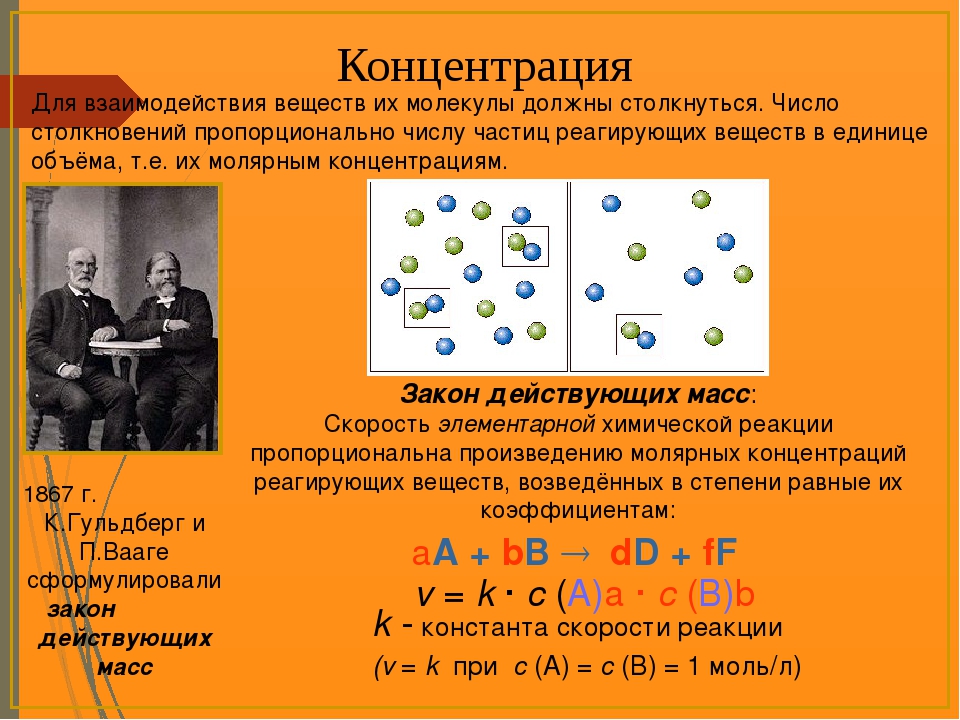 Установленные количественные зависимости были подтверждены многими экспериментальными наблюдениями. Вместе с тем одновременно накапливались и такие экспериментальные факты, которые эти зависимости уже не в состоянии было описать. Наблюдались химические реакции, протекавшие или значительно медленнее, или значительно быстрее, чем это вытекало из установленных соотношений. Понадобилось дальнейшее развитие кинетических представлений, отчасти связанных с некоторой детализацией простейшего молекулярного механизма, а в основном—с переходом на так называемый цепной механизм реакций, в котором основную роль играют [c.53]
Установленные количественные зависимости были подтверждены многими экспериментальными наблюдениями. Вместе с тем одновременно накапливались и такие экспериментальные факты, которые эти зависимости уже не в состоянии было описать. Наблюдались химические реакции, протекавшие или значительно медленнее, или значительно быстрее, чем это вытекало из установленных соотношений. Понадобилось дальнейшее развитие кинетических представлений, отчасти связанных с некоторой детализацией простейшего молекулярного механизма, а в основном—с переходом на так называемый цепной механизм реакций, в котором основную роль играют [c.53]
Фундаментом химической кинетики является закон действия масс, при идеальном соблюдении которого в разбавленных растворах скорость любой химической реакции пропорциональна произведению концентраций веществ, действительно участвующих в реакции. Она не зависит ни от концентраций других веществ, ни от наличия или отсутствия других реакций.
 Если вещество может реагировать само с собой, то, согласно этому закону, скорость реакции будет пропорциональна квадрату, кубу или даже более высоким степеням концентрации такого вещества. В частности, прямая и обратная реакции обратимого процесса являются независимыми, а суммарная скорость обратимой реакции равна разности скоростей прямой и обратной реакции. При этом для каждой реакции зависимость скорости от концентраций реагентов будет такой же, как и в отсутствие противоположного процесса. [c.71]
Если вещество может реагировать само с собой, то, согласно этому закону, скорость реакции будет пропорциональна квадрату, кубу или даже более высоким степеням концентрации такого вещества. В частности, прямая и обратная реакции обратимого процесса являются независимыми, а суммарная скорость обратимой реакции равна разности скоростей прямой и обратной реакции. При этом для каждой реакции зависимость скорости от концентраций реагентов будет такой же, как и в отсутствие противоположного процесса. [c.71]Скорость реакции зависит от концентраций А и В, однако заранее нельзя утверждать, что она прямо пропорциональна концентрации того или другого. Количественно зависимость между скоростью реакции и молярными концентрациями реагирующих веществ описывается основным законом химической кинетики — законом действующих масс [c.67]
Количественно зависимость между скоростью реакции и молярными концентрациями реагирующих веществ описывается основным законом химической кинетики — законом действующих масс. [c.90]
[c.90]
Закон действия масс. Основным законом химической кинетики является открытый в 1864—1867 гг. Гульдбергом и Вааге (Норвегия) закон действия масс, согласно которому скорость элементарной реакции пропорциональна произведению концентраций реагирующих веществ в степенях, равных стехиометрнческим коэффициентам. Такая зависимость скорости реакции от концентрации обусловлена тем, что вероятность столкновения молекул и, следовательно, нх взаимодействия, пропорциональна произведению концентраций реагентов. [c.214]
Зависимость скорости химических реакций от концентрации реагирующих веществ и соотношение между концентрациями про- дуктов реакции и реагентов в состоянии химического равновесия устанавливаются законом действующих масс, открытым Гульд-1 бергом и Вааге (1864 —1867) [c.32]
Одним из основных факторов, определяющих ско-рость химических реакций, является концентрация реагирующих веществ. Это объясняется тем, что для взаимодействия между молекулами необходимо их столкновение, поэтому чем выше концентрация реагирующих веществ, тем больше молекул находится в единице объема и тем чаще они сталкиваются друг с другом. Зависимость скорости наиболее простых химических реакций от концентрации определяется законом действия масс, по которому скорость химической реакции пропорциональна произведению концентраций реагирующих веществ, взятых в степени, равной стехиометрическому коэффициенту, стоящему перед формулой вещества в уравнении реакции. Нач пример, для реакции окчсления оксида азота ско [c.83]
Зависимость скорости наиболее простых химических реакций от концентрации определяется законом действия масс, по которому скорость химической реакции пропорциональна произведению концентраций реагирующих веществ, взятых в степени, равной стехиометрическому коэффициенту, стоящему перед формулой вещества в уравнении реакции. Нач пример, для реакции окчсления оксида азота ско [c.83]
В 1867 г. шведские ученые Г. Гульдберг и П. Вааге открыли закон действующих масс, устанавливающий зависимость скорости химической реакции от концентрации реагирующих веществ и выражающий соотношение между концентрациями веществ, участвующих в реакции при равновесии. [c.7]
Зависимость скорости элементарной реакции от концентрации реагирующих веществ выражает, как известно, закон действующих масс (Гульдберг и Вааге). В соответствии с этим законом, i.opo Tb химической реакции пропорциональна концентрациям [c.20]
Во второй половине XIX века были разработаны начала учения о скорости химических реакций — химической кинетике—и учения о равновесиях в химических системах. Вскоре после указанных выше работ Бекетова шведскими учеными Гульд-бергом и Вааге (1867) был открыт закон, количественно выражающий зависимость скорости реакции от концентрации реагирующих веществ и выражающий соотношение между концентрациями веществ, участвующих в реакции при равновесии, — закон действия масс. [c.17]
Вскоре после указанных выше работ Бекетова шведскими учеными Гульд-бергом и Вааге (1867) был открыт закон, количественно выражающий зависимость скорости реакции от концентрации реагирующих веществ и выражающий соотношение между концентрациями веществ, участвующих в реакции при равновесии, — закон действия масс. [c.17]
Основопологающим в химической кинетике является понятие о скорости химических реакций. Скорость химической 15сакции зависит от многих факторов, но важнейшими являются природа реагируюгцих веществ, концентрация, температура, давление и действие катализаторов. При постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ. Данное количественное соотношение известно как закон действующих масс. Зависимость скорости реакции от температуры выражается правилом Вант-Гоффа. Если процесс протекает только в одном направлении, то его называют необратимым. Процессы, протекающие в двух противоположных направлениях, называют обратимыми. Когда в обратимом процессе скорости прямой и обратной реакций становятся равными, то в системе устанавливается динамическое равновесие. Смещение химического равновесия осуществляется в соответствии с принципом Ле Шателье. [c.102]
Когда в обратимом процессе скорости прямой и обратной реакций становятся равными, то в системе устанавливается динамическое равновесие. Смещение химического равновесия осуществляется в соответствии с принципом Ле Шателье. [c.102]
Основным законом, устанавливающим количественную зависимость между концентрациями продуктов реакции и исходных веществ в условиях равновесия, является закон действующих масс, выведенный Н. Гульдбергом и П. Вааге (1867) скорость химических реакций, протекающих в однородной среде, при постоянной температуре прямо пропорциональна произведению концентраций (активностей) реагирующих веществ, возведенных в степень их стехисметрических коэффициентов. [c.41]
Скорость химической реакции и влияние на нее концентрации реагирующих веществ и температуры. Необратимые и обратимые реакции. Концентрация и действующая масса. Закон действия масс. Константа химического равновесия. Смйцение химического равновесия в зависимости от различных факторов. Принцип Ле Шателье. Скорость гетерогенных реакций и влияние на нее поверхности твердой фазы. Катализ. [c.71]
Принцип Ле Шателье. Скорость гетерогенных реакций и влияние на нее поверхности твердой фазы. Катализ. [c.71]
Закон действующих масс. В 1864 г. Гульберг и Вааге установили зависимость между скоростью химической реакции и концентрациями реагирующих веществ ( действующую массу эти исследователи считали пропорциональной концентрации). [c.117]
Зависимость скорости элементарной реакции от концентрации реагирующих веществ выражает, как известно, закон действующих масс (Гульдберг и Вааге). В соответствии с этим законом, скорость химической реакции пропорциональна концентрациям реагирующих веществ в степенях, равных их стехиометрическим коэффициентам [c.347]
Зависимость скорости простых реакций (т, е. реакций, протекающих через один элементарный акт) от концентрации описывается законом действующих масс, установленным К. Гульдбергом и П, Вааге в 1867г. скорость химической реакции прямо пропорциональна произведению концентрации реагирующих веществ, возведенных в степень их стехиометрических коэффициентов. [c.73]
[c.73]
Влияние концентраций реагирующих веществ. Уравнение, показывающее зависимость скорости реакции от концентрации реагируюй1их веществ и известное под названием закона действия масс, является основным законом химической кинетики. Рассмотрим приложение этого закона для различных реакций [c.106]
Зависимость скорости реакции от концентрации реагирующих веществ, сформулированная Гульдбергом и Вааге (1867), получила назв шие закона действующих масс скорость химической реакции прямо пропорциональна произведению молярных концентраций реагт -рующих веществ, возведенних в степени их стехиометрических коэффициентов. Например, для реакций, протекающих в водных растворах неэлектролитов или в разбавленных растворах электролитов, по уравнению [c.14]
Зависимость скорости реакции от концентраций веществ. Задачи 22
Задача 22.
Реакция идет по уравнению: 2NО + О2 = 2NО2
Начальные концентрации реагирующих веществ были (моль/л): С(NО) = 0,8; С(О2) = 0,6. Как изменится скорость реакции, если концентрацию кислорода увеличить до 0,9 моль/л, а концентрацию оксида азота (II) – до 1,2 моль/л?
Как изменится скорость реакции, если концентрацию кислорода увеличить до 0,9 моль/л, а концентрацию оксида азота (II) – до 1,2 моль/л?
Решение:
Зависимость скорости реакции от концентраций определяется законом действия масс: при постоянной температуре скорость химической реакции прямо пропорциональна произведению молярных концентраций реагирующих веществ.
v = k[NО]2[О2]
Обозначим скорость реакции до изменения концентраций v1, а после изменения концентраций v2.
Тогда
v1 = k[(0,82)2 . 0,6];
v2 = k[(1,2)2 . 0,9].
изменение скорости (v2/v1) равно:
v2/v1 = k[(1,2)2 . 0,9]/k[(0,82)2 .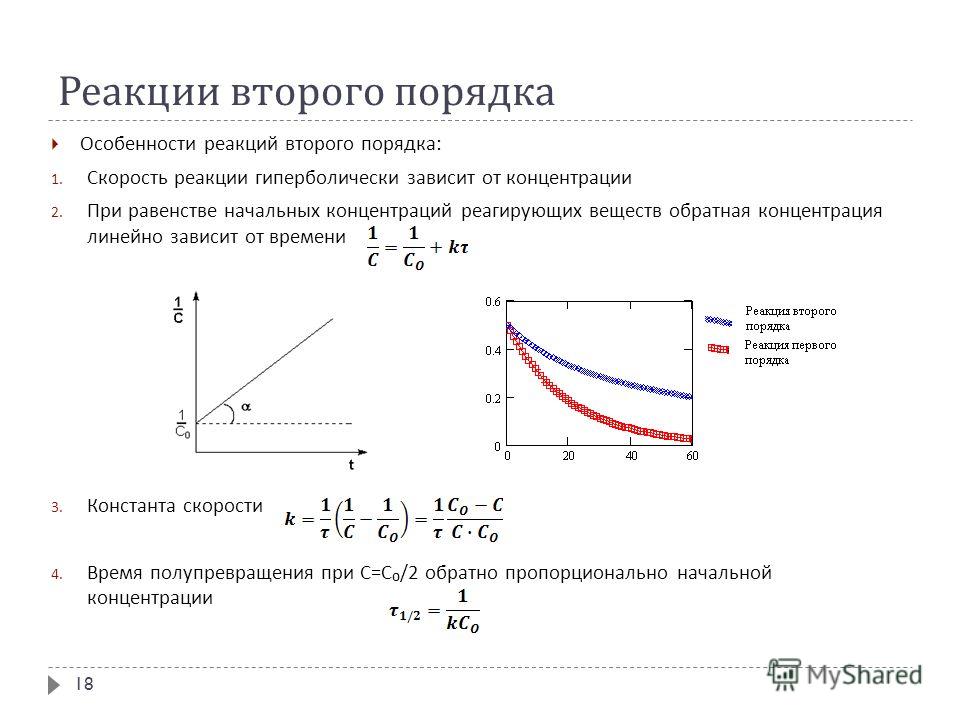 0,6] = 1,296/0,403 = 3,2.
0,6] = 1,296/0,403 = 3,2.
Ответ: Скорость реакции возрастет в 3,2 раза.
Задача 23.
Реакция между внщнствами А и В протекает по уравнению: 2А + В = С. Концентрация вещества А равна 6 моль/л, В – 5 моль/л. Константа скорости реакции равна 0,5 л2/моль.с. Вычислить скорость реакции в начальный момент и в тот момент, когда в реакционной смеси останется 45% вещества В.
Решение:
Зависимость скорости реакции от концентраций определяется законом действия масс: при постоянной температуре скорость химической реакции прямо пропорциональна произведению молярных концентраций реагирующих веществ.
v = k[А]2[В]
Обозначим скорость реакции до изменения концентраций v1, а после изменения концентраций — v2.
Тогда
v1 = (0,5 . 62. 5) = 90 моль/л.с
62. 5) = 90 моль/л.с
Для нахождения v2 надо рассчитать концентрацию веществ А и В :
По условию задачи в реакционной смеси 45% вещества В, что составляет (5 . 0,45) = 2,25 моль/л. Следовательно, прореагировало 2,25 моля вещества В.
Исходя из уравнения реакции вещества прореагировало в 2 раза больше — (2 . 2,25) = 4,5 моль/л. Следовательно, в реакционной смеси осталось:
(6 — 4,5) = 1,5 моль/л.
Отсюда
v2 = (0,5 . 1,52. 2,25) = 2,53 моль/л.с.
Ответ: v1 = 90 моль/л.с; v2 = 2,53 моль/л.с.
Зависимость скорости гомогенной химической реакции от концентрации реагирующих веществ
Чтобы произошло химическое взаимодействие, необходимо столкновение реагирующих частиц.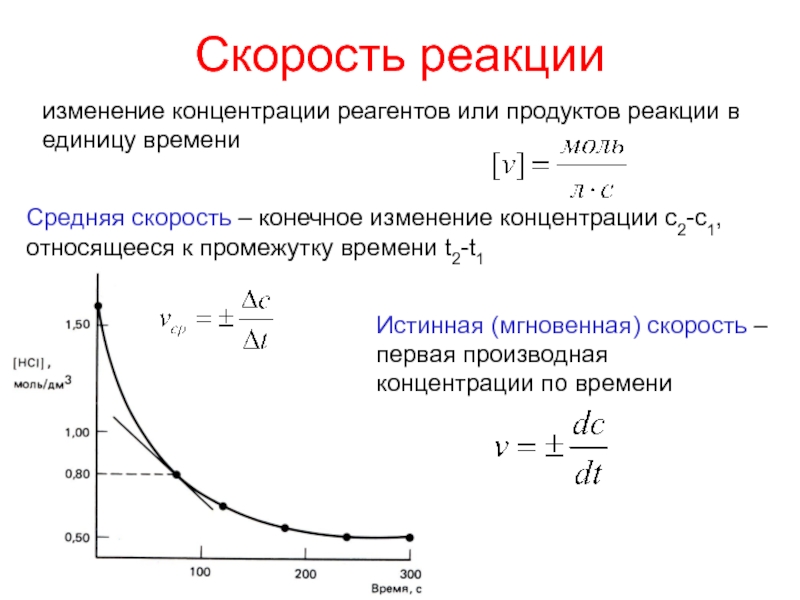 При одной и той же температуре количество столкновений растет с увеличением количества реагирующих частиц в единице объема, т.е. с возрастанием концентрации реагентов. Соответственно, скорость реакции повышается с увеличением концентрации реагирующих веществ.
При одной и той же температуре количество столкновений растет с увеличением количества реагирующих частиц в единице объема, т.е. с возрастанием концентрации реагентов. Соответственно, скорость реакции повышается с увеличением концентрации реагирующих веществ.
Выведенное на основе экспериментальных данных уравнение, выражающее зависимость скорости от концентраций реагирующих веществ, показывает, что скорость химической реакции пропорциональна произведению концентраций реагентов в степенях, называемых порядками реакции по реагентам и определяемых опытным путем.
Уравнение, устанавливающее зависимость скорости от концентрации реагирующих веществ, называется дифференциальным кинетическим уравнением реакции.
Например, для реакции аА + bB = cC + dD выражение для скорости реакции будет иметь следующий вид:
υ = k[A]n [B]m
(2.3)
где k – коэффициент пропорциональности, называемый константой скорости реакции; [A] и [B] молярные концентрации реагирующих веществ; n и m показатели степеней при концентрациях реагентов (порядки реакции по веществам А и B).
Общим порядком, или просто порядком реакции, называется величина, равная сумме показателей степеней при концентрациях реагентов в кинетическом уравнении реакции (n+m). Порядок реакции равен сумме порядков по реагирующим веществам.
Константа скорости k – постоянная величина (при T = const) и не зависит от концентрации реагентов. Она определяется природой реагирующих веществ и зависит от температуры.
Из уравнения (2.3) следует, что при единичных концентрациях реагирующих веществ (например, [A] = [B] = 1 моль/л) константа скорости реакции численно равна скорости реакции.
Из этого же уравнения видно, что размерность константы скорости реакции зависит от порядка реакции, поскольку размерность скорости реакции для всех гомогенных реакций одинакова. Единицу измерения константы скорости реакции определяют из анализа размерностей.
Порядок реакции зависит от ее сложности.
Для простой (элементарной) реакции стехиометрическое уравнение передает механизм процесса, стехиометрические коэффициенты уравнения реакции совпадают с порядками по реагентам, молекулярность совпадает с общим кинетическим порядком.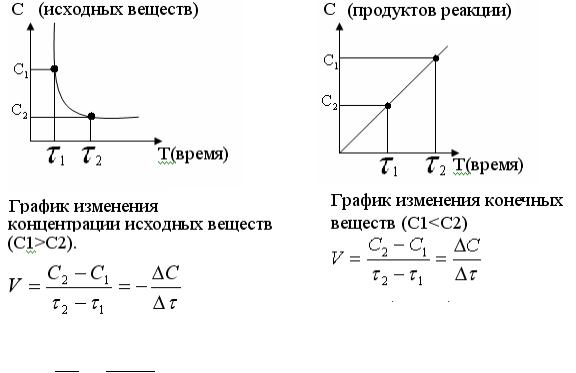
Для необратимой элементарной реакции зависимость скорости от концентрации реагентов выражается законом действующих масс.
При постоянной температуре скорость элементарной химической реакции пропорциональна произведению концентраций реагирующих веществ в степенях, равных их стехиометрическим коэффициентам.
Рассмотрим необратимые элементарные реакции разного вида и применим к ним закон действующих масс.
1. Скорость реакции первого порядка
А → продукты,
характеризуется кинетическим уравнением
υ = k [A].
Константа скорости реакции первого порядка имеет размерность
[с-1].
Например, для термораспада диметилового эфира
Ch4OCh4 → Ch5 + h3 + CO,
υ = k [Ch4OCh4]
2. Скорость реакции второго порядка в соответствии с законом действующих масс равна:
2А → продукты, υ = k [А]2;
А + В → продукты, υ = k [А] [В].
Размерность константы скорости реакции второго порядка
[л· моль-1·с-1].
Например, для реакции разложения иодида водорода
2 HI → h3 + I2
υ = k [ HI]2.
Или, для реакции этерификации уксусной кислоты этанолом
Ch4COOH + C2H5OH → Ch4COOC2H5 + h3O,
υ = k [Ch4COOH] [C2H5OH].
3. Скорость реакции третьего порядка
A + B + C → продукты, υ = k [А] [В] [C],
2A + B → продукты, υ = k [А]2 [B];
3A → продукты, υ = k [А]3.
Размерность константы скорости третьего порядка [л²· моль-2·с-1].
Например, реакция взаимодействия оксида азота с хлором
2NO + Cl 2 → 2NOCl,
υ = k [NO]2 [Cl 2].
Закон действующих масс справедлив только для элементарных реакций.
В большинстве случаев реакции многостадийны.
Для сложных (многостадийных) реакций порядки реакции по реагентам не совпадают со стехиометрическими коэффициентами, общий порядок реакции не равен сумме стехиометрических коэффициентов.
Порядок сложной реакции может быть целым, дробным числом и даже равным нулю.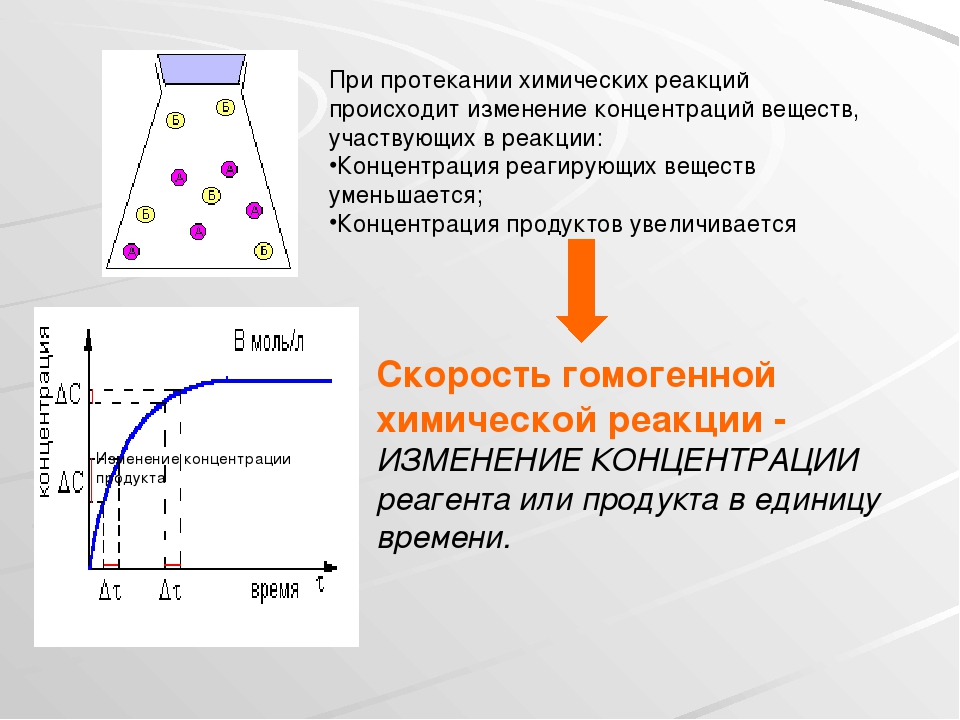
Порядок сложной реакции определяют экспериментально.
Например, реакция: 2N2O5 = 2N2O4 + O2 является сложной и протекает по стадиям:
N2O5 = N2O3 + O2 (а) N2O3 = NO2 + NO (б) NO + N2O5 = 3NO2 (в)
2NO2 = N2O4. (г)
Наиболее медленно протекает стадия (а), т.е. эта стадия является лимитирующей. Скорость стадии (а) и соответственно всей сложной реакции будет равна
υ ≈ υ =
a
k [N2O5].
a
Так, приведенная выше сложная реакция имеет первый порядок по оксиду азота (V) и общий первый порядок.
2.3. Графический метод определения констант дифференциального кинетического уравнения
Определим константы дифференциального кинетического уравнения для следующей реакции:
аА + bB → продукты.
Зависимость скорости от концентраций выражается уравнением
(2.3)
υ = k[A]n [B]m .
Прологарифмируем это выражение
ln υ = lnk + n ln[A] + m ln[B] .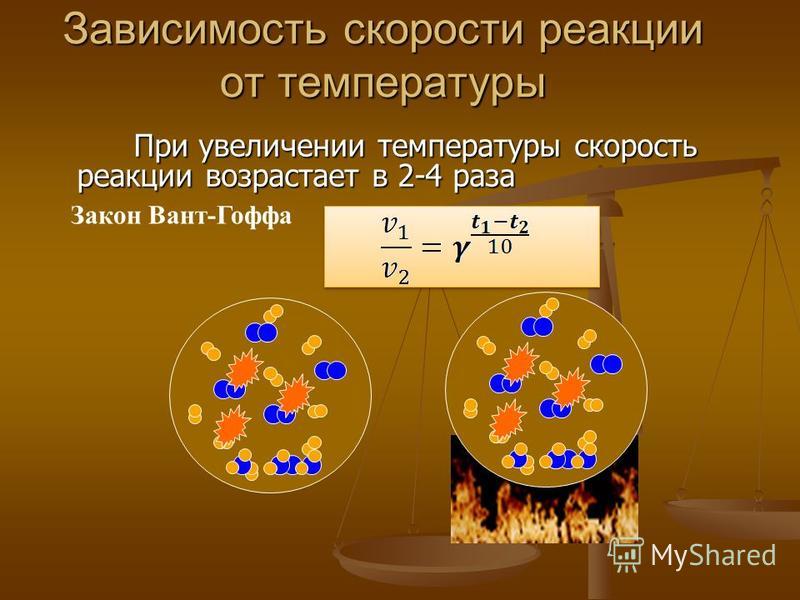 (2.4)
(2.4)
Так как величины k, n и m для рассматриваемой реакции (при T =
const) являются постоянными и не зависят от концентрации реагентов, то для их нахождения достаточно определить зависимость скорости реакции от концентрации одного из реагентов при фиксированной концентрации другого реагента.
Пусть в трех опытах концентрация вещества А будет постоянной
и равной [A]0, тогда в уравнении (2.4) сумма ( ln k + n ln[A]
0
величиной постоянной, обозначим ее
) будет тоже
ln k + n ln[A]
0
= D .
Тогда уравнение (2.4) можно переписать как
ln υ = m ln[B] + D . (2.5)
Зависимость (2.5) представляет собой в координатах ln[B] —
ln υ
уравнение прямой линии, тангенс угла наклона которой к оси абсцисс численно равен порядку реакции по веществу В.
По экспериментальным данным строят график зависимости от ln[B] (рис. 3) и находят порядок реакции по веществу B
ln υ
m = lnυ2 −
ln[B]2 −
lnυ1 .
ln[B]1
Рис.3. Определение порядка реакции по веществу В
В последующих опытах определяют скорость реакции при различных исходных концентрациях вещества А и постоянной концентрации [B]0. Находят порядок реакции по веществу А
n = ln υ2 −
ln[A]2 −
ln υ1 .
ln[A]1
Из уравнения (2.3) с учетом найденных порядков реакции по веществам А и В рассчитывают константу скорости
k = υi ,
i [A] n [B] m
i i
где
υi , [A]i, [B]i экспериментальные данные, относящиеся к одному
опыту.
2.4. Зависимость концентрации реагирующих веществ от времени для реакции первого порядка.
Интегральное кинетическое уравнение
На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции.
Рассмотрим эту задачу на примере реакции первого порядка
А → продукты.
Скорость такой реакции выражается следующим уравнением:
υ = k[A] . (2.6)
В дифференциальном виде
− d[A] = k[A] . (2.7)
dt
Перепишем это уравнение в следующем виде:
− d [A] =kdt ,
[A]
и возьмем определенный интеграл от обеих частей уравнения от исходного состояния ([A]0, t0 = 0) до текущего момента ([A]t, t):
[ A]t d[A] t
− ∫ = k ∫ dt .
[ A]0
[A] 0
Решение этого уравнения приводит к следующей зависимости:
или
[A]t
= [A
]0 •
e− kt
(2.8)
(2.9)
ln[A]t
= ln[ A]0 −
kt .
Соотношения (2.8) и (2.9) являются интегральными кинетическими уравнениями реакции первого порядка.
Зная исходную концентрацию вещества [A]0 и константу скорости реакции k, можно рассчитать концентрацию [A]t через любое время t после начала реакции.
Если же известны исходная концентрация [A]0 и концентрация реагирующего вещества [A]t через какое-то время t после начала реакции, то можно рассчитать константу скорости этой реакции
[A]
k = ln 0
t [A]t
. (2.10)
(2.10)
Часто для характеристики скорости реакции пользуются временем полупревращения t1/2 (для реакции первого порядка чаще говорят
«период полураспада»). t1/2 это время, за которое прореагирует по[A]0
ловина исходного вещества
[A]t =
2 . Тогда, исходя из уравнения
(2.10), получим следующие зависимости:
k = 1 ln
[A]0
= ln 2 = 0,693 ;
t1/ 2
[A]0 / 2
t1/ 2
t1/ 2
(2.11)
t
1/ 2
0,693
= .
k
(2.12)
Материал взят из книги Основы химической кинетики (К.И. Болячевская)
Скорость химических реакций — химия, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
Скорость химических реакций
Номер слайда 2
Некоторые понятия химической кинетики. Химическая кинетика – раздел химии, изучаю- щий скорость и механизмы химических реакций. Гомогенные реакции – реакции, протекающие в однородной среде (в растворе или газовой фазе) во всем объеме реакционной смеси. Гетерогенные реакции – реакции в неоднородных системах, как правило, благодаря участию твердого вещества. Реакция в таких системах протекает на границе раздела фаз.
Химическая кинетика – раздел химии, изучаю- щий скорость и механизмы химических реакций. Гомогенные реакции – реакции, протекающие в однородной среде (в растворе или газовой фазе) во всем объеме реакционной смеси. Гетерогенные реакции – реакции в неоднородных системах, как правило, благодаря участию твердого вещества. Реакция в таких системах протекает на границе раздела фаз.
Номер слайда 3
Что такое химические реакции? Химические реакции – превращения одних веществ в другие, отличающиеся по составу и (или) строению. При химических реакциях обязательно происходит изменение веществ, при котором рвутся старые и образуются новые связи между атомами. Признаки химических реакций: 1) Выделяется газ; 2) Выпадет осадок; 3) Изменяется окраска веществ; 4) Выделяется или поглощается тепло, свет.
При химических реакциях обязательно происходит изменение веществ, при котором рвутся старые и образуются новые связи между атомами. Признаки химических реакций: 1) Выделяется газ; 2) Выпадет осадок; 3) Изменяется окраска веществ; 4) Выделяется или поглощается тепло, свет.
Номер слайда 4
Химические реакции протекают с разными скоростями. Быстрые реакции протекают в водных растворах с участием растворимых веществ; также это реакции, сопровожда-ющиеся взрывом. Медленные реакции – разрушение горных пород, образование сталактитов и сталагмитов, коррозия металлов.
Номер слайда 5
Скорость гомогенной реакции определяется как изменение концентрации одного из веществ в единицу времени: Скорость гетерогенной реакции определяется как изменение количества вещества в единицу времени на единице поверхности: S — площадь поверхности соприкосновения веществ . Как оценить скорость реакции?
Номер слайда 6
Номер слайда 7
Номер слайда 8
Факторы, влияющие на скорость химической реакции.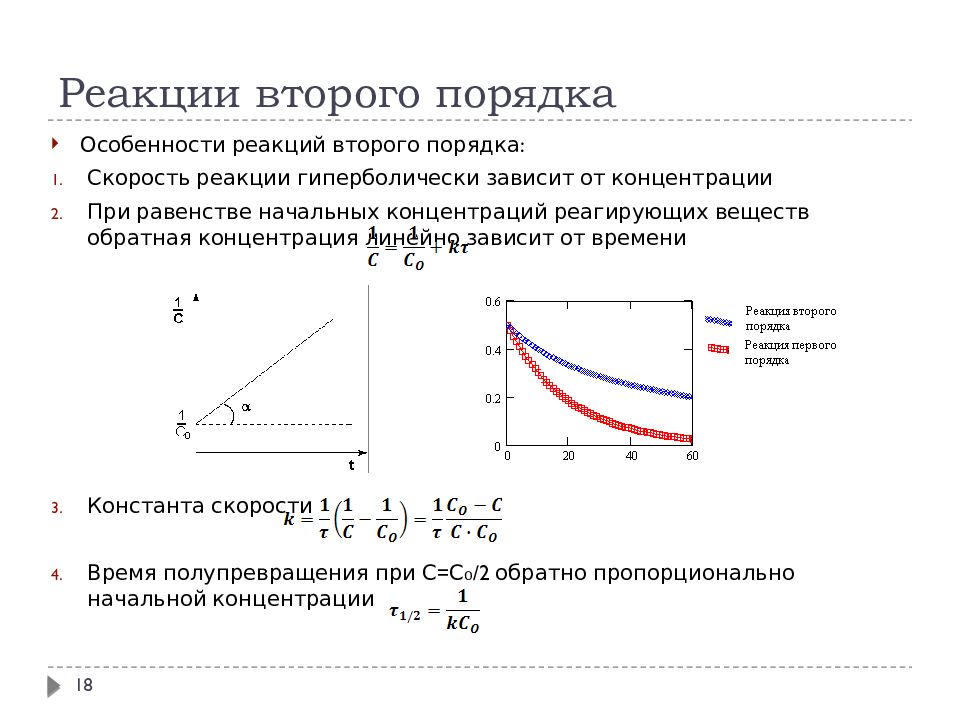 Природа реагирующих веществ Температура Концентрация реагирующих веществ Наличие катализатора (ингибитора) Площадь поверхности соприкосновения веществ
Природа реагирующих веществ Температура Концентрация реагирующих веществ Наличие катализатора (ингибитора) Площадь поверхности соприкосновения веществ
Номер слайда 9
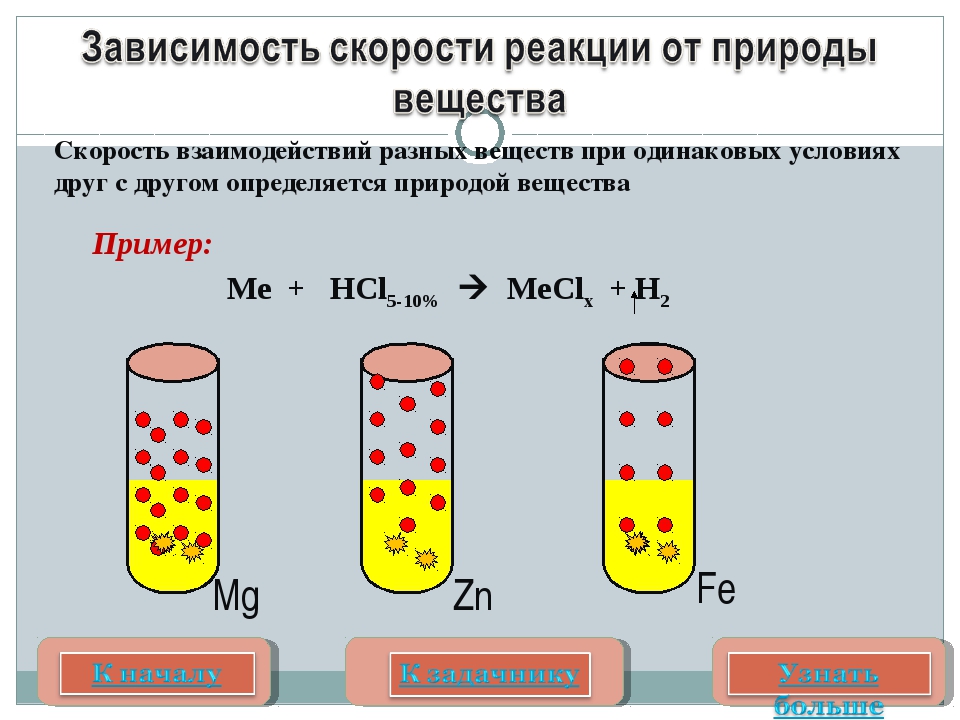
В случае c HCl реакция пойдет быстрее, т.к. соляная кислота – сильная, а уксусная – слабая. Природа реагирующих веществ В каком случае реакция пойдет с бОльшей скоростью: Zn + HCl или Zn + Ch4COOH Mg + HCl или Fe + HCl В случае c Mg реакция пойдет быстрее, т.к. магний более активный металл, чем железо.
Номер слайда 10
Температура Правило Вант-Гоффа: Повышение температуры на каждые 10 °С приводит к увеличению скорости реакции в 2–4 раза (эту величину называют температурным коэффициентом реакции). При повышении температуры резко повышается доля «активных» молекул, участвующих в эффективных соударениях, преодолевающих энергетический барьер реакции. Вант-Гофф Якоб Хендрик голландский химик, первая Нобелевская премия по химии, 1901 г.
При повышении температуры резко повышается доля «активных» молекул, участвующих в эффективных соударениях, преодолевающих энергетический барьер реакции. Вант-Гофф Якоб Хендрик голландский химик, первая Нобелевская премия по химии, 1901 г.
Номер слайда 11
Пример 1: Если температурный коэффициент реакции равен 2, то при повышении температуры с 200С до 500С скорость реакции возрастет в 8 раз. Температура Пример 2: Если скорость реакции возросла в 243 раза, а температурный коэффициент реакции равен 3, то температура была повышена на 50 0С.
Номер слайда 12
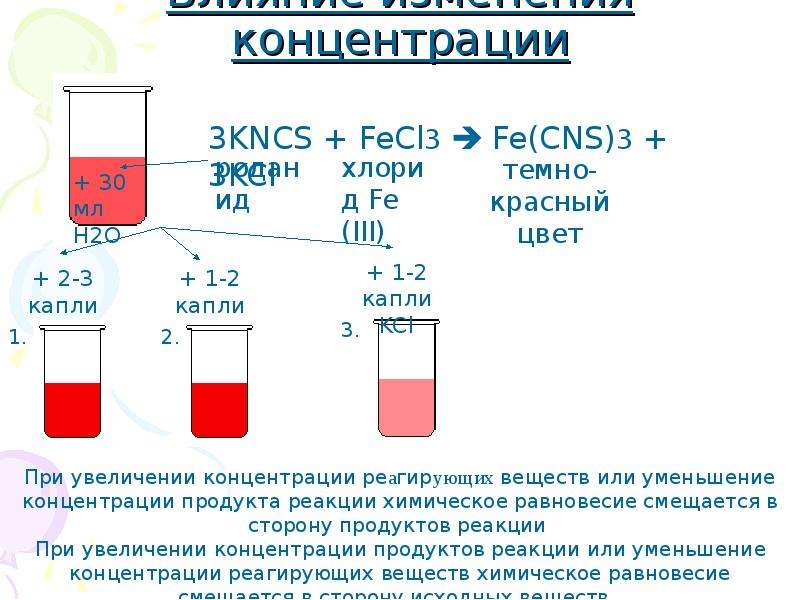
Концентрация реагирующих веществ Математически зависимость скорости от концентрации для реакции выражается законом действующих масс. Т.е. скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных стехиометрическим коээфициентам. СА, СВ – молярные концентрации веществ, k – константа скорости Для реакции: аА + bВ = cАВ Закон открыт в 1867 г. норвежскими учеными К.Гульдбергом и П.Вааге
Номер слайда 13
Концентрация реагирующих веществ 2SO2 + О2 2 SO3 + Q Пример: Если в реакции давление в системе увеличить в 2 раза, то скорость реакции возрастет в 8 раз. Для реакций с участием газообразных веществ повышение давления в системе или уменьшение объема равносильно повышению концентрации реагирующих веществ.
Для реакций с участием газообразных веществ повышение давления в системе или уменьшение объема равносильно повышению концентрации реагирующих веществ.
Номер слайда 14
Катализаторы Катализаторы – это вещества, участвующие в химической реакции и изменяющие ее скорость или направление, но по окончании реакции остающиеся неизменными. Изменение скорости химической реакции или ее направления с помощью катализатора называют катализом. Механизм действия катализаторов – образование промежуточных продуктов, имеющих более низкую энергию активации.
Номер слайда 15
Катализаторы 2SO2 + О2 2 SO3 + Q Реакция окисления сернистого газа в серный ангидрид в производстве серной кислоты протекает в контактном аппарате. На горизонтальных полках размещается катализатор – пятиокись ванадия V2O5. Автомобильные двигатели снабжены катализаторами полного сжигания топлива.
Номер слайда 16
Катализаторы Ферменты – биологически активные катализаторы. Используются в производстве детского питания, сыров, хлебопечении, виноделии и пивоварении. Нежелательные реакции необходимо замедлять. Для этого используют вещества – ингибиторы.
Используются в производстве детского питания, сыров, хлебопечении, виноделии и пивоварении. Нежелательные реакции необходимо замедлять. Для этого используют вещества – ингибиторы.
Номер слайда 17
Площадь соприкосновения реагирующих веществ В каком случае реакция пойдет с бОльшей скоростью: Feкусковое + HCl или Feпорошкообразное + HCl С порошкообразным железом реакция пойдет быстрее, т.к. больше площадь поверхности соприкосновения реагирующих веществ. Для гетерогенных реакций скорость не зависит от количества твердого продукта реакции, а зависит от степени его измельчения.
Номер слайда 18
Площадь соприкосновения реагирующих веществ В производстве серной кислоты при обжиге пирита (серного колчедана) 4FeS2 + 11O2 = 2Fe2O3 + 8SO2 для увеличении поверхности соприкосновения твердого компонента с воздухом используют принцип «кипящего слоя».
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Как вы работаете?
Вам нужно написать сообщение в WhatsApp . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.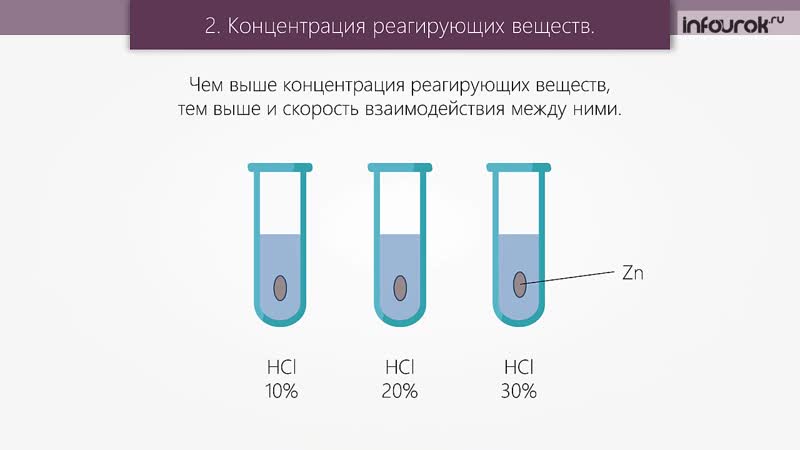
В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Whatsapp или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования.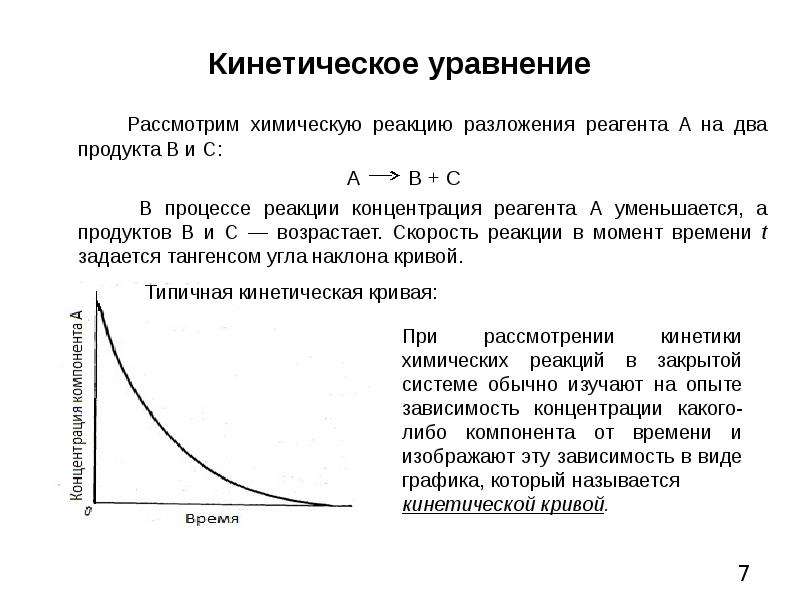 80% заказов сдаются раньше срока.
80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Зависимость скорости реакции от концентрации реагентов — Скорость процессов в химических реакциях Кинетика и равновесие
При повышении концентрации реагентов реакция протекает быстрее.
Повышение концентрации реагентов ускоряет реакцию. Чтобы произошла химическая реакция, должно существовать определенное количество молекул с энергиями, равными или превышающими энергию активации .С увеличением концентрации будет увеличиваться количество молекул с минимально необходимой энергией, а значит, будет возрастать и скорость реакции.
Закон скорости для химической реакции представляет собой уравнение, которое связывает скорость реакции с концентрациями или парциальными давлениями реагентов. Для общей реакции:
аА+бВ→С
Без промежуточных стадий в механизме реакции , что означает, что это элементарная реакция, закон скорости определяется следующим образом:
r=k[A] x [B] y
В этом уравнении [A] и [B] выражают концентрации A и B, соответственно, в единицах молей на литр.Показатели x и y различны для каждой реакции и должны быть определены экспериментально; они не связаны со стехиометрическими коэффициентами химического уравнения. Наконец, k известен как константа скорости реакции. Значение этого коэффициента k будет варьироваться в зависимости от условий, влияющих на скорость реакции, таких как температура, давление, площадь поверхности и т. д. Меньшая константа скорости указывает на более медленную реакцию, а большая константа скорости указывает на более быструю реакцию.
Порядок реакции — это зависимость между концентрацией частиц и скоростью реакции.Чтобы определить x и y в уравнении скорости, нам нужно рассмотреть экспериментальные данные, используя концентрации A и B, и изучить их влияние на скорость реакции. x и y известны как порядки и относятся к степенной зависимости скорости от концентрации каждого реагента.
r=k[A] x [B] y
Реакция первого порядка зависит от концентрации только одного реагента. Поэтому реакцию первого порядка иногда называют мономолекулярной реакцией.Хотя могут присутствовать и другие реагенты, каждый из них будет нулевого порядка, поскольку концентрации этих реагентов не влияют на скорость. Таким образом, закон скорости элементарной реакции первого порядка по реагенту А определяется выражением:
Реакция второго порядка — это когда общий порядок равен двум. Для реакции общего вида: аА+bВ→С реакция может быть второго порядка двумя возможными способами. Она может быть второго порядка как по А, так и по В, или первого порядка как по А, так и по В. Если бы реакция была второго порядка по любому из реагентов, она привела бы к следующим законам скорости:
Она может быть второго порядка как по А, так и по В, или первого порядка как по А, так и по В. Если бы реакция была второго порядка по любому из реагентов, она привела бы к следующим законам скорости:
Второй сценарий, в котором реакция имеет первый порядок как по А, так и по В, дает следующий закон скоростей:
Для реакции нулевого порядка увеличение концентрации реагирующих частиц не ускорит скорость реакции.Реакции нулевого порядка обычно обнаруживаются, когда материал, необходимый для протекания реакции, такой как поверхность или катализатор, насыщен реагентами.
Практические вопросы
Официальная подготовка MCAT (AAMC)
Онлайн-карточки по химии Вопрос 1
Пакет вопросов по химии, отрывок 10, вопрос 56
Практический экзамен 1 C/P Section Pass 9 Question 51
Практический экзамен 2 C/P Раздел 7 Вопрос 35
Практический экзамен 3 Раздел C/P Пассаж 6 Вопрос 31
Ключевые точки
• При повышении концентрации реагентов реакция протекает быстрее.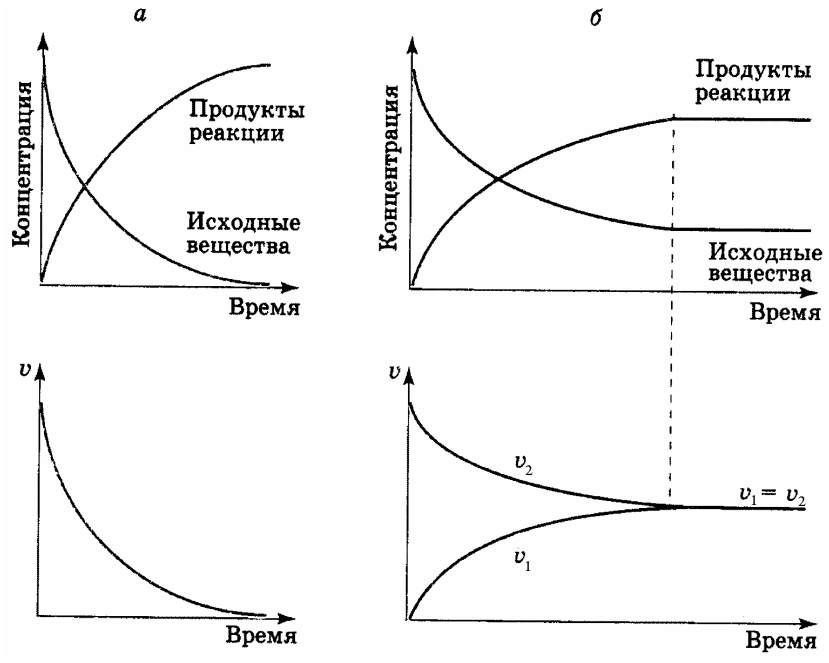 Это связано с увеличением числа молекул, обладающих минимально необходимой энергией.
Это связано с увеличением числа молекул, обладающих минимально необходимой энергией.
• Для общей реакции aA+bB→C без промежуточных стадий в механизме реакции (то есть элементарной реакции) скорость определяется как: r=k[A]x[B]y
• Уравнение скорости реакции с многостадийным механизмом, вообще говоря, нельзя вывести из стехиометрических коэффициентов общей реакции; это надо определять экспериментально.
• Порядок реакции относится к степенной зависимости скорости от концентрации каждого реагента, и реакция может быть 0, 1 или 2 порядка по отношению к реагентам и их влиянию на скорость
Основные термины
Энергия активации : Минимальная энергия, необходимая для протекания реакции.
Закон скорости : Уравнение, связывающее скорость химической реакции с концентрацией или парциальным давлением реагентов.
Механизм реакции : Пошаговая последовательность элементарных превращений, посредством которых происходит общее химическое изменение.
Константа скорости : Коэффициент пропорциональности, связывающий скорость химической реакции при данной температуре с концентрацией реагента (в мономолекулярной реакции) или с произведением концентраций реагентов.
Реакция первого порядка : Реакция, зависящая от концентрации только одного реагента (мономолекулярная реакция). Могут присутствовать и другие реагенты, но каждый из них будет нулевого порядка.
Реакция второго порядка : Реакция, которая зависит от концентрации (концентраций) одного реагента второго порядка или двух реагентов первого порядка.
Реакция нулевого порядка : Реакция, скорость которой не зависит от концентрации реагента(ов).
Зависимость от концентрации и порядок реакции — Концепция | Лаборатория: Химия
Химическая кинетика и закон скорости реакции
Химическая кинетика относится к скорости или скорости химической реакции. Скорость зависит от механизма, сложности и количества реагентов в реакции. Концентрация реагента также играет существенную роль в скорости реакции.
Скорость зависит от механизма, сложности и количества реагентов в реакции. Концентрация реагента также играет существенную роль в скорости реакции.
Закон скорости определяет эту взаимосвязь с помощью экспериментов. Каждый реагент способствует скорости реакции фактором, известным как порядок реакции. Этот коэффициент может варьироваться от нуля до двух и зависит от отношения этого реагента к скорости реакции.
r = k[A] m [B] n для aA + bB + … → СС
В этом уравнении r — скорость реакции, k — константа скорости реакции, [A] и [B] — концентрации реагентов A и B, а m и n — порядки реакции реагентов A и B соответственно. . Скорость реакции r определяется как изменение концентрации продукта во времени и выражается в молях на литр в секунду.
Заказ реакции
Порядок реакции описывает степенную зависимость концентрации реагентов от скорости реакции.Общий порядок реакции представляет собой сумму порядков реакции для каждого из реагентов. Важно помнить, что порядок реакции , а не , связанный со стехиометрическими факторами сбалансированного химического уравнения. Другими словами, стехиометрию нельзя использовать для определения порядка химической реакции. Порядок реакции должен быть определен экспериментально
Важно помнить, что порядок реакции , а не , связанный со стехиометрическими факторами сбалансированного химического уравнения. Другими словами, стехиометрию нельзя использовать для определения порядка химической реакции. Порядок реакции должен быть определен экспериментально
Чтобы определить порядок реакции, концентрацию второго реагента поддерживают постоянной, а концентрацию первого реагента меняют.Время, необходимое для возникновения реакции, измеряется в секундах; однако это время не соответствует времени, которое требуется реакции, чтобы перейти к завершению . Вместо этого это время, необходимое для реакции на start . Затем время реакции для различных концентраций реагентов сравнивается для определения порядка. Та же серия реакций проводится для определения порядка второго реагента, где концентрация первого реагента поддерживается постоянной, а концентрация второго реагента варьируется.
Путем сравнения времени реакции можно определить порядок реакции. Например, если время реакции остается постоянным, несмотря на изменение концентрации реагента, то реагент имеет нулевой порядок. Это означает, что скорость реакции равна коэффициенту скорости реакции k, который должен иметь единицы М/с. Если время реакции изменяется линейно с изменением концентрации (т. е. удвоение концентрации влияет на время реакции в 2 раза), то реагент имеет первый порядок.Это означает, что скорость реакции равна произведению коэффициента скорости реакции на концентрацию реагента. В этом случае k имеет единицы измерения 1/с. Наконец, если время реакции увеличивается в 4 раза при удвоении концентрации реагента, реагент имеет второй порядок. Это означает, что скорость реакции равна произведению константы скорости на квадрат концентрации реагента, образуя квадратичную зависимость. В этом случае единицами k должны быть 1/M⋅s.
Например, если время реакции остается постоянным, несмотря на изменение концентрации реагента, то реагент имеет нулевой порядок. Это означает, что скорость реакции равна коэффициенту скорости реакции k, который должен иметь единицы М/с. Если время реакции изменяется линейно с изменением концентрации (т. е. удвоение концентрации влияет на время реакции в 2 раза), то реагент имеет первый порядок.Это означает, что скорость реакции равна произведению коэффициента скорости реакции на концентрацию реагента. В этом случае k имеет единицы измерения 1/с. Наконец, если время реакции увеличивается в 4 раза при удвоении концентрации реагента, реагент имеет второй порядок. Это означает, что скорость реакции равна произведению константы скорости на квадрат концентрации реагента, образуя квадратичную зависимость. В этом случае единицами k должны быть 1/M⋅s.
Общий порядок реакции представляет собой сумму порядков отдельных реакций. Например, если реакция первого порядка по A, то m = 1. А если реакция нулевого порядка по B, то n = 0. Общий порядок реакции первый, потому что m + n = 1.
Общий порядок реакции первый, потому что m + n = 1.
Константа скорости реакции
Константа скорости k зависит от реакции и температуры, в которой проводится реакция. Константу скорости определяют из серии экспериментов.Используя измеренную скорость и начальные концентрации реагентов, уравнение скорости используется для определения константы скорости. Константа скорости зависит от температуры и определяется уравнением Аррениуса. Это уравнение описывает взаимосвязь между k и энергией активации E a , температурой T и постоянной идеального газа R. Константа A является константой пропорциональности, и ее не следует путать с реагентом A.
Каталожные номера
- Коц, Дж.К., Трейчел-младший, П.М., Таунсенд, младший (2012). Химия и химическая активность. Белмонт, Калифорния: Брукс/Коул, Cengage Learning.
- Зильдерберг, М.С. (2009). Химия: молекулярная природа материи и изменений.
 Бостон, Массачусетс: McGraw Hill.
Бостон, Массачусетс: McGraw Hill.
Кинетика
Показания для этого раздела
Петруччи: Главы 14:
Введение
В предыдущих главах по термодинамике мы в основном изучали разницу между конечным и начальным состояниями (функция состояния).У нас не было возможности использовать термодинамическую информацию, чтобы сказать нам, почему некоторые реакции, хотя спонтанно, не будет продолжаться, пока это делают другие. Это работа Kinetics.
Мы видели, что некоторые реакции бывают быстрыми (даже взрывоопасными), а другие довольно медленный (ржавление железа). В этом разделе мы собираемся изучить кинетику реакции и попытаться понять, как и почему скорость реакции такая, какая она есть. являются. Мы также рассмотрим, как кинетические исследования могут помочь нам понять механизмы реакций.
Изучим влияние концентрации, температуры и катализаторов на
скорость реакции. Этот тип информации позволит нам понять детали
химия, происходящая в ходе реакции.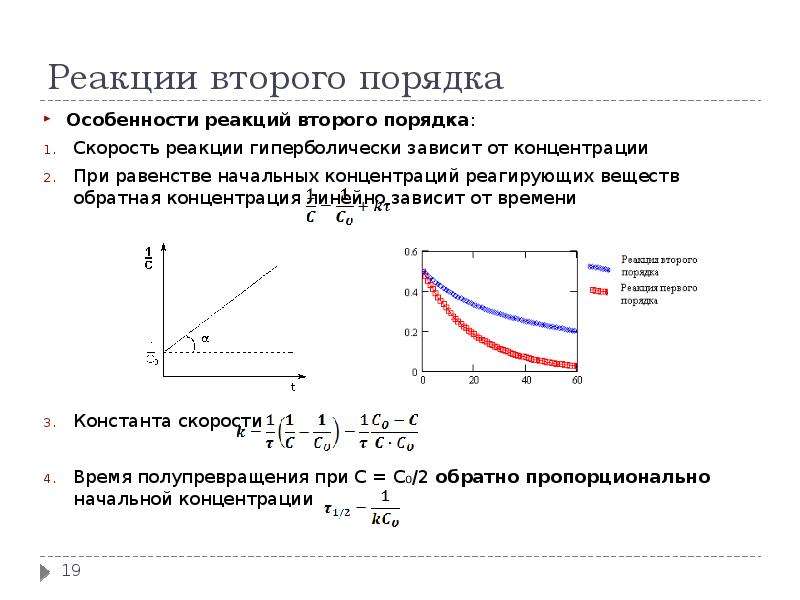
Вернуться к началу
Скорость $\Rightarrow$
Для автомобиля скорость – это пройденное расстояние (изменение положения), деленное на время. Для химических реакций мы определяем скорость (Rate) как изменение концентрация деленная на время. Более конкретно, мы используем либо концентрация продукта или реагента в нашем определении СКОРОСТИ для химическая реакция.
\[RATE=\frac{количество\;реакция}{реакция\;время}\]
Для данной химической реакции количество реакции измеряется с использованием изменений концентрации один измеримый реагент или продукт и могут быть определены из стехиометрии.
Рассмотрим: NO(g) + O 3 (g) $\rightarrow$ NO 2 (g) + О 2 (г)
Для каждой реакции мы получаем один NO 2 , то есть 1:1 переписка.Таким образом, количество реакции можно заменить на изменение концентрации NO 2 .
Если [NO 2 ] в t 1 равно [NO 2 ] 1 и @t 2 это [НОМЕР 2 ] 2 затем
Δ[№ 2 ] = [№ 2 ] 2 — [№ 2 ] 1
и
Δt = t 2 — t 1
и
скорость = Δ[NO 2 ]/Δt
Так как скорость всегда положительна и прямая реакция будет
производить № 2 , i. е. , Δ [№ 2 ]
положительно, знаки согласуются. Если бы мы использовали концентрацию реагента,
знаки бы поменялись местами. Если неединичное количество молей вещества
производится на один моль реакции, то нам нужно будет учитывать и это.
е. , Δ [№ 2 ]
положительно, знаки согласуются. Если бы мы использовали концентрацию реагента,
знаки бы поменялись местами. Если неединичное количество молей вещества
производится на один моль реакции, то нам нужно будет учитывать и это.
Для вышеуказанной реакции мы можем написать:
В реакции: N 2 (ж) + 3 H 2 (ж) $\rightarrow$
2NH 3 (г)
мы могли бы написать:
коэффициент 1/3 для H 2 вступает в игру, конечно, поскольку скорость потребления H 2 в три раза выше, чем скорость реакция.Коэффициент 1/2 для NH 3 существует по той же причине, скорость образования аммиака равна удвоенной скорости реакции, так как его коэффициент равен 2.
Приведенное выше определение скорости включает измеримый промежуток времени
Δt. За это время, возможно, фактическое
изменения курса. В этом случае приведенные выше уравнения фактически являются определениями
средние скорости за интервал времени Δt.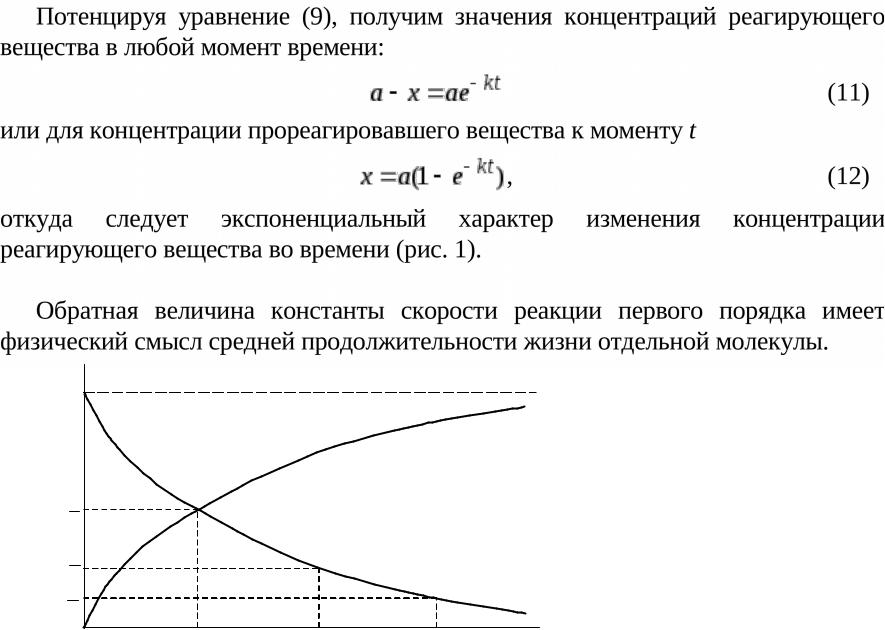 Чтобы получить
мгновенной скорости, нам нужно сократить временной интервал до
бесконечно малый диапазон, и, таким образом, скорость теперь может быть записана с использованием dC/dt
а не ΔC/Δt.
Чтобы получить
мгновенной скорости, нам нужно сократить временной интервал до
бесконечно малый диапазон, и, таким образом, скорость теперь может быть записана с использованием dC/dt
а не ΔC/Δt.
Для измерения скоростей мы обычно измеряем концентрации или что-то, связанное с концентрация.
Есть несколько методов, которые мы могли бы использовать для этого измерения.
- Мы можем взять небольшой образец из реакционной смеси в несколько раз, погасить реакцию (возможно, путем быстрого охлаждения) и затем измерение концентрации с использованием наиболее подходящего метода. удобен (как стандартные мокрые химические методы).
- Если один вид окрашен, мы может провести реакцию внутри клетки в спектрометре и измерить изменение поглощения.Закон Бера гласит, что степень поглощения пропорциональна концентрации.
- Для газофазных реакций мы можем измерить давление при постоянный объем.
- И многие другие. Разрабатываются некоторые новые
непрерывно.

Давайте рассмотрим пример реакции и рассмотрим изменения, происходящие в результате реакция (время) прогрессирует
Реакция CO(г) + NO 2 (г) $\rightarrow$ CO 2 (г) + NO(g) измеряется инициировано, и концентрации измеряются несколько раз со следующими результатами.
| Время/с | [СО] | [№ 2 ] | Средняя ставка Δ[CO]/Δt |
Мгновенная скорость д[СО]/дт |
| 0 | 0,100 | 0,100 | 0,0049 | |
| 0,0033 | ||||
| 10 | 0.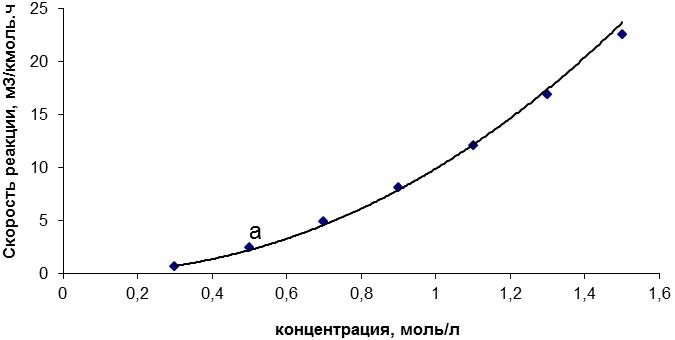 067 067 |
0,067 | 0,0022 | |
| 0,0017 | ||||
| 20 | 0,050 | 0,050 | 0,0012 | |
| 0,0010 | ||||
| 30 | 0.040 | 0,040 | ||
Вернуться к началу
Существует связь между кинетикой и химией, которая
реально происходящее.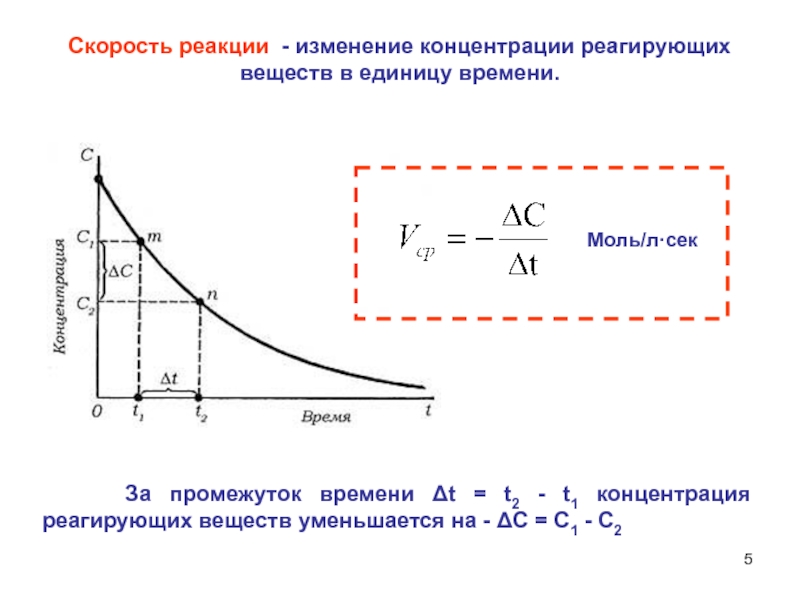 В этом разделе мы начнем исследовать эту связь
и научиться определять законы скорости и порядок реакции из кинетики реакции.
В этом разделе мы начнем исследовать эту связь
и научиться определять законы скорости и порядок реакции из кинетики реакции.
Рассмотрим реакцию
NO(г) + O 3 (г) $\rightarrow$ NO 2 (г) + O 2 (г) измерено при 25С.
Экспериментально установлено, что скорость реакции пропорциональна [NO] и [О 3 ]. Следовательно, мы можем написать уравнение:
Ставка = k [НЕТ] [O 3 ]
, где k — константа скорости (мера внутренней скорости). Для этой реакции при 25°C k = 1,610 7 моль -1 с -1 .
Эта реакция первого порядка по NO и O 3 и Общий второй заказ
|
Некоторые общие сведения о константах скорости и порядке реакции. Быстрые реакции имеют большие значения k Медленные реакции имеют небольшие значения k . Вообще за реакцию а А + б В + в С + … $\rightarrow$ продукты Ставка = k [A] x [B] y [C] z … Где x , y и z являются порядком реакции А, В и С соответственно и не обязательно связаны к коэффициентам a , b и c в сбалансированном химическая реакция. Суммарная реакция дает, по существу, начальное и конечное состояния (реагенты и продукты). кинетика представлять промежуточный процесс. |
Рассмотреть реакцию
2 N 2 O 5 (ж) $\rightarrow$ 4 НЕТ 2 (ж) + О 2 (г)
Собранные экспериментальные данные и некоторые расчетные скорости приведены здесь.
| т/мин | [Н 2 О 5 ] | Оценить |
| 0 | . 0172 0172 |
|
| 10 | .0113 | 3.410 -4 |
| 20 | .0084 | 2,510 -4 |
| 30 | .0062 | 1.810 -4 |
| 40 | .0046 | 1.310 -4 |
| 50 | .0035 | 1.010 -4 |
| 60 | .0026 | 0,810 -4 |
Если построить график [N 2 O 5 ] в зависимости от времени, мы найдем следующее:
По этому графику мы можем рассчитать скорость в различные моменты времени t (и, следовательно, в
различные концентрации [N 2 O 5 ]).Теперь мы строим курс против [N 2 O 5 ]
чтобы увидеть, получим ли мы прямую линию, как уравнение прямой линии
Rate = k [N 2 O 5 ].
Поскольку мы получаем прямую линию, мы знаем, что скорость прямо пропорциональна к [N 2 O 5 ], т.е. , порядок реакции 1.
Мы можем дважды проверить это, построив курс против других заказов [N 2 O 5 ], например, давайте попробуем order=2.
Очевидно, что Ставка не пропорциональна [N 2 O 5 ] 2 , т. е. , Ставка ≠ k [N 2 O 5 ] 2 . Поскольку мы не получаем прямую линию для любого другого заказа, мы можем быть уверены, что порядок реакции 1.
Метод начальной скорости
Некоторые реакции имеют более одного реагента. Это усложняет задачу, поскольку
все концентрации меняются одновременно, и мы не можем использовать описанный выше метод для
определить порядок реакции по любому одному реагенту.Кроме того,
иногда обратная реакция усложняет ситуацию, влияя на кажущуюся
ставки. Обе эти проблемы можно решить с помощью метода начальной ставки.
Обе эти проблемы можно решить с помощью метода начальной ставки.
Теперь из собранных данных о скорости мы можем видеть, как изменения влияют на скорость. в концентрации только одного из химических веществ за раз, и мы устранили обратная реакция в процессе.
Пример:
Экспериментальные данные скорости были собраны для следующих реакция.Определить закон скорости.
2 NO + Cl 2 $\rightarrow$ 2 NOCl
| Экспл. | [НЕТ] | [Кл 2 ] | Начальная ставка |
|---|---|---|---|
| 1 | 0,010 | 0.010 | 1.210 -4 |
| 2 | 0,010 | 0,020 |
2. 310 -4 310 -4 |
| 3 | 0,020 | 0,020 | 9.610 -4 |
Закон ставки будет иметь вид Скорость = k [NO] x [Cl 2 ] y .
Наша задача — определить x и y.
Давайте рассмотрим эти реакции парами, а именно парами, в которых разница заключается в концентрации только одного реагента. 1,2 и 2,3 такие пары.
| Эксперименты | Наблюдения | Выводы |
|---|---|---|
| Эксперименты 1 и 2 |
[NO] $\rightarrow$ константа
[Кл 2 ] $\rightarrow$ удваивает Ставка $\Rightarrow$ удваивается |
Скорость пропорциональна [Cl 2 ] Y = 1 |
| Эксперименты 2 и 3 |
[Cl 2 ] $\rightarrow$ постоянная
[НЕТ] $\rightarrow$ удваивается Оцените $\Rightarrow$ вчетверо |
Скорость пропорциональна [NO] 2 Х = 2 |
Наш закон скорости теперь может быть записан как
Ставка = k [НЕТ] 2 [Кл 2 ]
Общий порядок реакции — 3, порядок по NO — 2, а относительная — 2. Класс 2 1.
Класс 2 1.
Мы рассмотрим значение этого приказа реакции позже в разделе, посвященном механизмы реакции.
Приведенный выше пример был сделан здесь немного маханием рукой. если ты хотите увидеть более математически строгий вывод того же закона скорости, кликните сюда.
Пример
Какова константа скорости при 300К для следующей реакции:
2 NO + Cl 2 $\rightarrow$ 2 NOCl ?
Мы уже знаем, что закон скорости
Скорость = k [NO] 2 [Cl 2 ].Мы можем использовать значения из любого один из экспериментов из предыдущего примера. Мы будем использовать эксп. 1. (2 и 3 также должно давать такое же значение для k)
Какова скорость этой реакции, когда [NO] = 0,030 M и [Cl 2 ] = 0,040 М ?
Ставка = k [НЕТ] 2 [Кл 2 ]
= 1,210 2 M -2 с -1 (0,030) 2
(0. 040)
040)
= 4,310 -3 M с -1 .
Метод интегрированного закона ставок
Мы можем определить закон скорости, сравнивая наклоны (конц./т). Из этого график, мы можем затем определить скорость в любой момент времени t, а затем построить ее в зависимости от концентрация на различных мощностях. Из этих сил мы определяем сюжет, который является линейным и, следовательно, устанавливает порядок по реагенту.
Более прямой метод состоит в том, чтобы интегрировать уравнения закона скорости, как они были ранее выраженный (наклон конц.от времени == производная d[A]/dt) и от эти интегрированные выражения закона скорости отображают различные функции концентрации по сравнению со временем, чтобы увидеть, какой из них дает прямую линию. Кроме того, интегрированный Законы скорости помогают нам углубить наше понимание изменений концентрации которые происходят и приводят к определению периода полураспада реагента.
Во всех этих примерах рассматривается один вид реагентов А. Для многих реакций мы можем установить такие условия, что только один из реагентов
необходимо рассмотреть в любое время.Делаем это, запуская реакцию со всеми
виды, за исключением одного, в очень большом избытке. Таким образом, в ходе прогрессирования
реакции изменение концентраций большого избытка соединений будет
очень маленький. Следовательно, мы можем установить закон псевдоскорости. В других реакциях есть
только один реагент для рассмотрения. В любом случае действуют следующие законы ставок.
не являются общими и не должны восприниматься как единственно возможные формы.
Для многих реакций мы можем установить такие условия, что только один из реагентов
необходимо рассмотреть в любое время.Делаем это, запуская реакцию со всеми
виды, за исключением одного, в очень большом избытке. Таким образом, в ходе прогрессирования
реакции изменение концентраций большого избытка соединений будет
очень маленький. Следовательно, мы можем установить закон псевдоскорости. В других реакциях есть
только один реагент для рассмотрения. В любом случае действуют следующие законы ставок.
не являются общими и не должны восприниматься как единственно возможные формы.
Рассмотрим ситуацию первого порядка: A $\rightarrow$ продукты.{-кт}\]
Другими словами, концентрация А падает экспоненциально, как показано здесь
Мы можем построить график зависимости ln [A] t от t, чтобы получить график, который должен быть график прямой линии с наклоном = -k.
Теперь рассмотрим систему второго порядка.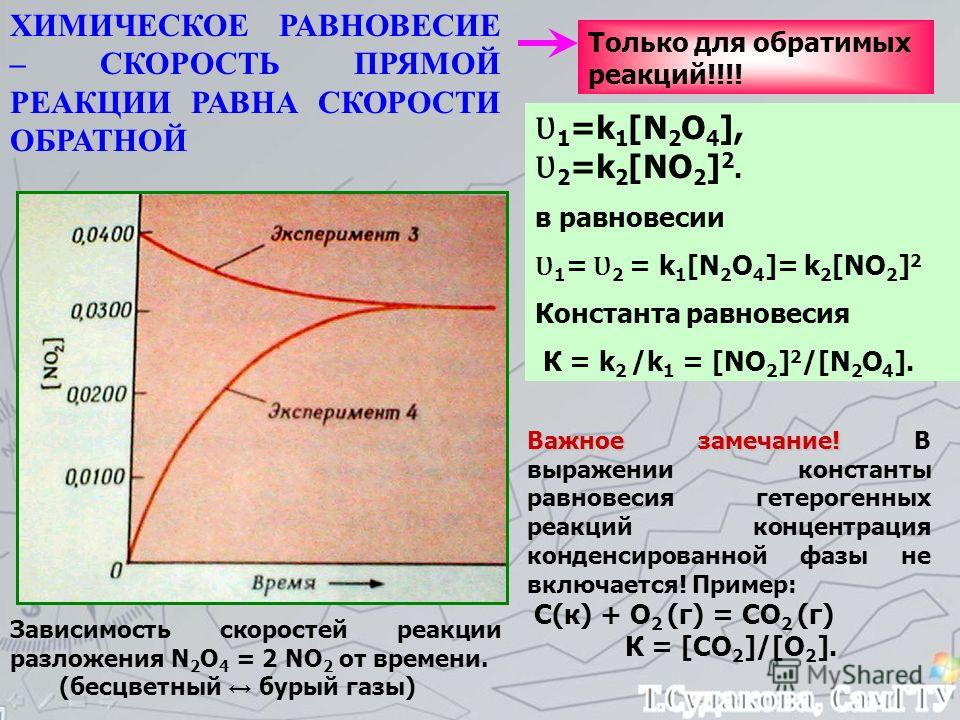
$\rightarrow$ товары
скорость = k 2 [A] 2 = -d[A]/dt
Интеграция дает нам
Если построить график зависимости 1/[A] от t, мы должны получить прямолинейный график с наклоном = к.
Более редкий случай: реакции нулевого порядка.
Этот тип закона скорости не предполагает зависимости скорости от концентрации. Этот чаще всего происходит, когда катализатор используется с большим избытком реагента. В В такой ситуации ставка зависит исключительно от общего количества места реагентов, доступные на катализаторе.
интегрирование дает
[А] т = -кт + [А] 0
График зависимости [A] от t дает прямую линию с наклоном = -k.
Период полураспада
Период полураспада химического вещества определяется как время, необходимое для
уменьшить концентрацию вида до половины исходного значения. В
математические термины, [A] t = [A] 0 /2 @ t = t 1/2 .
В
математические термины, [A] t = [A] 0 /2 @ t = t 1/2 .
Реакция первого порядка:
Ln [А] t = -кт + ln [А] 0
Аналогично, для второго порядка получаем
Для редкого случая нулевого порядка мы находим
Пример:
Гидролиз сахарозы до глюкозы и фруктозы катализируется ферментом сахароза.Это первый порядок по сахарозе. Если период полураспада измеряется 80 мин. @ 25C какая доля исходной сахарозы будет остаются после 160 и после 320 мин?
Первый порядок ==> Conc = 1/2 каждые 80 мин. временной интервал.
160 мин = 2 интервала по 80 мин. так что концентрация вдвое меньше.
С = 1/2 { 1/2 (С 0 )} = 1/4 С 0
Одна четверть сахарозы останется через 160 мин.
320 мин = 4 интервала по 80 мин.
С = (1/2) 4 С 0 = С 0 /16
Через 320 мин останется одна восьмая часть исходного количества сахарозы.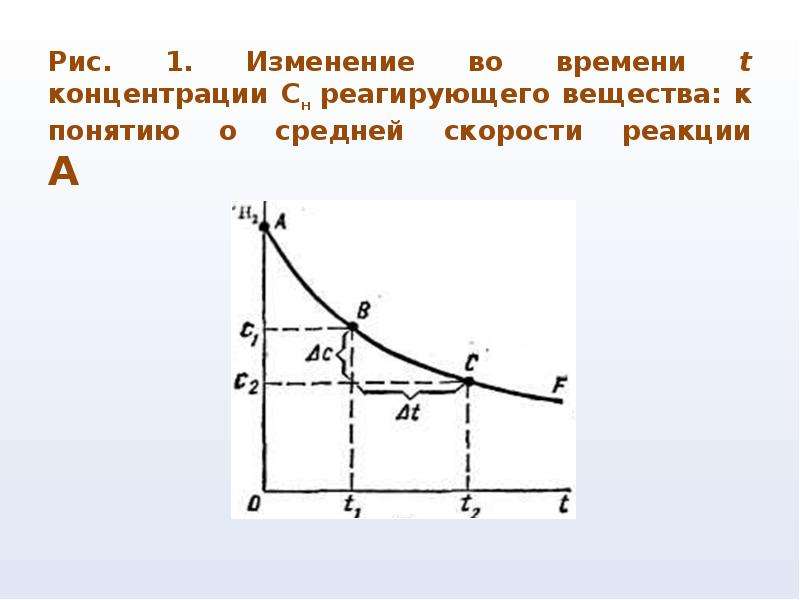
Другой пример
Период полураспада N 2 O 5 в первом порядке разложение при 25°С составляет 4,0310 4 с. Что такое постоянная скорость? Какой процент N 2 O 5 останется через сутки?
1 день равен 8.6410 4 с.
Из закона об интегрированных тарифах:
22,6 % остается через один день.
Вернуться к началу
Поскольку реакции включают как разрыв связей (требуется энергия), так и преобразование связывает (высвобождает энергию) почти всегда есть количество энергии, которое должно быть вход в молекулы до того, как реакция может быть инициирована. Мы могли бы представить это с использованием шкалы энергии в зависимости от коэффициента реакции следующим образом.
Теория, называемая теорией столкновений или теорией активированных комплексов, часто используется для
объяснить скорость реакции.Энергия чаще всего передается связям, которые
должны быть сломаны во время (или в результате) столкновения.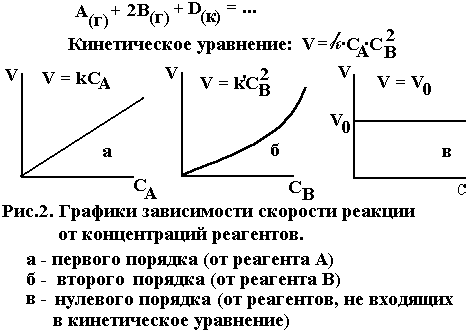 Эти столкновения наиболее
часто столкновения между самими реагирующими видами, но также могут быть
столкновения с другими нереагирующими молекулами газа и даже со стенкой
контейнер (горячая стенка). Мы ожидаем, что только столкновения с достаточной энергией
инициирует реакцию. Из этой диаграммы экзотермической реакции мы видим, что
минимальная энергия для инициирования реакции определяется значением активации
энергия E a .Следовательно, только столкновения между молекулами реагентов с
энергия > E a приведет к продуктам.
Эти столкновения наиболее
часто столкновения между самими реагирующими видами, но также могут быть
столкновения с другими нереагирующими молекулами газа и даже со стенкой
контейнер (горячая стенка). Мы ожидаем, что только столкновения с достаточной энергией
инициирует реакцию. Из этой диаграммы экзотермической реакции мы видим, что
минимальная энергия для инициирования реакции определяется значением активации
энергия E a .Следовательно, только столкновения между молекулами реагентов с
энергия > E a приведет к продуктам.
В газовой фазе происходит большое количество столкновений, которые имеют достаточно
энергии активации, но все еще не реагируют. Это связано с «стерическим» фактором. От
это, мы имеем в виду, что молекулы должны сталкиваться с правильной относительной ориентацией
до того, как произойдет реакция. Этот стерический фактор не зависит от температуры.
Есть и другие факторы, которые также влияют на скорость.В большой молекуле энергия
столкновения должны быть сосредоточены в связи или связях, которые должны быть разорваны. Это может занять время и определяется статистически. Это тоже не иждивенец
по температуре.
Это может занять время и определяется статистически. Это тоже не иждивенец
по температуре.
Если мы посмотрим на ансамбль молекул газа при определенной температуре, мы увидим распределение кинетической энергии. Это значит, что будет раздача кинетическая энергия сталкивающихся молекул. Энергия столкновения связана с полной кинетической энергии сталкивающихся атомов и углу падения.Как и в автомобиле, лобовое столкновение преобразует больше кинетической энергии в «столкновение». энергии, чем при скользящем (боковом) столкновении. Это другой вид стерический фактор и не зависит от температуры. Следовательно, единственный фактор, который реально зависящая от энергии средняя кинетическая энергия столкновения. Если мы график частоты столкновений в зависимости от энергии столкновения, мы видим распределение кривая, которая изменяется при изменении Т.
Мы видим, что число столкновений, происходящих при достаточно высокой энергии
(не менее E a ) меньше в случае низкотемпературной кривой (площадь
под кривой) по сравнению с кривой высоких энергий. Следовательно, при повышении температуры мы
ожидать, что скорость реакции будет расти.
Следовательно, при повышении температуры мы
ожидать, что скорость реакции будет расти.
Нажмите здесь, чтобы открыть электронную таблицу что демонстрирует этот принцип
Уравнение Аррениуса
Экспериментально можно показать, что температурная зависимость k можно выразить следующим образом:
k = A e — E a /RT .
Это известно как уравнение Аррениуса, где предэкспоненциальный множитель A содержит информацию о не зависящих от температуры элементах, рассмотренных выше и E a — энергия активации.Мы видим, что константа скорости (и поэтому скорость) реакции будет ниже при более высоких значениях E a и будет увеличиваться с увеличением Т.
Уравнение Аррениуса также можно записать в логарифмической форме следующим образом:
пер. к = пер.
Это линейное уравнение и из него мы видим, что если построить ln k
против 1/ T получим прямую с наклоном = — E a /R и
перехват = ln A .
Поскольку нас не часто интересует предэкспоненциальный множитель A, мы можем перепишите это уравнение, чтобы показать изменение от k 1 до k 2 при изменении температуры от T 1 до T 2 .
Пример:
Преобразование циклопропана в пропилен можно записать следующим образом.
Следующие данные были измерены экспериментально.
@300C k = 2.4110 -10 с -1
@400C k = 1,1610 -6 с -1
Что такое E и ?
Пример (продолжение)
Что такое k при 450C?
Вернуться к началу
Наконец-то мы подошли к тому моменту, когда можем посмотреть, как скорость законов и реакций
механизмы взаимосвязаны. Мы видели, что сбалансированная химическая реакция не
обязательно расскажите нам что-нибудь о фактическом законе скорости. Это потому, что
общая сбалансированная химическая реакция представляет собой только исходное состояние (реагенты)
и конечное состояние (продукты) и не касается процесса. Кинетика
относится к процессу.
Это потому, что
общая сбалансированная химическая реакция представляет собой только исходное состояние (реагенты)
и конечное состояние (продукты) и не касается процесса. Кинетика
относится к процессу.
Если реакция включает только одну стадию (элементарную реакцию), то есть прямая связь между законом скорости реакции и «молекулярностью» сама реакция. Другими словами, закон скорости элементарной реакции говорит нам какие именно молекулы участвуют.Так как для одноступенчатой реакции можно также связать это с реагентами, существует корреляция между уравновешенным реакция и закон скорости элементарных реакций.
Давайте рассмотрим несколько примеров элементарных реакций и посчитаем скорость законы для них.
Унимолекулярные реакции (общий порядок реакции = 1)
Для этой реакции требуется 262 кДж/моль. Эта энергия должна быть сконцентрирована в вибрациях. и вращения, которые участвуют в реакции.
Закон о скорости: Ставка = k[C 4 H 8 ]
Вообще для реакции A $\rightarrow$ продуктов
Коэффициент = k[A]
Бимолекулярные реакции (общий порядок реакции = 2)
NO(г) + О 3 (г) $\rightarrow$ NO 2 (г) + О 2 (г)
Закон о скорости: Скорость = k[NO][O 3 ]
Реакция первого порядка как по NO, так и по O 3 .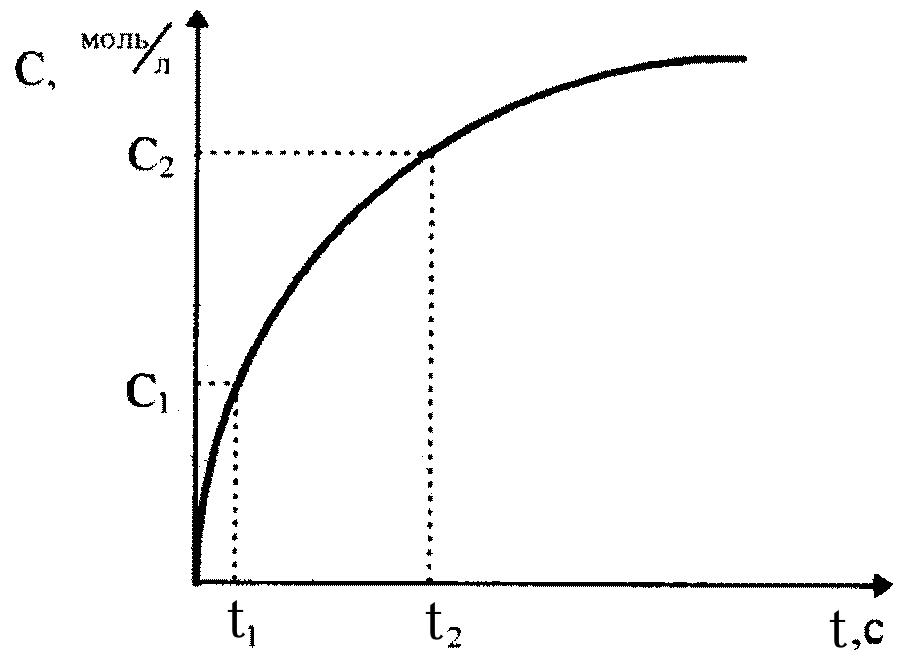 Этот
подразумевает, что одна молекула NO и одна молекула O 3 участвуют в
реакцию, точно так же, как показывает уравновешенная реакция.
Этот
подразумевает, что одна молекула NO и одна молекула O 3 участвуют в
реакцию, точно так же, как показывает уравновешенная реакция.
В общем случае для реакции A + B $\rightarrow$ Продукты Ставка = k[A][B]
для реакции 2A $\rightarrow$ Продукты Скорость = к[А] 2
Термолекулярные реакции (общий порядок реакции = 3)
Три молекулы должны столкнуться с достаточной энергией и все в правильном направлении. ориентация.Это очень редко. Если ту же реакцию можно провести используя несколько бимолекулярных стадий, то именно так это и произойдет.
Вообще,
для реакции A + B + C $\rightarrow$ Продукты Ставка = k[A][B][C]
2A + B $\rightarrow$ Продукты Скорость = k[A] 2 [B]
и т. д. .
Нет одностадийных реакций более высокого порядка.
Константы равновесия и механизмы реакций
Рассмотрим реакцию
NO(г) + O 3 (г) № 2 (г) + О 2 (г)
Поскольку было установлено, что оба прямая и обратная реакции одноступенчатые реакции, это легко для нас, чтобы написать закон скоростей для обеих реакций:
Скорость пересылки = k f [NO][O 3 ],
Скорость обратного хода = k r [NO 2 ][O 2 ].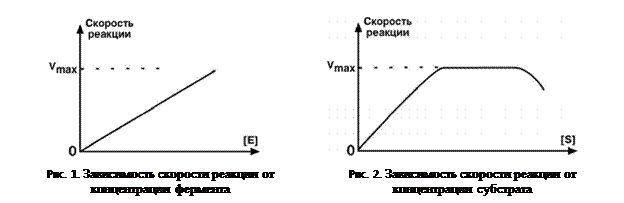
Если система находится в равновесии, то мы можем утверждать, что форвардный курс равняется обратному курсу.
k f [NO][O 3 ] = k r [NO 2 ][O 2 ]
, константа равновесия.
Многоступенчатые реакции не так просты, но все же дают правильные значения K из стехиометрия.
Многостадийные реакции
Экспериментально установлено, что химическая реакция (собственно, мы делали это ранее в этих заметках)
2 NO + Cl 2 $\rightarrow$ 2 NOCl
Имеет закон скорости
Скорость = k [NO] 2 [Cl 2 ].
Мы хотим попробовать создать модель (механизм реакции) это объяснит этот наблюдаемый закон скорости. Наша работа как ученых состоит в том, чтобы найти модель, которая работает, и убедиться, что это наилучшая модель.
Вот один из вариантов:
| 2 НО Н 2 О 2 | Быстрое равновесие с константой равновесия K 1 . |
| Н 2 О 2 + Кл 2 $\rightarrow$ 2 NOCl | Медленный шаг с константой скорости k 2 |
С медленного шага:
Ставка = k 2 [N 2 O 2 ][Cl 2 ]
Однако этот закон скорости включает концентрацию N 2 O 2 который является промежуточным продуктом реакции.Это не реагент и не продукт. Нам нужно попытаться заменить это какой-либо другой функцией концентрации реагентов.
Равновесие быстрое. Следовательно, всегда можно считать, что концентрации можно связать с константой равновесия следующим образом:
К 1 = [Н 2 О 2 ]/[НЕТ] 2 ==> [N 2 O 2 ] = K 1 [НО] 2
Теперь мы можем подставить это в закон скорости, который мы определили исключительно из
медленный шаг.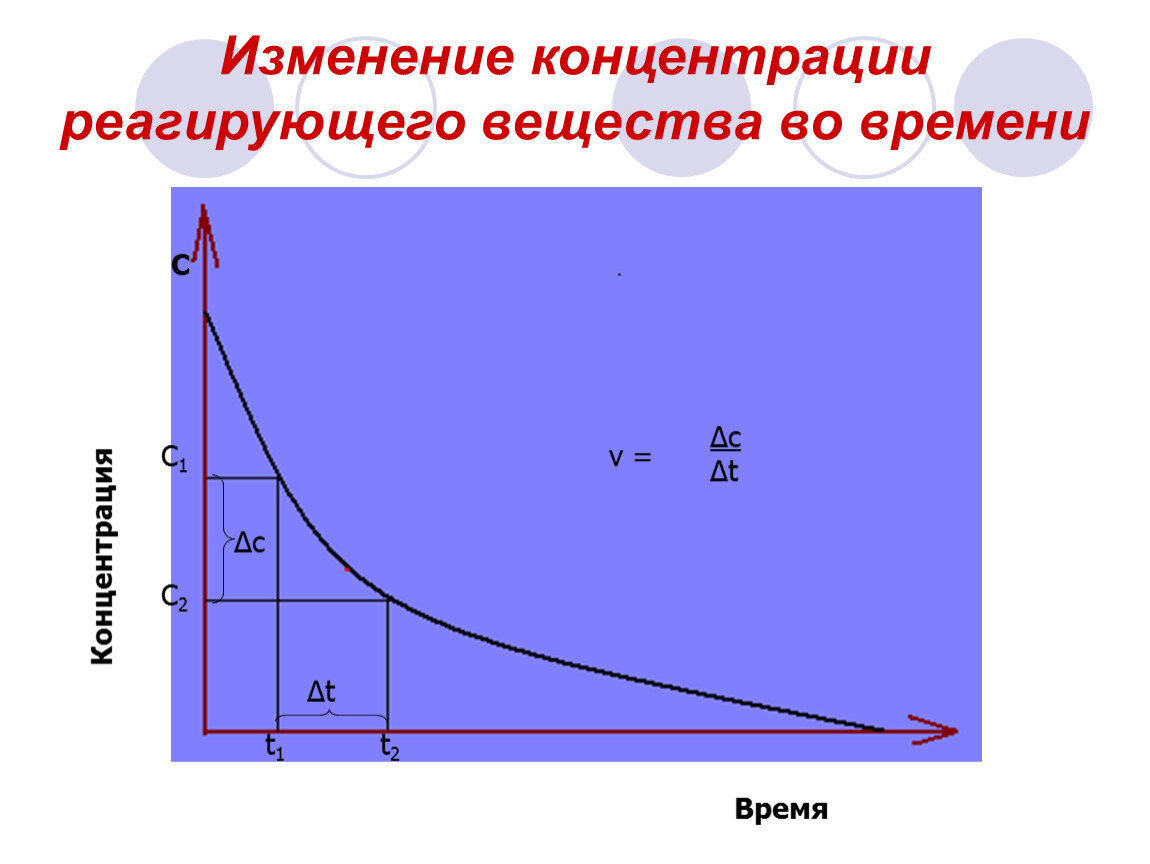
Ставка = k 2 K 1 [НО] 2 [Кл 2 ]
или
Ставка = k[NO] 2 [Cl 2 ], где k = k 2 K 1 .
Может быть и другая возможность. Мы можем представить, что следующий механизм правдоподобно.
NO + Cl 2 $\rightarrow$ NOCl + Cl slow — скорость постоянная. = к 1
NO + Cl $\rightarrow$ NOCl быстро — скорость конст.= к 2
Из скорости, определяющей медленный шаг:
Скорость = k 1 [NO][Cl 2 ].
Это не экспериментальный закон скорости. Этот механизм не является правильным.
Приближение устойчивого состояния.
В этом примере нам нужно будет сделать некоторые предположения относительно промежуточных концентраций для решения проблемы.
Разложение N 2 O 5 на NO 2 и O 2 получается в результате следующей химической реакции:
2 Н 2 О 5 $\rightarrow$ 4 НЕТ 2 + О 2
и имеет экспериментально
наблюдаемый закон скорости = k[N 2 O 5 ].
Поскольку очевидно, что нам нужно как минимум две молекулы N 2 O 5 чтобы закончить одну молекулу кислорода, мы не можем делать вид, что этот закон скорости указывает на одностадийную реакцию, даже если мы можем записать сбалансированную реакцию с коэффициент 1 перед N 2 O 5 .
В этом химическом процессе должно быть несколько стадий. Чтобы определить каков может быть действительный механизм, можно просто строить обоснованные догадки о механизм, а затем определяет закон скорости из постулируемого механизма.Если закон скорости постулируемого механизма совпадает с установленным экспериментально, мы иметь доказательства (не убедительные), что постулируемый механизм является действительным.
Постулируемый механизм этой реакции включает следующую одностадийную реакции.
1. Н 2 О 5 + М
Н 2 О 5 *
+ М
шаг активации k 1 и k -1 .
Этот этап является этапом активации, на котором некоторая молекула M сталкивается с N 2 O 5 и передает ему достаточную энергию для реагировать.
2. N 2 O 5 O 5 * $ \ pruralarrow $ no 2 + № 3 Медленно; к 2
3. НЕТ 2 + НЕТ 3 $\rightarrow$ НЕТ + НЕТ 2 + O 2 быстро
4.НЕТ + НЕТ 3 $\rightarrow$ 2 НЕТ 2 быстро
Так как быстрые реакции существенно «задерживаются» медленными шагами. будет быть медленными шагами, которые определяют скорость реакции. Очевидно, нам нужно иметь дело с тем фактом, что есть два шага, ни один из которых явно не является тарифообразующий.
Мы можем думать об этом как о двухэтапном процессе, в котором ставки
сопоставимо.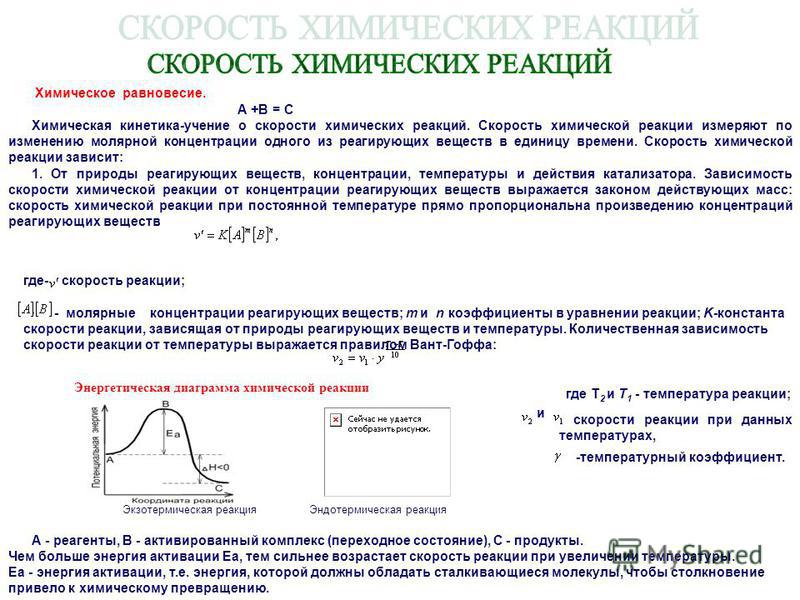 Мы можем получить несколько дифференциальных уравнений скорости из этого
система.
Мы можем получить несколько дифференциальных уравнений скорости из этого
система.
С шага 1:
1. = -k 1 [N 2 O 5 ][M] + к -1 [Н 2 О 5 *][М]
2. = k 1 [N 2 O 5 ][M] — k -1 [N 2 O 5 *][M] — к 2 [Н 2 О 5 * ]
и, предполагая, что шаги 3 и 4 идут до завершения сразу, мы можем использовать общую стехиометрию, чтобы определить еще одну скорость уравнение.
3. 1/2 = k 2 [N 2 O 5 * ]
У нас есть, казалось бы, неразрешимая проблема, так как есть больше неизвестных, чем уравнений. Однако существуют упрощения возможности.
Если у нас есть большое избыточное количество молекул M (высокое давление
системы), доступные для активации N 2 O 5
тогда шаг активации (1) будет быстрее, чем первая диссоциация
стадия (2) с участием активированной молекулы N 2 O 5 * .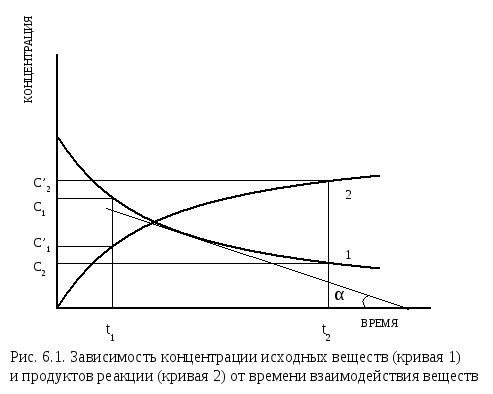 В этом случае скорость может быть определена из медленного шага (2) и будет
просто
В этом случае скорость может быть определена из медленного шага (2) и будет
просто
Ставка = k 2 [N 2 O 5 *]. и используя равновесие из шага 1, мы можем легко получить
К 1 = (к 1 /к -1 ) = [N 2 O 5 *] / [N 2 O 5 ]
Ставка = K 1 k 2 [N 2 O 5 ] = k [N 2 O 5 ].
Это означает, что существует только одна молекула N 2 O 5 участвуют в этапе определения скорости. Хотя даже в этой многостадийной реакции это может быть правдой, нет никакой гарантии, что мы можем связать порядок реакции с молекулярность в многостадийной реакции.
В случаях низкого или среднего давления мы не можем сделать упрощение
предположение, что шаг 2 является определяющим. мы должны рассмотреть оба
стадия активации и стадия диссоциации вместе.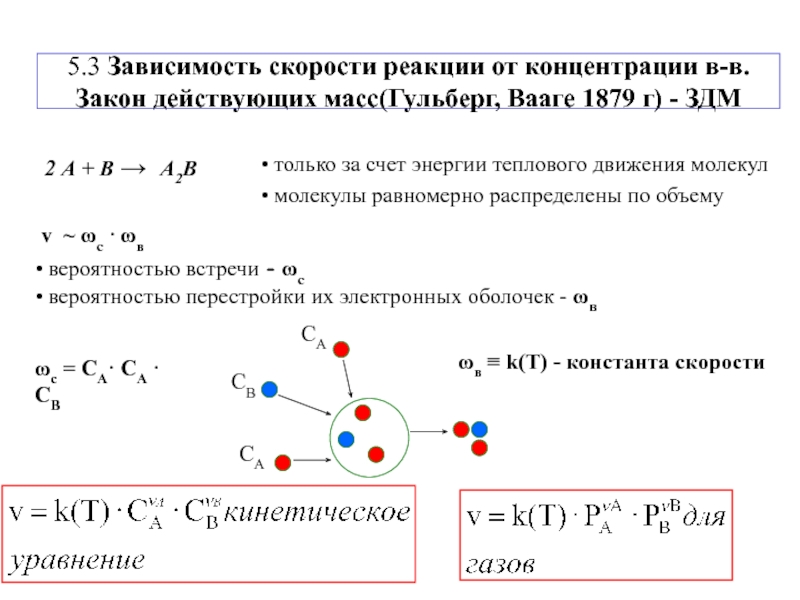
N 2 O 5 * производится и уничтожается шаг активации, а также израсходован на шаге диссоциации. Первое предположение, которое нам нужно будет сделать, состоит в том, чтобы предположить, что количество активированного молекулы N 2 O 5 * быстро достигает значения, которое остается постоянным на протяжении всей реакции. Это устойчивое состояние и математически записывается как
.= 0 = k 1 [N 2 O 5 ][M] — к — 1 [N 2 O 5 *][M] — k 2 [N 2 O 5 * ].
Нулевое значение означает, что мы не предполагали никаких изменений в концентрация во времени, а не нулевая концентрация.
Теперь мы можем найти [N 2 O 5 * ]
Теперь, используя приведенное выше уравнение 3, мы можем определить общую скорость.
Мы видим, что при низком давлении (малые количества M) можно считать, что k -1 [M] мало по сравнению с k 2 (в знаменателе) и нашим выражения упрощаются до
ставка = к 1 [N 2 O 5 ][M]
при высоких давлениях верно обратное и мы получаем
,
какой той же форме, которую мы предсказали в нашем первом упрощении выше.
Зависимость скорости и температуры
2 NO(г) + Cl 2 (г) $\rightarrow$ 2 NOCl(г)
экспериментальный закон скорости: Скорость = k[NO] 2 [Cl].
Хотя мы могли бы использовать это как доказательство того, что реакция является одноступенчатой
поскольку закон скоростей и показатели степени совпадают. Это было бы термолекулярным
реакция. Если можно придумать многоступенчатую систему, избегающую
молекулярных стадий и по-прежнему имеет тот же закон скорости, то реакция более
вероятно, пойдет по многоступенчатому пути.
Вот пример другого механизма. Кроме того, мы рассмотрим Температурный ход реакции.
2 НО + О 2 $\rightarrow$ 2НО 2
Имеет тарифный закон
Ставка = к [НЕТ] 2 [О 2 ],
, где k уменьшается с повышением температуры!
Следующий механизм объясняет как закон скорости, так и кажущуюся антиаррениусовское поведение.
| НЕТ + НЕТ N 2 O 2 | Быстрое равновесие с прямой/обратной скоростью константы к 1 / к -1 |
| Н 2 О 2 + О 2 $\rightarrow$ 2 НЕТ 2 | Константа скорости медленного шага = k 2 |
Второй (медленный) шаг определяет скорость, поэтому
Ставка = к 2 [N 2 O 2 ] [O 2 ].
Как и в предыдущем примере [N 2 O 2 ] является промежуточное звено, а не реагент или продукт. Было бы очень трудно измерить это концентрация с какой-либо уверенностью. Мы переформулируем закон ставки таким образом, чтобы использует только концентрации реагентов (или продуктов).
Так как первый шаг равновесия быстрый, мы можем сказать, что система всегда в равновесии, следовательно,
прямой курс = обратный курс
k 1 [НО] 2 = k -1 [N 2 O 2 ]
или
[N 2 O 2 ] = K 1 [НО] 2
где константа равновесия K 1 = k 1 /k -1 .о}})}{RT}\справа]\]
Мы сгруппировали факторы на основе их независимости от температуры.
Обратите внимание, что если мы переименуем первый фактор просто в A eff
а числитель показателя степени представляет собой «эффективную» энергию активации E a,eff , теперь мы можем написать
уравнение, похожее на уравнение Аррениуса. o\]
o\]
в показателе степени во втором множителе похоже на эффективную реакцию барьер E a,eff .
Это похоже на обычное уравнение Аррениуса, за исключением того, что эффективное энергия активации E a равна сумме E a2 плюс Δ Н 1 . Начиная с Δ H 1 может быть положительным или отрицательным, знак общего E a может быть отрицательно, если Δ H 1 достаточно отрицательно. В этом случае стадия 1 сильно экзотермична. Это даст эффективное отрицательный энергетический барьер и наблюдаемое антиаррениусовское поведение.
Альтернативный взгляд на это можно увидеть в свете теории Ле Штелье.
принцип. Равновесие на этапе 1 обеспечивает поставку реагента для этапа 2.
Так как положение равновесия смещается влево при повышении температуры
увеличивается (Энергия является продуктом шага 1), то запас (концентрация)
реагент для стадии 2 (стадия ограничения скорости) уменьшается по мере того, как температура
увеличивается. Если изменение концентрации достаточно велико, скорость второго шага
будет уменьшаться даже при повышении температуры.
Если изменение концентрации достаточно велико, скорость второго шага
будет уменьшаться даже при повышении температуры.
Вернуться к началу
Катализатор – это вещество, которое увеличивает скорость реакции, но не потребляется в этой реакции и не изменяет продукты реакции. А катализатор вполне может быть использован в реакции на каком-то этапе механизма реакции но если это так, то он регенерируется на более позднем этапе. Таким образом, нет чистого изменения в происходит количество катализатора. В некоторых случаях катализатор представляет собой просто соединение или химические вещества, находящиеся в той же фазе, что и сама реакционная смесь.Этот называется гомогенным катализатором . Другие катализаторы существуют как отдельные фазы, а реакция происходит на границе раздела фаз (поверхности) между реакционная смесь и катализатор. Это называется гетерогенным катализатором .
Пример гомогенного катализа можно найти в реакции, которая
видит, как цис-2-бутен превращается в транс-2-бутен.
Эта реакция имеет относительно низкую скорость реакции и активацию энергия E a = 262 кДж/моль.
Если мы добавим йод I 2 к реакционной смеси, мы обнаружим, что энергия активации снижается до E a = 115 кДж/моль.
Это можно объяснить следующим механизмом реакции.
Йод устанавливает собственное равновесие с радикалом йода.
я 2 2 я
Мы видим, что радикал йода, использованный в реакции, вызвал другой механизм реакции. Этот новый механизм имеет более низкую энергию активации. чем некатализируемый.Иодный радикал регенерируется в конце механизм и, следовательно, не израсходован, а используется.
В гетерогенной реакции чаще всего участвуют твердый катализатор и жидкий или
газообразная реакционная смесь. Рассмотрим каталитический нейтрализатор в выхлопной системе.
ваших автомобилей. Металлическая платина наносится на гранулированный материал подложки для
обеспечить, чтобы как можно больше платины подвергалось воздействию паров, проходящих через
выхлопная система.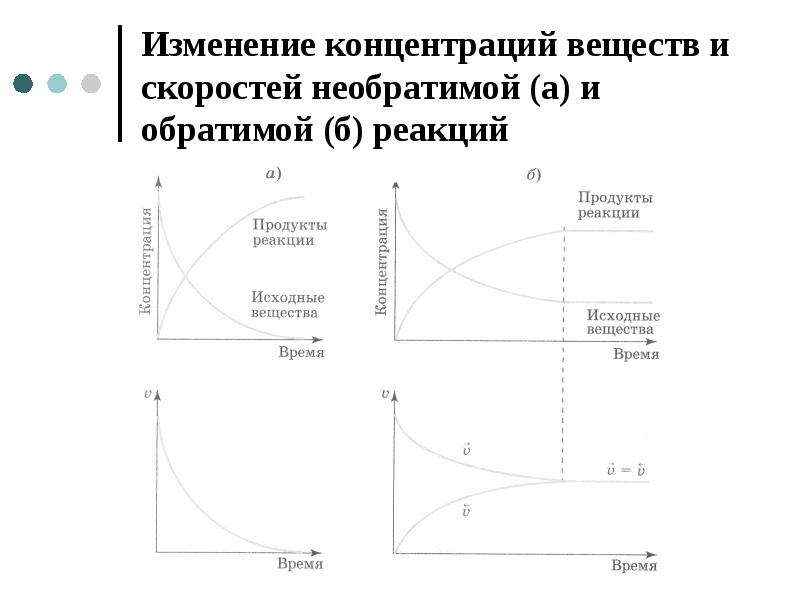 Эти пары часто содержат несгоревшие углеводороды и углекислый газ.
НЕТ газов.Катализатор помогает завершить их окисление до CO 2 ,
NO 2 и H 2 O. Вы часто замечаете много водяного пара, поступающего
из выхлопных систем современных автомобилей в холодный день, потому что он конденсирует
на холодном воздухе, чтобы стать видимым.
Эти пары часто содержат несгоревшие углеводороды и углекислый газ.
НЕТ газов.Катализатор помогает завершить их окисление до CO 2 ,
NO 2 и H 2 O. Вы часто замечаете много водяного пара, поступающего
из выхлопных систем современных автомобилей в холодный день, потому что он конденсирует
на холодном воздухе, чтобы стать видимым.
Я проиллюстрирую гетерогенный катализ со следующими пример.
C 2 H 4 + H 2 $\rightarrow$ C 2 H 6 Без катализатора очень медленно.
Используйте катализатор Pt или Ni.
Наши тела используют катализаторы, называемые ферментами, для облегчения многих видов
реакции. Например, окисление сахарозы C 12 H 22 O 11
с углекислым газом и водой происходит только при высокой температуре (сахароза горит)
если нет катализатора. Фермент сахараза (кодовое название, означающее «мы
не знаю что это, но он катализирует сахарозную реакцию») делает этот процесс
довольно быстро при температуре тела (более низкая энергия активации). Катализированный
реакция при температуре тела порядка в 10 20 раз быстрее
чем некатализируемый.
Катализированный
реакция при температуре тела порядка в 10 20 раз быстрее
чем некатализируемый.
Эти типы каталитических реакций не столь гетерогенны, как реакции, катализируемые металлами, так как ферменты растворяются в одном и том же растворы как реагенты и продукты, но их размер настолько велик, что они почти как твердая фаза по сравнению с крошечными реагентами и продуктами. Этот Тип реакции обычно просто классифицируется как реакция, катализируемая ферментами.
Вернуться к началу
Майкл Дж. Момбуркетт.
Авторское право 1997
Отредактировано: 05 сентября 2012 г.
Краткое введение в историю химической кинетики
1. Введение
Современная химическая (реакционная) кинетика – это наука, описывающая и объясняющая химическую реакцию в том виде, в каком мы ее понимаем в наши дни [1]. Его можно определить как изучение скорости химического процесса или превращения реагентов в продукты, происходящего по определенному механизму, т. е.е., механизм реакции [2]. Скорость химической реакции выражается изменением концентрации некоторых веществ во времени [3]. Можно также указать, что химические реакции также являются предметом изучения многих других химических и физико-химических дисциплин, таких как аналитическая химия, химическая термодинамика, технология и т. д. [2]. Термодинамика связана с общим изменением энергии между начальной и конечной стадиями процесса. Поскольку это изменение может появиться в результате через бесконечное время, термодинамика не имеет прямого отношения к предмету скорости реакции [3].
е.е., механизм реакции [2]. Скорость химической реакции выражается изменением концентрации некоторых веществ во времени [3]. Можно также указать, что химические реакции также являются предметом изучения многих других химических и физико-химических дисциплин, таких как аналитическая химия, химическая термодинамика, технология и т. д. [2]. Термодинамика связана с общим изменением энергии между начальной и конечной стадиями процесса. Поскольку это изменение может появиться в результате через бесконечное время, термодинамика не имеет прямого отношения к предмету скорости реакции [3].
В первой главе дается краткий экскурс в историю понимания природы, механизма, кинетики и термодинамики химических реакций, что привело к широко принятой сегодня теории переходного состояния (TST). Вторая глава закладывает основы теории ТСТ, включая термодинамическое описание активированного комплекса, формулировку статистической суммы и ограничения. Последняя глава посвящена введению простого подхода к расчету изменения массы при переходе реагентов в активированное состояние.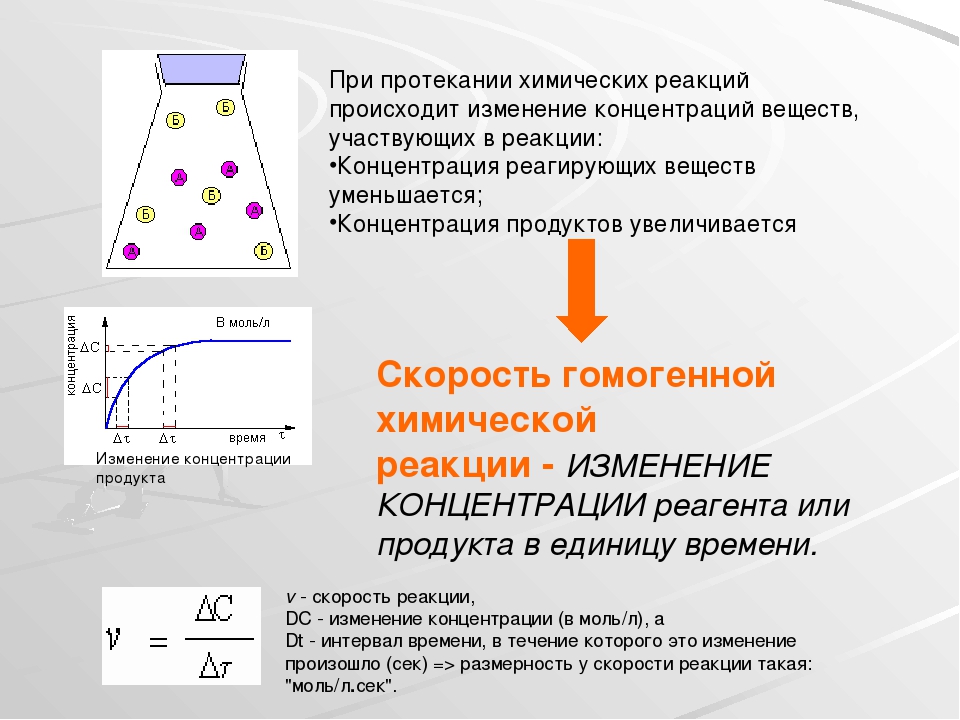 Обзор и упрощенная схема соотношения отдельных тем, которые описаны в этой главе, представлены на рис. 1.
Обзор и упрощенная схема соотношения отдельных тем, которые описаны в этой главе, представлены на рис. 1.
Рис. 1.
Упрощенная схема соотношения отдельных тем в этом трактате.
Объявление2. Краткий исторический экскурс в химическую кинетику
«Химия должна быть не только наукой и профессией, но и искусством. И только как художник может сохраниться личность ученого.” J. von Liebeg 1 [4]
Первое количественное исследование в области химической кинетики было проведено немецким ученым Людвигом Фердинандом Вильгельми (1812–1864) в 1850 г. [5], который использовал поляриметрию для исследования катализируемой кислотой конверсии сахарозы. В этом раннем исследовании Вильгельми установил, что скорость реакции (dZ/dt) пропорциональна концентрации сахарозы (Z) и кислоты (S) в соответствии с дифференциальным уравнением [5]:
−dZdt=MZS⇒logZ=− MSt+CE1
, где M – коэффициент трансформации сахарозы, отнесенный к единице времени, т. е.е., константа скорости реакции и C — константа интегрирования.
е.е., константа скорости реакции и C — константа интегрирования.
Однако английский химик Август Джордж Вернон Харкорт 2 (1934–1919, рис. 2а) считается первым ученым, внесшим значительный вклад в область химической кинетики 3 . Он был одним из первых, кто спланировал эксперименты, чтобы проследить ход химического изменения [6]:
Рисунок 2.
Фотографии (все эти изображения принадлежат к свободной работе в общественном достоянии) А.Г.В. Харкорт (а), Дж.Х. Вант-Гоффа Никола Першайд (немецкий фотограф (1864–1930), разработавший софт-фокус с открытой глубиной резкости (объектив Першайда) где-то около 1920 года) (б) и С.А. Аррениус (в).
«Каждое изменение, которое мы можем наблюдать, может рассматриваться как ставящее перед нами две проблемы: одна относится к способу или ходу изменения, а другая — к его результату. …В начале химии считалось достаточным количественное знание результатов химических превращений; прогресс науки начинается с введения точных количественных идей.В настоящее время то знание, которым мы обладаем, о ходе химических превращений и об их связи с условиями, при которых они происходят, носит чисто количественный характер».
…В начале химии считалось достаточным количественное знание результатов химических превращений; прогресс науки начинается с введения точных количественных идей.В настоящее время то знание, которым мы обладаем, о ходе химических превращений и об их связи с условиями, при которых они происходят, носит чисто количественный характер».
Для измерения скорости реакции. Несмотря на отсутствие у Харкорта математических навыков, он очень уважал ее и признавал важность применения математики к химической задаче 4 [7, 8, 9]. Сам Харкорт писал, что [10]:
«…мы занимаемся накоплением обширной коллекции рецептов приготовления различных веществ и фактов об их составе и свойствах, которые могут больше не служить обобщению наука, всякий раз, когда возникает наш Ньютон, чем, я полагаю, большинство звезд для концепции тяготения.
Харкорт сыграл большую роль в превращении химии из описательной в количественную [7]. Еще в 1868 г. он определил химию как науку, которая [11]:
«…исследует отношения различных видов материи друг к другу».
, а также изменения, происходящие при помещении веществ в разные условия или при помещении их друг с другом [7, 11].
Первая реакция была исследована Харкортом совместно с британским математиком Уильямом Эссоном 4 (1838–1916, ФРС 1869 г.) – процесс [6, 7, 12]:
K2Mn2O8+3h3SO4+5h3C2O4→K2SO4+2MnSO4 +10CO2+8h3OE2
Эта реакция, протекающая в очень разбавленном водном растворе, протекает с удобной скоростью при комнатной (постоянной) температуре, и ее можно начать в данный момент и резко остановить добавлением йодистого водорода, который высвобождает йод.Затем степень реакции можно было определить путем титрования количества йода раствором тиосульфата. Харкорт также понял, что реакция ускоряется за счет образования сульфата марганца, т. е. протекает более чем в одну стадию, и предложил следующую последовательность реакций [7, 12, 13]:
K2Mn2O8+3MnSO4+2h3O→K2SO4+2h3SO4+ 5MnOE3
MnO2+h3SO4+h3C2O4→MnSO4+2h3O+2CO2E4
Затем Эссон попытался найти математические уравнения, которые интерпретировали бы результаты на основе гипотезы о том, что: момент будет пропорционален оставшемуся тогда количеству вещества. ”
”
Из-за сложности реакций Ур. 2–4 (см. также работы H.F. Launer [14, 15]), Харкорт и Эссон добились лишь ограниченного успеха в интерпретации своих результатов. С другой стороны, их работы [16] важны тем, что содержат четкую математическую трактовку реакций первого и второго порядка и некоторых типов последовательных реакций. Математические процедуры Эссона используются и сегодня. Он составил соответствующие дифференциальные уравнения, выражающие связь между производной по времени концентрации реагирующего вещества и оставшейся концентрацией, и затем получил решения путем интегрирования [7].
К 1865 г. Харкорт и Эссон начали работу над кинетически более простой реакцией между перекисью водорода и иодоводородом [6, 7, 17]:
h3O2+2HI→2h3O+I2.E5
перекись натрия вносят в присутствии либо кислого, либо щелочного бикарбоната, происходит постепенное выделение йода. Если к раствору добавить гипосульфит натрия (тиосульфат натрия, Na 2 S 2 O 3 ), то он вновь превращает (восстанавливает) йод, как только он образуется, в йодид, но никак иначе не проявляется в влияют на ход реакции. Следовательно, если перекись присутствует в избытке над гипосульфитом, то весь последний под действием выделяющегося йода превращается в тетратионат. 5 После этого превращения в растворе появляется свободный йод, и его выделение можно наблюдать с помощью предварительно добавленного в жидкость небольшого количества крахмала (индикатор, образование йод-крахмального клатрата) [17].
Следовательно, если перекись присутствует в избытке над гипосульфитом, то весь последний под действием выделяющегося йода превращается в тетратионат. 5 После этого превращения в растворе появляется свободный йод, и его выделение можно наблюдать с помощью предварительно добавленного в жидкость небольшого количества крахмала (индикатор, образование йод-крахмального клатрата) [17]. Эссон нашел удовлетворительное уравнение, описывающее результаты опытов Харкорта. Их первая статья по этому вопросу появилась в 1866 г. [12], и хотя они продолжали работу над этой реакцией еще 30 лет, они не публиковали никаких данных об этом до 1895 г., когда Харкорт и Эссон совместно написали Бейкеровскую лекцию 6 [18]. поставлен в Королевском обществе [19].
Большая часть работы была посвящена влиянию температуры на скорость реакции [7, 20, 21]: коэффициент частоты) A ´, а также m (отношение d k / k к d T / T [21]) не зависят от температуры.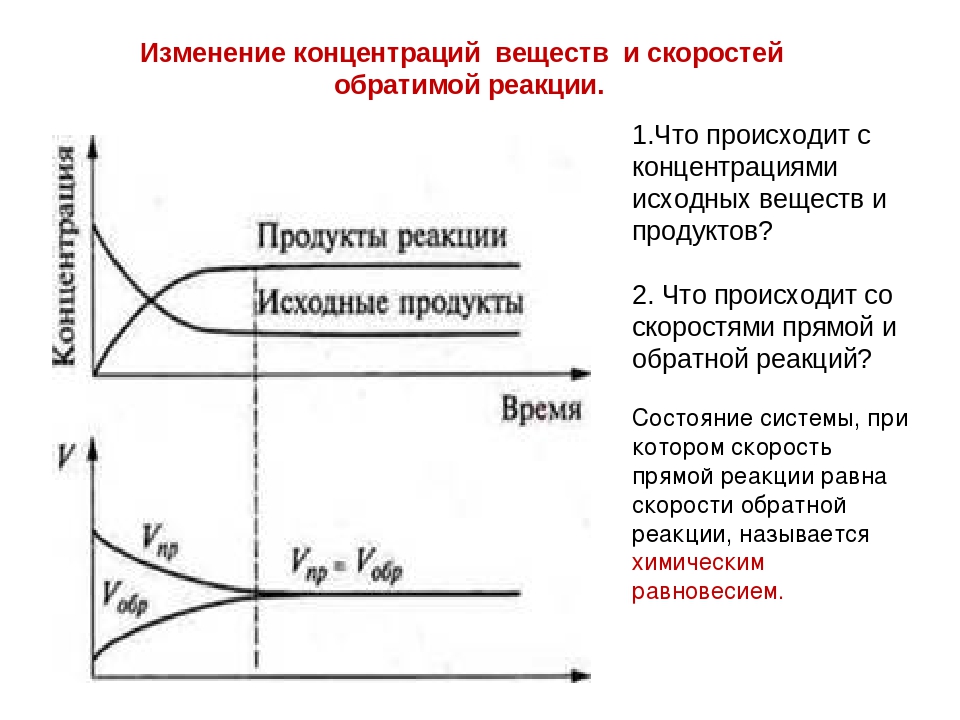
Ранее в 1884 г. Якоб Хенрикус вант-Гофф 7 (1852–1911, рис. 2б) предложил несколько альтернативных уравнений температурной зависимости [22, 23, 24], и одно из них было в 1889 г. принято С.А. Аррениус 8 (1859–1957, рис. 2в) [22]:
k=Aexp−EaRT;E7
где A , E a , R — константы 6ie, частотный фактор, энергия активации и универсальная газовая постоянная (8,314 Дж·(К·моль) -1 ) соответственно. В то время как уравнение 7 дает некоторое представление о механизме реакции, например, энергия активации — это минимальная энергия, необходимая для протекания реакции, уравнение Харкорта-Эссона 9 (ур.6) теоретически стерилен и м не имеет физического значения [7]. С другой стороны, интересным аспектом их работы является то, что они предсказали «кинетический абсолютный нуль», при котором все реакции прекратятся. Их значение для него составило -272,6°С, что замечательно согласуется с недавним значением -273,15°С для абсолютного нуля [7, 21]. Следует также отметить, что Харкорт вместе с его кинетическими работами был очень подробно рассмотрен М. К. Кингом [8, 25, 26] и Дж. Шортером [27].
Следует также отметить, что Харкорт вместе с его кинетическими работами был очень подробно рассмотрен М. К. Кингом [8, 25, 26] и Дж. Шортером [27].
Для более точного решения температурной зависимости константы скорости реакции, особенно тех, которые охватывают широкий диапазон температур, обычно допускается, чтобы A было пропорционально T m , так что уравнение 7 приводит к формуле [20]:
k=A’Tmexp-EaRT;E8
, где константа A ´ не зависит от температуры (см. также уравнение 24).
Вант-Гофф также указал, что реакции первого и второго порядка относительно распространены, тогда как реакции третьего порядка встречаются редко.Он привел пример, основанный на реакции 5, которая экспериментально ведет себя как реакция второго порядка, несмотря на то, что имеется три молекулы реагента. Далее реакция, скорее всего, протекает в две стадии с образованием короткоживущего интермедиата реакции (HOI) следующим образом [28]:
h3O2+HI→HOI+h3O;E9
Несмотря на то, что голландский ученый JH Вант-Гофф получил признание благодаря органической химии 10 за свои пионерские работы в области стереохимии [23, 29, 30, 31, 32]:
«Благодаря Вант-Гоффу химия становится трехмерной» ;
к концу 1870-х годов он больше не интересовался в основном изучением органических молекулярных структур. Его внимание переключилось на молекулярные превращения и исследование того, почему химические реакции протекают с очень разной скоростью. Чтобы понять химическое равновесие и химическое сродство, он начал десятилетние исследования в области термодинамики, химического равновесия и кинетики, то есть химической динамики 11 [33]. По словам Вант-Гоффа [34]:
Его внимание переключилось на молекулярные превращения и исследование того, почему химические реакции протекают с очень разной скоростью. Чтобы понять химическое равновесие и химическое сродство, он начал десятилетние исследования в области термодинамики, химического равновесия и кинетики, то есть химической динамики 11 [33]. По словам Вант-Гоффа [34]:
«…динамика посвящена взаимодействию нескольких веществ, т. е. химическому изменению, сродству, скорости реакции и химическому равновесию.
Немецкий химик Фридрих Вильгельм Оствальд 12 (1853–1932, рис. 3) определил аналогично [35]:
рис. ) В. Оствальда Никола Першайд (немецкий фотограф (1864–1930), разработавший мягкий фокус с открытой глубиной резкости (объектив Першайда) где-то около 1920 г.) (а), CN Хиншелвуд (б) и Н.Н. Семенов (с).
«…теория протекания химических реакций и теория химического равновесия.
Сегодня выражение «химическая кинетика» относится к изучению скоростей химических реакций, а не к свойствам химических систем, находящихся в равновесии [36].
Среди прочего, наиболее значительный вклад Дж.Х. Вант-Гоффа [23, 36, 37, 38, 39]:
-
Вывод математической модели для объяснения скоростей химических реакций на основе изменения концентрации реагентов во времени.
-
Вывод уравнения, связывающего теплоту реакции с константой равновесия 13 , широко известного как уравнение Вант-Гоффа
, где K — константа равновесия, T — температура, R — универсальная газовая постоянная и q — теплота, необходимая для диссоциации моля вещества в современных обозначениях, уравнение11 можно записать как:
dlnKdT=ΔH∘RT2;E12
где Δ H ° — стандартное изменение энтальпии реакции.
-
Предложение нового метода определения порядка (молекулярности) химической реакции 15 , заключающегося в измерении скорости (r) при различных концентрациях (c) реагента:
r=kcn;E13
порядок реакции ( n ) можно определить по наклону графика log r против log c .

-
Объяснение влияния температуры на равновесие реакции (уравнения 11 и 12) Х. Л. Ле Шателье показало применимость этого соотношения, которое теперь известно как принцип Вант-Гоффа — Ле Шателье. Закон обеспечивает важное качественное обсуждение того, как K зависит от температуры: если теплота выделяется, когда реакция протекает слева направо ( q отрицательно), константа равновесия будет уменьшаться при повышении температуры. .И наоборот, если q положительно, повышение температуры увеличит K .
-
Определение химического сродства с точки зрения максимальной внешней работы, совершаемой в химической реакции при постоянной температуре и давлении в качестве движущей силы реакции. Выводы Вант-Гоффа, Дж. Томсена и М. Бертольда 16 используются такими физиками, как Дж.В. Гиббса и Гельмгольца, чтобы распространить термодинамические принципы на химические системы.
-
(a) Значение E не зависит от температуры.
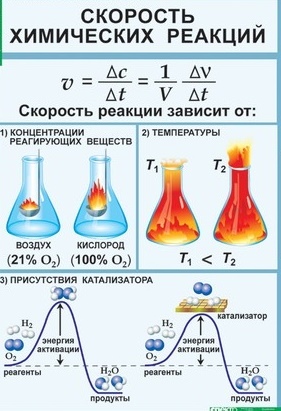 В этом случае уравнение 18 можно проинтегрировать (термин E/R∫dT/T2=-E/RT+const.), чтобы получить:
В этом случае уравнение 18 можно проинтегрировать (термин E/R∫dT/T2=-E/RT+const.), чтобы получить: -
или:
-
, где A — константа.
-
(б) Имеется параболическая зависимость E от температуры, т.е.т. е. зависимость, заданная формулой B + D T 2 , где B и D — константы. уравнение 18 можно проинтегрировать следующим образом:
-
или:
- 1 линейная зависимость между E и температурой, которая задается термином B + C T , что приводит к уравнению:
Вант-Гофф также указал, что химическая кинетика отличается от химической термодинамики, и немецкий физик Герман фон Гельмгольц выдвинул аналогичную теорию в 1882 году [23].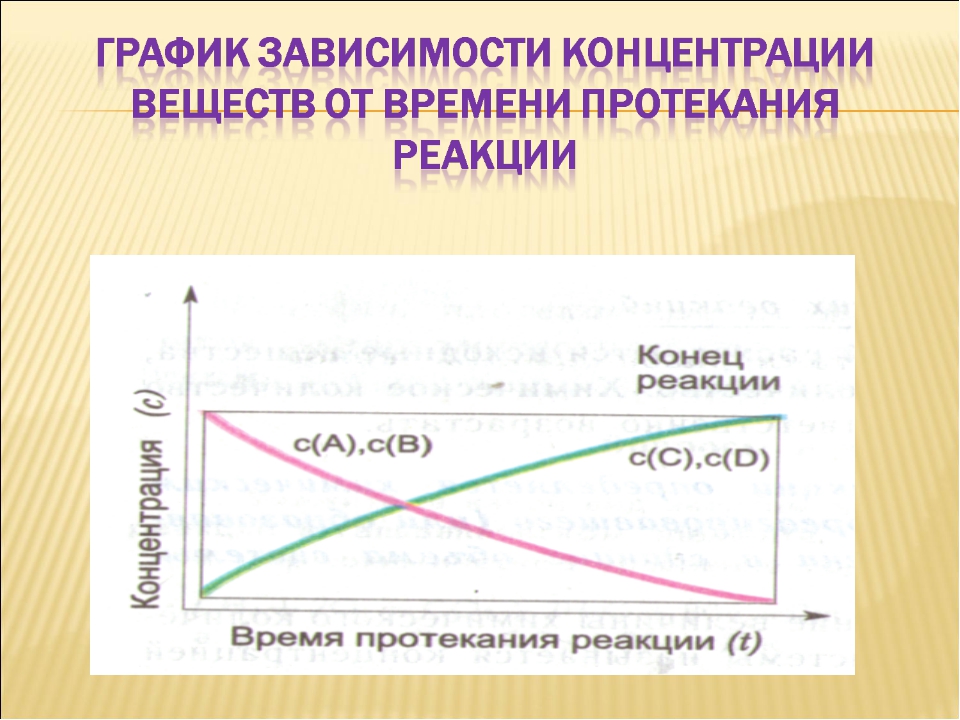
Поскольку отношение констант скорости прямой ( k 1 ) и обратной ( k − 1 ) реакций равно константе равновесия, уравнения 11 или 12 можно интерпретировать следующим образом [36]: −1 меняются в зависимости от температуры так же, как K .Другими словами, он рассматривал теплоту q как разность между двумя энергетическими терминами E 1 и E −1 :
q=E1−E−1;E15
3, поэтому: dlnk1dT-dlnk-1dT=E1RT2-E-1RT2.E16
Затем он утверждал, что первый член с каждой стороны можно приравнять, а второй член может быть:
dlnk1dT=E1RT2 and dlnk-1dT=E− 1RT2.E17
С опущенным нижним индексом мы можем записать влияние температуры на константу скорости следующим образом:
dlnkdT=ERT2.E18
Затем Вант-Гофф обсуждает три различные возможности:
lnk=-ERT+const;E19
k= Aexp-ERT;E20
lnk=-BRT+DTR+const.;E21
k=Aexp-B-DT2RT.E22
lnk=−BRT+CRlnT+const.;E23
-
или:
k=ATmexp−BRT;E24
где м = C/ R — константа. 17
Первая и простейшая из этих возможностей (а) того, что E не зависит от умеренной температуры, была принята в 1889 г. Аррениусом [36, 40], который применил ее к множеству экспериментальных результатов. Он также дал ему интересную интерпретацию с точки зрения равновесия между молекулами реагентов и активными молекулами, которые, как предполагалось, очень легко вступают в реакцию.В результате уравнение 20 теперь обычно называют уравнением Аррениуса 18 [36].
Аррениусом [36, 40], который применил ее к множеству экспериментальных результатов. Он также дал ему интересную интерпретацию с точки зрения равновесия между молекулами реагентов и активными молекулами, которые, как предполагалось, очень легко вступают в реакцию.В результате уравнение 20 теперь обычно называют уравнением Аррениуса 18 [36].
В 1893 г. немецкий физик Макс Карл Эрнст Людвиг Планк (1858–1947, Нобелевская премия 1918 г. за «открытие энергии квантов») предложил уравнение, разрешающее связь константы равновесия и давления ( p ) [7, 41, 42, 43].
dlnKdp=-ΔVRT;E25
где Δ V — молярное изменение объема в ходе реакции. Как указывал Вант-Гофф, это уравнение аналогично уравнениям14–17. С K — K 1 / K -1 Можно представить так называемый «возможная формула»:
DLNKDP = -ΔVRT; E26
без какой-либо интерпретации δ V № , что сегодня означает объем активации, т. е. изменение объема при переходе реагентов в активированное состояние [7].
е. изменение объема при переходе реагентов в активированное состояние [7].
Поскольку Харкорт сыграл большую роль в переходе химии от описательной эры к количественной, его учение повлияло на многих студентов, таких как Х.Б. Диксон, Д.Л. Чепмен и Н.В. Сиджвик. Гарольд Бейли Диксон (1852–1930) сыграл важную роль в развитии физической химии в Англии. Наиболее важные исследовательские вклады Диксона были посвящены изучению взрывной реакции между окисью углерода и газообразным кислородом. Он заставлял взрывы двигаться по металлическим трубам и измерял их скорость с помощью хронометра [36, 44, 45, 46].
Дэвид Леонард Чепмен (1869–1958), его первые исследования были посвящены кинетической теории газовой детонации. 19 Он использовал результаты Диксона о скоростях взрывных волн в газах для теоретического рассмотрения таких взрывов 20 [36, 47]. Область за детонационной волной до сих пор называют «слоем Чепмена-Жуге» или «условием Чепмена-Жуге» [36, 48]. Чепмен также разработал важную теорию распределения ионов на заряженной поверхности [36, 49]. Поскольку родственная работа [50] была выполнена французским физиком Жоржем Гуи (1854–1826), двойной электрический слой, рассматриваемый в их теориях, теперь известен как «слой Гуи-Чепмена» [36].
Поскольку родственная работа [50] была выполнена французским физиком Жоржем Гуи (1854–1826), двойной электрический слой, рассматриваемый в их теориях, теперь известен как «слой Гуи-Чепмена» [36].
Другая газофазная реакция, изученная Чепменом, включает разложение озона [51, 52], синтез формальдегида [53] и закиси азота [54]. Он также провел важные исследования термических и фотохимических реакций между водородом и хлором [36, 55, 56], исследовал аллотропную модификацию [57] и соединения фосфора [58, 59]. Одним из очень важных вкладов, сделанных Чепменом в 1913 г., было применение (впервые) стационарной обработки к составному механизму, включающему промежуточные соединения с коротким временем жизни [60].Эта процедура позже широко использовалась Максом Эрнстом Августом Боденштейном (1871–1942) [61], который смог защитить ее от критики [36].
Сирил Норман Хиншелвуд 21 (1897–1967, рис. 3b) был английским химиком-физиком:
«Химия: самое превосходное дитя интеллекта и искусства».
Он был удостоен Нобелевской премии по химии за 1956 г., а также внес важный вклад в химическую кинетику [62]:
очарование времени и перемен: это то, что выходит за пределы науки в поэзию, но наука, подчиненная жесткой необходимости всегда искать более близкое приближение к истине, сама содержит много поэтических элементов.
Среди прочих Хиншелвуд исследовал реакцию между водородом и кислородом 22 [63, 64]:
сообщает им некоторым физическим действием, таким как столкновение с другой молекулой, определенное критическое количество энергии. Этот процесс обычно называют «активацией». …в экзотермических реакциях, как было показано, возможен особый механизм, в котором освобождающаяся энергия передается молекулами, образовавшимися в реакции, непревращенным молекулам и немедленно активирует их, тем самым создавая так называемую реакционную цепь.
В первой работе этой серии [63] сделан вывод о том, что при протекании реакции между водородом и кислородом в кварцевом сосуде протекали два процесса, один на стенках сосуда и один в газовой фазе (цепные реакции 23 ) . Возможность разветвления цепи ранее поднималась датским физиком Х.А. Крамерс (1894–1952) и русский ученый Николай Николаевич Семенов 21 (Семенов или Семенов) (1896–1986, рис. 3в) [65], которые провели специальные эксперименты, показавшие существование нижнего предела давления кислорода при окислении фосфора. [7].В более поздней работе [65] было показано, что существует диапазон давлений, в пределах которого происходит взрыв («полуостров взрыва» [66]), а также нижний и верхний пределы давления, за пределами которых реакция идет медленнее. Дальнейшая работа была также проведена по окислению фосфина [67] и монооксида углерода [68]. Он также участвовал в исследованиях Гарольда Хартли 25 (1878–1772) по термическому разложению твердых тел [69, 70, 71].
Возможность разветвления цепи ранее поднималась датским физиком Х.А. Крамерс (1894–1952) и русский ученый Николай Николаевич Семенов 21 (Семенов или Семенов) (1896–1986, рис. 3в) [65], которые провели специальные эксперименты, показавшие существование нижнего предела давления кислорода при окислении фосфора. [7].В более поздней работе [65] было показано, что существует диапазон давлений, в пределах которого происходит взрыв («полуостров взрыва» [66]), а также нижний и верхний пределы давления, за пределами которых реакция идет медленнее. Дальнейшая работа была также проведена по окислению фосфина [67] и монооксида углерода [68]. Он также участвовал в исследованиях Гарольда Хартли 25 (1878–1772) по термическому разложению твердых тел [69, 70, 71].
Британский физико-химик Эдмунд («Тед») Джон Боуэн 24 (1898–1980) делал акцент на жидкостях и твердых телах, а не на газах.Его фотохимическая работа могла быть инициирована предположением Хартли 25 о возможности разделения изотопов хлора фотохимическими средствами.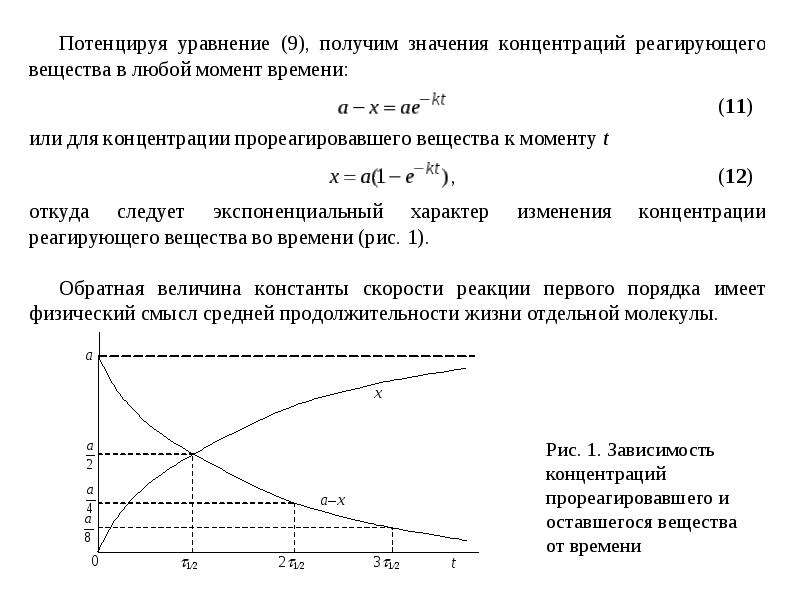 Поскольку эта попытка не увенчалась успехом, Боуэн начал свою фотохимическую работу, и принципы предмета стали яснее [7].
Поскольку эта попытка не увенчалась успехом, Боуэн начал свою фотохимическую работу, и принципы предмета стали яснее [7].
К тому времени было признано, что в фотохимических процессах 26 свет ведет себя как пучок частиц (фотонов) и что существует однозначное соответствие между поглощенными фотонами и молекулами, переведенными в активированное состояние или диссоциированными 27 .Иными словами, один фотон вызывал химическое превращение одной молекулы 28 в результате исследования разложения монооксида хлора (Cl 2 O) в синем и фиолетовом свете [7, 72], где он также писал [ 72]:
Редкость таких реакций, вероятно, преувеличена, поскольку наиболее яркими фотохимическими реакциями являются реакции высокой так называемой «светочувствительности».
К такому же выводу приводит и исследование фотохимического разложения диоксида хлора (ClO 2 ) [73, 74, 75] и нитрозилхлорида (NOCl) [76] в растворе тетрахлорида. Идея цепных реакций и их связь с принципом фотохимической эквивалентности стали признаваться (W.H. Nernst 29 [77], K.F. Bonhoeffer [78]) [7, 79]. В работе Боуэна с Г. Г. Уоттсом [80] показано, что квантовые выходы фотолиза альдегидов и кетонов в растворе значительно меньше, чем в газовой фазе 30 [7].
Идея цепных реакций и их связь с принципом фотохимической эквивалентности стали признаваться (W.H. Nernst 29 [77], K.F. Bonhoeffer [78]) [7, 79]. В работе Боуэна с Г. Г. Уоттсом [80] показано, что квантовые выходы фотолиза альдегидов и кетонов в растворе значительно меньше, чем в газовой фазе 30 [7].
Работа Боуэна по этой теме была недавно обобщена в основополагающей книге под названием «Химические аспекты света» [81, 82].
«Физика и химия начались с изучения поведения объектов обычного размера, но теперь они в основном занимаются материей в чрезвычайно малых масштабах, настолько малых, что обычные чувственные впечатления не могут с ними справиться.”
Фотохимические реакции обычно отличаются от тепловых тем, что энергия активации используется расточительно. Например, термическое разложение йодистого водорода:
2HI→h3+I;E27
, где для реакции двух сталкивающихся молекул требуется энергия 184,1 кДж. Фотохимический процесс:
HI+hv→H+I;E28
требует 283,3 кДж, чтобы поднять молекулу HI до электронно-возбужденного уровня. Этот пример также иллюстрирует очень распространенную особенность фотохимических реакций, т.е.е., образование свободных атомов или радикалов, последующие реакции которых обуславливают сложность измеряемых химических изменений [72, 81].
Этот пример также иллюстрирует очень распространенную особенность фотохимических реакций, т.е.е., образование свободных атомов или радикалов, последующие реакции которых обуславливают сложность измеряемых химических изменений [72, 81].
Эти вторичные процессы, например, для реакции, упомянутой выше (уравнение 28), включают реакции: M;E30
приводят к тому, что простого наблюдения за изменением давления или определения концентрации продукта титрованием часто недостаточно для отслеживания хода реакции, и обычно необходима сложная аналитическая процедура на различных стадиях реакции [81].
Боуэн исследовал также хемилюминесценцию, испускание излучения в результате химических реакций, например окисления паров фосфора в кислороде [83]. Вместе со своими учениками он также провел много исследований по кинетике процессов тушения флуоресценции в растворе [84, 85, 86, 87], но за всю свою исследовательскую карьеру Боуэн много писал по фотохимии и смежным темам, таким как усовершенствование фотоэлементов. и светофильтры для ртутной лампы [7, 88, 89], перенос энергии между молекулами в жестком растворителе [90] и влияние вязкости на выход флуоресценции растворов [91].
и светофильтры для ртутной лампы [7, 88, 89], перенос энергии между молекулами в жестком растворителе [90] и влияние вязкости на выход флуоресценции растворов [91].
Рональд («Ронни») Перси Белл 32 1907–1996) был врачом-химиком, особенно интересовавшимся катализом кислот и оснований, но он также внес важный вклад в понимание эффектов растворителей [7, 92, 93, 94, 95] и квантово-механического туннелирования 33 [96].
Белл одним из первых понял, что при легком водороде; но не тяжелый водород (дейтерий 34 ), переносится в химической реакции, может иметь место особый процесс, известный как «квантово-механическое туннелирование», при котором атом водорода проходит через энергетический барьер, а не над ним.В нескольких теоретических работах он рассмотрел барьеры различной формы и рассмотрел скорость, с которой водород может туннелировать через барьер [7].
Белла также интересовала проблема, которой занимались Хиншелвуд и Мелвин-Хьюз 35 [97, 98], т. е. влияние растворителя на скорость реакции:
е. влияние растворителя на скорость реакции:
люди. Богатых мало, бедных много». 36
Hinshelwood и Moelwyn-Hughes предложили модификацию обычной формулы (ур.20), где предэкспоненциальный множитель рассматривался как частота столкновений, вычисленная из кинетической теории газов 37 , следующим образом:
k=PAexp-EaRT;E31
fudge factor», т. е. величина ad hoc, предназначенная для выражения особых условий 38 , необходимых для реакции молекул после столкновения.
Белл меньше полагался на старую теорию столкновений, 39 , которая была независимо разработана Максом Траутцем (1880–1960) в 1916 году [99] и Уильямом Льюисом (1885–1956) в 1918 году, и больше на теорию переходного состояния. как только он был сформулирован в 1935 г.Он быстро понял, что вместе с формулировкой скоростей Бренстеда 40 в терминах коэффициентов активности теория переходного состояния привела к полезному способу интерпретации эффектов растворителя. Сделав оценки коэффициентов активности веществ в растворе и используя термодинамические параметры, он смог очень удовлетворительным образом связать скорости в растворе со скоростями в газовой фазе. Ранее это было сделано М.Г. Эванс 41 и М. Поланьи [7, 100].
Сделав оценки коэффициентов активности веществ в растворе и используя термодинамические параметры, он смог очень удовлетворительным образом связать скорости в растворе со скоростями в газовой фазе. Ранее это было сделано М.Г. Эванс 41 и М. Поланьи [7, 100].
Хиншелвуд, продолжавший изучение реакции в течение ряда лет, заинтересовался факторами, влияющими на величину P и A (уравнение 31), в частности характером реакции, структурой реагентов. и растворитель. Он также исследовал возможные корреляции между P и E a [7]. Незадолго до этого работы Генри Айринга 42 (1901–1981) [101, 102] и венгерско-британского химика Майкла Поланьи (1891–1976) [103] внесли важный вклад в построение поверхности потенциальной энергии, которая предоставил ценный способ предвидеть ход реакции.В 1977 году Айринг писал [104]:
«Таким образом, мы получили захватывающую, хотя и приблизительную, потенциальную поверхность и вместе с ней получили доступ в совершенно новый мир химии, испытав весь энтузиазм, вдохновленный такой перспективой. Мы сразу поняли роль энергии нулевой точки в кинетике реакции, и наш метод… позволил распространить наши расчеты на все виды реакций».
Мы сразу поняли роль энергии нулевой точки в кинетике реакции, и наш метод… позволил распространить наши расчеты на все виды реакций».
Позже Айринг, Эванс и Поланьи независимо друг от друга разработали то, что стало называться теорией переходного состояния (теорией абсолютной скорости), которая позволяет вычислять предэкспоненциальный множитель для химических реакций всех видов [7, 105]. ].
Хиншелвуд также опубликовал статью, в которой обсуждался корреляционный эффект между P и E a с точки зрения поверхностей потенциальной энергии [106], и в этой работе он также заявил, что:
нет принципиальной разницы между результатами кинетической и термодинамической обработки. …метод переходного состояния и кинетический метод решения проблемы скорости реакции гораздо больше похожи, чем может показаться на первый взгляд.Преимущество термодинамического метода часто состоит в большей формальной элегантности его уравнений и большей общности».
В связи с этим попытка термодинамической формулировки скорости реакции описана в статье П. Конштамма и Ф.Е.К. Шеффера [107, 108], где также отмечалось, что:
«…не сам термодинамический потенциал, а экспоненциальная его функция будет функцией, характерной для реакции».
Эта тема также глубоко освещена в работе М.Пекарж [109].
Поскольку ограниченное пространство этой главы не позволяет представить неизмеримый вклад многих других ученых в области кинетики реакций и термодинамики, было бы уместно закончить эту главу цитатой, которую сказал сам Вант-Гофф 43 [36, 110]:
«Известное имя имеет такую особенность, что оно постепенно становится меньше, особенно в естественных науках, где каждое последующее открытие неизменно затмевает предыдущее.
Скорость реакций – химия
СКОРОСТИ ХИМИЧЕСКИХ РЕАКЦИЙ
Скорость химической реакции – это количество прореагировавшего реагента или количество продукта, образовавшегося в единицу времени. Часто количество может быть выражено в терминах концентрации или какого-либо свойства, пропорционального концентрации.
Часто количество может быть выражено в терминах концентрации или какого-либо свойства, пропорционального концентрации.
Для такой реакции, как A → 2B, мы могли бы измерить либо скорость, с которой [B] увеличивается, либо скорость, с которой [A] уменьшается.
Скорость образования B = увеличение концентрации/временной интервал = Δ[B]/Δt
Скорость реакции A = увеличение концентрации/временной интервал = -Δ[A]/Δt
Обратите внимание, что скорость всегда выражается положительным числом (это причина отрицательного знака перед Δ[A]).
Кроме того, эти две скорости различаются. Если [A] уменьшается со скоростью 0,1 моль•л⁻¹мин⁻¹, [B] увеличивается со скоростью 0,2 моль•л⁻¹мин⁻¹. Скорость реакции должна быть одинаковой, как бы мы ее ни измеряли. Мы должны учитывать стехиометрию реакции. Таким образом, мы делим ставку по компоненту на его коэффициент в уравновешенном уравнении. Таким образом, измеряем ли мы [A] или [B], скорость реакции составляет 0,1 моль•л⁻¹мин⁻¹.
Для такой реакции, как aA + bB → cC + dD, наше новое определение принимает вид
Скорость реакции = -(1/a)Δ[A]/Δt = -(1/b)Δ[B]/Δt = ( 1/c)Δ[C]/Δt = (1/d)Δ[D]/Δt
В зависимости от временного интервала между измерениями скорости называются
начальная скорость: мгновенная скорость в начале эксперимента
средняя скорость: скорость, измеренная между длинными временными интервалами
мгновенная скорость: скорость, измеренная между очень короткими интервалами
ИЗМЕРЕНИЕ СКОРОСТИ РЕАКЦИИ
Чтобы измерить скорость реакции, мы обычно отслеживаем изменение продукта или реагента.Мы можем контролировать любую физическую характеристику, связанную с количеством или концентрацией продукта или реагента.
ПРИМЕР
N2O3(г) разлагается на NO2(г) и NO(г) в соответствии с реакцией
N2O3(г) → NO2(г) + NO(г)
За реакцией следят, измеряя [NO₂] в разное время . Получаются следующие данные.
т/с [NO₂]/моль•/л⁻¹
0,,,,,,,,,,,0
884,,,,,,0,193
Какова средняя скорость образования NO₂ за этот промежуток времени? Какова средняя скорость реакции за этот промежуток времени?
Δ[NO₂]/Δt = (0. 193 – 0) моль•л⁻¹/(884 – 0) с = 0,193/884 моль•л⁻¹с⁻¹ =
193 – 0) моль•л⁻¹/(884 – 0) с = 0,193/884 моль•л⁻¹с⁻¹ =
2,18 × 10⁻⁴ моль•л⁻¹с⁻¹
Поскольку коэффициент NO₂ в сбалансированном уравнении равен 1,
Скорость реакции = (1/1)Δ[NO₂]/Δt = 2,18 × 10⁻⁴ моль•л⁻¹с⁻¹
%PDF-1.3 % 1213 0 объект > эндообъект внешняя ссылка 1213 80 0000000016 00000 н 0000002972 00000 н 0000001938 00000 н 0000003119 00000 н 0000003248 00000 н 0000003292 00000 н 0000003822 00000 н 0000003850 00000 н 0000004002 00000 н 0000004420 00000 н 0000005578 00000 н 0000006025 00000 н 0000006420 00000 н 0000006498 00000 н 0000007135 00000 н 0000007221 00000 н 0000007265 00000 н 0000007303 00000 н 0000008517 00000 н 0000008925 00000 н 0000010068 00000 н 0000010245 00000 н 0000010422 00000 н 0000010599 00000 н 0000010733 00000 н 0000010934 00000 н 0000011122 00000 н 0000011424 00000 н 0000011734 00000 н 0000012868 00000 н 0000013998 00000 н 0000014985 00000 н 0000015231 00000 н 0000015511 00000 н 0000016662 00000 н 0000016952 00000 н 0000016990 00000 н 0000017387 00000 н 0000018504 00000 н 0000019891 00000 н 0000022562 00000 н 0000024569 00000 н 0000026570 00000 н 0000026748 00000 н 0000026932 00000 н 0000028898 00000 н 0000031569 00000 н 0000031870 00000 н 0000042785 00000 н 0000042999 00000 н 0000043300 00000 н 0000056646 00000 н 0000056855 00000 н 0000057156 00000 н 0000065241 00000 н 0000065450 00000 н 0000065752 00000 н 0000075774 00000 н 0000075986 00000 н 0000076289 00000 н 0000083159 00000 н 0000083371 00000 н 0000083672 00000 н 0000089901 00000 н 00000 00000 н 00000
Влияние концентрации на скорость реакции
Предположим, что в любой момент времени 1 частица из миллиона имеет энергию, достаточную для того, чтобы равняться или превышать энергию активации. Если бы у вас было 100 миллионов частиц, 100 из них реагировали бы. Если бы у вас было 200 миллионов частиц в том же объеме, 200 из них теперь реагировали бы. Скорость реакции удвоилась за счет удвоения концентрации.
Если бы у вас было 100 миллионов частиц, 100 из них реагировали бы. Если бы у вас было 200 миллионов частиц в том же объеме, 200 из них теперь реагировали бы. Скорость реакции удвоилась за счет удвоения концентрации.
Случаи, когда изменение концентрации не влияет на скорость реакции
На первый взгляд это кажется очень удивительным!
Там, где катализатор уже работает так быстро, как только может
Предположим, вы используете небольшое количество твердого катализатора в реакции и достаточно высокую концентрацию реагента в растворе, чтобы поверхность катализатора была полностью загромождена реагирующими частицами.
Дальнейшее увеличение концентрации раствора не может дать никакого эффекта, так как катализатор уже работает на пределе своих возможностей.
В некоторых многостадийных реакциях
Это более важный эффект с точки зрения уровня A’. Предположим, у вас есть реакция, которая происходит в виде серии небольших шагов. Эти шаги, вероятно, будут иметь очень разную скорость — некоторые быстрые, некоторые медленные.
Эти шаги, вероятно, будут иметь очень разную скорость — некоторые быстрые, некоторые медленные.
Например, предположим, что два реагента A и B реагируют вместе на этих двух стадиях:
Общая скорость реакции будет зависеть от того, насколько быстро A разделится на X и Y.Это описывается как определяющая скорость стадия реакции.
Если вы увеличите концентрацию A , вы повысите вероятность того, что этот шаг произойдет по причинам, которые мы рассмотрели выше.
Если вы увеличите концентрацию B , это, несомненно, ускорит второй шаг, но вряд ли это изменит общую скорость. Вы можете представить, что второй шаг уже происходит так быстро, что как только формируется любой X, он немедленно набрасывается на B .Эта вторая реакция уже «ждет» появления первой.
.