Теория к ЕГЭ по математике » 4ЕГЭ
Методические материалы по математике, нацеленные главным образом на подготовку к ЕГЭ.Алгебра и анализ
Метод интервалов: interval.pdf
Уравнения и неравенства с модулем: modul.pdf
Что такое функция: function.pdf
Чтение графика функции: grafik.pdf
Степени и корни: power.pdf
Производная: der.pdf
Геометрический смысл производной: dergeom.pdf
Тригонометрия
Тригонометрический круг: trigcircle.pdf
Тригонометрические формулы: trigform.pdf
Простейшие тригонометрические уравнения. 1: treq1.pdf
Простейшие тригонометрические уравнения. 2: treq2.pdf
Тригонометрические уравнения: trigequations.pdf
Углы в тригонометрии: trigangles.pdf Задачи: protrigangles.pdf
Тригонометрическая окружность: trigok.pdf Задачи: protrigok.pdf
Тригонометрические функции. Синус и косинус: sincos.pdf
Тригонометрические функции. Тангенс и котангенс: tangens.pdf Задачи: protrigfun. pdf
pdf
Основное тригонометрическое тождество: ott.pdf Задачи: proott.pdf
Формулы сложения: fadd.pdf Задачи: profadd.pdf
Формулы приведения: fpriv.pdf Задачи: profpriv.pdf
Формулы двойного и половинного угла: fda.pdf Задачи: profda.pdf
Суммы и произведения тригонометрических функций: trigsum.pdf Задачи: protrigsum.pdf
Тригонометрические формулы (резюме): trigform.pdf
Обратные тригонометрические функции: trigeqprost.pdf
Тригонометрические уравнения: trigequations.pdf
Планиметрия
О первичных понятиях, или Зачем аксиомы в геометрии: primaries.pdf
Стереометрия
Многогранники в задаче С2: sm.pdf
Пирамида: piramida.pdf
Призма: prizma.pdf
Взаимное расположение прямых в пространстве: ll.pdf
Угол между скрещивающимися прямыми: lla.pdf Задачи: prolla.pdf
Взаимное расположение прямой и плоскости: lp.pdf
Теорема о трёх перпендикулярах: ttp.pdf
Угол между прямой и плоскостью: lpa.pdf Задачи: lpa.pdf
Взаимное расположение плоскостей: pp. pdf
pdf
Угол между плоскостями: ppa.pdf Задачи: proppa.pdf
Расстояние от точки до прямой: dpl.pdf Задачи: prodpl.pdf
Расстояние от точки до плоскости: dpp.pdf Задачи: prodpp.pdf
Расстояние между скрещивающимися прямыми: dll.pdf Задачи: prodll.pdf
Метод объёмов: vol.pdf
Задачи на сечения многогранников: prosec.pdf
mathus.ru
2.4.1. Основные понятия тригонометрии
Глава 2. Алгебраические выражения
2.4.
2.4.1.
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Пусть одна сторона угла α с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l, на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
Пусть одна сторона угла α с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l, на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле:
Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2πR, то всей окружности соответствует угол
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
градусов:
И наоборот,
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
и от радианного измерения к градусному:
Обозначение «рад» при записи часто опускают и вместо, например, 180° = π рад пишут просто 180° = π.
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
Пример 1Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.
Снова рассмотрим на координатной плоскости окружность радиуса R с центром O в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями.
| 1 |
| Рисунок 2.4.1.1. Окружность радиуса R |
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора
против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.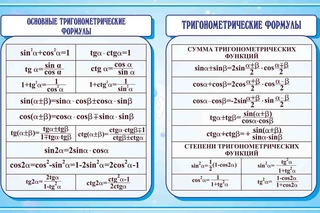
| 2 |
| Рисунок 2.4.1.2 |
Докажем, что отношения
и
не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку
такую, что
Построим окружность с центром в начале координат радиуса
Построенная окружность пересекает радиус-вектор
в точке
Так как векторы
и
коллинеарны и одинаково направлены, то
Однако равные векторы имеют равные координаты, следовательно,
Откуда следует после деления обеих частей последних равенств на R1, что
Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора.
|
Модель 2.6. Координатная окружность |
Ввиду всего вышесказанного, рассмотренные отношения и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.
|
Модель 2.8. Функция y = cos x |
|
Модель 2. |
|
Модель 2.9. Функция y = tg x |
|
Модель 2.10. Функция y = ctg x |
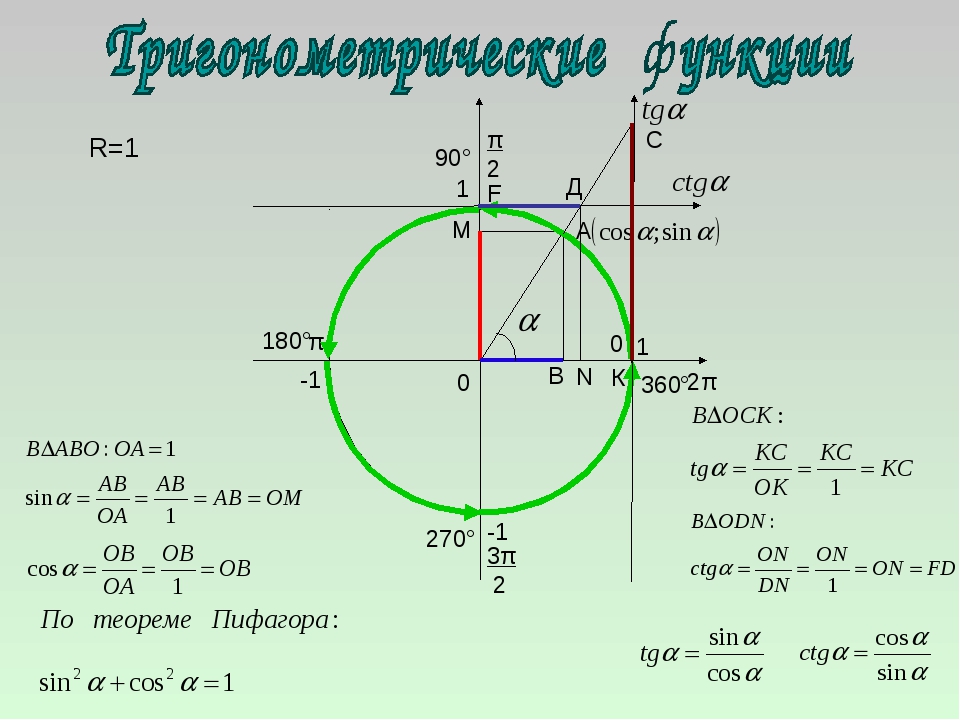
Ясно, что для данного угла α функции sin α, cos α, tg α и ctg α, которые называются тригонометрическими функциями, определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin α и cos α определены для любого угла α, то функции tg α и ctg α определены только для тех углов, для которых не равен нулю знаменатель дробей и Значит, tg α не определён для углов вида где ctg α не определён для углов вида
Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:
|
|||||||||||||||||||||||||||||
Таблица 2. 4.1.2 4.1.2 |
|||||||||||||||||||||||||||||
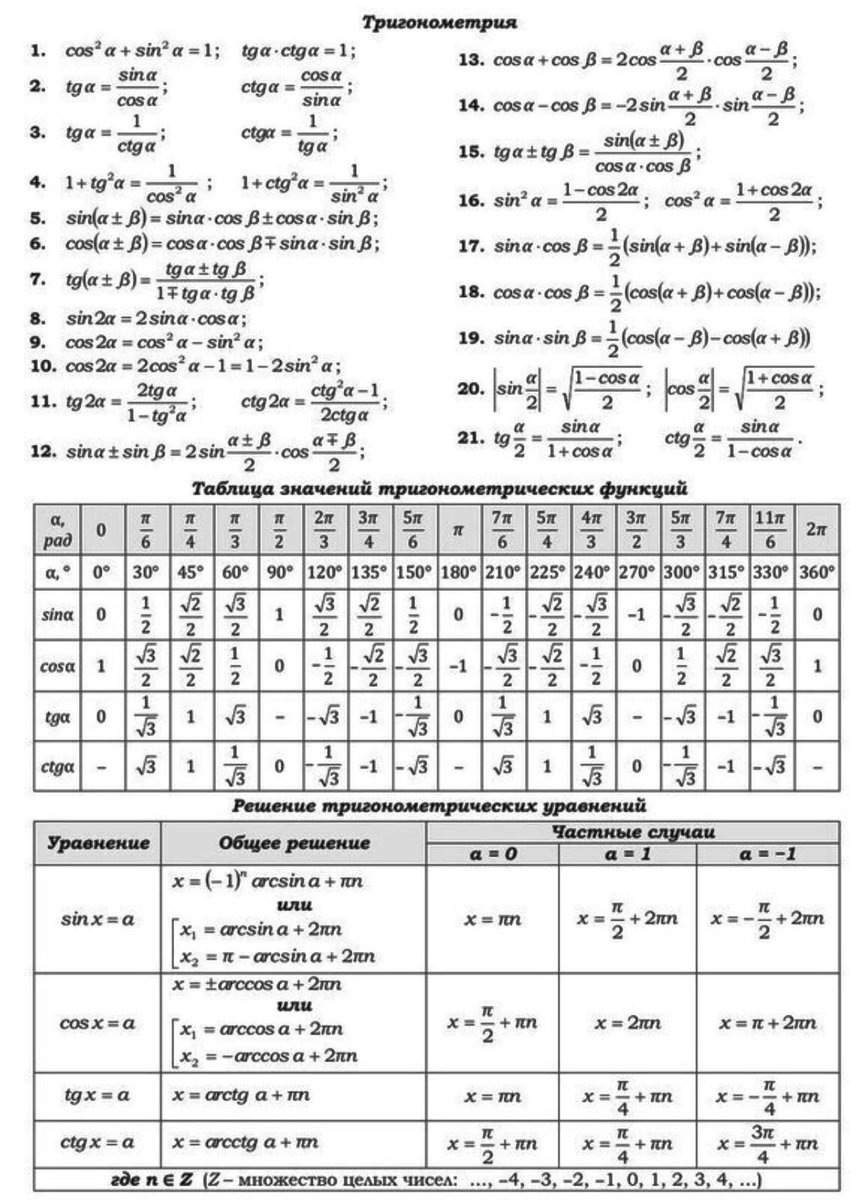
Вычисление тригонометрических функций некоторых углов
| 3 |
| Рисунок 2.4.1.3. Вычисление углов |
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка A, имеет координаты (1; 0). Поэтому cos 0° = 1, sin 0° = 0, tg 0° = 0, ctg 0° не определён. Совершенно аналогично рассматриваются точки B (0; 1), C (–1; 0) и D (0; –1), что даёт:
-
sin 90° = 1, cos 90° = 0, ctg 90° = 0, tg 0° не определён.
- sin 180° = 0, cos 180° = –1, tg 180° = 0, ctg 180° не определён.
-
sin 270° = –1, cos 270° = 0, ctg 270° = 0, tg 270° не определён.
Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе:
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе:
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка O – совпадёт с началом координат, а точка A будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу OA = 1), то геометрическое определение синуса примет вид:
Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
| 4 |
| Рисунок 2.4.1.4. Прямоугольный треугольник |
| 5 |
| Рисунок 2.4.1.5. Правильный треугольник |
Рассмотрим правильный треугольник ABC со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты BH равна
| 6 |
| Рисунок 2.4.1.6. Прямоугольный равнобедренный треугольник |
Значит, Рассматривая угол ABH, найдём, что Соответственно,
Рассмотрим теперь прямоугольный равнобедренный треугольник ABC с катетами, равными CA = CB = 1, CAB = 45°. Тогда по теореме Пифагора
и
Следовательно,
Тогда по теореме Пифагора
и
Следовательно,
Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили.
Пример 2Найдите значения выражений
1)
2)
|
Имеем: 1) 2) Ответ. 1) 1; 2) |
Периодические функции
Если функция f имеет период T, то она, очевидно, имеет период nT, где
Поэтому говорят о наименьшем положительном периоде (НПП) функции f. Существуют периодические функции, не имеющие НПП. Так, например, f (x) = C, где C − произвольная постоянная, является периодической, однако любое положительное число является её периодом. Очевидно, среди них нет наименьшего.
Очевидно, среди них нет наименьшего.
Доказать, что НПП функции y = sin x является 2π.
|
Из определения функции следует, что у точек x и x + 2π одинаковая ордината, следовательно, sin x = sin (x + 2π), а это означает, что 2π является периодом функции sin x. Пусть T − некоторый период функции y = sin x. Тогда для всех x должно выполняться равенство sin x = sin (x + T). При x = 0 имеем sin T = 0. Значит, T может принимать значения только πn, где Нас интересуют T < 2π. Таким периодом может быть только T = π, однако T = π не является периодом данной функции, так как равенство sin x = sin (x + π) неверно при Значит, НПП функции y = sin x является T = 2π. |
Аналогично можно показать, что функция y = cos x также имеет НПП T = 2π. А функции y = tg x и y = ctg x имеют НПП T = π.
Свойства обратных тригонометрических функций
- Главная
- Справочник
- Тригонометрия
- Свойства обратных тригонометрических функций
Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.
Арксинус
Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Областью определения функции арксинус является отрезок \( [-1;1].
 \)
\) - Областью значений функции арксинус является отрезок \( [-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус строго возрастающая функция.
- \( \sin \left (\arcsin a \right )=a,\;|a|\leqslant 1. \)
- \( \arcsin\left (\sin \alpha \right )=\alpha,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус является нечетной функцией: \( \arcsin(-a)=-\arcsin a,\;|a| \leqslant 1. \)
- \( \arcsin a>0,\;a\in(0;1]. \)
- \( \arcsin a=0,\;a=0. \)
- \( \arcsin a<0,\;a\in[-1;0). \)
Арккосинус
Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)
- Областью определения функции арккосинус является отрезок \( [-1;1]. \)
- Областью значений функции арккосинус является отрезок \( [0;\pi]. \)
- Арккосинус строго убывающая функция.
- \( \cos \left (\arccos a \right )=a,\;|a|\leqslant 1.
 \)
\) - \( \arccos\left (\cos \alpha\right )=\alpha,\;\alpha\in[0;\pi]. \)
- Арккосинус является индифферентной функцией: \( \arccos (-a)=\pi-\arccos a,\;|a|\leqslant 1. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
- \( \arccos a>0,\;a\in[-1;1). \)
- \( \arccos a=0,\;a=1. \)
Арктангенс
Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{tg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Областью определения функции арктангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арктангенс является интервал \( \left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс строго возрастающая функция.
- \( \text{tg}\left (\text{arctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\left (\text{tg}\,\alpha \right ) =\alpha,\;\alpha\in\left ( -\frac{\pi}{2};\frac{\pi}{2} \right ).
 \)
\) - Арктангенс является нечетной функцией: \( \text{arctg}\left (-a \right ) =-\text{arctg}\,a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\,a>0,\;a\in(0;\infty ). \)
- \( \text{arctg}\,a=0,\;a=0. \)
- \( \text{arctg}\,a<0,\;a\in(-\infty;0). \)
Арккотангенс
Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{ctg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (0;\pi \right ). \)
- Областью определения функции арккотангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арккотангенс является интервал \( \left (0;\pi \right ). \)
- Арккотангенс строго убывающая функция.
- \( \text{ctg}\left (\text{arcctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arcctg}\left (\text{ctg}\,\alpha \right ) =\alpha,\;\alpha\in\left (0;\pi \right ). \)
- Арккотангенс является индифферентной функцией: \( \text{arcctg}\left (-a \right ) =\pi-\text{arcctg}\,a,\;a\in\mathbb{R}.
 k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
или \( \left[\begin{matrix} x&=&\arcsin\,a+2\pi k,&\;k\in\mathbb{Z}\\ x&=&\pi-\arcsin\,a+2\pi l,&\;l\in\mathbb{Z} \end{matrix}\right. \)
\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arctg}\,a+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arcctg}\,a+\pi k,\;k\in\mathbb{Z} \)
Частные случаи
\( \sin x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \cos x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=1\Rightarrow x=\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=-1\Rightarrow x=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=-1\Rightarrow x=-\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=-1\Rightarrow x=\frac{3\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsboxMathematica & Wolfram Language for Math Students—Fast Intro
Для базовых тригонометрических функций используются стандартные обозначения (первые буквы в именах функций — заглавные):
In[1]:= ⨯ Sin[x]/Cos[x] == Tan[x]
Out[1]= Добавим ключевое слово “Arc” для получения обратных функций:
In[2]:= ⨯ ArcTan[1]
Out[2]= Для работы с радианами зачастую необходимо использовать константу Pi:
(Наберите ESCpiESC для ввода символаπ.)In[1]:= ⨯ Sin[\[Pi]/2]
Out[1]= Или наберите ESCdegESC для использования встроенного символа Degree:
In[2]:= ⨯ Sin[90 \[Degree]]
Out[2]= Разложим (или упростим) тригонометрические выражения, используя известные тождества:
In[1]:= ⨯ TrigExpand[Sin[2 x]]
Out[1]= Выполним факторизацию тригонометрического полинома:
In[2]:= ⨯ TrigFactor[Cos[x]^2 - Sin[x]^2]
Out[2]= Такие функции, как Solve, также позволяют решать подобные уравнения:
In[1]:= ⨯ Solve[Cos[x]^2 + Sin[x]^2 == x]
Out[1]= Уточним интересующую область решений:
In[2]:= ⨯ Solve[{Tan[x] == 1, 0 < x < 2 Pi}]Out[2]= Справочная информация: Тригонометрические функции
»Hands–on Start to
Wolfram Mathematica »Полная документация »
Demonstrations Project »
Тригонометрические функции с примерами решения и образцами выполнения
Тригонометрические функции — служат прежде всего для описания разнообразных периодических процессов.
 С периодически повторяющимися ситуациями человек сталкивается повсюду. Его жизнь сопровождают различные астрономические явления — восход и заход Солнца, изменение фаз Луны, чередование времен года, положение звезд на небе, затмения и движения планет. Человек давно заметил, что все эти явления возобновляются периодически. Жизнь на Земле тесно связана с ними, и поэтому неудивительно, что астрономические наблюдения явились источником многих математических открытий.
С периодически повторяющимися ситуациями человек сталкивается повсюду. Его жизнь сопровождают различные астрономические явления — восход и заход Солнца, изменение фаз Луны, чередование времен года, положение звезд на небе, затмения и движения планет. Человек давно заметил, что все эти явления возобновляются периодически. Жизнь на Земле тесно связана с ними, и поэтому неудивительно, что астрономические наблюдения явились источником многих математических открытий.Биение сердца, цикл в жизнедеятельности организма, вращение колеса, морские приливы и отливы, заполненность городского транспорта, эпидемии гриппа — в этих многообразных примерах можно найти общее: эти процессы периодичны.
Открывая утром газету, мы часто читаем сообщение об очередном запуске искусственного спутника Земли. Обычно в сообщении указываются наименьшее и наибольшее расстояния спутника от поверхности Земли и период его обращения. Если сказано, что период обращения спутника составляет 92 мин, то мы понимаем, что его положение относительно Земли в какой-то момент времени и через каждые 92 мин с этого момента будет одинаковым.
 Так мы приходим к понятию периодической функции как функции, обладающей периодом, т. е. таким числом Т, что значения функции при значениях аргумента, отличающихся на Т, 2Т, ЗТ и т. д., будут одинаковыми.
Так мы приходим к понятию периодической функции как функции, обладающей периодом, т. е. таким числом Т, что значения функции при значениях аргумента, отличающихся на Т, 2Т, ЗТ и т. д., будут одинаковыми.Астрономия, которая дает нам наиболее наглядное представление о периодических процессах, определяет положение объектов в небесной сфере с помощью углов. Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов.
Область определения и множество значений тригонометрических функций
Вы знаете, что каждому действительному числу х соответствует единственная точка единичной окружности, получаемая
поворотом точки (1; 0) на угол х радиан. Для этого угла
определены sin х и cos х. Тем самым каждому действительному числу х поставлены в соответствие числа sin х и cos х, т. е. на множестве R всех действительных чисел определены функции
е. на множестве R всех действительных чисел определены функцииy = sin x и у = cos x.
Таким образом, областью определения функций y = sin x и
у = cos x является множество R всех действительных чисел.
Чтобы найти множество значений функции y = sin х, нужно
выяснить, какие значения может принимать у при различных значениях х, т. е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение
sin x = a имеет корни, если , и не имеет корней, если
|а |> 1 .Томсон Уильям, лорд Кельвин (1824— 1907) — английский физик, президент Лондонского королевского общества. Дал одну из формулировок второго начала термодинамики, предложил абсолютную шкалу температур (шкалу Кельвина).
Следовательно, множеством значений функции у = sin x
является отрезокАналогично множеством значений функции у = сos x также
является отрезокЗадача:
Найти область определения функции
Найдем значения х, при которых выражение —
не имеет смысла, т. е. значения х, при которых знаменатель равен
е. значения х, при которых знаменатель равен
нулю. Решая уравнение sin x + cos х = 0, находим tg x = — 1,
Следовательно, областью определения данной функции являются все значенияЗадача:
Найти множество значений функции y = 3 + sin х cos х.
Нужно выяснить, какие значения может принимать у при
различных значениях х, т. е. установить, для каких значений а
уравнение 3 + sin х cos х = а имеет корни. Применяя формулу
синуса двойного угла, запишем уравнение так:откуда sin2x = 2a — 6. Это уравнение имеет корни, если
|2а — 6| = 1, т. е. если , откудаСледовательно, множеством значений данной функции является промежуток
Функция y = tg x определяется формулой
Эта функция определена при тех значениях х, для которых
Известно, что cos x = 0 приСледовательно, областью определения функции y = tg х является множество чисел
Так как уравнение tg x = a имеет корни при любом
действительном значении а, то множеством значений функции
y = tg х является множество R всех действительных чисел.
Функции y = sin x, у = cos x, y = tg x называются
тригонометрическими функциями.Задача:
Найти область определения функции y = sin Зх + tg 2х.
Нужно выяснить, при каких значениях х выражение
sin 3x + tg 2х имеет смысл. Выражение sin Зх имеет смысл при
любом значении х, а выражение tg 2х — при т. е. приСледовательно, областью определения данной функции является множество действительных чисел
Задача:
Найти множество значений функции
у = 3 sin x + 4 cos х.Выясним, при каких значениях а уравнение 3 sin x + 4 cos x = a имеет корни. Поделим уравнение на
Так как то очевидно найдется такой угол первой четверти , что (этот угол )
Тогда откуда
так как .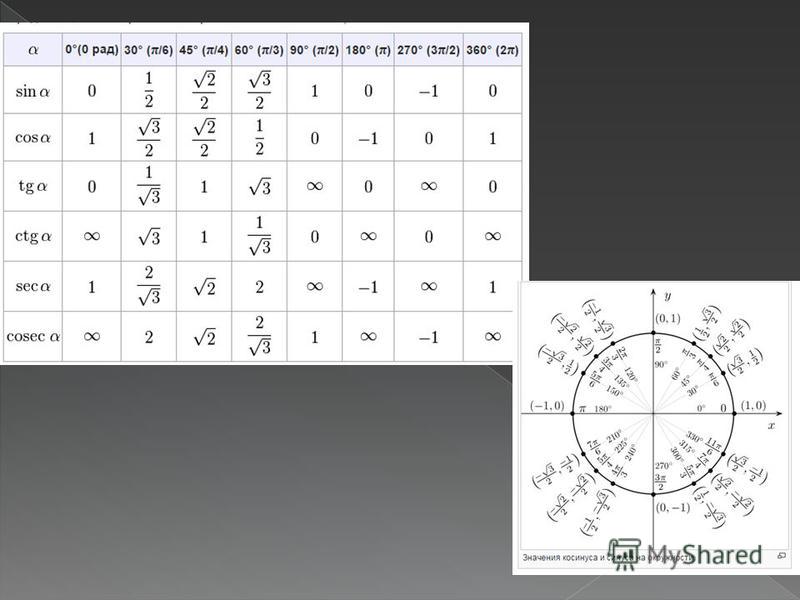 Уравнение примет вид т. e. Это уравнение имеет корни, если
Уравнение примет вид т. e. Это уравнение имеет корни, если Ответ.
Четность, нечетность, периодичность тригонометрических функций
Вы знаете, что для любого значения х верны равенства
sin ( — x ) = — sin x, cos ( — x) = — cos x.Следовательно, y = sin х — нечетная функция, а у = cos х —
четная функция. Так как для любого значения х из области
определения функции y — tg x верно равенство tg (— х)= — tg х,
то y = tg х — нечетная функция.Задача:
Выяснить, является ли функция
четной или нечетной.
Используя формулу приведения, запишем данную функцию
так:Имеем , т. е. данная функция является четной. ▲
Известно, что для любого значения х верны равенства
Из этих равенств следует, что значения синуса и косинуса
периодически повторяются при изменении аргумента на
Такие функции называются периодическими с периодомФункция f (x) называется периодической, если существует такое число что для любого х из области определения этой функции выполняется равенство f (х — T) = f (x) = f( x+ T ).

Число 7 называется периодом функции f (х).
Из этого определения следует, что если х принадлежит области определения функции f (х), то числа х + T , х — Т и вообще
числа х + Tn , также принадлежат области определения
этой периодической функции и f (х + Tn ) = f (х),Покажем, что число является наименьшим положительным периодом функции у = cos х.
Пусть T > 0 — период косинуса, т. е. для любого х выполняется равенство cos (х + T) = cos х. Положив х = 0, получим
cos T = 1 . ОтсюдаТак как T > 0 , то T может принимать значения … и поэтому период не может быть меньше
Можно доказать, что наименьший положительный период функции у = sin х также равен
Задача:
Доказать, что f (x) = sin 3 x — периодическая
функция с периодомЕсли функция f (х) определена на всей числовой оси, то для
того, чтобы убедиться в том, что она является периодической
с периодом T, достаточно показать, что для любого х верно
равенство f (х + T ) = f (х). Данная функция определена для всех и
Данная функция определена для всех и Покажем, что функция tg х является периодической с периодом
Если х принадлежит области определения этой функции, т. е. то по формулам приведения получаем:
Таким образом,
Следовательно, — период функции tg х.
Покажем, что — наименьший положительный период функции tg х.
Пусть T — период тангенса, тогда tg ( x + T ) = tg x , откуда
при х = 0 получаем:Так как наименьшее целое положительное k равно 1, то —
наименьший положительный период функции tg х.Задача:
Доказать, что периодическая функция
с периодомТак как то — периодическая функция с периодом
Периодическими функциями описываются многие физические
процессы (колебания маятника, вращение планет, переменный
ток и т. д.).
д.).
На рисунке 34 изображены графики некоторых периодических функций.
Отметим, что на всех последовательных отрезках числовой
прямой, длина которых равна периоду, график периодической
функции имеет один и тот же вид.Функция у = cos x, ее свойства и график
Напомним, что функция у = cos х определена на всей числовой прямой и множеством ее значений является отрезок [— 1; 1].
Следовательно, график этой функции расположен в полосе между прямыми у = — 1 и у = 1.
Так как функция у = cos х периодическая с периодом , то
достаточно построить ее график на каком-нибудь промежутке длиной , например на отрезке тогда на
промежутках, получаемых сдвигами выбранного отрезка на график будет таким же.
Функция у = cos х является четной. Поэтому ее график симметричен относительно оси Оу. Для построения графика на отрезке достаточно построить его для а затем симметрично отразить относительно оси Оу.
Для построения графика на отрезке достаточно построить его для а затем симметрично отразить относительно оси Оу.Прежде чем перейти к построению графика, покажем, что
функция у = cos х убывает на отрезкеВ самом деле, при повороте точки Р (1; 0) вокруг начала координат против часовой стрелки на угол от 0 до абсцисса точки,
т. е. cos х, уменьшается от 1 до — 1. Поэтому если то (рис. 35). Это и означает, что функция у = cos х убывает на отрезке .Используя свойство убывания функции y = cos x на отрезке и найдя несколько точек, принадлежащих графику,
построим его на этом отрезке (рис. 36).
Пользуясь свойством четности функции у = cos х, отразим
построенный на отрезке график симметрично относительно оси Оу, получим график этой функции на отрезке (рис. 37).Так как у = cos х — периодическая функция с периодом
и ее график построен на отрезке длиной, равной периоду, распространим его по всей числовой прямой с помощью сдвигов на и т.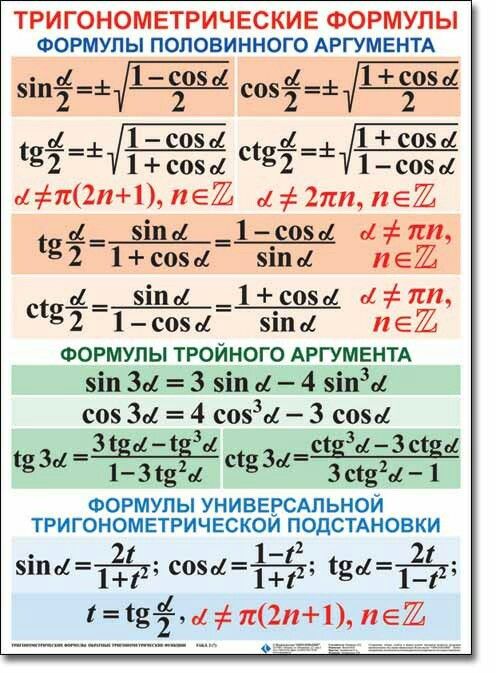 д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).
д. вправо, на и т. д. влево, т. е. вообще на (рис. 38).Итак, график функции у = cos x: построен геометрически на
всей числовой прямой, начиная с построения его части на отрезке
. Поэтому свойства функции у = cos х можно получить,
опираясь на свойства этой функции на отрезке . Например, функция y = cosx возрастает на отрезке так как она убывает на отрезке и является четной.
Перечислим основные свойства функции у = cos х;
1) Область определения — множество R всех действительных
чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = cos х периодическая с периодом .
4) Функция у = cos х четная.
5) Функция у = cos х принимает:
— значение, равное 0, при
— наибольшее значение, равное 1, при
— наименьшее значение, равное — 1, при
— положительные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на …;
— отрицательные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на …;
6) Функция у = cos х:
— возрастает на отрезке и на отрезках, получаемых
сдвигами этого отрезка на , … ;
— убывает на отрезке и на отрезках, получаемых
сдвигами этого отрезка на , … .
Задача:
Найти все корни уравнения
принадлежащие отрезку
Построим графики функций у = сos х и — на данном
отрезке (рис. 39). Эти графики пересекаются в трех точках,
абсциссы которых являются корнями уравненияНа отрезке корнем уравнения является число . Из рисунка видно, что точки и симметричны относительно оси Оу, т. е. а
.Ответ.
Задача:
Найти все решения неравенства принадлежащие отрезку
Из рисунка 39 видно, что график функции у = cos x лежит
выше графика функции на промежутках иОтвет.
Функция y=sin x, ее свойства и график
Функция y = sin x определена на всей числовой прямой, является нечетной и периодической с периодом . Ее график можно
построить таким же способом, как и график функции у = cos x,
начиная с построения, например, на отрезке . Однако проще воспользоваться следующей формулой:
Однако проще воспользоваться следующей формулой:Эта формула показывает, что график функции у = sin х можно
получить сдвигом графика функции у = соs х вдоль оси абсцисс
вправо на (рис. 40).График функции у = sin х изображен на рисунке 41.
Кривая, являющаяся графиком функции у = sin х, называется
синусоидой.Так как график функции у = sin х получается сдвигом графика функции у = соs х, то свойства функции у = sin х можно получить из свойств функции у = соs x.
Перечислим основные свойства функции у = sin х :
1) Область определения — множество Я всех действительных чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = sin x периодическая с периодом .
4) Функция у = sin х нечетная.5) Функция y = sin x принимает:
— значение, равное 0 , при
— наибольшее значение, равное 1, при
— наименьшее значение, равное — 1, при
— положительные значения на интервале и на
интервалах, получаемых сдвигами этого интервала на , … ;
— отрицательные значения на интервале и на
интервалах, получаемых сдвигами этого интервала
на , … .
6) Функция у = sin х:
— возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на и на отрезках, получаемых сдвигами этого отрезка на , …
Задача:Найти все корни уравнения
принадлежащие отрезкуПостроим графики функций у = sin х и — на данном
отрезке (рис. 42). Эти графики пересекаются в двух точках,
абсциссы которых являются корнями уравненияНа отрезке уравнение имеет корень
Второй корень так как
Ответ .
Задача:
Найти все решения неравенства
принадлежащие отрезкуИз рисунка 42 видно, что график функции y = sin x лежит
ниже графика функции на промежутках иОтвет.
Функция y=tg x, ее свойства и график
Напомним, что функция y = tg x определена при является нечетной и периодической с периодом .
 Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .
Поэтому достаточно построить ее график на промежутке . Затем, отразив его симметрично относительно начала координат, получить график на интервале .Наконец, используя периодичность, построить график функции
y = tgx на всей области определения.Прежде чем строить график функции на промежутке ,
покажем, что на этом промежутке функция y = tg x возрастает.Пусть Покажем, что т. е.
По условию откуда по свойствам функции
у = sin х, имеем а по свойствам функции
y = cos x имеем откудаПеремножив неравенства и получим
Используя свойство возрастания функции y = tg x на промежутке и найдя несколько точек, принадлежащих графику, построим его на этом промежутке (рис. 43).
Пользуясь свойством нечетности функции y = tg x, отразим
построенный на промежутке график симметрично относительно начала координат; получим график этой функции на интервалеНапомним, что при функция y = tg x не определена.

Если и х приближается к , то sin х приближается к 1,
a cos х, оставаясь положительным, стремится к 0. При этом дробь неограниченно возрастает, и поэтому график функцииу = tg х приближается к вертикальной прямой . Аналогично при отрицательных значениях х, больших и приближающихся к , график функции y = tg x приближается к вертикальной прямой .
Перейдем к построению графика функции у = tg х на всей области определения. Функция y = tg х периодическая с периодом .
Следовательно, график этой функции получается из ее графика
на интервале (рис. 44) сдвигами вдоль оси абсцисс
на (рис. 45).Итак, весь график функции у = tg х строится с помощью
геометрических преобразований его части, построенной на
промежутке .Поэтому свойства функции y = tg x можно получить, опираясь
на свойства этой функции на промежутке .Например,
функция y = tg x возрастает на интервале , так как
эта функция возрастает на промежутке и является
нечетной.
Перечислим основные свойства функции y = tg x:
1) Область определения — множество всех действительных
чисел2) Множество значений — множество R всех действительных
чисел.
3) Функция у = tg х периодическая с периодом
4) Функция y = tg x нечетная.
5) Функция у = tg x принимает:
— значение, равное 0, при
— положительные значения на интервалах — отрицательные значения на интервалах
6) Функция у = tg х возрастает на интервалахЗадача:
Найти все корни уравнения tg х = 2, принадлежащие отрезку
Построим графики функций y = tg х и у = 2 на данном отрезке (рис. 46, а) . Эти графики пересекаются в трех точках, абсциссы которых являются корнями уравнения tg x = 2.

На интервале уравнение имеет корень
Так как функция у = tg х периодическая с периодом , тоОтвет.
Задача:
Найти все решения неравенства
принадлежащие отрезкуИз рисунка 46, а видно, что график функции y = tg х лежит
не выше прямой у = 2 на промежуткахи .
Ответ.
Задача:
Решить неравенство tg х > 1.
Построим графики функций y = tg x и у = 1 (рис. 46, б).
Рисунок показывает, что график функции y = tgx лежит выше
прямой у = 1 на промежутке , а также на промежутках,
полученных сдвигами его на и т. д.Ответ.
Тригонометрические функции широко применяются в математике, физике и технике. Например, многие процессы, такие, как колебание струны, колебание маятника, напряжение в цепи
Углы и их измерение
переменного тока и т. д., описываются функцией, которая задается формулой Такие процессы называют
гармоническими колебаниями, а описывающие их функции —
гармониками (от греческого harmonikos — соразмерный). График
График
функции получается из синусоиды y = sin x
сжатием или растяжением ее вдоль координатных осей и
сдвигом вдоль оси Ох. Обычно гармоническое колебание является
функцией времени: где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.Геометрический угол — это часть плоскости, ограниченная двумя лучами, выходящими из одной точки, вершины угла. Чтобы сравнивать углы, удобно закрепить их вершины в одной точке и вращать стороны.
Как измеряют углы? В качестве единицы измерения геометрических углов принят градус часть развернутого угла.
Конкретные углы удобно измерять в градусах с помощью транспортира. Многие оптические приборы также используют градусную меру угла. Углы, получающиеся при непрерывном вращении, удобно измерять не в градусах, а с помощью таких чисел, которые отражали бы сам процесс построения угла, т.
 е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.
е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.Представим себе, что зафиксирована не только вершина угла, но и один из образующих его лучей. Заставим второй луч вращаться вокруг вершины. Ясно, что получающиеся углы будут зависеть от скорости вращения и времени. Можно считать, что вращение происходит равномерно (с постоянной угловой скоростью). Тогда поворот будет определяться путем, который пройдет какая-либо фиксированная точка подвижного луча.
Если расстояние точки от вершины равно /?, то при вращении точка движется по окружности радиуса R. Отношение пройденного пути к радиусу R не зависит от радиуса и может быть взято за меру угла. Численно она равна пути, пройденному точкой по окружности единичного радиуса.
Итак, пусть угол получен вращением подвижного луча от некоторого начального положения. Его величина численно равна пути, который пройдет точка этого луча, находящаяся на единичном расстоянии от вершины.

Развернутый угол измеряется половиной длины единичной окружности. Это число обозначается буквой л. Число я было известно людям с глубокой древности и с довольно большой точностью. Первые десятичные знаки этого числа таковы:
π = 3,14159265358….
Угол величиной π часто используется как самостоятельная единица измерения углов — прямой угол равен угол в равностороннем треугольнике равен .
Часто встречаются записи меры углов в виде и т. д. Угол, мера которого равна числу 1, называют радианом. Он соответствует некоторому углу, чуть меньшему, чем , ведь ≈ 1,047.
АННА ВОВК u715078663 ДЕЛАЕТ АЛГЕБРУ №2 (дополнительная)
Гаусс Карл Фридрих
(1777—1855) — немецкий математик, астроном и физик. Еще студентом написал «Арифметические исследования», определившие развитие теории чисел до нашего времени. В 19 лет определил, какие правильные многоугольники можно построить циркулем и линейкой.
 Занимался геодезией и вычислительной астрономией. Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.
Занимался геодезией и вычислительной астрономией. Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.Так как на практике приходится иметь дело как с градусной, так и с радианной мерой, то на микрокалькуляторе обычно есть рычажок, регулирующий способ измерения используемого в вычислениях угла. Фактически микрокалькулятор умеет переводить градусы в радианы и обратно.
Выведем формулы для этого перевода. Достаточно сравнить меры одного и того же угла, например прямого:
Откуда
Обратно можно выразить единицу (т. е. один радиан) в градусной мере:
В географии, астрономии и других прикладных науках используют доли градуса — минуту и секунду. Минута — это градуса, а секунда — минуты. Запишем соотношения между различными единицами измерения углов:
Заметим еще, что обозначение градуса (минуты, секунды) нельзя пропускать в записи, а обозначение радиана опускают. С физической точки зрения угол — безразмерная величина, поэтому имеют смысл записи: а = 0,23, а = 3,14, а=0,01.
 Во всех этих записях подразумевается, что угол а измерен в радианах. Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.
Во всех этих записях подразумевается, что угол а измерен в радианах. Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.Движение точки по окружности во многом аналогично движению точки по прямой. Чтобы определить положение точки на прямой, недостаточно знать путь, пройденный ею от начальной точки, нужно указать еще направление движения. Обычно на прямой фиксируют положительное направление, а положение точки определяют одним числом, которое может быть не только положительным (как путь), но и отрицательным.
Аналогично поступают и с вращательным движением. В качестве положительного направления движения по окружности выбирается движение против часовой стрелки. Угол задают числом t (которое может принимать произвольное значение). Чтобы построить угол t, на единичной окружности от неподвижной точки откладывают путь, равный|t|, в направлении, определяемом знаком числа t.
 Таким образом, для произвольного числа t мы построили угол t, определяемый двумя лучами — неподвижным и тем, который проходит через построенную точку (рис. 84).
Таким образом, для произвольного числа t мы построили угол t, определяемый двумя лучами — неподвижным и тем, который проходит через построенную точку (рис. 84).При таком обобщении понятия угла постепенно отходят от его геометрического образа как части плоскости, лежащей между двумя лучами. Фактически слово «угол» становится для нас синонимом слова «число». Угол t (т. е. произвольное число t) может выступать у нас в качестве аргумента тригонометрических функций. Изображать угол t нам будет удобно не в виде пары лучей, а в виде точки единичной окружности. Для этого мы подробно рассмотрим вращательное движение.
Вращательное движение и его свойстваПредставим себе маленький шарик, который равномерно вращается по единичной окружности в положительном направлении (т. е. против часовой стрелки). Будем считать, что в момент времени t = О шарик находился в положении А и что за время t = 1 он проходит по окружности расстояние, равное 1. Половину окружности шарик проходит за время, равное π, а всю окружность — за время 2 π.

Обозначим через Pt точку на окружности, в которой шарик находится в момент времени t. Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t <0. Рассмотрим примеры.
1.Пусть t=. Отложим по окружности от точки Р0 в положительном направлении путь длиной .
Так как длина всей окружности равна 2 π, то точка является серединой дуги АВ (рис. 85).
2. Пусть . Отложим от точки Р0 путь длиной
Заметим, что Пройдя путь длиной 2 π, мы опять попадаем в точку А. Пройдя оставшийся путь, мы попадаем в середину дуги АВ. Таким образом, точка совпадает с точкой .
3. Найдем теперь точку Для этого нам необходимо пройти в отрицательном направлении путь длиной
Таким образом, мы для каждого значения t можем построить точку Рt. На языке механики аргумент t — это время, на языке геометрии t — это угол.

Оси координат делят плоскость на четыре части. В зависимости от того, в какую часть плоскости попадает точка Рt, говорят о том, в какую четверть попадает угол t. При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения.
Свойство 1. Для всякого целого числа k точка Рt совпадает с точкой Это свойство выражает периодичность вращательного движения: если моменты времени отличаются на число, кратное 2 π, то шарик в эти моменты времени занимает одно и то же положение.
Свойство 2. Если , то найдется такое целое число k, что
Свойство 3. Для всякого значения t точки Рt и Рt+π диаметрально противоположны.Свойство 4. Для всякого значения t точки Рt и Р_t симметричны друг другу относительно оси абсцисс.
Свойство 5. Для всякого значения t точки Рt и Р_t+π симметричны относительно оси ординат.
Свойство 6. Для всякого значения t точки Рt и симметричны друг другу относительно биссектрисы первого и третьего координатных углов.

Эти свойства легко объяснить с помощью рисунка 86. Сделаем лишь пояснение к свойству 6. Возьмем две точки Р0 и
Они симметричны друг другу относительно биссектрисы первого и третьего координатных углов. Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку , надо на такое же
расстояние двигаться от точки , но в противоположном направлении. Ясно, что при этом точки Рt и при всяком t будут
оставаться симметричными друг другу относительно указанной прямой.
Определение тригонометрических функций
Тригонометрические функции определяются с помощью координат вращающейся точки. Рассмотрим на координатной плоскости ху единичную окружность, т. е. окружность единичного радиуса с центром в начале координат. Обозначим через Ро точку единичной окружности с координатами (1; 0) (рис. 87). Точку Ро будем называть начальной точкой. Возьмем произвольное число t. Повернем начальную точку на угол t.
 Получим точку на единичной окружности, которую обозначим через Рt.
Получим точку на единичной окружности, которую обозначим через Рt.Определение. Синусом числа t называется ордината точки Pt, косинусом числа t называется абсцисса точки Pt, где Р, получается поворотом начальной точки единичной окружности на угол t.
Если обозначить координаты точки Р, через х и у, то мы получим x = cost y = sint или можно записать, что точка Рt имеет координаты (cos t; sin t).
Так как координаты точки Р, (х; у), лежащей на единичной окружности, связаны соотношением х2 + у2 = 1, то sin t и cos t связаны соотношением
которое называют основным тригонометрическим тождеством.
Определение. Тангенсом числа t называется отношение синуса числа t к его косинусу, т. е. по определению
Котангенсом числа t называется отношение косинуса числа t к его синусу, т. е. по определению
Тангенс числа t определен для тех значений t, для которых cos t ≠ 0.
Периодичность Котангенс числа t определен для тех значений t, для которых sin t ≠ 0.
Котангенс числа t определен для тех значений t, для которых sin t ≠ 0.Тригонометрические функции являются периодическими функциями.
Теорема:
Число 2π является периодом синуса и косинуса.
Доказательство. Необходимо доказать тождества
Значения тригонометрических функций определяются с помощью координат вращающейся точки. Так как точки Pt и Рt+2π совпадают, то совпадают и их координаты, т. е. cos t = cos (t + 2π) и sin t = sin (t + 2π), что и требовалось доказать.
Следствие:
Верны тождества
Действительно, Аналогично доказывается и второе тождество. Это означает, что 2π является одним из периодов тангенса и котангенса.
Равенство sin (t + 2π) = sin t верно при всех значениях t. Подставляем в это равенство вместо t число t+2π, получаем цепочку равенств sin(t+ 2 π +2 π ) = sin (t + 2 π ) = sin t, т. е. равенство sin (t + 4 π ) = sin t также верно при всех значениях t.
 Аналогично, подставляя вместо t число t— 2 π , получим тождество sin (t —2 π ) = sin t. Можно сказать так, что раз 2 π является периодом синуса, то и 2-2 π , —2 π также являются его периодами. Получаем, что всякое число вида 2πk {k ∈ Z) является периодом синуса.
Аналогично, подставляя вместо t число t— 2 π , получим тождество sin (t —2 π ) = sin t. Можно сказать так, что раз 2 π является периодом синуса, то и 2-2 π , —2 π также являются его периодами. Получаем, что всякое число вида 2πk {k ∈ Z) является периодом синуса.Число 2π выделяется тем, что это наименьший положительный период синуса. Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.
Знаки тригонометрических функцийЗнаки тригонометрических функций определяются в зависимости от того, в какой четверти лежит рассматриваемый угол.
Синус числа t есть ордината точки Рt. Поэтому синус положителен в первой и второй четвертях и отрицателен в третьей и четвертой.
Косинус числа t как абсцисса точки Рt положителен в первой и четвертой четвертях и отрицателен во второй и третьей.Тангенс и котангенс являются отношением координат.
Четность Поэтому они положительны тогда, когда эти координаты имеют одинаковые
Поэтому они положительны тогда, когда эти координаты имеют одинаковые
знаки (первая и третья четверти), и отрицательны, когда разные (вторая и четвертая четверти). Знаки тригонометрических функций по четвертям приведены на рисунке 88.Теорема:
Синус — нечетная функция, т. е. при всех t выполнено равенство sin (— t) = — sin t.
Косинус — четная функция, т. е. при всех t выполнено равенство cos ( — t) =cos t.
Доказательство:
Действительно, мы знаем, что для всякого значения t точки Р, и Р_( симметричны друг другу относительно оси абсциссы (т. е. cos t = cos ( — t)), а ординаты противоположны (т. е. sin t=— sin ( — t)), что и требовалось доказать.
Следствие. Тангенс и котангенс — нечетные функции.
Действительно, . Аналогично доказывается нечетность котангенса.
Формулы приведенияЗначения тригонометрических функций острых углов можно вычислить по таблицам или с помощью прямоугольного треугольника.
 Их вычисление для любого значения аргумента можно привести к вычислению значений для аргумента
Их вычисление для любого значения аргумента можно привести к вычислению значений для аргумента Соответствующие формулы так и называются — формулы приведения. Они основаны на симметрии вращательного движения.
Основные формулы:
Формула (1) —это запись в координатной форме свойства 3 вращательного движения, формула (2) — это запись свойства 5, а формула (3) — запись свойства 6.
С помощью периодичности и формул (1) — (3) можно привести вычисление синуса и косинуса любого числа t к их вычислению для t, лежащего между 0 и .
Из основных формул (1) — (3) можно вывести и другие формулы приведения:
Доказательство:
Аналогично выводятся формулы
Формулы приведения для тангенса и котангенса получаются как следствие аналогичных формул для синуса и косинуса. Например:
Мнемоническое правило для запоминания формул приведения следующее:
1) Название функции не меняется, если к аргументу левой части добавляется — π или + π, и меняется, если добавляется число ± или
2) Знак правой части определяется знаком левой, считая, что
Примеры.
1.Вычислить sin . Представим так:
Далее,
Значения тригонометрических функцийВычисление значений тригонометрических функций имеет длинную историю. Потребности точных астрономических наблюдений вызвали к жизни появление огромных таблиц, позволявших производить вычисления с четырьмя, пятью и даже семью и более знаками. На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности.
Некоторые соображения о значениях тригонометрических функций надо помнить всегда, так как они облегчают вычисления.
1) С помощью формул приведения вычисление значения тригонометрической функции любого числа можно свести к вычислению функции угла, лежащего в первой четверти.
2) Достаточно знать значение лишь одной из тригонометрических функций.
 С помощью основных тождеств и зная четверть, в которой лежит значение аргумента, легко найти значения остальных функций.
С помощью основных тождеств и зная четверть, в которой лежит значение аргумента, легко найти значения остальных функций.Примеры:
3) Полезно помнить значения тригонометрических функций для углов двух «знаменитых» прямоугольных треугольников —для равнобедренного и для треугольника с углами 30° () и 60° (). Эти значения обычно записывают с помощью радикалов и при необходимости эти радикалы заменяют их приближенными значениями
Сведем их в таблицу, дополнив ее значениями t = 0 и t=.
Решение простейших тригонометрических уравненийДля решения некоторых,особенно простых, но важных уравнений достаточно вспомнить определение тригонометрической функции.
Примеры:
- sin t = 0. Вращающаяся точка Рt имеет нулевую ординату в моменты времени t—0, π, 2 π, …, а также t— π, —2 π…..В общем виде множество этих значений можно записать в виде t=πk, k ∈ Z. Таким образом, решением уравнения sin t = 0 будут числа t = πk, k ∈ Z.
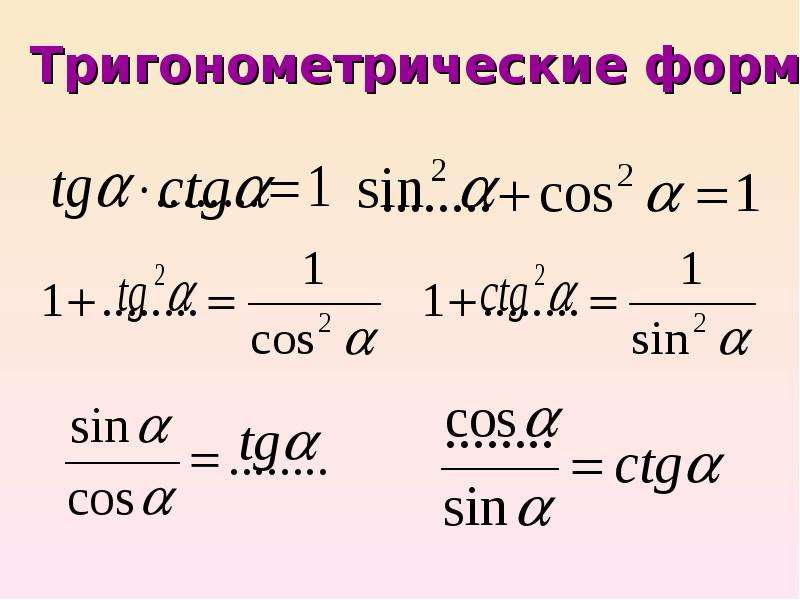
Запишем кратко решения еще нескольких уравнений, правильность которых предлагается проверить самостоятельно.
Все рассмотренные уравнения имеют бесчисленное множество решений. Эти решения записываются в виде бесконечных серий с помощью переменной (в наших примерах к), которая может принимать любые целые значения.
Теперь легко доказать, что 2π является наименьшим положительным периодом синуса и косинуса. Действительно, формула 3 показывает, что значение 1 синус принимает только в точках
Расстояние между соседними точками этой последовательности равно 2 π, поэтому синус не может иметь положительный период, меньший 2 π. Рассуждения для косинуса аналогичны.
Исследование тригонометрических функций
Основные свойства синуса и косинусаПри введении тригонометрических функций мы обозначали аргумент буквой t, так как буквы х и у были заняты — они обозначали координаты вращающейся точки Рt. Сейчас при исследовании мы вернемся к обычным обозначениям: х — аргумент, у — функция.

Рассмотрим функции y = sinx и y = cosx.
1) Область определения. Синус и косинус числа х задаются как координаты точки Рх, получающейся из точки Ро (1; 0) поворотом на угол х. Так как поворот возможен на любой угол, то областью определения синуса и косинуса является множество R всех вещественных чисел.
2) Промежутки монотонности. Проследим за характером изменения координат точки Рх, движущейся по окружности. При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= точка займет положение Р (0; 1). Итак, в первой четверти синус (ордината) возрастает от 0 до 1, а косинус (абсцисса) убывает от 1 до 0.
Когда точка переходит во вторую четверть, ордината начинает убывать от 1 до 0. Абсцисса становится отрицательной и растет по абсолютной величине, значит, косинус продолжает убывать от 0 до — 1. В третьей четверти синус становится отрицательным и убывает от 0 до —1, а косинус начинает возрастать от — 1 до 0.

Наконец, в четвертой четверти синус возрастает от — 1 до 0 и косинус возрастает от 0 до 1. Монотонность синуса и косинуса по четвертям показана на схеме VIII.
3) Точки экстремума. Координаты вращающейся точки меняются между —1 и +1. Эти числа являются наименьшими и наибольшими значениями синуса и косинуса. Если требуется указать абсциссы точек экстремума, то надо решить уравнения sin х = ±1 и cos х= ± 1.
4) Промежутки постоянного знака и корни функции. Мы повторим их еще раз при построении графика.
5) Множество значений. Синус и косинус принимают любые значения от —1 до +1, так как являются координатами точки, движущейся по единичной окружности.
Графики синуса и косинусаДля приближенного построения синусоиды можно поступить так. Разделим первую четверть на 8 равных частей и на столько же частей разделим отрезок [0; ]оси абсцисс. Удобно при этом начертить окружность слева, как на рисунке 89.
 Перенесем значения синуса (проекции на ось у точек деления окружности) к соответствующим точкам оси х. Получим точки, лежащие на синусоиде, которые нужно плавно соединить и продолжить кривую дальше, пользуясь симметрией.
Перенесем значения синуса (проекции на ось у точек деления окружности) к соответствующим точкам оси х. Получим точки, лежащие на синусоиде, которые нужно плавно соединить и продолжить кривую дальше, пользуясь симметрией.Так мы получим график синуса на промежутке [0;]. Так
как sin (—х = sin +x). то график синуса должен быть
симметричен относительно прямой x=. Это позволяет построить
график синуса на отрезке [-; π]. Воспользовавшись нечетностью
синуса, получим график синуса на отрезке [ — π; 0] симметричным отражением построенной части синусоиды относительно начала координат. Так как отрезок [— π; π] имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельными переносами построенной кривой.
График синуса мы построили, воспользовавшись его свойствами. При этом к определению синуса мы обращались только при построении графика на отрезке [0; ].
Построение графика на всей оси потребовало знания симметрии вращательного движения (формулы приведения, нечетность, периодичность).
 После того как график построен, полезно вернуться к свойствам синуса и посмотреть, как они проявляются на графике.
После того как график построен, полезно вернуться к свойствам синуса и посмотреть, как они проявляются на графике.Функция y = sin х имеет период 2 π. На графике это свойство отражается следующим образом: если мы разобъем ось х на отрезки длиной 2 π, например, точками… —4 π, —2 π, 0, 2 π, 4 π, …, то весь график разобьется на «одинаковые» части, получающиеся друг из друга параллельным переносом вдоль-оси х. При этом видно, что 2 π — наименьший положительный период синуса.
Функция y = sin x: нечетна. На графике это свойство проявляется так: синусоида симметрична относительно начала координат.
Функция y = sin x обращается в нуль при х = πk, k ∈ Z. На графике это точки пересечения синусоиды с осью абсцисс.
Функция y = sin x положительна при и отрицательна при или третьей-четвертой четвертям (sin х<0).
Функция y = sin х возрастает при и убывает при
Указанные отрезки соответствуют четвертой-первой и второй-третьей четвертям.

Множеством значений функции y = sinx является отрезок [— 1; 1]. Действительно, проекции вращающейся точки на ось заполняют отрезок [—1; 1]. На графике это свойство проявляется так: синусоида расположена в полосе и при этом проекции точек графика на ось у целиком заполняют отрезок [— 1; 1].
График косинуса можно построить так же, как и график синуса. Возможен и другой путь. Формулы приведения показывают, что синус и косинус связаны между собой простыми соотношения-
ми. Воспользуемся, например, формулой cosx = sin (x+)
Эта формула показывает, что график косинуса получается сдвигом синусоиды на влево по оси х (схема VIII).Если изображать графики синуса и-косинуса в системе координат с одинаковым масштабом по осям, то синусоида получается очень растянутой. Однако на практике величины х и у, связанные с помощью тригонометрических функций, имеют различные единицы измерения и необязательно изображать их в одном масштабе.
Если аргумент умножить на некоторое число, то синусоида будет, как гармоника, сжиматься и растягиваться по оси х.
 Примеры такого преобразования приведены на рисунке 90.
Примеры такого преобразования приведены на рисунке 90.Если значение синуса умножить на число, то будет происходить растяжение (сжатие) по оси у.
Графики функций вида у = А sin ( ω х + а) при различных А, ω, а являются синусоидами. Эти функции описывают так называемые гармонические колебания — движение проекции вращающегося шарика на ось или колебания конца упругой пружины.
Постоянные величины А, ω, а, задающие колебания, имеют наглядный физический смысл: А — амплитуда колебания, ω — его частота, а — начальная фаза.
Исследование тангенса и котангенсаЕсли свойства синуса и косинуса мы получили, рассматривая свойства движения точки по окружности, то для исследования тангенса и котангенса нам нет необходимости возвращаться к механической модели.
По определению тангенс числа х задается как отношение sin х и cos х. Изучим свойства тангенса.
1.Областью определения функции является
множество всех вещественных чисел, за исключением тех, в которых косинус обращается в нуль.
 Мы запишем это множество следующим образом:
Мы запишем это множество следующим образом:2. Тангенс — периодическая функция с периодом π:
3. Тангенс — нечетная функция, т. е. tg ( — х)= — tg х.
4. Функция y = tg x обращается в нуль одновременно с синусом, т. е. при x=πk, k ∈ Z.
5. Функция у= tg x: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
Выберем для дальнейшего изучения тангенса какой-либо промежуток числовой оси длиной, равной периоду, т. е. числу π. Можно было бы выбрать отрезок от 0 до π, но это неудобно, так как внутри этого отрезка есть точка x= в которой тангенс не определен. Лучше выбрать промежуток ( —; ).
6. Тангенс возрастает в первой четверти. Действительно, пусть
Тогда (возрастание синуса) и (убывание косинуса). Так как значения косинуса положительны, то по свойству неравенств имеем
Умножим это неравенство на неравенство с положительными членами: sin х1<sin х2. Получим tg x1<tg x2.

Тангенс возрастает также и в четвертой четверти. Действительно, пусть Тогда имеем
Теперь числа (— х2) и ( — х1) лежат в первой четверти, и мы можем воспользоваться тем, что в первой четверти тангенс возрастает: tg (— x2)<tg (— x1). Но так как тангенс — нечетная функция, получим:
На промежутке (—; 0 ] тангенс отрицателен и возрастает. На тангенс становится положительным и возрастает.
В итоге тангенс возрастает на промежутке (-; ).
7. Какие же значения принимает тангенс? Когда х возрастает от 0 до тангенс возрастает. При этом когда х приближается к синус х близок к единице, а косинус близок к нулю. Поэтому отношение становится сколь угодно большим. То, что любое вещественное число может быть значением тангенса, видно из рисунка 91. Построим ось, параллельную оси ординат с началом в точке Ро. Возьмем на этой оси точку, соответствующую произвольно выбранному числу а. Соединим 0 с а. Получим точку Р на окружности. Пусть х — число, принадлежащее и такое, что (cos х; sin х) — координаты Р.
 Тогда
ТогдаМы показали, что областью значений тангенса является вся числовая ось R.
Вообще на этой оси, которую часто называют осью тангенсов, можно проследить все свойства тангенса.
8. Построим график тангенса. На промежутке график
тангенса можно построить по точкам, учтя, что тангенс строго возрастает, в нуле обращаясь в нуль, а при приближении к становится сколь угодно большим (рис. 92).Отразив построенную часть графика относительно начала координат (тангенс — нечетная функция), получим график тангенса на промежутке . Для построения полного графика
разобьем числовую ось на отрезки, перенося вправо
и влево на π, 2 π, З π и т. д.График тангенса распадается на отдельные, не связанные между собой части. Это вызвано тем, что в точках тангенс не определен.
Замечание (о монотонности тангенса).
Мы доказали, что функция тангенс возрастает на .Можно ли сказать, что тангенс возрастает на всей области определения? Нет.
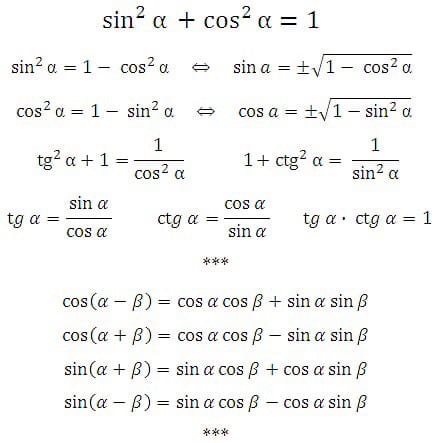 Достаточно посмотреть на график. Если взять
Достаточно посмотреть на график. Если взятьХотя х1 <х2, но tg х1 >tg х2.
Нарушение монотонности связано с тем, что между точками х1 и х2 лежала точка х = в которой тангенс не определен.
Однако можно сказать, что тангенс возрастает на каждом промежутке, который целиком попадает в его область определения.
Свойства котангенса получаются так же, как и свойства тангенса. Перечислим кратко эти свойства, оставляя их доказательство для самостоятельной работы.
1.Функция определена при
2. Функция у = ctg х периодична. Ее периодом является число π:
3. Функция у = ctg x нечетна: ctg ( — х)= — ctg х.
4. Функция у = ctg х обращается в нуль одновременно с косинусом, т. е. при х = + лk, k ∈ Z.
5. Функция у = ctgx: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
6. Функция y=ctgx убывает на промежутке (0; π). Перенося его на kπ, получаем, что котангенс убывает на каждом промежутке ( πk; π + πk).
7. Область значений котангенса — множество R всех вещественных чисел.
8. График котангенса изображен на рисунке 93.
Производные тригонометрических функцийПусть точка А движется с единичной скоростью . по окружности радиуса 1 с центром в начале координат О в положительном направлении. Координаты точки А в момент времени t равны cos t и sin t. Вектор мгновенной скорости точки А в момент времени t направлен по касательной к окружности в точке А (рис. 94), и в силу теоремы о перпендикулярности касательной к радиусу, проведенному в точку касания, вектор перпендикулярен вектору .
Вычислим координаты вектора . Отложив от точки О вектор , мы получим вектор , координаты которого равны координатам вектора . Далее, так как движение точки А по окружности происходит с единичной скоростью, то длина вектора и равна 1, поэтому длина вектора также равна 1. Следовательно, точка В лежит на окружности.
Вектор перпендикулярен вектору, поэтому если A = Pt,
то .
 Таким образом, координаты вектора = равны
Таким образом, координаты вектора = равныС другой стороны, координаты скорости являются производными от координат точки А, следовательно,
Найдем производную функции y = A sin ( ωt + а):
Рассмотрим примеры.
Вычислим теперь производную функции y = tgx. Так как то по теореме о производной частного получаем:
Следовательно,
Аналогично
Таким образом,
Примеры:
Приближенные формулыГлавная приближенная формула: вблизи нуля sin t ≈ t.
Доказательство. Дифференциал функции y = sin х равен dy = cos х dx. Найдем dy при х = 0. Так как cos 0=1, то при х = 0 dy = dx. Найдем приращение функции:
∆y = sin ∆х — sin 0 = sin ∆х.
Так как ∆y ≈ dy, то получим ∆y = sin ∆х ≈ dy=dx = ∆х. Вместо ∆х можно написать t и получить sin t ≈ t.
Эта формула дает тем точнее значение синуса, чем ближе t к нулю.
 Возможность заменять sin t на t при маленьких значениях угла t широко употребляется в приближенных вычислениях. Можно дать различные интерпретации этой приближенной формулы.
Возможность заменять sin t на t при маленьких значениях угла t широко употребляется в приближенных вычислениях. Можно дать различные интерпретации этой приближенной формулы.1. — это запись того, что отношение приращения
функции к его главной части стремится к единице при стремлении к нулю приращения аргумента.
2. Рассмотрим единичный круг. Пусть для простоты t>0. Тогда длина дуги АВ равна t, а длина отрезка ВС равна sin t. Удвоим дугу АВ и отрезок ВС — дуга BD имеет длину 2t, а хорда BD — длину 2 sin t. Соотношение sin t ≈ t означает, что отношение длины хорды к длине стягиваемой ею дуги стремится к единице, когда дуга стягивается в точку (рис. 95).
3. Рассмотрим касательную к синусоиде в начале координат. Так как (sin x)’=cos х, a cos 0= 1, то уравнение этой касательной у — х. Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.
Для получения других приближенных формул выпишем дифференциалы тангенса и косинуса:
При x = 0 получим приближенное значение тангенса:
Применяя этот же прием к косинусу, мы получим, что дифференциал косинуса при x=0 равен —sin0 • dx т.
 е. равен 0. Это означает, что главная часть приращения косинуса равна нулю и в первом приближении cos x ≈ cos 0 = 1. Можно получить более точную формулу таким путем. Запишем cos х так:
е. равен 0. Это означает, что главная часть приращения косинуса равна нулю и в первом приближении cos x ≈ cos 0 = 1. Можно получить более точную формулу таким путем. Запишем cos х так:Заменим в этой формуле sin х на х и воспользуемся приближенной формулой для квадратного корня:
Полученная приближенная формула для косинуса вблизи точки x = 0 весьма точна.
Более точные приближения можно получить с помощью формул
Примеры:
- Вычислить приближенно sin 0,03 • tg 0,12. sin 0,03 ≈ 0,03, tg 0,12 ≈ 0,12, sin 0,03 • tg 0,12 ≈ 0,0036 ≈ 0,004.
- Вычислить приближенно sin 2°. Переводим 2° в радианную меру: 2° ≈ 0,034. sin 2° ≈ 0,034.
Тождественные преобразования
Формулы сложенияТригонометрические функции связаны между собой многочисленными соотношениями. Первая серия тождеств описывает связь между координатами точки окружности — это так называемые основные соотношения.
 Эти соотношения позволяют выразить значения одних функций через другие (при одном и том же значении аргумента). Вторая серия тождеств происходит от симметрии и периодичности в движении точки по окружности. Отсюда мы получаем формулы приведения. Третий источник тригонометрических формул — это изучение поворотов. Поворот точки на угол а + β можно составить из композиции двух поворотов — на угол а и на угол β. Есть простые формулы, связывающие координаты точек Эти формулы называются формулами сложения.
Эти соотношения позволяют выразить значения одних функций через другие (при одном и том же значении аргумента). Вторая серия тождеств происходит от симметрии и периодичности в движении точки по окружности. Отсюда мы получаем формулы приведения. Третий источник тригонометрических формул — это изучение поворотов. Поворот точки на угол а + β можно составить из композиции двух поворотов — на угол а и на угол β. Есть простые формулы, связывающие координаты точек Эти формулы называются формулами сложения.Нашей целью является вывод формул, связывающих sin (а ± β), cos (а ± β), tg (а ± β), ctg (а ± β) с тригонометрическими функциями углов а и β. Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.
Теорема. Косинус разности двух углов равен произведению косинусов этих углов, сложенному с произведением синусов:
cos (а — β) =cos а cos β + sin а sin β.
Доказательство. Построим углы а и β помощью единичной окружности, т.
 е. точки Ра и Рβ , такие, что векторы образуют углы а и β с положительным направлением оси абсцисс. Угол между векторами равен а — β (рис. 96).
е. точки Ра и Рβ , такие, что векторы образуют углы а и β с положительным направлением оси абсцисс. Угол между векторами равен а — β (рис. 96).Вычислим скалярное произведение этих векторов. По определению скалярного произведения
(так как векторы имеют длину, равную 1).
Теперь вычислим это же скалярное произведение с помощью координат:
Сравнивая результаты вычислений, получаем требуемую формулу:
Доказательство теоремы закончено. Выведем остальные формулы.
Косинус суммы. Сумму а + β представим как разность а — ( — β) и подставим в формулу для косинуса разности:
Воспользуемся тем, что cos( —p) = cos p (четность косинуса), a sin( —p)=—sin p (нечетность синуса). Получим:
Синус суммы. Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности получим:
Окончательно
В качестве примера вычислим sin 15°. Представим 15° как разность 45° —30°.
 Получим sin 15° = sin (45° — 30°) = sin 45° cos 30°
Получим sin 15° = sin (45° — 30°) = sin 45° cos 30° Тангенс суммы и разности. По определению tg(a + β) формулам синуса и косинуса суммы имеем:
Разделив числитель и знаменатель этой дроби на cos a cos β, получим:
Заменяя β на ( — β) и пользуясь нечетностью тангенса, получаем:
Формулы удвоенияФормулы сложения являются одними из основных формул, связывающих тригонометрические функции. Из них можно вывести различные следствия. Полагая а = р, получим так называемые формулы удвоения.
Тригонометрические функции половинного угла
Заметим, что в формуле для cos 2a можно заменить на 1 — или на 1 — . Получим две новые формулы:Из формул двойных углов можно получить формулы для синуса и косинуса половинного угла. Сначала запишем:
Затем в этих формулах подставив вместо а, получим:
Извлекая корень, получим:
(Для того чтобы раскрыть модули, надо знать, в какой четверти лежит угол ).

Обилие тригонометрических формул связано с тем, что между основными тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом — есть соотношения, которые позволяют по-разному написать одно и то же выражение. Возникает вопрос: нельзя ли выбрать одну какую-то функцию и через нее выражать все остальные? Если в качестве такой функции мы выберем синус, то во многих формулах появятся квадратные корни. Так, например, выражая sin 2а через sin а, мы получим sin 2а = 2 sin а cos а = 2 sin а . Такие формулы неудобны.
Оказывается, что все тригонометрические функции от аргумента х (и от nх при целом n) выражаются через тангенс угла рационально, без квадратных корней. Выведем эти полезные формулы.
Напишем формулы двойного угла для исходного угла
Представим число 1 в виде и поделим на 1 правые части последних формул
Поделим теперь числитель и знаменатель каждой дроби на
Пользуясь этими формулами, можно функцию вида у = а sin x + b cos x + c представить в виде рациональной функции от tg .

Пример. Выразить у = 2 sin х + З cos х — 1 в виде функции от tg .
Преобразование суммы тригонометрических функций в произведение и обратные преобразованияПусть требуется преобразовать сумму sin a + sin β в произведение. Используем следующий искусственный прием: напишем тождества
заменим а и β выражениями, стоящими справа, в формулах для синуса суммы и разности:
Аналогично выводятся еще три формулы:
Выпишем подряд четыре формулы сложения:
Вычитая почленно из четвертого равенства третье, получим:
Складывая третье и четвертое равенства, получим:
Складывая два первых равенства, получим:
Мы рассмотрели различные тождества, связывающие тригонометрические функции. Все их запомнить трудно, и приходится обращаться к таблицам и справочникам. Важнее запомнить не сами формулы, а то, какие функции между собой они связывают, что с их помощью можно получить.

Тригонометрические уравнения
Простейшим тригонометрическим уравнением называется уравнение вида sinx=a, где cos x=a, tgx=a, где a — некоторое действительное число.
АрксинусРассмотрим уравнение sin x = a. Так как областью значений синуса является отрезок [—1; 1], то это уравнение не имеет решений при |a| > 1. Пусть теперь |а|< 1. Построим на одном чертеже графики у = а и y = sin x (рис. 97).
По рисунку ясно, что прямая у = а пересечет синусоиду бесконечно много раз. Это означает, что при |a| ≤ 1 уравнение sin x = a имеет бесконечно много корней. Так как синус имеет период 2π, то достаточно найти все решения в пределах одного периода. По графику видно, что при |a| < 1 на отрезке [0; 2π] есть два числа, или, можно сказать, два угла, синус которых равен а.
Если один из таких углов а, то другой π—а. Все другие решения уравнения sin х = а, где |a| < 1, получаются из двух найденных с помощью свойства периодичности синусa.
Итак, пусть а — какое-либо решение уравнения sin х = а, где |a| < 1. Тогда все решения этого уравнения получаются по формулам
Эти две серии решений иногда записываются одной формулой:
Пример. Решить уравнение
Одно решение этого уравнения Все остальные решения получаются по формулам
Как мы уже выяснили, уравнение sinx=a при |а| ≤ 1 имеет бесконечно много решений. Для одного из них имеется специальное название — арксинус.
Определение. Пусть число а по модулю не превосходит единицы. Арксинусом числа а называется угол х, лежащий в пределах от , синус которого равен а.
Обозначение: х = arcsin а.
Итак, равенство x = arcsin a равносильно двум условиям: sin z = a и
Обратим еще раз внимание на то, что arcsin а существует лишь, если |а|≤ 1.
Примеры:
Теперь решения уравнения sin х = а (при |а| ≤ 1) можно записать так: х = arcsin а+2πk, х= π — arcsin а+2πk, или в виде одной формулы:
Запишем некоторые тождества для арксинуса.

- sin arcsin а = а.
Это тождество вытекает из определения арксинуса (arcsin а — это такой угол х, что sin х=а).
Действительно, обозначим sin х через а. Тогда наше тождество будет равносильно определению арксинуса: arcsin а = х, если и sinx = a. Заметим, что выражение arcsin (sin х) имеет смысл при любом х, однако при оно не равно х.
Действительно, синусы от правой и левой частей равны: sin (arcsin ( —а)) = —а и sin ( — arcsin а)= —sin (arcsin а)= —а. В то же время правая часть доказываемого равенства — это угол, принадлежащий отрезку . Поэтому левая и правая части равны между собой.
АрккосинусТак же как и в предыдущем пункте, при |а|>1 уравнение cosx = a решений не имеет; если |а| ≤ 1 то решений уравнения бесконечно много.
Если a — какое-либо решение уравнения cos х=а, то —а также есть решение этого уравнения, так как cos a = cos ( — a). По графику или на единичном круге видно, что при |а|< 1 в пределах одного периода уравнение cos х=а имеет два решения.

Если a — одно из решений уравнения cos х = а, то все решения исчерпываются двумя сериями:
Эти серии обычно записывают в виде одной формулы:
Пример. Решить уравнение
Одно решение находится легко: .
Запишем все решения так:
Так же как и для синуса, выделяется одно определенное решение уравнения cos х = а и ему дается специальное название — арккосинус.
Определение. Пусть а — число, по модулю не превосходящее единицы. Арккосинусом числа а называется угол х, лежащий в пределах от 0 до π, косинус которого равен а.
Обозначение: х= arccos а.
Равенство x = arccos a равносильно двум условиям: cos x = a и 0 ≤ х ≤ π. Арккосинус числа а существует лишь при |а| ≤ 1 .
Пример:
Решение уравнения cos х=а (при |а| ≤ 1) можно записать теперь в общем виде:
По каким причинам для значений арксинуса был выбран отрезок , а для арккосинуса отрезок [0; π]?
Это объясняется тем, что на этих отрезках, во-первых, синус и косинус принимают все возможные значения от — 1 до 1 и, во-вторых, каждое значение принимается ровно один раз.
 Отрезков с этими условиями бесконечно много, но при этом выбраны отрезки «поближе к нулю».
Отрезков с этими условиями бесконечно много, но при этом выбраны отрезки «поближе к нулю».Для арккосинуса можно вывести ряд тождеств.
- cos (arccos а) = а.
Это тождество следует из определения арккосинуса.
Обозначим cos x = а. Получим определение арккосинуса: arccos а = х, если x ∈ [0; π ] и cos х = а.
Сначала вычислим косинус от левой и правой частей:
Если равны косинусы двух чисел, то это еще не означает, что равны сами числа. Проверим, что правая часть принадлежит отрезку [0; π]. (Так как левая часть тоже принадлежит этому отрезку, то из равенства косинусов двух чисел теперь уже будет следовать равенство самих чисел.) Итак, надо доказать, что π —arccos а принадлежит [0; π]. Действительно, arccos а ∈ [0; π — arccos а ∈ [ — π ; 0], π— arccos а ∈ [0; π], что и требовалось доказать.
АрктангенсОбласть значений тангенса (котангенса) — вся числовая ось. Поэтому уравнения tgx = a, ctg х — а имеют решения при любом а.
 В пределах одного периода π тангенс и котангенс принимают каждое значение ровно один раз. Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:
В пределах одного периода π тангенс и котангенс принимают каждое значение ровно один раз. Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:где a — какое-либо решение соответствующего уравнения. Примеры. Решить уравнения:
Определения арктангенса и арккотангенса вводятся аналогично определениям арксинуса и арккосинуса, поэтому мы проведем его короче.
Определение. Арктангенсом числа а называется угол тангенс которого равен а. Арккотангенсом числа а называется угол x ∈ (0; π), котангенс которого равен а.
Обозначения: х = arctg а и x = arcctg а. Примеры.
2. Решить уравнения:
Тождества:
Решение тригонометрических уравненийТригонометрические уравнения встречаются в задачах, в которых из соотношений между тригонометрическими функциями требуется найти неизвестные углы.
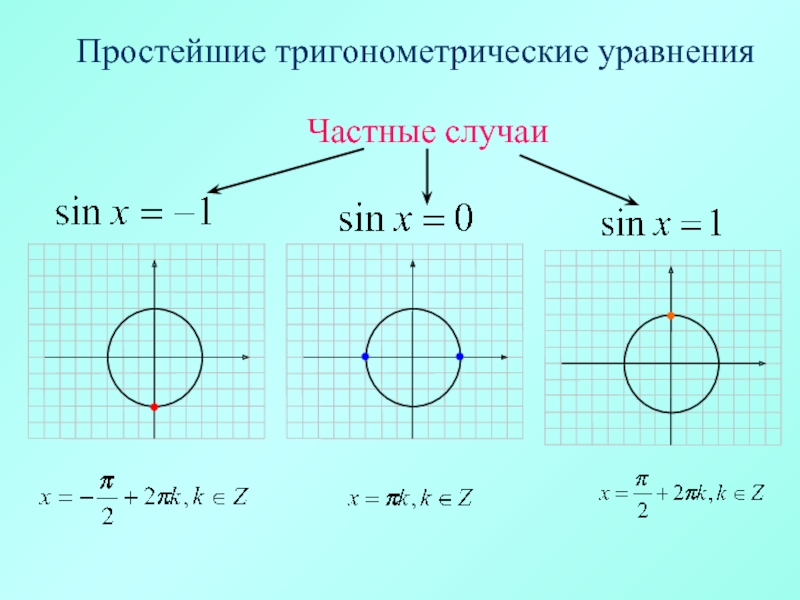 Основными, чаще всего встречающимися тригонометрическими уравнениями являются уравнения простейшего типа sin х — а, cos х = а, tg х = а и ctg х = а, которые уже рассмотрены в предыдущих пунктах. Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.
Основными, чаще всего встречающимися тригонометрическими уравнениями являются уравнения простейшего типа sin х — а, cos х = а, tg х = а и ctg х = а, которые уже рассмотрены в предыдущих пунктах. Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.Более сложные тригонометрические уравнения обычно решаются сведением их к простейшим с помощью различных алгебраических и тригонометрических формул и преобразований. Рассмотрим некоторые приемы решения тригонометрических уравнений.
а) Уравнения, алгебраические относительно одной из тригонометрических функций.
Примеры решения уравнений.
Это уравнение является квадратным относительно sin х. Корни этого квадратного уравнения и sin x= — 2. Второе из полученных простейших уравнений не имеет решений, так как |sinx| ≤ 1, решение первого можно записать так:
Если в уравнении встречаются разные тригонометрические функции, то надо пытаться заменить их все через какую-нибудь одну, используя тригонометрические тождества.

Так как квадрат синуса легко выражается через косинус, то, заменяя sin2 х на 1 —cos2 х и приводя уравнение к квадратному относительно cos х, получим 2 (1 —cos2 х) — 5 cos х — 5 = 0, т. е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которого
Уравнение решений не имеет. Решения уравнения cos x= — 1 запишем в виде
Заменив ctg x на и приведя к общему знаменателю, получим квадратное уравнение , корни которого tg x=l, tg х = 3, откуда
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используют формулы, выражающие синус и косинус через тангенс половинного угла, т. е.
Делая замену, получаем уравнение относительно
Квадратное уравнение имеет корни откуда
б) Уравнения, решаемые понижением их порядка.
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла.
 Такие замены делать выгодно, так как они понижают порядок уравнения.
Такие замены делать выгодно, так как они понижают порядок уравнения.Примеры решения уравнений.
- Решить уравнение
Можно заменить cos 2х на 2 — 1 и получить квадратное уравнение относительно cos х, но проще заменить на и получить линейное уравнение относительно cos 2х:
2. Решить уравнение
Подставляя вместо их выражение через cos 2x, получим:
в) Уравнения, решаемые после преобразований с помощью тригонометрических формул.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы преобразования суммы в произведение.
Примеры решения уравнений.
Преобразуем произведение синусов в сумму:
Полученное уравнение можно решить разными способами. Можно воспользоваться формулами сложения и преобразовать в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 2х и 6х:
Получим два уравнения:
Проверьте, что решения второй серии содержат в себе все решения первой серии.
 Учитывая это, ответ можно записать короче:
Учитывая это, ответ можно записать короче:г) Однородные уравнения.
Решим уравнение
Если считать, что sin х и cos х — члены первой степени, то каждое слагаемое имеет вторую степень. Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.)
Гармонические колебанияГармонические колебания — это процесс, который может быть описан функцией вида у = A sin (ω + а).
Примеры:
1) Колебания упругой пружины. Конец упругой пружины (точка Р) при ее сжатии или растяжении описывает колебательные движения. Если на прямой, по которой движется точка Р, ввести координату х так, чтобы в положении равновесия xр = 0, оттянуть конец пружины в положительном направлении на расстояние A и в момент времени t = 0 отпустить его, то зависимость координаты точки Р от времени t (рис.
 98) будет иметь следуюший вид: , где ω — некоторый коэффициент, характеризующий упругость пружины.
98) будет иметь следуюший вид: , где ω — некоторый коэффициент, характеризующий упругость пружины.2) Электрический колебательный контур. Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора С и катушки индуктивности L (рис. 99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени.
Таким образом, гармоническое колебание у=А sin (ωt + a) определяется тремя параметрами: амплитудой A>0, угловой скоростью ω>0 и так называемой начальной фазой а. Часто вместо угловой скорости ω говорят о частоте колебаний v, которая связана с угловой скоростью ω (или иначе круговой частотой) формулой ω = 2πv.
 Функция у периодична. Ее основной период равен
Функция у периодична. Ее основной период равен Колебания приходится складывать. В механике это связано с тем, что на точку может действовать несколько сил, каждая из которых вызывает гармонические колебания. В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функций
есть функция того же вида:
Достаточно научиться складывать функции вида у = A1 sin ωt и
y = A2 cos ωt. Для их сложения применяется прием введения вспомогательного угла. Итак, рассмотрим выражение у = A1 sin ωt + A2 cos ωt. Оно похоже на формулу синуса суммы: sin (ωt + a) = sin ωt cos a+ cos ωt sin a. Числа A1 и A2 нельзя считать косинусом и синусом, однако если их разделить на число то тогда это будет возможно. Введем угол а с помощью соотношении
Сделаем преобразование:
Примеры:
Периодические функцииТригонометрические функции являются периодическими.
 В общем виде функция y = f(x) называется периодической, если существует такое число Т ≠ О, что равенство f (x+T)=f (х) выполняется тождественно при всех значениях х.
В общем виде функция y = f(x) называется периодической, если существует такое число Т ≠ О, что равенство f (x+T)=f (х) выполняется тождественно при всех значениях х.Обычно среди периодов периодической функции можно выделить наименьший положительный период, который часто называют основным периодом. Все другие периоды функции являются целыми кратными основного. График периодической функции состоит из повторяющихся кусков, поэтому достаточно построить его на отрезке изменения аргумента длиной, равной основному периоду. На рисунке 100 изображены графики различных периодических функций.
Приведем пример одной интересной периодической функции. Всякое число х можно представить в виде суммы его целой и дробной частей. Целая часть числа х определяется как наибольшее целое число, не превосходящее х, и обозначается [х]. Например, [3]=3; [3,14]=3; [ — 3,14]=— 4. Дробная часть обозначается {x} и равна по определению x — [x]. Функция у — {х)=х — [х] является периодической с основным периодом, равным единице.
 Ее график изображен на рисунке 101.
Ее график изображен на рисунке 101.Если функция y — f (х) периодична и ее периодом является число Т, то и функция y=f (kx) будет периодической, причем ее пе-риодом будет число Действительно, рассмотрим функцию y=g(x), где g(x) = f{kx). Вычислим
Сдвиг аргумента не меняет период функции. Отсюда следует, что функция у=А sin (ωt + а), задающая гармоническое колебание, имеет период
Если Т является общим периодом двух функций f и g, то Т остается периодом их суммы, произведения, частного. Правда, как мы видим на примере тангенса, если Т является основным периодом f и g, то это может быть не так для новых функций, полученных из f и g арифметическими операциями.
Сумма двух функций с различными периодами необязательно будет периодической. Интересен случай сложения двух функций с различными, но очень близкими периодами. Рассмотрим, например, сумму функций близки друг к другу. Складывая синусы, получим
Так как
Поэтому при маленьких значениях t и
Однако с ростом t множитель будет убывать.

«Ровное» гармоническое колебание типа у1 заменится «биением», график которого изображен на рисунке 102. Можно представить себе, что «биение» — это колебание, амплитуда которого медленно (и тоже периодически) меняется. Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.
Разложение на гармоникиЧистый звуковой тон представляет собой колебание с некоторой постоянной частотой. Музыка, которую мы слышим, представляет собой наложение различных чистых тонов, т. е. получается сложением колебаний с различными частотами. Преобладание звука той или иной частоты (скажем, низких звуков или высоких) связано с амплитудой соответствующих колебаний. Это знакомое нам разложение звуков на чистые тона часто встречается при изучении различных колебательных процессов.

Можно сказать так: простейшие гармонические колебания являются теми кирпичиками, из которых складывается любое колебание. На языке математики это означает, что любую периодическую функцию можно представить с наперед заданной точностью как сумму синусов.
Эйлер Леонард
(1707—1783) — швейцарский математик и механик, академик Петербургской Академии наук, автор огромного количества научных открытий во всех областях математики. Эйлер первым применил средства математического анализа в теории чисел, положил начало топологии.
«Математика, вероятно, никогда не достигла бы такой высокой степени совершенства, если бы древние не приложили столько усилий для изучения вопросов, которыми сегодня многие пренебрегают из-за их мнимой бесплодности».
Л. Эйлер
Этот замечательный факт обнаружен еще в XVIII в. Д. Бернулли при решении задачи о колебании струны. Это показалось удивительным и невозможным по отношению к любой функции даже такому гениальному математику, как Л.
 Эйлер, который, кстати, является автором всей современной символики тригонометрии. Систематически разложения периодических функций в сумму синусов (или, как говорят, на гармоники) изучал в начале XIX в. французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.
Эйлер, который, кстати, является автором всей современной символики тригонометрии. Систематически разложения периодических функций в сумму синусов (или, как говорят, на гармоники) изучал в начале XIX в. французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.В качестве примера на рисунке 103 изображено приближение к периодической функции y = {x) в виде суммы нескольких гармоник. Разложение произвольного периодического сигнала на гармоники является главным математическим аппаратом радиотехники.
Тригонометрические и обратные тригонометрические функции
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Как школьнику понять тригонометрию? | Хакнем Школа
#хакнем_знайка (👈 рубрика, которая пробуждает и формирует вкус к учёбе)
Вероятно, в истории математики второй, после арифметики, возникла геометрия.
 Из неё выросли тригонометрия и теория функций комплексного переменного, «перебежавшие» в алгебру и зажившие там самостоятельно, аналитически. С собой они захватили тригонометрическую форму теоремы Пифагора — основное тождество тригонометрии и многое другое.
Из неё выросли тригонометрия и теория функций комплексного переменного, «перебежавшие» в алгебру и зажившие там самостоятельно, аналитически. С собой они захватили тригонометрическую форму теоремы Пифагора — основное тождество тригонометрии и многое другое. Разделение привело к некоторым трудностям освоения тригонометрии теми, кто образы воспринимает лучше формул, поэтому многие её разделы бывает полезно изучать совместно с геометрическими аналогами. При умелом использовании геометрия создаёт для тригонометрии зрительные образы, а тригонометрия для геометрии аналитический аппарат.
Как геометрические представления могут помочь освоению тригонометрических формул и даже вывести их, покажем на примере вывода формул для синусов и косинусов суммы и разности двух углов, α и β. Для простоты примем все рассматриваемые углы достаточно малыми, чтобы они помещались в первом квадранте координатной окружности. На рисунке показаны углы α и β, их сумма и разность, а также прямоугольные треугольники OAD, OBE, OCF, построенные на соответствующих им точках на координатной окружности, начале и осях координат, хорде AC.

Сверху показаны маленькие треугольники AGB и BHC. Их гипотенузы равны катетам треугольников OAB и OBC, противолежащим углам β, а углы при их верхних вершинах равны α в силу перпендикулярности сторон этих треугольников соответствующим сторонам треугольника OBE. Поскольку радиус координатной окружности принимается равным единице, искомые функции суммы и разности углов равны катетам треугольников OAD и OCF, а все стороны изображенных на рис. прямоугольных треугольников выражаются в виде тригонометрических функций, подписанных на них.
Непосредственно из рис. видно:
Школьник, который рассмотрит совместно рисунок и формулы, не удивится росту синуса и уменьшению косинуса небольших углов при их сложении, что вполне соответствует виду синусоид и косинусоид. Для углов, порознь или вместе выходящих за первый квадрант, соотношения сохраняются, но чтобы получить геометрические их представления, чертежи потребуется делать дополнительно.

#хакнем_знайка (👈 в этой рубрике мы размещаем заметки, которые помогают учиться. Если вы хорошо разбираетесь в каком-то предмете и готовы помочь другим участникам сообщества разобраться — пришлите свою заметку, мы опубликуем её от вашего имени)
Автор: #сергей_игоревич_рыбников , доктор технических наук, профессор
👇 От партнёра Хакнем Школы 👇👇 От партнёра Хакнем Школы 👇
Регистрируйтесь на бесплатный вводный урок — преподаватели со стажем из онлайн-школы ТЕТРИКА научат вас решать даже самые сложные задания из ОГЭ/ЕГЭ!Тригонометрия
Главная > Учебные материалы > Математика: Тригонометрия
1. Тригонометрия.
Тригонометрия.
2.Тригонометрические функции.1 2 3 4 5 6 7 8 9 1. Тригонометрия – раздел математики, изучающий зависимости между углами и сторонами в треугольниках и тригонометрические функции.
Основная задача тригонометрии — вычисление неизвестных величин треугольника, если известны значения других его величин.
 В тригонометрии также решают задачу о вычислении углов треугольника, если известны его стороны, задачу о вычислении сторон треугольника и т.д.
В тригонометрии также решают задачу о вычислении углов треугольника, если известны его стороны, задачу о вычислении сторон треугольника и т.д.Для измерения углов между сторонами треугольника используется такая единица измерения, как градус. Вся окружность с центром в точке О составляет 360°. Помимо градусной меры углов, также используется радианная мера. 1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.
Радианная и градусная меры связаны зависимостью 180°=π радиан. Угол в n° равен πn/ 180 радиан.
Для того, чтобы рассчитать длину дуги угла α, используется следующая формула:
l= αr
где
l – длина дуги окружности
α – угол в радианах
r – радиус окружности.
Площадь S сектора круга радиуса r, дуга которого содержит α радиан, рассчитывается так:
S = αr² / 2
где
S – площадь сектора круга радиуса rПлощадь сектора круга.

2. Тригонометрические функции.
Тригонометрические функции — математические функции от величины угла. Они используются при изучении геометрии, а также при исследовании переодических процессов в разных областях науки. Тригонометрические функции определяют отношения сторон прямоугольного треугольника в единичной окружности.
Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY . Возьмем в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OМ поворачивается на произвольный угол α вокруг центра O. Так как треугольник ОМВ прямоугольный, то тригонометрические функции угла α определяется из соотношений в прямоугольном треугольнике.
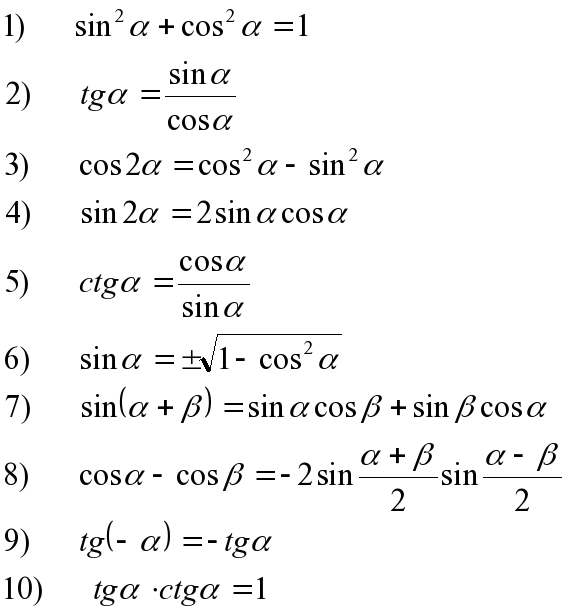 Тогда:
Тогда:Синусом угла α называется отношение противолежащего катета к гипотенузе или отношение координаты y точки М к длине отрезка OМ=R, где R — радиус окружности. Синус угла α обозначают sinα. Так как длина отрезка OМ=1, следовательно sinα = y.
Косинусом угла α называется отношение прилежащего катета к гипотенузе или отношение координаты х точки М к длине отрезка OМ. Косинус угла α обозначают cosα. Так как ОМ=1, то cosα = х.
Тангенсом угла α называется отношение противолежащего катета к прилежащему или координаты y точки М к x. Тангенс угла α обозначают tgα. Так как y = sin α и x = cos α, то tgα= sin α / cos α.
Котангенсом угла α называется отношение прилежащего катета к противолежащему или отношение координаты х точки М к y. Котангенс угла α обозначают ctgα. Так как y = sin α и x = cos α, то ctgα= cosα / sinα. Из последних двух соотношений следует: ctg α= 1 / tg αsin, cos, tg, ctg на тригонометрическом круге.
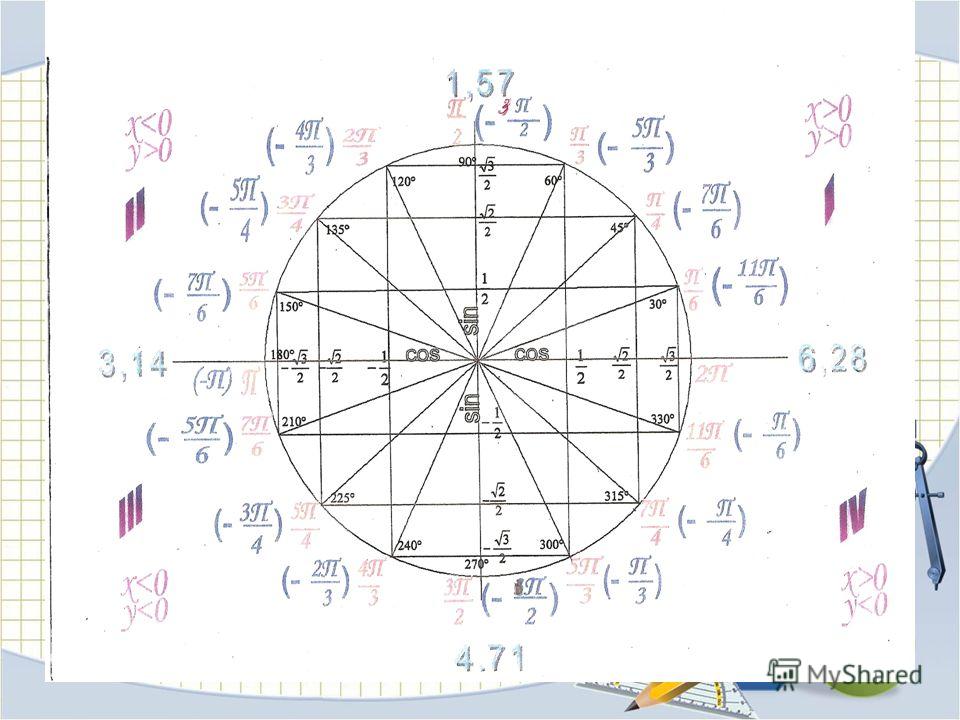
y = sin x
Область определения функции sin x — множество всех действительных чисел. Областью значений функции синус является отрезок [-1;1].График функции sin.
y = cos x
Область определения функции cos x — множество всех действительных чисел. Областью значений функции синус является отрезок [-1;1].График функции cos.
y = tg x
Область определения функции tg x — (-π/2 + πn, π/2 + πn) nϵZ;
область значений (-∞; ∞)График функции tg.

y = ctg x
Область определения функции ctg x — (πn, π + πn) nϵZ;
область значений (-∞; ∞)График функции сtg.
Значения синуса и косинуса для некоторых углов.

Значения тангенса и котангенса для углов 30, 45 и 60 находятся аналогично. Пример 1
Пример 2 1 2 3 4 5 6 7 8 9 Тригонометрия
Треугольники могут показаться простыми фигурами, но математика, лежащая в их основе, достаточно глубока, чтобы рассматривать их как отдельную тему: тригонометрия.

Как следует из названия, тригонометрия — это изучение треугольников. В частности, тригонометрия занимается отношениями между углами и сторонами в треугольниках.
Как ни странно, тригонометрические отношения также могут обеспечить более глубокое понимание кругов. Эти соотношения часто используются в расчетах, а также во многих областях науки, включая физику, инженерию и астрономию.
Ресурсы в этом руководстве охватывают основы тригонометрии , включая определение тригонометрических соотношений и функций. Затем они рассказывают, как использовать эти функции в задачах и как их построить в виде графиков.
Наконец, , это справочное руководство завершается объяснением наиболее распространенных тригонометрических идентичностей.
Базовая тригонометрия
Тригонометрия, в частности, имеет дело с отношениями сторон прямоугольного треугольника , которые можно использовать для определения меры угла.
 Эти отношения называются тригонометрическими функциями, а самые основные из них — синус и косинус.
Эти отношения называются тригонометрическими функциями, а самые основные из них — синус и косинус. Эти две функции используются для определения других хорошо известных тригонометрических функций : тангенса, секанса, косеканса и котангенса.
Этот раздел начинается с обзора прямоугольных треугольников и объяснения основных тригонометрических функций. Это также объясняет их взаимность. В теме также рассказывается, как оценивать тригонометрические углы, особенно специальные углы в 30, 45 и 60 градусов.
Наконец, в руководстве по этой теме рассказывается, как обращаться с обратными тригонометрическими функциями и два наиболее распространенных способа измерения углов.
- Определите стороны прямоугольных треугольников
- Тригонометрические функции или триггер. Отношения
- Синус
- Косинус
- Касательная
- Обзор синуса, косинуса и тангенса
- Секанс, косеканс, котангенс
- Sin, Cos, Tan, Sec, Csc, Cot
- Со-функции
- Вычислить тригонометрические углы
- Специальные углы: 30 градусов, 45 градусов, 60 градусов
- Использование калькулятора
- Обратная тригонометрия
- Градусы и радианы
Применения тригонометрии
На самом деле существует множество теоретических и практических приложения для тригонометрических функций.
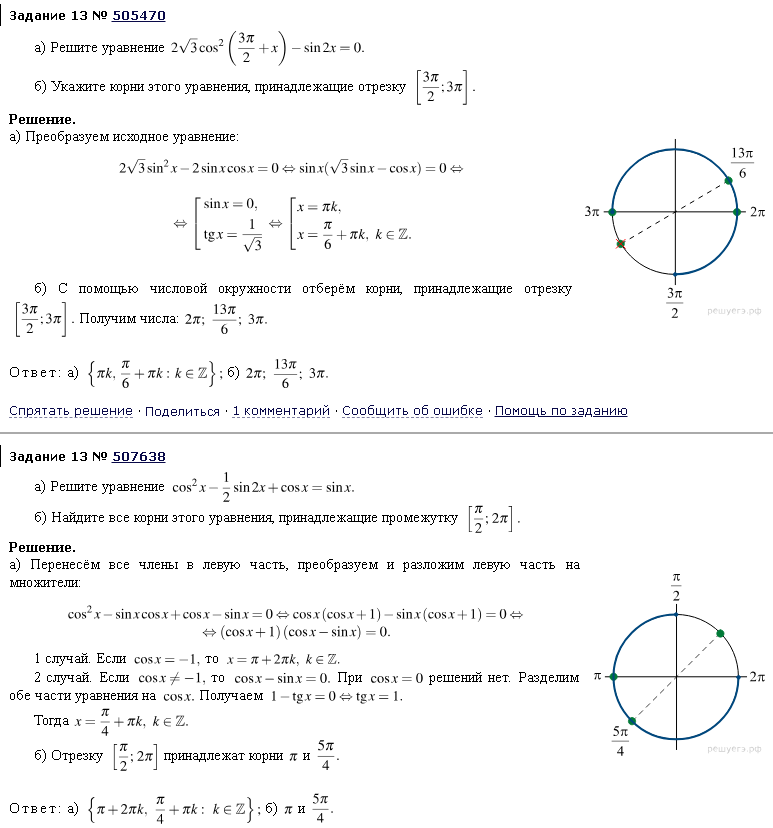 Их можно использовать для поиска недостающих сторон или углов в треугольнике, но их также можно использовать для определения длины опорных балок моста или высоты высокого объекта на основе тени.
Их можно использовать для поиска недостающих сторон или углов в треугольнике, но их также можно использовать для определения длины опорных балок моста или высоты высокого объекта на основе тени. В этом разделе рассматриваются различные типы тригонометрических задач и способы использования основных тригонометрических функций для поиска неизвестных длин сторон. Здесь также рассказывается, как их можно использовать для определения углов и даже площади треугольника.
Наконец, этот раздел завершается подтемами о законах синусов и косинусов.
- Задачи тригонометрии
- Задачи синуса
- Задачи косинуса
- Задачи касательной
- Найти неизвестные стороны прямых углов
- Найти высоту объекта с помощью тригонометрии
- Приложения тригонометрии
- Угол возвышения и понижения
- Площадь треугольника функция синуса
- Закон синусов или правило синуса
- Закон косинусов или правило косинуса
Тригонометрия в декартовой плоскости
Тригонометрия в декартовой плоскости центрируется вокруг единичной окружности.
 То есть окружность с центром в точке (0, 0) и радиусом 1. Любая линия, соединяющая начало координат с точкой на окружности, может быть построена как прямоугольный треугольник с гипотенузой длины 1. Длины катетов треугольника дают представление о тригонометрических функциях. Циклический характер единичного круга также выявляет закономерности в функциях, которые полезны для построения графиков.
То есть окружность с центром в точке (0, 0) и радиусом 1. Любая линия, соединяющая начало координат с точкой на окружности, может быть построена как прямоугольный треугольник с гипотенузой длины 1. Длины катетов треугольника дают представление о тригонометрических функциях. Циклический характер единичного круга также выявляет закономерности в функциях, которые полезны для построения графиков. Этот раздел начинается с описания углов в стандартном положении и боковых углов перед объяснением единичной окружности и опорных углов.Затем он описывает, как значения тригонометрических функций меняются в зависимости от квадранта декартовой плоскости. Наконец, этот раздел заканчивается объяснением того, как единичная окружность и плоскость xy могут использоваться для решения задач тригонометрии.
- Углы в стандартном положении и концевые углы
- Единичная окружность
- Базовый угол
- Тригонометрические отношения в четырех квадрантах
- Нахождение квадранта, в котором лежит угол
- Котерминальные углы
- Тригонометрические функции в декартовой плоскости
- Градусы и радианы
- Оценка тригонометрических функций для углов по заданной точке
- Оценка тригонометрических функций с использованием опорного угла
- Нахождение тригонометрических значений по одному тригонометрическому значению / другая информация
- Оценка тригонометрических функций для важных углов
Графики тригонометрических функций
Хотя единичный круг на декартовой плоскости обеспечивает тригонометрические функции, каждая из этих функций также имеет свой собственный график.Эти графы имеют циклический характер. Как правило, графики триггерных функций имеют наибольший смысл, когда ось x делится на интервалы пи радиан, а ось y по-прежнему делится на интервалы целых чисел.
В этом разделе рассматриваются основные графики синуса, косинуса и тангенса. Затем обсуждаются преобразования этих графов и их свойства. Наконец, тема завершается подтемой о графиках обратных величин основных триггерных функций.
- Тригонометрические графики
- Синусоидальный график
- Косинусный график
- Касательный график
- Преобразования тригонометрических графиков
- Графический синус и косинус с разными коэффициентами
- Максимальные и минимальные значения функций синуса и косинуса
- График , Период, вертикальный и горизонтальный сдвиги
- Касательный, котангенс, секущий, косекансный графики
Тригонометрические тождества
Это точка, в которой тригонометрические функции живут сами по себе, кроме своей основы в соотношениях сторон треугольника.Функции содержат множество идентификаторов, которые раскрывают взаимосвязь между различными типами триггерных функций.
Эти идентификаторы могут использоваться для поиска значений углов вне общих опорных углов. Фактически, они были основным инструментом, доступным для этого до калькуляторов.
В этом разделе рассказывается о тригонометрических идентичностях, а также о том, как их найти и запомнить. Здесь также объясняется, как использовать тождества для упрощения выражений, что требует значительного количества алгебраических манипуляций.
В руководстве объясняется, как найти значения различных углов на основе опорных углов с помощью тождеств суммы и разности, а также формул двойного угла и половинного угла. Тема продолжается и заканчивается дополнительными способами упрощения, факторизации и решения тригонометрических уравнений.
- Тригонометрические тождества
- Тригонометрические тождества: как их вывести / запомнить
- Использование тригонометрических тождеств для упрощения выражений
- Тождества сумм и разностей
- Формулы двойного и полууглового углов
- Тригонометрические уравнения
- Упрощение тригонометрических уравнений Тригонометрические тождества
- Упрощение тригонометрических выражений с участием дробей
- Упрощение произведений биномов с использованием тригонометрических функций
- Факторинг и упрощение тригонометрических выражений
- Решение тригонометрических уравнений
- Решение тригонометрических уравнений с использованием нечетных тригонометрических или четных выражений
- Доказательство тригонометрической идентичности
Новый взгляд на тригонометрию ›News in Science (ABC Science)
Новости науки
Понедельник, 19 сентября 2005 г. Анна Саллех
ABC
Архитекторы используют тригонометрию, чтобы убедиться, что углы и стены находятся там, где они должны быть.Но могли ли они использовать что-нибудь попроще? (Изображение: iStockphoto)
Математическое изучение треугольников стало намного проще, по словам исследователя, который говорит, что его новая теория тригонометрии проще в использовании и более точна.
Доцент Норман Вильдбергер из Университета Нового Южного Уэльса в Сиднее, Австралия, говорит, что его теория «рациональной тригонометрии» больше похожа на алгебру, поскольку вы можете подставить числа в уравнение и получить точный результат.
«Мы собираемся взглянуть на тригонометрию по-новому», — говорит Вильдбергер.
«Мы собираемся оставить синусы и косинусы для части математики кругового движения, а не навязывать ее треугольникам».
Вильдбергер говорит, что тригонометрия, которую мы знаем и любим (или ненавидим) сегодня, имеет свои исторические корни в работах древних астрономов, таких как Птолемей, изучавших движение планет.
В этом случае угол между двумя точками на небе, если смотреть с Земли, был разумным способом вычисления расстояния между ними, говорит он.
Но, говорит Вильдбергер, проблема возникла, когда другие применили эти теории, разработанные для сферической геометрии, к изучению плоских треугольников.
«Это очень хорошо, если вы работаете со сферой или кругом, но когда мы на самом деле изучаем треугольники, там нет кругов», — говорит он.
Новые концепции
Основная цель тригонометрии — понять отношения между углами и сторонами треугольников.
Сегодня он используется в таких областях, как геодезия, проектирование и строительство.
Классическая тригонометрия называет разделение между двумя линиями «углом», который представляет собой длину дуги окружности между двумя линиями.
Угол можно рассчитать с помощью уравнения, которое связывает углы треугольника (используя понятия синуса, косинуса или тангенса) с длиной (расстоянием) противоположной стороны.
Но Вильдбергер говорит, что расстояние — не лучший способ измерить расстояние между двумя точками, а угол — не лучший способ измерить разделение двух линий.
«Это не концепция, которая приводит к тому, что математика является самой приятной, самой полезной и самой точной», — говорит он.
Вместо расстояния в тригонометрии Вильдбергера используется понятие «quandrance», квадрат расстояния.
Вместо угла он использует понятие «разброса», вычисляемое путем деления одного квадранта на другой.
Разброс между двумя линиями — это число от 0 (представляющее параллельные линии) до 1 (представляющее линии под прямым углом).
Вильдбергер говорит, что можно было бы сделать новый транспортир, который измеряет разброс, а не угол.
Затем вы вставляете значения квадранта и распределяете их в его систему уравнений.
Более точный
Что лучше в системе, говорит Вильдбергер, так это то, что все члены в уравнениях могут быть вычислены точно или являются «рациональными», отсюда и термин для его новой теории «рациональная тригонометрия».
Но синус, косинус и тангенс обычно только аппроксимируются, говорит он, что делает их «трансцендентными функциями».
Это означает, что любое сложное вычисление с использованием классической тригонометрии может привести к значительному накоплению ошибок.
Вильдбергер надеется, что «рациональная тригонометрия» предоставит старшеклассникам более простой способ думать о треугольниках, который будет более точным и легким для выполнения.
И он говорит, что повышенная точность будет важна в другом месте, например, при GPS-съемке или при проектировании устройств инженерами.
Вильдбергер говорит, что разработал новую теорию, изучая более сложную математику.
«Дело не в том, что я намеревался это сделать. Это было просто случайностью, в каком-то смысле, когда я понял:« Эй, эти идеи могут изменить элементарную тригонометрию »».
На этой неделе выходит книгаВильдбергера « Божественные пропорции: от рациональной тригонометрии к универсальной геометрии », изданная издательством Wild Egg books.
Теги: наука и технологии, компьютеры и технологии, математика
Написать редактору
Используйте эти ссылки в социальных сетях, чтобы поделиться Новый угол тригонометрии .2 $ описывает круг. Конечно, если вы математический робот, уравнения достаточно. Остальным из нас, с органическим мозгом, наполовину посвященным обработке зрения, кажется, нравятся образы. А «TOA» вызывает потрясающую красоту абстрактного соотношения.
Думаю, вы заслуживаете лучшего, и вот что сделало триггерный клик для меня.
- Визуализируйте купол, стену и потолок
- Триггерные функции — это процентное соотношение к трем формам
Мотивация: Триггер — это анатомия
Представьте себе Боба-инопланетянина, который посещает Землю, чтобы изучить наш вид.
Без новых слов трудно описать людей: «Наверху есть сфера, которая иногда царапается» или «Два удлиненных цилиндра, кажется, обеспечивают движение».
После создания конкретных терминов для анатомии Боб может записать типичные пропорции тела:
- Размах рук (от кончика пальца до кончика пальца) примерно равен высоте
- Голова шириной 5 глаз
- Взрослые, рост 8 голов
Чем это полезно?
Ну, когда Боб находит куртку, он может поднять ее, протянуть руки и оценить рост владельца.И размер головы. И шириной глаз. Один факт связан с множеством выводов.
Еще лучше, человеческая биология объясняет человеческое мышление. У столов есть ноги, у организаций есть голова, у криминальных авторитетов есть мускулы. Наша биология предлагает готовые аналогии, которые появляются в творениях рук человека.
А теперь поворот сюжета: вы, , инопланетянин Боб, изучаете существ в математической стране!
Общие слова, такие как «треугольник», не слишком полезны. Но обозначение синуса, косинуса и гипотенузы помогает нам заметить более глубокие связи.И ученые могут изучать гаверсин, эксеканс и гамзин, как биологи, которые находят связь между вашей голенью и ключицей.
И поскольку треугольники появляются в кругах…
… и круги появляются циклически, наша терминология треугольников помогает описать повторяющиеся узоры!
Trig — это книга по анатомии «математических» объектов. Если нам удастся найти метафорический треугольник, мы получим армаду выводов бесплатно.
Синус / косинус: купол
Вместо того, чтобы смотреть на треугольники сами по себе, как замороженный во льду пещерный человек, представьте их в сценарии охоты на этого мамонта.
Представьте, что вы находитесь в центре купола и собираетесь повесить киноэкран. Вы указываете на какой-то угол «x», и именно там экран будет висеть.
Угол, на который вы указываете, определяет:
- синус (x) = sin (x) = высота экрана, свисающего как знак
- косинус (x) = cos (x) = расстояние до экрана по земле [«cos» ~ насколько «близко»]
- гипотенуза, расстояние до верхнего края экрана всегда одинаково
Хотите максимально большой экран? Укажите прямо вверх.Он находится в центре, на вашей голове, но это большой дагнаббит.
Хотите, чтобы экран находился как можно дальше? Конечно. Укажите прямо под углом 0 градусов. В этом положении экран имеет нулевую высоту и находится далеко, как вы и просили.
Высота и расстояние меняются в противоположных направлениях: поднесите экран ближе, и он станет выше.
Совет: триггерные значения — это проценты
Никто никогда не говорил мне, когда я учился в школе: синус и косинус — это проценты .Они варьируются от + 100% до 0 до -100% или от максимального положительного значения до нуля до максимального отрицательного.
Допустим, я заплатил 14 долларов в виде налога. Вы даже не представляете, дорого ли это. Но если я скажу, что заплатил 95% налога, вы знаете, что меня ограбят.
Абсолютная высота бесполезна, но если ваше значение синуса 0,95, я знаю, что вы почти на вершине своего купола. Довольно скоро вы достигнете максимума, а затем снова начнете снижаться.
Как вычислить процент? Просто: разделите текущее значение на максимально возможное (радиус купола, он же гипотенуза).
Это , почему нам говорят: «Синус = противоположность / гипотенуза». Это для того, чтобы получить процент! Лучшая формулировка: «Синус — это ваш рост в процентах от гипотенузы». (Синус становится отрицательным, если ваш угол указывает «под землю». Косинус становится отрицательным, когда ваш угол направлен назад.)
Давайте упростим расчет, предположив, что мы находимся на единичной окружности (радиус 1). Теперь мы можем пропустить деление на 1 и просто сказать синус = высота.
Каждый круг на самом деле представляет собой единичный круг, увеличенный или уменьшенный до разного размера.Так что проработайте связи на единичном круге и примените результаты к вашему конкретному сценарию.
Попробуйте сами: подключите угол и посмотрите, какой процент высоты и ширины он достигает:
Линия роста синуса не является ровной. Первые 45 градусов покрывают 70% высоты, а последние 10 градусов (от 80 до 90) покрывают только 2%.
Это должно иметь смысл: при 0 градусах вы двигаетесь почти вертикально, но когда вы добираетесь до вершины купола, ваша высота меняется на горизонт.
Касательная / секущая: стена
Однажды ваш сосед ставит стену рядом с вашим куполом. Ага, твой взгляд! Ваша стоимость при перепродаже!
Но можем ли мы извлечь максимальную пользу из плохой ситуации?
Конечно. Что, если мы повесим киноэкран на стену? Вы указываете под углом (x) и получаете:
- касательная (x) = tan (x) = высота экрана на стене
- расстояние до экрана: 1 (экран всегда на одинаковом расстоянии от земли, верно?)
- секанс (x) = sec (x) = «лестничное расстояние» до экрана
У нас есть новые причудливые термины.Представьте, что вы видите Витрувианского «ДЖЕНТЛЬМЕНА», проецируемого на стену. Вы поднимаетесь по лестнице, чтобы убедиться, что вы можете «ВИДЕТЬ, НЕ МОЖЕТЕ?». (Да, он голый … не забудете теперь аналогию, ладно?)
Обратите внимание на касательную высоту экрана.
-
Начинается с 0 и идет бесконечно высоко. Вы можете продолжать указывать на стену все выше и выше, чтобы получить бесконечно большой экран! (Это будет стоить вам.)
-
Касательная — это просто увеличенная версия синуса! Он никогда не становится меньше, и хотя синусоида «достигает вершины» по мере изгиба купола, касательная продолжает расти.
Как насчет секущей, лестничного расстояния?
- Секущая начинается с 1 (лестница от пола к стене) и растет оттуда
- Секущая всегда длиннее касательной. Наклонная лестница, по которой крепится экран, должна быть длиннее самого экрана, верно? (При огромных размерах, когда лестница почти вертикальна, они близки. Но секущая всегда немного длиннее.)
Помните, значения процентов . Если вы указываете под углом 50 градусов, tan (50) = 1.19. Ваш экран на 19% больше, чем расстояние до стены (радиус купола).
(Подключите x = 0 и проверьте свою интуицию, что tan (0) = 0, а sec (0) = 1.)
Котангенс / косеканс: потолок
Удивительно, но теперь ваш сосед решает построить потолок на вершине вашего купола, далеко за горизонтом. ( Что с этим парнем? Ах, случай с голым мужчиной на стене… )
Что ж, пора построить пандус до потолка и немного поболтать.Вы выбираете угол для построения и тренировки:
- котангенс (x) = кроватка (x) = насколько далеко простирается потолок до того, как мы соединим
- косеканс (x) = csc (x) = как долго мы идем по рампе
- пройденное расстояние по вертикали всегда 1
Касательная / секущая описывает стену, а СО-касательная и СО-секанс описывают потолок.
Наши интуитивные факты аналогичны:
- Если вы выберете угол 0, ваш пандус будет плоским (бесконечным) и никогда не достигнет потолка.Облом.
- Самый короткий «наклон» — это когда вы указываете вверх под углом 90 градусов. Котангенс равен 0 (мы не двигались по потолку), а косеканс — 1 («длина пандуса» минимальна).
Визуализируйте связи
Недавно у меня было ноль «интуитивных выводов» о косеканте. Но с помощью метафоры купол / стена / потолок мы видим следующее:
Ого, это тот же треугольник, только увеличенный до стены и потолка.2 $) мы видим, как связаны стороны каждого треугольника.
И из-за сходства, отношения, такие как «высота к ширине», должны быть одинаковыми для этих треугольников. (Интуиция: отойдите от большого треугольника. Теперь он кажется меньше в вашем поле зрения, но внутренние соотношения не могли измениться.)
Вот как мы находим «синус / косинус = тангенс / 1».
Я всегда пытался запомнить эти факты, когда они просто выскакивают на нас при визуализации. SOH-CAH-TOA — хороший ярлык, но сначала получите настоящее понимание!
Попался: вспомни другие углы
Psst … не зацикливайтесь на одной диаграмме, касательная к мысли всегда меньше единицы. 2 $, за исключением глупых тестов, которые ошибочно принимают пустяки за понимание.В этом случае потратьте минуту, чтобы нарисовать схему купола / стены / потолка, заполните метки (загорелый джентльмен, вы же видите, не так ли?) И создайте шпаргалку для себя.
В дальнейшем мы узнаем о построении графиков, дополнениях и использовании формулы Эйлера, чтобы найти еще больше связей.
Приложение: Исходное определение тангенса
Вы можете увидеть касательную, определяемую как длина касательной от окружности к оси x (любители геометрии могут с этим справиться).
Как и ожидалось, в верхней части окружности (x = 90) касательная линия никогда не может достигать оси x и является бесконечно длинной.
Мне нравится эта интуиция, потому что она помогает нам запомнить название «касательная», и вот хорошее интерактивное руководство по триггерам для изучения:
Тем не менее, очень важно расположить касательную вертикаль и распознать, что это просто синус, спроецированный на заднюю стену (вместе с другими соединениями треугольника). {- 1} $ или $ \ arcsin $ («арксинус»), и часто записываются как
asinна различных языках программирования.Если наша высота составляет 25% от купола, какой у нас угол?
Если вставить asin (0,25) в калькулятор, получается угол 14,5 градусов.
А что насчет чего-нибудь экзотического, например, обратной секущей? Часто он недоступен как функция калькулятора (даже тот, который я построил, вздох).
Глядя на нашу шпаргалку по триггерам, мы находим простое соотношение, в котором мы можем сравнить секанс с 1. Например, секанс с 1 (гипотенуза по горизонтали) совпадает с 1 по косинусу:
Предположим, что наш секанс равен 3.5, то есть 350% радиуса единичной окружности. Какой угол к стене?
Приложение: несколько примеров
Пример: найти синус угла x.
Аку, какой скучный вопрос. Вместо того, чтобы «найти синус», подумайте: «Какая высота в процентах от максимума (гипотенузы)?».
Во-первых, обратите внимание, что треугольник «перевернут». Это нормально. У него все еще есть высота, зеленая.
Какая максимальная высота? По теореме Пифагора мы знаем
Хорошо! Синус — это высота в процентах от максимума, равная 3/5 или.60.
Продолжение: Найдите угол.
Конечно. У нас есть несколько способов. Теперь, когда мы знаем, что синус = 0,60, мы можем просто сделать:
Вот еще один подход. Вместо использования синуса обратите внимание, что треугольник «упирается в стену», поэтому можно использовать касательную. Высота 3, расстояние до стены 4, поэтому касательная высота 3/4 или 75%. Мы можем использовать арктангенс, чтобы снова превратить процентное значение в угол:
Пример: Сможете ли вы добраться до берега?
Вы находитесь на лодке, у которой достаточно топлива, чтобы проплыть 2 мили.Вы сейчас находитесь в 0,25 милях от берега. Какой самый большой угол вы можете использовать и при этом дотянуться до земли? Кроме того, единственная доступная ссылка — это Сборник арккосинов Губерта, 3-е изд. . (Поистине адское путешествие.)
Ок. Здесь мы можем визуализировать пляж как «стену», а «расстояние по лестнице» до стены — это секущая.
Во-первых, нам нужно все нормализовать в процентах. У нас есть 2 / 0,25 = 8 «единиц гипотенузы» топлива. Итак, наибольшая секущая, которую мы могли допустить, составляет 8-кратное расстояние до стены.
Мы бы назвали , чтобы спросить: «У какого угла секущая 8?». Но мы не можем, поскольку у нас есть только книга арккосинусов.
Мы используем нашу шпаргалку, чтобы связать секанс с косинусом: А, я вижу, что «sec / 1 = 1 / cos», поэтому
Секанс 8 означает косинус 1/8. Угол с косинусом 1/8 равен arccos (1/8) = 82,8 градуса, это самый большой угол, который мы можем себе позволить.
Неплохо, правда? До аналогии купола / стены / потолка я бы тонул в беспорядке вычислений.Визуализация сценария позволяет легко и даже весело увидеть, какой приятель по триггеру может нам помочь.
В своей задаче подумайте: меня интересует купол (sin / cos), стена (tan / sec) или потолок (cot / csc)?
Счастливая математика.
Обновление: Владелец Gray Matters собрал интерактивные диаграммы для аналогий (перетащите ползунок слева, чтобы изменить угол):
Спасибо!
Другие сообщения из этой серии
- Как интуитивно научиться тригонометрии
- Идентификации Easy Trig с формулой Эйлера
- Интуиция к закону косинусов
- Интуиция к закону синуса
Тригонометрия — обзор | Темы ScienceDirect
ТРАДИЦИОННОЕ ПРОИСХОЖДЕНИЕ ФОРМУЛЫ
Традиционно применение тригонометрии для определения происхождения ударного события, в результате которого распространились капли крови, основывалось на серии теорем и предположений:
- 1.
-
Сферическая капля образует эллиптическое поперечное сечение при контакте с поверхностью (рисунок 4-2).
Рисунок 4-2. Традиционная техника рисования сферической капли, образующей овальное (эллиптическое) поперечное сечение, контактирующее с поверхностью.
- 2.
-
Прямая, пересекающая параллельные прямые, образует равные углы.
- 3.
-
Диаметр капли крови равен ширине проецируемого эллипса.
- 4.
-
Длину эллипса можно определить, используя форму первого контакта капли крови с поверхностью и завершая форму эллипса, как показано.
- 5.
-
Можно построить прямоугольный треугольник из линий контакта, проведенных от теоретической капли крови к приближенному эллипсу (рис. 4-3).
Рисунок 4-3. Вращение теоретических контактных линий в соответствии с тригонометрической моделью.
- 6.
-
Измерение ширины пятна и деление на длину дает число меньше единицы (<1), которое можно использовать с карманным калькулятором или журнальной таблицей, чтобы найти синус дуги, который является угол падения исходной капли крови.
- 7.
-
Используя несколько измеренных пятен, можно вернуться назад от углов падения и определить место происхождения события удара с распределением крови.
Студенты время от времени указывали на фундаментальную проблему этой модели. Поперечное сечение капли крови не может быть таким же, как у капли крови, которую она оставляет. Это связано с тем, что капля является трехмерной, в то время как пятно, по сути, двумерным, с сохранением объема, распространяющимся на более широкую площадь.Пятно крови всегда должно быть больше капли (рис. 4-4). Прямоугольный треугольник все еще может быть построен на основе результирующего пятна крови, но задействованные углы не включают касательную (длину пятна и гипотенузу треугольника) через параллельные линии, поэтому не включают равные углы, внутренние и внешние. Причина построения прямоугольного треугольника состоит в том, чтобы определить первый падающий угол контакта, который является внешним (вне прямоугольного треугольника) углом. Только если внешний вид равен внутреннему, мы можем рассчитать угол падения, измерив пятно.
Рисунок 4-4.
Большинство инструкторов отвечают на вопросы о разнице в размерах, утверждая, что пропорциональность остается неизменной. Это может оправдать процесс, но не было найдено конкретного исследования, которое бы показало, что пропорциональность действительно существует. Сторонники этого метода утверждают, что, поскольку эллипс завершается на основе местоположения начального угла контакта, угол будет таким же на нижнем конце дублированной кривизны. Это приводит к следующей проблеме.
Первый контакт между каплей крови и поверхностью на самом деле не эллиптический.Когда сферическая капля крови впервые касается поверхности, это происходит в результате схлопывания хорды (произносимого шнура) сферы. Наблюдение за тем, как капли крови соприкасаются под узким углом сбоку, подразумевает, что контакт имеет форму капли слезы, хотя на самом деле контакт представляет собой серию поперечных сечений сферы (то есть кругов; рис. 4-5). Еще более важно то, что диаметр хорды контакта зависит от скорости капли, что следует логике Пола Кирка о форме пятна, на которую влияет скорость капли. Об этом свидетельствуют опубликованные фотоработы. 1
Рисунок 4-5. Хорда (произносится как «шнур») нанесенного шара в зависимости от скорости падения.
К сожалению, в исследованиях капель в основном использовалась кровь, капающая из капельниц на наклонные цели. Капли включают большие капли, падающие в свободном падении только под действием силы тяжести. В источниках указано, что форма эллипса зависит от угла, под которым капля крови встречается с поверхностью цели. 2 Это может иметь меньшее значение, чем первоначальное наблюдение доктора Кирка о том, что скорость капли крови влияет на форму последнего пятна.Чем быстрее капля крови движется при контакте с целью, тем меньший первоначальный отпечаток оставит сфера. Чем медленнее движется капля при первоначальном контакте, тем больше диаметр хорды сферы будет записан вначале. Это видно даже по тому, как кровь капает на изогнутый картон. Чем шире пятно, тем больше открыт угол, потому что соотношение больше. Чем быстрее капля движется до тех пор, пока весь поступательный импульс не рассеется, это удлиняет пятно крови, а также сужает его, создавая явно меньший градусный угол контакта.Распределенные ударные брызги при выстреле (GDIS) создают полосы при записи, даже если они могут быть обнаружены под тем, что должно было быть рассчитанным углом к исходной точке.
Теория предельной скорости была введена как средство достижения известной или, по крайней мере, постоянной скорости для капель крови. Кровь капала на наклонные цели с большей высоты, чтобы создать капли крови с известной скоростью, падающие на поверхность под известными углами. Конечная скорость применяется, если объект падает за пределы определенного расстояния.Объект будет ускоряться в соответствии с силой тяжести до тех пор, пока не достигнет точки, за которой ускорение будет в равновесии со сдвигом ветра и другими силами. Падение, продолжающееся после достижения равновесия, будет происходить с постоянной скоростью. К сожалению, точка конечной скорости зависит от массы свободно падающего объекта в воздухе. Только в вакууме можно игнорировать массу. В воздухе, поскольку состав и масса капли крови неоднородны, и они не могут быть известны для какой-либо конкретной капли крови, распределенной во время насильственного преступления, конечная скорость будет изменяться.Однако главная проблема с введением предельной скорости состоит в том, что он не имеет отношения к каплям крови, выбрасываемым силой. Единственное применение — для капель (LVIS, пассивные пятна, следы капель, гравитационные капли).
Было сделано предположение, что разница в массе капли крови мала. Это основано на ложном представлении 3 о том, что кровь однородна по соотношению эритроцитов (гематокриту) или в разумных пределах превышает нормальный диапазон. Однако распределение крови не ограничивается кровью людей с нормальным здоровьем.Анемичные, истощенные бездомные, алкоголики, наркоманы, пожилые люди, дети, абортированные плоды и люди, страдающие сердечными приступами, — все они могут значительно выходить за пределы нормальных диапазонов для соотношений эритроцитов, и это часто упоминается в исследованиях виктимизации. 4 Кроме того, в Blood Dynamics 5 и включенном в приложение здесь указано, что соотношения эритроцитов сильно различаются для разных органов тела. Предположение, что кровь, распределяемая во время насильственных преступлений, всегда имеет нормальный уровень гематокрита эритроцитов, нереалистично.
Попытки найти математическое обоснование исходной логики не увенчались успехом. Наиболее близким приближением может быть проекция сферы в виде тени (рис. 4-6). Эллиптическая тень, кажется, поддается рисованию точек контакта от шара до длины и ширины тени (рис. 4-7). Однако оценка угла не является функцией контакта между сферой и поверхностью, а зависит от расположения источника света (рис. 4-8).Хотя тень проецируется из сферы, плоский круг будет производить такой же эффект. Это не та динамика, что трехмерная капля жидкости, контактирующая с поверхностью под определенным углом, образуя двумерное эллиптическое пятно. Формулу проекционного изображения нельзя применять к переносу вещества.
Рисунок 4-6. Проекция тени создает из сферического шара овальную форму.
Рисунок 4-7. Тень подвешенного шара выглядит неплохо и показывает контакты параллельных линий, проведенных к овалу (эллипсу).
Рисунок 4-8. Проблема с формулой проекции заключается в том, что тень является функцией источника света, а не отношениями между сферой и ее контактом с поверхностью.
Упражнение, демонстрирующее невозможность создания овального поперечного сечения из сферы, состоит в том, чтобы взять сферический объект и попытаться сделать один прямой диагональный разрез поперек него, образуя овал или эллипс. В результате на самом деле всегда будет хорда сферы с кругом в качестве формы поперечного сечения.Независимо от того, как вы его разрезаете, любое поперечное сечение сферы будет кругом, а не овалом (эллипсом). Физически невозможно и вопреки геометрии разрезать сферу так, чтобы получилось овальное поперечное сечение (рис. 4-9).
Рисунок 4-9. Независимо от того, как вы разрезаете сферу, в результате получится круговое поперечное сечение.
По этой логике следуют два вопроса. Почему аналитики до сих пор используют тригонометрические выводы и почему исследователи не заметили отсутствия логики в традиционных теориях? Вероятный ответ заключается в том, что эта техника, кажется, работает, когда применяется к имитации места преступления, а имитация сцены строилась преимущественно с помощью ударов тупым предметом, а не с применением огнестрельного оружия, две совершенно разных степени скорости.Чтобы проверить ответ относительно сравнительных скоростей, 15 июля 2005 года на полигоне Калифорнийской дорожной патрульной академии в Сакраменто была проведена серия экспериментов.
Frontiers | Обучение решению задач тригонометрии, требующих навыков алгебраического преобразования, посредством обучения по аналогии и обучения по сравнению
Введение
Тема тригонометрии входит в учебную программу средней математики. Тригонометрия является необходимым условием для изучения математического анализа в старших классах математики и необходима студентам, желающим изучать курсы естествознания, технологий, инженерии и математики (STEM).Изучение задач тригонометрии требует понимания множества взаимосвязанных математических понятий, таких как навыки алгебраического преобразования , знания геометрии и обоснование графического представления концепций . Из-за необходимости изучать несколько взаимосвязанных понятий, студенты испытывают большие трудности при изучении задач тригонометрии (Blackett and Tall, 1991; Kendal and Stacey, 1998). Наша цель в этой статье концептуального анализа — подчеркнуть важность навыков алгебраических преобразований для облегчения начального этапа изучения задач тригонометрии.Основное внимание здесь уделяется вычислению неизвестной стороны прямоугольного треугольника по известной стороне и углу, что может стать проблемой для многих студентов. В частности, мы утверждаем, что у некоторых студентов могут возникнуть трудности при решении sin30 ° = x /5, скажем, несмотря на то, что они узнали, как решить аналогичную задачу, например, x /4 = 3. Для более сложных задач тригонометрии, Например, sin30 ° = 12/ x , где местоимение является знаменателем, студентов учили «заменять» x на sin30 °, а затем, исходя из этого, решать для x (Источник: личное сообщение).
Мы утверждаем, что такая детализированная стратегия обучения для задач тригонометрии не соответствует навыкам алгебраического преобразования, которые требуются для решения задач тригонометрии. Например, он не пытается связать предварительные знания учащегося о решении линейных уравнений с дробью с решением задач тригонометрии. Помимо этого, учащиеся могут столкнуться с большими трудностями, когда они попытаются различить два типа задач тригонометрии, которые выглядят одинаково, но концептуально отличаются друг от друга, следовательно, из-за относительного положения местоимения (т.е., числитель против знаменателя) (Kendal and Stacey, 1998). Исходя из этого, преподавателям важно рассмотреть различные теоретические подходы, педагогические стратегии и / или образовательные программы, которые могут помочь учащимся приобрести соответствующие навыки для решения задач тригонометрии, которые различаются по расположению местоимения (т. Е. Числитель vs знаменатель). Одна из возможностей, например, связана с использованием различных, но сопоставимых теорий обучения, которые могут способствовать эффективному обучению и способствовать осмысленному пониманию.Таким образом, цель этой статьи, расположенной в контексте актуальной темы тригонометрии, состоит в том, чтобы мы исследовали эффективность двух теорий обучения: обучение по аналогии, и обучение по сравнению с . Мы утверждаем, что этот анализ может стать основой для дальнейшего развития исследований, теоретических, эмпирических, концептуальных и / или методологических, в целях эффективного применения различных теорий обучения.
Концепция обучения по аналогии
Обучение по аналогии , подкрепленное теорией отображения структуры (Gentner, 1983), обеспечило теоретическую основу для развития исследований в области изучения проблем со словами (Reed et al., 1985, 2012; Рид, 1987; Росс и Кеннеди, 1990; Cummins, 1992). Теория структурных отображений подчеркивает построение «реляционных общностей» между исходным примером (изученная проблема) и целевой проблемой (новая проблема) с точки зрения структуры проблемы. Проблемы, состоящие из двух слов, могут иметь разные контексты проблемы, но имеют схожую структуру проблемы, например: (i) «Если 20% моей экономии составляет 300 долларов, какова моя экономия?» vs. (ii) «Джошуа платит 260 долларов в неделю за аренду, что составляет 25% его недельной заработной платы.Сколько зарабатывает Джошуа в неделю? » Используя подход Алгебры , мы можем составить два уравнения, например, 20% x = 300 долларов США и 25% x = 260 долларов США, соответственно, и решить для x . Поскольку эти два уравнения имеют общие реляционные элементы, они используют одну и ту же процедуру решения. Аналогичный перенос вероятен, если учащиеся смогут успешно сопоставить элементы отношений между исходным примером и целевой проблемой. Действительно, рассуждение по аналогии изученной проблемы и новой проблемы позволяет учащимся извлечь схему для изученной проблемы, которая применима для решения новой проблемы.
Holyoak (1984) и Holyoak and Koh (1987) выделили четыре задачи для облегчения обучения по аналогии: построить мысленное представление исходного примера и целевой проблемы (Задача 1), получить исходный пример как аналог целевой проблемы (Задача 2), сопоставьте реляционные элементы исходного примера и целевой проблемы (Задача 3) и расширьте сопоставление для решения целевой проблемы (Задача 4). Авторы не предложили определенную последовательность для реализации этих четырех задач и не указали, какие задачи или задачи являются критическими для стимулирования аналогичного обучения.
Research сообщило о преимуществах включения вспомогательных сигналов , таких как подсказка (Novick and Holyoak, 1991) или напоминание (Ross, 1984) для доступа к исходному примеру. Таким образом, подсказка обращается к Задаче 2. В исследовании, проведенном Cummins (1992), практика извлечения сходных понятий между исходным примером и целевой проблемой привела к аналогичному переносу. Мы можем приписать извлечение аналогичных концепций деятельности по картированию, которая обращается к Задаче 3.Другие исследователи также подчеркивали процесс картирования для достижения аналогичного переноса (Gentner et al., 2003). Участники, заполнившие диаграмму, выделяющую элементы взаимосвязи между двумя сценариями переговоров, превзошли тех участников, которые просто изучали эти два сценария переговоров. В отличие от этого, Рид (1989) не смог найти доказательств аналогичного переноса для словесных задач, несмотря на то, что он обратился к Заданиям 2 и 3: (1) предоставил студентам подсказку для доступа к исходному примеру, (2) потребовал, чтобы студенты построили концептуальную — сопоставление задач между исходным примером и целевой проблемой.
Исследование, проведенное одним из нас несколько лет назад (Ngu and Yeung, 2012), показало, что наличие нескольких компонентов в исходном примере (например, символические уравнения, категоризация) или целевой проблеме (например, подсказка, категоризация) или и то, и другое фактически способствовало отображению символьных уравнений исходного примера на целевую задачу, что привело к эффективности аналогичного переноса. Полученные данные, как мы утверждаем, предоставили новое теоретическое понимание обучения по аналогии, подчеркнув важность наличия нескольких компонентов, а не одного компонента, для содействия аналоговой передаче для словесных задач.
В свете предшествующих исследований обучения по аналогии, использование подсказок для доступа к исходному примеру кажется критически важной задачей по аналогии для облегчения передачи. Тем не менее, использование подсказки для доступа к источнику станет излишним, если исходный пример остается видимым, в то время как учащиеся занимаются отображением исходного примера и целевой проблемы (Richland et al., 2007). Ряд исследователей (Gentner et al., 2003; Rittle-Johnson and Star, 2007; Richland and McDonough, 2010) отметили преимущество представления двух примеров одновременно, а не последовательно.В этом случае одновременное представление двух примеров устраняет необходимость подсказывать учащимся, как получить доступ к исходному примеру. Представление примеров в последовательной манере, напротив, требует возможной необходимости предоставить соответствующие подсказки, чтобы напомнить учащимся об исходном примере.
Действительно, сопоставление двух проработанных примеров не только делает ненужным поиск исходного примера, но также дает учащимся возможность участвовать в сложном сравнении. В своем исследовании Kurtz et al.(2001) выступали за реализацию взаимного согласования, чтобы способствовать абстракции лежащей в основе общей структуры в двух частично понятых сценариях. Участники, которые совместно интерпретировали два сценария в сочетании с перечислением конкретных соответствий, продемонстрировали большую взаимную согласованность, чем те участники, которые либо совместно, либо по отдельности интерпретировали два сценария. Более того, взаимное согласование двух частично понятых текстовых примеров способствовало аналогичной передаче сложной научной концепции (Orton et al., 2012).
Очевидно, что из предыдущих разделов исследование поддержало использование сопоставления двух примеров для продвижения обучения по аналогии. Тем не менее, эффективность выполнения однозначного сопоставления зависит от ориентации двух изображений (Kurtz and Gentner, 2013) или объектов в двух примерах (Matlen et al., 2020). Выравнивание двух примеров в одной ориентации вместо разных ориентаций в этом случае способствует прямому согласованию процесса сопоставления, что повышает эффективность рассуждений по аналогии.
Концепция обучения путем сравнения
Основываясь на теории отображения структуры (Gentner, 1983), чтобы способствовать аналогичной передаче, ряд исследований недавно выявил положительные эффекты обучения по сравнению с (Alfieri et al., 2013; Ziegler and Stern, 2014; Rittle-Johnson et al. др., 2017). Например, Дуркин и Риттл-Джонсон (2012) исследовали эффект сравнения правильных и неправильных примеров для изучения десятичных чисел. Отображение правильных десятичных и неправильных десятичных понятий одновременно помогло учащимся исправить свои неправильные представления о величине десятичных чисел.Аналогичное направление исследований включало просьбу учащихся обосновать, почему конкретный шаг решения был хорошим шагом (например, 1 = 2 x — 5, 6 = 2 x ) или неправильным шагом (например, 3 = 6 x — 2, 3 = 3 x ), помог студентам консолидировать и уточнить свое понимание концептуальных знаний, которые использовались при решении линейных уравнений (Booth et al., 2013). Более того, Große и Renkl (2007) продемонстрировали положительный эффект от использования правильных и неправильных рабочих примеров в области проблем вероятности.Они утверждали, что обучение на правильных и неправильных примерах дает учащимся возможность различать сходства и различия между двумя типами проработанных примеров.
Вместо сравнения правильных и неправильных проработанных примеров для облегчения изучения математики, сравнение двух противоположных выражений алгебры (например, y 3 + y 3 = 2 y 3 vs. y 3 × y 3 = y 6 ) бок о бок также помогли учащимся различать внешне похожие (например,g., буква, число), но концептуально разные концепции (например, сложение или умножение) в двух противоположных рабочих примерах (Ziegler and Stern, 2014). Студенты, изучавшие противоположные выражения алгебры одновременно, превзошли тех студентов, которые изучали выражения алгебры последовательно. Таким образом, в целом развитие исследований на сегодняшний день подтвердило преимущество использования обучения в сравнении для повышения эффективности обучения математике.
Обучение по аналогии и обучение по сравнению в классе математики
Помимо проведения лабораторных тестов, исследователи также изучили межнациональные различия при использовании обучения по аналогии на уроках математики для восьмиклассников (Richland et al., 2007). Например, учителя в странах с высокими показателями по математике (например, Гонконг, Япония), как правило, используют гораздо больше визуально-пространственных опор и связывающих жестов, чтобы подчеркнуть аналогичные сравнения, чем их коллеги из США. Частое использование визуально-пространственных опор и связующих жестов, которые направляют внимание студентов на аналог источника, может помочь снизить требования к когнитивной обработке, поскольку устраняет необходимость поиска аналога источника (Richland et al., 2017).
Вместо того, чтобы проводить обучение путем сравнения в неповрежденных классах, которое длилось несколько дней, Star et al.(2015), напротив, реализовали одногодичное вмешательство между учебной программой «сравнения» и учебной программой «как обычно». Учебная программа сравнения была включена в обычную учебную программу в качестве дополнительных материалов. Более широкое использование сравнительных материалов коррелировало с более высоким ростом процедурных знаний. Тем не менее, было непросто побудить учителей постоянно использовать сравнительные материалы в течение года.
Действительно, исходя из вышесказанного, аналогичные рассуждения облегчаются использованием вспомогательных сигналов (например,g., подсказка), чтобы привлечь внимание учащихся к соответствующему исходному примеру, в котором описана процедура решения, аналогичная целевой задаче. Тем не менее, мы могли бы исключить подсказку для доступа к исходному примеру, если бы мы поместили исходный пример и целевую задачу рядом (например, Rittle-Johnson and Star, 2007). Сопоставление реляционных общностей между исходным примером и целевой проблемой — еще одна важная задача по аналогии, которая облегчает передачу по аналогии. Однако успешный аналогичный перенос зависит от активного процесса сравнения (например,g., совместная интерпретация плюс список конкретных соответствий) (например, Kurtz et al., 2001) и прямое согласование примеров (например, Matlen et al., 2020). Тем не менее, интересно отметить, что из нашего изучения литературы, построение мысленного представления исходного примера на начальном этапе обучения по аналогии (Holyoak and Koh, 1987) получило минимальное внимание с точки зрения исследования и / или преподавания. разработка.
Отличительной чертой обучения путем сравнения, напротив, является одновременное отображение двух проработанных примеров бок о бок, что затем позволяет учащимся идентифицировать сходства и различия между двумя процедурами решения двух проработанных примеров (Rittle-Johnson et al. al., 2017). Следовательно, обучение путем сравнения может улучшить понимание учащимся математических концепций (или заблуждений), а также конкретных процедур, относящихся к двум проработанным примерам (например, Booth et al., 2013).
Интересно отметить, что с методологической точки зрения обучение по аналогии и обучение по сравнению состояли из использования различных типов вмешательств. Что касается обучения по аналогии, исследователи внедрили меры вмешательства в лабораторных и учебных классах (Alfieri et al., 2013) и также включали использование визуально-пространственных опор и связывающих жестов (Richland et al., 2007). Аналогичным образом, для обучения путем сравнения исследователи проводили как краткосрочные вмешательства (например, Rittle-Johnson and Star, 2007), так и долгосрочные (например, один календарный год), чтобы улучшить изучение алгебры (Star и др., 2015). Таким образом, в целом мы утверждаем, что педагогические практики, которые включают использование обучения по аналогии и обучения по сравнению, эффективны, помогая облегчить изучение математики учащимися.Какой подход более уместен и / или эффективен? С нашей точки зрения, мы признаем, что два педагогических подхода дополняют друг друга — сила одного подхода может противостоять слабости другого подхода, и поэтому этот «дополнительный баланс» может отражать целостную позицию, когда человек узнает, как для решения задач тригонометрии.
Задачи тригонометрии
Наша цель для обсуждения — предложить эффективные инструкции, которые могли бы облегчить изучение двух разных типов задач тригонометрии, которые различаются из-за относительного положения местоимения, например, cos60 ° = x /2, где местоимение числитель, а sin30 ° = 8/ x , где местоимение является знаменателем.Как отмечалось ранее, задачи тригонометрии аналогичны линейным уравнениям с дробью. В ходе нашего исследования мы обнаружили, что сложнее решать линейные уравнения, содержащие дробь, особенно когда местоимение является знаменателем, а не числителем, поскольку первое включает больше шагов решения (Ngu and Phan, 2016).
Несмотря на важность задач тригонометрии в учебной программе средней школы по математике, исследования, касающиеся эффективного преподавания и обучения этому типу задач, относительно немногочисленны (Kendal and Stacey, 1998; Weber, 2005; Weber et al., 2008). Исследования показали, что студенты испытывают большие трудности, когда им нужно научиться решать оба типа задач тригонометрии (например, sin30 ° = 8/ x против cos60 ° = x /2) (Kendal and Stacey, 1998). . Чтобы решить эту проблему, Кендал и Стейси (1998) сравнили метод единичного круга и метод отношения с особым вниманием к трудностям студентов в применении навыков алгебраического преобразования для решения задач тригонометрии с местоимениями в качестве знаменателей.Для метода единичного круга авторы создали прямоугольный треугольник, который имеет те же свойства, что и данный прямоугольный треугольник. Требовалось несколько навыков для создания масштабного коэффициента, который позволил бы решать задачи тригонометрии с местоимениями в качестве знаменателей (например, выровнять два прямоугольных треугольника с точки зрения аналогичных свойств). Для метода отношения, напротив, на основе информации, представленной в прямоугольном треугольнике, студенты должны были выразить тригонометрическое соотношение в уравнении (например,g., cos60 ° = x /2), а затем решите относительно x . Результаты пост-тестирования показали, что метод единичного круга уступает методу отношения, независимо от типа задач тригонометрии (то есть sin30 ° = 8/ x или cos60 ° = x /2).
Хорошо известно, что научиться решать тригонометрические задачи, требующие навыков алгебраического преобразования, является повсеместной проблемой, которая по-прежнему сохраняется для многих учащихся средних школ (Weber, 2005).Эта трудность, возможно, усугубляется существующими учебными материалами, которые описаны и рекомендованы в учебниках (например, Vincent et al., 2012). Например, Винсент и др. (2012) подробно описали процедуру решения задач тригонометрии, в которых числителями являются местоимения (например, cos50 ° = x /8): умножьте обе стороны на 8, что включает одну операцию. Напротив, когда местоимение является знаменателем (например, sin30 ° = 12/ x ), авторы рекомендовали две операции: (i) умножить обе стороны на x и (ii) разделить обе стороны на sin30 °.Мы утверждаем, что представление процедуры решения обоих типов задач тригонометрии логично. Сказав это, однако, отметим, что Винсент и др. (2012) не пытались связать два типа задач тригонометрии с предварительным знанием студентами линейных уравнений с дробью.
Мы утверждаем, что важно учитывать степень, в которой обучение по аналогии, которое может опираться на предварительные знания учащегося о решении линейных уравнений с дробью, может способствовать эффективному решению задач тригонометрии, требующих навыков алгебраических преобразований.В то же время мы также рассматриваем эффективность обучения путем сравнения, чтобы различать различные процедуры решения для задач тригонометрии, которые имеют местоимение в качестве знаменателя (например, sin30 ° = 8/ x ) или числителей (например, cos60 ° = x /2). Мы обсудим процедуру решения линейных уравнений с дробью в следующем разделе, учитывая, что они связаны с задачами тригонометрии.
Процедура решения линейных уравнений
В соответствии с предыдущими исследованиями (e.г., Нгу и др., 2015; Ngu and Phan, 2016), мы используем реляционную и рабочую строку для описания процедуры решения линейного уравнения. Линия отношения относится к «количественному отношению, в котором левая часть уравнения приравнивается к правой части уравнения». Операционная строка, напротив, относится к использованию «операции, которая изменяет состояние уравнения, и, следовательно, такой процедурный шаг сохранит равенство уравнения». Например, обращаясь к формуле.1 на рисунке 1, строки 1 и 3 являются линиями отношений, тогда как, напротив, линия 2 — это рабочая линия. Более того, для этого примера мы используем обратный метод , чтобы проиллюстрировать процедуру решения уравнений, содержащих дробь (рисунок 1). Наше предыдущее исследование подтвердило использование обратного метода, а не метода баланса для решения линейных уравнений, особенно тех уравнений, которые включают несколько шагов решения (Ngu et al., 2015, 2018). Основное различие между обратным методом и балансовым методом в этом смысле заключается в оперативной строке (т.е.g., × 4 с обеих сторон по сравнению с ÷ 2 становится × 2) (см. рисунок 1 для обратного метода). Центральное место в природе обратного метода занимает сама обратная операция. Концептуализация обратной операции деления в данном случае — умножение (т.е. ÷ 2 становится × 2). По словам Динга (2016), интересно, что понимание обратной операции в младшие школьные годы может помочь в изучении математики в старших классах (например, дифференциация и интеграция в исчислении). Обратный метод, как мы выяснили из нашего существующего исследования, вероятно, вызовет меньшую когнитивную нагрузку, чем метод баланса, особенно для линейных уравнений, которые имеют несколько шагов решения.
Рисунок 1. Три варианта исходных примеров.
Задачи тригонометрии с местоимением в числителе
В этом разделе статьи подробно описывается наша основная посылка, которая «приравнивает» задачу тригонометрии, в которой числителем является местоимение (например, sin30 ° = x /6), с задачей линейного уравнения с дробью (например, х /4 = 3). Используя существующие исследования (Holyoak, 1984; Holyoak, Koh, 1987; Kurtz et al., 2001; Нгу и Йунг, 2012; Альфиери и др., 2013; Риттл-Джонсон и др., 2017; Matlen et al., 2020), мы предлагаем два основных этапа, чтобы облегчить аналогичное обучение для задач тригонометрии, которые включают навыки алгебраического преобразования. Теперь мы подробно обсудим каждый из приведенных ниже этапов.
Первый этап: три варианта исходных примеров
В соответствии с разработкой учебной программы и расписанием мы предполагаем, что студенты выучили бы линейные уравнения с дробью до того, как они изучат тему тригонометрии (Винсент и др., 2012). Такое упорядочение является преимуществом, поскольку оно позволяет преподавателям проводить параллель между изученной задачей, такой как линейное уравнение с дробью, x /4 = 3 (исходный пример), и новой задачей, такой как задача тригонометрии, sin30 ° = x /6 (целевая задача). Однако начинающие ученики не обязательно могут распознать сходство между исходным примером и целевой проблемой без поддержки учителя. Чтобы облегчить обучение по аналогии, первый этап включает мысленное представление трех вариантов исходных примеров в терминах процедуры решения (рис. 1).В данном случае цель состоит в том, чтобы помочь учащимся выбрать соответствующий исходный пример из трех различных вариантов исходных примеров, который затем может служить руководством для решения целевой проблемы.
Все три варианта исходных примеров представляют собой одношаговые уравнения, которые имеют одну рабочую строку и две строки отношения (Ngu and Phan, 2016, 2017). Мы помещаем три уравнения рядом, чтобы облегчить процесс картирования (Курц и др., 2001; Риттл-Джонсон и Стар, 2009; Матлен и др., 2020).Кроме того, мы помечаем шаги решения, например, строки 1, 2 и 3 в уравнении. 1 (Ngu and Phan, 2016, 2017), чтобы дать четкую подсказку (Richland et al., 2017), которая будет поощрять и облегчать активное сравнение. По сути, уравнение. 1 является основным примером источника, тогда как уравнения. 2 и 3 являются производными уравнения. 1. Уровень сложности трех вариантов увеличивается по сравнению с уравнениями 1–3. Уравнение 1 отличается от уравнения. 2 с точки зрения относительного положения пронумерала (т. Е. Левая сторона по сравнению с правой). Различная ориентация пронумерала может препятствовать прямому выравниванию реляционных элементов (Kurtz, Gentner, 2013; Matlen et al., 2020), и, следовательно, это отрицательно скажется на эффективности аналогичного сравнения. Напротив, отображение уравнений. 2 и 3 в той же ориентации, при которой местоимение расположено в правой части уравнения, позволило бы прямое выравнивание реляционных элементов и, таким образом, облегчило бы процесс сопоставления (Kurtz and Gentner, 2013). Следует отметить, что уравнение. 2 (например, 2 = x /5) соответствует целевой задаче (например, sin30 ° = x /6), учитывая, что обе задачи имеют местоимения, расположенные в правой части уравнения.Уравнение 3, напротив, отличается от уравнения 2, поскольку первое имеет десятичное число. Расположение местоимения в правой части уравнения и наличие десятичного числа считаются особенностями одношаговых уравнений; Эти особенности, как мы утверждаем, создают серьезные проблемы для многих студентов (Ngu and Phan, 2017).
В соответствии с рекомендацией Kurtz et al. (2001), чтобы облегчить рассуждение по аналогии, наша концептуализация требует, чтобы учащиеся выполнили три задачи (см. Рисунок 1).Наша цель — побудить студентов к углубленной обработке трех исходных примеров. Для выполнения первого задания учащиеся должны сравнить и описать сходства и различия между тремя уравнениями по отношению к Строке 1. Цель состоит в том, чтобы помочь учащимся провести глубокие аналогичные рассуждения, ведущие к идентификации общей структуры отношений во всей системе. три уравнения. Сравнение формул. 1 и 2, например, раскрывают различное расположение местоимения (т. Е., левая сторона против правой). Сравнение формул. 2 и 3, напротив, показали бы, что эти уравнения не демонстрируют взаимно однозначного соответствия с точки зрения атрибута элементов из-за присутствия десятичного числа в уравнении. 3. Следует отметить, что уравнение. 3 (1,2 = x /3) соответствует целевой задаче (sin30 ° = x /6), учитывая, что обе задачи имеют местоимения, расположенные в правой части уравнения, и что sin30 ° можно выразить в виде десятичной дроби. . Кроме того, как мы видим, математическая операция для строки 1 (например,g., ÷ 2 становится × 2 в уравнении. 1) одинаков во всех трех уравнениях. Таким образом, сравнив строку 1 трех уравнений, мы ожидаем, что учащиеся поймут, что эти три уравнения принадлежат к одной и той же категории линейных уравнений, что требует использования одной и той же математической операции для решения.
Что касается второй задачи, студенты должны генерировать параллельные шаги решения, такие как строки 2 и 3 уравнений. 2 и 3, которые совпадают со строками 2 и 3 в уравнении. 1 (Курц и др., 2001).Создание параллельных шагов решения для уравнений. 2 и 3 привлекут внимание студентов к взаимно однозначному соответствию со ссылкой на элементы взаимосвязи между тремя уравнениями. Третье задание, напротив, требует от студентов ответа на наводящий вопрос, например: «Почему может быть полезно сравнить уравнения. 1–3? » Мы ожидаем, что такая задача укрепит понимание учащимися сходства между тремя уравнениями с точки зрения схемы для процедуры совместного решения. Короче говоря, выполнив три задачи, мы ожидаем, что студенты сделают вывод и осознают, что три уравнения имеют схожую процедуру решения, несмотря на относительное положение местоимения (т.е., правая сторона против левой) и разница в формате числа (например, 2 против 1,2). После того, как учащиеся мысленно представили три варианта исходных примеров и вывели схему для общей процедуры решения, мы ожидаем, что они выберут соответствующий исходный пример (1,2 = x /3) и впоследствии будут использовать его для решения целевой задачи тригонометрии. (sin30 ° = x /6). Это будет вторым этапом в аналогичном процессе обучения.
Второй этап: сопоставление соответствующего исходного примера и целевой проблемы
Мы предполагаем, что учащиеся выучили бы определение тригонометрических соотношений до того, как научились решать задачи тригонометрии, требующие навыков алгебраического преобразования.Каждое тригонометрическое соотношение представляет собой число (т.е. дробь или десятичное число), которое определяется как одна сторона над другой стороной в прямоугольном треугольнике.
Как показано на рисунке 2, при размещении соответствующего исходного примера (1,2 = x /3) и целевой задачи (sin30 ° = x /6) рядом друг с другом нет необходимости предоставлять подсказку. для доступа к соответствующему примеру источника (Rittle-Johnson and Star, 2009; Matlen et al., 2020). И снова мы даем явную подсказку (Richland et al., 2017), в которых мы используем строки 1, 2, 3 и так далее для обозначения процедуры решения. Для первого задания учащиеся должны изучить шаги решения строк 1, 2 и 3 в соответствующем исходном примере, а затем сгенерировать параллельные шаги решения для целевой проблемы, которые обозначены строками 2, 3 и 4. Изучив целевую задачу, мы ожидаем, что студенты восстановят свои предварительные знания о выражении sin30 ° в десятичном числе, а затем заполнят Строку 2 целевой задачи. При этом студенты, вероятно, заметят сходство между строкой 1 соответствующего исходного примера (1.2 = x /3) и первый шаг решения целевой задачи (0,5 = x /6). Следовательно, посредством действий по сопоставлению мы утверждаем, что это будет направлять создание шагов решения для строк 3 и 4 целевых проблем, которые аналогичны шагам решения строк 2 и 3 соответствующего исходного примера. Соответственно, с нашей точки зрения, наилучшее согласование между соответствующим исходным примером и первым шагом решения целевой проблемы могло бы произойти, поскольку оба они имеют схожие объекты и отношения (Richland et al., 2006).
Рисунок 2. Процедура решения соответствующего исходного примера и целевой проблемы.
Сгенерировав недостающие параллельные шаги решения целевой проблемы, студенты переходят ко второму заданию. Мы рекомендуем использовать открытые вопросы в качестве дополнительных вспомогательных сигналов для размышлений, консолидации и понимания — например, «Почему может быть полезно сравнить соответствующий исходный пример и целевую проблему?» Мы утверждаем, что вопросы для размышления могут помочь учащимся глубоко проанализировать соответствующий исходный пример и целевую проблему (Rittle-Johnson and Star, 2007).В конечном итоге, выполнив обе задачи на рисунке 2, мы ожидаем, что студенты сделают вывод со ссылкой на схему для общей процедуры решения линейного уравнения с дробью (например, 1,2 = x /3) и первого шага решения Задача тригонометрии (например, 0,5 = x /6), при которой sin30 ° в цели заменен десятичным числом.
Сводка
Мы предлагаем мысленное представление трех вариантов исходных примеров, ведущее к выбору подходящего исходного примера для целевой проблемы.Наше предложение отличается от предыдущих исследований (Holyoak and Koh, 1987; Ngu and Yeung, 2012), которые предполагают мысленное представление только одного примера источника. Существующие рекомендации подчеркивают взаимно однозначное сопоставление случаев или примеров для облегчения обучения по аналогии (Alfieri et al., 2013; Goldwater and Schalk, 2016). Однако, в отличие от существующих рекомендаций, мы подчеркиваем общую процедуру решения между соответствующим исходным примером и первым шагом решения целевой проблемы (т. Е., подмножество целевой задачи).
В соответствии с концепцией обучения путем сравнения (Rittle-Johnson et al., 2017) мы помещаем соответствующий исходный пример и целевую задачу рядом. Мы также помечаем процедуру решения соответствующего исходного примера, а также отсутствующую процедуру параллельного решения целевой проблемы. Наша цель здесь, в этом анализе, — привлечь внимание студентов к важнейшей особенности шагов решения, которая составляет общую структуру между релевантным источником и целевой проблемой.Активное аналогичное сравнение будет результатом, когда студенты генерируют недостающие параллельные шаги решения для целевых задач. Предоставление наводящего вопроса в сочетании с генерацией недостающих параллельных шагов решения для целевой проблемы, с нашей точки зрения, поможет студентам вывести схему общей процедуры решения между соответствующим исходным примером и первым шагом решения. целевой проблемы.
В целом, мы утверждаем, что предложенные нами два основных этапа обеспечивают важные идеи, которые могут способствовать аналогичному обучению: (i) мысленное представление трех вариантов исходных примеров с последующим выбором среди них подходящего исходного примера и (ii) выполнение картографических действий между соответствующим исходным примером и целевой проблемой.Мы утверждаем, что наше предложение, в отличие от существующих исследований, информативно благодаря своей структурированной последовательности, позволяющей учащимся выстраивать свое понимание при решении задач тригонометрии, которые включают навыки алгебраического преобразования, используя как обучение по аналогии, так и обучение через концепции сравнения.
Исследование эффекта обращения опыта сделало акцент на конкретном взаимодействии между методом обучения и опытом учащегося в соответствующей области (Kalyuga et al., 2003). Вкратце, с акцентом на обратном эффекте опыта, следует отметить, что учащимся с разным уровнем знаний потребуются разные типы учебных методов. Соответственно, учащимся-экспертам не обязательно нужно мысленно представлять три варианта исходных примеров и выбирать соответствующий исходный пример и / или мысленно представлять целевую проблему плюс ее первый шаг решения. Обладая глубокими знаниями и пониманием линейных уравнений и тригонометрических соотношений, опытные ученики могут понять, что sin20 ° = x /6 аналогично 3 = x /8.Как только они поймут, что sin20 ° является десятичным числом, у них будет решение для sin20 ° = x /6. В самом деле, обнаружение сходства между sin20 ° = x /6 и 3 = x /8 приведет к тому, что опытные учащиеся получат выученную процедуру решения для решения 3 = x /8, которую затем можно использовать для решить sin20 ° = x /6.
Теоретическое обоснование, объясняющее процедуру решения задач тригонометрии с местоимением в качестве числителя, может быть применено к задачам тригонометрии, которые имеют местоимение в качестве знаменателя, при условии, что оба типа задач тригонометрии связаны с линейными уравнениями с дробью.В следующем разделе мы подробно исследуем решение задач тригонометрии, в знаменателе которых используются местоимения.
Задачи тригонометрии с местоимением в знаменателе
Как отмечалось ранее, относительное расположение местоимения (т. Е. Числитель против знаменателя) определяет сложность задачи тригонометрии. Шаги дифференциального решения отдают предпочтение задачам тригонометрии, в которых числитель является местоимением. В частности, задачи тригонометрии, в которых местоимение является знаменателем, более сложны, чем задачи тригонометрии, в которых местоимение используется в качестве числителя.В этом анализе у первого больше операционных линий (2 против 1) и линий отношений (3 против 2) по сравнению со вторым (см. Рисунки 2, 4). Обоснование для продвижения аналогичного обучения для двух типов задач тригонометрии, которые различаются расположением местоимения (то есть числитель против знаменателя), аналогично одинаково. Поэтому, как и в случае обучения тому, как решать тригонометрические задачи с местоимениями в качестве числителя (например, sin30 ° = x /6), мы утверждаем, что обучение решению cos60 ° = 4/ x потребует от учащихся вовлечения в следующем: (i) мысленно представить три варианта исходных примеров, а затем выбрать соответствующий исходный пример из этих исходных примеров (рисунок 3), (ii) сопоставить соответствующий исходный пример и целевую проблему (рисунок 4).
Рисунок 3. Три варианта исходных примеров.
Рисунок 4. Сопоставление релевантного исходного примера и целевой проблемы.
Три варианта исходных примеров представляют собой одношаговые линейные уравнения с двумя операционными линиями и тремя линиями отношения (рисунок 3). Уравнения 1, 2 аналогичны, за исключением расположения пронумерали (левая или правая сторона). Для уравнения. 2 расположение местоимения находится в правой части уравнения (4 = 32/ x ), что аналогично расположению местоимения для целевой задачи (Cos60 ° = 4/ x ) (Kurtz и Гентнер, 2013).Уравнения 2 и 3 аналогичны, за исключением десятичного числа для последнего. Как отмечалось ранее, наличие специальных функций (например, местоимение, расположенное в правой части уравнения, десятичное число и т. Д.) Усложняет одношаговые уравнения. Соответственно, три варианта линейных уравнений увеличивают сложность по сравнению с уравнениями. 1–3. Следует отметить, что обоснование выполнения задач на рисунках 3, 4 для изучения задач тригонометрии с местоимением в качестве знаменателя аналогично обоснованию выполнения задач на рисунках 1, 2 для изучения задач тригонометрии с местоимением в числителе. .Таким образом, мы не будем здесь отдельно обсуждать задачи на рисунках 3, 4.
Изучение процедуры решения двух типов задач тригонометрии (т. Е. Местоимение в числителе и местоимение в знаменателе) позволяет предположить, что есть несколько заметных различий. Как отмечалось ранее, например, разностное число реляционных (3 против 4) и операционных (1 против 2) благоприятствует задачам тригонометрии, в которых местоимение используется в числителе (Ngu and Phan, 2016). Следовательно, исходя из этого несоответствия, мы утверждаем, что научиться решать Cos60 ° = 4/ x будет сложнее, чем научиться решать sin30 ° = x /6 (т.е., см. рисунок 2 в сравнении с рисунком 4). Однако, сказав это, мы утверждаем, что предварительные знания (например, знания алгебраических преобразований) помогли бы учащемуся сократить количество реляционных линий. Например, обращаясь к рисунку 4, учащийся может пропустить Строку 2 соответствующего исходного примера (т. Е. 2,4 × x = 3) и соответствующую Строку 3 целевой задачи (т. Е. 0,5 × x = 4). . Следует отметить, что опытные ученики также могут распознать и понять, что cos40 ° = 5/ x и 3 = 12/ x похожи друг на друга.Как только они поймут, что cos60 ° является десятичным числом (т.е. 0,5), они бы поняли, что для решения обеих задач можно использовать один и тот же метод.
Как мы можем помочь учащимся различать два типа задач тригонометрии: местоимение в качестве числителя (например, sin30 ° = x /6) и местоимение в качестве знаменателя (например, cos60 ° = 4/ x ) )? Предыдущие исследования показали, что учащиеся средней школы лучше учатся, когда местоимение является числителем, а не знаменателем (Kendal and Stacey, 1998; Weber, 2005).Количество операционных и реляционных линий, как мы утверждали, отражает сложность процедуры решения. Как отмечалось ранее, задачи тригонометрии, в которых местоимение является числителем, имеют меньше рабочих (например, 1 против 2) и относительных (3 против 4) строк, чем задачи тригонометрии, в которых местоимение является знаменателем.
Различение двух типов задач тригонометрии
Концепция обучения путем сравнения, с нашей точки зрения, может помочь учащимся различать два типа задач тригонометрии.Мы предлагаем расположить два типа задач тригонометрии бок о бок и проинструктировать учащихся определять сходства и различия между ними (Rittle-Johnson et al., 2017). Например, со ссылкой на рисунок 5 мы могли бы попросить учащихся указать основные сходства и / или различия. На наш взгляд, существует ряд возможностей: (i) расположение местоимения (т. Е. Числитель против знаменателя), (ii) sin30 ° аналогичен cos50 °, оба из которых являются десятичными числами, (iii ) как только мы заменим sin30 ° или cos50 ° на десятичное число, оно превратится в линейное уравнение с дробью (например,g., рисунки 2, 4), (iv) различное количество реляционных линий (т. е. 2 против 3) и рабочих линий (т. е. 1 против 2) способствует решению задачи тригонометрии, в которой местоимение используется в качестве числителя, и ( v) обратный метод используется для решения обоих типов задач тригонометрии. После того, как учащиеся сравнили и определили сходства и различия между двумя типами задач тригонометрии, мы прогнозируем, что они заметили бы навыки дифференциально-алгебраического преобразования, используемые при решении этих двух типов задач тригонометрии.
Рисунок 5. Сравнение процедуры решения двух типов задач тригонометрии.
Для начинающих учеников, напротив, мы утверждаем, что в качестве основного шага для понимания было бы идеально сравнить линейные уравнения с дробью бок о бок, чтобы определить их сходства и / или различия (см. Рисунок 6). Одна примечательная характеристика для идентификации в данном случае связана с расположением местоимения (т.е.как числитель vs.знаменатель), который влияет на навыки алгебраического преобразования, необходимые для решения этих двух типов линейных уравнений. Мы утверждаем, что изучение и освоение этого базового шага может облегчить понимание задач тригонометрии, в которых местоимения используются как в числителе, так и в знаменателе. Например, сравнение cos60 ° = 2/ x и cos60 ° = x /2 бок о бок указывает на то, что основное различие заключается в расположении местоимения, то есть 2/ x vs х /2.Эта идентификация, в свою очередь, подготовит новичков к решению обоих типов задач тригонометрии — в данном случае sin30 ° = 8/ x против cos60 ° = x /2.
Рисунок 6. Сравнение уравнения с местоимением в качестве числителя и уравнения с местоимением в качестве знаменателя.
Обсуждение
Тригонометрия действительно является сложной темой для многих учащихся средних школ, особенно когда мы смешиваем проблемы тригонометрии с расположением местоимения (т.е., числитель против знаменателя) (Kendal and Stacey, 1998). Мы утверждаем, что можно противостоять этой распространенной проблеме, рассматривая использование теорий обучения — в данном случае обучения по аналогии и обучения по концепциям сравнения (Kurtz et al., 2001; Rittle-Johnson and Star, 2007; Alfieri et al. ., 2013). Наша концептуализация, подробно описанная в предыдущих разделах, предлагала мысленное представление трех вариантов исходных примеров. Из этих трех вариантов исходных примеров мы выбираем один релевантный исходный пример для целевой задачи.Мы выделяем сопоставление соответствующего исходного примера и первого шага решения целевой проблемы, чтобы достичь оптимального согласования между этими двумя проблемами. Наше предложение, в его совокупности, продвинуло изучение обучения по аналогии для его обсуждения на соответствующем исходном примере из трех вариантов исходных примеров. Это педагогическое утверждение отличается от предыдущего исследования (например, Holyoak and Koh, 1987), в котором акцент делается на использовании примера из одного источника. Более того, мы выделяем подмножество целевой проблемы, а не всю целевую проблему с целью реализации задачи сопоставления «один-к-одному» между соответствующим исходным примером и первым шагом решения целевой проблемы.Поэтому мы рекомендуем сравнение исходного примера и подмножества целевой задачи, чтобы облегчить обучение по аналогии.
В то же время, опираясь на важность обучения путем сравнения, мы рассматриваем возможность использования сравнения в контексте задач тригонометрии из-за их сходства и различий. Наша концептуализация, которую на сегодняшний день исследователи не изучили, является новаторской, поскольку в ней делается упор на одновременное сравнение различных типов задач тригонометрии.Это сравнение двух типов задач тригонометрии бок о бок, в частности, направлено на преодоление давних трудностей изучения задач тригонометрии, которые различаются из-за относительного положения местоимения (то есть числитель против знаменателя). Имея это в виду, мы призываем преподавателей рассмотреть возможность использования учебных практик, которые помогают учащимся распознавать и понимать два основных типа задач тригонометрии.
Как концепции обучения по аналогии и обучения по сравнению могут помочь нам в нашей педагогической практике в других областях математики? Рассмотрим в этом случае изучение задачи с выражением алгебры , которая представлена на рисунке 7.В данном случае фокус понимания связан с нашим предыдущим упоминанием сравнения, то есть параллельное сравнение проводится между «2 (3 + 5)» и « a (2 + b )». Мы постулируем, что выравнивание реляционных элементов может помочь учащимся понять логику манипулирования переменными. Например, как показано, 2 a просто означает, что 2 умножается на a (переменная). Исходя из этого, в средней школе ученик может сравнить два уравнения бок о бок и сделать вывод, что 2 равно a , а 5 равно b .В том же ключе мы утверждаем, что полезно рассматривать обучение путем сравнения в качестве учебного инструмента, который может облегчить изучение линейных уравнений . В качестве точки сравнения линейных уравнений, которые имеют дробную часть (например, рисунок 7), мы, например, отметим, что меньшее количество шагов решения (метод 1) более выгодно, поскольку это приведет к более низкой когнитивной нагрузке (Ngu et al., 2018 ).
Рисунок 7. Примеры обучения математике через обучение по аналогии и обучение по сравнению.
В заключение, как преподаватели, мы признаем важную тему тригонометрии. Более того, исходя из нашего профессионального опыта, мы признаем, что существует распространенная проблема, когда в задачах тригонометрии есть местоимения, которые действуют как числитель, так и знаменатель. Это различие (т.е. местоимение в качестве числителя и местоимение в качестве знаменателя), как мы утверждаем, является относительно уникальным, затрудняя понимание учащимися того, как решать различные типы задач тригонометрии, требующие навыков алгебраического преобразования.На основе наших существующих эмпирических исследований и запросов и открытий других исследователей мы получили педагогическую концепцию, которая могла бы помочь студентам понять сложность задач тригонометрии. В этом анализе, рассматривая эффективность обучения по аналогии и обучения по сравнению, мы предложили ученикам альтернативную последовательность шагов. Мы рекомендуем преподавателям реализовать и изучить возможности нашего предложения при обучении двум типам задач тригонометрии, которые различаются относительным расположением местоимения (т.е., числитель против знаменателя).
Авторские взносы
BN и HP были ответственны за концептуализацию и редактирование этой рукописи. Оба автора внесли свой вклад в статью и одобрили представленную версию.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы хотели бы выразить нашу признательность и благодарность двум рецензентам и редактору за их проницательные комментарии.
Список литературы
Альфиери, Л., Нокс-Малах, Т. Дж., И Шунн, К. Д. (2013). Обучение через сравнение случаев: метааналитический обзор. Educ. Psychol. 48, 87–113. DOI: 10.1080 / 00461520.2013.775712
CrossRef Полный текст | Google Scholar
Бехер Т. (1987). «Дисциплинарное формирование профессий», Академическая профессия , изд. Б. Р. Кларк (Беркли, Калифорния: Калифорнийский университет Press), 271–303.
Google Scholar
Блэкетт, Н.и Толл Д. О. (1991). «Гендер и разностороннее изучение тригонометрии с использованием компьютерного программного обеспечения», в Труды 15-го заседания Международной группы психологии математического образования , изд. Ф. Фурингетти (Италия: PME), 144–151.
Google Scholar
Бут, Дж. Л., Ланге, К. Э., Кёдингер, К. Р., Ньютон, К. Дж. (2013). Использование примеров задач для улучшения обучения студентов алгебре: различение правильных и неправильных примеров. Учиться. Instr. 25, 24–34. DOI: 10.1016 / j.learninstruc.2012.11.002
CrossRef Полный текст | Google Scholar
Камминс, Д. Д. (1992). Роль рассуждений по аналогии в индукции категорий проблем. J. Exp. Psychol. Учиться. Mem. Cogn. 18, 1103–1124. DOI: 10.1037 / 0278-7393.18.5.1103
CrossRef Полный текст | Google Scholar
Дин, М. (2016). Возможности учиться: обратные отношения в учебниках США и Китая. Math.Считать. Учиться. 18, 45–68. DOI: 10.1080 / 10986065.2016.1107819
CrossRef Полный текст | Google Scholar
Дуркин, К., Риттл-Джонсон, Б. (2012). Эффективность использования неправильных примеров для поддержки изучения десятичной величины. Учиться. Instr. 22, 206–214. DOI: 10.1016 / j.learninstruc.2011.11.001
CrossRef Полный текст | Google Scholar
Гентнер Д. (1983). Структурное отображение: теоретическая основа для аналогии. Cogn.Sci. 7, 155–170. DOI: 10.1207 / s15516709cog0702_3
CrossRef Полный текст | Google Scholar
Гентнер Д., Левенштейн Дж. И Томпсон Л. (2003). Изучение и передача: общая роль аналогового кодирования. J. Educ. Psychol. 95, 393–405. DOI: 10.1037 / 0022-0663.95.2.393
CrossRef Полный текст | Google Scholar
Große, C. S., and Renkl, A. (2007). Обнаружение и исправление ошибок в отработанных примерах: может ли это способствовать результатам обучения? Учиться.Instr. 17, 612–634. DOI: 10.1016 / j.learninstruc.2007.09.008
CrossRef Полный текст | Google Scholar
Холиоук, К. Дж. (1984). «Аналогичное мышление и человеческий интеллект», в Advances in the Psychology of Human Intelligence , ed. Р. Дж. Стернберг (Хиллсдейл, Нью-Джерси: Эрлбаум), 199–230.
Google Scholar
Калюга С., Эйрес П., Чендлер П. и Свеллер Дж. (2003). Эффект отмены экспертизы. Educ. Psychol. 38, 23–31.DOI: 10.1207 / s15326985ep3801_4
CrossRef Полный текст | Google Scholar
Кендал М. и Стейси К. (1998). Обучение тригонометрии. Austral. Математика. Учат. 54, 34–39.
Google Scholar
Курц, К. Дж., И Гентнер, Д. (2013). Обнаружение аномальных свойств в сложных стимулах: роль структурированного сравнения. J. Exp. Psychol. Прил. 19, 219–232. DOI: 10.1037 / a0034395
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Курц, К.J., Miao, C.-H., и Gentner, D. (2001). Обучение с помощью аналогичного бутстрэппинга. J. Learn. Sci. 10, 417–446. DOI: 10.1207 / s15327809jls1004new_2
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., Чунг, С. Ф., Юнг, А. С. (2015). Познавательная нагрузка в алгебре: интерактивность элементов при решении уравнений. Educ. Psychol. 35, 271–293. DOI: 10.1080 / 01443410.2013.878019
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х.П. (2016). Распаковка сложности линейных уравнений с точки зрения теории когнитивной нагрузки. Educ. Psychol. Ред. 28, 95–118. DOI: 10.1007 / s10648-015-9298-2
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х. П. (2017). Будет ли трудной задачей для учащихся 8-х классов научиться решать одношаговые уравнения? Внутр. J. Math. Educ. Sci. Technol. 48, 876–894. DOI: 10.1080 / 0020739x.2017.1293856
CrossRef Полный текст | Google Scholar
Нгу, Б.Х., Фан, Х. П., Йунг, А. С., Чунг, С. Ф. (2018). Управление интерактивностью элементов при решении уравнений. Educ. Psychol. Rev. 30, 255–272. DOI: 10.1007 / s10648-016-9397-8
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Йунг, А. С. (2012). Содействие передаче по аналогии: многокомпонентный подход к решению задач алгебры в контексте химии. Contemp. Educ. Psychol. 37, 14–32. DOI: 10.1016 / j.cedpsych.2011.09.001
CrossRef Полный текст | Google Scholar
Новик, Л.Р. и Холиоук К. Дж. (1991). Решение математических задач по аналогии. J. Exp. Psychol. Учиться. Mem. Cogn. 17, 398–415.
Google Scholar
Ортон, Дж. М., Анггоро, Ф. К., и Джи, Б. Д. (2012). Взаимное сопоставление сравнения облегчает абстрагирование и передачу сложной научной концепции. Educ. Stud. 38, 473–477. DOI: 10.1080 / 03055698.2011.643104
CrossRef Полный текст | Google Scholar
Рид, С. К. (1987). Модель отображения структуры для текстовых задач. J. Exp. Psychol. Учиться. Mem. Cogn. 13, 124–139. DOI: 10.1037 / 0278-7393.13.1.124
CrossRef Полный текст | Google Scholar
Рид, С. К. (1989). Ограничения на абстракцию решений. J. Educ. Psychol. 81, 532–540. DOI: 10.1037 / 0022-0663.81.4.532
CrossRef Полный текст | Google Scholar
Рид, С. К., Демпстер, А., Эттингер, М. (1985). Полезность аналогичных решений для решения словесных задач алгебры. J. Exp.Psychol. Учиться. Mem. Cogn. 11, 106–125. DOI: 10.1037 / 0278-7393.11.1.106
CrossRef Полный текст | Google Scholar
Рид, С. К., Стебик, С., Коми, Б., и Кэрролл, Д. (2012). Обнаружение сходств и различий в решениях словесных задач. J. Educ. Psychol. 104, 636–646. DOI: 10.1037 / a0027181
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., Беголли, К. Н., Симмс, Н., Фраузель, Р. Р., Лайонс, Э. А. (2017). Поддерживающие математические дискуссии: роли сравнения и познавательная нагрузка. Educ. Psychol. Rev. 29, 41–53. DOI: 10.1007 / s10648-016-9382-2
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., и МакДонаф, И. М. (2010). Обучение по аналогии: различение потенциальных аналогов. Contemp. Educ. Psychol. 35, 28–43. DOI: 10.1016 / j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., и МакДонаф, И. М. (2010). Обучение по аналогии: различение потенциальных аналогов. Contemp. Educ. Psychol. 35, 28–43. DOI: 10.1016 / j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., Моррисон, Р. Г., и Холиоук, К. Дж. (2006). Развитие у детей рассуждений по аналогии: выводы из задач по аналогии со сценой. J. Exp. Детская психол. 94, 249. DOI: 10.1016 / j.jecp.2006.02.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б., и Стар, Дж. Р. (2007).Облегчает ли сравнение методов решения концептуальные и процедурные знания? Экспериментальное исследование по обучению решению уравнений. J. Educ. Psychol. 99, 561–574. DOI: 10.1037 / 0022-0663.99.3.561
CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б. и Стар, Дж. Р. (2009). По сравнению с чем? Влияние различных сравнений на концептуальные знания и процедурную гибкость при решении уравнений. J. Educ. Psychol. 101, 529–544. DOI: 10.1037 / a0014224
CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., Дуркин, К. (2017). «Сила сравнения в обучении математике: экспериментальные данные из классных комнат», в Mathematical Cognition and Learning: Acquisition of Complex Arithmetic Skills and High Order Mathematics Concepts , eds DC Geary, DB Berch, and KM Koepke (Waltham, MA: Эльзеви), 273–295. DOI: 10.1016 / b978-0-12-805086-6.00012-6
CrossRef Полный текст | Google Scholar
Росс, Б.Х. (1984). Напоминания и их влияние на обучение когнитивным навыкам. Cogn. Psychol. 16, 371–416. DOI: 10.1016 / 0010-0285 (84)
-8
CrossRef Полный текст | Google Scholar
Росс, Б. Х., и Кеннеди, П. Т. (1990). Обобщение использования предыдущих примеров при решении проблем. J. Exp. Psychol. Учиться. Mem. Cogn. 16, 42–55. DOI: 10.1037 / 0278-7393.16.1.42
CrossRef Полный текст | Google Scholar
Стар, Дж. Р., Поллак, К., Дуркин, К., Риттл-Джонсон, Б., Линч, К., Ньютон, К. и др. (2015). Учимся на сравнении в алгебре. Contemp. Educ. Psychol. 40, 41–54. DOI: 10.1016 / j.cedpsych.2014.05.005
CrossRef Полный текст | Google Scholar
Винсент, Дж., Прайс, Б., Карузо, Н., Ромерил, Г., и Тайнан, Д. (2012). MathsWorld 9 Австралийский учебный план. Южная Ярра, Виктория: Макмиллан.
Google Scholar
Вебер, К. (2005). Понимание учащимися тригонометрических функций. Math. Educ. Res. J. 17, 91–112. DOI: 10.1007 / bf03217423
CrossRef Полный текст | Google Scholar
Вебер К., Нотт Л. и Эвиттс Т. А. (2008). Обучение тригонометрическим функциям: уроки, извлеченные из исследований. Math. Учат. 102, 144–150.
Google Scholar
Циглер, Э., Стерн, Э. (2014). Отложенные преимущества изучения элементарных алгебраических преобразований посредством контрастных сравнений. Учиться. Instr. 33, 131–146.DOI: 10.1016 / j.learninstruc.2014.04.006
CrossRef Полный текст | Google Scholar
тригонометрия | Что нового
Следующий набор заметок: Примечания 1.
Известно, что Кронекер сказал: «Бог создал натуральные числа; все остальное — дело рук человека ». Истинность этого утверждения (буквального или иного) спорна; но, безусловно, можно рассматривать другие стандартные системы счисления как (повторяющиеся) пополнения натуральных чисел в различных смыслах. Например:
Эти описания стандартных систем счисления элегантны и концептуальны, но не совсем подходят для построения систем счисления некруглым способом на более примитивных основаниях.Например, нельзя полностью определить действительные числа с нуля как метрическое завершение рациональных чисел, потому что определение самого метрического пространства требует понятия действительных чисел! (Конечно, можно построить другие средства, например, используя дедекиндовы разрезы или используя равномерные пространства вместо метрических пространств.) Определение комплексных чисел как алгебраического завершения вещественных чисел не страдает от такой некруглости. вопрос, но для работы с этим определением на начальном этапе требуется определенный объем теории поля.Таким образом, для целей быстрого построения комплексных чисел более традиционно сначала определять как квадратичное расширение действительных чисел, а точнее как расширение, образованное присоединением квадратного корня из действительных чисел, то есть решение уравнение . Не сразу очевидно, что это расширение на самом деле алгебраически замкнуто; это содержание известной фундаментальной теоремы алгебры, которую мы докажем позже в этом курсе.
Два эквивалентных определения — как алгебраическое замыкание и как квадратичное расширение вещественных чисел соответственно — раскрывают важные особенности комплексных чисел в приложениях.Поскольку он алгебраически замкнут, все многочлены над комплексными числами полностью расщепляются, что приводит к хорошей спектральной теории как для конечномерных матриц, так и для бесконечномерных операторов; в частности, ожидается возможность диагонализации большинства матриц и операторов. Применение этой теории к обыкновенным дифференциальным уравнениям с постоянными коэффициентами приводит к единой теории таких решений, в которой поведение ОДУ с действительными переменными, такое как экспоненциальный рост или спад, полиномиальный рост и синусоидальные колебания, становятся аспектами одного объекта, комплексного экспоненциального ( или, в более общем смысле, матрица экспоненты).Применяя эту теорию в более общем плане для диагонализации произвольных трансляционно-инвариантных операторов над некоторой локально компактной абелевой группой, мы приходим к анализу Фурье, который, таким образом, наиболее естественно выражается в терминах комплекснозначных функций, а не действительных. Если отказаться от предположения, что основная группа является абелевой, вместо этого откроется теория представлений унитарных представлений, которую проще изучать, чем действительный аналог ортогональных представлений.По тесно связанным причинам теория комплексных групп Ли проще, чем теория вещественных групп Ли.Между тем, тот факт, что комплексные числа являются квадратичным расширением вещественных чисел, позволяет рассматривать комплексные числа геометрически как двумерную плоскость над реалами (плоскость Аргана). В то время как точечная особенность на реальной прямой разъединяет эту линию, точечная особенность на плоскости Аргана оставляет остальную часть плоскости связанной (хотя, что важно, проколотая плоскость больше не является односвязной).Как мы увидим, этот факт приводит к тому, что особенности в комплексных аналитических функциях ведут себя лучше, чем особенности реальных аналитических функций, что в конечном итоге приводит к мощному исчислению вычетов для вычисления комплексных интегралов. Примечательно, что это исчисление в сочетании с типичной техникой комплексных переменных смещения контура также можно использовать для вычисления некоторых (хотя, конечно, не всех) определенных интегралов от действительных -значных функций, которые было бы гораздо сложнее вычислить. чисто методами вещественных переменных; это яркий пример известного изречения Адамара о том, что «кратчайший путь между двумя истинами в реальной области проходит через сложную область».
Другой важной геометрической особенностью плоскости Аргана является угол между двумя касательными векторами к точке на плоскости. Как оказалось, операция умножения на комплексный скаляр сохраняет величину и ориентацию таких углов; тот же факт верен для любого невырожденного комплексного аналитического отображения, что можно увидеть, выполнив разложение Тейлора до первого порядка. Этот факт тесно связывает изучение сложных отображений с изучением конформной геометрии плоскости (и в более общем плане двумерных поверхностей и областей).В частности, можно использовать сложные аналитические отображения для конформного преобразования одной двумерной области в другую, что, в частности, приводит к знаменитой теореме об отображении Римана и классификации римановых поверхностей.
Если Тейлор расширяет комплексные аналитические отображения до второго порядка, а не до первого порядка, обнаруживается еще одно важное свойство этих отображений, а именно то, что они гармоничны. Этот факт делает класс сложных аналитических карт чрезвычайно жестким и хорошо анализируемым; действительно, вся теория эллиптических уравнений в частных производных теперь вступает в игру, давая такие полезные свойства, как эллиптическая регулярность и принцип максимума.Фактически, благодаря магии исчисления вычетов и сдвига контура, мы уже получили эти свойства для отображений, которые являются просто комплексно дифференцируемыми, а не комплексно аналитическими, что приводит к поразительному факту, что комплексные дифференцируемые функции автоматически аналитичны (в отличие от реальных -переменный случай, когда реальные дифференцируемые функции могут быть очень далеки от аналитических).
Геометрическая структура комплексных чисел (и в более общем плане комплексных многообразий и комплексных многообразий) в сочетании с алгебраическим замыканием комплексных чисел приводит к прекрасному предмету комплексной алгебраической геометрии , который мотивирует гораздо более общую теорию развит в современной алгебраической геометрии.Однако мы не будем здесь развивать алгебро-геометрические аспекты комплексного анализа.
И последнее, но не менее важное: из-за хорошего поведения рядов Тейлора в комплексной плоскости комплексный анализ представляет собой отличную среду для манипулирования различными производящими функциями, в частности рядами Фурье (которые можно рассматривать как граничные значения мощности (или Лорана). ) серии), а также серии Дирихле. Теория контурного интегрирования представляет собой очень полезный словарь между асимптотическим поведением последовательности и сложным аналитическим поведением рядов Дирихле или Фурье, особенно в отношении его полюсов и других особенностей.Оказывается, это особенно удобный словарь в аналитической теории чисел, например, связывающий распределение простых чисел с дзета-функцией Римана. В настоящее время многие результаты аналитической теории чисел, впервые полученные посредством комплексного анализа (например, теорема о простых числах), также могут быть получены с помощью других методов «вещественных переменных»; однако комплексно-аналитическая точка зрения по-прежнему чрезвычайно ценна и поучительна.
Мы часто будем касаться многих из этих связей с другими областями математики в этих конспектах лекций.Тем не менее, это в основном второстепенные замечания, предназначенные для обеспечения контекста, и, безусловно, можно пропустить большинство из этих касательных и при желании сосредоточиться исключительно на материале сложного анализа в этих примечаниях.
Примечание: комплексный анализ — это очень наглядный предмет, и при его изучении нужно рисовать много картинок. Однако я не планирую помещать в эти заметки слишком много изображений, отчасти потому, что это несколько неудобно делать в этом блоге с технической точки зрения, а также потому, что изображения, которые вы рисуете самостоятельно, вероятно, будут для вас гораздо более полезными. чем картинки, предоставленные кем-то другим.
Читать оставшуюся часть записи »
Развитие тригонометрии | Encyclopedia.com
ОбзорДаже во времена древних вавилонян и египтян теоремы о соотношении сторон подобных треугольников широко использовались для измерения, построения и для попытки понять движение в небесах. Греки начали систематическое изучение углов и длин, связанных с этими углами, снова на службе астрономии.История тригонометрии тесно связана с историей астрономии, являющейся ее основным математическим инструментом. Тригонометрия со временем станет отдельным разделом математики, как изучение современных тригонометрических функций.
ПредпосылкиЛюди древних цивилизаций в Египте и Месопотамии смотрели в небеса. Небеса сказали людям, когда сажать, а когда собирать урожай. Чтобы отметить важные события, людям нужен был годовой календарь.Наблюдение за положением Солнца необходимо для составления календаря. Чтобы узнать время суток, нужно смотреть на длину теней. Эти длины теней измеряются с помощью вертикальной палки в земле и измерения длины ее тени. Тригонометрия берет свое начало в вычислении этих измерений. Действительно, современное градусное измерение дуг и углов берет свое начало в вавилонских измерениях.
Знаменитая вавилонская глиняная табличка, ныне известная как Плимптон 322, датируется примерно 1700 годом до нашей эры.c. Эта табличка наиболее известна своим списком троек Пифагора, списком сторон и соответствующей гипотенузой прямоугольных треугольников. Менее известен тот факт, что один из столбцов на планшете содержит квадрат отношения диагонали к одной из сторон, и по мере движения вниз по столбцу это отношение уменьшается почти равномерно. Если посмотреть на квадраты этих отношений как на квадрат косеканса соседнего угла, то этот угол увеличивается почти равномерно от примерно 45 ° до 58 °.Используется ли Plimpton 322 частично как тригонометрический стол?
Большая часть наших знаний о ранней египетской математике получена из папируса Райнда (или Ахмеса). Папирус был куплен в 1858 году в курортном городке Нила шотландцем Александром Генри Райндом, отсюда и его название. Его иногда называют папирусом Ахмеса в честь писца, переписавшего его около 1650 г. до н. Э. Задачи с 56 по 60 этого папируса иллюстрируют происхождение тригонометрии в Древнем Египте. Эти проблемы касаются квадратных пирамид, которые, естественно, очень интересовали египтян.При построении пирамиды грани должны выдерживать постоянный наклон. Слово seqt или seked часто встречается в этих задачах, и для современного читателя оно означает отношение горизонтального расстояния наклонной линии от вертикали к высоте, во многом подобно тому, как проход на подъем в современное понятие уклона. Можно также представить себе seqt как котангенс угла между основанием пирамиды и ее гранью. Однако египтяне не думали о seqt таким образом.Для них это было просто длиной. Тригонометрические функции как отношения (в том виде, в каком мы их понимаем сегодня) в то время еще не появились.
Использование геометрии подобных прямоугольных треугольников, а не тригонометрии, также является особенностью математики ранней Греции. Фактически, эти идеи могли прийти непосредственно из вавилонской цивилизации. Говорят, что Фалес Милетский (ок. 624-547 до н. Э.) Вычислил высоту пирамиды, сравнив длину ее тени с длиной вертикального стержня.Книга II Евклида Элементы (ок. 300 г. до н. Э.) Содержит предложения, эквивалентные закону косинусов, хотя и на геометрическом языке. Теорема Архимеда (ок. 287–212 до н. Э.) О разорванной хорде может быть переформулирована как формула для синуса разности двух углов.
Греческие астрономы также работали с этими геометрическими инструментами. Аристарх Самосский (310-230 до н.э.) заметил, что, когда Луна наполовину полная, угол между линиями взгляда на Солнце и Луну почти прямой, 87 °.Используя это наблюдение, Аристарх подсчитал, что Солнце было в 18-20 раз дальше от Земли, чем Луна. Хотя сегодня для нас это было бы проблемой тригонометрии (используя прямоугольный треугольник 3 ° -87 ° -90 °, состоящий из Земли, Луны и Солнца), для Аристарха это была проблема геометрии. Используя эти измерения расстояний, Аристарх также смог найти отношение размеров Солнца и Луны к Земле. Чтобы рассчитать размеры Солнца и Луны, нужен был размер Земли. Это измерение было предоставлено Эратосфеном Киренским (276-195 гг. До н. Э.)c.), который нашел его, используя отношения между углами и дугами окружности и углами и хордами окружности.
Эти отношения между углами, дугами и хордами составляют основу наблюдательной астрономии. Они помогают дать метод измерения положения звезд и планет на небе или, альтернативно, на «небесной сфере», границе сферической вселенной, с Землей в ее центре, которая вращается вокруг Земли и где объекты в небо расположены. Вавилоняне были ответственны за эту «эклиптическую систему» определения местоположения небесных тел, и греческие астрономы также использовали ее.Для работы с этой системой нужна сферическая тригонометрия. Однако, чтобы понять это, сначала необходимо было понять тригонометрию плоскости. Например, теорема Менелая дает взаимосвязь между дугами больших окружностей на сфере и доказывается, сначала показывая, как взаимосвязь работает с сегментами на плоскости.
Само понятие тригонометрии возникло у астронома Гиппарха из Вифинии (190-120 гг. До н.э.). Начнем с того, что Гиппарх представил грекам вавилонское градусное измерение углов и дуг окружностей.Он также был первым, кто дал таблицу длин, связанных с углами, которая позволила бы решить плоские треугольники. Гиппарх создал эту таблицу для выполнения своих астрономических расчетов. К сожалению, таблица Гиппарха утеряна, но по другим работам, относящимся к нему и его работам, мы можем восстановить, как должен был выглядеть его стол.
Гиппарх считал, что каждый треугольник вписан в круг с фиксированным радиусом. Это означало, что каждая сторона треугольника представляет собой хорду круга.Единственной тригонометрической функцией в тригонометрии Гиппарха была функция хорды, теперь сокращенно crd (α), где α — центральный угол напротив хорды. В своей таблице Гиппарх рассчитал длину хорды каждого угла от 7,5 ° до 180 ° с шагом 7,5 °. Эти длины хорды также меняются в зависимости от радиуса окружности, поэтому радиус необходимо было зафиксировать. Гиппарх использовал фиксированный радиус R = 57 + 18/60. Этот радиус получен из расчета 2π R = 360 × 60, что соответствует количеству минут на окружности круга.При вычислении используется приближение 3 + 8/60 + 30/60 2 = 3,1416 … для π. Это означает, что хордовая функция связана с современной синусоидальной функцией соотношением crd (α) = 2 R sin (α / 2). Обратите внимание, что хорда — это длина, а не соотношение длин.
Гиппарх начал свою таблицу аккордов с хорды под углом 60 °. Этот угол создает равносторонний треугольник с вершиной в центре круга, поэтому длина хорды равна радиусу круга.Отсюда Гиппарх использовал два геометрических результата: crdα 2 (180 — α) = (2 R ) 2 — crdα 2 (α), что является просто повторением теоремы Пифагора; и crdα 2 (α / 2) = R (2 R — crd (180 — α)), что происходит от подобия прямоугольного треугольника, вписанного в полукруг, с треугольниками, образованными путем отбрасывания перпендикуляра от вершина гипотенузы.
После Гиппарха следующей крупной фигурой в развитии тригонометрии был астроном Менелай Александрийский (ок.объявление. 100), написавшего аккорд круга, , который мы потеряли, и Sphaerica, — работу по сферической тригонометрии. В Sphaerica, Менелай устанавливает множество утверждений для сферических треугольников (образованных дугами больших окружностей на сфере), которые аналогичны утверждениям для плоских треугольников. Теорема Менелая появляется в этой работе, и эта теорема является фундаментальной для области сферической тригонометрии.
Кульминация греческой тригонометрии происходит в работе, которая также является кульминацией греческой астрономии, Syntaxis Mathematikos (Математический сборник) Клавдия Птолемея, более известного у Птолемея (ок.объявление. 100-178). Много веков спустя исламские ученые называли этот труд al-magisti, «величайший», и это имя, переведенное на латынь, стало Almagest, , под которым он известен с тех пор. Птолемей понял, что хорда в круге связана со сторонами как сферических, так и плоских треугольников, поэтому его работа потребовала от него построения таблицы аккордов.
Таблица Птолемея была более полной, чем таблица Гиппарха. Таблица Птолемея рассчитывала хорды дуги от 0.От 5 ° до 180 ° с шагом 0,5 °. Птолемей использовал значение 60 для своего фиксированного радиуса. Птолемей начал свою таблицу с вычисления хорд, используя правильные многоугольники, вписанные в круг радиуса 60. Сторона правильного треугольника дает crd (120 °), сторона правильного квадрата дает crd (90 °), правильный пятиугольник, crd ( 72 °) и правильный десятиугольник crd (36 °). Затем Птолемей разработал формулы для crd (180 — α), crd (α / 2) и crd (α ± β) (последний с использованием теоремы Птолемея) и использовал эти формулы для завершения своей таблицы. Эта таблица позволила Птолемею решать плоские треугольники так же, как тригонометрические таблицы теперь позволяют нам решать плоские треугольники.Он также мог рассчитать значения, необходимые в эксцентрической модели неба, где Солнце вращается вокруг Земли не по кругу, а по кругу с центром вдали от Земли. С помощью этого расчета Птолемей мог предсказать положение Солнца и других небесных объектов на небе в разное время. Хотя тригонометрия Птолемея будет модифицирована математиками на Востоке, его концепции астрономии сохранялись еще 1400 лет, до времен Коперника (1473-1543).
Во времена Птолемея северная Индия была завоевана и управлялась Кушанской империей, установившей торговые пути с Римом.Историки считают, что именно этими путями в Индию была передана греческая астрономия. Правители Гуптов в Индии (с четвертого по шестой века н.э.) также поддерживали регулярное общение с наследниками греко-римской культуры. Самая ранняя известная индуистская работа по тригонометрии — это Paitāmmaha Siddhānta, , написанная в начале пятого века. Это произведение содержит таблицу полуккордов, или на санскрите джья-ардха. Интересно, что это слово в конечном итоге стало нашим современным термином синус. Слово джья-ардха было сокращено до джья или джива. Когда это было позже переведено на арабский исламскими учеными, они перевели его как джиба, и написали jb, , поскольку гласные не были написаны. Позже это было интерпретировано как jaib, , что означает «грудь» или «складка», и было переведено на латынь как sinus. Эта таблица полуаккордов, кажется, произошла от таблицы аккордов Гиппарха, поскольку в ней используется то же значение радиуса, что и у него.
Первой работой, в которой синусоида была упомянута (хотя все еще как длина в круге с фиксированным радиусом, а не как отношение длин), была Aryabhatiya индуистского астронома Арьябхата I, написанная около 510 года. Его таблица синусов была на самом деле таблица значений R sin (α). В завершении таблицы Арьябхате помогли разработать эквивалент современной идентичности sin [( n + 1) α] — sin ( n α) sin ( n α) sin [( n — 1) α] -1/225 sin ( n α).Индусские таблицы строятся с использованием таких рекурсивных соотношений для синуса. Арьябхата также ввел функции косинуса и версин, опять же как длины, а не отношения; используя современные R cos (α) для их функции косинуса. Версия versine или функция «проверенного синуса» определяется как vers (α) = R (1 — cos (α)). И снова упор в этой работе был сделан на использование тригонометрии в астрономии и создании календарей.
Эти греческие и индуистские сочинения были переведены на арабский язык в восьмом веке и позже.Исламские астрономы способствовали изучению тригонометрии как в астрономических, так и в религиозных целях, поскольку мусульмане должны знать направление на Мекку из любого места, где они окажутся. Эти работы, в свою очередь, вернулись на Запад, и тригонометрия превратилась в раздел математики, изучаемый сегодня.
УдарС развитием тригонометрии астрономия превратилась из наблюдательной качественной науки в предсказательную количественную науку.Это преобразование продвинуло идею о возможности математического описания природных явлений. Впервые данные наблюдений можно было преобразовать в математические модели. Птолемей Альмагест был вехой в этом отношении, служа для прикладной математики той же ролью, которую Евклидовы Элементы сыграли для теоретической математики. Математика применялась для решения задач и раньше, но тригонометрия была разработана для прикладной математики и продолжает делать это все более и более изощренными способами.
Хотя тенденция к применению приложений совпала с упадком греческой математики, эти приложения привлекли внимание индуистских и исламских ученых, главным образом потому, что они имели отношение к религии и составлению календаря. Математика в этих двух культурах находилась на подъеме, и благодаря им большая часть наследия классических греков была возвращена на Запад.
По мере того как тригонометрия и астрономия развивались как наука о прогнозировании как на Востоке, так и на Западе, было важно, чтобы таблицы вычислений становились все более и более точными, а вычисления — менее громоздкими.
- sin t = 0. Вращающаяся точка Рt имеет нулевую ординату в моменты времени t—0, π, 2 π, …, а также t— π, —2 π…..В общем виде множество этих значений можно записать в виде t=πk, k ∈ Z. Таким образом, решением уравнения sin t = 0 будут числа t = πk, k ∈ Z.

 7.
Функция y = sin x
7.
Функция y = sin x