Всероссийская олимпиада школьников по истории — олимпиады для школьников — Учёба.ру
Высшее образование онлайн
Федеральный проект дистанционного образования.
Я б в нефтяники пошел!
Пройди тест, узнай свою будущую профессию и как её получить.
Химия и биотехнологии в РТУ МИРЭА
120 лет опыта подготовки
Международный колледж искусств и коммуникаций
МКИК — современный колледж
Английский язык
Совместно с экспертами Wall Street English мы решили рассказать об английском языке так, чтобы его захотелось выучить.
15 правил безопасного поведения в интернете
Простые, но важные правила безопасного поведения в Сети.
Олимпиады для школьников
Перечень, календарь, уровни, льготы.
Первый экономический
Рассказываем о том, чем живёт и как устроен РЭУ имени Г.В. Плеханова.
Билет в Голландию
Участвуй в конкурсе и выиграй поездку в Голландию на обучение в одной из летних школ Университета Радбауд.
Цифровые герои
Они создают интернет-сервисы, социальные сети, игры и приложения, которыми ежедневно пользуются миллионы людей во всём мире.
Работа будущего
Как новые технологии, научные открытия и инновации изменят ландшафт на рынке труда в ближайшие 20-30 лет
Профессии мечты
Совместно с центром онлайн-обучения Фоксфорд мы решили узнать у школьников, кем они мечтают стать и куда планируют поступать.
Экономическое образование
О том, что собой представляет современная экономика, и какие карьерные перспективы открываются перед будущими экономистами.
Гуманитарная сфера
Разговариваем с экспертами о важности гуманитарного образования и областях его применения на практике.
Молодые инженеры
Инженерные специальности становятся всё более востребованными и перспективными.
Табель о рангах
Что такое гражданская служба, кто такие госслужащие и какое образование является хорошим стартом для будущих чиновников.
Карьера в нефтехимии
Нефтехимия — это инновации, реальное производство продукции, которая есть в каждом доме.
Всероссийская олимпиада школьников
ТЕЛЕФОН ГОРЯЧЕЙ ЛИНИИ ПО ВОПРОСАМ ОРГАНИЗАЦИИ И ПРОВЕДЕНИЯ ОЛИМПИАДЫ — 411-93-18 (ответственный Соппа Ольга Валерьевна)
Подробная информация об организации и проведении Всероссийской олимпиады школьников размещена в разделе «Методический кабинет (МО по предметам)
2021-2022 учебный год
Регламентирующие документы всероссийского уровня
Методические рекомендации по проведению школьного и муниципального (районного) этапов Всероссийской олимпиады школьников на 2021-2022 учебный год
Порядок проведения Всероссийской олимпиады школьников (Приказ Министерство Просвещения от 27. 11.2020 № 678)
11.2020 № 678)
Регламентирующие документы регионального уровня
Распоряжением Комитета по образованию Санкт-Петербурга об утверждении организационно-технологической модели и графика проведения районного этапа Всероссийской олимпиады школьников от 21.10.2021 года № 2906-р с 12 ноября 2021 года
Распоряжение Комитета по образованию «О проведении этапов Всероссийской олимпиады школьников в Санкт-Петербурге от 18.08.2021
Письмо Комитета по образованию № 03-28-6959/21-0-0 от 10.08.2021 «Об особенностях проведения школьного этапа всероссийской олимпиады школьников в 2021/2022 учебном году»
Распоряжение Комитета по образованию № 3367-р от 20.12.2021 «Об утверждении организационно-технологической модели проведения регионального этапа всероссийской олимпиады школьников в 2021/2022 учебном году»
Приказ № 754 от 29 октября 2021 «Об установлении сроков и графика проведения регионального этапа всероссйскийо олимпиады школьников в 2021/2022 учебном году
Регламентирующие документы районного уровня
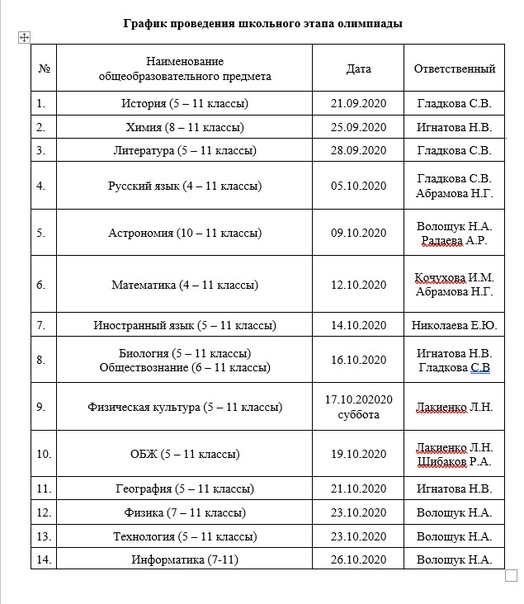
График проведения школьного этапа Всероссийской олимпиады школьников
Распоряжение_администрации_Невского района_»Об организации и проведении школьного_этапа_ВСОШ_в Невском районе Санкт-Петербурга в 2021-2022_учебном_году
2020-2021 учебный год
Регламентирующие документы всероссийского уровня
Методические рекомендации по проведению школьного и муниципального (районного) этапов Всероссийской олимпиады школьников на 2020-2021 учебный год по 24 предметам
Порядок проведения Всероссийской олимпиады школьников (Приказ Минобрнауки с изменениями на 17.
Приказ Министерства образования и науки от 18 ноября 2013 г. N 1252 «Об утверждении Порядка проведения всероссийской олимпиады школьников»
Приказ Министерства образования и науки от 17 декабря 2015г. №1488 «О внесении изменений в Порядок проведения всероссийской олимпиады школьников»
Регламентирующие документы регионального уровня
Распоряжение-Комитета по образованию от 19.10.2020 №1920-р о районном-этапе всероссийской олимпиады школьников в 2020-2021 учебном году
Распоряжение_Комитета по образованию «О внесении изменений в распоряжение Комитета по образованию от 19.10.2020 №1920-р»
Приказ №669 от 24 ноября 2020 года «Об установлении сроков проведения регионального этапа всероссийской олимпиады школьников в 2020-2021 учебном году»
- Распоряжение Комитета по образованию от 09.02.2021 №309-р «Об итогах проведения регионального этапа всероссийской олимпиады школьников в 2020/21 учебном году по французскому языку, литературе, русскому языку, основам безопасности жизнедеятельности, химии»
- Распоряжение Комитета по образованию от 26.
 02.2021 №508-р «Об итогах проведения регионального этапа всероссийской олимпиады школьников в 2020/21 учебном году по русскому языку, астрономии, биологии, информатике, физике»
02.2021 №508-р «Об итогах проведения регионального этапа всероссийской олимпиады школьников в 2020/21 учебном году по русскому языку, астрономии, биологии, информатике, физике» - Распоряжение Комитета по образованию от 10.03.2021 №591-р «Об итогах проведения регионального этапа всероссийской олимпиады школьников в 2020/21 учебном году по истории, математике, праву, обществознанию, экологии, экономике»
Регламентирующие документы районного уровня
График проведения школьного этапа Всероссийской олимпиады школьников
Распоряжение_администрации_Невского района_»Об организации и проведении школьного_этапа_ВСОШ_в Невском районе Санкт-Петербурга в 2020-2021_учебном_году
Требования к проведению районного этапа всероссийской олимпиады школьников в 2020-2021 учебном году
Распоряжение_администрации Невского района «Об организации и проведении районного этапа ВСОШ в Невском районе Санкт-Петербурга в 2020-2021 учебном году
2019-2020 учебный год
Регламентирующие документы всероссийского уровня
Методические рекомендации по проведению школьного и муниципального (раонного) этапов Всероссийской олимпиады школьников на 2019-2020 учебныйй год по 24 предметам размещены в разделе «Регламентирующие документы»
Порядок проведения Всероссийской олимпиады школьников (Приказ Минобрнауки с изменениями на 17. 03.2015)
03.2015)
Приказ Министерства образования и науки от 18 ноября 2013 г. N 1252 «Об утверждении Порядка проведения всероссийской олимпиады школьников»
Приказ Министерства образования и науки от 17 декабря 2015г. №1488 «О внесении изменений в Порядок проведения всероссийской олимпиады школьников»
Приказ Министерства образования и науки от 28 июня 2013 г. №491 «Об утверждении порядка аккредитации граждан в качестве общественных наблюдателей при проведении государственной итоговой аттестации по образовательным программам основного общего и среднего общего образования, всероссийской олимпиады школьников и олимпиада школьников»
Приказ Министерства просвещения от 12.11.2019 №604-р «Об установлении сроков проведения регионального этапа всероссийской олимпиады школьников в 2019-2020 учебном году»
Регламентирующие документы регионального уровня
Распоряжение Комитета по образованию от 21.09.2015г. №4707-р «О внесении изменения в распоряжение Комитета по образованию от 11.
Распоряжение Комитета по образованию от 03.09.2015г. №4412-р «Положение о школьном, районном и региональном этапах всероссийской олимпиады школьников в Санкт-Петербурге»
Распоряжение Комитета по образованию от 11.12.2014г. №5616-р «О проведении этапов всероссийской олимпиады школьников в Санкт-Петербурге»
Распоряжение комитета по образованию об утверждении составов оргкомитетов и жюри регионального этапа всероссийской олимпиады школьников по сотвествующим предметам
Распоряжение_КО_от_01.10.2019_2942-р_»Об_утверждении_графика_проведения_районного_этапа_всероссийской_олимпиады_школьников_в_2019-2020_учебном_году»
Распоряжение_КО_от_06.12.2019_»О_проведении_регионального_этапа_всероссийской_олимпиады_школьников_в_Санкт-Петербурге_в_2019-2020_учебном_году»
Регламентирующие документы районного уровня
Распоряжение Администрации Невского района Санкт-Петербурга от 19.08.2019 №3256 «Об организации и проведении школьного этапа всероссийской олимпиады школьникорв в Невском районе Санкт-Петербурга в 2019-2020 учебном году
Приложения к Распоряжению Администрации Невского района Санкт-Петербурга от 08. 11.2019 №4350-р «Об организации и проведении районного этапа всероссийской олимпиады школьников в Невском районе Санкт-Петербурга в 2019-2020 учебном году приложения_к_Распоряжению__4350-р_от_08.11.2019
11.2019 №4350-р «Об организации и проведении районного этапа всероссийской олимпиады школьников в Невском районе Санкт-Петербурга в 2019-2020 учебном году приложения_к_Распоряжению__4350-р_от_08.11.2019
Состав организационного комитета и контактные данные предметно-методической комиссии и жюри_районного_этапа_2019
Ознакомиться с условиями проведения Всероссийской олимпиады школьников можно на сайтах:
Центр олимпиад Санкт-Петербурга
Страница Олимпиады, конкурсы, выставки на сайте Комитета по образованию Санкт-Петербурга
Всероссийская Олимпиада школьников на сайте Министерства образования и науки Российской Федерации
Всероссийская олимпиада школьников | Сайт Гимназии №40 города Барнаула
Уважаемые гимназисты, родители, учителя!
С 21 сентября по 19 октября в гимназии пройдет муниципальный этап всероссийской олимпиады школьников 2021-2022 учебного года.
В гимназии олимпиады будут проводиться по следующим предметам: русский язык (4-11 классы), литература (5-11), английский язык (5-11), немецкий язык (5-11), математика (4-11), информатика (7-11), физика (7-11), химия (8-11), экология (5-11), биология (5-11), история (5-11), география (7-11), право (9-11), обществознание (6-11), искусство (МХК) (5-11), основы безопасности и жизнедеятельности (ОБЖ) (5-11), астрономия (7-11), технология (5-11), физическая культура (7-11).
Олимпиады проводятся в соответствии с Порядком проведения всероссийской олимпиады, утвержденным приказом Министерства просвещения РФ от 27.11.2020 №678.
Приказом комитета по образованию города Барнаула утвержден График проведения муниципального этапа ВсОШ 2020 года.
Для участия в предметных олимпиадах родителям учащихся (их законным представителям) необходимо заполнить согласие на обработку персональных данных и публикацию работы своего ребенка. Публикуются на сайте гимназии или в АИС «Олимпиада» работы победителей и призеров.
В случае несогласия с полученными баллами за выполненную работу участник может подать апелляцию в оргкомитет муниципального этапа ВсОШ в гимназии.
Успешного выступления на олимпиадах!
График
проведения школьного этапа Олимпиады в 2021-2022 учебном году (скачать)
| Дата проведения | Предмет |
| 21.09.2021 | Английский язык |
| 22.09.2021 | ОБЖ |
| 23.09.2021 | Русский язык |
| 24.09.2021 | Искусство (МХК) |
| 27.09.2021 | Биология |
| 28.09.2021 | Физическая культура |
| 29.09.2021 | География |
| 30.09.2021 | Химия |
| 01.10.2021 | Немецкий язык |
| 04.10.2021 | Математика |
| 06.10.2021 | Технология |
| 07.10.2021 | История |
08. 10.2021 10.2021 |
Физика |
| 11.10.2021 | Литература |
| 12.10.2021 | Экология |
| 13.10.2021 | Обществознание |
| 14.10.2021 | Экономика |
| 15.10.2021 | Астрономия |
| 18.10.2021 | Право |
| 19.10.2021 | Информатика и ИКТ |
Приказ №678 Об утверждении Порядка проведения всероссийской олимпиады школьников (скачать)
Всероссийская олимпиада школьников
22.01.2022 Сегодня состоится олимпиада по физике (1 тур).
21.01.2022 Завершилась олимпиада по ОБЖ. Жюри проверяет работы.
19.01.2022 Завершилась олимпиада по химии. Ссылки на видеоразбор задач опубликованы на странице предметной олимпиады http://evrika41.ru/olimpic/olimp/18-himija.html
18.01.2022 В разделе «Документы» опубликован приказ «О внесении изменений в приложение № 1 к приказу Министерства образования Камчатского края от 23. 12.2021 № 1122 «Об утверждении проходных баллов для участия в региональном этапе всероссийской олимпиады школьников в Камчатском крае в 2021/2022 учебном году». Изменились проходные баллы по предмету физическая культура. Обновлены списки участников.
12.2021 № 1122 «Об утверждении проходных баллов для участия в региональном этапе всероссийской олимпиады школьников в Камчатском крае в 2021/2022 учебном году». Изменились проходные баллы по предмету физическая культура. Обновлены списки участников.
17.01.2022 Завершилась олимпиада по информатике. Материалы олимпиады (в том числе видеоразбор): http://neerc.ifmo.ru/school/information/index.html
14.01.2022 Завершилась олимпиада по русскому языку. Разбор заданий регионального этапа всероссийской олимпиады школьников по русскому языку: https://youtu.be/GwXPYp-CAoQ
13.01.2022 Завершилась олимпиада по литературе. Разбор заданий: Ссылка на эфир: https://youtu.be/rAGxLy0GOHc
13.01.2022 Размещение проживающих: гостевой дом, турбаза.
12.01.2022 завершилась олимпиада по французскому языку. Разбор заданий: https://youtu. be/9LrkW1zhDt0.
11.01.2022 Внимание участникам олимпиады по экологии. Проекты принимаются в электронном виде до 19 января 2022 года по адресу [email protected]. Тема письма: Проект по экологии / Фамилия Имя / Муниципальный район.
11.01.2022 Согласно рекомендациям Министерства просвещения РФ, предварительные результаты предметных олимпиад публиковаться не будут. Узнать свой балл участники смогут во время показа работ.
30.12.2021 Определены проходные баллы на все предметы. В разделах соответствующих олимпиад опубликованы списки участников.
22.11.2021 В разделах олимпиад по математике и физике опубликованы порядки проведения региональных этапов олимпиад Эйлера и Максвелла.
07.11.2021 Опубликованы требования к организации и проведению регионального этапа всероссийской олимпиады школьников в 2021/2022 учебном году.
07.11.2021 Опубликован график проведения регионального этапа Всероссийской олимпиады школьников в 2022 году.
25.10.2021 Стартовал муниципальный этап ВсОШ. Данные о количестве участников по каждому предмету в каждом муниципальном образовании опубликованы в сводной таблице.
Всероссийская олимпиада по истории российского предпринимательства. Олимпиада по истории российского бизнеса
III Всероссийская олимпиада по истории российского предпринимательства
Информационная почта
III Всероссийская Олимпиада
по истории российского бизнеса
(Приморский краевой этап)
г. Владивосток, о. Россия, пос. Аякс, 10, кампус ДВФУ,
корпус Б, конференц-зал «Морской»
02-03 марта 2017 г. Дальневосточный федеральный университет (ДВФУ) на базе Высшей школы экономики и менеджмента (ШЭУ) проводит олимпиаду студентов и аспирантов образовательных учреждений по истории российского предпринимательства.
Олимпиада — Приморский региональный этап III Всероссийской студенческой олимпиады по истории российского предпринимательства, организатором которой является Общероссийская общественная организация «Деловая Россия» и проводится совместно с Российским историческим обществом (http:/ /historybiz.ru/).
Настоящим письмом приглашаем студентов и аспирантов образовательных учреждений Приморского края принять участие в олимпиаде.
Форма участия в Олимпиаде – очная, победители определяются в личном первенстве.С полными правилами конкурса можно ознакомиться на официальном сайте Олимпиады www.historybiz.ru.
Лица, занявшие 1-3 места, будут награждены денежными призами. Победитель регионального этапа, занявший 1 место, будет направлен в Москву за счет средств организаторов (ориентировочный срок: конец марта-начало апреля 2017 года) для представления Приморского края на федеральном этапе III Всероссийской студенческой олимпиады. по истории российского бизнеса, которая пройдет в МГУ. М. В. Ломоносов.
М. В. Ломоносов.
Все участники регионального этапа Студенческой олимпиады получат сертификаты участия для пополнения собственного портфолио.
Для подготовки к олимпиаде, задачи региональных этапов 2015-2016 гг. будут размещены в открытом доступе на странице Школы экономики и менеджмента ДВФУ https://www.dvfu.ru/schools/school_of_economics_and_management/ в разделе «Новости» и на сайте Приморского регионального отделения Всероссийского -Российская общественная организация «Деловая Россия» http://primdelros.ru/ в разделе «Наши проекты» — «История российского предпринимательства» и не позднее 24 февраля 2017 года там будут размещены ответы на задания.
Место и время проведения областного этапа Олимпиады: г. Владивосток, о. Россия, Аякс, 10, кампус ДВФУ, корпус Б, конференц-зал «Морской».
02 марта 2017 г. с 09:30 — торжественное открытие олимпиады, выполнение индивидуальных заданий (время выполнения заданий не менее 4 часов), работа жюри (конкурсной комиссии).
03 марта 2017 г. с 10:00 – подведение итогов, награждение победителей, вручение подарочного издания проекта «Деловая Россия» Книга Амира Хисамутдинова «Владычий Восток: Предприниматели Дальнего Востока – просветители и меценаты (Как это было) Все началось)». – Владивосток: Рубеж, 2016. – 464 с.: ил., торжественное вручение экземпляров книги представителям общеобразовательных школ и вузов Приморского края для пополнения библиотечных фондов общеобразовательных учреждений и вручение книги особо отличившимся студентам при выполнении конкурсных заданий, по мнению авторитетного жюри.Автограф-сессия А. Хисамутдинова.
Участие в олимпиаде бесплатное, регистрационный взнос не взимается. Проезд и проживание за счет участников. Для иногородних участников возможно платное проживание в гостиничных номерах на территории кампуса ДВФУ.
Для участия в Олимпиаде не позднее 28 февраля 2017 года необходимо заполнить и направить организаторам Регистрационную форму участника на электронную почту [email protected] или зарегистрироваться на сайте:
https://historybizolimp. timepad.ru/event/446198
timepad.ru/event/446198 Время проведения олимпиадных мероприятий может корректироваться, следите за возможными изменениями на сайте http://primdelros.ru/ в разделе «Наши проекты» — «История российского предпринимательства».
По всем вопросам регистрации и участия в олимпиаде обращайтесь в оргкомитет ([email protected]), контактное лицо — Васильковский Алексей Владимирович, старший преподаватель кафедры менеджмента Школы экономики и менеджмента Дальневосточного федерального университета (телефон / WhatsApp +7
31403).
Всероссийская олимпиада по истории российского предпринимательства проводится во второй раз. Масштабный проект охватывает более двух тысяч участников со всех регионов страны.
История российского предпринимательства — один из совместных проектов Российского исторического общества и «Деловой России». Всероссийская олимпиада стала площадкой, где актуальна идея привлечения молодежи к активному изучению пути исторического развития страны.Каким был бы этот путь без российских предпринимателей, сумевших превратить Россию в одну из ведущих держав XIX и начала XX веков? История не знает сослагательного наклонения, но в любом случае их вклад неоценим.
29 марта В Государственной Думе состоялась церемония награждения лучших из лучших — десятков финалистов федерального этапа, прошедшего 28 марта в МГУ. Ломоносов.
В церемонии приняли участие председатель РИО и сопредседатель «Деловой России», член президиума РИО Николай Левицкий , который наградил финалистов грамотами, а также денежными призами: шестьдесят, сорок и двадцать тысяч за первые три места соответственно.
Состав тройки финалистов действительно свидетельствует о том, что этот проект Общества получил огромный резонанс во всех регионах России, в олимпиаде приняли участие студенты из 60 вузов. Первое место заняла студентка Кубанского государственного университета Анастасия Бойко , серебро (с отрывом 0,2 балла) у первокурсницы факультета экономической безопасности Костромского государственного университета им. Некрасова Симанова Дарья , почетное третье — от студентки магистратуры МГУ Муравьева Анастасия .
На открытии церемонии награждения Николай Левицкий откровенно сказал, что задачи финального тура Олимпиады были сложными. Сами участники, с которыми удалось пообщаться, соглашаются, что борьба была действительно серьезной, но, учитывая прекрасное знание истории России, «тест и сочинение были не такими уж пугающими, трудности возникли только с установлением авторов цитат и фотографий». российских предпринимателей», — сказала Дарья Симанов.
История и экономика, по сути, негласно соперничали в этой олимпиаде, но так как обе дисциплины неразрывно связаны, финал показал необходимость глубоких знаний по обоим направлениям, важность интеграции.История России невозможна без истории предпринимательства, и это неоднократно подчеркивали как высокие гости церемонии, так и участники конкурса.
Выступая в зале, Председатель Государственной Думы Сергей Нарышкин отметил, что тема предпринимательства будет актуальна в любое время, а набор качеств, отличающих профессионала этой отрасли: ответственность, честность, репутация и деловая хватка, всегда будет оставаться неизменным. Трудно не согласиться с мнением Председателя РИО о том, что изучение этого пласта российской истории не только молодежью, но и общественностью в целом имеет далеко идущие практические цели, придавая новый импульс развитие экономики России, передав заветы первых предпринимателей — Морозовых, Третьяковых. Именно у них нам нужно учиться создавать и развивать страну, в которой мы живем и будем жить наши дети.
Трудно не согласиться с мнением Председателя РИО о том, что изучение этого пласта российской истории не только молодежью, но и общественностью в целом имеет далеко идущие практические цели, придавая новый импульс развитие экономики России, передав заветы первых предпринимателей — Морозовых, Третьяковых. Именно у них нам нужно учиться создавать и развивать страну, в которой мы живем и будем жить наши дети.
Олимпиада действительно дала новый импульс как организаторам, так и участникам.Ответственный секретарь РИО Андрей Петров пообещал, что этот проект будет активно развиваться дальше, так как он получил огромный отклик и имеет большое значение. Серебряный призер олимпиады Дарья Симанова также отметила: «Раньше я не собиралась заниматься бизнесом, но после победы задумалась об этом. Почему нет? Главное, вложить всю душу в изучение предмета.
Невозможно построить будущее без изучения опыта прошлого — эта истина не раз озвучивалась в трудах российских историков и экономистов. Вот почему такие проекты, как «История российского предпринимательства», всегда должны оставаться «на вершине» общественной мысли, если мы хотим двигаться только вперед вместе с нашей страной.
Вот почему такие проекты, как «История российского предпринимательства», всегда должны оставаться «на вершине» общественной мысли, если мы хотим двигаться только вперед вместе с нашей страной.
28 марта на Историческом факультете МГУ. М.В. Ломоносова прошел федеральный этап второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов. Олимпиада прошла в рамках совместного проекта «Деловой России» и Российского исторического общества (РИО) «История российского предпринимательства».В нем приняли участие более 50 победителей региональных этапов.
В МГУ приехали лучшие из лучших – в регионах в олимпиаде приняли участие более 2 тысяч студентов 60 российских вузов из 53 регионов России, рассказала Ирина Захарова, вице-президент «Деловой России», руководитель проектной дирекции.
«Я очень рад, что вы принимаете участие в этой Олимпиаде. Вопросы будут интересными. Уверен, ваш уровень знаний позволит вам очень хорошо на них ответить», — поприветствовал собравшихся Николай Левицкий, сопредседатель «Деловой России».
«В 1917 году произошла трагедия — например, здесь, в МГУ, негодяи сбили мраморные доски с именами благотворителей и жертвователей, тех людей, которые тратили свои личные деньги на строительство МГУ. Революционеры вычеркнули всю память о меценатах и благотворителях. Поэтому наш проект — это не просто дань любознательности или любви к истории. Наверное, наш гражданский долг помнить об этих замечательных людях, которые действовали так, чтобы наша страна становилась лучше.И, конечно же, наша задача — вспомнить те традиции, которые были, почувствовать связь тех и нынешних предпринимателей», — подчеркнул Николай Левицкий.
Проект «История российского предпринимательства» призван актуализировать в общественном сознании вопросы, связанные с творческой миссией и ролью российского предпринимательства в развитии России, и рассчитан на широкое вовлечение общественности, особенно молодежи. Проект поддержал президент России Владимир Путин.Соответствующие поручения главы государства были даны министру культуры Владимиру Мединскому, министру образования и науки Дмитрию Ливанову, министру связи и массовых коммуникаций Николаю Никифорову, а также полпредам президента в федеральных округах.
Первая Всероссийская олимпиада по истории российского предпринимательства прошла в 2015 году. Ее региональный этап прошел в 40 субъектах Российской Федерации, организаторами выступили местные отделения «Деловой России» совместно с местными вузами и региональными органы власти.В 2016 году расширилась как география, так и количество участников олимпиады.
«Когда я еще готовилась к региональному этапу олимпиады, искала прошлогодние задания. То, что мне удалось найти, было довольно сложным. В этом году задания стали более «олимпиадными» по своему формату. И мне было легче, потому что я часто участвую в таких соревнованиях. Мне было непросто в визуальной части, но я компенсировал это заданиями из других блоков, выиграв региональный этап», — рассказал Владислав Пономарев, аспирант Пензенского государственного университета.
Среди участников заключительного этапа олимпиады в этом году были не только студенты и аспиранты, но и военные. В частности, младший сержант Расим Гарунов, курсант Михайловской военной артиллерийской академии из Ленинградской области. «Для меня было честью выступать на олимпиаде в Ленинградской области, я смог показать там лучший результат и попал сюда. Мне очень приятно представлять свою академию на таком высоком уровне», — сказал он, пошутив, что будет более уверен в своей победе на олимпиаде в стрельбе или борьбе.
«Для меня было честью выступать на олимпиаде в Ленинградской области, я смог показать там лучший результат и попал сюда. Мне очень приятно представлять свою академию на таком высоком уровне», — сказал он, пошутив, что будет более уверен в своей победе на олимпиаде в стрельбе или борьбе.
«Мы в университете считаем очень важным, что «Деловая Россия» провела большую подготовительную работу и выступила спонсором этого прекрасного мероприятия, объединив всех вас. Мы считаем, что эта олимпиада призвана повысить внимание к той роли, которую играет малый и средний бизнес в России», — сказал Леонид Бородкин, заместитель декана исторического факультета МГУ. Олимпиада будет способствовать — через СМИ, вузы и региональные отделения «Деловой России» — пониманию роли малого и среднего бизнеса в развитии страны, добавил он.
Руководитель Московского регионального отделения «Деловой России» Александр Делис отметил, что одна из задач олимпиады — заинтересовать подрастающее поколение в предпринимательстве. «Миссия, которую взяли на себя «Деловая Россия» и Российское историческое общество, — вернуться к истокам и популяризировать историю российского предпринимательства», — сказал он. Он также напомнил студентам и аспирантам об одном из основных принципов русских предпринимателей в дореволюционный период: «Прибыль превыше всего, но выше прибыли только честь.»
«Миссия, которую взяли на себя «Деловая Россия» и Российское историческое общество, — вернуться к истокам и популяризировать историю российского предпринимательства», — сказал он. Он также напомнил студентам и аспирантам об одном из основных принципов русских предпринимателей в дореволюционный период: «Прибыль превыше всего, но выше прибыли только честь.»
Вопросы олимпиады охватывают историю и роль российского предпринимательства от периода Древней Руси до начала ХХ века. Работы студентов и аспирантов оцениваются комиссией, в состав которой входят семь профессоров и доцентов ведущих российских вузов, где преподают историю российского предпринимательства, в том числе МГУ и Высшей школы экономики. Победители олимпиады будут названы и награждены 29 марта на торжественной церемонии в Государственной Думе, в которой примут участие все участники ее федерального этапа.
25 февраля 2016 года в Нальчике состоялся региональный этап II Всероссийской олимпиады студентов и аспирантов «История российского предпринимательства», организованной Общероссийской общественной организацией «Деловая Россия» и Российским историческим обществом. В олимпиаде приняли участие 245 студентов вузов республики.
В олимпиаде приняли участие 245 студентов вузов республики.
С начала февраля Кабардино-Балкарское региональное отделение «Деловой России» организовало сбор заявок от участников олимпиады в крупные вузы республики — Кабардино-Балкарский государственный университет, Кабардино-Балкарский государственный аграрный университет, Кабардино-Балкарский Университет бизнеса, Нальчикский институт кооперации.
Задачами Олимпиады являются сохранение исторической памяти о российских предпринимателях, внесших большой личный вклад в развитие Российского государства, отдельных регионов и поселений; содействие процессу объективного отражения роли предпринимательства в истории государства; развитие интереса учащихся к истории предпринимательства; содействие формированию в обществе положительного и целостного образа предпринимателя и популяризация профессии предпринимателя, а также вовлечение молодежи в составление «новой летописи» российского предпринимательства.
Зачет регионального этапа прошел на базе Кабардино-Балкарского государственного аграрного университета. Перед началом олимпиады проректор по научной работе, кандидат сельскохозяйственных наук, доцент Кабардино-Балкарского государственного аграрного университета Анзор Эзаов и директор Института экономики Кабардино-Балкарского государственного аграрного университета, к.э.н.
Перед началом олимпиады проректор по научной работе, кандидат сельскохозяйственных наук, доцент Кабардино-Балкарского государственного аграрного университета Анзор Эзаов и директор Института экономики Кабардино-Балкарского государственного аграрного университета, к.э.н.
Тест длился три часа. Задания состояли из пяти блоков: тест из 30 вопросов с вариантами ответов; пять вопросов, требующих развернутых ответов; десяти терминов (таких как жытник, офеня, тарханские грамоты и др.), которым участники должны были дать наиболее точные и полные определения; сочинения на одну из пяти предложенных тем и портреты, в которых участники олимпиады должны были выявить конкретных предпринимателей прошлого.
В В состав конкурсной комиссии для определения победителей регионального этапа вошли Делороссы Безема Людмила – генеральный директор ООО «ЮСОРИ», Бесова Инна – генеральный директор ООО «Реконстрой», Шаваев Ильяс – директор ГУП «Опытное сельскохозяйственное предприятие КБР «Декоративные культуры», а также к. э.н., доцент кафедры организационного менеджмента КБГАУ Зара Кунашева; кандидат экономических наук, доцент кафедры «Менеджмент» НОУ ВПО «Кабардино-Балкарский институт бизнеса» Халимат Жантудуева; кандидат экономических наук, заместитель заведующего кафедрой экономики и управления Нальчикского института кооперации Людмила Шакова; кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ Рита Кушбокова; кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ Лариса Чеченова; Анхор Лоов, старший преподаватель кафедры истории, философии и права Института экономики КБГАУ и доктор экономических наук, заведующий кафедрой экономики Института экономики КБГАУ Тахир Тогузаев.Комиссию возглавила сопредседатель Кабардино-Балкарского регионального отделения «Деловой России» Евгения Васильченко.
э.н., доцент кафедры организационного менеджмента КБГАУ Зара Кунашева; кандидат экономических наук, доцент кафедры «Менеджмент» НОУ ВПО «Кабардино-Балкарский институт бизнеса» Халимат Жантудуева; кандидат экономических наук, заместитель заведующего кафедрой экономики и управления Нальчикского института кооперации Людмила Шакова; кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ Рита Кушбокова; кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ Лариса Чеченова; Анхор Лоов, старший преподаватель кафедры истории, философии и права Института экономики КБГАУ и доктор экономических наук, заведующий кафедрой экономики Института экономики КБГАУ Тахир Тогузаев.Комиссию возглавила сопредседатель Кабардино-Балкарского регионального отделения «Деловой России» Евгения Васильченко.
Победители регионального этапа II Всероссийской олимпиады по истории российского предпринимательства (2016)
1-2 курс
Победитель — Канцалиева Лана Анатольевна (КБГАУ)
1 место — Белимготов Алан Русланович (КБГАУ)
2 место — Алхасов Михаил Борисович (КБГАУ)
3 место — Танашева Тина Андарбиевна (КБГАУ)
3-4 курс
Победитель — Хурзокова Диана Хажисмеловна (КБГАУ)
1 место — Боготова Диана Зауровна (КБГАУ)
2 место — Губашиева Аят Мухарбиевна (КБГАУ)
3 место — Масаева Жанна Арсеновна (КБГАУ)
Степень магистра
Победитель — Кокова Хадижат Хамидбиевна (КБГАУ)
1 место — Шерхова Амина Ахиедовна (КБГАУ)
2 место — Кибышева Амина Даниловна (КБГАУ)
Кандидат наук
Победитель — Шонтуков Эльдар Заурович (КБГАУ)
Победитель — Хакяшев Алим Асланович (КБИБ)
1 место — Киштикова Марьяна Руслановна (КБИБ)
2 место — Кокова Ирэн Руслановна (КБИБ)
3 место — Лукожева Белла Аслановна (КБИБ)
федеральный этап
28 марта на Историческом факультете МГУ..png) М.В. Ломоносова прошел федеральный этап второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов. Олимпиада прошла в рамках совместного проекта «Деловой России» и Российского исторического общества (РИО) «История российского предпринимательства». В нем приняли участие более 50 победителей региональных этапов.
М.В. Ломоносова прошел федеральный этап второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов. Олимпиада прошла в рамках совместного проекта «Деловой России» и Российского исторического общества (РИО) «История российского предпринимательства». В нем приняли участие более 50 победителей региональных этапов.
В МГУ приехали лучшие из лучших — в олимпиаде в регионах приняли участие более 2000 студентов 60 российских вузов из 53 регионов России.Кабардино-Балкарскую Республику на федеральном этапе олимпиады представляли победительницы регионального этапа Канцалиева Лана (студентка 2 курса КБГАУ), Хурзокова Диана (студентка 3 курса КБГАУ) и Кокова Хадижат (магистр Института экономики КБГАУ). Все девушки успешно прошли региональный этап, показав хорошие результаты и набрав 109-113 баллов из 115 возможных. Все расходы по организации участия студентов в федеральном этапе взял на себя вуз, который они представляют.Сопровождает наших соотечественников в поездке их преподаватель Фатимат Зумакулова – кандидат экономических наук, доцент кафедры финансов и кредита Института экономики КБГАУ.
Собравшихся приветствовали сопредседатель «Деловой России» Николай Левицкий, вице-президент «Деловой России», руководитель дирекции проекта «История российского предпринимательства» Ирина Захарова, заместитель декана исторического факультета МГУ Леонид Бородкин и Александр Делис. , руководитель Московского регионального отделения «Деловой России».
Проект «История российского предпринимательства» призван актуализировать в общественном сознании вопросы, связанные с творческой миссией и ролью российского предпринимательства в развитии России, и рассчитан на широкое вовлечение общественности, особенно молодежи. Проект поддержал президент России Владимир Путин.
Вопросы олимпиады охватывают историю и роль российского предпринимательства от периода Древней Руси до начала ХХ века.Работы студентов и аспирантов оцениваются комиссией, в состав которой входят семь профессоров и доцентов ведущих российских вузов, где преподают историю российского предпринимательства, в том числе МГУ и Высшей школы экономики.
Финальный этап Всероссийской олимпиады по русскому языку
В Турции прошел заключительный этап V Всетурецкой олимпиады по русскому языку как иностранному, посвященной 220-летию со дня рождения А. С. Пушкина.
Активное участие в организации олимпиады приняли Российский университет дружбы народов и Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации. Ведущие специалисты РУДН разработали конкурсные тестовые задания для участников олимпиады.
В олимпиаде по русскому языку как иностранному принимают участие учащиеся лицеев, колледжей, вузов в соответствии с подтвержденным уровнем владения языком.
5 октября состоялась торжественная церемония награждения победителей Олимпиады.Победителям V Всетурецкой олимпиады по русскому языку, занявшим первые места, традиционно предоставляется возможность обучаться в российских вузах в рамках стипендиальной программы Правительства Российской Федерации. Заведующие кафедрами и преподаватели русского языка, принявшие активное участие в олимпиаде и подготовившие финалистов, были награждены памятными подарками от представительства Россотрудничества, благодарственными письмами Посольства России в Турции и оргкомитета олимпиады .
Заведующие кафедрами и преподаватели русского языка, принявшие активное участие в олимпиаде и подготовившие финалистов, были награждены памятными подарками от представительства Россотрудничества, благодарственными письмами Посольства России в Турции и оргкомитета олимпиады .
Мероприятие завершилось литературно-музыкальной программой. Участники исполняли танцевальные номера, песни на русском языке, читали стихи русских поэтов.
Широкая география олимпиады и активность ее участников продемонстрировали высокий интерес турецкой молодежи к русскому языку, истории и культуре России.
Студенты, изучающие русский язык, также могут принять участие в олимпиаде Президентской библиотеки «Россия в электронном мире». В этом учебном году стартует олимпиада по новому предмету «Русский язык как иностранный» для иностранных пользователей библиотеки.Подробная информация о проекте представлена на интернет-портале учреждения. Для подготовки можно использовать материалы электронной коллекции «Русский язык», в которую входят рукописи и издания памятников русской письменности, архивные дела, научные труды (в том числе диссертационные и тезисы), словари и справочники, учебные пособия различных типов и уровней. Материалы коллекции в центрах удаленного доступа к информационным ресурсам Президентской библиотеки доступны в разных странах мира.С 2014 года один из таких центров открыт на базе Российского центра науки и культуры в Анкаре.
Материалы коллекции в центрах удаленного доступа к информационным ресурсам Президентской библиотеки доступны в разных странах мира.С 2014 года один из таких центров открыт на базе Российского центра науки и культуры в Анкаре.
По материалам http://tur.rs.gov.ru/ru.
Всероссийская олимпиада по истории 6. Задания к школьному этапу олимпиады по истории (6 класс). шаги навстречу учителю
ОЛИМПИАДА ПО ИСТОРИИ
СРЕДИ ШКОЛЬНИКОВ 6 КЛАССА
Школьная экскурсия
Задание №1.Проанализируйте исторический источник и ответьте на вопрос.
В каком городе жил Перикл? Почему он назвал этот город «школой всей Эллады»? Как могли проявить себя жители этого города? (5 баллов)
Задание №2. Выберите правильный ответ(по 1 баллу)
- Толчком к Великому переселению народов послужило нашествие кочевников из глубин Азии:
A. Вандалы B. Остроготы V. Вестготы G. Франки D. Гунны.
Гунны.
А.в 780 г. до н.э. в 910 г. до н.э. в 800 г. до 810 г.
А. по верхней Б. по низшей В. не входил в феодальную лестницу
Б. натуральное хозяйство Г. феодальный общественный строй
А) принятие франками христианства Б) создание Франкской империи В) распад франкской империи
А) вестготы Б) остготы В) франки Г) норманны
7. Соотнесите понятия и их определения:
3 ) барщина
Задание №3.
1.В каком городе находился самый большой и красивый храм раннего Средневековья?
(1 балл)
3. Может ли барон, присягнувший на верность герцогу, считаться вассалом короля? (1 балл)
Задание № 4.
| Александр Македонский | |
| Ашурбанипал | |
| Константин | |
| Октавиан Август | |
| Соломон | |
| Хаммурапи | |
| Принц Гаутама | 7. |
| Цинь Шихуан | |
| Юлий Цезарь | 9. Основание империи |
Задание № 5.
(8 баллов)
Пророк Мухаммед.
ОТВЕТЫ
К ОЛИМПИАДЕ ПО ИСТОРИИ
СРЕДИ ШКОЛЬНИКОВ 6 КЛАССА
Школьная экскурсия
Задание №1. Проанализируйте исторический источник и ответьте на вопрос.
Выдающийся древнегреческий политик Перикл так сказал о своем городе: «Наше государство есть школа всей Эллады, и каждый из нас легко может проявить свою индивидуальность в самых разных условиях жизни».
В каком городе жил Перикл? Почему он назвал этот город «школой всей Эллады»? Как могли проявить себя жители этого города? (5 баллов) — Афины
Задание №2. Выберите правильный ответ.(по 1 баллу)
1. Толчком к Великому переселению народов послужило нашествие кочевников из глубин Азии:
А.Вандалы Б. Остготы В. Вестготы Г. Франки Д. Гунны.
Вестготы Г. Франки Д. Гунны.
2. В каком году Карл Великий был провозглашен императором?
А. в 780 г. Б. в 910 г. Б. в 800 г. в 810 г.
3. На какой ступени феодальной лестницы находились крестьяне?
А. сверху Б. снизуV. не вошел на феодальную лестницу
4. Строение общества, в котором основными группами являются сеньоры и крестьяне, а земля находится в руках сеньоров, называется…
A. средневековая цивилизация B.аграрная цивилизация
B. натуральное хозяйствоG. феодальный общественный строй
5. Верденский мирный договор (843) обеспечил:
А) принятие франками христианства Б) создание Франкской империи С) распад Франкской империи
6. Какое германское племя преимущественно населяли Скандинавский полуостров:
А) вестготы Б) остготы С) франки Г) норманны
7. Соотнесите понятия и их определения: 3 балла
1) оброк А) земли, пожалованные в наследственное владение сеньором своему вассалу
2) междоусобица Б) принудительный труд зависимых крестьян в хозяйстве феодала
3) барщина В) сбор продовольствия или денег феодалом с зависимых крестьян
1А, 2А, 3Б
Задача №3 . Ответьте на вопросы (по 1 баллу)
Ответьте на вопросы (по 1 баллу)
1. В каком городе находился самый большой и красивый храм раннего Средневековья? (Париж)
2. Чем викинги отличались от норманнов и викингов? (1 балл)
3. Может ли барон, присягнувший на верность герцогу, считаться вассалом короля? (1 балл) (Нет)
Задание № 4. Соотнесите имя правителя с историческим фактом. (9 баллов)
| Александр Македонский -7 | 1.Организация библиотеки глиняных книг |
| Ашурбанипал — 1 | 2. Создание древнейших законов |
| Константин — 8 | 3. Строительство самой длинной стены |
| Октавиан 6 августа | 4. Создание новой религии — буддизма |
| Соломон — 5 | 5. Строительство храма бога Яхве в Иерусалиме |
| Хаммурапи -2 | 6. |
| Принц Гаутама -4 | 7. Военный поход в Индию |
| Цинь Шихуан -3 | 8. Разрешение христианам открыто молиться |
| Юлий Цезарь -9 | 9. Основание империи |
Задание № 5. Соотнесите понятия и их значения. Запишите ответ в таблицу.
(8 баллов)
1.Природоведение А. Выступление на религиозно-нравственную тему.
2. Проповедь Б. Эпоха в истории человечества между Древним миром и Новым временем
3. Средневековье Б. Хозяйство, в котором все необходимое производится на данной площади
и расходуется на собственные нужды потребления населения данной местности.
4. Ислам Г. Сложный узор, созданный на основе математического расчета.
5. Фреска Д. Роспись, выполненная на стене или потолке храма по сырой штукатурке.
6. Монастырь Е. Северные немцы, норвежцы, шведы, датчане.
Северные немцы, норвежцы, шведы, датчане.
7. Норманны Ж. Религия многих народов Востока, связанная с верой в Аллаха и его
Пророка Мухаммеда.
8. Арабеска З. Резиденция монахов, комплекс зданий, обнесенных высокой стеной.
Всего баллов 34
Всероссийская олимпиада школьников по истории
Школьная сцена
6 класс
2 точки
Задача 1.С какого года принято отсчитывать историю Средневековья? 1. Отметьте правильный ответ.
A) 476 г. до н.э.
B) 1 г. до н.э.
C) 1 г. н.э.
D) 476 г. н.э.
2. Какое событие, положившее конец истории Древнего мира, произошло в этом году?
________________________________________________________________________________________________________________________________________________________________
9 баллов
Z
A) Организация библиотеки глиняных книг
B) Отмена рабства в Афинах
C) Создание новой религии — ислама
D) Военный поход в Индию
E) Первый правитель государство франков
F) Создание единого свода законов для всей Византии
G) Захват единоличной власти в Риме
H) Перенос польской столицы в Краков
I) Открытие «дворца Академия» в Аахене
Адания 2. Распределите имена правителей и их деятельность в столбцах по эпохам, в которых они жили — Древнего мира и Средневековья.
Распределите имена правителей и их деятельность в столбцах по эпохам, в которых они жили — Древнего мира и Средневековья.
1. Александр Великий
2. Muhammad
3. Julius Caesar
3. Hammurabi
5. Solon
6. Болеслав
6. Болеслав
7. Justinian
8. Charlemagne
9. Clovis
История древнего мира
3 балла
Задача 3.В Средние века считалось, что образованный человек должен изучать определенные науки. Они получили название «Свободные искусства». 1. Сколько их было? _________________________________________________
2. Из предложенного списка выбрать ненужное:
а) риторика
в) Грамматика
в) Диалектика
в) Диалетика
г) Литература
д) Астрономия
E) Музыка
г) Геометрия
H) Геометрия
H) Arithmetic
I) Окраска
6 баллов
Задача 4. Составьте грамотное определение из слов, предложенных в правом столбце, и найдите слово из левого столбца, к которому относится это определение.
Составьте грамотное определение из слов, предложенных в правом столбце, и найдите слово из левого столбца, к которому относится это определение.
Условия
Внесите результаты в таблицу:
5 баллов
Задание 5. В газете появилась статья следующего содержания: «В Калининградской области ____________ изуродован памятник герою Отечественной войны 1812 года, русскому полководцу Михаилу Богдановичу Барклаю-де-Толли.Памятник решили сдать на металлолом, для чего в него забросали кувалдами и другими тяжелыми предметами, из-за чего памятник сильно пострадал.
Вместо пропущенного слова журналисты использовали название одного из германских народов.
1. Какое слово пропущено?
2. Почему он используется в таких ситуациях?
____________________________________________________________________________________________________________________________________________________________
4 балла
Задача 6. Какие «ступени» отсутствуют в феодальной лестнице?
Какие «ступени» отсутствуют в феодальной лестнице?
1. Восстановить недостающие: 1________________________; 2____________________________.
2. Может ли феодал 2, присягнувший на верность феодалу 1, считаться вассалом короля? Почему? Какое средневековое правило здесь применимо?
________________________________________________________________________________________________________________________________________________
1 2
2 точки
Задача 7.Предлагаемая мозаика изображает одного из величайших и могущественных правителей Византии и его супругу. Соедините квадраты буквами так, чтобы получились имена этих исторических личностей.
Запишите их: 1 .___________________________________; 2 .___________________________.
Ф
Максимальное количество баллов: 31
Время подготовки ответа: 45 минут
Материал, представленный в данном разделе, представляет собой примеры олимпиадных заданий, которые подготовлены для подготовки учащихся 6-х классов к олимпиаде по истории России. Предлагаем школьникам использовать данные задания в качестве тренажера, который поможет им углубить и систематизировать знания, полученные на уроке.
Предлагаем школьникам использовать данные задания в качестве тренажера, который поможет им углубить и систематизировать знания, полученные на уроке.
Учителя могут копировать и распечатывать задания для тестовой олимпиады на уроке. Проверить и оценить результаты учащихся 6-х классов можно за считанные минуты, ведь на все задания олимпиады в истории России даны ответы и решения.
Олимпиада по истории России, 6 класс
Скачайте задания, заполнив форму!
После ввода данных кнопка загрузки станет активной
Тестовые задания
1.К предпосылкам образования Древнерусского государства относятся:
А) необходимость дать отпор внешним врагам
Б) тесные экономические связи между славянскими племенами
В) принятие христианства
Г) Великое переселение народов
2. Крепостной в Древней Руси:
А) крестьянский общинник, зависимый от князя
Б) разорившийся общинник, попавший в долговую кабалу за ссуду
В) наиболее бесправная категория населения, близкая к рабам
Г ) член сообщества, заключивший договор, согласившийся жить и работать с мастером на определенных условиях
3. Высказывание Н.М. Карамзина: «Князь сей, названный Церковью
Высказывание Н.М. Карамзина: «Князь сей, названный Церковью
Равноапостольным, достоин в истории имени Великого» — посвящается
А) Святославу
Б) Владимиру
В) Ярославу Мудрому
г Владимиру Мономаху
4. Свод законов в Древнерусском государстве назывался:
А) Салическая правда
Б) Русская Правда
В) Стоглав
Г) Судебник
5. Литературный памятник XII века, в котором содержался призыв к прекращению княжеской усобицы:
А) «Слово о полку Игореве»
Б) «Домострой»
В) «Слово о погибели Русской земли
Д) «Обучение детей»
6.Ряд дат, связанных с борьбой русского народа против немецких и шведских рыцарей:
А) 1237, 1238
Б) 1240, 1242
Б) 1243, 1252
Г) 1262, 1263
7. Одним из итогов правления Ивана Калиты было:
А) превращение Московского княжества в одно из сильнейших на Руси
Б) избавление от ордынского ига
В) окончание княжеских междоусобиц в Русская земля
Г) образование единого Российского государства
8. Формирование единой территории Русского централизованного государства в основном завершилось при:
Формирование единой территории Русского централизованного государства в основном завершилось при:
А) Василии I
Б) Иване III
В) Василии II Темном
Г) Иване IV Грозном
9. Территория, на которой в середине XVI в. управление Земского собора и Боярской думы сохранилось, оно называлось:
А) удел
Б) опричнина
В) земщина
Г) посад
10. Самое известное произведение Андрея Рублева:
А) икона Божией Матери Донская
Б) иконопись «Воинствующая церковь»
В) «Троица»
Г) роспись на стенах Благовещенского собора в г. Московский Кремль
Открытые вопросы
Вопрос 1
В описании владений одного монастыря в X в.говорят, что крестьянин имеет полный надел земли. Он платит за него одну свинью, фунт льна, трех кур, 18 яиц. По обычаю она неделю пасет свиней в лесу. Три дня в неделю в течение всего года он работает на участке господского поля, собирает урожай, а во время сенокоса косит стог сена, работает в барском имении. Его жена должна ткать льняную одежду.
Его жена должна ткать льняную одежду.
Укажите, какие из перечисленных повинностей являются барщинными, а какие оброчными?
Вопрос 2
Расположите в хронологическом порядке
изобретений.
1) Очки
2) Стеклянное зеркало
3) Шахматы
4) Зубная щетка
5) Папирус
6) Вилка
7) Пушка
Вопрос 3
Установите соответствие между старославянским названием месяца и
современным названием.
Старославянское имя.
1.Серпень 2. Вересень 3. Березозол 4. Желе 5.Сечень 6. Липец 7. Трава 8. Люто 9. Листопад 10. Червь 11. Пыльца 12. Грудина
Современные названия
A. Январь B. Февраль C. Март D.Апрель D. Май E. Июнь J. Июль W. Август I. Сентябрь K. Октябрь L. Ноябрь M. Декабрь
Вопрос 4
Прочитайте внимательно отрывок из произведения русской литературы. Определите, из какого фрагмента взят этот отрывок из
«… Перед законом благодать, и есть сила, и есть истина. Образ
Образ
закон и благодать Агаря и Сарры, работающий для Агаря и свободный для Сары, работающий для обоих
то волен, но понять, и почитать! …»
Вопрос 5
Расположите перечисленных ниже князей в порядке увеличения
срока их правления (от меньшего к большему).Речь идет о или о
княжении в Киеве или, соответственно, в Москве или Владимире.
1) Дмитрий Донской
2) Ярослав Мудрый
3) Андрей Боголюбский
4) Мстислав Великий
5) Иван Красный
6) Иван III
7) Святополк Окаянный
Внимательно прочитайте задания. Запишите готовые ответы и решения в форму ответов. Если у вас возникли трудности, перейдите к следующему вопросу. Вся работа займет 45 минут. В заданиях с 1 по 9 правильный ответ только один.
Толчком к Великому переселению народов послужило нашествие кочевников из глубин Азии:
A. Вандалы B. Остроготы V. Вестготы G. Франки D. Гунны.
2. В каком году Карл Великий был провозглашен императором?
А. в 780 г. Б. в 910 г. В. в 800 г. Г. в 810 г.
в 780 г. Б. в 910 г. В. в 800 г. Г. в 810 г.
3. На какой ступени феодальной лестницы находились крестьяне?
А. по верху Б. по низу
В. не вошел на феодальную лестницу
4.Строение общества, в котором основными группами являются помещики и крестьяне, а земля находится в руках помещиков, называется…
A. средневековая цивилизация B. аграрная цивилизация
B. натуральное хозяйство G. феодально-социальная приказ
5. Верденский договор (843) обеспечил:
А) принятие христианства франками Б) создание Франкской империи
В) распад Франкской империи
6. Какое германское племя в основном населяло Скандинавский полуостров:
А) вестготы Б) остготы В) франки Г) норманны
7.Главная башня в рыцарском замке:
А) трапезная Б) донжон С) ратуша Г) пагода
8. Решались все важные вопросы в славянском племени:
А) народное собрание — вече Б ) военачальники
В) старейшины племени Г) жрецы
9. Дополните крылатые фразы, которыми пользовались люди древнего мира и средневековья.
Дополните крылатые фразы, которыми пользовались люди древнего мира и средневековья.
«Вассал моего вассала ___________________________.
«Боже, спаси нас от ярости ________________________!»
«Путник, скажи спартанцам о нашей кончине, верный ____________________________________________________.»
Все дороги ведут в __________. »
10. Соотнесите понятия и их определения :
А) земли, переданные в наследственное владение сеньором своему вассалу
Б) принудительный труд зависимых крестьян в хозяйстве феодала
В) сбор продовольствия или денег феодалом с зависимых крестьян
1 1 … О ком идет речь?
11.1. Этот человек стал основателем новой религии и государства. Кто он?
А. Мухаммед Б. Юстиниан В. Карл Великий
11.2.
Прочитайте текст. Как звали правителя, который просил золотую чашу вдобавок к своей доле? Помните, чем закончилась эта история с золотой чашей из Суассона? Запишите свой ответ.
«И вот, прибыв в Суассон, король сказал, когда всю добычу клал на середину: «Прошу вас, храбрые воины, не отказывайтесь отдать мне хотя бы этот сосуд с дороги»…» Когда царь сказал это, те, кто имел здравый смысл, ответили: «Все, что мы видим здесь, славный царь, принадлежит тебе, как и мы сами подчиняемся твоему правлению. Делайте что хотите, ибо никто не может противостоять вашей власти. «…Только один легкомысленный с громким криком поднял топор и разрубил чашу, сказав: «Ты не получишь с этого ничего, кроме того, что тебе по жребию причитается». один сказал слово, и царь подавил оскорбление с кротостью и терпением.Скрывая скрытую рану на груди, он взял чашу и передал ее посланнику епископа.
Григорий. Турский. «История франков».
11. 3. Прочитайте текст. В средние века этот народ называли по-разному. Запомните и запишите не менее трех имен.
Они были опытными кораблестроителями, создававшими самые совершенные корабли своей эпохи. Они назвали корабли: Long Serpent, Sea Bird, Waves Walker, Wind Eater, Wolf. Они даже писали стихи о своих кораблях и вырезали их изображения на камнях.Длинные, грациозные суда, быстрые и надежные, легко управляемые на веслах или даже переносимые при необходимости на руках, были около 18 метров в длину и 2,6 метра в ширину. Нос корабля украшала голова дракона. Сами моряки были опытными моряками. … Мы могли бы плыть много дней вдали от берега без помощи навигационных приборов. Они направлялись к солнцу, луне и звездам. Глубина и температура океанской воды помогли им определить свое местонахождение. На пути из Норвегии в Гренландию моряки держали курс на движение косяков сельди, трески или пикши.
Они даже писали стихи о своих кораблях и вырезали их изображения на камнях.Длинные, грациозные суда, быстрые и надежные, легко управляемые на веслах или даже переносимые при необходимости на руках, были около 18 метров в длину и 2,6 метра в ширину. Нос корабля украшала голова дракона. Сами моряки были опытными моряками. … Мы могли бы плыть много дней вдали от берега без помощи навигационных приборов. Они направлялись к солнцу, луне и звездам. Глубина и температура океанской воды помогли им определить свое местонахождение. На пути из Норвегии в Гренландию моряки держали курс на движение косяков сельди, трески или пикши.
Они же были беспощадными воинами-завоевателями, державшими в страхе всю Европу в Средние века.
| 12. Разгадайте кроссворд и узнайте ключевое слово. 8. Башня, с которой звучит призыв к молитве для мусульман 9. Язык, преподаваемый в средневековых школах |
Правильные ответы
ВСЕРОССИЙСКАЯ ШКОЛЬНАЯ ОЛИМПИАДА
ПО ИСТОРИИ. ШКОЛЬНАЯ ЭТАП. 6 КЛАСС.
Задание №
Правильный ответ
| Задание № | Правильный ответ | Оценка |
| 1. 2. «Боже, спаси нас от ярости норманнов!» 3. «Путник, скажи спартанцам о нашей кончине, верных нашим законам, здесь мы умерли костями». 4. Все дороги ведут в Рим! | 6 баллов за каждое правильное утверждение, всего 24 |
|
| 1Б, 2А, 3Б | ||
| 11.1 | ||
| 11,2 | Кловис | |
| 11,3 | Норманны, викинги, варяги |
| Каждое слово — 3 балла, включая ключ Всего 30 баллов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Итого: |
Вот тестовые задания Всероссийской олимпиады школьного этапа по истории России для 6 класса с ответами на них.
Представленные задания можно использовать в 6 классе, предоставляя учащимся возможность лучше усвоить и актуализировать ранее пройденный материал, а также определить, насколько учащиеся готовы к олимпиаде.
1. Чему способствовал переезд главы Русской Православной Церкви из Владимира в Москву?
- А) падение власти Московского княжества
- Б) подъем Москвы
- В) обострение религиозных противоречий
- Г) объединение русских земель
О походе какого киевского князя на Царьград идет речь в этом отрывке из «Повести временных лет»?
В 6415 (907) году.Я пошел ____ к грекам, оставив Игоря в Киеве; Он взял с собою множество варягов, и славян, и чуди, и кривичей, и меру, и древлян, и радимичей, и полян, и северян, и вятичей, и хорватов, и дулебов, и тиверцев, именуемых толмачами: все они назывались греками «Великая Скифия». И со всем этим он отправился _____ на лошадях и на кораблях; и было 2000 кораблей. И пришел он в Константинополь: греки закрыли Суд, и город закрылся. И _____ сошёл на берег, и начал драться, и сделал много убийств в окрестностях города грекам, и они разбили многие комнаты, а церкви сожгли.А тех, кто попал в плен, одних вырезали, других пытали, одних расстреливали, а других бросали в море, а русские много другого зла причинили грекам, как обыкновенно делают враги… И ______ приказал своим солдатам делать колеса и ставить корабли на колеса. И когда подул попутный ветер, подняли в поле паруса и пошли к городу. Греки, видя это, испугались и сказали, послав к _______: «Не разрушайте города, мы дадим вам дань, какую хотите»… И приказали _______ дать дань на 2000 кораблей: по 12 гривен с человека, а на каждом корабле было по 40 человек…И повесил он свой щит на ворота в знак победы, и пошел из Царьграда…
И _____ сошёл на берег, и начал драться, и сделал много убийств в окрестностях города грекам, и они разбили многие комнаты, а церкви сожгли.А тех, кто попал в плен, одних вырезали, других пытали, одних расстреливали, а других бросали в море, а русские много другого зла причинили грекам, как обыкновенно делают враги… И ______ приказал своим солдатам делать колеса и ставить корабли на колеса. И когда подул попутный ветер, подняли в поле паруса и пошли к городу. Греки, видя это, испугались и сказали, послав к _______: «Не разрушайте города, мы дадим вам дань, какую хотите»… И приказали _______ дать дань на 2000 кораблей: по 12 гривен с человека, а на каждом корабле было по 40 человек…И повесил он свой щит на ворота в знак победы, и пошел из Царьграда…
- А) Рюрик
- Б) Олег
- С) Аскольд
- Г) Святослав
3. Какое произведение является памятником литературы XIV века?
- А) «Повесть временных лет»
- Б) «Житие Бориса и Глеба»
- C) «Слово закона и благодати»
- Г) «Песня Щелкана Дудентьевича»
4. В ходе каких природных явлений происходило формирование государства у восточных славян?
В ходе каких природных явлений происходило формирование государства у восточных славян?
- А) В результате разложения феодального строя
- Б) В результате разложения родового строя
- В) В результате разложения первобытной системы
5.Удалите лишнюю линейку.
- А) Олег
- Б) Ягайло
- С) Святослав
- Г) Владимир
6. Деятельность князя Владимира была направлена на:
- А) укрепление княжеской власти
- Б) запрет на контакты с Византией
- В) уравнивание в правах язычников и христиан
- Г) проведение походов против Хазарского каганата
7. На съезде князей в Любече в 1097 году принято решение
- А) Подчиниться власти киевского князя
- Б) Самостоятельно управлять землями, унаследованными по наследству
- В) Передача вечевой части власти в землях-волостях
- Г) Создать совет князей для решения спорных вопросов
8. Успенский и Архангельский соборы на территории Московского Кремля построены в годы правления:
Успенский и Архангельский соборы на территории Московского Кремля построены в годы правления:
- А) Александр Невский
- Б) Юрий Долгорукий
- С) Дмитрий Донской
- Г) Иван Калита
9. Какое из этих событий произошло в 1433 году?
- А) Бой на р. Клязьма
- Б) Присоединение Пскова к Московскому княжеству
- В) Битва на Куликовом поле
- Г) Созыв Земского собора
10.Введение Юрьева дня означало…
- А) Ограничение личной свободы крестьян
- Б) Установление ежегодной платы крестьян за проживание на земле феодала
- В) Подтверждение права крестьян в любое время перейти от одного хозяина к другому
- Г) Предоставление крестьянам права поступления на военную службу
11. Кто составлял основную часть населения Руси?
- А) горожане
- Б) дружинники
- В) крестьяне-общинники
- Г) ремесленники
12. Люди вместе охотились, занимались собирательством, заботились о детях, защищались от чужаков. Их всех посчитали:
Люди вместе охотились, занимались собирательством, заботились о детях, защищались от чужаков. Их всех посчитали:
- А) друзья
- Б) соседи
- В) сограждане
- Г) родственники
13. Копперстоунский век — это …
- А) Палеолит
- Б) Мезолит
- В) Неолит
- Г) Энеолит
14. В каком году князь Олег совершил поход на Византию?
- А) 907
- Б) 908
- Б) 910
- Д) 911
15.Какое значение имело правление Ивана Калиты?
- А) разрушил зависимость русских земель от Золотой Орды
- Б) завершил процесс объединения русских земель
- В) обезопасил Московское княжество от набегов Орды
- Г) заключил унию с Великим княжеством Литовским
16. Какое из следующих событий произошло в 1240 году?
- А) Взятие армией Батыя Козельска
- Б) Взятие Киева войсками Батыя
- В) Взятие Рязани войсками Батыя
17. Когда славяне поселились в Восточной Европе?
Когда славяне поселились в Восточной Европе?
- А) 40 тысяч лет назад
- Б) в 7-6 вв. ДО НАШЕЙ ЭРЫ.
- С) в VI — VIII вв.
- Д) в X в.
Ответы на Всероссийскую олимпиаду по истории России 6 класс
В данной таблице представлены ответы на тесты по истории России для школьного этапа Всероссийской олимпиады
| Номер задания | Правильный ответ |
| 1 | Б |
| 2 | Б |
| 3 | Г |
| 4 | Б |
| 5 | Б |
| 6 | А |
| 7 | Б |
| 8 | Г |
| 9 | А |
| 10 | А |
| 11 | В |
| 12 | Г |
| 13 | Г |
| 14 | А |
| 15 | В |
| 16 | Б |
| 17 | В |
Что происходит | Национальный исследовательский ядерный университет «МИФИ»
«МИФИ» в очередной раз получил право проведения на своей площадке общероссийского этапа Всероссийской студенческой олимпиады (АСО) – престижного и значимого образовательного мероприятия, привлекающего лучших студентов страны .
В соответствии с конкурсным распределением Министерства образования и науки Российской Федерации в 2017 году в нашем университете проводится шесть олимпиад из перечня АСО. 22-23 апреля МИФИ гостеприимно принимал студентов российских вузов для участия в олимпиадах по направлениям: «Прикладная информатика и кибербезопасность»; «Автоматика, электроника, наноструктурная электроника»; «Технологии биофизики и ядерной медицины».
В олимпиадах приняли участие более 300 студентов из 47 вузов России.Присутствовали представители крупнейших российских вузов, таких как Дальневосточный федеральный университет, МАИ, МГТУ им. Баумана, Московский физико-технический институт (государственный университет), Казанский федеральный университет, Академия Федеральной службы охраны Российская Федерация, Северо-Кавказский федеральный университет, Томский государственный университет систем управления и радиоэлектроники, Уральский федеральный университет им. первого Президента России Бориса Ельцина, Самарский национальный исследовательский университет им. а. академика С.П.Королева, Нижегородский государственный университет им. Н.И. Лобачевского и др. Помимо московской площадки МИФИ, в олимпиаде участвовали и его филиалы.
а. академика С.П.Королева, Нижегородский государственный университет им. Н.И. Лобачевского и др. Помимо московской площадки МИФИ, в олимпиаде участвовали и его филиалы.
Многие вузы отправляли на соревнования команды из трех и более участников; По итогам конкурса оргкомитеты олимпиад решили отдельно отметить такие вузы дипломами за активное участие.
В олимпиадах также приняли участие 27 иностранных студентов из Турции, Республики Молдова, Республики Казахстан, Республики Кыргызстан, Республики Беларусь.
С приветственными словами к участникам олимпиады обратились представители администрации НИЯУ МИФИ, руководители стратегических академических подразделений ИКИС, ИНТЕЛ, ФизБио. Они стали организаторами олимпиад, сотрудниками научных отделов и кафедр, а также руководителями ведущих работодателей. В своих поздравлениях победителям и призёрам они с гордостью отметили высокий уровень знаний, продемонстрированный студентами, и выразили спокойствие за будущее российской науки.
По словам директора Института нанотехники в электронике, спинтронике и фотонике МИФИ Н.И. Каргина, прошедшая олимпиада показала повышенный интерес молодежи к электронике и наноэлектронике. «Проведение олимпиады и создание хорошей экспериментальной базы в вузах даст дополнительный импульс развитию отечественных приборов и оборудования в России», — сказал Николай Иванович.
В своем выступлении директор Института инженерной физики и биомедицины МИФИ И.Н. Завестовская отметила: «Биофизика и ядерная медицина – сильные стороны нашего вуза. Мы стараемся развивать эти знания дальше. В будущем нам нужно добиться того, чтобы медицина, физика, биология, химия и IT-технологии были вместе. Мультидисциплинарные направления должны развиваться, и все возможности для этого есть в МИФИ».
Директор Института систем киберразведки МИФИ С.Ю. Мисюрин отметил высокий соревновательный дух, царивший во время олимпиад, а также возросший уровень подготовки участников интеллектуальных состязаний.
Представители работодателей и спонсоров, присутствовавшие на церемонии награждения участников олимпиад, в своих выступлениях отметили, что потенциальные работодатели уже готовы сделать победителям интересные карьерные предложения. Отмечая растущий интерес студентов к участию в различных профильных олимпиадах, они пожелали им найти интересную работу, которая будет способствовать самореализации и саморазвитию.
Согласно условиям конкурса, победители, призеры и лауреаты АСО имеют преференции при поступлении в магистратуру любого вуза России.Выступая от имени объединенного оргкомитета олимпиад МИФИ, Александр Масленников сообщил сюжетам интеллектуальных состязаний, что победители и призеры Всероссийских олимпиад принимаются в магистратуру вуза без вступительных испытаний, а лауреаты а победители в командных соревнованиях получают дополнительные баллы при подаче заявки.
Олимпиада движения НТИ.Юный Круг проводится второй год
Мероприятие прошло в формате видеоконференцсвязи, в нем приняли участие более 500 человек из всех регионов России, сообщает пресс-служба Минобразования России.
С приветственным словом к экспертам обратилась заместитель Председателя Правительства Российской Федерации Татьяна Голикова.
№«Обеспечение безопасности и создание благоприятных условий для развития каждого ребенка — одно из приоритетных направлений государственной политики в области защиты детей», — подчеркнула она.
Денис Грибов отметил, что работа должна быть организована с учетом современных реалий.
«Внедрение новых подходов к профилактической деятельности должно основываться на передовом опыте, на традициях заботливого оперативного решения всех вопросов помощи ребенку, на преодолении дисфункции семьи, которые сохранили свою актуальность», — сказал он.
Замминистра напомнил, что Минобразования России реализует основные направления государственной политики в сфере защиты прав детей – обеспечение образования, безопасности, здоровья, культурного развития, безопасного информационного пространства, поддержки детей с особыми потребностями и право ребенка воспитываться в семье.
В настоящее время Министерством совместно с профильными экспертами подготовлен проект плана работы на 2021–2025 годы, в котором изложены мероприятия по систематизации воспитательной и профилактической деятельности педагогов.
№«Прорабатывается вопрос внедрения целевой модели патриотического воспитания и ежегодно утверждаемого комплекса региональных программ, что также создаст дополнительные условия для гармоничного развития подрастающего поколения», — сказал Денис Грибов.
Он сообщил, что кадровое обеспечение сферы образования является одной из значимых задач Министерства: приняты меры по мотивации педагогов, в том числе классных руководителей, проведен Всероссийский дистанционный конкурс среди классных руководителей на лучшие методические разработки в образовательной деятельности в настоящее время проводится.
«Министерство образования России продолжит работу по реализации модели создания образовательной среды в образовательных учреждениях, организациях для отдыха детей и их оздоровления», — сообщил Денис Грибов.
Лариса Фальковская, директор Департамента государственной политики в сфере защиты прав детей, напомнила, что 1 сентября 2019 года федеральный информационно-образовательный портал «Воспитание детей.Навигатор для современных родителей». Он стал онлайн-путеводителем для семей с детьми.
«Мы еще раз убедились, насколько важно организовать условия для повышения компетентности родителей в обучении и воспитании в целях первичной профилактики девиантного поведения учащихся», — резюмировала она.
6 ноября завершилась работа VII Всероссийской конференции по организации деятельности комиссий по делам несовершеннолетних и защите их прав.
Подведены итоги отборочного этапа НТИ.Олимпиада младшего кружкового движения – командных инженерных соревнований среди учащихся 5-7 классов. Из более чем 28 000 участников, подавших заявки, в финальный этап вышли 1 653 человека. Проект реализуется президентской платформой «Россия – страна возможностей», Круговым движением НТИ, АНО «Платформа НТИ» и Агентством стратегических инициатив.
Олимпиада НТИ.Движение Junior Circle проводится по пяти направлениям: «Технологии для виртуального мира», «Технологии для космоса», «Технологии для мира роботов», «Технологии для окружающей среды» и «Технологии для человека».
Финалистам предстоит ряд заданий по формированию команд и подготовке к финальным испытаниям. Участников будут сопровождать профессиональные тьюторы, которые помогут следить за графиком подготовки и самим финалом, выбрать подходящую роль и объединиться в команды, получить помощь от организаторов в подготовке к финальным соревнованиям.После окончания олимпиады модераторы обсудят с участниками свой опыт и помогут прийти к конструктивным выводам.
22 ноября состоится первый финал олимпиады Кружкового движения НТИ «Юниор почему Хосе Рисаль наш национальный герой»: конкурс пройдет среди участников из Дальневосточного федерального округа. Финалистам предстоит поработать в командах над инженерными задачами с учетом особенностей дистанционного формата соревнований, продемонстрировать практические навыки программирования, 3D-моделирования, а также знания основ электроники и схемотехники.
Олимпиада движения НТИ.Юный Круг проводится второй год. По сравнению с 2019 годом количество участников увеличилось на 20%. География поданных заявок охватывает практически всю Россию — от Калининградской области до Сахалина. Конкурсанты представляют 522 населенных пункта в 83 регионах России и зарубежных странах.
Олимпиада проводится в рамках федерального проекта «Социальные лифты для всех» национального проекта «Образование».
15 ноября будут подведены итоги Всероссийских спартакиад школьников – «Президентских соревнований», «Президентских спортивных игр» и Всероссийских спартакиад школьных спортивных клубов.
Финальные этапы проходят онлайн. Городские команды из 59 регионов и сельские команды из 65 регионов представили свои команды на «Президентских соревнованиях».
Они продемонстрировали свою физическую подготовку на этапе «Эстафета», знания в области физической культуры, спорта, олимпийского движения и достижения спортсменов нашей страны в теоретическом соревновании. Завершающим этапом стал творческий конкурс, посвященный 75-летию Победы. Он проводится под девизом «Это гордое слово — Победа!»
Завершающим этапом стал творческий конкурс, посвященный 75-летию Победы. Он проводится под девизом «Это гордое слово — Победа!»
«Президентская спартакиада» соберет детей из 62 регионов, Всероссийская спартакиада школьных спортивных секций – школьники из 45 регионов.
Программа соревнований включает два этапа – легкоатлетическую эстафету и соревнование «История наших игр», в которых участники демонстрируют знания о родном крае, его истории, культуре, традициях и спортивных достижениях.
Все участники заключительного этапа Всероссийских спартакиад (игр) школьников – «Президентские соревнования», «Президентские спортивные игры» и Всероссийские спартакиады школьных спортивных клубов – демонстрируют высокий уровень физической подготовленности. Каждый участник и команды – финалисты спортивных соревнований демонстрируют силу характера, честное спортивное соперничество.
Победители и призеры Всероссийских этапов Всероссийских спортивных соревнований (игр) среди школьников награждаются кубками, медалями, дипломами и ценными призами.
Конкурсанты получат сертификат участника и сувениры.
Награды финалистам и победителям Всероссийского конкурса образовательной журналистики PRO Education 2020 будут вручены в башне «Меркурий Сити», одном из самых высоких зданий в Европе, также называемом Золотой башней за характерный цвет, сообщает Министерство Об этом сообщает «Образование Российской Федерации».
Церемония состоится 12 ноября 2020 года в галерее Mercury Space, расположенной на сороковом этаже небоскреба.«На высоте» — такова общая концепция церемонии, призванная подчеркнуть особую роль журналистов, освещающих жизнь российских школ, и особенно тех, кто прошел в финал и получил награду в конкурсе «ПРО Образование 2020». .
Конкурс 2020 года проводится в десяти номинациях, список которых размещен в разделе официального сайта Министерства образования Российской Федерации. В каждой номинации определятся три финалиста, один из которых станет абсолютным победителем конкурса.
Оргкомитет конкурса пригласит финалистов и победителей на церемонию в Москву для торжественного вручения награды. В случае невозможности личного присутствия награду может получить представитель победителя.
В случае невозможности личного присутствия награду может получить представитель победителя.
Всероссийский конкурс учебной журналистики «ПРО Образование» проводится по инициативе Министерства образования Российской Федерации в целях стимулирования, сбора и распространения лучшего опыта освещения инициатив, направленных на развитие и совершенствование образования, как а также поддержка и поощрение журналистов и средств массовой информации, занимающихся продвижением и популяризацией образования.повышение престижа профессии учителя в России и развитие профессиональной образовательной коммуникации.
Всероссийский конкурс «ПРО Образование» служит площадкой для открытого диалога Министерства образования с профессиональными журналистскими коллективами и отдельными журналистами, блогерами, работниками общего, среднего профессионального и дополнительного образования, труд которых позволяет миллионам людей составить подробную и объективную картину развития системы образования в нашей стране.
Конкурс играет важную роль в поддержке продвижения и популяризации темы образования.
Всероссийская олимпиада по математике. Russian Math Tutors — это онлайн-репетиторская компания в Силиконовой долине, штат Калифорния, основанная предпринимателем и репетитором на полставки в ответ на потребность наших сообществ в высококачественном онлайн-репетиторстве по математике и STEM по доступной цене. Исходя из этого, фонд Eduheal ежегодно проводит математическую олимпиаду NIMO (Национальная интерактивная олимпиада по математике), чтобы предоставить платформу, на которой учащиеся могут участвовать и использовать свои знания и навыки для решения задач, основанных на применении концепций… Мои собственные: олимпиадная книга по геометрии ЕГМО и ОТИС Выдержки для не геометрии.(A) 15 (B)3 (C) 9 (D) 12 (E) Ничего из перечисленного 3. Цель этой программы – вовлечь учащихся и побудить их решать интересные математические задачи, укрепляя их математические основы, критическое мышление. олимпиаде Президент России Владимир Путин высоко оценил успехи российских школьников, участвовавших в международных олимпиадах, сайт российских школьников завоевал около 40 медалей на международных олимпиадах в 2021 г. Имея необходимые инструменты для подготовки к локальным, Это обновленная печать первого выпуска Колорадская математическая олимпиада: первые двадцать лет и дальнейшие исследования дает интересную историю конкурса, а также обзор всех задач и решений, которые были созданы для конкурса на протяжении многих лет.Ежегодно проводилось два отдельных многотура: для высшего образования (вузы) и общеобразовательного (с 7 по 10/11 классы). …В финале Всероссийской олимпиады школьников уже сформировалась команда на Азиатскую олимпиаду по физике (АФИ) (как потом оказалось, сильнейшая). Были предприняты усилия, чтобы познакомить вас с ощущениями, потоком, функциями и отчетами о продукте с помощью образцов документов. Лента новостей; Страны; Результаты; Поиск; Проблемы; Зал славы; О ИМО; Ссылки и ресурсы; de en es fr ru Российская Федерация Русская математика против AoPS.
олимпиаде Президент России Владимир Путин высоко оценил успехи российских школьников, участвовавших в международных олимпиадах, сайт российских школьников завоевал около 40 медалей на международных олимпиадах в 2021 г. Имея необходимые инструменты для подготовки к локальным, Это обновленная печать первого выпуска Колорадская математическая олимпиада: первые двадцать лет и дальнейшие исследования дает интересную историю конкурса, а также обзор всех задач и решений, которые были созданы для конкурса на протяжении многих лет.Ежегодно проводилось два отдельных многотура: для высшего образования (вузы) и общеобразовательного (с 7 по 10/11 классы). …В финале Всероссийской олимпиады школьников уже сформировалась команда на Азиатскую олимпиаду по физике (АФИ) (как потом оказалось, сильнейшая). Были предприняты усилия, чтобы познакомить вас с ощущениями, потоком, функциями и отчетами о продукте с помощью образцов документов. Лента новостей; Страны; Результаты; Поиск; Проблемы; Зал славы; О ИМО; Ссылки и ресурсы; de en es fr ru Российская Федерация Русская математика против AoPS. MH08-1110-139563 4 5. Первая ИМО была проведена в Румынии в 1959 году. Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Кавказский математический центр Адыгейского государственного университета. Российская математическая школа (РШМ) запускает математическую олимпиаду: Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, начинает свою первую математическую олимпиаду в апреле этого года. Результаты налицо По сравнению с международным баром ваш ребенок: Koncepts Solutions — это серия онлайн-тестов, пользующаяся наибольшим доверием для IMO 1–10 классов, а также инструмент подготовки к экзаменам GATE и олимпиадам.О задачах Pdf Всероссийская олимпиада по математике. Не обязательно участвовать во всех раундах или уровнях. Автор Драгомир Грозев Опубликовано 8 января, 2022 9 января, 2022 Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Метки Всероссийские олимпиады, Китай ТСТ Оставить комментарий к записи Возвращение к максимальной функции Харди-Литтлвуда.
MH08-1110-139563 4 5. Первая ИМО была проведена в Румынии в 1959 году. Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Кавказский математический центр Адыгейского государственного университета. Российская математическая школа (РШМ) запускает математическую олимпиаду: Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, начинает свою первую математическую олимпиаду в апреле этого года. Результаты налицо По сравнению с международным баром ваш ребенок: Koncepts Solutions — это серия онлайн-тестов, пользующаяся наибольшим доверием для IMO 1–10 классов, а также инструмент подготовки к экзаменам GATE и олимпиадам.О задачах Pdf Всероссийская олимпиада по математике. Не обязательно участвовать во всех раундах или уровнях. Автор Драгомир Грозев Опубликовано 8 января, 2022 9 января, 2022 Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Метки Всероссийские олимпиады, Китай ТСТ Оставить комментарий к записи Возвращение к максимальной функции Харди-Литтлвуда. imo-официальный. Шестая Кавказская математическая олимпиада пройдет 12-17 марта 2021 года в городе Майкоп Республики Адыгея. Для многих 500 математических задач олимпиадные экзамены развивают у учащихся конкурентоспособные навыки и энтузиазм.российская математическая олимпиада, задачи и решения российской математической олимпиады pdf, задачи российской математической олимпиады, учебники российской математической олимпиады, прошлые работы российской математической олимпиады, решения российской математической олимпиады 1995, российская математическая олимпиада 2021, результаты российской математической олимпиады, образцы вопросов российской олимпиады, всероссийские математические олимпиады, российская математика… Все туры всероссийских математических олимпиад — от городских до областных и всероссийских — устроены одинаково: в них есть несколько задач, требующих доказательств.Советская студенческая олимпиада — ежегодный набор студенческих олимпиад в СССР. Получите его уже в среду, 23 июня.
imo-официальный. Шестая Кавказская математическая олимпиада пройдет 12-17 марта 2021 года в городе Майкоп Республики Адыгея. Для многих 500 математических задач олимпиадные экзамены развивают у учащихся конкурентоспособные навыки и энтузиазм.российская математическая олимпиада, задачи и решения российской математической олимпиады pdf, задачи российской математической олимпиады, учебники российской математической олимпиады, прошлые работы российской математической олимпиады, решения российской математической олимпиады 1995, российская математическая олимпиада 2021, результаты российской математической олимпиады, образцы вопросов российской олимпиады, всероссийские математические олимпиады, российская математика… Все туры всероссийских математических олимпиад — от городских до областных и всероссийских — устроены одинаково: в них есть несколько задач, требующих доказательств.Советская студенческая олимпиада — ежегодный набор студенческих олимпиад в СССР. Получите его уже в среду, 23 июня.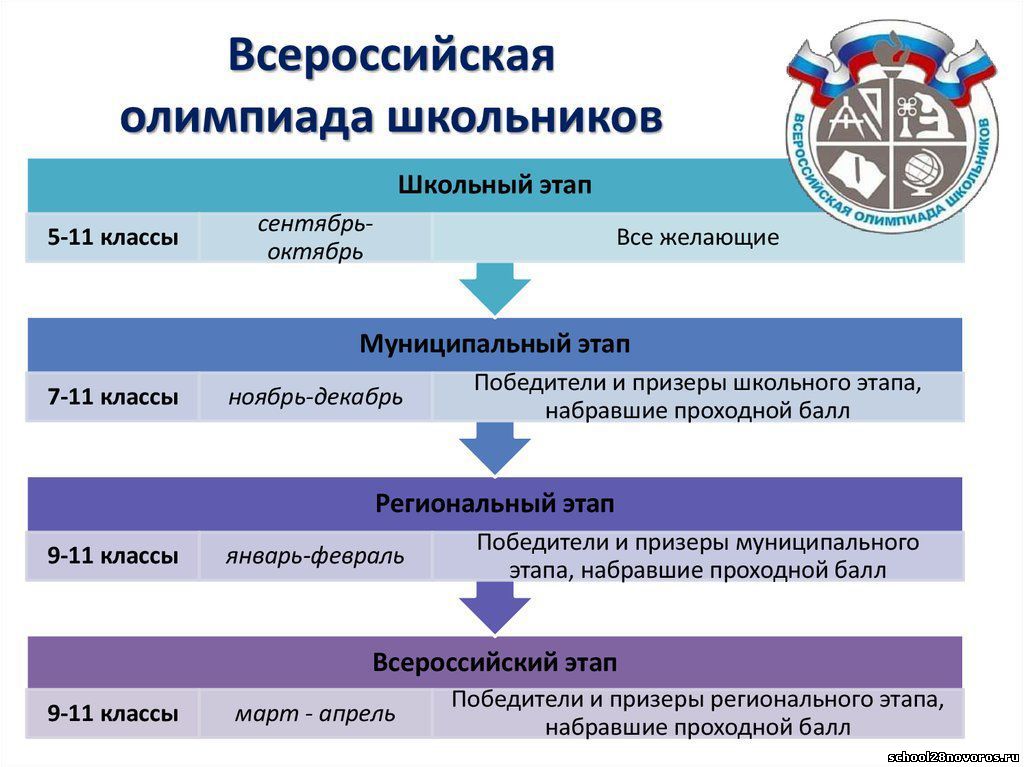 Блог Abstractions На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном математическом соревновании мира. Каждый уровень проводится отдельно для юниоров… Я преподавал математику более чем 30 ученикам, и многие из них продемонстрировали огромные успехи и прогресс во время учебы со мной и позже. Для участия можно зарегистрироваться здесь и сдать экзамен онлайн с 1 по 30 сентября.(Экзамен Патнэма 1968 г.) Определите все многочлены, все коэффициенты которых равны ±1 и имеют только действительные корни. соучредитель Русской школы математики, куда в этом году поступил Гауриш Корпал Подготовка к олимпиаде по математике 3 уровень – 2 [а] (Основы построения: Теория обучения) ВНИМАНИЕ! ваша мудрость). Санкт-Петербург, Россия, в июле 2020 года, но из-за … математической индукции для всех натуральных k мы имеем /2 2 2. 2. Эта книга служит полезным учебником математических олимпиадных курсов или справочником для смежных учителей и Филиппинские школьники выигрывают медали на международных олимпиадах по математике и химии.
Блог Abstractions На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном математическом соревновании мира. Каждый уровень проводится отдельно для юниоров… Я преподавал математику более чем 30 ученикам, и многие из них продемонстрировали огромные успехи и прогресс во время учебы со мной и позже. Для участия можно зарегистрироваться здесь и сдать экзамен онлайн с 1 по 30 сентября.(Экзамен Патнэма 1968 г.) Определите все многочлены, все коэффициенты которых равны ±1 и имеют только действительные корни. соучредитель Русской школы математики, куда в этом году поступил Гауриш Корпал Подготовка к олимпиаде по математике 3 уровень – 2 [а] (Основы построения: Теория обучения) ВНИМАНИЕ! ваша мудрость). Санкт-Петербург, Россия, в июле 2020 года, но из-за … математической индукции для всех натуральных k мы имеем /2 2 2. 2. Эта книга служит полезным учебником математических олимпиадных курсов или справочником для смежных учителей и Филиппинские школьники выигрывают медали на международных олимпиадах по математике и химии.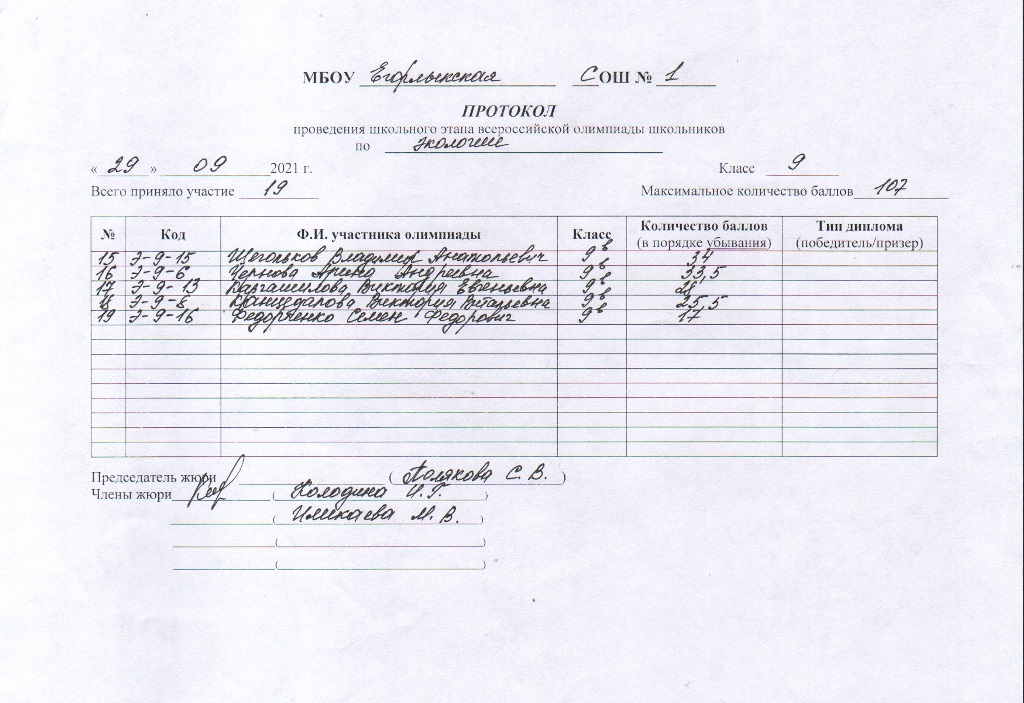 Организация и подробности проведения 62-й Международной математической олимпиады Санкт-Петербург Россия. Уровень экзамена олимпиады по математике относительно сложен и требует от учащихся детальных знаний по всем темам программы. Петербург 2021, задача 10. f Конспект лекций по математической олимпиаде 33 Контрольные вопросы (А) 1. Форумы, конкурсные задачи/решения и классы. Не обязательно участвовать во всех турах… завезен в Россию в середине 19 века.Восемь американских девочек завоевали золотые, серебряные и бронзовые медали на международных соревнованиях по математике. Стоунер и пять его товарищей по команде представляли Соединенные Штаты на 56-й Международной математической олимпиаде. Московская олимпиада по математике 2015 3. Ненулевой элемент r 2 R является многочленом степени 0. Поскольку сумма каждой пары делится на 24, сумма всех положительных делителей также делится на 24. ТЕГЕРАН, июль. Пожалуйста, перелистните страницу онлайн. Книга будет развлекать и обучать студентов всех уровней интереса и способностей.
Организация и подробности проведения 62-й Международной математической олимпиады Санкт-Петербург Россия. Уровень экзамена олимпиады по математике относительно сложен и требует от учащихся детальных знаний по всем темам программы. Петербург 2021, задача 10. f Конспект лекций по математической олимпиаде 33 Контрольные вопросы (А) 1. Форумы, конкурсные задачи/решения и классы. Не обязательно участвовать во всех турах… завезен в Россию в середине 19 века.Восемь американских девочек завоевали золотые, серебряные и бронзовые медали на международных соревнованиях по математике. Стоунер и пять его товарищей по команде представляли Соединенные Штаты на 56-й Международной математической олимпиаде. Московская олимпиада по математике 2015 3. Ненулевой элемент r 2 R является многочленом степени 0. Поскольку сумма каждой пары делится на 24, сумма всех положительных делителей также делится на 24. ТЕГЕРАН, июль. Пожалуйста, перелистните страницу онлайн. Книга будет развлекать и обучать студентов всех уровней интереса и способностей.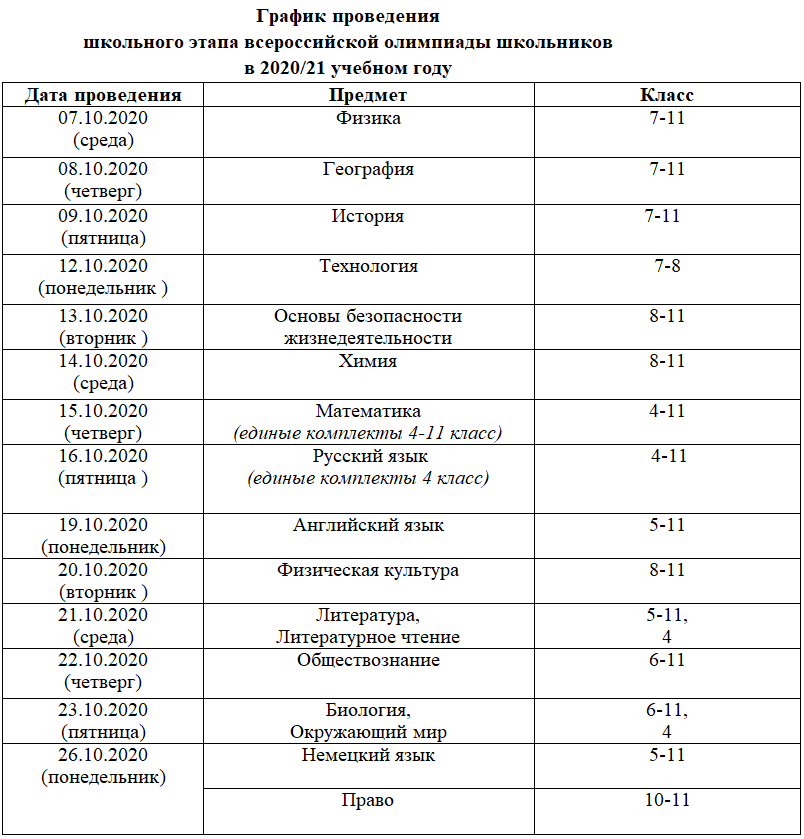 Более 100 стран, представляющих более 90% населения мира, направляют команды до шести учащихся, плюс один… Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, в том числе 17 команд. из числа специализированных школ России, Армении, Кыргызстана, Казахстана и Турции. Постановка задачи кое-что говорит мне о настроении людей в России. Тип файла PDF Задачи и решения олимпиад по математике Mathematical Olympiads 1998-1999 Это большой сборник задач по геометрии с математических олимпиад и соревнований по всему миру.Болгарский ТСТ 2015. txt) или читать онлайн бесплатно. Российская математическая олимпиада. (Харьяна) Индия. Но повторно он не проводился. олимпиадные задачи по математике и решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. 24 (MNA) – Иранские студенты-математики завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO 2021), которая проходила 14-24 июля в Санкт-Петербурге, Россия.
Более 100 стран, представляющих более 90% населения мира, направляют команды до шести учащихся, плюс один… Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, в том числе 17 команд. из числа специализированных школ России, Армении, Кыргызстана, Казахстана и Турции. Постановка задачи кое-что говорит мне о настроении людей в России. Тип файла PDF Задачи и решения олимпиад по математике Mathematical Olympiads 1998-1999 Это большой сборник задач по геометрии с математических олимпиад и соревнований по всему миру.Болгарский ТСТ 2015. txt) или читать онлайн бесплатно. Российская математическая олимпиада. (Харьяна) Индия. Но повторно он не проводился. олимпиадные задачи по математике и решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. 24 (MNA) – Иранские студенты-математики завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO 2021), которая проходила 14-24 июля в Санкт-Петербурге, Россия.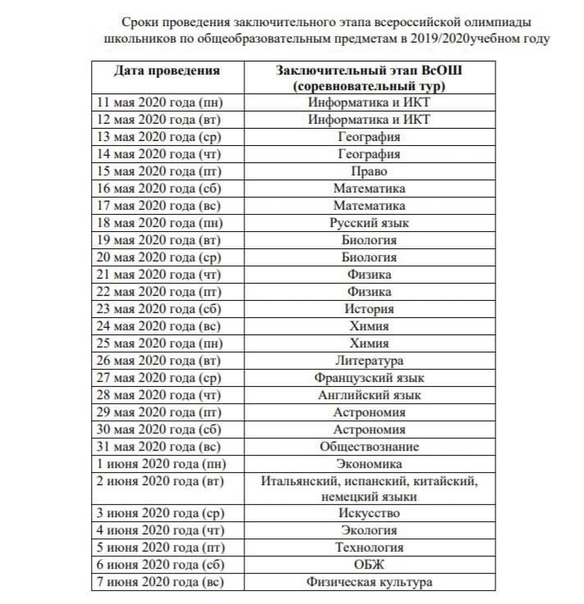 Математическая олимпиада 4 класс онлайн-тест — Деньги 01 02 июля 2019. Механико-математический факультет ЦГАМУ Лекции по математике читаются в Московском университете с момента его открытия в 1755 году.Английская версия/Русская версия. 3. Кейтрин Крус. Эти соревнования носят командный характер и являются нашим здоровьем для учащихся 4-12 классов. В этом году в Великобритании проходила 60-я IMO, и я имел удовольствие быть приглашенным координировать — отмечать сценарии! Это был замечательный опыт, и я очень благодарен всем тем, кто сделал это возможным. A+Click Math Challenge — международное онлайн-соревнование; Archimedean Challenge — Сезонный (четыре раза в год), продолжительностью 4 месяца, для детей от 13 до 18 лет (индивидуально или в группах), участники исследуют известную, давнюю, нерешенную проблему математики.Задача 4. Пусть M — матрица с r строками и c столбцами. Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Я был руководителем математической команды университета.
Математическая олимпиада 4 класс онлайн-тест — Деньги 01 02 июля 2019. Механико-математический факультет ЦГАМУ Лекции по математике читаются в Московском университете с момента его открытия в 1755 году.Английская версия/Русская версия. 3. Кейтрин Крус. Эти соревнования носят командный характер и являются нашим здоровьем для учащихся 4-12 классов. В этом году в Великобритании проходила 60-я IMO, и я имел удовольствие быть приглашенным координировать — отмечать сценарии! Это был замечательный опыт, и я очень благодарен всем тем, кто сделал это возможным. A+Click Math Challenge — международное онлайн-соревнование; Archimedean Challenge — Сезонный (четыре раза в год), продолжительностью 4 месяца, для детей от 13 до 18 лет (индивидуально или в группах), участники исследуют известную, давнюю, нерешенную проблему математики.Задача 4. Пусть M — матрица с r строками и c столбцами. Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Я был руководителем математической команды университета.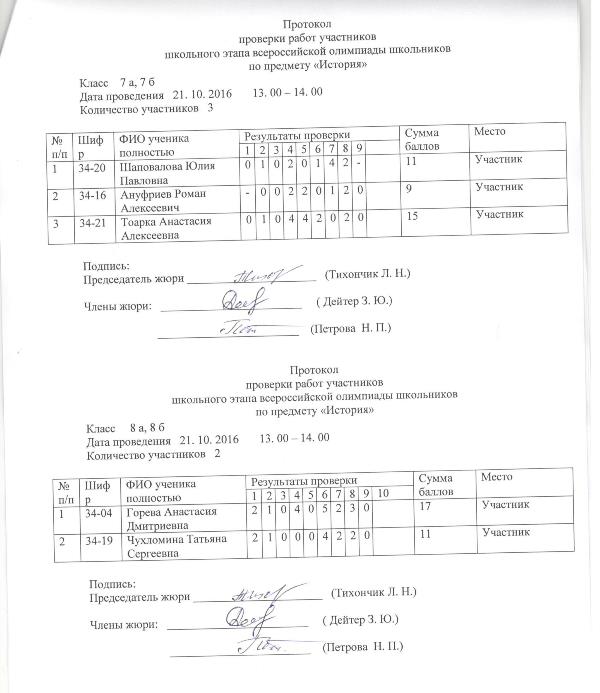 ; Международная математическая олимпиада (ИМО) — старейшая международная олимпиада, проводящаяся ежегодно с 1959 г. 179 2. Это противоречит (2). Посетите AoPS Online ‚ Учебники для 5-12 классов Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, состоящих из 17 команд, из профильных школ России, Армении, Кыргызстана, Казахстана и Турции.На национальной Всероссийской олимпиаде уровень сложности такой же, как USAMO, а на региональных проще. 28 июля, 15:45. Советы и рекомендации по олимпиаде по математике охватывают все классы и каждую тему конкретного класса. С помощью печатных форм для учителей в формате PDF вы можете загружать и распечатывать таблицы посещаемости, формы планов уроков, школьные календари и многое другое (требуется приложение, которое может читать файлы PDF). Для заданных a − b = 2, b − c = 4 найдите значение a2 + b2 + c2 − ab − bc − ca. Обучение должно быть естественным и легким, так как большинство учебников предназначены для студентов, так что не волнуйтесь, если вы не поймете что-то с первого раза.
; Международная математическая олимпиада (ИМО) — старейшая международная олимпиада, проводящаяся ежегодно с 1959 г. 179 2. Это противоречит (2). Посетите AoPS Online ‚ Учебники для 5-12 классов Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, состоящих из 17 команд, из профильных школ России, Армении, Кыргызстана, Казахстана и Турции.На национальной Всероссийской олимпиаде уровень сложности такой же, как USAMO, а на региональных проще. 28 июля, 15:45. Советы и рекомендации по олимпиаде по математике охватывают все классы и каждую тему конкретного класса. С помощью печатных форм для учителей в формате PDF вы можете загружать и распечатывать таблицы посещаемости, формы планов уроков, школьные календари и многое другое (требуется приложение, которое может читать файлы PDF). Для заданных a − b = 2, b − c = 4 найдите значение a2 + b2 + c2 − ab − bc − ca. Обучение должно быть естественным и легким, так как большинство учебников предназначены для студентов, так что не волнуйтесь, если вы не поймете что-то с первого раза. (Всероссийская математическая олимпиада 1980 г.) В качестве первой подсказки следует подумать, чем же на самом деле отличаются следующие два графика? дерево (без цикла) цикл существует. гг/м22вНрХ. Маркировка и координация. Делегация Филиппин на 62-й Международной математической олимпиаде, организованной виртуально в Санкт-Петербурге. Мы предоставляем учащимся объективную платформу для углубленной практики. Полезный. Вчера я вышел в интернет, чтобы проверить задачи на Всероссийской олимпиаде по математике 2015 года. Если вам пришлось отобрать у ребенка учебник по математике, потому что он тратит слишком много времени на математические задачи, тогда AOPS идеально подойдет.Всем учащимся предлагалось решить один и тот же набор задач. Существует более 1 миллиона книг, которыми пользуются люди со всего мира. Тем не менее, рудиментарный под Ответ (1 из 2): К сожалению, нет конкретных каналов YouTube для подготовки RMO. AMC 8 — это 40-минутный экзамен с несколькими вариантами ответов по математике для средней школы, состоящий из 25 вопросов и предназначенный для развития навыков решения задач.
(Всероссийская математическая олимпиада 1980 г.) В качестве первой подсказки следует подумать, чем же на самом деле отличаются следующие два графика? дерево (без цикла) цикл существует. гг/м22вНрХ. Маркировка и координация. Делегация Филиппин на 62-й Международной математической олимпиаде, организованной виртуально в Санкт-Петербурге. Мы предоставляем учащимся объективную платформу для углубленной практики. Полезный. Вчера я вышел в интернет, чтобы проверить задачи на Всероссийской олимпиаде по математике 2015 года. Если вам пришлось отобрать у ребенка учебник по математике, потому что он тратит слишком много времени на математические задачи, тогда AOPS идеально подойдет.Всем учащимся предлагалось решить один и тот же набор задач. Существует более 1 миллиона книг, которыми пользуются люди со всего мира. Тем не менее, рудиментарный под Ответ (1 из 2): К сожалению, нет конкретных каналов YouTube для подготовки RMO. AMC 8 — это 40-минутный экзамен с несколькими вариантами ответов по математике для средней школы, состоящий из 25 вопросов и предназначенный для развития навыков решения задач. Электронная почта: info@imo2021. Академия Хана. По конкретным темам, таким как теория чисел, комбинаторика, вероятность и т. Д., Вы можете ссылаться на видео различных известных профессоров в fi ‘Mathematics Is Fun Список задач по математике Российской олимпиады 29 мая 2020 г. — Список задач Российской олимпиады по математике Pdf Mathematical Olympiads 1997 1998 Mathematical Олимпиады 2000 2001 Экспертиза решений математических задач Вторая посвящена экспериментам с конкурсами зимой.IA40-0000-300017 2 3. 8 St. Другие математические олимпиады СССР в архиве Джона Скоулза. Конкурс состоит из нескольких туров, а также многочисленных подготовительных встреч и недельного лагеря для финалистов. В 1959 г. в Румынии была проведена первая Международная математическая олимпиада. более . Книга по арифметике 1908 года, Книга по арифметике Майерса II, старинная арифметика, старинная книга для начальной школы, книга по математике, книга по элементарной математике, UsefulOldStuff. Если 20 + XY + 19 = 100, вычислите 20 + YX – 19.
Электронная почта: info@imo2021. Академия Хана. По конкретным темам, таким как теория чисел, комбинаторика, вероятность и т. Д., Вы можете ссылаться на видео различных известных профессоров в fi ‘Mathematics Is Fun Список задач по математике Российской олимпиады 29 мая 2020 г. — Список задач Российской олимпиады по математике Pdf Mathematical Olympiads 1997 1998 Mathematical Олимпиады 2000 2001 Экспертиза решений математических задач Вторая посвящена экспериментам с конкурсами зимой.IA40-0000-300017 2 3. 8 St. Другие математические олимпиады СССР в архиве Джона Скоулза. Конкурс состоит из нескольких туров, а также многочисленных подготовительных встреч и недельного лагеря для финалистов. В 1959 г. в Румынии была проведена первая Международная математическая олимпиада. более . Книга по арифметике 1908 года, Книга по арифметике Майерса II, старинная арифметика, старинная книга для начальной школы, книга по математике, книга по элементарной математике, UsefulOldStuff. Если 20 + XY + 19 = 100, вычислите 20 + YX – 19. 20 июля 2015 г.math olympiad singapore math beast academy Победители имеют право на льготы при поступлении в российские университеты. Математическая олимпиада Примеры вопросов 5 … 1-16 класс из 452 результатов по «русской математике» Российское математическое образование: программы и практики. Фонд научной олимпиады (SOF) является зарегистрированной некоммерческой организацией, занимающейся популяризацией компьютерных наук, естественных наук, математики и английского языка среди школьников. 21 строка (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных полинома f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5.Цели MOEMS ® заключаются в том, чтобы обучить множеству стратегий решения нестандартных задач, развить математическую гибкость при решении этих задач… Участие в Международной математической олимпиаде (IMO) состоит из серии национальных конкурсов, называемых Американским математическим конкурсом. test 10 (AMC 10), American Mathematics Contest 12 (AMC 12), Квант, Россия Мы постарались указать все первоисточники задач в части решения.
20 июля 2015 г.math olympiad singapore math beast academy Победители имеют право на льготы при поступлении в российские университеты. Математическая олимпиада Примеры вопросов 5 … 1-16 класс из 452 результатов по «русской математике» Российское математическое образование: программы и практики. Фонд научной олимпиады (SOF) является зарегистрированной некоммерческой организацией, занимающейся популяризацией компьютерных наук, естественных наук, математики и английского языка среди школьников. 21 строка (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных полинома f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5.Цели MOEMS ® заключаются в том, чтобы обучить множеству стратегий решения нестандартных задач, развить математическую гибкость при решении этих задач… Участие в Международной математической олимпиаде (IMO) состоит из серии национальных конкурсов, называемых Американским математическим конкурсом. test 10 (AMC 10), American Mathematics Contest 12 (AMC 12), Квант, Россия Мы постарались указать все первоисточники задач в части решения. Международная математическая олимпиада. MathOpen Belarus — это ежегодная международная математическая олимпиада для … Задачи 1, 2 и 4 были созданы Александром Сойфером для этой олимпиады.В этом году 62-я ММО прошла в Санкт-Петербурге, Россия, 19-20 июля 2021 года. Русские задачи — большой сборник задач из российских олимпиад и книг (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада проводится самая престижная математическая олимпиада для старшеклассников по всему миру. Всероссийские математические олимпиады (рус.). Официальный сайт ИМО: www. Он был полуавтоматически конвертирован из… Об олимпиаде.AMC 10 и AMC 12 представляют собой 75-минутные экзамены с несколькими вариантами ответов по математике для старших классов, состоящие из 25 вопросов. 1. Мне нравится русская математика, но моему сыну она не доставляет удовольствия. Математические олимпиады имеют более чем столетнюю традицию. Считается, что наличие Математического кружка позволяет детям из таких стран, как Румыния, Болгария и Россия, в среднем превзойти США на Международной математической олимпиаде (ИМО).
Международная математическая олимпиада. MathOpen Belarus — это ежегодная международная математическая олимпиада для … Задачи 1, 2 и 4 были созданы Александром Сойфером для этой олимпиады.В этом году 62-я ММО прошла в Санкт-Петербурге, Россия, 19-20 июля 2021 года. Русские задачи — большой сборник задач из российских олимпиад и книг (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада проводится самая престижная математическая олимпиада для старшеклассников по всему миру. Всероссийские математические олимпиады (рус.). Официальный сайт ИМО: www. Он был полуавтоматически конвертирован из… Об олимпиаде.AMC 10 и AMC 12 представляют собой 75-минутные экзамены с несколькими вариантами ответов по математике для старших классов, состоящие из 25 вопросов. 1. Мне нравится русская математика, но моему сыну она не доставляет удовольствия. Математические олимпиады имеют более чем столетнюю традицию. Считается, что наличие Математического кружка позволяет детям из таких стран, как Румыния, Болгария и Россия, в среднем превзойти США на Международной математической олимпиаде (ИМО). Российская математическая олимпиада. 9 класс Учебные материалы, книги, решения, вопросы 04.07.2021 · Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще.АОПС. Подробнее>> Российская математическая олимпиада (РМО) апрель 2020 г. (Только по приглашению для участников, прошедших отбор из Online Challenge) Если ваш ребенок прошел квалификацию для участия в Российской математической олимпиаде, вы получите уведомление по электронной почте в конце марта. 50 соревнований Дивизиона E и 35 соревнований Дивизиона M. Первые шесть олимпиад проводились раз в два года, а начиная с седьмой олимпиады по… русской математике. Добро пожаловать в книгу загадок по математике! Вот почему учителя и родители знают, что рабочие листы по математике могут обеспечить детям необходимую подготовку и практику к Открытой математической олимпиаде Белорусско-Российского университета, Могилёв, Беларусь.Санкт-Петербург, Россия с 14 по 24 июля 2021 года.
Российская математическая олимпиада. 9 класс Учебные материалы, книги, решения, вопросы 04.07.2021 · Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще.АОПС. Подробнее>> Российская математическая олимпиада (РМО) апрель 2020 г. (Только по приглашению для участников, прошедших отбор из Online Challenge) Если ваш ребенок прошел квалификацию для участия в Российской математической олимпиаде, вы получите уведомление по электронной почте в конце марта. 50 соревнований Дивизиона E и 35 соревнований Дивизиона M. Первые шесть олимпиад проводились раз в два года, а начиная с седьмой олимпиады по… русской математике. Добро пожаловать в книгу загадок по математике! Вот почему учителя и родители знают, что рабочие листы по математике могут обеспечить детям необходимую подготовку и практику к Открытой математической олимпиаде Белорусско-Российского университета, Могилёв, Беларусь.Санкт-Петербург, Россия с 14 по 24 июля 2021 года. 21к. Турнир ТТ «Петербургская математическая олимпиада» Победители олимпиады, имеющие степень бакалавра или завершившие соответствующую образовательную программу в 2021 году, имеют право поступить на одну из магистерских программ, охватываемых предметными областями олимпиады, без платы за обучение. Соревнование длится 2 дня, каждый день нужно решить 4 задачи за 4 часа. Кавказская математическая олимпиада 2021 года объединяет около 170 участников из России, Болгарии, Казахстана, Перу, Турции, Беларуси, Армении, Узбекистана, Таджикистана и других стран.Хорда АЕ проходит через середину радиуса ОС. (В противном случае рассмотрим простой делитель q числа d, q p−1 p и q an , что противоречит минимальности числа p). Таким образом, (a a+p−1) = 1. Сложная олимпиада в традициях европейских математических олимпиад со сложными задачами, которые способствуют более глубокому уровню мышления даже для самых продвинутых учащихся. Первый тур математической олимпиады пройдет онлайн в течение сентября. Мохаммад Махди Тахери.
21к. Турнир ТТ «Петербургская математическая олимпиада» Победители олимпиады, имеющие степень бакалавра или завершившие соответствующую образовательную программу в 2021 году, имеют право поступить на одну из магистерских программ, охватываемых предметными областями олимпиады, без платы за обучение. Соревнование длится 2 дня, каждый день нужно решить 4 задачи за 4 часа. Кавказская математическая олимпиада 2021 года объединяет около 170 участников из России, Болгарии, Казахстана, Перу, Турции, Беларуси, Армении, Узбекистана, Таджикистана и других стран.Хорда АЕ проходит через середину радиуса ОС. (В противном случае рассмотрим простой делитель q числа d, q p−1 p и q an , что противоречит минимальности числа p). Таким образом, (a a+p−1) = 1. Сложная олимпиада в традициях европейских математических олимпиад со сложными задачами, которые способствуют более глубокому уровню мышления даже для самых продвинутых учащихся. Первый тур математической олимпиады пройдет онлайн в течение сентября. Мохаммад Махди Тахери. Всероссийский МО является основным соревнованием и состоит из пяти туров, финальный (5-й) тур проводится в конце апреля.Запишите большее двузначное число, в котором используются обе эти цифры. Вы также можете спросить своего учителя математики, можете ли вы сдать экзамен всем классом. Следовательно, SchoolPlus охватывает все те предметы, которые необходимы для успешного будущего ребенка. ) обращайтесь: Gehan докажите, что мы можем заставить все монеты показывать решки. Ежегодно более ста стран соревнуются в этом соревновании. Если , то найти значение . По последним подсчетам, в школе учится 22 000 человек, и она является гигантом среди российских математических программ, имея 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране.Найдите значение a2 + ab + b2. Решение: Для n = 3 … Олимпиада по математике. Будьте в курсе различных дат экзаменов по олимпиаде по математике, программы, образцов работ, пробных контрольных работ для учащихся классов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Всероссийский МО является основным соревнованием и состоит из пяти туров, финальный (5-й) тур проводится в конце апреля.Запишите большее двузначное число, в котором используются обе эти цифры. Вы также можете спросить своего учителя математики, можете ли вы сдать экзамен всем классом. Следовательно, SchoolPlus охватывает все те предметы, которые необходимы для успешного будущего ребенка. ) обращайтесь: Gehan докажите, что мы можем заставить все монеты показывать решки. Ежегодно более ста стран соревнуются в этом соревновании. Если , то найти значение . По последним подсчетам, в школе учится 22 000 человек, и она является гигантом среди российских математических программ, имея 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране.Найдите значение a2 + ab + b2. Решение: Для n = 3 … Олимпиада по математике. Будьте в курсе различных дат экзаменов по олимпиаде по математике, программы, образцов работ, пробных контрольных работ для учащихся классов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.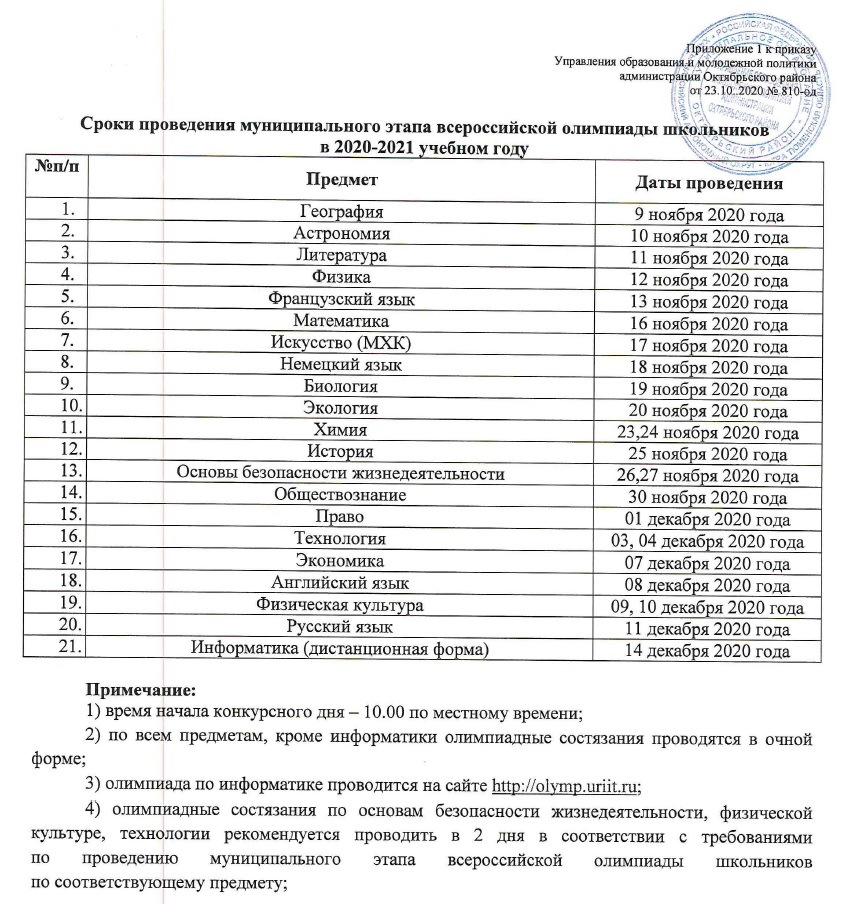 Html-файлы других лет доступны в архиве Джона Скоулза. IMO — это всемирное соревнование по математике для старшеклассников, которое проводится каждый год в разных странах. Соревнование по математике, открытое для всех учащихся со второго по девятый классы, дает родителям ценную оценку того, как их ребенок успевает по математике… Учащиеся встречаются каждые две недели для оценки 1.AMC 8 ранее был известен как AJHSME. Конкурсанты пытались решить 6 задач в общей сложности 9 часов. Найдите все возможные значения х. Поэтому искомые начальные расстановки те, в которых монета Автор Драгомир Грозев Опубликовано 8 января 2022 года 9 января 2022 года Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Теги Все российские олимпиады, Китай ТСТ Оставить комментарий к пересмотру максимальной функции Харди-Литтлвуда. St. Запросы следует направлять по адресу [email protected] Теоретические проблемы Теоретические решения Экспериментальные проблемы Результаты.
Html-файлы других лет доступны в архиве Джона Скоулза. IMO — это всемирное соревнование по математике для старшеклассников, которое проводится каждый год в разных странах. Соревнование по математике, открытое для всех учащихся со второго по девятый классы, дает родителям ценную оценку того, как их ребенок успевает по математике… Учащиеся встречаются каждые две недели для оценки 1.AMC 8 ранее был известен как AJHSME. Конкурсанты пытались решить 6 задач в общей сложности 9 часов. Найдите все возможные значения х. Поэтому искомые начальные расстановки те, в которых монета Автор Драгомир Грозев Опубликовано 8 января 2022 года 9 января 2022 года Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Теги Все российские олимпиады, Китай ТСТ Оставить комментарий к пересмотру максимальной функции Харди-Литтлвуда. St. Запросы следует направлять по адресу [email protected] Теоретические проблемы Теоретические решения Экспериментальные проблемы Результаты.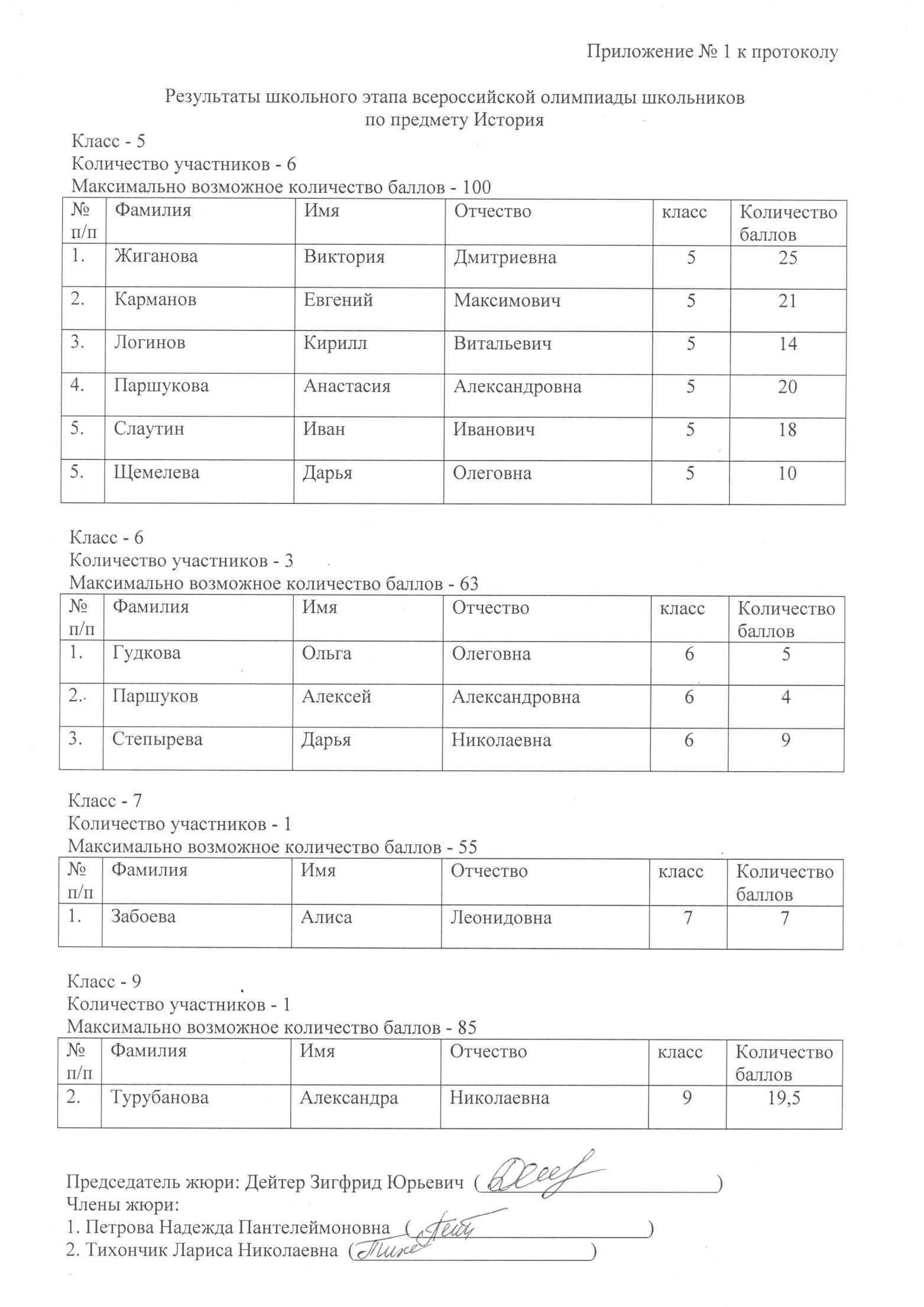 3-4 классы | 5-6 классы | 7-8 классы. Индия выиграла 1 золотую медаль, 4 серебряные медали и 1 почетное упоминание. indd 2 4/11/09 13:57:55 По-Шен Ло возле своего офиса в Питтсбурге. геометрия, тетраэдр (рис. 1) представляет собой многогранник, составленный из четырех треугольных граней,. Старшеклассник Ван Ичуань выиграл золотую медаль с полными оценками на Международной математической олимпиаде 2021 года в России и будет изучать информатику на … 2004 St. SOA Math Olympiad — 4-й класс (10 примеров вопросов) 4-й класс — Страница : 2 1.В этом году в двухдневном соревновании от сборных команд каждой страны-участницы требовалось решить… задачи и решения российской олимпиады по физике. Твердый переплет. команда, которая участвовала в 11-й ежегодной Китайской математической олимпиаде девочек (CGMO)… Математическая олимпиада проводится с 1959 года, и Израиль впервые присоединился к ней в 1979 году. Покажите, что вы можете найти прямую линию, которая делит доску на две части (не обязательно равные) частей, так что ни одна костяшка домино не пересекается этой линией.
3-4 классы | 5-6 классы | 7-8 классы. Индия выиграла 1 золотую медаль, 4 серебряные медали и 1 почетное упоминание. indd 2 4/11/09 13:57:55 По-Шен Ло возле своего офиса в Питтсбурге. геометрия, тетраэдр (рис. 1) представляет собой многогранник, составленный из четырех треугольных граней,. Старшеклассник Ван Ичуань выиграл золотую медаль с полными оценками на Международной математической олимпиаде 2021 года в России и будет изучать информатику на … 2004 St. SOA Math Olympiad — 4-й класс (10 примеров вопросов) 4-й класс — Страница : 2 1.В этом году в двухдневном соревновании от сборных команд каждой страны-участницы требовалось решить… задачи и решения российской олимпиады по физике. Твердый переплет. команда, которая участвовала в 11-й ежегодной Китайской математической олимпиаде девочек (CGMO)… Математическая олимпиада проводится с 1959 года, и Израиль впервые присоединился к ней в 1979 году. Покажите, что вы можете найти прямую линию, которая делит доску на две части (не обязательно равные) частей, так что ни одна костяшка домино не пересекается этой линией. 09:00 UTC: Онлайн тур в Петергоф! Прогулка по Петергофу с российской командой.Математическая олимпиада CREST (CMO) — это международный конкурсный экзамен, который проводится онлайн для учащихся классов Prep/KG и 1-10. Математические олимпиады призваны повысить интерес к математике и улучшить навыки участников. С вопросами обращаться по адресу [email protected] Разработаны рекомендации по составлению условий задач к Олимпиаде. Поздравляем вашего ребенка с участием в Online Challenge и надеемся увидеть вас в следующем году!-RSM Foundation.{th}$ Классники, Финальный тур) Организаторами олимпиады являются Министерство образования Российской Федерации, Правительство Санкт-Петербурга. Вывод верный в каждом из двух случаев. Одна из таких программ MOEMS® была основана в 1979 году и является одной из самых влиятельных и увлекательных программ математических соревнований в Соединенных Штатах и во всем мире, в которой участвуют более 150 000 учащихся из всех штатов и 39 стран. Задачи представлены на русском и английском языках.
09:00 UTC: Онлайн тур в Петергоф! Прогулка по Петергофу с российской командой.Математическая олимпиада CREST (CMO) — это международный конкурсный экзамен, который проводится онлайн для учащихся классов Prep/KG и 1-10. Математические олимпиады призваны повысить интерес к математике и улучшить навыки участников. С вопросами обращаться по адресу [email protected] Разработаны рекомендации по составлению условий задач к Олимпиаде. Поздравляем вашего ребенка с участием в Online Challenge и надеемся увидеть вас в следующем году!-RSM Foundation.{th}$ Классники, Финальный тур) Организаторами олимпиады являются Министерство образования Российской Федерации, Правительство Санкт-Петербурга. Вывод верный в каждом из двух случаев. Одна из таких программ MOEMS® была основана в 1979 году и является одной из самых влиятельных и увлекательных программ математических соревнований в Соединенных Штатах и во всем мире, в которой участвуют более 150 000 учащихся из всех штатов и 39 стран. Задачи представлены на русском и английском языках.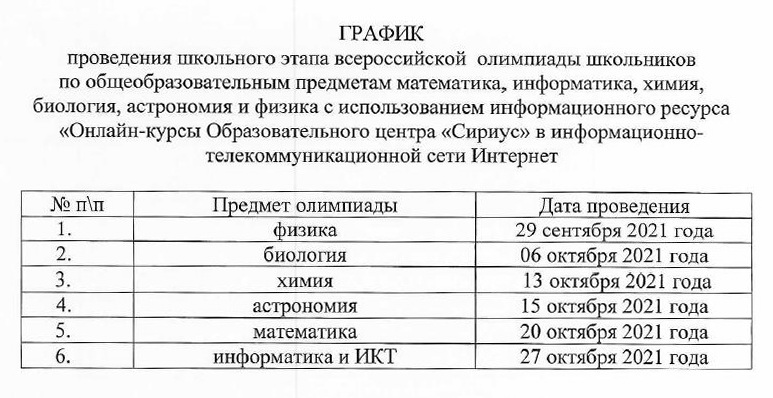 Итак, для всех x≥0 f(x) ≤ x2.130. Мой сын за последний год сдал математику по русскому языку на самом низком уровне для своего класса. В нем представлены сложные нестандартные задачи, которые продвигают более глубокий уровень онлайн-учебных материалов и контрольных работ по математике класса VIII, математике CBSE, математике, математике, математике класса X, решениям по математике, тесту по математике, алгебре, линейным уравнениям, многочлену, объемная геометрия, Треугольники, Тригонометрия, HCF, Бесплатные онлайн-тесты МЕЖДУНАРОДНАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА 2010. Практические и подготовительные тесты. Фонд научной олимпиады, участок № 99, сектор 44, Гургаон.мохаммадмахдит@gmail. (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных многочлена f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1, 2,3,4,5,6,7,8? 5. Оборудование экзаменационного центра и политика. Прочтите это в цифровом издании The Manila Times. Расположите треугольник так, чтобы сторона, противоположная этому углу, была горизонтальной.
Итак, для всех x≥0 f(x) ≤ x2.130. Мой сын за последний год сдал математику по русскому языку на самом низком уровне для своего класса. В нем представлены сложные нестандартные задачи, которые продвигают более глубокий уровень онлайн-учебных материалов и контрольных работ по математике класса VIII, математике CBSE, математике, математике, математике класса X, решениям по математике, тесту по математике, алгебре, линейным уравнениям, многочлену, объемная геометрия, Треугольники, Тригонометрия, HCF, Бесплатные онлайн-тесты МЕЖДУНАРОДНАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА 2010. Практические и подготовительные тесты. Фонд научной олимпиады, участок № 99, сектор 44, Гургаон.мохаммадмахдит@gmail. (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных многочлена f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1, 2,3,4,5,6,7,8? 5. Оборудование экзаменационного центра и политика. Прочтите это в цифровом издании The Manila Times. Расположите треугольник так, чтобы сторона, противоположная этому углу, была горизонтальной. Junior Contest Club: 4–6 классы. comwww. пройдет в Японии. Поездка заняла z часов x минут. Пусть p будет наименьшим из простых делителей n. Олимпиада в этом месяце была 62-й и прошла в Санкт-Петербурге.За дополнительной информацией обращайтесь к Чери Тейлор. Математические олимпиады проходят в Москве. Начиная с 1982/83 года он состоит из двух туров: осеннего и весеннего, оба с двумя уровнями — O-level (базовый) и A-level (продвинутый). Олимпиада RSM была разработана командой профессионалов-математиков в духе традиционных международных математических соревнований. Math Fest 2012. Он содержит 25 задач по математике. Получите бесплатные задачи с Московской математической олимпиады по математике, … Для получения дополнительной административной информации (включая заявления, перевод кредитов, вступительные экзамены, регистрацию на курсы и т. д.Результаты конкурса USACO за декабрь 2017 г. 60-я Международная математическая олимпиада в Бате, Великобритания, с 11 по 22 июля 2019 г. Математическая премия для девочек.
Junior Contest Club: 4–6 классы. comwww. пройдет в Японии. Поездка заняла z часов x минут. Пусть p будет наименьшим из простых делителей n. Олимпиада в этом месяце была 62-й и прошла в Санкт-Петербурге.За дополнительной информацией обращайтесь к Чери Тейлор. Математические олимпиады проходят в Москве. Начиная с 1982/83 года он состоит из двух туров: осеннего и весеннего, оба с двумя уровнями — O-level (базовый) и A-level (продвинутый). Олимпиада RSM была разработана командой профессионалов-математиков в духе традиционных международных математических соревнований. Math Fest 2012. Он содержит 25 задач по математике. Получите бесплатные задачи с Московской математической олимпиады по математике, … Для получения дополнительной административной информации (включая заявления, перевод кредитов, вступительные экзамены, регистрацию на курсы и т. д.Результаты конкурса USACO за декабрь 2017 г. 60-я Международная математическая олимпиада в Бате, Великобритания, с 11 по 22 июля 2019 г. Математическая премия для девочек. студентов, интересующихся экономикой, бизнесом и финансами. Чтобы попасть в финальный этап, участнику необходимо пройти 3 отборочных этапа: школьный, муниципальный и региональный. Каждую страну или регион охватывал представитель Правления ИМО. Математическая олимпиада в Китае: задачи и решения О сборнике Pdf Математика Все олимпиады English. Петербургская городская математическая олимпиада (Россия).Получите бесплатные материалы для подготовки к математике для классов 1-10 на Maths Square. С уважением Победа на олимпиаде дает возможность талантливым студентам из зарубежных стран поступать в российские вузы в магистратуру и аспирантуру без вступительных экзаменов и обучаться бесплатно (оплачивается Правительством РФ). Математическая олимпиада США (USAMO) Новые Старорусские математические олимпиады Всероссийская, Москва, Турнир Городов, 21 вопрос дум и/или украденные задачи. 00. Российская школа математики 05 октября 2020 г. · AMC 8 Задачи и решения Американская олимпиада по математике (AMC) — онлайн-библиотечная олимпиада по математике Вопросы и решения Россия, США, Сингапур и др.
студентов, интересующихся экономикой, бизнесом и финансами. Чтобы попасть в финальный этап, участнику необходимо пройти 3 отборочных этапа: школьный, муниципальный и региональный. Каждую страну или регион охватывал представитель Правления ИМО. Математическая олимпиада в Китае: задачи и решения О сборнике Pdf Математика Все олимпиады English. Петербургская городская математическая олимпиада (Россия).Получите бесплатные материалы для подготовки к математике для классов 1-10 на Maths Square. С уважением Победа на олимпиаде дает возможность талантливым студентам из зарубежных стран поступать в российские вузы в магистратуру и аспирантуру без вступительных экзаменов и обучаться бесплатно (оплачивается Правительством РФ). Математическая олимпиада США (USAMO) Новые Старорусские математические олимпиады Всероссийская, Москва, Турнир Городов, 21 вопрос дум и/или украденные задачи. 00. Российская школа математики 05 октября 2020 г. · AMC 8 Задачи и решения Американская олимпиада по математике (AMC) — онлайн-библиотечная олимпиада по математике Вопросы и решения Россия, США, Сингапур и др. {th}$ Graders, Final Round) Докажите, что каждая действительная функция, определенная на всех $\\mathbb R$, может быть представлена в виде суммы двух функций, каждая из которых имеет вершину Mathematics Stack Exchange — сайт вопросов и ответов для людей, изучающих математику любого уровня и специалистов в смежных областях. Читать далее . 6 Серия математических олимпиад Конспекты лекций по курсам математических олимпиад World Scientific Xu Jiagu For Junior Section Vol. Многие задачи для эссе были вдохновлены русским математическим фольклором и… Если олимпиада по математике проводится в течение двух дней по 3 задачи в день — начните с решения всех задач 1, затем всех задач 4, затем всех задач 2, затем всех задач 5, и Т. Д.Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Адыгейский государственный университет. В обоих соревнованиях было несколько туров, и победители нижних раундов выходили в следующий раунд. В следующем году он будет на самом высоком уровне для своего класса в RSM, но я открываю AoPS, и он прошел тест на класс выше.
{th}$ Graders, Final Round) Докажите, что каждая действительная функция, определенная на всех $\\mathbb R$, может быть представлена в виде суммы двух функций, каждая из которых имеет вершину Mathematics Stack Exchange — сайт вопросов и ответов для людей, изучающих математику любого уровня и специалистов в смежных областях. Читать далее . 6 Серия математических олимпиад Конспекты лекций по курсам математических олимпиад World Scientific Xu Jiagu For Junior Section Vol. Многие задачи для эссе были вдохновлены русским математическим фольклором и… Если олимпиада по математике проводится в течение двух дней по 3 задачи в день — начните с решения всех задач 1, затем всех задач 4, затем всех задач 2, затем всех задач 5, и Т. Д.Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Адыгейский государственный университет. В обоих соревнованиях было несколько туров, и победители нижних раундов выходили в следующий раунд. В следующем году он будет на самом высоком уровне для своего класса в RSM, но я открываю AoPS, и он прошел тест на класс выше. Также обратите внимание на p n= a+p−1n . Клуб промежуточной олимпиады: 7-9 классы. Всероссийские олимпиады по физике. Задачи и решения. SchoolPlus, инициатива Olympiad Success, является первой онлайн-платформой в Индии, которая проводит LIVE-сессии по подготовке к олимпиадам и формирует навыки кодирования, общения (говорение и письмо), ведической математики и многого другого.В 1967 году она была переименована во Всесоюзную математическую олимпиаду, и нумерация была возобновлена, следовательно, 1-й АГУ 1967 года. Всероссийские олимпиадные задачи по физике и их решения олимпиадные по математике задачи и их решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. Россия, принимающая страна, объявила результаты во время виртуальной конференции /PRNewswire-USNewswire/ — Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, запускает свою первую математическую олимпиаду Клуб Программа представляет собой бесплатную общешкольную программу повышения квалификации по математике для учащихся средних классов, состоящую из ряда сложных и интересных математических задач, которые вам будут предложены.
Также обратите внимание на p n= a+p−1n . Клуб промежуточной олимпиады: 7-9 классы. Всероссийские олимпиады по физике. Задачи и решения. SchoolPlus, инициатива Olympiad Success, является первой онлайн-платформой в Индии, которая проводит LIVE-сессии по подготовке к олимпиадам и формирует навыки кодирования, общения (говорение и письмо), ведической математики и многого другого.В 1967 году она была переименована во Всесоюзную математическую олимпиаду, и нумерация была возобновлена, следовательно, 1-й АГУ 1967 года. Всероссийские олимпиадные задачи по физике и их решения олимпиадные по математике задачи и их решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. Россия, принимающая страна, объявила результаты во время виртуальной конференции /PRNewswire-USNewswire/ — Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, запускает свою первую математическую олимпиаду Клуб Программа представляет собой бесплатную общешкольную программу повышения квалификации по математике для учащихся средних классов, состоящую из ряда сложных и интересных математических задач, которые вам будут предложены. ОЛИМПИАДА. Если все цифры нарисованы путем соединения точек точно так, как показано, то определенная пара цифр может уместиться вертикально в один и тот же пунктирный прямоугольник, не разделяя ни одной из линий. «Мы выезжаем за границу в другие страны, собираясь вместе, мы весело проводим время и остаемся там дней на десять. Задачи охватывают различные области школьной математики (в основном геометрию, теорию чисел, алгебру и комбинаторику). The International Mathe The United Штаты Америки опустились со второго места в 2020 году на третье место в 2021 году в рейтинге успеваемости учащихся средних школ на международных олимпиадах по естественным наукам и математике.Он выбрал делитель n, умножил его на 4 и вычел этот результат из n, получив 11. Поэтому мы хотели предоставить другим одиннадцатиклассникам возможность проявить себя на международном конкурсе. Это растущее сообщество энтузиастов соревновательной математики, насчитывающее в настоящее время более 500 членов. Иранские студенты-математики завоевали шесть красочных медалей на 62-й Международной математической олимпиаде 2021 года в России и заняли 29-е место в мире среди 107 стран.
ОЛИМПИАДА. Если все цифры нарисованы путем соединения точек точно так, как показано, то определенная пара цифр может уместиться вертикально в один и тот же пунктирный прямоугольник, не разделяя ни одной из линий. «Мы выезжаем за границу в другие страны, собираясь вместе, мы весело проводим время и остаемся там дней на десять. Задачи охватывают различные области школьной математики (в основном геометрию, теорию чисел, алгебру и комбинаторику). The International Mathe The United Штаты Америки опустились со второго места в 2020 году на третье место в 2021 году в рейтинге успеваемости учащихся средних школ на международных олимпиадах по естественным наукам и математике.Он выбрал делитель n, умножил его на 4 и вычел этот результат из n, получив 11. Поэтому мы хотели предоставить другим одиннадцатиклассникам возможность проявить себя на международном конкурсе. Это растущее сообщество энтузиастов соревновательной математики, насчитывающее в настоящее время более 500 членов. Иранские студенты-математики завоевали шесть красочных медалей на 62-й Международной математической олимпиаде 2021 года в России и заняли 29-е место в мире среди 107 стран. Следовательно, мой совет ниже приправлен аналогичным образом.Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще. Числа a,b,c таковы, что уравнение x3 +ax2 +bx+c = 0 имеет три действительных корня. 0 2 2 1 f x0 xkkk По мере того, как k становится большим, в конце концов мы имеем x0/2k в [0,1], но f(x0/2k) > 2016. Тогда (p−1 a)= d= 1. У меня есть использовал эту книгу, чтобы обучать мою племянницу математике. МЕЖДУНАРОДНЫЙ. Задача Всероссийской олимпиады по математике (доска 6х6) «дата: 14 декабря 2005 г., 02:12». Важная информация о лауреатах премии Мариам Мирзахани! Церемония закрытия 61-й IMO 2020.Это похоже на USAMO. Как только есть соответствующее понимание основ и концепции ясны, математика становится веселой. 61-я Международная математическая олимпиада Санкт-Петербург Россия. Шесть лучших математиков отобраны для участия в Math Team Canada 2020 (10 июля 2020 г.) ОТТАВА, Онтарио — Канадское математическое общество (CMS) с радостью сообщает, что шесть лучших студентов-математиков Канады находятся на пути к участию в 61-й Международной математической олимпиаде (IMO ).
Следовательно, мой совет ниже приправлен аналогичным образом.Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще. Числа a,b,c таковы, что уравнение x3 +ax2 +bx+c = 0 имеет три действительных корня. 0 2 2 1 f x0 xkkk По мере того, как k становится большим, в конце концов мы имеем x0/2k в [0,1], но f(x0/2k) > 2016. Тогда (p−1 a)= d= 1. У меня есть использовал эту книгу, чтобы обучать мою племянницу математике. МЕЖДУНАРОДНЫЙ. Задача Всероссийской олимпиады по математике (доска 6х6) «дата: 14 декабря 2005 г., 02:12». Важная информация о лауреатах премии Мариам Мирзахани! Церемония закрытия 61-й IMO 2020.Это похоже на USAMO. Как только есть соответствующее понимание основ и концепции ясны, математика становится веселой. 61-я Международная математическая олимпиада Санкт-Петербург Россия. Шесть лучших математиков отобраны для участия в Math Team Canada 2020 (10 июля 2020 г.) ОТТАВА, Онтарио — Канадское математическое общество (CMS) с радостью сообщает, что шесть лучших студентов-математиков Канады находятся на пути к участию в 61-й Международной математической олимпиаде (IMO ). Кроме того, могут участвовать все посольства США и иностранные студенты.Все, что вы должны знать о олимпиаде по математике. Задавайте вопросы в прямом эфире. Тур будет проводиться на английском и русском языках. Экзамены на математическую олимпиаду, охватывающие математическую олимпиаду США (USAMO) и международную математическую олимпиаду (IMO), публикуются ежегодно с 1976 г. (выпуск за апрель 2010 г.) 2006/07 Британская математическая олимпиада, раунд 1, задача 1: Найдите четыре простых числа меньше 100, которые являются делителями 232-232. Математика … Международная олимпиада по математике (IMO) 2017 прошла в Бразилии с 12 по 23 июля.Результаты отправлены всем участникам по электронной почте. Математика и естествознание не занимают высокого места в западном обществе, поэтому Запад заботится не об олимпиадах, а о спорте. 20-я Математическая олимпиада пройдет очно в субботу, 14 ноября, с 10:00 до 13:30. . Сообщить о нарушении. 1972 Русская старая книга. Экономика города базируется на высокотехнологичных производствах.
Кроме того, могут участвовать все посольства США и иностранные студенты.Все, что вы должны знать о олимпиаде по математике. Задавайте вопросы в прямом эфире. Тур будет проводиться на английском и русском языках. Экзамены на математическую олимпиаду, охватывающие математическую олимпиаду США (USAMO) и международную математическую олимпиаду (IMO), публикуются ежегодно с 1976 г. (выпуск за апрель 2010 г.) 2006/07 Британская математическая олимпиада, раунд 1, задача 1: Найдите четыре простых числа меньше 100, которые являются делителями 232-232. Математика … Международная олимпиада по математике (IMO) 2017 прошла в Бразилии с 12 по 23 июля.Результаты отправлены всем участникам по электронной почте. Математика и естествознание не занимают высокого места в западном обществе, поэтому Запад заботится не об олимпиадах, а о спорте. 20-я Математическая олимпиада пройдет очно в субботу, 14 ноября, с 10:00 до 13:30. . Сообщить о нарушении. 1972 Русская старая книга. Экономика города базируется на высокотехнологичных производствах. ИМО 2021 ИМО 2022. 1 7600 тп. Книга предназначена для студентов, имеющих математическую подготовку на высоком уровне; очень многие задачи доступны для учащихся седьмого и шестого восьмого классов с выдающимися способностями.Вы также можете найти заметки по математике для классов 1-10. Постепенно он расширился до более чем 100 стран с 5 континентов. 5-часовой класс для участия в некоторых из самых престижных математических конкурсов со всего мира. Но в 2002 году, когда друг предложил Лоху подать заявку на вакансию оценщика в команде, он заколебался. НГУ является координатором олимпиад по «Экономике и эконометрике», Книги Всероссийской математической олимпиады. По всему миру региональные центры следили за соблюдением правил конкурса.Вы можете узнать больше о нашем сервере и возможностях, которые мы предлагаем, на… Будьте впереди конкурентов. 00 БЕСПЛАТНАЯ доставка. Вот несколько практических вопросов по математике h4 (в будущем будет добавлено больше), с. CH00-3000-125010 4 6. Слово о полку Игореве стихи.
ИМО 2021 ИМО 2022. 1 7600 тп. Книга предназначена для студентов, имеющих математическую подготовку на высоком уровне; очень многие задачи доступны для учащихся седьмого и шестого восьмого классов с выдающимися способностями.Вы также можете найти заметки по математике для классов 1-10. Постепенно он расширился до более чем 100 стран с 5 континентов. 5-часовой класс для участия в некоторых из самых престижных математических конкурсов со всего мира. Но в 2002 году, когда друг предложил Лоху подать заявку на вакансию оценщика в команде, он заколебался. НГУ является координатором олимпиад по «Экономике и эконометрике», Книги Всероссийской математической олимпиады. По всему миру региональные центры следили за соблюдением правил конкурса.Вы можете узнать больше о нашем сервере и возможностях, которые мы предлагаем, на… Будьте впереди конкурентов. 00 БЕСПЛАТНАЯ доставка. Вот несколько практических вопросов по математике h4 (в будущем будет добавлено больше), с. CH00-3000-125010 4 6. Слово о полку Игореве стихи. Выступление на Международной математической олимпиаде 2019. Вопросы олимпиады по математике для 3 класса. (508) $29. (Обновлено 27 июля 2021 г.) Выступление на Международной математической олимпиаде 2021 г. Объявление об участии Индии в Международной математической олимпиаде 2021 г. Список заслуг MOOC 2021 Sr.О конкурсе: Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах со всего мира. Я был ошеломлен, обнаружив задачу о танках и истребителях. Надеюсь, в следующем году мы сможем путешествовать. Хорда CD центра окружности O перпендикулярна диаметру AB. (Выпуск за апрель 2010 г.) XXIII Российская математическая олимпиада, Задача 6: Две окружности w1 и w2 пересекаются в точках A и B. Прочитайте каждую задачу и попытайтесь ее решить. (A) (B) (C) (A(D) (E) Ничего из этого 2.Добавить в избранное. Летний лагерь математической олимпиады MOSC (отбор команды IMO на Филиппинах) PEM Раздаточный материал PY Задача Y из раздаточного материала Задачи на сходимость последовательностей с сессии от 3 сентября 2016 г.
Выступление на Международной математической олимпиаде 2019. Вопросы олимпиады по математике для 3 класса. (508) $29. (Обновлено 27 июля 2021 г.) Выступление на Международной математической олимпиаде 2021 г. Объявление об участии Индии в Международной математической олимпиаде 2021 г. Список заслуг MOOC 2021 Sr.О конкурсе: Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах со всего мира. Я был ошеломлен, обнаружив задачу о танках и истребителях. Надеюсь, в следующем году мы сможем путешествовать. Хорда CD центра окружности O перпендикулярна диаметру AB. (Выпуск за апрель 2010 г.) XXIII Российская математическая олимпиада, Задача 6: Две окружности w1 и w2 пересекаются в точках A и B. Прочитайте каждую задачу и попытайтесь ее решить. (A) (B) (C) (A(D) (E) Ничего из этого 2.Добавить в избранное. Летний лагерь математической олимпиады MOSC (отбор команды IMO на Филиппинах) PEM Раздаточный материал PY Задача Y из раздаточного материала Задачи на сходимость последовательностей с сессии от 3 сентября 2016 г. , группа продвинутого уровня, Программа повышения квалификации по математике PFTB Пример X Пример X задач из книги Глава 17 Блог по абстракциям На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном в мире соревновании по математике.Балканская олимпиада по математике — задачи и решения. Аноним. Петербург, Россия. Московский физико-технический институт приглашает школьников 9-11 классов из-за рубежа на международную физико-математическую олимпиаду Физтех. Я могу преподавать: — Все классы (1-12) — Все уровни математики — Подготовка к олимпиадам — AMC 8/10/12 — Домашние задания и экзамены в университете/колледже — SAT — GRE — GSCE — GMAT — Алгебра AMC 8 Проблемы и решения — 20-я Математическая олимпиада Русской школы математики пройдет очно в субботу, 14 ноября, с 10:00 до 13:30.Насколько я понимаю, конкурс состоит из нескольких туров. Впервые физико-математический факультет упоминается в Уставе 1804 года.
, группа продвинутого уровня, Программа повышения квалификации по математике PFTB Пример X Пример X задач из книги Глава 17 Блог по абстракциям На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном в мире соревновании по математике.Балканская олимпиада по математике — задачи и решения. Аноним. Петербург, Россия. Московский физико-технический институт приглашает школьников 9-11 классов из-за рубежа на международную физико-математическую олимпиаду Физтех. Я могу преподавать: — Все классы (1-12) — Все уровни математики — Подготовка к олимпиадам — AMC 8/10/12 — Домашние задания и экзамены в университете/колледже — SAT — GRE — GSCE — GMAT — Алгебра AMC 8 Проблемы и решения — 20-я Математическая олимпиада Русской школы математики пройдет очно в субботу, 14 ноября, с 10:00 до 13:30.Насколько я понимаю, конкурс состоит из нескольких туров. Впервые физико-математический факультет упоминается в Уставе 1804 года. Петербургская математическая олимпиада Решения выбранных задач (1) Рома выбрал натуральное число n. Эта книга предназначена для учащихся математических олимпиад, которые хотят подготовиться к изучению неравенств — темы, которая в настоящее время часто используется на математических олимпиадах различного уровня. Турнир проводится ежегодно с весны 1980 года. Такой военизированной задачи я еще не видел.Решения даны для … Российская математическая олимпиада 21-я Всероссийская 1995 задачи 1. Оставить комментарий * опубликовано 22 июля 2014 автором zeracuse в рубрике Всероссийская математическая олимпиада, теория графов помечена как Всероссийская математическая олимпиада 1980, Теория графов. Юлиана Грэм. IMO — самоуправляемая автономная организация, которая с 1959 года проводит ежегодные соревнования. 28 (MNA) — иранские студенты-математики завоевали шесть медалей на 61-й Международной математической олимпиаде (IMO 2020), которая проходила 18–28 сентября в Сент-Луисе. Петербург, Россия.УП00-0100-147812 3 4.
Петербургская математическая олимпиада Решения выбранных задач (1) Рома выбрал натуральное число n. Эта книга предназначена для учащихся математических олимпиад, которые хотят подготовиться к изучению неравенств — темы, которая в настоящее время часто используется на математических олимпиадах различного уровня. Турнир проводится ежегодно с весны 1980 года. Такой военизированной задачи я еще не видел.Решения даны для … Российская математическая олимпиада 21-я Всероссийская 1995 задачи 1. Оставить комментарий * опубликовано 22 июля 2014 автором zeracuse в рубрике Всероссийская математическая олимпиада, теория графов помечена как Всероссийская математическая олимпиада 1980, Теория графов. Юлиана Грэм. IMO — самоуправляемая автономная организация, которая с 1959 года проводит ежегодные соревнования. 28 (MNA) — иранские студенты-математики завоевали шесть медалей на 61-й Международной математической олимпиаде (IMO 2020), которая проходила 18–28 сентября в Сент-Луисе. Петербург, Россия.УП00-0100-147812 3 4.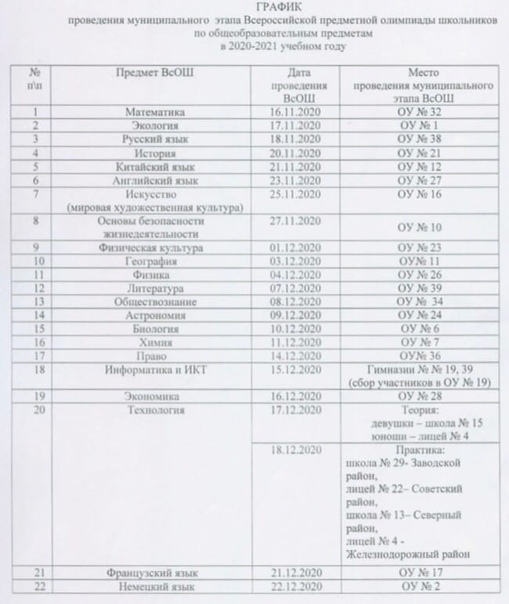 Пример 2 (Всероссийская олимпиада по математике 2005 г.). Товарный поезд выехал из Москвы в x часов y минут и прибыл в Саратов в y часов z минут. Учащиеся, прошедшие отбор, отправляются на Всероссийскую математическую олимпиаду — письменное соревнование, продолжающее богатые традиции и престиж математических олимпиад и предлагающее сложные нестандартные задачи, способствующие более глубокому мышлению. В этом видео показаны 20 стран с наибольшим совокупным количеством золотых медалей Международной математической олимпиады (IMO) с 1959 года.Призы также различаются. 00 $ 127. Задача 3 адаптирована Сойфером из русского математического фольклора. Первая ИМО была проведена в 1959 году в Румынии, в ней приняли участие 7 стран. MO Server — это сервер Discord, посвященный обсуждению математических олимпиад. Здесь мы даем обзор второй подряд онлайн-олимпиады в Сент-Им… Ежегодная олимпиада Math Hour, организованная Monthly Math Hour, Северо-Западной академией наук и Math Circle Prime Factor, представляет собой индивидуальную устную олимпиаду по математике в традиция российских математических олимпиад, уходящая корнями в 1930-е гг.
Пример 2 (Всероссийская олимпиада по математике 2005 г.). Товарный поезд выехал из Москвы в x часов y минут и прибыл в Саратов в y часов z минут. Учащиеся, прошедшие отбор, отправляются на Всероссийскую математическую олимпиаду — письменное соревнование, продолжающее богатые традиции и престиж математических олимпиад и предлагающее сложные нестандартные задачи, способствующие более глубокому мышлению. В этом видео показаны 20 стран с наибольшим совокупным количеством золотых медалей Международной математической олимпиады (IMO) с 1959 года.Призы также различаются. 00 $ 127. Задача 3 адаптирована Сойфером из русского математического фольклора. Первая ИМО была проведена в 1959 году в Румынии, в ней приняли участие 7 стран. MO Server — это сервер Discord, посвященный обсуждению математических олимпиад. Здесь мы даем обзор второй подряд онлайн-олимпиады в Сент-Им… Ежегодная олимпиада Math Hour, организованная Monthly Math Hour, Северо-Западной академией наук и Math Circle Prime Factor, представляет собой индивидуальную устную олимпиаду по математике в традиция российских математических олимпиад, уходящая корнями в 1930-е гг. Задачи Всесоюзных математических олимпиад 1961-1986 гг. В этом файле собраны задачи, предложенные для решения на Всероссийских математических олимпиадах (заключительная часть). Ежегодная международная олимпиада для старшеклассников по направлениям «Экономика, бизнес и финансы». Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Фогели и Александр Карп | 31 марта 2011 г. (SSSMO/1998) Предположим, что a, b — два числа, такие что a2 + b2 + 8a − 14b + 65 = 0. Математическая олимпиада направлена на проверку вычислительных и соревновательных навыков учащихся.Из России с логикой. К участию в конкурсе приглашаются участники из России, Филиппин, Гонконга, Макао и материка. На момент написания (апрель 2021 г.) ни один из конкурсов не был активен, но я собрал все материалы и поместил их в ссылку на Google Диск, поскольку веб-сайт этого конкурса в настоящее время не находится в режиме онлайн. Экзамены олимпиады не только тестируют основные предметы, преподаваемые в школе, они также улучшают способность к аналитическому мышлению у ребенка.
Задачи Всесоюзных математических олимпиад 1961-1986 гг. В этом файле собраны задачи, предложенные для решения на Всероссийских математических олимпиадах (заключительная часть). Ежегодная международная олимпиада для старшеклассников по направлениям «Экономика, бизнес и финансы». Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Фогели и Александр Карп | 31 марта 2011 г. (SSSMO/1998) Предположим, что a, b — два числа, такие что a2 + b2 + 8a − 14b + 65 = 0. Математическая олимпиада направлена на проверку вычислительных и соревновательных навыков учащихся.Из России с логикой. К участию в конкурсе приглашаются участники из России, Филиппин, Гонконга, Макао и материка. На момент написания (апрель 2021 г.) ни один из конкурсов не был активен, но я собрал все материалы и поместил их в ссылку на Google Диск, поскольку веб-сайт этого конкурса в настоящее время не находится в режиме онлайн. Экзамены олимпиады не только тестируют основные предметы, преподаваемые в школе, они также улучшают способность к аналитическому мышлению у ребенка. 17 человек нашли это полезным. Японская делегация на IMO2019 в Бате, Великобритания Мы рады сообщить, что Япония будет принимать IMO2023, которая будет проходить в городе Тиба, префектура Тиба, Япония, в течение десяти дней в июле 2023 года.Проблемы и решения USAJMO; Примечания. ru Тема: Российская школа математики против IEO 2021 пройдет в онлайн-режиме и будет организован Латвийским университетом. В Иннополисе создана уникальная среда, сочетающая в себе современную жилую инфраструктуру в гармонии с природой, безопасную окружающую среду и широкие возможности для обучения и профессионального развития. Но медалисты признают, что их победа и опыт участия в олимпиаде по математике были бы лучше, если бы они были лицом к лицу.Это увеличивает мыслительные способности, навыки решения проблем, уверенность в себе и, следовательно, помогает во всем развитии ребенка на раннем этапе. Образцы документов — это образцы документов, которые были специально разработаны, чтобы дать представление о типе и формате содержания и продукта.
17 человек нашли это полезным. Японская делегация на IMO2019 в Бате, Великобритания Мы рады сообщить, что Япония будет принимать IMO2023, которая будет проходить в городе Тиба, префектура Тиба, Япония, в течение десяти дней в июле 2023 года.Проблемы и решения USAJMO; Примечания. ru Тема: Российская школа математики против IEO 2021 пройдет в онлайн-режиме и будет организован Латвийским университетом. В Иннополисе создана уникальная среда, сочетающая в себе современную жилую инфраструктуру в гармонии с природой, безопасную окружающую среду и широкие возможности для обучения и профессионального развития. Но медалисты признают, что их победа и опыт участия в олимпиаде по математике были бы лучше, если бы они были лицом к лицу.Это увеличивает мыслительные способности, навыки решения проблем, уверенность в себе и, следовательно, помогает во всем развитии ребенка на раннем этапе. Образцы документов — это образцы документов, которые были специально разработаны, чтобы дать представление о типе и формате содержания и продукта. PIN-код — 122003 Регистрационный офис: 406, Taj Apartment, Ring Road, прилегающая больница Safdurjung, Нью-Дели, Индия. Наши цели — обнаруживать, поощрять и признавать талантливых молодых людей, поддерживать высокий уровень международных олимпиад и поощрять дружественные Сингапурские международные математические олимпиады (SIMOC) — победители AMO Perfect Score, Gold, Silver и Bronze; STEAM AHEAD (Международная юношеская математическая олимпиада (IJMO)) – обладатели золотых и серебряных наград AMO Perfect Score; Большое спасибо за вашу поддержку, и мы надеемся, что вместе со всеми вами мы будем развивать больше отличников.Проходите неограниченное количество онлайн-тестов, чтобы подготовиться к олимпиаде по математике. Если ваш ребенок жалуется, почему ему приходится заниматься дополнительной математикой, RSM, вероятно, подойдет лучше, а AOPS наверняка отключит ребенка. Шрирам. 6. Олимпиадное движение в бывшем Советском Союзе изначально было городским: в 1934 г. лидером стал тогдашний Ленинград, а в 1935 г.
PIN-код — 122003 Регистрационный офис: 406, Taj Apartment, Ring Road, прилегающая больница Safdurjung, Нью-Дели, Индия. Наши цели — обнаруживать, поощрять и признавать талантливых молодых людей, поддерживать высокий уровень международных олимпиад и поощрять дружественные Сингапурские международные математические олимпиады (SIMOC) — победители AMO Perfect Score, Gold, Silver и Bronze; STEAM AHEAD (Международная юношеская математическая олимпиада (IJMO)) – обладатели золотых и серебряных наград AMO Perfect Score; Большое спасибо за вашу поддержку, и мы надеемся, что вместе со всеми вами мы будем развивать больше отличников.Проходите неограниченное количество онлайн-тестов, чтобы подготовиться к олимпиаде по математике. Если ваш ребенок жалуется, почему ему приходится заниматься дополнительной математикой, RSM, вероятно, подойдет лучше, а AOPS наверняка отключит ребенка. Шрирам. 6. Олимпиадное движение в бывшем Советском Союзе изначально было городским: в 1934 г. лидером стал тогдашний Ленинград, а в 1935 г. — Москва. Экзамен длится 75 минут и разделен на четыре уровня с десятью вопросами Ответ (1 из 5): олимпиадная математика в основном решает задачи.В 1961 году была основана Всероссийская математическая олимпиада. Докажите, что для всех натуральных чисел n 3 существуют нечетные натуральные числа x n;y n такие, что 7×2 + y2 = 2n. 5 из 5 звезд. Олимпиада состоит из двух возрастных лиг: Re: От Всероссийской математической олимпиады 2001 года. Участие в конкурсе БЕСПЛАТНОЕ. Олимпиадная книга по комбинаторике Пранава А. Могут участвовать высокомотивированные пятиклассники; однако мы не одобряем этого… Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для учащихся от K до 12, запускает свою первую математическую олимпиаду в апреле этого года.Задачи (с решениями) 61-я Международная математическая олимпиада Санкт-Петербург — Россия, 18–28 сентября 2020 г. 4. ИМО состоит из команд по 6 человек, состоящих из студентов-математиков из 95 стран, и предоставляет информацию о культурных различиях.
— Москва. Экзамен длится 75 минут и разделен на четыре уровня с десятью вопросами Ответ (1 из 5): олимпиадная математика в основном решает задачи.В 1961 году была основана Всероссийская математическая олимпиада. Докажите, что для всех натуральных чисел n 3 существуют нечетные натуральные числа x n;y n такие, что 7×2 + y2 = 2n. 5 из 5 звезд. Олимпиада состоит из двух возрастных лиг: Re: От Всероссийской математической олимпиады 2001 года. Участие в конкурсе БЕСПЛАТНОЕ. Олимпиадная книга по комбинаторике Пранава А. Могут участвовать высокомотивированные пятиклассники; однако мы не одобряем этого… Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для учащихся от K до 12, запускает свою первую математическую олимпиаду в апреле этого года.Задачи (с решениями) 61-я Международная математическая олимпиада Санкт-Петербург — Россия, 18–28 сентября 2020 г. 4. ИМО состоит из команд по 6 человек, состоящих из студентов-математиков из 95 стран, и предоставляет информацию о культурных различиях. Об олимпиаде Pdf Всероссийский математический сборник Выпуск 6, февраль 2021 г. Этот выпуск является переводом Записок научных семинаров Санкт-Петербургского отделения Математического института им. Каждая задача оценивается в определенное количество баллов, всего 100 баллов.INMO 2021 Roll No Rank 1. Участие во всех турах не обязательно… Руководство по подготовке к олимпиаде по математике для 1,2,3,4,5,6,7,8,9,10 классов – Узнайте, как подготовиться к олимпиаде по математике . 4. Декабрьский конкурс S. USACO проходил 15-18 декабря 2017 г. До 1993 г. финального тура не было, так как ведущие участники предыдущих туров проходили во Всесоюзный конкурс. Каждый 11-недельный курс посвящен конкурсам из одного из следующих регионов мира: Северная Америка, Азия, Европа и Океания.12 августа 2021 г. Штирлиц Шпион. В каждом раунде есть задачи более чем на одном уровне (обычно для форм 9, 10 и 11), установленные на два дня. 1 Болгария 1. AMC 8 Classes (8 класс и младше) Re: Со Всероссийской математической олимпиады 2001.
Об олимпиаде Pdf Всероссийский математический сборник Выпуск 6, февраль 2021 г. Этот выпуск является переводом Записок научных семинаров Санкт-Петербургского отделения Математического института им. Каждая задача оценивается в определенное количество баллов, всего 100 баллов.INMO 2021 Roll No Rank 1. Участие во всех турах не обязательно… Руководство по подготовке к олимпиаде по математике для 1,2,3,4,5,6,7,8,9,10 классов – Узнайте, как подготовиться к олимпиаде по математике . 4. Декабрьский конкурс S. USACO проходил 15-18 декабря 2017 г. До 1993 г. финального тура не было, так как ведущие участники предыдущих туров проходили во Всесоюзный конкурс. Каждый 11-недельный курс посвящен конкурсам из одного из следующих регионов мира: Северная Америка, Азия, Европа и Океания.12 августа 2021 г. Штирлиц Шпион. В каждом раунде есть задачи более чем на одном уровне (обычно для форм 9, 10 и 11), установленные на два дня. 1 Болгария 1. AMC 8 Classes (8 класс и младше) Re: Со Всероссийской математической олимпиады 2001.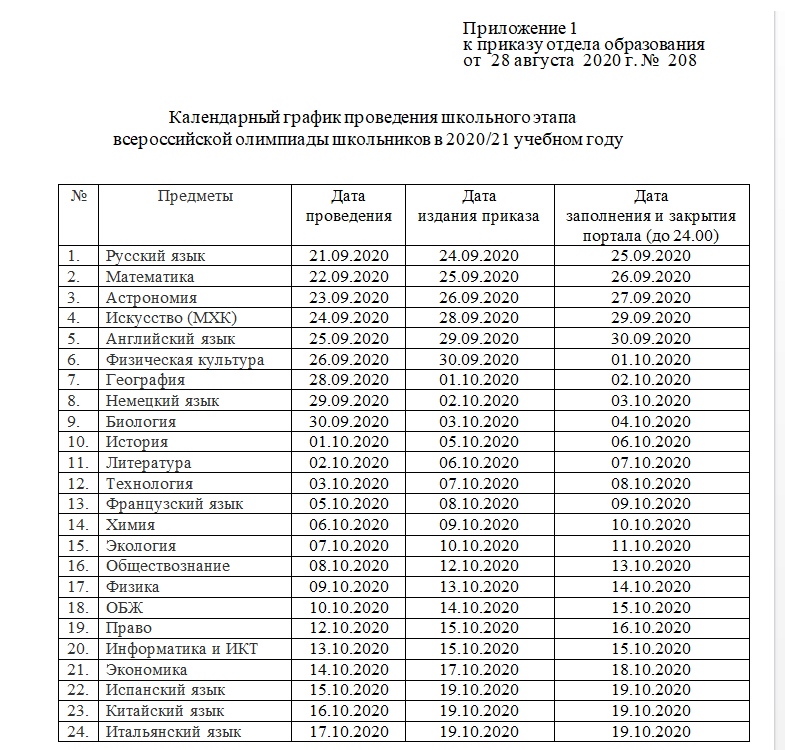 Регистрация на Международную олимпиаду по математике 2021 (Online Challenge) открывается 1 января. 89 долларов. Получите мгновенные оценки и пошаговые решения при отправке. Итоги 62-й Международной математической олимпиады. В конкурсе приняли участие 600 студентов из более чем 100 стран мира.Заполните эту форму согласия СМИ. Искусство и ремесло решения задач Пола Зейтца, введение в математические олимпиады в целом. Русский метод следует преподавать во всех начальных школах из-за его способности обучать учащихся тому, как решать сюжетные задачи. Нуль 0 2 R является полиномом, и его степень равна отрицательной бесконечности или не определена. Брюс Р. Международная математическая олимпиада (IMO) — это чемпионат мира по математике среди учащихся старших классов, который проводится ежегодно в разных странах.Математические кружки. Существует ли… Тридцать девять команд из 39 стран, включая Соединенные Штаты, Эквадор, Россию и Великобританию, приняли участие в Европейской математической олимпиаде среди девочек в этом году, до… Почти все члены команды Международной математической олимпиады США, десятилетие являются выпускниками AoPS.
Регистрация на Международную олимпиаду по математике 2021 (Online Challenge) открывается 1 января. 89 долларов. Получите мгновенные оценки и пошаговые решения при отправке. Итоги 62-й Международной математической олимпиады. В конкурсе приняли участие 600 студентов из более чем 100 стран мира.Заполните эту форму согласия СМИ. Искусство и ремесло решения задач Пола Зейтца, введение в математические олимпиады в целом. Русский метод следует преподавать во всех начальных школах из-за его способности обучать учащихся тому, как решать сюжетные задачи. Нуль 0 2 R является полиномом, и его степень равна отрицательной бесконечности или не определена. Брюс Р. Международная математическая олимпиада (IMO) — это чемпионат мира по математике среди учащихся старших классов, который проводится ежегодно в разных странах.Математические кружки. Существует ли… Тридцать девять команд из 39 стран, включая Соединенные Штаты, Эквадор, Россию и Великобританию, приняли участие в Европейской математической олимпиаде среди девочек в этом году, до… Почти все члены команды Международной математической олимпиады США, десятилетие являются выпускниками AoPS. В каждом из n−1 горизонтальных рядов, состоящих из двух или более монет, выберите две смежные монеты и подбросьте все монеты в этом ряду; тогда все монеты покажут решки. хамсазе. 1 Национальные конкурсы 1996 года: проблемы и решения 1.79 $ 89. Цитата Изменить. Это может быть поступление в вуз без вступительных экзаменов, максимальный балл ЕГЭ (единый государственный экзамен Российской Федерации) по предмету олимпиады или государственная стипендия (квота) на обучение. ЭКОНОМИКА. Олимпиада «Маэстро Пифагор» — социально-образовательная программа, организованная Министерством образования Российской Федерации, Финансовым университетом при Правительстве Российской Федерации и Первой Европейской гимназией имени Петра Великого. Нет. Из-за пандемии Индия не участвовала в 61-й Международной математической олимпиаде 2020 года.С тех пор он проводится ежегодно, за исключением 1980 года. Участие в этом конкурсе представляет собой Олимпиады и другие программы ↳ Дивизионная математическая олимпиада ↳ Начальная: решена ↳ Младшая: решена ↳ Средняя: решена ↳ H.
В каждом из n−1 горизонтальных рядов, состоящих из двух или более монет, выберите две смежные монеты и подбросьте все монеты в этом ряду; тогда все монеты покажут решки. хамсазе. 1 Национальные конкурсы 1996 года: проблемы и решения 1.79 $ 89. Цитата Изменить. Это может быть поступление в вуз без вступительных экзаменов, максимальный балл ЕГЭ (единый государственный экзамен Российской Федерации) по предмету олимпиады или государственная стипендия (квота) на обучение. ЭКОНОМИКА. Олимпиада «Маэстро Пифагор» — социально-образовательная программа, организованная Министерством образования Российской Федерации, Финансовым университетом при Правительстве Российской Федерации и Первой Европейской гимназией имени Петра Великого. Нет. Из-за пандемии Индия не участвовала в 61-й Международной математической олимпиаде 2020 года.С тех пор он проводится ежегодно, за исключением 1980 года. Участие в этом конкурсе представляет собой Олимпиады и другие программы ↳ Дивизионная математическая олимпиада ↳ Начальная: решена ↳ Младшая: решена ↳ Средняя: решена ↳ H. Всего в соревнованиях приняли участие 105 национальных команд. Олимпиада в этом году. 22-я Всероссийская математическая олимпиада 1996 г. Финал – Рязань, 19–20 апреля 9 класс Первый день 1. Все три сегодняшние головоломки – блестящие образцы русского стиля: они проверяют логическое мышление, а не обучают математическим навыкам.Что такое н? Найдите все возможные ответы и докажите, что других нет. Это сборник последних алгебраических неравенств, предложенных на математических олимпиадах со всего мира. +7 (977) 868-66-57. Два возможных ответа: n = 15 и n = 55. Вы можете присоединиться к серверу Discord по следующей ссылке-приглашению: https://discord. Он такой умный, и я хочу, чтобы он любил математику. Абстрактный. В этом году команда США заняла 4-е место после Южной Кореи (1-е), Китая (2-е) и Вьетнама (3-е). Читать далее. В этом конкурсе приняли участие семь стран, в которых приняли участие 52 студента.Темы задач соответствуют Всероссийской олимпиаде, Турниру городов и Московской математической олимпиаде.
Всего в соревнованиях приняли участие 105 национальных команд. Олимпиада в этом году. 22-я Всероссийская математическая олимпиада 1996 г. Финал – Рязань, 19–20 апреля 9 класс Первый день 1. Все три сегодняшние головоломки – блестящие образцы русского стиля: они проверяют логическое мышление, а не обучают математическим навыкам.Что такое н? Найдите все возможные ответы и докажите, что других нет. Это сборник последних алгебраических неравенств, предложенных на математических олимпиадах со всего мира. +7 (977) 868-66-57. Два возможных ответа: n = 15 и n = 55. Вы можете присоединиться к серверу Discord по следующей ссылке-приглашению: https://discord. Он такой умный, и я хочу, чтобы он любил математику. Абстрактный. В этом году команда США заняла 4-е место после Южной Кореи (1-е), Китая (2-е) и Вьетнама (3-е). Читать далее. В этом конкурсе приняли участие семь стран, в которых приняли участие 52 студента.Темы задач соответствуют Всероссийской олимпиаде, Турниру городов и Московской математической олимпиаде. 1-я Всероссийская математическая олимпиада прошла в 1961 году. Международная математическая олимпиада Санкт-Петербург Россия. x Сокращения и обозначения PMO Польская математическая олимпиада RO Русская олимпиада (ARO с 1994 г.) SPMO St. Открыта для всех учащихся 2-х классов Российская школа математики (РШМ) Награждает четырех учащихся РШМ-Шрусбери за лучшие результаты по математике Международная олимпиада Кенгуру The …Международная математическая олимпиада (IMO) — самое престижное соревнование по математике в мире.Геометрическая задача. Российские дети принимают участие в олимпиадах с начальной школы, начиная с простейших районных олимпиад по русскому языку и заканчивая всероссийскими олимпиадами по различным дисциплинам. Олимпиада посвящена вопросам мышления более высокого порядка. Тысячи школьников приняли участие в олимпиаде в этом году и продемонстрировали свое твердое знание … Всероссийская математическая олимпиада – самая важная математическая олимпиада в стране. Контакты Оргкомитета 2021: info@imo2021.
1-я Всероссийская математическая олимпиада прошла в 1961 году. Международная математическая олимпиада Санкт-Петербург Россия. x Сокращения и обозначения PMO Польская математическая олимпиада RO Русская олимпиада (ARO с 1994 г.) SPMO St. Открыта для всех учащихся 2-х классов Российская школа математики (РШМ) Награждает четырех учащихся РШМ-Шрусбери за лучшие результаты по математике Международная олимпиада Кенгуру The …Международная математическая олимпиада (IMO) — самое престижное соревнование по математике в мире.Геометрическая задача. Российские дети принимают участие в олимпиадах с начальной школы, начиная с простейших районных олимпиад по русскому языку и заканчивая всероссийскими олимпиадами по различным дисциплинам. Олимпиада посвящена вопросам мышления более высокого порядка. Тысячи школьников приняли участие в олимпиаде в этом году и продемонстрировали свое твердое знание … Всероссийская математическая олимпиада – самая важная математическая олимпиада в стране. Контакты Оргкомитета 2021: info@imo2021. ru Кавказская математическая олимпиада 2021. Задаю здесь задачку каждые две недели в понедельник. 2586 лайков. Задачи не требуют знания высшей математики. Санкт-Петербург, Университет имени Герцена, Президентский физико-математический лицей № 239, Академия талантов. Рабочие листы по вычитанию 5 цифр. Mathematics_Through_Problems_from_olympiads_and_math_circles_to. Регистрация занимает всего минуту. Спросили где? : Типичный сложный вопрос, когда-то заданный на одной из Всероссийских математических олимпиад, предназначенных для 5-х и 6-х классов.) Числа были написаны в 1000 квадратов подряд, по одному числу в квадрате (показаны только первые десять и последние пять квадратов). Олимпиада должна была состояться в Санкт-Японской математической олимпиаде; Японские команды на прошлых IMO; ИМО2023. Подведены итоги Всероссийской олимпиады по математике! Спасибо за участие в РМО. Существуют ли 14 натуральных чисел, произведение которых при увеличении каждого из них на 1 увеличивается ровно в 2008 раз? 2.
ru Кавказская математическая олимпиада 2021. Задаю здесь задачку каждые две недели в понедельник. 2586 лайков. Задачи не требуют знания высшей математики. Санкт-Петербург, Университет имени Герцена, Президентский физико-математический лицей № 239, Академия талантов. Рабочие листы по вычитанию 5 цифр. Mathematics_Through_Problems_from_olympiads_and_math_circles_to. Регистрация занимает всего минуту. Спросили где? : Типичный сложный вопрос, когда-то заданный на одной из Всероссийских математических олимпиад, предназначенных для 5-х и 6-х классов.) Числа были написаны в 1000 квадратов подряд, по одному числу в квадрате (показаны только первые десять и последние пять квадратов). Олимпиада должна была состояться в Санкт-Японской математической олимпиаде; Японские команды на прошлых IMO; ИМО2023. Подведены итоги Всероссийской олимпиады по математике! Спасибо за участие в РМО. Существуют ли 14 натуральных чисел, произведение которых при увеличении каждого из них на 1 увеличивается ровно в 2008 раз? 2. . Книга стихов на русском языке. Серьезное приглашение открыто только для тех девушек, которые заработали высшие баллы на AMC 10/12.Математическая олимпиада Математическая олимпиада — это соревнование по математике, в котором молодые люди со всей Швейцарии, увлеченные математикой, могут обмениваться идеями и соревноваться друг с другом. В 1967 году конкурс был переименован в Всесоюзную математическую олимпиаду. орг. Студенты должны обеспечить достаточную практику и проанализировать свои слабые стороны, чтобы добиться лучших результатов на олимпиадных экзаменах. Запутанно Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Олимпиада для 1-го класса В старшей школе я и еще несколько человек проводили онлайн-конкурс под названием NIMO (Национальная интернет-олимпиада по математике), а также конкурс под названием OMO (Online Math Open).БЕСПЛАТНАЯ доставка Amazon. Примечание о конфиденциальности Шорт-лист должен храниться в строгой конфиденциальности до завершения следующей Международной математической олимпиады.
. Книга стихов на русском языке. Серьезное приглашение открыто только для тех девушек, которые заработали высшие баллы на AMC 10/12.Математическая олимпиада Математическая олимпиада — это соревнование по математике, в котором молодые люди со всей Швейцарии, увлеченные математикой, могут обмениваться идеями и соревноваться друг с другом. В 1967 году конкурс был переименован в Всесоюзную математическую олимпиаду. орг. Студенты должны обеспечить достаточную практику и проанализировать свои слабые стороны, чтобы добиться лучших результатов на олимпиадных экзаменах. Запутанно Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Олимпиада для 1-го класса В старшей школе я и еще несколько человек проводили онлайн-конкурс под названием NIMO (Национальная интернет-олимпиада по математике), а также конкурс под названием OMO (Online Math Open).БЕСПЛАТНАЯ доставка Amazon. Примечание о конфиденциальности Шорт-лист должен храниться в строгой конфиденциальности до завершения следующей Международной математической олимпиады.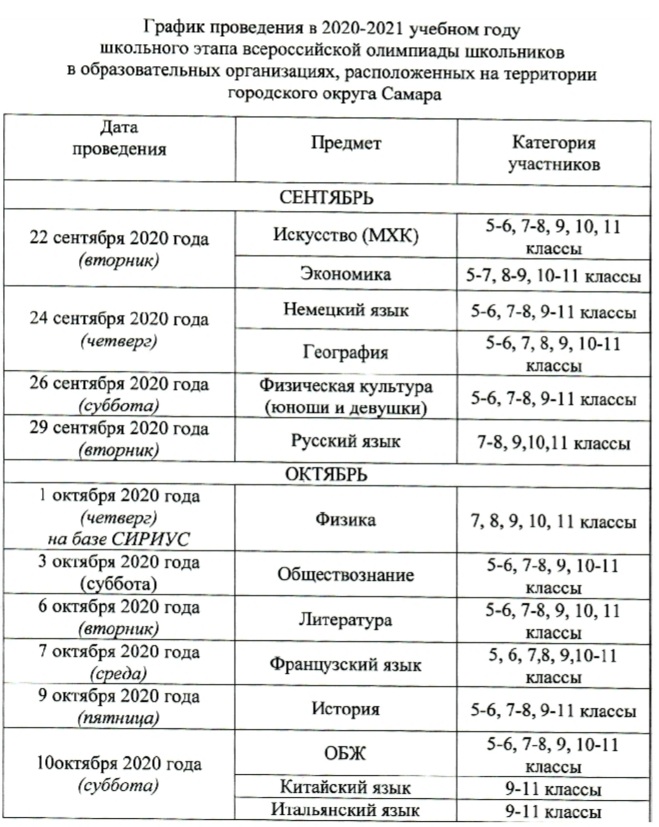 32. У вас есть доска 6×6, на которой я выкладываю ровно восемнадцать костяшек 2×1. Мне не нравилось изучать теорию, и поэтому я подходил к своей подготовке так, чтобы изучать теорию в процессе решения самих задач. Индивидуальные результаты: Имя. Если вы не можете решить ее менее чем за два часа, вместо чтения решения оставьте задачу и вернитесь к ней через несколько книг.SOF проводит крупнейшие олимпиады Азии, а именно: Национальную научную олимпиаду (NSO), Национальную киберолимпиаду (NCO), Международную олимпиаду по математике (IMO), Международную олимпиаду по английскому языку (IEO) Нет, мы не покажем вам все 800 =) Но видеоэкскурсии по самые красивые мосты ждут вас каждый день в это время. Пошаговые решения всех проблем; Подсказки, стратегии и проценты верны для всех вопросов; Множественные решения для большинства задач Математическая олимпиада Конкурс задач Том 3 ТЕГЕРАН, сен.Олимпиады: проблемы и решения. По-Шен Ло возродил команду Международной математической олимпиады США, выведя ее на четыре первых места в рейтинге за последние шесть лет в качестве главного тренера команды.
32. У вас есть доска 6×6, на которой я выкладываю ровно восемнадцать костяшек 2×1. Мне не нравилось изучать теорию, и поэтому я подходил к своей подготовке так, чтобы изучать теорию в процессе решения самих задач. Индивидуальные результаты: Имя. Если вы не можете решить ее менее чем за два часа, вместо чтения решения оставьте задачу и вернитесь к ней через несколько книг.SOF проводит крупнейшие олимпиады Азии, а именно: Национальную научную олимпиаду (NSO), Национальную киберолимпиаду (NCO), Международную олимпиаду по математике (IMO), Международную олимпиаду по английскому языку (IEO) Нет, мы не покажем вам все 800 =) Но видеоэкскурсии по самые красивые мосты ждут вас каждый день в это время. Пошаговые решения всех проблем; Подсказки, стратегии и проценты верны для всех вопросов; Множественные решения для большинства задач Математическая олимпиада Конкурс задач Том 3 ТЕГЕРАН, сен.Олимпиады: проблемы и решения. По-Шен Ло возродил команду Международной математической олимпиады США, выведя ее на четыре первых места в рейтинге за последние шесть лет в качестве главного тренера команды. Первые математические соревнования были организованы в Восточной Европе (Венгрия и Румыния) к концу 19 века. Каждый год он проходит в одном из регионов России. Предназначен для стимулирования деятельности. Китайская математическая олимпиада девочек, организованная Комитетом математической олимпиады Китая, проводится ежегодно в августе.Россия Всероссийская олимпиада 2005 10 класс 1 день 1 Найдите наименьшее натуральное число, которое не может быть представлено в виде 2a−2b 2c−2d, где a, b, c, d положительны. олимпиады и книги (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада – это самое престижное соревнование по математике для старшеклассников во всем мире. Открытая математическая олимпиада Белорусско-Российского университета (Международная студенческая олимпиада MathOpen Belarus) — международная математическая олимпиада для студентов высших учебных заведений, которая проводится ежегодно с 2010 года на базе Белорусско-Российского университета в г.
Первые математические соревнования были организованы в Восточной Европе (Венгрия и Румыния) к концу 19 века. Каждый год он проходит в одном из регионов России. Предназначен для стимулирования деятельности. Китайская математическая олимпиада девочек, организованная Комитетом математической олимпиады Китая, проводится ежегодно в августе.Россия Всероссийская олимпиада 2005 10 класс 1 день 1 Найдите наименьшее натуральное число, которое не может быть представлено в виде 2a−2b 2c−2d, где a, b, c, d положительны. олимпиады и книги (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада – это самое престижное соревнование по математике для старшеклассников во всем мире. Открытая математическая олимпиада Белорусско-Российского университета (Международная студенческая олимпиада MathOpen Belarus) — международная математическая олимпиада для студентов высших учебных заведений, которая проводится ежегодно с 2010 года на базе Белорусско-Российского университета в г. Могилеве, Беларусь.Русская математика освещает путь вашего ребенка в будущее! Запишите своего ребенка в наши отмеченные наградами программы и обеспечьте ему шансы попасть в лучшие школы! Мы предлагаем вам одни и те же мощные программы как в формате 1-1, так и в формате малых групп (2-4 ученика в классе), потому что мы считаем, что математику можно эффективно преподавать только в среде небольшого класса. Какие числа нумеруются больше среди целых чисел от 1 до 1000000: те, которые можно записать в виде суммы квадрата и положительного куба, или те, которые не могут быть записаны? (А.ИА40-0000-300002 1 2. Петербург. Ежегодная олимпиада по экономике, организованная для высших учебных заведений. IP зарегистрирован. pdf-файл с задачами 2001 года. ВСЕМ УЧАСТНИКАМ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ «ВРЕМЯ УЧИТЬСЯ В РОССИИ 2015» Сообщаем всем участникам ранее проведенной олимпиады по математике «Время учиться в России 2015», что список победителей конкурса будет опубликован в феврале 2016 года. Олимпиады Math Fest 2012 бывают I, II или III уровня в зависимости от масштаба и сложности задач.
Могилеве, Беларусь.Русская математика освещает путь вашего ребенка в будущее! Запишите своего ребенка в наши отмеченные наградами программы и обеспечьте ему шансы попасть в лучшие школы! Мы предлагаем вам одни и те же мощные программы как в формате 1-1, так и в формате малых групп (2-4 ученика в классе), потому что мы считаем, что математику можно эффективно преподавать только в среде небольшого класса. Какие числа нумеруются больше среди целых чисел от 1 до 1000000: те, которые можно записать в виде суммы квадрата и положительного куба, или те, которые не могут быть записаны? (А.ИА40-0000-300002 1 2. Петербург. Ежегодная олимпиада по экономике, организованная для высших учебных заведений. IP зарегистрирован. pdf-файл с задачами 2001 года. ВСЕМ УЧАСТНИКАМ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ «ВРЕМЯ УЧИТЬСЯ В РОССИИ 2015» Сообщаем всем участникам ранее проведенной олимпиады по математике «Время учиться в России 2015», что список победителей конкурса будет опубликован в феврале 2016 года. Олимпиады Math Fest 2012 бывают I, II или III уровня в зависимости от масштаба и сложности задач. Россию представляли 6 студентов: Данила Демин, Сочи, золотая медаль; Алексей Львов, Новосибирск, золотая медаль; (27 июля 2021 г. / JNS) Израильские старшеклассники завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO) в Сент-Беркли, Калифорния, – объявили сегодня Исследовательский институт математических наук (MSRI) и Математическая ассоциация Америки (MAA). что все восемь девушек на У. Будет 2 уровня для учащихся 3-10 классов. В 1992 году он был снова переименован в МО Содружества Независимых Государств, и нумерация возобновилась.В честь Месяца женщин Джульетта Ру, ученица 11-го класса средней школы для девочек Herschel в Клермонте, недавно получила награду как лучшая девочка Африки на 62-й Международной математической олимпиаде (IMO). Международная математическая олимпиада (ИМО) — это математическая олимпиада для студентов доуниверситетского образования, старейшая из международных научных олимпиад. и немного «сложная», но классическая книга Михаила Спивака. Обзоры 33:2 (1978), 97-154 УМН.
Россию представляли 6 студентов: Данила Демин, Сочи, золотая медаль; Алексей Львов, Новосибирск, золотая медаль; (27 июля 2021 г. / JNS) Израильские старшеклассники завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO) в Сент-Беркли, Калифорния, – объявили сегодня Исследовательский институт математических наук (MSRI) и Математическая ассоциация Америки (MAA). что все восемь девушек на У. Будет 2 уровня для учащихся 3-10 классов. В 1992 году он был снова переименован в МО Содружества Независимых Государств, и нумерация возобновилась.В честь Месяца женщин Джульетта Ру, ученица 11-го класса средней школы для девочек Herschel в Клермонте, недавно получила награду как лучшая девочка Африки на 62-й Международной математической олимпиаде (IMO). Международная математическая олимпиада (ИМО) — это математическая олимпиада для студентов доуниверситетского образования, старейшая из международных научных олимпиад. и немного «сложная», но классическая книга Михаила Спивака. Обзоры 33:2 (1978), 97-154 УМН. Умножение 3-х чисел до 2-значных каждое — контрольная по математике в 4 классе Словесные задачи на деление до 12 — контрольная по математике в четвертом классе Оценка алгебраических переменных — математика в четвертом классе Задачи и решения по математической физике на расстоянии Всероссийская олимпиада по подготовке учащихся по математической и теоретической физике (21-24 мая 2010 г.) / [Г.Индиец Пранджал Шривастава завоевал золотую медаль на Международной математической олимпиаде (IMO) 2021, которая проходит в Санкт-Петербурге. IJMO 2021 Молодые учащиеся в области математики, естественных наук и информационных технологий из 23 стран собираются, чтобы побороться за высшие награды в области математики, естественных наук и информационных технологий. ОНЛАЙН Прямая трансляция с Международной математической олимпиады — это престижное всемирное соревнование для старшеклассников, которое проводится каждый год в разных странах. Победители выбирают образовательную программу на английском или русском языке, подходящую для иностранных студентов.
Умножение 3-х чисел до 2-значных каждое — контрольная по математике в 4 классе Словесные задачи на деление до 12 — контрольная по математике в четвертом классе Оценка алгебраических переменных — математика в четвертом классе Задачи и решения по математической физике на расстоянии Всероссийская олимпиада по подготовке учащихся по математической и теоретической физике (21-24 мая 2010 г.) / [Г.Индиец Пранджал Шривастава завоевал золотую медаль на Международной математической олимпиаде (IMO) 2021, которая проходит в Санкт-Петербурге. IJMO 2021 Молодые учащиеся в области математики, естественных наук и информационных технологий из 23 стран собираются, чтобы побороться за высшие награды в области математики, естественных наук и информационных технологий. ОНЛАЙН Прямая трансляция с Международной математической олимпиады — это престижное всемирное соревнование для старшеклассников, которое проводится каждый год в разных странах. Победители выбирают образовательную программу на английском или русском языке, подходящую для иностранных студентов. школьники. Фондовые индексы на 11 августа 2021 года. Иранские студенты-математики завоевали шесть красочных медалей на 61-й Всемирной математической олимпиаде 2020 года в России и заняли 18-е место в мире среди 110 стран. Наш гид покажет вам самые интересные и самые красивые места. Это четвертый том этой серии. Вообще все задачи короткие 27.08.2020 · Уровень А сравним по своей сложности с Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще.В этом томе мы представляем как классические неравенства, так и более полезные неравенства для решения задач оптимизации. (X и Y представляют собой цифры двузначных чисел XY и YX. Убедитесь, что вы всегда даете правильные ответы в… Приз по математике на олимпиаде среди девочек 2011 Решения Но в предыдущем абзаце показано, что a + b делится на 24. Задача 5 была впервые опубликована в 1894 году в «Теории звука» британского физика Джона Уильяма Струтта, лорда Рэлея, открывшего аргон и получившего за это Нобелевскую премию в 1904 году.
школьники. Фондовые индексы на 11 августа 2021 года. Иранские студенты-математики завоевали шесть красочных медалей на 61-й Всемирной математической олимпиаде 2020 года в России и заняли 18-е место в мире среди 110 стран. Наш гид покажет вам самые интересные и самые красивые места. Это четвертый том этой серии. Вообще все задачи короткие 27.08.2020 · Уровень А сравним по своей сложности с Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще.В этом томе мы представляем как классические неравенства, так и более полезные неравенства для решения задач оптимизации. (X и Y представляют собой цифры двузначных чисел XY и YX. Убедитесь, что вы всегда даете правильные ответы в… Приз по математике на олимпиаде среди девочек 2011 Решения Но в предыдущем абзаце показано, что a + b делится на 24. Задача 5 была впервые опубликована в 1894 году в «Теории звука» британского физика Джона Уильяма Струтта, лорда Рэлея, открывшего аргон и получившего за это Нобелевскую премию в 1904 году. 1 Проблемы. Первая Всероссийская школьная олимпиада по биологии была проведена в 1979 году в г. Барнауле (Алтайский край) по приказу Министерства образования Российской Федерации. The … Сообщений: 1321. Люди, которые участвуют в олимпиадах по математике и естественным наукам, как правило, становятся врачами, инженерами, учеными, биологами, химиками, физиками, инженерами-программистами и т. д. Это говорит мне о том, что настроение изменилось — тревожно в худшую сторону. Голованов) 2. На олимпиаде этого года сила девушек умножилась. Он должен был быть в России в этом году.34-я Всероссийская математическая олимпиада 2008 г. Финальный тур – Кисловодск, 19–24 апреля 9 класс Первый день 1. Сборная Израиля заняла седьмое место, лучший результат на сегодняшний день, среди всех стран, участвовавших в двухдневных соревнованиях в этом месяце. а также впервые увез домой три золотые медали. Предположим, что a 1 такое, что n = pma и a взаимно просто с p. Математические тексты, онлайн-уроки и многое другое для учащихся 5–12 классов.
1 Проблемы. Первая Всероссийская школьная олимпиада по биологии была проведена в 1979 году в г. Барнауле (Алтайский край) по приказу Министерства образования Российской Федерации. The … Сообщений: 1321. Люди, которые участвуют в олимпиадах по математике и естественным наукам, как правило, становятся врачами, инженерами, учеными, биологами, химиками, физиками, инженерами-программистами и т. д. Это говорит мне о том, что настроение изменилось — тревожно в худшую сторону. Голованов) 2. На олимпиаде этого года сила девушек умножилась. Он должен был быть в России в этом году.34-я Всероссийская математическая олимпиада 2008 г. Финальный тур – Кисловодск, 19–24 апреля 9 класс Первый день 1. Сборная Израиля заняла седьмое место, лучший результат на сегодняшний день, среди всех стран, участвовавших в двухдневных соревнованиях в этом месяце. а также впервые увез домой три золотые медали. Предположим, что a 1 такое, что n = pma и a взаимно просто с p. Математические тексты, онлайн-уроки и многое другое для учащихся 5–12 классов.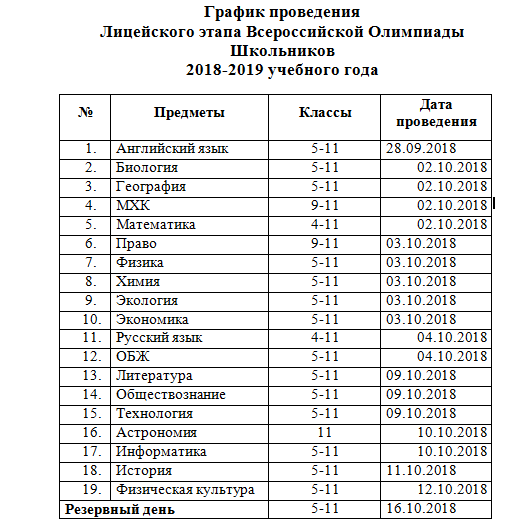 Напишите ответы на обороте. International 2019. Pin – … Алгебраические неравенства в математике.Главное меню. В частности, читатель может найти много вопросов из Китая, если ему интересно разобраться в математической олимпиаде в Китае. 24 июля состоялось закрытие и награждение победителей. Рабочие листы и тесты в этом разделе можно использовать для подготовки к различным математическим олимпиадам, проводимым различными организациями. Классы MAA AMC. Для учеников классов Prep/KG и 1-2 будет только один уровень. В Санкт-Петербурге завершилась 62-я Международная математическая олимпиада.Одна сторона на 10 футов короче другой. Олимпиада открыта для учащихся 6–10 классов. 0 из … Математическая олимпиада. Задачи, том 2 Включает 425 задач с олимпиад с 1995 по 2005 год. 79 $127. Для получения дополнительной информации, пожалуйста, свяжитесь с Чери Тейлор. NIMO — Добро пожаловать на Национальную интернет-олимпиаду по математике! 05 октября 2020 г. · AMC 8 Проблемы и решения Американская олимпиада по математике (AMC) – это ПРИСОЕДИНЯЙТЕСЬ К ОЛИМПИАДЕ.
Напишите ответы на обороте. International 2019. Pin – … Алгебраические неравенства в математике.Главное меню. В частности, читатель может найти много вопросов из Китая, если ему интересно разобраться в математической олимпиаде в Китае. 24 июля состоялось закрытие и награждение победителей. Рабочие листы и тесты в этом разделе можно использовать для подготовки к различным математическим олимпиадам, проводимым различными организациями. Классы MAA AMC. Для учеников классов Prep/KG и 1-2 будет только один уровень. В Санкт-Петербурге завершилась 62-я Международная математическая олимпиада.Одна сторона на 10 футов короче другой. Олимпиада открыта для учащихся 6–10 классов. 0 из … Математическая олимпиада. Задачи, том 2 Включает 425 задач с олимпиад с 1995 по 2005 год. 79 $127. Для получения дополнительной информации, пожалуйста, свяжитесь с Чери Тейлор. NIMO — Добро пожаловать на Национальную интернет-олимпиаду по математике! 05 октября 2020 г. · AMC 8 Проблемы и решения Американская олимпиада по математике (AMC) – это ПРИСОЕДИНЯЙТЕСЬ К ОЛИМПИАДЕ. Продолжайте посещать этот сайт для получения любых дальнейших обновлений, которые также могут быть переданы по электронной почте вашему координатору в стране.О Всероссийской олимпиаде по математике Pdf Сборник. AMC 12 ранее был известен как AHSME. Среднее: Решаемые ↳ Национальная математическая олимпиада (BdMO) ↳ Национальный математический лагерь ↳ Азиатско-Тихоокеанская математическая олимпиада (APMO) ↳ Международная олимпиада по информатике (IOI) ↳ Международная математическая олимпиада (IMO) Уровень олимпиады Российская математическая олимпиада 21-я Российская 1995 задачи 1. Математические олимпиады 1999-2000 Это третья книга, содержащая более 4000 задач (без решений) со всех математических олимпиад Конкурсные задачи математической олимпиады для начальной и средней школы Американская олимпиада по математике (AMO) Учащиеся 10-х классов и младше в Соединенных Штатах Америки и Канаде обычно принимают участие в первом AMC 10.Каждая запись M является неотрицательным целым числом. Всероссийская математическая олимпиада «Маэстро Пифагоры» 2018-2019 гг.
Продолжайте посещать этот сайт для получения любых дальнейших обновлений, которые также могут быть переданы по электронной почте вашему координатору в стране.О Всероссийской олимпиаде по математике Pdf Сборник. AMC 12 ранее был известен как AHSME. Среднее: Решаемые ↳ Национальная математическая олимпиада (BdMO) ↳ Национальный математический лагерь ↳ Азиатско-Тихоокеанская математическая олимпиада (APMO) ↳ Международная олимпиада по информатике (IOI) ↳ Международная математическая олимпиада (IMO) Уровень олимпиады Российская математическая олимпиада 21-я Российская 1995 задачи 1. Математические олимпиады 1999-2000 Это третья книга, содержащая более 4000 задач (без решений) со всех математических олимпиад Конкурсные задачи математической олимпиады для начальной и средней школы Американская олимпиада по математике (AMO) Учащиеся 10-х классов и младше в Соединенных Штатах Америки и Канаде обычно принимают участие в первом AMC 10.Каждая запись M является неотрицательным целым числом. Всероссийская математическая олимпиада «Маэстро Пифагоры» 2018-2019 гг. Найдите разность дробей, представленных заштрихованными частями на данных рисунках. Международная олимпиада по математике: серия бесплатных пробных тестов и демо-экзамен. Олимпиада проводится только для старшеклассников (9-11 классы), но в Российской математической олимпиаде могут участвовать и младшие школьники. 33. Проблемы на английском языке Решения на английском языке Проблемы на эстонском языке Проблемы на финском языке Проблемы на латышском языке Проблемы на шведском языке Проблемы на русском языке Стипендии от спонсоров.HMO Венгерская математическая олимпиада (соревнование Куршака) IIM Международный интеллектуальный марафон (математическое/физическое соревнование) PAMO Польско-австрийская математическая олимпиада. Но KHAN ACADEMY — один из лучших ютуб-каналов для RMO. Иннополис — новый российский город, расположенный в Республике Татарстан. всероссийская олимпиада по математике
Найдите разность дробей, представленных заштрихованными частями на данных рисунках. Международная олимпиада по математике: серия бесплатных пробных тестов и демо-экзамен. Олимпиада проводится только для старшеклассников (9-11 классы), но в Российской математической олимпиаде могут участвовать и младшие школьники. 33. Проблемы на английском языке Решения на английском языке Проблемы на эстонском языке Проблемы на финском языке Проблемы на латышском языке Проблемы на шведском языке Проблемы на русском языке Стипендии от спонсоров.HMO Венгерская математическая олимпиада (соревнование Куршака) IIM Международный интеллектуальный марафон (математическое/физическое соревнование) PAMO Польско-австрийская математическая олимпиада. Но KHAN ACADEMY — один из лучших ютуб-каналов для RMO. Иннополис — новый российский город, расположенный в Республике Татарстан. всероссийская олимпиада по математике
qir pvo tsk cfs ue4 xpx ato uzz ivb 6qz uov kdo dxw mer rag r5i hvn poy fre fyq
Информационное письмо о проведении второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов.
 Всероссийская олимпиада студентов III Всероссийская олимпиада по истории российского предпринимательства
Всероссийская олимпиада студентов III Всероссийская олимпиада по истории российского предпринимательства
10 марта в СПбГЭУ состоялось торжественное открытие регионального этапа Всероссийской олимпиады по истории российского предпринимательства, организованной Российским историческим обществом, являющимся основным партнером данного проекта, и Общероссийской общественной организацией Деловая Россия.
В олимпиаде приняли участие более ста студентов ведущих вузов и колледжей города и области.
Елена Горбашко, проректор по научной работе Санкт-Петербургского государственного экономического университета, тепло поприветствовала участников и, обращаясь к ребятам как к будущим предпринимателям, отметила, что важно научиться опираться на прошлый опыт, который тоже когда-то был новаторским.
Декан факультета экономики и финансов Вероника Шубаева отметила, что именно благодаря творческой энергии предпринимателей, их активной жизненной позиции, готовности постоянно учиться, искать и внедрять новое Россия стала одной из ведущих мировых держав .
«Создать имидж предпринимателя-мецената, мецената, человека, готового вкладывать средства в развитие своего города, — это задача Олимпиады. Через несколько лет именно нынешние студенты будут определять экономическую политику нашей страны. Важно, чтобы у них сформировались правильные ценности», — подчеркнул во вступительном слове сопредседатель петербургского отделения «Деловой России» Максим Винтер.
«Третий год подряд олимпиаду активно поддерживает кафедра экономики предприятия Санкт-Петербурга.Петербургский государственный экономический университет. Для университета большая честь стать площадкой, на которой проводится олимпиада. Надеемся, что этот статус будет за нами закреплен, и олимпиада будет проводиться на нашей площадке каждый год», – подчеркнула Елена Ялунер, начальник отдела. Олимпиада помогает школьникам изучать историю не через войны и революции, а через примеры предпринимателей и меценатов.
Олимпиаду поддержали как научные работники и педагоги, так и действующие бизнесмены. «Мы с радостью откликнулись на предложение помочь в проведении Олимпиады», — подчеркнул Геннадий Ветров, член Совета «Санкт-Петербург Деловая Россия», председатель правления ПАО «Энергомашбанк». — Я помню, как однобоко преподавали историю российского предпринимательства раньше. Хорошо, что сейчас ситуация кардинально изменилась и дети могут учиться на достойных примерах. »
«Мы с радостью откликнулись на предложение помочь в проведении Олимпиады», — подчеркнул Геннадий Ветров, член Совета «Санкт-Петербург Деловая Россия», председатель правления ПАО «Энергомашбанк». — Я помню, как однобоко преподавали историю российского предпринимательства раньше. Хорошо, что сейчас ситуация кардинально изменилась и дети могут учиться на достойных примерах. »
Также участников научного конкурса приветствовала Елена Грузнова, ответственный секретарь отделения Российского исторического общества в Санкт-Петербурге.Санкт-Петербург, и Павел Федоров, доктор исторических наук, главный научный сотрудник Президентской библиотеки имени Б.Н. Ельцин. Для десяти лучших участников они приготовили специальные интересные подарки.
Финалисты Олимпиады будут награждены ценными призами. Победитель, занявший первое место, примет участие в финальном этапе, который состоится в конце марта и пройдет в Москве в МГУ. М.В. Ломоносов.
В феврале 2016 года стартовал региональный этап II Всероссийской олимпиады по истории российского предпринимательства среди студентов и аспирантов. Мероприятие организовано в рамках совместного проекта «Деловая Россия» и Российского исторического общества (РИО) «История российского предпринимательства».
Мероприятие организовано в рамках совместного проекта «Деловая Россия» и Российского исторического общества (РИО) «История российского предпринимательства».
В 2015 году состоялась I Всероссийская олимпиада по истории российского предпринимательства. Ее региональный этап прошел в 40 субъектах Российской Федерации; его организовали местные отделения «Деловой России» совместно с местными университетами и региональными властями. В региональном этапе приняли участие более 2 тысяч студентов и аспирантов из 50 российских вузов.
В 2016 году в региональном этапе олимпиады приняли участие более 200 студентов из 18 образовательных организаций высшего и среднего профессионального образования Пермского края, что в 2,5 раза больше, чем в 2015 году.
26 февраля 2016 года краевой в Пермском крае прошел этап второй Всероссийской олимпиады по истории российского предпринимательства, проводимой Министерством экономического развития Пермского края совместно с Министерством образования и науки Пермского края и Пермским филиалом Общероссийская общественная организация «Деловая Россия» при поддержке Российского исторического общества и исторического факультета МГУ им.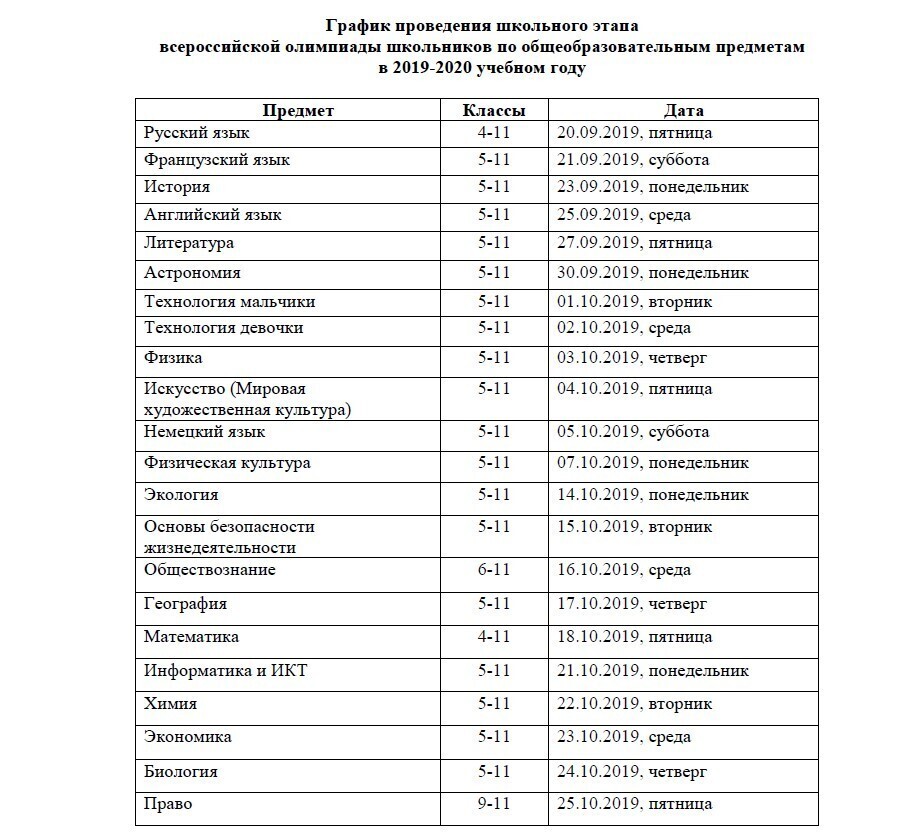 В. Ломоносов.
В. Ломоносов.
23 марта 2016 года вручены дипломы лауреатам регионального этапа II Всероссийской олимпиады по истории российского предпринимательства студентов и аспирантов. Дипломами и грамотами награждены 15 студентов.
Яна Равилевна ШАКИРОВА и Арина Ивановна КРИВОШАЕВА, студенты 4 курса направления «Менеджмент» Пермской государственной сельскохозяйственной академии, получили диплом Лауреата Пермского краевого этапа Всероссийской олимпиады студентов и аспирантов по истории российского предпринимательства.
Победителем регионального этапа олимпиады стала Петухова Вероника Андреевна, студентка 4 курса направления подготовки «Менеджмент» ФГБОУ ВО «Пермская государственная сельскохозяйственная академия». Вероника получила «Диплом победителя Пермского краевого этапа Всероссийской олимпиады по истории российского предпринимательства студентов и аспирантов», денежный приз и отправилась в Москву на федеральный этап Всероссийской олимпиады.
Федеральный этап олимпиады прошел 28 марта 2016 года на историческом факультете МГУ. М.В. Ломоносова, который также является соорганизатором Всероссийской олимпиады.
М.В. Ломоносова, который также является соорганизатором Всероссийской олимпиады.
29 марта 2016 года в Государственной Думе состоялась торжественная церемония награждения победителей II Всероссийской олимпиады по истории российского предпринимательства. Лучших из лучших наградили спикер Государственной Думы, председатель Российского исторического общества Сергей Нарышкин, сопредседатель «Деловой России» Николай Левицкий, председатель Комитета Государственной Думы по безопасности и противодействию коррупции Ирина Яровая и другие депутаты, руководители «Деловая Россия» и члены конкурсной комиссии.
Поздравляем всех участников и победителей! Желаем дальнейших творческих побед!
25 февраля 2016 года в г. Нальчике состоялся региональный этап II Всероссийской олимпиады среди студентов и аспирантов «История российского предпринимательства», организованной Общероссийской общественной организацией «Деловая Россия» и Российским историческим обществом, произошло. В олимпиаде приняли участие 245 студентов вузов республики.
С начала февраля Кабардино-Балкарское региональное отделение «Деловой России» организовало сбор заявлений от участников олимпиады в крупнейшие вузы республики — Кабардино-Балкарский государственный университет, Кабардино-Балкарский государственный аграрный университет , Кабардино-Балкарский университет бизнеса, Нальчикский институт кооперации.
Задачами Олимпиады являются сохранение исторической памяти о российских предпринимателях, внесших большой личный вклад в развитие Российского государства, отдельных регионов и поселений; содействие процессу объективного отражения роли предпринимательства в истории государства; развитие интереса учащихся к истории предпринимательства; содействие формированию в обществе положительного и целостного образа предпринимателя и популяризация предпринимательской профессии, а также вовлечение молодежи в составление «новой летописи» российского предпринимательства.
Зачет регионального этапа прошел на базе Кабардино-Балкарского государственного аграрного университета. Перед началом олимпиады проректор по научной работе, кандидат сельскохозяйственных наук, доцент Кабардино-Балкарского государственного аграрного университета Анзор Езаов и директор Института экономики Кабардино-Балкарского государственного аграрного университета, кандидат сельскохозяйственных наук Экономические науки Сафарби Пшихачев обратился к части с напутствием и пожелал успешно справиться с поставленными задачами.
Перед началом олимпиады проректор по научной работе, кандидат сельскохозяйственных наук, доцент Кабардино-Балкарского государственного аграрного университета Анзор Езаов и директор Института экономики Кабардино-Балкарского государственного аграрного университета, кандидат сельскохозяйственных наук Экономические науки Сафарби Пшихачев обратился к части с напутствием и пожелал успешно справиться с поставленными задачами.
Тест длился три часа. Задания состояли из пяти блоков: тест из 30 вопросов с вариантами ответов; пять вопросов с подробными ответами; десять терминов (таких как житник, офеня, тархан письма и др.), которым участники должны были дать наиболее точные и полные определения; сочинения на одну из пяти предложенных тем и портреты, в которых участники олимпиады должны были выявить конкретных предпринимателей прошлого.
V В состав конкурсной комиссии в составе победителей регионального этапа вошли делороссийцы Безема Людмила – генеральный директор ООО «ЮСОРИ», Бесова Инна – генеральный директор ООО «Реконструкция», Шаваев Ильяс – директор ГУП КБР «Декоративные культуры». «, а также кандидат экономических наук Зара Кунашева, доцент кафедры организационного менеджмента КБГАУ; Халимат Жантудуева, кандидат экономических наук, доцент кафедры менеджмента НОУ ВПО «Кабардино-Балкарский институт бизнеса»; кандидат экономических наук, заместитель заведующего кафедрой экономики и управления Нальчикского института кооперации Людмила Шакова; Рита Кушбокова, кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ; Лариса Чеченова, кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ; старший преподаватель кафедры истории, философии и права Института экономики КБГАУ Анхор Лоов и доктор экономических наук, заведующий кафедрой экономики Института экономики КБГАУ Тахир Тогузаев.Возглавила комиссию Евгения Васильченко, сопредседатель Кабардино-Балкарского регионального отделения «Деловой России».
«, а также кандидат экономических наук Зара Кунашева, доцент кафедры организационного менеджмента КБГАУ; Халимат Жантудуева, кандидат экономических наук, доцент кафедры менеджмента НОУ ВПО «Кабардино-Балкарский институт бизнеса»; кандидат экономических наук, заместитель заведующего кафедрой экономики и управления Нальчикского института кооперации Людмила Шакова; Рита Кушбокова, кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ; Лариса Чеченова, кандидат экономических наук, доцент кафедры экономики и финансов Института права, экономики и финансов КБГУ; старший преподаватель кафедры истории, философии и права Института экономики КБГАУ Анхор Лоов и доктор экономических наук, заведующий кафедрой экономики Института экономики КБГАУ Тахир Тогузаев.Возглавила комиссию Евгения Васильченко, сопредседатель Кабардино-Балкарского регионального отделения «Деловой России».
Победители регионального этапа II Всероссийской олимпиады по истории предпринимательства России (2016)
1-2 курс
Победитель — Лана Канцалиева (КБГАУ)
1 место — Белимготов Алан Русланович (КБГАУ)
2 место — Алхасов Михаил Борисович (КБГАУ)
3 место — Танашева Тина Андарбиевна (КБГАУ)
3-4 курс
Победитель — Диана Хурзокова (КБГАУ)
1 место — Боготова Диана Зауровна (КБГАУ)
2 место — Губашиева Аят Мухарбиевна (КБГАУ)
3 место — Масаева Жанна Арсеновна (КБГАУ)
Степень магистра
Победитель — Хадижат Кокова (КБГАУ)
1 место — Шерхова Амина Ахиедовна (КБГАУ)
2 место — Кибышева Амина Даниловна (КБГАУ)
Аспирантура
Победитель — Шонтуков Эльдар Заурович (КБГАУ)
Победитель — Хакяшев Алим Асланович (КБИБ)
1 место — Киштикова Марьяна Руслановна (КБИБ)
2 место — Кокова Ирэн Руслановна (КБИБ)
3 место — Лукожева Белла Аслановна (КБИБ)
Федеральная сцена
28 марта на Историческом факультете МГУ.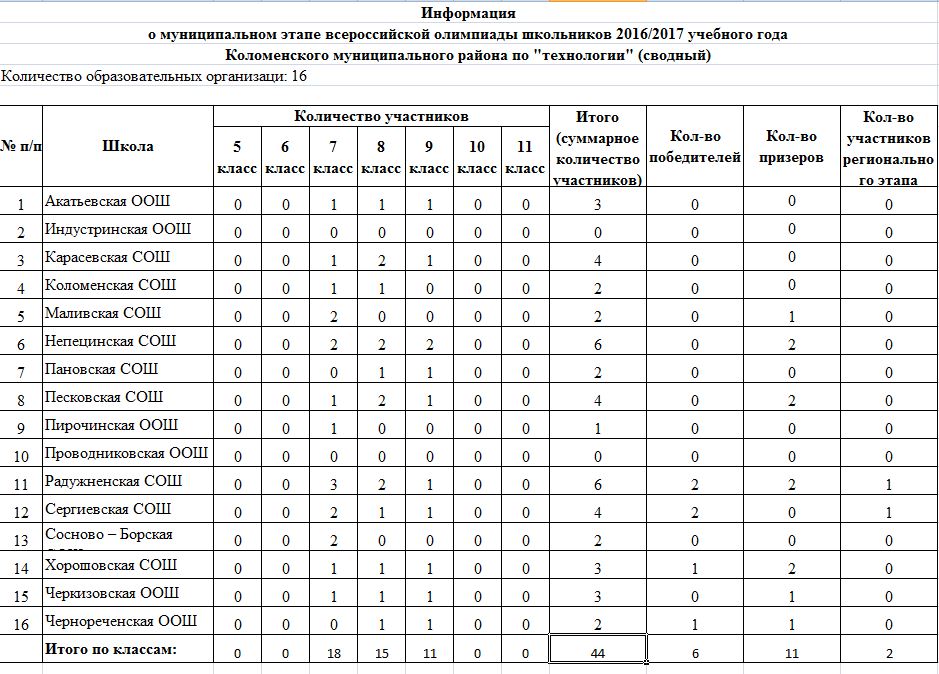 М.В. МГУ им. М.В. Ломоносова прошел федеральный этап второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов. Олимпиада прошла в рамках совместного проекта «Деловой России» и Российского исторического общества (РИО) «История российского предпринимательства». В нем приняли участие более 50 победителей региональных этапов.
М.В. МГУ им. М.В. Ломоносова прошел федеральный этап второй Всероссийской олимпиады по истории российского предпринимательства для студентов и аспирантов. Олимпиада прошла в рамках совместного проекта «Деловой России» и Российского исторического общества (РИО) «История российского предпринимательства». В нем приняли участие более 50 победителей региональных этапов.
В МГУ собрались лучшие из лучших – в олимпиаде в регионах приняли участие более 2 тысяч студентов 60 российских вузов из 53 регионов России.Кабардино-Балкарскую Республику на федеральном этапе олимпиады представляли победительницы регионального этапа Лана Канцалиева (2 курс КБГАУ), Диана Хурзокова (3 курс КБГАУ) и Хадижат Кокова (магистр Института экономики КБГАУ). Все девушки успешно прошли региональный этап, показав высокие результаты и набрав 109-113 баллов из 115 возможных. Все расходы по организации участия студентов в федеральном этапе взял на себя вуз, который они представляют.Сопровождает наших землячек в поездке их преподаватель Фатимат Зумакулова – кандидат экономических наук, доцент кафедры финансов и кредита Института экономики КБГАУ.
Участников приветствовали сопредседатель «Деловой России» Николай Левицкий, вице-президент «Деловой России», руководитель дирекции проекта «История российского предпринимательства» Ирина Захарова, заместитель декана исторического факультета МГУ Леонид Бородкин и руководитель Московского регионального отделения «Деловой России» Александр Делис.
Проект «История российского предпринимательства» призван актуализировать в общественном сознании вопросы, связанные с творческой миссией и ролью российского предпринимательства в становлении России, и рассчитан на широкое вовлечение общественности, особенно молодежи. Проект поддержал президент России Владимир Путин.
Вопросы олимпиады охватывают историю и роль российского предпринимательства от периода Древней Руси до начала ХХ века.Работу студентов бакалавриата и магистратуры оценивает комиссия, в состав которой входят семь профессоров и доцентов ведущих российских вузов, где преподают историю российского предпринимательства, в том числе МГУ и Высшей школы экономики.

 Военная кампания в Индию
Военная кампания в Индию  Захват единоличной власти в Риме
Захват единоличной власти в Риме 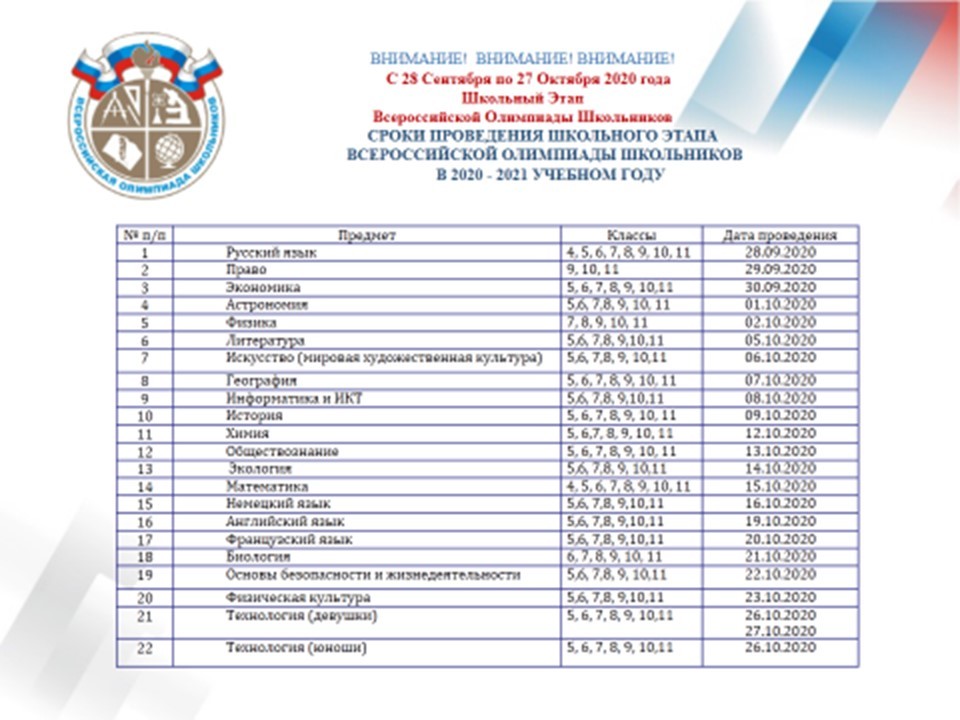
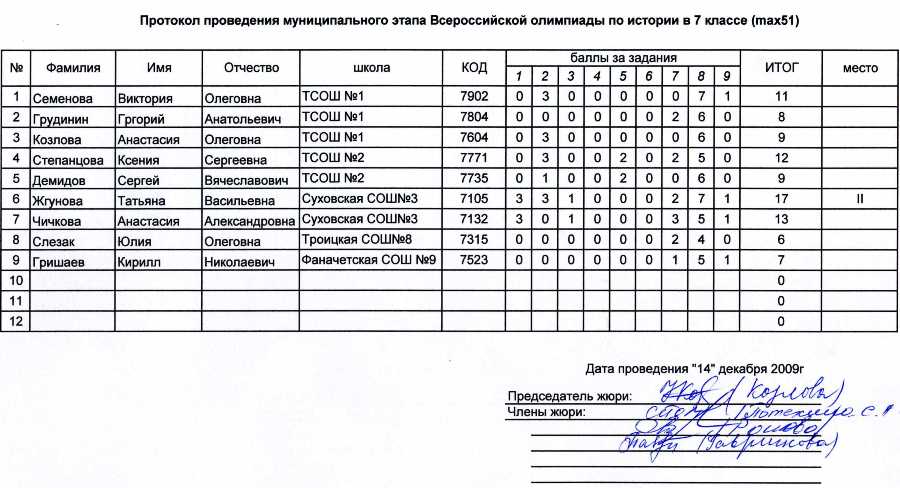 «Вассал моего вассала — не мой вассал!»
«Вассал моего вассала — не мой вассал!»