Вращательное движение: определение, расчет, формула расчета
Физика твердого тела изучает множество различных видов движения. Основные из них — это поступательное движение и вращение по неподвижной оси. Также существуют и их комбинации: свободное, плоское, криволинейное, равноускоренное и другие разновидности. Каждое движение имеет свои особенности, но и сходство между ними, конечно, есть. Рассмотрим, какое движение называется вращательным и приведем примеры такого движения, проведя аналогию с движением поступательным.
Законы механики в действии
На первый взгляд кажется, что вращательное движение, примеры которого мы наблюдаем в повседневной деятельности, нарушает законы механики. В чем можно заподозрить это нарушение и каких законов?
Например, закон инерции. Всякое тело, когда на него не действуют неуравновешенные силы, должно или находиться в состоянии покоя, или совершать равномерное прямолинейное движение. Но если дать глобусу боковой толчок, он начнет вращаться. И он, скорее всего, вращался бы вечно, если бы не трение. Как и отличный пример вращательного движения – земной шар – вращается постоянно, никем не подталкиваемый. Получается, что первый закон Ньютона в этом случае не действует? Это не так.
И он, скорее всего, вращался бы вечно, если бы не трение. Как и отличный пример вращательного движения – земной шар – вращается постоянно, никем не подталкиваемый. Получается, что первый закон Ньютона в этом случае не действует? Это не так.
Что движется: точка или тело
Вращательное движение отличается от поступательного, но между ними есть и много общего. Стоит сопоставить и сравнить эти виды, рассмотреть примеры поступательного и вращательного движения. Для начала следует строго разграничить механику материального тела и механику материальной точки. Вспомним определение поступательного движения. Это такое движение тела, при котором каждая его точка движется одинаково. Это означает, что все точки физического тела в каждый конкретный момент времени имеют одинаковую по модулю и направлению скорость и описывают одинаковые траектории. Поэтому, поступательное движение тела можно рассматривать как движение одной точки, а точнее, движение его центра масс. Если на такое тело (материальную точку) не будут действовать другие тела, то оно находится в покое, или движется прямолинейно и равномерно.
Сравнение формул для вычисления
Примеры вращательного движения тел (глобус, колесо) показывают, что вращение тела характеризуется угловой скоростью. Она обозначает, на какой угол оно повернется за единицу времени. В технике угловую скорость часто выражают числом оборотов в минуту. Если угловая скорость постоянна, то можно говорить, что тело вращается равномерно. Когда угловая скорость равномерно возрастает, то вращение называется равноускоренным. Сходство законов поступательного и вращательного движений очень значительно. Отличаются только буквенные обозначения, а формулы вычисления – одинаковы. Это хорошо видно в таблице.
| Поступательное движение | Вращательное движение | |
| Скорость v Путь s Время t Ускорение a | Угловая скорость ω Угловое перемещение φ Время t Угловое ускорение ą | |
| s = v * t | φ = ω * t | |
| v = a * t S = a*t2 / 2 | ω = ą * t φ = ą*t2 / 2 |
Все задачи по кинематике как поступательного, так и вращательного движения аналогично решаются по этим формулам.
Роль силы сцепления
Рассмотрим примеры вращательного движения в физике. Возьмем движение одной материальной точки – тяжелого металлического шарика от шарикоподшипника. Можно ли сделать так, чтобы он двигался по окружности? Если толкнуть шарик, то он покатится по прямой. Можно вести шарик по окружности, все время его поддерживая. Но стоит только убрать руку, и он продолжит движение по прямой линии. Из этого следует вывод, что точка может двигаться по окружности только под действием силы.
Это движение материальной точки, но в твердом теле не одна точка, а множество. Они связаны между собой, так как на них действуют силы сцепления. Именно эти силы и удерживают точки на круговой орбите. При отсутствии силы сцепления материальные точки вращающегося тела разлетелись бы, как грязь слетает с вращающегося колеса.
Линейная и угловая скорости
Эти примеры вращательного движения позволяют провести еще одну параллель между вращательным и поступательным движением. Во время поступательного движения все точки тела двигаются в определенный момент времени с одинаковой линейной скоростью. При вращении тела все его точки двигаются с одинаковой угловой скоростью. При вращательном движении, примеры которого – спицы вращающегося колеса, угловые скорости всех точек вращающейся спицы будут одинаковы, а линейные – различны.
Во время поступательного движения все точки тела двигаются в определенный момент времени с одинаковой линейной скоростью. При вращении тела все его точки двигаются с одинаковой угловой скоростью. При вращательном движении, примеры которого – спицы вращающегося колеса, угловые скорости всех точек вращающейся спицы будут одинаковы, а линейные – различны.
Ускорение – не в счет
Вспомним, что в равномерном движении точки по окружности всегда присутствует ускорение. Такое ускорение называется центростремительным. Оно показывает только изменение направления скорости, но не характеризует изменение скорости по модулю. Поэтому можно говорить о равномерном вращательном движении с одной угловой скоростью. В технике, при равномерном вращении маховика или ротора электрического генератора, угловую скорость считают постоянной. Только постоянное количество оборотов генератора может обеспечить постоянное напряжение в сети. А такое число оборотов маховика гарантирует плавный и экономичный ход машины. Тогда вращательное движение, примеры которого приведены выше, характеризуется только угловой скоростью, без учета центростремительного ускорения.
Тогда вращательное движение, примеры которого приведены выше, характеризуется только угловой скоростью, без учета центростремительного ускорения.
Сила и ее момент
Есть еще одна параллель между поступательным и вращательным движением – динамическая. Как гласит второй закон Ньютона, ускорение, получаемое телом, определяется как деление приложенной силы на массу тела. При вращении изменение угловой скорости зависит от силы. Ведь при завинчивании гайки определяющую роль играет вращающее действие силы, а не то, куда эта сила приложена: к самой гайке или к рукоятке гаечного ключа. Таким образом, показателю силы в формуле поступательного движения при вращении тела соответствует показатель момента силы. Наглядно это можно отобразить в виде таблицы.
| Поступательное движение | Вращательное движение |
| Сила F | Момент силы M=Fl, где l — плечо силы |
| Работа A = F * s | Работа A = M * φ |
| Мощность N=Fs/t=Fv | Мощность N=Mφ/t=Mω |
Масса тела, его форма и момент инерции
В приведенной таблице не проводится сравнение по формуле второго закона Ньютона, так как это требует дополнительного объяснения. В эту формулу входит показатель массы, который характеризует степень инертности тела. При вращении тела его инертность не характеризуется его массой, а определяется такой величиной, как момент инерции. Этот показатель находится в прямой зависимости не столько от массы тела, сколько от его формы. То есть имеет значение то, как в пространстве масса тела распределена. Тела различной формы будут иметь разные значения момента инерции.
В эту формулу входит показатель массы, который характеризует степень инертности тела. При вращении тела его инертность не характеризуется его массой, а определяется такой величиной, как момент инерции. Этот показатель находится в прямой зависимости не столько от массы тела, сколько от его формы. То есть имеет значение то, как в пространстве масса тела распределена. Тела различной формы будут иметь разные значения момента инерции.
При вращении материального тела по окружности его момент инерции будет равен произведению массы вращающегося тела на квадрат радиуса оси вращения. Если точка переместится от оси вращения на вдвое большее расстояние, то показатель момента инерции и устойчивость вращения увеличатся в четыре раза. Вот почему маховые колоса делают большими. Но и слишком сильно увеличивать радиус колеса нельзя, так как при этом растет центростремительное ускорение точек его обода. Образующая это ускорение сила сцепления молекул может стать недостаточной для удержания их на круговом пути, и колесо разрушится.
Итоговое сравнение
При проведении параллели между вращательным и поступательным движением, следует понять, что при вращении роль массы тела играет момент инерции. Тогда динамический закон вращательного движения, соответствующий второму закону Ньютона, будет гласить, что момент силы равен произведению момента инерции и углового ускорения.
Теперь можно провести сравнение всех формул основного уравнения динамики, импульса и кинетической энергии при поступательном и вращательном движении, примеры расчета которых уже известны.
| Поступательное движение | Вращательное движение |
| Основное уравнение динамики F = m * a | Основное уравнение динамики M = I * ą |
| Импульс p = m * v | Импульс p = I * ω |
| Кинетическая энергия Ek = mv2 / 2 | Кинетическая энергия Ek = Iω2 / 2 |
Поступательное и вращательное движения имеют много общего. Нужно только разобраться, как в каждом из этих видов ведут себя физические величины. При решении задач используются очень похожие формулы, сравнение которых приведено выше.
Нужно только разобраться, как в каждом из этих видов ведут себя физические величины. При решении задач используются очень похожие формулы, сравнение которых приведено выше.
Вращательное движение — Физическая энциклопедия
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
твёрдого тела — 1) В. д. вокруг неподвижной оси — движение твёрдого тела, при
к-ром все его точки, двигаясь в параллельных плоскостях, описывают окружности
с центрами, лежащими на одной
неподвижной прямой, наз.
осью вращения. Тело, совершающее В. д., имеет одну степень свободы, и его положение
относительно данной системы отсчёта определяется углом поворота
между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом,
проведёнными через ось вращения (рис. 1). В. д. задаётся ур-нием
, где t — время. Осн. кинематич. характеристики В.д. тела: его угловая
скорость
и угловое ускорение . Для любой точки тела, находящейся на расстоянии h от оси вращения,
линейная скорость ,
касат. ускорение
, нормальное ускорение ,
полное ускорение .
Т.о., скорости и ускорения всех точек тела пропорциональны их расстояниям от
оси вращения.
ускорение
, нормальное ускорение ,
полное ускорение .
Т.о., скорости и ускорения всех точек тела пропорциональны их расстояниям от
оси вращения.
Осн. динамич. характеристиками
В. д. тела являются его гл. моменты кол-в движения относительно связанных с
телом осей х, у, z (z — ось вращения), равные:
и кинетич. энергий
где Ix —
осевой, а 1хz, Iyz — центробежные моменты инерции.
2) В. д. вокруг точки (или
сферич. движение) — движение твёрдого тела, имеющего одну неподвижную точку
0 (напр., движение гироскопа ,закреплённого в кардановом подвесе).
Каждая из точек тела при этом В. д. перемещается по поверхности сферы с центром
в точке 0. В. д. тела вокруг точки слагается из серии элементарных или
мгновенных В. д. вокруг мгновенных осей вращения, проходящих через эту точку.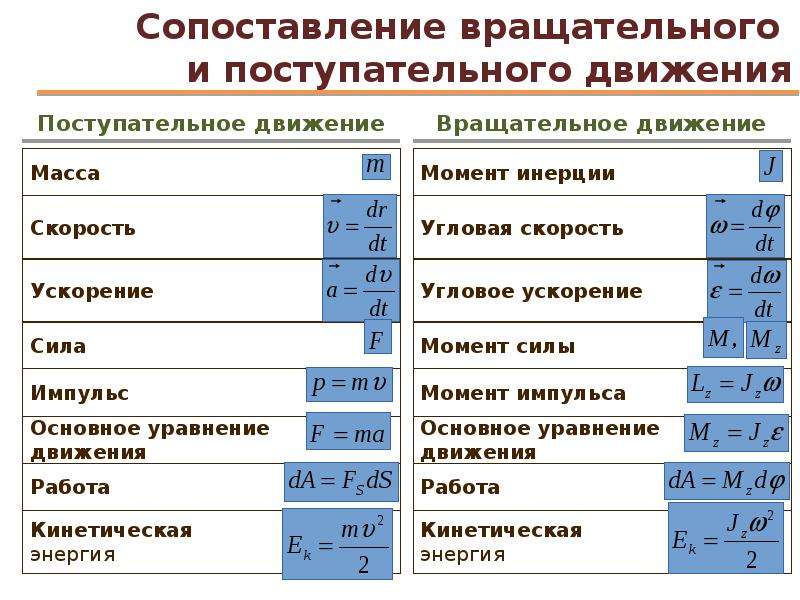
Тело с неподвижной точкой
имеет 3 степени свободы, и его положение по отношению к данной системе отсчёта
определяется тремя параметрами, напр. Эйлера углами . Закон движения тела задаётся в этом случае ур-ниями
Кинематич. характеристиками
движения являются вектор угл. скорости ,
направленный в каждый момент времени вдоль мгновенной оси вращения, и вектор
угл. ускорения ,
направленный параллельно касательной к годографу вектора.
Если движение задано ур-ниями (*), то проекции вектора
на прямоугольные оси  ур-ниями Эйлера
ур-ниями Эйлера
I
где
— производные от углов Эйлера по времени t. Векторы линейной скорости
и ускорения
любой точки тела равны
где
— радиус-вектор, проведённый в данную точку тела из неподвижной точки 0. Проекции вектора v на оси Oxyz определяются ф-лами Эйлера
Осн. динамич. характеристиками
тела с неподвижной точкой 0 являются моменты количеств движения относительно
гл. осей инерции х, у, z, проведённых в точке 0:
и кинетич. энергия
где Ix, Iy,
Iz — моменты инерции тела относительно упомянутых гл. осей;
— проекции на
эти оси. Кол-во движения тела при любом виде движения равно ,
где
т — масса тела, —
скорость центра масс.
Теория В. д. имеет важные
приложения в небесной механике, внеш. баллистике, теории гироскопа, кинематике
и динамике механизмов и машин и при решении др. техн. задач.
Лит.: см. при ст.
Кинематика и Динамика. С. M. Тарг.
Предметный указатель >>
Движение вращательное — Энциклопедия по машиностроению XXL
Из трех возможных относительных движений звеньев пар плоских механизмов вращательные и поступательные пары исключают по два движения. Вращательная пара исключает возможность поступательных движений вдоль двух осей, лежащих в плоскости движения звеньев. Поступательная пара исключает одно поступательное движение и одно вращательное (вокруг оси, перпендикулярной к плоскости движения звеньев).На рис. 2.30 показан трехзвенный винтовой механизм.
 Звенья этого механизма имеют возможность только двух движений вращательного вокруг оси А — А и поступательного вдоль этой же оси. Таким образом, на звенья механизма наложено четыре
[c.50]
Звенья этого механизма имеют возможность только двух движений вращательного вокруг оси А — А и поступательного вдоль этой же оси. Таким образом, на звенья механизма наложено четыре
[c.50]Так как относительное движение звена 2 около точки В есть движение вращательное, то очевидно, что относительные ускорения всех точек звена 2 будут образовывать с радиусами-векторами, выходящими из точки В, постоянный угол 1-1, удовлетворяющий соотношению [c.86]
Движение вращательное одностороннее Вращение вала одностороннее [c.267]
Технологический метод формообразования поверхностей заготовок точением характеризуется двумя движениями вращательным движением заготовки (скорость резания) и поступательным движением режущего инструмента — резца (движение подачи). Движение подачи осуществляется параллельно оси вращения заготовки (продольная подача), перпендикулярно к оси вращения заготовки (поперечная подача), под углом к оси вращения заготовки (наклонная подача).
Особенность построения горизонтальной проекции конической винтовой линии (черт, 188) состоит в том, что горизонтальная проекция движущейся точки определяется с учетом двух движений вращательного — вместе с образующей и поступательного — вдоль образующей. [c.84]
Б. Переносное движение вращательное. Покажем, как вычисляется а в, когда переносное движение является вращением вокруг неподвижной оси. [c.164]
Найдем переносное ускорение точки М. Так как переносное движение вращательное, то, следовательно,
Мы вывели формулу (109) в предположении, что переносное движение вращательное. Она остается без изменений и при всяком ином непоступательном переносном движении. [c.201]
Количество 48 Движение вращательное — Кинематические параметры 25 — Схема 25 — Характеристики 25 [c.754]
Плоское движение твердого тела имеет большое значение в технике, так как звенья большинства механизмов и машин, применяемых в технике, совершают плоское движение.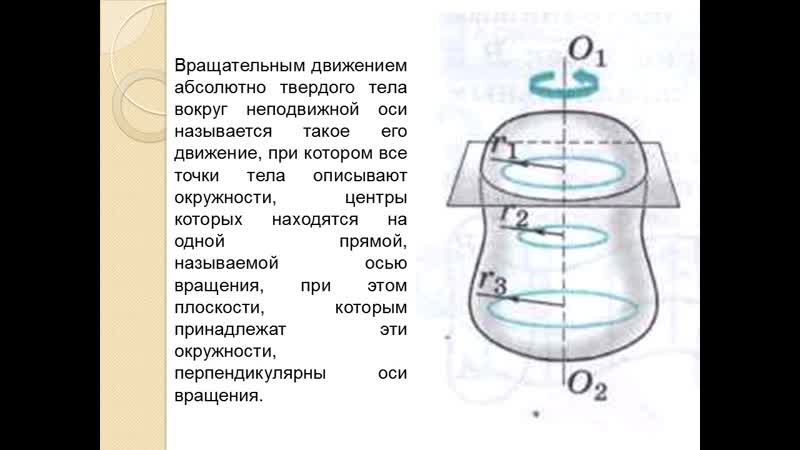 Вращательное движение твердого тела вокруг неподвижной оси можно считать частным случаем плоского движения.
[c.134]
Вращательное движение твердого тела вокруг неподвижной оси можно считать частным случаем плоского движения.
[c.134]
Когда мгновенные центры скоростей и ускорений звена совпадают и при работе механизма не меняют своего положения, это соответствует частному случаю плоского движения — вращательному (рис. 16.1). Вектор скорости произвольной точки А звена определится по величине и направлению из условий [c.189]
В плоскопараллельном движении вращательное ускорение следует отличать от касательного. 2. Вращательное ускорение направлено перпендикулярно центростремительному (в сторону вращения фигуры вокруг полюса, если вращение ускоренное, и в противоположную — при замедленном вращении). [c.15]
Равнопеременное вращательное движение. Вращательное движение называется равнопеременным, если угловое ускорение [c.110]
Если тело вращается равномерно, то ё=0 и, следовательно, во все время движения вращательное ускорение точек тела равно нулю ускорение сводится к осестремительному.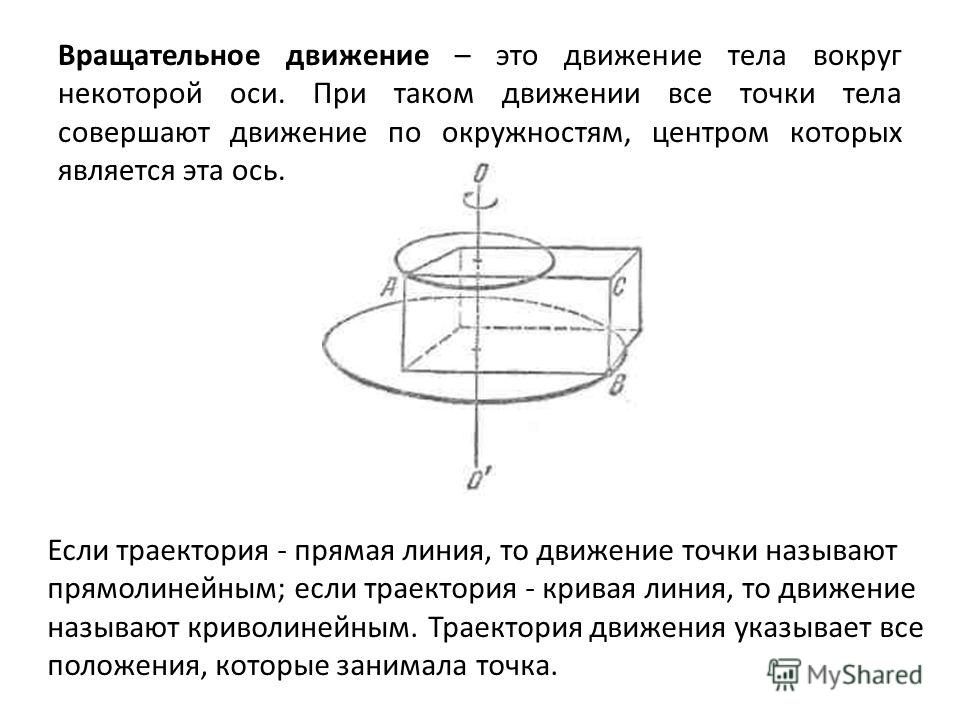 [c.218]
[c.218]
Итак, всякое движение твердого тела можно рассматривать как винтовое, т. е. как совокупность поступательного движения и движения вращательного вокруг оси, параллельной направлению поступательного движения. Ось, вокруг которой тело в данный момент поворачивается и параллельно которой перемещается поступательно, называется мгновенной винтовой осью.
Сопоставляя плоскопараллельное движение с простейшим видом движения — вращательным вокруг неподвижной оси, — приходим к следующим выводам. [c.351]
Под действием силы, приложенной к твердому телу, последнее совершает поступательное и вращательное движение. Вращательный эффект силы, приложенной к телу, определяется ее моментом относительно точки или оси. [c.154]
Остановимся на дополнительном пояснении второго вида движения-вращательного. Угловую скорость вращения элементарных объемов жидкости относительно своих мгновенных осей обозначим через С1, а компоненты ее — через А,, Найдем соответствующие выражения для величин Оу и С этой целью выделим элементарный объем жидкости в виде прямой треугольной призмы аЬс (рис.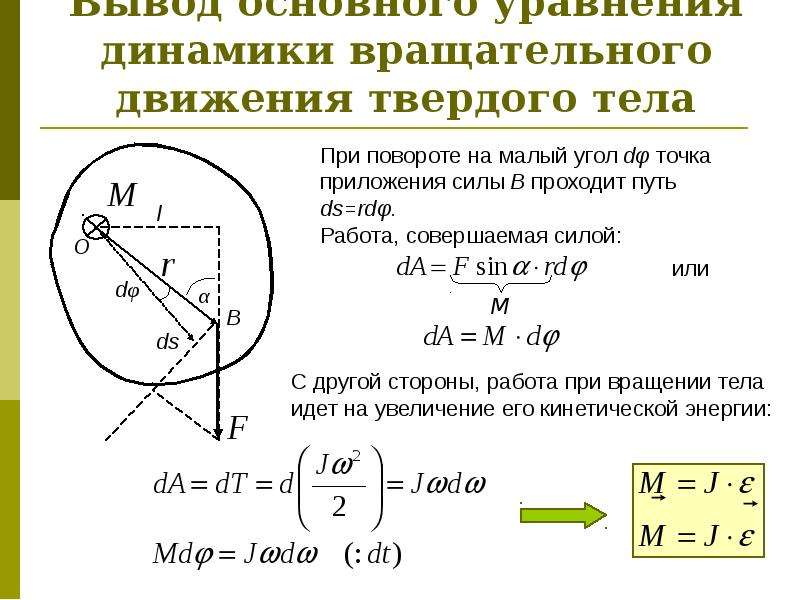
Движение звена характеризуется I) видом движения-, вращательным, поступательным, плоскопараллельным и сложным пространственным-, 2) наибольшей величиной угла поворота звена или наибольшей величиной линейного перемещения 5 ах заданной точки 3) угловым перемещением ср, рад, скоростью со, рад/с, ускорением е, рад/с звена-, 4) линейными перемещениями S, м, скоростями V, м/с, ускорениями а, м/с точек звеньев. [c.19]
Структурно-кинематической схемой (моделью) механизма или машины назьшается условное изображение взаимосвязанных неподвижных и подвижных звеньев, выполненное в принятом стандартном масштабе длин с применением условных обозначений кинематических пар, буквенных наименований кинематических пар, указанием входных звеньев (обозначаются дуговыми или прямолинейными стрелками в зависимости от вида движения — вращательного или поступательного, совершаемого входными звеньями).
Даламбера принцип 81, 84 Движение вращательное, основное уравнение 86 [c.363]
Кинетическую энергию сателлитов в относительном движении (вращательном движении относительно оси, проходящей через собственный центр инерции сателлита), воспользовавшись вторым уравнением связи (4.5), представим в виде [c.129]
Процесс загрузки заготовок в автоматическом технологическом комплексе (АТК) можно расчленить на отдельные элементарные движения — вращательные и поступательные. Даже такая простая операция, как загрузка заготовок в зажимное устройство токарного станка, требует четырех поступательных и двух вращательных движений, не считая движения захвата и зажима детали (рис. 6.15). Для осуществления этих движений с относительно большими скоростями и ускорениями необходимы соответствующие приводы, объединенные системой управления.
[c. 160]
160]
Скоростью резания v называют расс юяние, пройденное точкой режущей кромки инструмента относительно заготовки в единицу времени. Скорость резания имеет размерность м/мин или м/с. Если главное движение вращательное (точение), то скорость резания, м/ми и [c.257]
Е5ннтовые канавки фрезеруют при непрерывном вращении шпинделя делительной головки, которое он получает от винта продольной подачи стола универсально-фрезерного станка через сменные колеса а, Ь, с, d (рис. 6.61). Заготовку устанавливают в центрах делительной головки и задней бабки. В процессе обработки заготовка получает два движения — вращательное и поступательное вдоль оси. Оба движения согласованы так, что прн перемещении на шаг нарезаемой винтовой канавки заготовка делает один оборот. [c.334]
Поток газа (воздуха) в одном направлении Движение прямолинейное одноетороннее Движение вращательное одностороннее
[c. 454]
454]
Кроме этих составляющих абсолютного ускорения, имеется ускорение Корио-лиса, так как переносное движение вращательное [c.205]
Относительное движение прямолинейно, поэтому = О и йг = а т = Vr. Переносное вращательное движение равномерно,, поэтому а т- = О и г = переносное ускорения направлены по оси Ох. и спроецировались на нее в полную величину. Но вследствие того, что переносное движение вращательное (хотя относительное движение прямолинейно), меняется направление относительной скорости и вследствие перемещения точки по вращающемуся стержню меняется модуль переносной скорости (хотя переносное вращение равномерное). Оба эти фактора учтены ускорением Корнолиса, которое получим, взяв проекции на ось Оу [c.89]
Передаточные механизмы могут выполнять и другие функции а) приводить в движение несколько исполнительных органов (с различными скоростями движения) от одного двигателя б) преобразовьшать усилия и вращающие моменты (увеличивать их на выходе при уменьшении скорости движения выходного звена и наоборот) в) преобразовывать вид движения (вращательное в поступательное и др. ).
[c.288]
).
[c.288]
Если одна из переменных qi является циклической, то соответствующий ей импульс будет постоянным. Соответствующая траектория в плоскости qipi будет тогда горизонтальной прямой линией, не имеющей ясно выраженного периодического характера. Такое движение можно рассматривать как предельный случай периодического движения вращательного типа, причем координате qi можно здесь приписать любой период. Но так как во вращательном движении координатой всегда служит угол, то естественным периодом такой циклической координаты является величина 2я. Поэтому интеграл (9.34) должен в этом случае вычисляться от нуля до 2я и, следовательно, [c.320]
Но из соотношения (10) вытекает также, что это движение вращательное в самом дме, оно обнаруяшвает, что все точки Р, для которых вектор 2Р параллелен постоянному направлению со (т. е. точки прямой, проходящей через 2 и параллельной вектору со), имеют скорость, равную нулю, т. е. остаются неподвижными. [c.165]
[c.165]
После всего изложенного возвратимся к движению твердой плоскости р по себе самой в промежутке времени от i до рассмотрим одновременно как действительно происшедшее движение, так и фиктивное вращательное или поступательное движение (предполагая его, например, равномерным), которое осуществляет то же конечное смещение. Если, сохраняя момент г, мы будем неограниченно уменьшать М, то фиктивное движшше будет от момента к моменту изменяться в пределе оно будет стремиться к некоторому бебконечно малому движению, вращательному или поступательному, которое производит то же бесконечно малое перемещение (1А любой точки А, что и действительное движение за элемент времени от t до а потому совпадает с ним. Таким образом доказано, что всякое состояние плоского твердого движения является в каждый момент вращательным, или в частном случае, поступательным. [c.222]
Чтобы уменьшить шум, сопутствующий работе почти каждой машины, конструкторы заменяют поступательное движение вращательным, устанавливают механизмы на звукоизоляционные подкладки, применяют шумопоглощающие кожухи, требуют более тщательной подгонки частей, используют глушители, буфера и другие устройства. Строители помогают конструкторам, возводя нерезонирующие стены и покрывая их звукопоглощающими материалами.
[c.255]
Строители помогают конструкторам, возводя нерезонирующие стены и покрывая их звукопоглощающими материалами.
[c.255]
Технология машиностроения (1987) — [ c.19 ]
Курс теоретической механики Ч.1 (1977) — [ c.199 ]
Курс теоретической механики 1973 (1973) — [ c.164 ]
Курс теоретической механики 1981 (1981) — [ c.52 ]
Основные законы механики (1985) — [ c.18 , c.150 ]
Курс теоретической механики. Т.1 (1972) — [ c.102 ]
Физические основы механики и акустики
(1981) — [
c.13
,
c.14
,
c. 60
]
60
]
Гидравлика и аэродинамика (1975) — [ c.301 ]
Гидравлика и аэродинамика (1987) — [ c.320 ]
Курс теоретической механики Том 2 Часть 1 (1951) — [ c.38 ]
Теплоэнергетика и теплотехника Общие вопросы Книга1 (2000) — [ c.216 , c.217 ]
Курс теоретической механики (1965) — [ c.277 ]
Гидравлика Основы механики жидкости (1980) — [ c.120 , c.123 ]
Введение в теорию концентрированных вихрей (2003) — [ c.25 ]
Курс теоретической механики Том1 Изд3
(1979) — [
c. 187
]
187
]
Теоретическая механика (2002) — [ c.129 ]
Курс лекций по теоретической механике (2001) — [ c.93 ]
Механика жидкости и газа Издание3 (1970) — [ c.61 ]
Пневматические приводы (1969) — [ c.9 , c.229 , c.243 ]
Динамика системы твёрдых тел Т.1 (1983) — [ c.72 ]
Краткий справочник по физике (2002) — [ c.9 , c.27 ]
Справочное руководство по физике (0) — [ c.14 ]
Инженерная графика Издание 3
(2006) — [
c. 251
]
251
]
Справочник по элементарной физике (1960) — [ c.15 ]
Теоретическая механика (1981) — [ c.36 ]
Курс теоретической механики Изд 12 (2006) — [ c.159 ]
Справочник машиностроителя Том 1 Изд.2 (1956) — [ c.376 ]
Техническая энциклопедия Том 1 (0) — [ c.173 ]
Вращательное движение
Механика Вращательное движение
просмотров — 132
Поступательное движение
Тема 1.9. Простейшие движения твердого тела
ЛЕКЦИЯ 11
Иметь представление о поступательном движении, его особенностях и параметрах, о вращательном движении тела и его параметрах.
Знать формулы для определения параметров поступательного и вращательного движений тела.
Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела.
Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению (рис. 11.1, 11.2).
При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. По этой причине для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.
При вращательном движении все точки тела описывают окружности вокруг общей неподвижной оси.
Неподвижная ось, вокруг которой вращаются все точки тела, принято называть осью вращения.
При этом каждая точка движется по окружности, радиус которой равен расстоянию точки до оси вращения. Точки на оси вращения не перемещаются.
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис. 11.3):
φ — угол поворота тела, [φ] = рад;
ω — угловая скорость, определяет изменение угла поворота в единицу времени, [ω] = рад/с.
Для определения положения тела в любой момент времени используется уравнение φ = f(t).
Следовательно, для определения угловой скорости можно пользоваться выражением
ω = dφ/dt.
Иногда для оценки быстроты вращения используют угловую частоту вращения п, которая оценивается в оборотах в минуту.
Угловая скорость и частота вращения физически близкие величины:
Изменение угловой скорости во времени определяется угловым ускорением ε, [ε] = рад/с2;
Читайте также
Твердое тело — это система материальных точек, расстояние между которыми остается неизменным при взаимодействии системы с другими телами.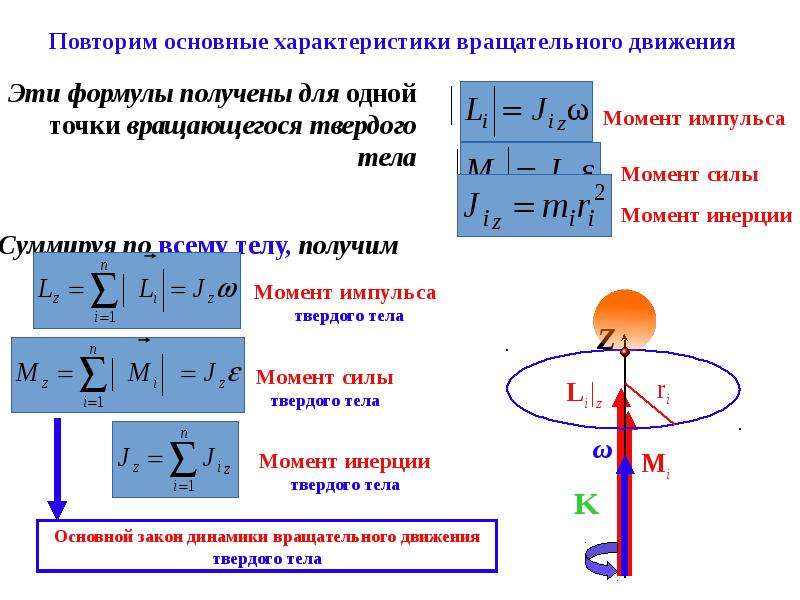 Движение твердого тела бывает поступательным и вращательным. Всякое движение твердого тела можно представить как сумму движения… [читать подробенее]
Движение твердого тела бывает поступательным и вращательным. Всякое движение твердого тела можно представить как сумму движения… [читать подробенее]
Твердое тело — это система материальных точек, расстояние между которыми остается неизменным при взаимодействии системы с другими телами. Движение твердого тела бывает поступательным и вращательным. Всякое движение твердого тела можно представить как сумму движения… [читать подробенее]
1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к… [читать подробенее]
1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к… [читать подробенее]
Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к… [читать подробенее]
Закон сохранения момента импульса Анализируя уравнение моментов относительно произвольного центра и неподвижной оси, мы говорили уже об условиях, при которых момент импульса системы не будет меняться во времени. Сформулируем эти условия ещё раз, собрав их… [читать подробенее]
Вращательным вокруг неподвижной оси называют движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения. Положение тела определяется углом поворота j (рис.2.9 ). Единица измерения угла – радиан. (Радиан -… [читать подробенее]
Кинематика вращательного и колебательного движения
Лекция 2Рассмотрим движение м. т. по окружности радиусом R с постоянной линейной скоростью вокруг неподвижной оси Z (рис. 1.8).
Положение точки определяется радиус-вектором , проведенным из начала координат. За малый… [читать подробенее]
т. по окружности радиусом R с постоянной линейной скоростью вокруг неподвижной оси Z (рис. 1.8).
Положение точки определяется радиус-вектором , проведенным из начала координат. За малый… [читать подробенее]
Поступательное движение тела Поступательным относительно данной системы отсчёта движением называется такое движение, при котором любая прямая, взятая в этом теле, остаётся параллельной самой себе во все время движения. Примерами поступательного движения являются:… [читать подробенее]
ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и ой же прямой, называемой осью вращения. Для изучения динамики вращательного к известным кинематическим… [читать подробенее]
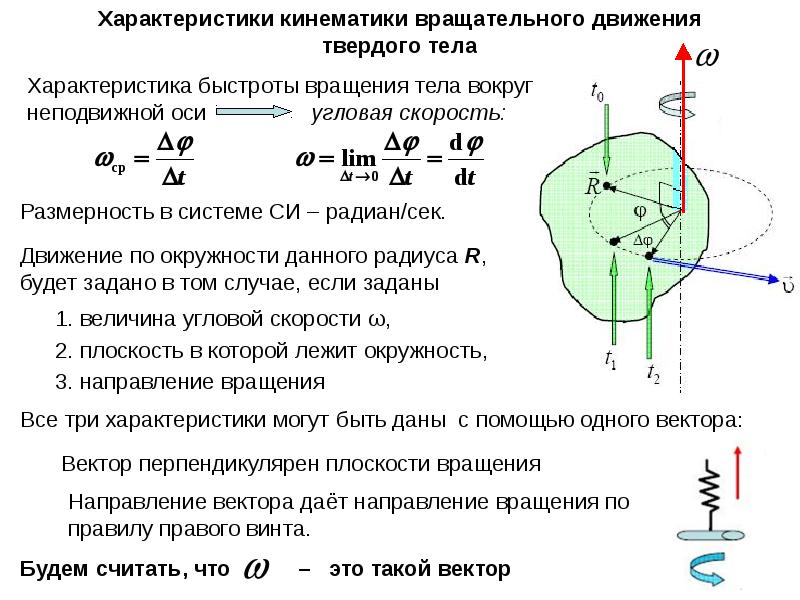
Поступательное движение твердого тела Кинематика твердого тела В отличие от кинематики точки в кинематике твердых тел решаются две основные задачи: — задание движения и определение кинематических характеристик тела в целом; -… [читать подробенее]
вращательное движение Archives — Физика дома
Задача на вращательное движение тела может быть интересна всем тем, кто готовится к экзаменам по физике и после 9-го класса, и после 11-го.
Определить радиус колеса, если при вращении скорость точек на ободе колеса равна 10 м/с, а точек, лежащих на 42 см ближе к его оси, 4 м/с. (подробнее…)
Автор: admin. Рубрики: Олимпиады. Опубликовано: Февраль 17th, 2013Данная задача на вращение камня в вертикальной плоскости была предложена на физической олимпиаде в старших классах. Задача может быть интересна и тем учащимся, кто сдаёт ЕГЭ.
Мальчик вращает в вертикальной плоскости камень на нити длиной 1,2 м. После обрыва нити камень летит вертикально вверх. На какую максимальную высоту поднимается камень, если в этот момент полное ускорение камня было направлено под углом 450 с вертикалью?
(подробнее…)
Комбинированная задача на равномерное и вращательное движение двух тел: пули и шара. Задача может быть интересна тем, кто готовится к сдаче ГИА по физике.
Тонкостенный шар радиусом 1 м вращается с угловой скоростью 628 рад/с относительно оси, проходящей через его центр. С какой минимальной скоростью должна лететь пуля, чтобы в оболочке шара было одно отверстие? Траектория пули проходит через центр шара. (подробнее…)
Задача на движение конического маятника может быть интересна и тем, кто сдает ЕГЭ по физике, и тем, кто сдает ГИА. Комбинированная задача на законы Ньютона и формулы движения тела по окружности.
Комбинированная задача на законы Ньютона и формулы движения тела по окружности.
Конический маятник имеет длину 1 м. может ли его период равняться 1 с? 3с? Дать решение . (подробнее…)
Задача может быть интересна будущим космонавтам (шутка!). При старте космических кораблей, космонавты испытывают многократные перегрузки (превышение веса над силой тяжести).
Еще одна комбинированная задача на совместное использование законов Ньютона и вращательного движения.
Для подготовки летчиков – космонавтов к перегрузкам применяют специальные центрифуги. Сколько оборотов в минуту должна делать центрифуга радиусом 2 м, чтобы космонавт испытывал десятикратную перегрузку? (подробнее…)
Автор: admin. Рубрики: Задачи 28 (С2). Опубликовано: Октябрь 19th, 2012Задачи на закон всемирного тяготения чаще всего встречались в части А не экзамене. Но эта задача, заслуживает внимания и проработки.
Но эта задача, заслуживает внимания и проработки.
Звезда и массивная планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найти массу планеты m, если известно, что скорость планеты v1, а скорость движения звезды равна v2 и Т соответственно. (подробнее…)
Автор: admin. Рубрики: Задачи 28 (С2). Опубликовано: Сентябрь 22nd, 2012Комбинированная задача С2, подготовка к ЕГЭ по физике. Задача может быть интересна учащимся и 10-х, и 11-х классов.
Вокруг невесомой горизонтальной оси может вращаться невесомый стержень, плечи которого равны L и 2L. На концах стержня укреплены грузы одинаковой массы. Чему будет равна линейная скорость одного из грузов в нижней точке при повороте на 900 под действием силы тяжести, если первоначально стержень находился в горизонтальном положении и был неподвижен.
(подробнее…)
Для тех, кто готовится сдавать физику в 2014 году, думаю, пригодится решение одного из вариантов, который был на ЕГЭ 13 июня 2012 года. (подробнее…)
(подробнее…)
Поступательное и вращательное движение твердого тела
Рис. 1.1
При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φмежду плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
Рис. 1.3
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.
Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
 Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
где k – единичный вектор оси вращения.
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
Рис. 1.4
- Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и εсовпадают, оба они направлены в положительную сторону оси вращения Oz.

- При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и εсовпадают, оба они направлены в отрицательную сторону оси вращения Oz.
- Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
- Если ε >0 при
ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны. - Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения
φ=φ0+ωt
- Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращенияи уравнение, выражающее угловую скорость в любой момент времениω=ω0+εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

Самый быстрый словарь в мире | Vocabulary.com
вращательное движение акт вращения как бы вокруг оси
возмездие заслуженное наказание
замедление темп замедления или отставания
реформирование улучшение состояния институтов или практики
повторное подтверждение возобновленное подтверждение
опровержение Отречение или отказ от предыдущего утверждения
Реформация религиозное движение XVI века, начавшееся как попытка реформирования римско-католической церкви и закончившееся созданием протестантских церквей
коннотация идея, которая подразумевается или предлагается
Празднование Успения в Восточной Православной Церкви вознесения Девы Марии на небо по окончании ее земной жизни; соответствует Успению в Римско-католической церкви и также отмечается 15 августа
повторение действие или случай повторения чего-либо
вращение акт поворота как бы вокруг оси
переформирование формирование снова ; обновление и восстановление
ретроспективная ссылка на прошлое
ретрофлексия акт изгиба назад
движение вперед акт движения вперед (как к цели)
диффамация оскорбительное нападение на репутацию или доброе имя человека
радиоизлучение: электромагнитная волна с длиной волны от 0.от 5 см до 30 000 м
поступательное движение акт движения вперед (как к цели)
ретикулярная формация сложная нервная сеть в центральном ядре ствола мозга; следит за состоянием организма и функциями в таких процессах, как бодрствование и сон, внимание и мышечный тонус
аффирмация: акт утверждения или утверждения чего-либо
Что такое вращательное движение
Поворотные столы являются популярными и полезными инструментами, которые используются уже давно. Они применимы во многих различных отраслях промышленности и могут помочь в различных процессах производства, изготовления и гравировки.
Они применимы во многих различных отраслях промышленности и могут помочь в различных процессах производства, изготовления и гравировки.
Многие компании по всему миру полагаются на эти машины для улучшения результатов своего бизнеса, даже не задумываясь о том, как эти машины работают на самом деле.
Главным здесь является вращательное движение, так как эти машины используют этот тип движения для достижения различных рабочих возможностей. Вращательное движение также известно как круговое движение и вращательное движение.Это хлеб с маслом каждого поворотного стола и всех подобных машин, у которых вращающаяся часть прикреплена к оси.
Сегодня мы собираемся копнуть немного глубже и посмотреть, что такое вращательное движение, как оно работает и почему оно предлагает такой большой потенциал для различных производственных процессов. Итак, начнем.
Вращательное движение включает в себя физическое движение определенного объекта, который вращается вокруг собственной оси. Вращательное движение анализируется аналогично линейному движению.Когда мы говорим, что некий объект имеет равномерное вращательное движение, равномерное круговое движение или равномерное вращательное движение, это означает, что направление, в котором движется объект, не меняется.
Вращательное движение анализируется аналогично линейному движению.Когда мы говорим, что некий объект имеет равномерное вращательное движение, равномерное круговое движение или равномерное вращательное движение, это означает, что направление, в котором движется объект, не меняется.
В то же время это также означает, что скорость этого движения также постоянна. Этот тип движения часто используется с поворотными столами в производственных целях, поскольку компании обычно производят идентичные продукты, которые должны демонстрировать постоянство, а равномерное движение дает стабильные результаты.
Однако это не так просто, как кажется, так как даже у самых лучших поворотных столов всегда есть изменения в их скорости во время работы.Инерция оказывает большое влияние на вращательное движение и вызывает различные изменения скорости, которые приводят к различным результатам работы.
Проще говоря, инерцию определенного вращающегося объекта можно описать как сопротивление, которое он оказывает при изменении вращательного движения. Поворотным столам с высокой инерцией потребуется больше энергии для изменения их положения или скорости на оси вращения.
Поворотным столам с высокой инерцией потребуется больше энергии для изменения их положения или скорости на оси вращения.
Инерция является очень важным элементом вращательного движения, так как она имеет решающее значение для лучшего объяснения движения и поведения объектов при вращательном движении.
Вот почему не все поворотные столы имеют одинаковую производительность и элементы управления. Материал вращающейся части и материал, из которого она сделана, важны для ее веса и поведения. Более тяжелым колесам нужны гораздо более мощные двигатели, чтобы контролировать их движения и быть более отзывчивыми.
Однако более тяжелые поворотные столы также обладают большей мощностью, так как сама инерция от веса и скорости требует больше энергии для замедления. Вот почему существует так много различных типов поворотных столов и их конструкций.
Например, давайте рассмотрим инерцию велосипедного колеса и сравним ее с инерцией вращающегося колеса. Велосипедное колесо, как правило, намного легче, и каждый может легко поворачивать на велосипеде, замедляться и ускоряться в удобной манере.
С другой стороны, вращающиеся колеса на поворотных столах могут быть намного тяжелее и в большей степени сопротивляться изменению скорости. В то же время вращающееся колесо достигает гораздо более высоких скоростей вращения, а это означает, что они сами по себе увеличивают силу инерции и требуют больше энергии для изменения движения или скорости.
Инерция также оказывает большое влияние на движение оси вращения или положение вращающегося объекта. Мы можем снова взять пример с велосипедным колесом и посмотреть, как инерция влияет на него через этот аспект вращательного движения.
Когда человек сидит на велотренажере, может быть невозможно удержать равновесие, и ему придется использовать свои ноги, чтобы не упасть.
Большинство людей думают, что это как-то связано с нами и тем, как мы сохраняем равновесие при езде на велосипеде, но на самом деле все из-за вращательного движения колес или его отсутствия.Когда колеса не вращаются, инерции нет, а это означает, что ничто не препятствует изменению положения.
С другой стороны, при движении на велосипеде колеса имеют большую инерцию, и все изменения вертикального положения естественным образом сопротивляются колесу. Это означает, что у человека, едущего на велосипеде, больше шансов сохранить равновесие.[
Это то, что вам нужно знать о вращательном движении с точки зрения поворотных столов и о том, как они работают в своей основе.
Вращательное движение – обзор
11.3.7 Гидравлические двигатели
Гидравлические двигатели преобразуют давление жидкости во вращательное движение. Жидкость под давлением из гидравлического насоса вращает выходной вал двигателя, нажимая на шестерни, поршни или лопасти гидравлического двигателя. Гидравлические двигатели можно использовать для прямого привода, где имеется достаточный крутящий момент, или с редуктором. Большинство гидравлических двигателей должны работать в условиях реверсивного вращения и торможения.Гидравлические двигатели часто должны работать при относительно низкой скорости и высоком давлении и могут испытывать большие колебания температуры и скорости при нормальной работе. Гидравлические двигатели могут создавать чрезвычайно высокие крутящие моменты. В приводах ворот гидравлические двигатели часто сочетаются с механическими приводами (рис. 3.151b и 11.23), в частности с шестернями. Схематическое изображение на рис. 11.23 показывает гидравлический двигатель, приводящий в движение ведущую шестерню секторных ворот LPV 149 в Новом Орлеане. Это относится ко многим секторным воротам в Соединенных Штатах и множеству роллетных ворот в Европе.В рулонных воротах гидравлические двигатели часто являются движущей силой механической лебедки (рис. 11.8). Гидромоторы также могут быть входом для редуктора, как показано на фото на рис. 11.24. Это система, используемая в шлюзовой камере рыболовного порта Бремерхафена для привода роллетных ворот.
Гидравлические двигатели могут создавать чрезвычайно высокие крутящие моменты. В приводах ворот гидравлические двигатели часто сочетаются с механическими приводами (рис. 3.151b и 11.23), в частности с шестернями. Схематическое изображение на рис. 11.23 показывает гидравлический двигатель, приводящий в движение ведущую шестерню секторных ворот LPV 149 в Новом Орлеане. Это относится ко многим секторным воротам в Соединенных Штатах и множеству роллетных ворот в Европе.В рулонных воротах гидравлические двигатели часто являются движущей силой механической лебедки (рис. 11.8). Гидромоторы также могут быть входом для редуктора, как показано на фото на рис. 11.24. Это система, используемая в шлюзовой камере рыболовного порта Бремерхафена для привода роллетных ворот.
Рис. 11.24. Гидравлический двигатель, приводящий в движение редуктор для рулонных ворот Бремерхафен, Германия.
Существует три типа гидравлических двигателей: шестеренчатые, поршневые и лопастные. Редукторные двигатели компактны и обеспечивают непрерывную работу при номинальном уровне мощности с умеренным КПД. Они обладают высокой устойчивостью к загрязнению гидравлического масла, что важно для применения в загрязненной среде. Мотор-редукторы с внешним редуктором состоят из пары согласованных шестерен, заключенных в один корпус. Обе шестерни имеют одинаковую форму зубьев и приводятся в движение жидкостью под давлением. Одна шестерня соединена с выходным валом, а другая с промежуточным валом. Жидкость под давлением поступает в корпус в месте зацепления шестерен. Он заставляет шестерни вращаться и следует по пути наименьшего сопротивления по периферии корпуса.Жидкость выходит под низким давлением на противоположной стороне двигателя. Жесткие допуски между шестернями и корпусом помогают контролировать утечку жидкости и повышают объемную эффективность. Существует несколько вариантов редукторного двигателя, в том числе геротор, дифференциальный мотор-редуктор и роликовый геротор. Все эти варианты обеспечивают более высокий крутящий момент с меньшими потерями на трение.
Они обладают высокой устойчивостью к загрязнению гидравлического масла, что важно для применения в загрязненной среде. Мотор-редукторы с внешним редуктором состоят из пары согласованных шестерен, заключенных в один корпус. Обе шестерни имеют одинаковую форму зубьев и приводятся в движение жидкостью под давлением. Одна шестерня соединена с выходным валом, а другая с промежуточным валом. Жидкость под давлением поступает в корпус в месте зацепления шестерен. Он заставляет шестерни вращаться и следует по пути наименьшего сопротивления по периферии корпуса.Жидкость выходит под низким давлением на противоположной стороне двигателя. Жесткие допуски между шестернями и корпусом помогают контролировать утечку жидкости и повышают объемную эффективность. Существует несколько вариантов редукторного двигателя, в том числе геротор, дифференциальный мотор-редуктор и роликовый геротор. Все эти варианты обеспечивают более высокий крутящий момент с меньшими потерями на трение.
Все гидравлические поршневые двигатели доступны в версиях с фиксированным и переменным объемом. Наиболее распространенным типом гидравлического двигателя является аксиально-поршневой тип.Аксиально-поршневые гидромоторы имеют высокий объемный КПД. Это обеспечивает постоянную скорость при переменном крутящем моменте или условиях вязкости жидкости. Аксиально-поршневые гидравлические двигатели также являются одними из наиболее приспособленных к переменным условиям нагрузки. Они доступны в двух основных типах конструкции, включая наклонную шайбу и изогнутую ось. Конструкция с наклонной шайбой является наиболее доступной, но конструкция с изогнутой осью является наиболее надежной и, как правило, более дорогой.
Наиболее распространенным типом гидравлического двигателя является аксиально-поршневой тип.Аксиально-поршневые гидромоторы имеют высокий объемный КПД. Это обеспечивает постоянную скорость при переменном крутящем моменте или условиях вязкости жидкости. Аксиально-поршневые гидравлические двигатели также являются одними из наиболее приспособленных к переменным условиям нагрузки. Они доступны в двух основных типах конструкции, включая наклонную шайбу и изогнутую ось. Конструкция с наклонной шайбой является наиболее доступной, но конструкция с изогнутой осью является наиболее надежной и, как правило, более дорогой.
Радиально-поршневые гидромоторы имеют корпус цилиндра, прикрепленный к ведомому валу, и обычно могут создавать больший крутящий момент, чем аксиально-поршневые гидромоторы.Однако они имеют ограниченный диапазон скоростей и более чувствительны к загрязнению гидравлической жидкости. Ствол содержит несколько поршней, которые совершают возвратно-поступательное движение в радиальном отверстии. Внешние концы поршня упираются в упорное кольцо, и жидкость под давлением течет через штифт в центре цилиндра, выталкивая поршни наружу. Поршни упираются в упорное кольцо, и силы реакции вращают ствол. Рабочий объем двигателя изменяется путем смещения ползуна вбок для изменения хода поршня.Когда осевые линии корпуса цилиндра и корпуса совпадают, поток жидкости отсутствует, и поэтому корпус цилиндра останавливается. Перемещение ползуна за центр изменяет направление вращения двигателя. Радиально-поршневые двигатели чрезвычайно эффективны и рассчитаны на относительно высокий крутящий момент. Во многих приводах ворот сектора USACE используются радиально-поршневые гидромоторы. Гидравлический двигатель, показанный на рис. 11.23, представляет собой радиально-поршневой двигатель и обеспечивает крутящий момент 260 Нм/бар. Номинальная скорость 50 об/мин. Гидравлический двигатель приводит в движение ведущую шестерню, которая, в свою очередь, приводит в движение зубчатую рейку на секторных воротах.
Внешние концы поршня упираются в упорное кольцо, и жидкость под давлением течет через штифт в центре цилиндра, выталкивая поршни наружу. Поршни упираются в упорное кольцо, и силы реакции вращают ствол. Рабочий объем двигателя изменяется путем смещения ползуна вбок для изменения хода поршня.Когда осевые линии корпуса цилиндра и корпуса совпадают, поток жидкости отсутствует, и поэтому корпус цилиндра останавливается. Перемещение ползуна за центр изменяет направление вращения двигателя. Радиально-поршневые двигатели чрезвычайно эффективны и рассчитаны на относительно высокий крутящий момент. Во многих приводах ворот сектора USACE используются радиально-поршневые гидромоторы. Гидравлический двигатель, показанный на рис. 11.23, представляет собой радиально-поршневой двигатель и обеспечивает крутящий момент 260 Нм/бар. Номинальная скорость 50 об/мин. Гидравлический двигатель приводит в движение ведущую шестерню, которая, в свою очередь, приводит в движение зубчатую рейку на секторных воротах.
Лопастные двигатели компактны, просты по конструкции, надежны и имеют хороший общий КПД при номинальных условиях. Однако они имеют ограниченные низкоскоростные возможности. Лопастные двигатели используют пружины или давление жидкости для выдвижения лопастей. Лопастные двигатели имеют ротор с прорезями, установленный на приводном валу, который приводится в движение ротором. Лопасти, плотно вставленные в пазы ротора, перемещаются в радиальном направлении, уплотняя кулачковое кольцо. Кольцо имеет два больших и два малых радиальных участка, соединенных переходными участками или пандусами.В лопастных двигателях обычно используется двух- или четырехпортовая конфигурация. Четырехпортовые двигатели генерируют вдвое больший крутящий момент примерно на половине скорости двухпортовых двигателей. Высокая эффективность пускового момента двигателей лопастного типа позволяет адаптировать их к приводам подъемных лебедок, позволяя запускать двигатель при высокой нагрузке. Лопастные двигатели обеспечивают хороший КПД, но не такой высокий, как у поршневых двигателей. Срок службы лопастного двигателя обычно меньше, чем у поршневого двигателя.
Срок службы лопастного двигателя обычно меньше, чем у поршневого двигателя.
Изучение крутящего момента и вращательного движения
Крутящий момент является важной биомеханической концепцией, но также и одной из наиболее часто неправильно истолковываемых.Я регулярно слышу, как массажисты говорят о неблагоприятном воздействии крутящего момента на некоторые структуры мягких тканей. Я даже помню, как учитель в школе массажа неоднократно подчеркивал, как плохо стоять с вывернутой задней ногой в передней стойке, потому что это «затянет поясницу». его принципы эффективно применяются в нашей практике.
Что такое крутящий момент?
Крутящий момент иногда определяют просто как силу кручения.Однако это определение недостаточно полно. В физике это определяется как скорость изменения углового момента объекта.
может показаться немного сложным, так что давайте погрузимся глубже и посмотрим, что это означает применительно к биомеханике и кинезиологии.
Если сила приложена к объекту в линейном направлении и этот объект не зафиксирован ни в одной точке, результирующее движение объекта будет в том же линейном направлении, что и сила. Например,
, если толкнуть книгу по столу, книга скользит в том же направлении, что и ваша рука (предполагается, что вы оказываете давление близко к центру книги, а не к одному из ее краев).Этот тип движения называется линейным движением. Линейное движение происходит от толкающих или тянущих сил.
Что такое вращательное движение?
Существует еще один вид движения тела, называемый вращательным. Вращательное движение возникает, когда к одной части объекта прикладывается сила, а другая часть (например, другой конец) остается неподвижной. В организме это происходит, когда мышца натягивает один конец кости, а другой конец фиксируется (удерживается). Результатом является движение незакрепленного конца.Например, когда проксимальный конец подколенного сухожилия удерживается неподвижно в области таза, а дистальный конец натягивает большеберцовую и малоберцовую кости, в коленном суставе происходит вращательное движение (сгибание).
Крутящий момент – это сила, создаваемая вращательным движением. Величина крутящего момента может варьироваться в зависимости от нескольких различных факторов. Простой пример включает ключ с длинной ручкой и ключ с короткой ручкой
. Предположим, у вас есть болт, который очень туго затянут, и вы пытаетесь его ослабить.Гаечный ключ с длинной ручкой более эффективен для ослабления, потому что он может создавать больший крутящий момент. Причина, по которой он создает больший крутящий момент, описывается относительно простым уравнением.
В приведенном выше примере болт считается осью вращения. Ось вращения похожа на ось колеса. Это центральная точка, вокруг которой вращается колесо. Сила, прилагаемая рукой к ключу, называется приложенной силой, а расстояние между вашей рукой (приложенной силой) и осью вращения называется плечом рычага (рис. 1).Плечо рычага также называют силовым плечом, моментным плечом или моментным плечом. Чем больше длина плеча рычага, тем большее усилие он может создать. Этот принцип иллюстрируется уравнением: T=F(d), и если вы немного заржавели в математике, это означает, что Крутящий момент равен Силе, умноженной на Расстояние.
Этот принцип иллюстрируется уравнением: T=F(d), и если вы немного заржавели в математике, это означает, что Крутящий момент равен Силе, умноженной на Расстояние.
В этом уравнении T — это крутящий момент, который может быть создан, F — приложенная сила, а d — расстояние от оси вращения до точки приложения силы. Важный момент, упомянутый выше и проиллюстрированный в уравнении, заключается в том, что чем больше расстояние (d), тем больший крутящий момент может быть создан.
Биомеханика и крутящий момент
Итак, как эта информация преобразуется во что-то значимое при рассмотрении функции тела? Специалисты в области биомеханики приложили немало усилий, чтобы изучить, как крутящие силы играют роль в нормальных и патологических функциях организма. Одним из примеров полезности этой информации является анализ сил, необходимых для получения травмы плеча.
Предположим, что Роберт держит руку перед собой, сгибая плечо на 90 градусов.Внезапно ему приходится ловить тяжелый груз, который падает с полки над ним. Если он поймает этот груз близко к своему плечу, плечо рычага будет относительно коротким, и сила крутящего момента не будет такой сильной (точка А на рисунке 2). Если вместо этого он поймает груз возле своих ладоней с полностью вытянутыми руками, плечо рычага для поглощения груза будет намного больше (точка B на рисунке 2). В любом случае плечевые мышцы будут нести ответственность за поглощение силы нагрузки. Однако во втором примере нагрузка крутящего момента на его плечо намного больше, потому что плечо рычага намного длиннее, хотя вес, который он поймал, был одинаковым в обоих примерах (рис. 2).Следовательно, травма плеча во втором сценарии, вероятно, будет значительно хуже.
Если он поймает этот груз близко к своему плечу, плечо рычага будет относительно коротким, и сила крутящего момента не будет такой сильной (точка А на рисунке 2). Если вместо этого он поймает груз возле своих ладоней с полностью вытянутыми руками, плечо рычага для поглощения груза будет намного больше (точка B на рисунке 2). В любом случае плечевые мышцы будут нести ответственность за поглощение силы нагрузки. Однако во втором примере нагрузка крутящего момента на его плечо намного больше, потому что плечо рычага намного длиннее, хотя вес, который он поймал, был одинаковым в обоих примерах (рис. 2).Следовательно, травма плеча во втором сценарии, вероятно, будет значительно хуже.
Мы можем применить тот же принцип рычага к процессу оценки или лечения. Если мы пытаемся оценить травму плеча с сопротивлением отведению, усилие клиента должно быть намного больше, если терапевт сопротивляется движению клиента, надавливая на его запястье, по сравнению с
сопротивлением отведению выше локтя в верхней части тела. рука. Если вы сопротивляетесь движению запястья клиента, от практикующего требуется гораздо меньше усилий.Однако, если вы сопротивляетесь движению выше локтя в верхней части руки, клиенту не нужно прилагать столько усилий. Каждая ситуация имеет свои преимущества и недостатки, но недооценка разницы в требуемом крутящем моменте поможет вам выбрать наиболее подходящую стратегию.
рука. Если вы сопротивляетесь движению запястья клиента, от практикующего требуется гораздо меньше усилий.Однако, если вы сопротивляетесь движению выше локтя в верхней части руки, клиенту не нужно прилагать столько усилий. Каждая ситуация имеет свои преимущества и недостатки, но недооценка разницы в требуемом крутящем моменте поможет вам выбрать наиболее подходящую стратегию.
Биомеханика играет фундаментальную роль в клиническом ортопедическом массаже и гораздо полезнее, когда ее концепции применяются правильно и точно. Существует множество применений соответствующих концепций крутящего момента для оценки травм, стратегий лечения, положений для растяжки или рекомендаций по хорошему домашнему уходу после лечения.
6.3 Вращательное движение — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать вращательные кинематические переменные и уравнения и связать их с их линейными аналогами
- Опишите крутящий момент и плечо рычага
- Решение задач на крутящий момент и кинематику вращения
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам освоить следующие стандарты:
-
(4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
Кроме того, руководство по физике для средней школы рассматривает содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
Основные термины раздела
| угловое ускорение | кинематика вращательного движения | рычаг |
| тангенциальное ускорение | крутящий момент |
Кинематика вращения
Служба поддержки учителей
Служба поддержки учителей
[BL][OL] Повторить уравнения линейной кинематики.
Предупреждение о неправильном представлении
Учащиеся могут запутаться между замедлением и увеличением ускорения в отрицательном направлении.
В разделе, посвященном равномерному круговому движению, мы обсуждали движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Однако бывают случаи, когда угловая скорость непостоянна — вращательное движение может ускоряться, замедляться или изменять направление. Угловая скорость не является постоянной, когда вращающийся фигурист тянет руки, когда ребенок толкает карусель, чтобы заставить ее вращаться, или когда компакт-диск останавливается при выключении.Во всех этих случаях угловое ускорение возникает из-за изменения угловой скорости ωω. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα – скорость изменения угловой скорости. В форме уравнения угловое ускорение равно
Угловая скорость не является постоянной, когда вращающийся фигурист тянет руки, когда ребенок толкает карусель, чтобы заставить ее вращаться, или когда компакт-диск останавливается при выключении.Во всех этих случаях угловое ускорение возникает из-за изменения угловой скорости ωω. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα – скорость изменения угловой скорости. В форме уравнения угловое ускорение равно
где ΔωΔω — изменение угловой скорости, а ΔtΔt — изменение во времени. Единицы углового ускорения: (рад/с)/с или рад/с 2 . Если ωω увеличивается, то αα положительно. Если ωω уменьшается, то αα отрицательно.Имейте в виду, что по соглашению против часовой стрелки — это положительное направление, а по часовой стрелке — отрицательное направление. Например, фигуристка на рис. 6.9 вращается против часовой стрелки, если смотреть сверху, поэтому ее угловая скорость положительна. Ускорение будет отрицательным, например, когда объект, вращающийся против часовой стрелки, замедляется. Было бы положительно, если бы объект, вращающийся против часовой стрелки, ускорялся.
Было бы положительно, если бы объект, вращающийся против часовой стрелки, ускорялся.
Рис. 6.9 Фигуристка вращается против часовой стрелки, поэтому ее угловая скорость обычно считается положительной.(Luu, Wikimedia Commons)
Соотношение между величинами тангенциального ускорения a и углового ускорения
α,isa=rαorα=ar.α,isa=rαorα=ar.6.10
Эти уравнения означают, что величины тангенциального ускорения и углового ускорения прямо пропорциональны друг другу. Чем больше угловое ускорение, тем больше изменение тангенциального ускорения, и наоборот. Например, рассмотрим всадников в своих капсулах на колесе обозрения в состоянии покоя.Колесо обозрения с большим угловым ускорением даст гонщикам большее тангенциальное ускорение, потому что по мере того, как колесо обозрения увеличивает скорость вращения, оно также увеличивает свою тангенциальную скорость. Обратите внимание, что радиус вращающегося объекта также имеет значение. Например, для данного углового ускорения αα меньшее колесо обозрения приводит к меньшему тангенциальному ускорению для гонщиков.
Советы для достижения успеха
Тангенциальное ускорение иногда обозначается a t .Это линейное ускорение в направлении, касательном к окружности в интересующей точке при круговом или вращательном движении. Помните, что тангенциальное ускорение параллельно тангенциальной скорости (либо в том же направлении, либо в противоположном направлении). Центростремительное ускорение всегда перпендикулярно тангенциальной скорости.
До сих пор мы определили три вращательные переменные: θθ, ωω и αα. Это угловые версии линейных переменных x , v и a .Таблица 6.2 показывает, как они связаны.
| Поворотный | Линейный | Отношения |
|---|---|---|
| θθ | х | θ=xrθ=xr |
| ωω | v | ω=vrω=vr |
| αα | и | α=арα=ар |
Таблица 6. 2 Вращательные и линейные переменные
2 Вращательные и линейные переменные
Теперь мы можем начать видеть, как вращательные величины, такие как θθ, ωω и αα, связаны друг с другом. Например, если колесо мотоцикла, находящееся в состоянии покоя, имеет большое угловое ускорение в течение достаточно долгого времени, оно в конечном итоге начинает быстро вращаться и делает много оборотов. Выражая это в терминах переменных, если угловое ускорение колеса αα велико в течение длительного периода времени t , то конечная угловая скорость ωω и угол поворота θθ велики.В случае линейного движения, если объект находится в состоянии покоя и испытывает большое линейное ускорение, то он имеет большую конечную скорость и пройдёт большое расстояние.
Кинематика вращательного движения описывает соотношения между углом поворота, угловой скоростью, угловым ускорением и временем. Это только описывает движение — оно не включает никаких сил или масс, которые могут повлиять на вращение (это часть динамики). Вспомним уравнение кинематики для линейного движения: v=v0+atv=v0+at (константа a ).
Вспомним уравнение кинематики для линейного движения: v=v0+atv=v0+at (константа a ).
Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение αα также является постоянным, поскольку a=rαa=rα. Уравнение кинематической зависимости между ωω, αα и t равно
ω=ω0+αt(константаα),ω=ω0+αt(константаα),
, где ω0ω0 — начальная угловая скорость. Обратите внимание, что уравнение идентично линейной версии, за исключением угловых аналогов линейных переменных. Фактически все уравнения линейной кинематики имеют вращательные аналоги, которые приведены в таблице 6.3. Эти уравнения могут быть использованы для решения задач вращательной или линейной кинематики, в которых a и αα являются постоянными.
| Поворотный | Линейный | |
|---|---|---|
| θ=ω¯tθ=ω¯t | х=v¯tx=v¯t | |
| ω=ω0+αtω=ω0+αt | v=v0+αtv=v0+αt | константа αα, a |
| θ=ω0t+12αt2θ=ω0t+12αt2 | х=v0t+12αt2x=v0t+12αt2 | константа αα, a |
| ω2=ω02+2αθω2=ω02+2αθ | v2=v02+2αxv2=v02+2αx | константа αα, a |
Таблица 6.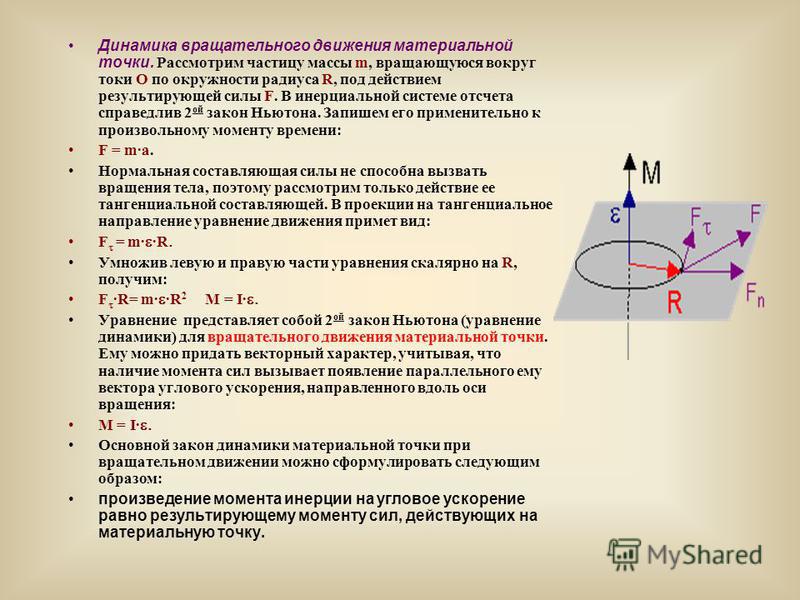 3 Уравнения вращательной кинематики
3 Уравнения вращательной кинематики
В этих уравнениях ω0ω0 и v0v0 — начальные значения, t0t0 равно нулю, а средняя угловая скорость ω¯ω¯ и средняя скорость v¯v¯ равны
ω¯=ω0+ω2иv¯=v0+v2.ω¯=ω0+ω2иv¯=v0+v2.6.11
Fun In Physics
Погоня за штормом
Рис. 6.10 Торнадо спускаются из облаков в виде воронок, которые сильно вращаются. (Дафна Зарас, Национальное управление океанических и атмосферных исследований США)
Охотники за штормами, как правило, попадают в одну из трех групп: любители, гоняющиеся за торнадо в качестве хобби, атмосферные ученые, собирающие данные для исследований, наблюдатели за погодой для средств массовой информации или ученые, развлекающиеся под видом работы.Погоня за штормом — опасное времяпрепровождение, потому что торнадо может быстро изменить курс без малейшего предупреждения. Поскольку за разрушениями, оставленными торнадо, следуют охотники за штормами, замена спущенных шин из-за обломков, оставленных на шоссе, является обычным явлением. Наиболее активная часть мира для торнадо, называемая переулок торнадо , находится в центральной части Соединенных Штатов, между Скалистыми горами и Аппалачами.
Наиболее активная часть мира для торнадо, называемая переулок торнадо , находится в центральной части Соединенных Штатов, между Скалистыми горами и Аппалачами.
Торнадо — прекрасный пример вращательного движения в действии в природе.Они появляются во время сильных гроз, называемых суперячейками, которые имеют столб воздуха, вращающийся вокруг горизонтальной оси, обычно около четырех миль в поперечнике. Разница в скорости ветра между сильными холодными ветрами выше в атмосфере в струйном течении и более слабыми ветрами, движущимися на север от Мексиканского залива, заставляет столб вращающегося воздуха смещаться так, что он вращается вокруг вертикальной оси, создавая торнадо.
Торнадо создают скорость ветра до 500 км/ч (приблизительно 300 миль/ч), особенно внизу, где воронка самая узкая, поскольку скорость вращения увеличивается по мере уменьшения радиуса.Они сдувают дома, как если бы они были сделаны из бумаги, и, как известно, протыкают стволы деревьев кусочками соломы.
Проверка захвата
Какой физический термин обозначает глаз бури? Почему ветры в эпицентре торнадо слабее, чем на его внешнем краю?
- Глаз бури — центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость прямо пропорциональна радиусу кривизны.
- Глаз бури — центр вращения.Ветры слабее в глазу торнадо, потому что тангенциальная скорость обратно пропорциональна радиусу кривизны.
- Глаз бури — центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость прямо пропорциональна квадрату радиуса кривизны.
- Глаз бури — центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость обратно пропорциональна квадрату радиуса кривизны.
Момент затяжки
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила. Чем дальше сила приложена от точки поворота (или точки опоры), тем больше угловое ускорение. Например, дверь открывается медленно, если вы нажимаете слишком близко к петле, но открывается легко, если вы нажимаете далеко от петли. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается; это потому, что угловое ускорение обратно пропорционально массе.Эти отношения очень похожи на отношения между силой, массой и ускорением из второго закона Ньютона. Поскольку мы уже рассмотрели угловые версии расстояния, скорости и времени, вы можете задаться вопросом, что такое угловая версия силы и как она соотносится с линейной силой.
Чем дальше сила приложена от точки поворота (или точки опоры), тем больше угловое ускорение. Например, дверь открывается медленно, если вы нажимаете слишком близко к петле, но открывается легко, если вы нажимаете далеко от петли. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается; это потому, что угловое ускорение обратно пропорционально массе.Эти отношения очень похожи на отношения между силой, массой и ускорением из второго закона Ньютона. Поскольку мы уже рассмотрели угловые версии расстояния, скорости и времени, вы можете задаться вопросом, что такое угловая версия силы и как она соотносится с линейной силой.
Угловой версией силы является крутящий момент ττ, который представляет собой поворачивающую эффективность силы. См. Рисунок 6.11. Уравнение для величины крутящего момента:
, где r — величина плеча рычага, F — величина линейной силы, а θθ — угол между плечом рычага и силой. Плечо рычага — это вектор от точки вращения (точка вращения или точка опоры) к месту приложения силы. Поскольку величина плеча рычага представляет собой расстояние, его единицы измерения — метры, а крутящий момент — Н⋅м. Крутящий момент является векторной величиной и имеет то же направление, что и создаваемое им угловое ускорение.
Плечо рычага — это вектор от точки вращения (точка вращения или точка опоры) к месту приложения силы. Поскольку величина плеча рычага представляет собой расстояние, его единицы измерения — метры, а крутящий момент — Н⋅м. Крутящий момент является векторной величиной и имеет то же направление, что и создаваемое им угловое ускорение.
Рис. 6.11 Человек толкает карусель за ее край и перпендикулярно плечу рычага для достижения максимального крутящего момента.
Применение большего крутящего момента приведет к большему угловому ускорению.Например, чем сильнее человек толкает карусель на рис. 6.11, тем быстрее она ускоряется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Если человек хочет максимизировать воздействие своей силы на карусель, он должен толкнуть ее как можно дальше от центра, чтобы получить наибольшее плечо рычага и, следовательно, наибольший крутящий момент и угловое ускорение. Крутящий момент также максимизируется, когда сила приложена перпендикулярно плечу рычага.
Поддержка учителя
Поддержка учителя
[BL][OL][AL] Продемонстрируйте физические взаимосвязи между крутящим моментом, силой, углом приложения силы и длиной плеча рычага, используя рычаги разной длины. Помогите учащимся установить связь между физическими наблюдениями и математическими соотношениями. Например, крутящий момент максимален, когда сила приложена точно перпендикулярно плечу рычага, потому что sinθ=1sinθ=1 для θ=90θ=90 градусов.
Решение задач кинематики вращения и крутящего момента
Точно так же, как линейные силы могут уравновешиваться, создавая нулевую результирующую силу и линейное ускорение, то же самое верно и для вращательного движения.Когда два крутящих момента одинаковой величины действуют в противоположных направлениях, нет ни чистого крутящего момента, ни углового ускорения, как вы можете видеть в следующем видео. Если нулевой чистый крутящий момент действует на систему, вращающуюся с постоянной угловой скоростью, система будет продолжать вращаться с той же угловой скоростью.
Watch Physics
Знакомство с крутящим моментом
В этом видеоролике крутящий момент определяется с точки зрения плеча момента (которое совпадает с плечом рычага). Он также охватывает проблему с силами, действующими в противоположных направлениях вокруг точки поворота.(На этом этапе вы можете игнорировать ссылки Сэла на работу и механические преимущества.)
Проверка захвата
Если бы чистый крутящий момент, действующий на линейку из примера, был бы положительным, а не нулевым, что бы это сказало об угловом ускорении? Что произойдет с правителем со временем?
- Линейка находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет равно нулю.
- Линейка не находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс.
 Таким образом, угловое ускорение будет равно нулю.
Таким образом, угловое ускорение будет равно нулю. - Линейка не находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
- Линейка находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
Теперь давайте рассмотрим примеры применения вращательной кинематики к рыболовной катушке и концепции крутящего момента к карусели.
Рабочий пример
Расчет времени остановки вращения рыболовной катушки
Глубоководный рыбак использует удочку с катушкой радиусом 4,50 см. Большая рыба берет наживку и уплывает от лодки, вытягивая леску из своей рыболовной катушки. По мере разматывания лески с катушки катушка вращается с угловой скоростью 220 рад/с. Рыбак тормозит спиннинговую катушку, создавая угловое ускорение −300 рад/с 2 .Сколько времени требуется барабану, чтобы остановиться?
Рыбак тормозит спиннинговую катушку, создавая угловое ускорение −300 рад/с 2 .Сколько времени требуется барабану, чтобы остановиться?
Стратегия
Нас просят найти время t для остановки барабана. Величина начальной угловой скорости ω0=220ω0=220 рад/с, а величина конечной угловой скорости ω=0ω=0 . Величина углового ускорения со знаком равна α=−300α=−300 рад/с 2 , где знак минус указывает на то, что оно действует в направлении, противоположном угловой скорости.Глядя на кинематические уравнения вращения, мы видим, что все величины, кроме t , известны в уравнении ω=ω0+αtω=ω0+αt, что делает его самым простым уравнением для решения этой задачи.
Решение
Используемое уравнение: ω=ω0+αtω=ω0+αt .
Алгебраически решаем уравнение для t , а затем подставляем известные значения.
6.12
Обсуждение
Время остановки барабана очень мало, потому что ускорение довольно большое. Леска иногда рвется из-за прилагаемой силы, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Усталая рыба будет медленнее, ей потребуется меньшее ускорение и, следовательно, меньшая сила.
Рабочий пример
Расчет крутящего момента карусели
Рассмотрим человека, толкающего игровую карусель на рис. 6.11. Он прикладывает силу 250 Н на краю карусели и перпендикулярно радиусу, который равен 1,50 м. Какой крутящий момент он выдает? Предположим, что трение, действующее на карусель, пренебрежимо мало.
Стратегия
Чтобы найти крутящий момент, обратите внимание, что приложенная сила перпендикулярна радиусу и что трением можно пренебречь.
Решение
τ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅мτ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅м6.13
Обсуждение
Человек максимизирует крутящий момент, прикладывая силу перпендикулярно плечу рычага, так что θ=π2θ=π2 и sinθ=1sinθ=1 . Мужчина также максимизирует свой крутящий момент, нажимая на внешний край карусели, так что он получает максимально возможное плечо рычага.
Практические задачи
15.Какой крутящий момент создаст человек, если он приложит силу 12\,\text{N} на расстоянии 1,0\,\text{м} от точки вращения, перпендикулярно плечу рычага?
- \frac{1}{144}\,\text{Н-м}
- \frac{1}{12}\,\text{Н-м}
- 12\,\text{Н-м}
- 144\,\text{Нм}
Угловая скорость объекта изменяется с 3 рад/с по часовой стрелке до 8 рад/с по часовой стрелке за 5 с. Каково его угловое ускорение?
Каково его угловое ускорение?
- 0,6 рад/с 2
- 1,6 рад/с 2
- 1 рад/с 2
- 5 рад/с 2
Проверьте свое понимание
17.Что такое угловое ускорение?
- Угловое ускорение — это скорость изменения углового смещения.
- Угловое ускорение — скорость изменения угловой скорости.
- Угловое ускорение — это скорость изменения линейного смещения.
- Угловое ускорение — скорость изменения линейной скорости.
Какое уравнение для углового ускорения, α ? Предположим, что θ — угол, ω — угловая скорость, а t — время.
- α=ΔωΔtα=ΔωΔt
- α=ΔωΔtα=ΔωΔt
- α=ΔθΔtα=ΔθΔt
- α=ΔθΔtα=ΔθΔt
Что из следующего лучше всего описывает крутящий момент?
- Это вращательный эквивалент силы.
- Это сила, влияющая на линейное движение.
- Это вращательный эквивалент ускорения.
- Именно ускорение влияет на линейное движение.
Какое уравнение для крутящего момента?
- \тау = {F\,cos\тета}\,{r}
- \тау = \фрак{F\sin\theta}{r}
- \тау = rF\!\cos\тета
- \тау = rF\!\sin\тета
Служба поддержки учителей
Служба поддержки учителей
Используйте вопросы «Проверить ваше понимание», чтобы оценить, справляются ли учащиеся с целями обучения в этом разделе. Если учащиеся борются с определенной целью, эти вопросы помогут определить, какая цель вызывает проблему, и направить учащихся к соответствующему содержанию.
Если учащиеся борются с определенной целью, эти вопросы помогут определить, какая цель вызывает проблему, и направить учащихся к соответствующему содержанию.
Круговое движение | Вращательное движение | Кинематика | Физика с Алкой | by Alka
Круговое движение и вращательное движение относятся к типам движения. Всегда было так запутанно различать эти два термина. Потому что они почти похожи друг на друга. Без сомнения, мы можем немного различать их в повседневной жизни.Но в физике становится трудно определить их отдельно. Поэтому студенты всегда оставляют эту тему или подготовку к экзаменам. Но эта статья предоставит вам полное и простое определение кругового движения и вращательного движения на примере. Итак, просто продолжайте читать, прокрутив вниз, и наслаждайтесь темой.
Когда частица или тело с точечной массой движется по круговой траектории, это называется круговым движением. Если вы обратите внимание на это утверждение, то увидите, что я использовал слово «тело с точечной массой». Цель использования этого слова здесь в том, что иногда мы смешиваем его с вращательным движением.Потому что его определение похоже на определение кругового движения. Посмотрим как?
Цель использования этого слова здесь в том, что иногда мы смешиваем его с вращательным движением.Потому что его определение похоже на определение кругового движения. Посмотрим как?
Определяется как движение, при котором тело, не являющееся телом с точечной массой, движется так, что все составляющие его частицы движутся одновременно по концентрическим окружностям. А центры этих концентрических окружностей лежат на линии, называемой осью вращения и сдвига на равные углы за равные промежутки времени.
- Круговое движение тела рассматривается как отдельная частица независимо от того, состоит ли оно из множества составляющих частиц или нет.Приходится пренебрегать движением этих частиц. Но в случае вращательного движения будет учитываться движение всех составляющих частиц.
- Также в случае кругового движения траектория движения очень велика по сравнению с размером движущегося тела. Но при Вращательном движении путь вращения сравним с размером тела.
- Ось вращения при круговом движении лежит вне корпуса.
 В то время как при вращательном движении ось вращения может лежать как внутри, так и снаружи тела.
В то время как при вращательном движении ось вращения может лежать как внутри, так и снаружи тела.
Давайте разберемся на примере. На рисунке (а) движение человека круговое, потому что путь его движения явно намного больше, чем его размер. И в этом случае движением составляющих его частиц можно пренебречь. Кроме того, ось вращения проходит через центр окружности, находящейся вне тела человека.
картинка (а)
картинка (б)
вращательное движение в предложении
Эти примеры взяты из корпусов и из источников в Интернете.Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Вращательное движение двигателя было преобразовано в линейное движение с помощью ползунково-кривошипного механизма.
Он преобразовал вращательное движение звеньев тела в линейное движение и смог подготовить робота к прыжку через препятствие.
Эти стимулы содержат смесь радиального и вращательного движения вокруг некоторого заданного центра.
Рычажный механизм передал вращательное движение электродвигателя на поступательное движение пружины.
Например, функцию двигателя можно описать как «обеспечивать механическую энергию», «преобразовывать электрическую энергию в механическую», «обеспечивать вращение движение » и так далее.
Одна из больших проблем заключалась в том, как преобразовать возвратно-поступательное линейное движение поршня двойного действия (двухтактного) в непрерывное вращательное движение колеса.
Пока машина предназначена для распыления шкур, зачем включать такие слова, как «возвратно-поступательное или вращательное движение »?
В описании используются слова «возвратно-поступательное или вращательное движение ».
Ранние ветряные мельницы использовали энергию ветра для создания вращения движения для фрезерных операций.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
При этом он должен изменить вращательное движение первичного двигателя на возвратно-поступательное движение насосной штанги.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Это может быть линейное или вращательное движение .
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Ему было доступно несколько механизмов для преобразования вращательного движения в синусоидальное движение.
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Другое значение относится к машинам, которые используют вращательное движение дисков или зубьев для достижения аналогичного результата.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Он был неспособен к типичной четвероногой походке, так как передним конечностям не хватало необходимого диапазона.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Здесь возвратно-поступательное движение было преобразовано во вращательное движение .
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Кольцевая пила и кольцевая пила также используют вращающееся движение , но отличаются от циркулярной пилы.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Коробка передач на вершине башни и коленчатый вал преобразовывали вращательное движение в возвратно-поступательное движение, передаваемое вниз через шток к цилиндру насоса внизу.
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.В качестве альтернативы, четвертьоборотный привод создает крутящий момент для обеспечения вращения движения для управления четвертьоборотным клапаном.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
.
